
Global Patch Search Boosts Video Denoising
Thibaud Ehret, Pablo Arias and Jean-Michel Morel
CMLA, ENS Cachan, Cachan, France
{thibaud.ehret, pablo.arias, morel}@cmla.ens-cachan.fr
Keywords:
Video Denoising, Patch-based Methods, Patch Search, Nearest Neighbors Search.
Abstract:
With the increasing popularity of mobile imaging devices and the emergence of HdR video surveillance, the
need for fast and accurate denoising algorithms has also increased. Patch-based methods, which are currently
state-of-the-art in image and video denoising, search for similar patches in the signal. This search is generally
performed locally around each target patch for obvious complexity reasons. We propose here a new and
efficient approximate patch search algorithm. It permits for the first time to evaluate the impact of a global
search on the video denoising performance. A global search is particularly justified in video denoising, where
a strong temporal redundancy is often available. We first verify that the patches found by our new approximate
search are far more concentrated than those obtained by exact local search, and are obtained in comparable
time. To demonstrate the potential of the global search in video denoising, we take two patch-based image
denoising algorithms and apply them to video. While with a classical local search their performance is poor,
with the proposed global search they even improve the latest state-of-the-art video denoising methods.
1 INTRODUCTION
Patch-based methods are among the state-of-the-art
both in image (Dabov et al., 2007d; Lebrun et al.,
2013a; Mairal et al., 2009) and video denoising
(Dabov et al., 2007a; Maggioni et al., 2012a; Li et al.,
2011; Buades et al., 2016). These methods exploit the
self-similarity of images and videos and filter together
groups of similar patches which are then aggregated
to create an estimate of the clean signal. Most contri-
butions in the area have focused on how to model and
filter the groups of similar patches, but little attention
has been given to how these groups are built. Typi-
cally similar patches are grouped by selecting a refer-
ence patch and searching exhaustively for the similar
ones in a local 2D, or 3D for videos, neighborhood.
The size of the search region is a parameter of the al-
gorithm which trades off quality of the result for com-
putational cost.
In the case of a single image, a local search region
is justified by the fact that similar patches are likely
to be close to each other in the image domain. Videos
however, have an additional strong source of redun-
dancy given by the temporal consistency. A patch is
expected to have similar patches along its motion tra-
jectory, even in distant frames. It seems intuitive that
patch-based methods should benefit from this larger
set of similar exemplars. Some methods estimate the
motion in the video to tackle this problem. A mo-
tion compensated search window can track the patch
trajectories for a certain number of frames (Liu and
Freeman, 2010b; Buades et al., 2016). Nevertheless,
the size of these search regions is still limited by the
computational cost and the accumulation of errors in
the estimated motion.
In this work we focus on the patch search. We
present an efficient global approximate search tech-
nique and demonstrate its impact on video denoising.
To that end we take two patch-based image denoising
methods, namely BM3D (Dabov et al., 2007d) and
NL-Bayes (Lebrun et al., 2013a) and adapt them to
video (simply by searching similar patches in multi-
ple frames instead of just the current one). We provide
an extensive experimental evaluation in grayscale and
color sequences. Our results show that substantial
gains in performance are obtained by searching glob-
ally in the video sequence, indicating that video de-
noising still has significant room for improvement
by using clever global search methods. In partic-
ular, the NL-Bayes method with global search out-
performs state-of-the-art methods such as V-BM3D
(Dabov et al., 2007b) and V-BM4D (Maggioni et al.,
2012b) by a significant margin, and the recently pro-
posed SPTWO (Buades et al., 2016) by a lower mar-
gin.
In recent years several efficient techniques for ap-
proximate nearest neighbor search have been pro-
124
Ehret T., Arias P. and Morel J.
Global Patch Search Boosts Video Denoising.
DOI: 10.5220/0006175601240134
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 124-134
ISBN: 978-989-758-225-7
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Figure 1: The plots show the position in the spatio-temporal video domain of the matches found for a sample patch query for
different search methods. From left to right: the best matches found with a global exhaustive search, with a local exhaustive
search in a window centered at the query, and with the VPLR search, the heuristic proposed in this paper. Notice how the
latter discovers the patch trajectories similar to those of the global exhaustive search.
posed, after the introduction of the PatchMatch algo-
rithm by Barnes et al. (Barnes et al., 2009). These
methods compute a nearest neighbor field for patches
located in a dense or semi-dense grid, and use heuris-
tics that benefit from the overlap of adjacent patches
in the grid. Most of these works focus on finding the
nearest neighbor, but they can be extended to handle
k nearest neighbors (Barnes et al., 2010). In practice
k is kept small since even with these efficient tech-
niques, computing a large number k of nearest neigh-
bors for a dense grid of patches remains too costly.
In this work we focus on a significantly different
problem: compute a large number, namely k, of near-
est neighbors for a single query patch. By allowing
independent queries, our technique is more flexible,
and is straightforward to apply to patch-based denois-
ing methods. In particular, this is useful for certain de-
noising algorithms which save computations by pro-
cessing a sparse set of reference patches dynamically
determined during the execution of the algorithm, and
also makes parallelization easier.
The rest of the paper is organized as follows: in
§2 we describe briefly two state-of-the-art image de-
noising algorithms (NL-Bayes (Lebrun et al., 2013a)
and BM3D (Dabov et al., 2007c)) which we selected
to demonstrate our global search. In §3 we pro-
pose a new heuristic to accelerate approximate near-
est neighbor search for patches in images and videos.
A comparison with state-of-the-art methods is per-
formed in §4. Concluding remarks are given in §5.
2 NL-Bayes AND BM3D
BM3D and NL-Bayes are patch based methods which
follow the same overall framework to denoise an im-
age. For each patch in a set of patches to be de-
noised, they first search for similar patches inside the
image. This search region is usually rectangular and
centered on the query patch. The patches found dur-
ing the search are then processed to compute an es-
timate of the corresponding clean patches. The de-
noised patches are then aggregated on an basic esti-
mate of the clean image. This process is then iterated
once. In the second step, the basic estimate is used as
a pilot for the patch search and the processing of the
similar patches.
To test the proposed global search, we consider
extensions to video of these algorithms by searching
for similar 2D patches in a spatio-temporal volume
in the video, as proposed in (Dabov et al., 2007b),
(Arias and Morel, 2015). This framework is presented
in Algorithm 1.
The main difference between BM3D and NL-
Bayes algorithms lies in the processing of the set of
similar patches. NL-Bayes learns a Gaussian a priori
model for the set of patches and computes the patches
as the maximum a posteriori estimate. BM3D stacks
the patches in a 3D signal which is denoised using
shrinkage on a transformed domain.
We use a slight modification of video NL-Bayes
(Arias and Morel, 2015) which caps the rank of the
patch covariance matrices for the groups of similar
patches. This improves both performance and speed
of this algorithm, and adds a rank parameter r to each
step.
We modified the search (corresponding to steps
2 and 7 in Algorithm 1) by considering three differ-
ent approaches: a local approach which uses the lo-
cal search in a spatio-temporal volume centered at
the reference patch for both denoising iterations; a
global approach which searches in the full video vol-
ume for both steps of the algorithm; and mixed ap-
proach which uses the local search in the first step
and the global in the second iteration (step 7 in the
pseudocode). The global patch search heuristic is pre-
sented in Section 3.
In the Section 4 we shall compare these ap-
proaches among them and also with other video
extensions of BM3D and NL-Bayes which use so-
Global Patch Search Boosts Video Denoising
125

Algorithm 1: Image/video denoising framework.
Require: Noisy image/video v, noise level σ
Ensure: Estimate of noiseless image/video ˆv
1: for all patch q in v do
2: Retrieve n nearest neighbors to q
3: Process the set of similar patches and compute
a denoised estimate q
0
of q
4: Aggregate estimated patches on v
0
to compute
the basic estimate
5: end for
6: for all patch q in v
0
do
7: Retrieve n nearest neighbors to q
8: Process the set of similar patches and compute
a denoised estimate ˆq of q
9: Aggregate estimated patches on ˆv to compute
the final estimate
10: end for
11: return ˆv
phisticated local patch search regions, V-BM3D and
SPTWO.
V-BM3D (Dabov et al., 2007b) is the direct ex-
tension of BM3D to video using predictive block
matching to define the search region. An initial set
of matches is first found in a 7 × 7 neighborhood
of the reference patch. Then, for the adjacent for-
ward/backward frames, the search is carried out in
the union of 5 × 5 neighborhoods centered around
the position of the matches found in the preced-
ing/subsequent frame. This scheme can track patches
on moving objects as long as the displacement be-
tween frames is smaller than two pixels while keeping
the search region small. V-BM4D (Maggioni et al.,
2012b) is an extension of V-BM3D for 3D patches.
SPTWO (Buades et al., 2016) is based on NL-
Bayes but performs a more elaborate search. First,
the optical flow towards the adjacent 6 frames is com-
puted and used to warp them to the reference frame.
A s ×s ×13 3D patch is then associated to each s ×s
patch in the reference frame by extending its tempo-
ral dimension on the volume defined by the warped
frames. Then, k extended patches closest to the ref-
erence one are searched for in a local neighborhood.
The final set of matches is given by the 13k 2D slices
from the newly found extended patches (some of them
might be discarded by an occlusion detection step).
The usage of these extended patches reduces the noise
in the distance while still keeping a small spatial patch
(the patch spatial size is s = 5). Furthermore, the
patches are warped by the optical flow. This is use-
ful in cases where the motion is not translational. On
the downside, this method relies heavily on the optical
flow.
3 HEURISTICS FOR GLOBAL
PATCH SEARCH
There are already a number of efficient patch search
techniques which exploit the so-called image co-
herency: Neighboring query patches, since they over-
lap, have high chances of having neighboring matches
in the database image. Thus knowing the position of
a good match for a patch helps in determining good
matches for its neighbors. This idea was first ap-
plied by (Barnes et al., 2009) to compute a nearest
neighbor field (NNF), assigning the closest k patches
to each patch in the image. The original algorithm
was presented for images but can easily be extended
to video. More recent works reported significant im-
provements (between one and two orders of magni-
tude) by combining PatchMatch with more classic
search data structures such as partition trees (more
specifically KD-trees) (Olonetsky and Avidan, 2012;
He and Sun, 2012) and locality sensitive hashing (Ko-
rman and Avidan, 2011; Barnes et al., 2015).
All these methods compute a dense k-NNF, typ-
ically for a small k. The reason is that when k is
large (e.g. k > 20) computing a dense NNF is too
costly. In such cases it is preferable (if the application
allows to) to compute the k nearest neighbors for a
small set of patches. In particular, for image/video de-
noising, a common speed-up strategy of patch-based
methods is to reduce the number of query patches. For
instance, in (Dabov et al., 2007d) the query patches
form a regular subgrid, and in (Lebrun et al., 2013a)
the query patches are irregularly located and are de-
termined during the evolution of the algorithm. To
handle such cases, it would be desirable to be able to
conduct independent patch queries. There is a vast lit-
erature on data structures for nearest neighbor search
on generic metric spaces or vector spaces; but these
classical tools do not exploit the image coherency. In
this section we briefly review one of such approaches,
namely partition trees, and show a simple yet effective
modification for a fast approximate k-nearest neigh-
bor search of image patches.
3.1 Partition Trees
A partition tree is an inductive data structure encoding
the position of a set of n points in R
d
(the database).
Once the partition tree has been built it is used to
search for the nearest neighbors of a point (the query).
Nodes in the tree can either be leaves (also called
bins) containing a maximum number of elements, or
a split value between two subtrees: the “left” subtree
and the “right” subtree. A partition tree splits recur-
sively the data space by applying a simple split at each
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
126
node (with the exception of the leaves). At each split-
ting operation, the set of elements in the current sub-
tree is split in two equally sized subsets which are then
used to construct the child subtrees. The construction
of the tree is fully specified by a split value function
and a split function. The split value function assigns
a split value to a set of elements, whereas the split
function assigns one of two groups to an element.
A partition tree can be directly used to search for
the exact k-nearest neighbors with expected complex-
ity of O(log(n)), where n is the number of points. In
practice when the dimensionality of the elements is
too large, its performance drops and becomes compa-
rable to a linear search, this problem was shown with
image patches by Kumar et al. in (Kumar et al., 2008).
This is indeed the case for image and video patches,
so we shall rule out exact search and settle with the
so-called first bin heuristic: The candidates for the k-
nearest neighbors are taken only from the bin of the
query patch. On its own, the first bin heuristic does
not suffice to provide good quality matches, but this
will be solved by combining it with other heuristics
that exploit the fact that patches lie on images.
3.2 Partition Tree Search with Local
Refinement
We propose to use the first bin search in a partition
tree (or a forest) to obtain a first set of m ≈ k initial
candidates matches, and refine this set of candidates
as follows: For each of the elements of the candidate
list, we search in a small local region in the image cen-
tered at the candidate. We call the resulting strategy
Partition Tree with Local Refinement (PTRL). The
complete pseudocode for this technique is presented
in Algorithm 2.
Note that the proposed approximate search heuris-
tic can in principle be applied in conjunction to other
data structures for nearest neighbor search such as
those based on hashing (Andoni and Indyk, 2006; An-
doni et al., 2014). We do not pursue this in the present
work.
3.3 Search Parameters
The choice of the partition tree has a strong impact on
the performance. The most common partition tree is
the KD-tree (Bentley, 1975). However, it has been
shown that VP-trees (Yianilos, 1993) produce bet-
ter results when working with image patches (Kumar
et al., 2008).
The VP-tree is characterized by the split value be-
ing a hyperball and the split function being the indi-
cator function of this ball. The VP-tree splits the
Algorithm 2: PTLR search heuristic.
Require: v an input video, F a Partition tree forest
constructed with the patches from v, p a request
patch from v, κ×κ the size of local search region
Ensure: A list of matches for p
1: Retrieve the list {ϕ
1
,...,ϕ
k
} of k best matches
from the forest F using the retrieval algorithm
from a partition tree forest
2: for i = 1 to k do
3: Search in the image region of size κ ×κ cen-
tered in ϕ
i
for better matches
4: end for
5: return the list {ϕ
0
1
,. . .,ϕ
0
k
} of k best matches af-
ter the update using the PTLR search
data set according to the distance of each point to a
vantage point. The vantage point is one of the data
points, chosen according to some criteria. By ran-
domizing the construction of these trees, forests can
be built, therefore improving the quality of the el-
ements retrieved using the first bin search. Forests
of VP-trees where the vantage point is chosen at ran-
dom have been shown to have a good retrieval power
(O’Hara et al., 2013).
For our experiments, we used a forest of four VP-
trees, randomized as in (O’Hara et al., 2013). We set
the size of the bins to 2n, where n is the number of
nearest neighbors of the query. The trees are con-
structed using all patches in the video. For the query,
the local refinement area is of size 8×8×3. We found
these parameters to give a reasonable trade-off be-
tween computational cost and search accuracy. In the
following, we will use the abbreviation VPLR instead
PTLR to remind that the partition tree is specifically
a VP-tree.
0
0.01
0.02
0.03
0.04
0.05
0.06
0 50 100 150 200 250 300
Globalexhaustivesearch
Localsearch
VP-treeforestsearch
VPLRsearch
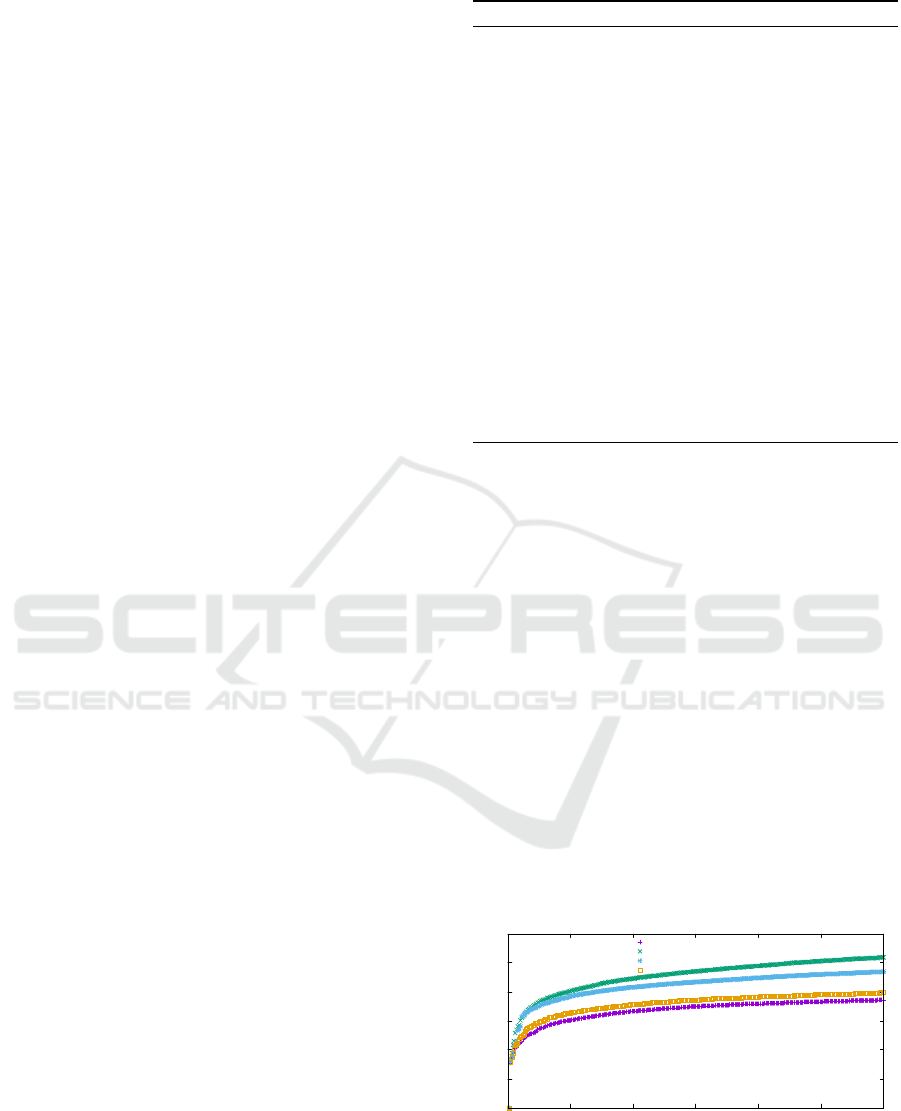
Figure 2: Comparison of the quality of the matches. The
plots show the normalized distance to the ith nearest neigh-
bor i = 1,...,300, averaged over 1000 query patches sam-
pled randomly in the bus video.
In Figure 2 we compare the results obtained with
Global Patch Search Boosts Video Denoising
127

the local search, the “first bin” search, and the pro-
posed VPLR search for the classical test sequence
bus
1
. The plot shows the Euclidean distances to the
n = 300 nearest neighbors averaged over 1000 query
patches randomly chosen in the same video. The
patches are of size s ×s with s = 10, RGB (thus their
dimensionality is 300) and their distance is rescaled
between 0 and 1 as d(p,q) = kp −qk/(255
√
3s).
The first conclusion is that the local exhaustive
search finds worse matches than the approximate
search methods (the search window of the local search
is of size 45 ×45 ×5). The best method is the VPLR
search, performing much better than the basic VP-
forest “first bin” approximate search. This result
shows the effectiveness of the proposed search heuris-
tic. We computed the corresponding plot on the other
videos and always found the same qualitative behav-
ior.
It is also interesting to visualize the position of the
matches found by each method in the spatio-temporal
domain of the video. Figure 1 presents the position of
the nearest patches found for a specific query in the
bus video. Note how the matches found by searching
globally are organized in trajectories.
For the same parameters, the number of distance
computations for each method is 10125 and around
20000 for respectively the local search and the VPLR
search for the first step of the algorithm (an equivalent
local search region would be close to 63 ×63 ×5).
4 EXPERIMENTAL RESULTS
We evaluated the effect of the global search on the
BM3D and NL-Bayes image denoising algorithms.
Since the source code of BM3D is not public we use
the implementation available in (Lebrun, 2012). We
adapted it to process image sequences and modify
only the patch search as explained in §2. For NL-
Bayes (referred as NLB in the following), we built
our implementation upon (Lebrun et al., 2013b) , and
modified to limit the rank of the a priori covariance
matrix (see §2).
For each method we considered the three versions
depending on the type of search used in each step:
the local and global versions use the correspond-
ing search in both denoising steps, and an additional
mixed approach, which uses the local search in the
first step and the global one in the second. The reason
for this will be explained later.
We compared these methods against V-BM3D
(Dabov et al., 2007b), V-BM4D (Maggioni et al.,
1
https://media.xiph.org/video/derf/
2012b) and SPTWO (Buades et al., 2016), which rep-
resent the current state-of-the-art in video denoising.
Regarding the parameters, we considered 2D
patches of size 10 ×10 for NL-Bayes and 8 ×8 for
BM3D. For the local search we used a window of size
45 ×45 ×5 for NL-Bayes and 32 ×32 ×5 for BM3D.
The remaining parameters for NL-Bayes are the
number of similar patches used in each step n
1
,n
2
and
the maximum ranks of the a priori covariance matrix
r
1
,r
2
. For BM3D we also needed to specify n
1
,n
2
, in
addition to the hard threshold in the first step λ
1
as
well as the distance threshold in both steps, τ
1
and τ
2
.
The values for λ
1
, τ
1
and τ
2
are the same as the ones
in VBM3D. The rest of the parameters were tuned by
optimizing the PSNR on a training set consisting of
short videos. The optimal parameters depend on the
noise level. Table 1 synthesizes the different parame-
ters as a function of the noise.
32
32.5
33
33.5
34
34.5
35
35.5
36
36.5
0 20 40 60 80 100 120 140 160
VBM3D
VBM4D
NL-Bayes local
NL-Bayes global
BM3D local
BM3D mix
SPTWO
Figure 3: Comparison of the PSNR frame by frame for dif-
ferent methods on the grayscale bus sequence with noise
10.
29
29.5
30
30.5
31
31.5
32
32.5
33
33.5
34
0 20 40 60 80 100 120 140 160
VBM4D
NL-B local
NL-B global
BM3D local
BM3D mix
Figure 4: Comparison of the PSNR frame by frame for dif-
ferent methods on color mobile sequence with noise 20.
These patches are somewhat larger than the typ-
ical sizes used by patch-based methods. The reason
for this is that the global search is more sensitive to
the noise in the patch distance. Consider for example
a noisy flat image. Since the image is flat, the closest
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
128

Table 1: Parameters used for the algorithms used.
Method σ n
1
n
2
r
1
r
2
NLB-local grayscale
all 160 40 +
4
7
(σ −6) max{8, 48 −
16
21
(σ −6)} max{8, 16 −
4
9
(σ −6)}
NLB-global grayscale
6 10 100 60 16 16
> 10 100 60 16 8
NLB-local/global color
all 350 150 full rank 40 −(σ −10)/3
BM3D-mix
6 20 4 ×2
σ/10
32 - -
> 20 32 32 - -
BM3D-global
all 32 32 - -
neighbors to a patch are the ones with the closest noise
pattern. If enough nearest neighbors share the same
noise pattern, it will be interpreted as a signal com-
ponent and will not be filtered out. The global search
increases the probability of finding a large number of
matches with a similar noise pattern. In practice, this
becomes an issue for patches in homogeneous regions
and high noise values. This problem can be mitigated
by involving a larger number of similar patches. An
interesting aspect of global search is that it is still pos-
sible to find many similar patches even for large patch
sizes.
Our quantitative comparison criterion was the
PSNR. We first evaluated the effect of the global
search for NL-Bayes and BM3D. Tables 2 and 3 show
the gain in PSNR with a global search, on grayscale
and color sequences.
2
. In almost all cases the global
search performed significantly better than the local
for NL-Bayes. This is also true, but to a minor ex-
tent for BM3D. For NL-Bayes the highest gain was
obtained using the global search in both steps of the
denoising algorithm: The average gain between NLB-
global and NLB-local is of around 1dB for grayscale
sequences and of 1.5dB for color sequences. This
gain is consistent across the different noise levels we
used in our tests. For BM3D the best alternative is
BM3D-mix, which uses the global search only in the
second step. The performance of BM3D-global is su-
perior for σ = 10, but drops severely when the noise
increases, becoming comparable or even worse than
BM3D-local for the highest levels of noise.
A possible reason for this is that BM3D uses a
much smaller number of similar patches n than NL-
Bayes. As explained before, for patches with low
SNR, the global search increases the risk of finding
a set of nearest neighbors sharing a similar noise pat-
tern, particularly for small n.
2
The color sequences are from https://media.xiph.org/
video/derf/. The grayscale sequences are from http://www.
cs.tut.fi/
∼
foi/GCF-BM3D/, except for football and mobile,
which have been obtained by averaging the channels from
the corresponding RGB sequences.
Note also that the performance of BM3D is worse
than that of NL-Bayes, and in most cases worse than
the authors’ implementation, denoted V-BM3D see
Table 4. Our version of BM3D is an adaptation to
video of the one published in (Lebrun, 2012). In par-
ticular, the search strategies of our BM3D-local and
V-BM3D differ, since V-BM3D uses the predictive
block matching described in §2.
We compared the performance of NLB-local and
NLB-global with the state-of-the-art methods V-
BM3D (Dabov et al., 2007b), V-BM4D (Maggioni
et al., 2012b) for grayscale (Table 4) and color (Table
5) videos. The sequences used in these tables were the
same as in Tables 2 and 3. The results of V-BM3D
3
and V-BM4D were computed using the authors’ im-
plementation.
4
For grayscale sequences and σ = 10,
NLB-global has the best performance. The exception
is tennis, where both NLB variants show problems in
reconstructing the texture of a wallpaper present in the
scene (possibly due to the use of too large patches.)
On average NLB-global has a PSNR .78dB higher
than V-BM4D. When the noise increases, the gap be-
tween NLB-global and the V-BMxD methods closes.
For most sequences, better results can be obtained
with NLB using a larger patch for higher noise lev-
els. This suggest that the problem comes from the
distance estimation in these high noise cases.
We also include a comparison with SPTWO in Ta-
ble 6. We computed the result of our algorithm for
some of the sequences used in (Buades et al., 2016).
Note that the sequences in Table 6 have 30 frames and
that the values shown correspond to the PSNR of the
central frame of the sequence. The results depends
largely on the sequence. In particular SPTWO per-
forms better in tennis, and bus. The fact that the bus
sequence has a very fast motion which can be easily
estimated might explain the perfomance gap in favor
of motion estimation on this sequence.
3
For V-BM3D we show only grayscale results since
there are no Linux binaries for the color version of V-
BM3D.
4
http://www.cs.tut.fi/
∼
foi/GCF-BM3D/
Global Patch Search Boosts Video Denoising
129

Table 2: Comparison between search strategies on grayscale sequences. For each sequence and noise level, we show the
PSNR obtained with the local search, and the difference in PSNR between each global search strategy and the local search.
σ Method Bus Fore. Sales. Tennis Foot. Mobi. Ave.
10
NLB-local 34.85 36.33 35.87 33.94 35.29 34.29 35.10 ± 0.92
NLB-mix 0.54 0.36 0.90 0.42 0.06 1.30 0.60 ± 0.44
NLB-global 0.94 0.50 2.01 0.64 -0.02 1.60 0.95 ± 0.75
BM3D-local 34.25 35.77 35.79 33.55 35.15 32.97 34.58 ± 1.18
BM3D-mix 0.15 0.55 1.08 0.09 -0.08 0.81 0.43 ± 0.46
BM3D-global 0.09 0.92 1.66 -0.03 -0.19 1.54 0.67 ± 0.82
20
NLB-local 30.75 32.59 32.06 30.12 31.36 29.80 31.11 ± 1.09
NLB-mix 0.53 0.62 1.15 0.50 0.11 1.91 0.80 ± 0.64
NLB-global 0.70 0.69 1.96 0.70 -0.05 2.46 1.08 ± 0.94
BM3D-local 30.28 32.17 31.84 29.90 31.23 29.02 30.74 ± 1.21
BM3D-mix 0.17 0.52 0.74 0.19 0.05 0.81 0.41 ± 0.32
BM3D-global 0.05 0.50 0.78 0.13 -0.14 1.52 0.47 ± 0.61
30
NLB-local 28.46 30.53 29.86 27.99 29.26 26.95 28.84 ± 1.30
NLB-mix 0.46 0.06 0.55 0.63 -0.14 2.24 0.63 ± 0.84
NLB-global 0.41 0.04 0.84 0.73 -0.33 2.68 0.73 ± 1.05
BM3D-local 28.06 29.92 29.38 28.12 29.18 26.47 28.52 ± 1.24
BM3D-mix 0.23 0.48 0.63 0.45 0.15 0.65 0.43 ± 0.20
BM3D-global 0.00 0.07 0.38 0.34 -0.19 0.92 0.25 ± 0.39
Table 3: Comparison between search strategies on color sequences. For each sequence and noise level, we show the PSNR
obtained with the local search, and the difference in PSNR between each global search strategy and the local search.
σ Method Bus City Cont. Mobile Tennis Fore. Coast. Ave.
10
NLB-local 36.47 37.35 38.29 34.76 35.30 38.34 36.60 36.73 ± 1.38
NLB-mix 0.64 1.37 1.16 1.46 0.74 1.18 0.52 1.01 ± 0.37
NLB-global 0.83 2.06 1.72 2.25 0.97 1.64 0.75 1.46 ± 0.61
BM3D-local 35.57 36.50 37.26 33.59 34.61 37.60 35.73 35.84 ± 1.43
BM3D-mix 0.22 0.73 1.08 0.44 0.40 0.57 0.22 0.52 ± 0.31
BM3D-global 0.12 1.02 1.44 0.76 0.19 0.70 0.21 0.63 ± 0.49
20
NLB-local 32.42 33.31 34.47 30.74 31.52 35.09 32.69 32.89 ± 1.54
NLB-mix 0.73 1.76 1.77 1.58 0.67 1.04 0.67 1.17 ± 0.51
NLB-global 0.90 2.34 2.34 2.58 0.84 1.37 0.86 1.60 ± 0.79
BM3D-local 31.72 32.75 33.68 29.75 30.87 34.39 31.99 32.16 ± 1.60
BM3D-mix 0.21 0.71 1.30 0.55 0.24 0.72 0.26 0.57 ± 0.39
BM3D-global -0.01 0.43 1.68 1.21 -0.04 0.62 0.17 0.58 ± 0.65
40
NLB-local 28.52 29.24 30.79 26.62 28.25 32.18 29.09 29.24 ± 1.80
NLB-mix 0.71 1.32 2.33 1.93 0.64 0.83 0.75 1.22 ± 0.67
NLB-global 0.73 1.28 2.78 2.93 0.59 0.82 0.82 1.42 ± 1.00
BM3D-local 27.89 28.45 30.23 26.07 27.62 31.04 28.34 28.52 ± 1.66
BM3D-mix 0.35 0.48 1.49 0.80 0.53 1.00 0.47 0.73 ± 0.40
BM3D-global -0.13 -0.54 1.79 1.28 0.25 0.54 0.11 0.47 ± 0.81
Two examples of denoised results are presented in
Figures 5 and 6. Comparing the different results of
denoising, we can see that the VPLR search allows
a better detail reconstruction. In particular, in Fig-
ure 5 the numbers of the calendar do not show a blur
around them compared to the other methods based on
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
130
Table 4: Comparison with V-BM3D and V-BM4D on grayscale sequences. PSNR of the full sequence. See text for details.
Results with a star were computed using the binary provided by the author.
σ Method Bus Fore. Sales. Tennis Foot. Mobi. Ave.
10
V-BM3D* 33.32 36.02 37.21 34.68 34.82 34.09 35.02 ± 1.39
V-BM4D-mp* 33.85 36.36 37.48 34.78 34.95 34.11 35.26 ± 1.40
NLB-local 34.85 36.33 35.87 33.94 35.29 34.29 35.09 ± 0.91
NLB-global 35.79 36.83 37.88 34.58 35.27 35.89 36.04 ± 1.07
20
V-BM3D* 29.57 32.87 34.04 31.20 31.04 30.35 31.51 ± 1.65
V-BM4D-mp* 30.00 33.11 33.46 30.70 31.06 30.49 31.47 ± 1.45
NLB-local 30.75 32.59 32.06 30.12 31.36 29.80 31.11 ± 1.09
NLB-global 31.45 33.28 34.02 30.82 31.31 32.26 32.19 ± 1.24
30
V-BM3D* 27.59 30.85 31.68 29.22 29.04 27.85 29.37 ± 1.62
V-BM4D-mp* 27.96 31.06 31.02 28.74 28.98 27.99 29.29 ± 1.41
NLB-local 28.46 30.53 29.86 27.99 29.26 26.95 28.84 ± 1.30
NLB-global 28.87 30.57 30.70 28.72 28.93 29.63 29.57 ± 0.88
Table 5: Comparison with V-BM4D on color sequences. PSNR of the full sequence. See text for details. Results with a star
were computed using the binary provided by the author.
σ Method Bus City Cont. Mobile Tennis Fore. Coast. Ave.
10
V-BM4D-mp* 35.39 37.14 38.78 34.18 35.91 37.95 36.05 36.49 ± 1.57
NLB-local 36.47 37.35 38.29 34.76 35.30 38.34 36.60 36.73 ± 1.38
NLB-global 37.30 39.41 40.01 37.01 36.27 39.98 37.35 38.19 ± 1.56
20
V-BM4D-mp* 31.35 33.41 34.94 30.47 31.99 34.53 32.14 32.69 ± 1.66
NLB-local 32.42 33.31 34.47 30.74 31.52 35.09 32.69 32.89 ± 1.54
NLB-global 33.32 35.65 36.81 33.32 32.36 36.46 33.55 34.50 ± 1.77
30
V-BM4D-mp* 29.04 31.04 32.63 28.35 29.73 32.54 29.97 30.47 ± 1.66
NLB-local 30.10 30.92 32.32 28.33 29.53 33.37 30.55 30.73 ± 1.69
NLB-global 30.92 32.79 34.97 31.17 30.24 34.42 31.38 32.27 ± 1.83
40
V-BM4D-mp* 27.44 29.31 30.94 26.79 28.15 31.08 28.49 28.89 ± 1.65
NLB-local 28.52 29.24 30.79 26.62 28.25 32.18 29.09 29.24 ± 1.80
NLB-global 29.25 30.52 33.57 29.55 28.84 33.00 29.91 30.66 ± 1.87
50
V-BM4D-mp* 26.24 27.97 29.60 25.52 27.03 29.90 27.34 27.66 ± 1.63
NLB-local 27.33 27.98 29.59 25.29 27.31 31.22 27.99 28.10 ± 1.88
NLB-global 27.99 28.77 32.39 28.22 27.86 31.87 28.79 29.41 ± 1.90
Table 6: Comparison with SPTWO. As in (Buades et al., 2016), only the first 30 frames of the sequence are considered,
and the shown PSNRs corresponding to the frame 15 of each sequences (indexing starts with 1). The values in each cell
correspond to SPTWO, NLB-local and NLB-global.
σ Bus Tennis Salesman Bike Average
10 36.07 34.89 35.60 34.69 32.86 34.31 36.38 35.92 37.10 36.74 37.10 38.30 35.97 35.19 36.33
20 32.24 30.75 31.02 30.59 28.23 28.71 32.95 32.02 34.45 33.01 33.39 35.56 32.20 31.10 32.44
30 30.05 28.48 28.87 27.48 26.24 26.63 30.95 29.92 31.49 31.62 31.17 33.28 30.02 28.95 30.07
a local search. For the example from grayscale bus,
the improvements can be seen mostly for the woman
inside the bus, who is more distinct with the global
search than with the local search; but also on the ad
where most details of the singer’s face are better re-
constructed.
In section 3.3, we briefly discussed the compu-
tation complexity (in number of distance computa-
Global Patch Search Boosts Video Denoising
131

Figure 5: Results of denoising for mobile (zoom on frame 37, noise 20). Top: ground truth, NL-Bayes local, BM3D local,
VBM4D; bottom: Noisy, NL-Bayes global and BM3D mix.
Figure 6: Results of denoising for grayscale bus (zoom on frame 70, noise 20). Top: ground truth, NL-Bayes local, BM3D
local, VBM4D; bottom: Noisy, NL-Bayes global, BM3D mix and VBM3D.
tion) of each search method per query. When these
searches are integrated into the denoising algorithm,
the full computation time (including the construction
of the VP-tree) is of the same order of magnitude than
the one when using the local search. Nevertheless,
NL-Bayes based methods are reasonably slower than
V-BM3D and V-BM4D when using the ”normal pro-
file”.
5 CONCLUSIONS
We studied the performance gain obtained by ex-
panding the local patch search into a global one for
patch-based video denoising algorithm. To the best
of our knowledge, this is the first time that denois-
ing results using global patch search were reported
in videos with hundreds of frames. With the global
search the patches found can follow long trajectories
in the video, thus fully benefiting from the temporal
redundancy of videos.
Our analysis of the most common patch search al-
gorithms showed that an approach based on a global
tree structure, more specifically based on a VP-tree,
performed very well compared to the local search.
Exact global search in the VP-tree is still too costly
for the denoising application, which is why we pro-
posed a simple heuristic for efficient approximate
search, the VPLR search (VP-tree search with local
refinement).
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
132

We then applied it to extend to video BM3D and
NL-Bayes, two image denoising algorithms, to video.
We obtained a significant boost on the denoising per-
formance. This performance boost is only slightly
more costly than a local exhaustive search, including
the time spent building the tree thanks to an easy par-
allelization.
Latest contributions in video denoising advocate
for the use of 3D patches as a mechanism to im-
pose temporal consistency in the video (Protter and
Elad, 2009; Liu and Freeman, 2010a; Maggioni et al.,
2012a). Yet, in this work we showed that state-of-
the-art results can be obtained with 2D patches, using
global search. The results obtained are visually better
frame-by-frame, but can suffer from a flickering arti-
fact due to the lack of temporal consistency. This is
most noticeable for higher values of noise. Ongoing
work focuses on extending the current results to 3D
patches and video specific algorithms. One of the cur-
rent limiting factors associated to the global search is
that it increases the risk of matching the noise pattern
for patches with low SNR. We were able to alleviate
this problem in most cases by using large 2D patches,
but this causes problems with random, low-contrasted
textures which are better denoised with small patches.
3D patches can reduce the spatial patch size while still
keeping accurate distances (same dimension than the
2D patches), and therefore be more appropriate for
these types of textures.
The proposed heuristics for approximate global
patch search are not limited to the denoising appli-
cation, and could be useful for other applications re-
quiring a large number of nearest neighbors but not
requiring a dense or semi-dense NNF.
ACKNOWLEDGEMENTS
This work is supported by the ”IDI 2016” project
funded by the IDEX Paris-Saclay, ANR-11-IDEX-
0003-02. This Work is also partly founded by
BPIFrance and R
´
egion Ile de France in the FUI 18
Plein Phare project, the Office of Naval research
(ONR grant N00014-14-1-0023).
REFERENCES
Andoni, A. and Indyk, P. (2006). Near-optimal hashing al-
gorithms for approximate nearest neighbor in high di-
mensions. In Foundations of Computer Science, 2006.
FOCS’06. 47th Annual IEEE Symposium on, pages
459–468. IEEE.
Andoni, A., Indyk, P., Nguyen, H. L., and Razenshteyn, I.
(2014). Beyond locality-sensitive hashing. In Pro-
ceedings of the Twenty-Fifth Annual ACM-SIAM Sym-
posium on Discrete Algorithms, pages 1018–1028.
SIAM.
Arias, P. and Morel, J.-M. (2015). Towards a bayesian video
denoising method. In ACIVS, volume 9386 of Lecture
Notes in Computer Science, pages 107–117. Springer.
Barnes, C., Shechtman, E., Finkelstein, A., and Goldman,
D. (2009). Patchmatch: a randomized correspondence
algorithm for structural image editing. ACM Transac-
tions on Graphics-TOG, 28(3):24.
Barnes, C., Shechtman, E., Goldman, D. B., and Finkel-
stein, A. (2010). The generalized patchmatch cor-
respondence algorithm. In Computer Vision–ECCV
2010, pages 29–43. Springer.
Barnes, C., Zhang, F.-L., Lou, L., Wu, X., and Hu, S.-M.
(2015). Patchtable: Efficient patch queries for large
datasets and applications. In ACM Transactions on
Graphics (Proc. SIGGRAPH).
Bentley, J. L. (1975). Multidimensional binary search trees
used for associative searching. Communications of the
ACM, 18(9):509–517.
Buades, A., Lisani, J. L., and Miladinovi, M. (2016). Patch-
based video denoising with optical flow estimation.
IEEE Transactions on Image Processing, 25(6):2573–
2586.
Dabov, K., Foi, A., and Egiazarian, K. (2007a). Video de-
noising by sparse 3D transform-domain collaborative
filtering. In EUSIPCO, pages 145–149.
Dabov, K., Foi, A., and Egiazarian, K. (2007b). Video de-
noising by sparse 3D transform-domain collaborative
filtering. In Proc. 15th European Signal Processing
Conference, volume 1, page 7.
Dabov, K., Foi, A., Katkovnik, V., and Egiazarian, K.
(2007c). Image denoising by sparse 3-D transform-
domain collaborative filtering. Image Processing,
IEEE Transactions on, 16(8):2080–2095.
Dabov, K., Foi, A., Katkovnik, V., and Egiazarian, K.
(2007d). Image denoising by sparse 3d transform-
domain collaborative filtering. IEEE Trans. on IP,
16(8):2080–2095.
He, K. and Sun, J. (2012). Computing Nearest-Neighbor
Fields via Propagation-Assisted KD-trees. In Com-
puter Vision and Pattern Recognition (CVPR), 2012
IEEE Conference on, pages 111–118. IEEE.
Korman, S. and Avidan, S. (2011). Coherency sensitive
hashing. In Computer Vision (ICCV), 2011 IEEE In-
ternational Conference on, pages 1607–1614. IEEE.
Kumar, N., Zhang, L., and Nayar, S. (2008). What is a
good nearest neighbors algorithm for finding similar
patches in images? In Computer Vision–ECCV 2008,
pages 364–378. Springer.
Lebrun, M. (2012). An Analysis and Implementation of the
BM3D Image Denoising Method. Image Processing
On Line, 2:175–213.
Lebrun, M., Buades, A., and Morel, J.-M. (2013a). A Non-
local Bayesian Image Denoising Algorithm. SIAM
Journal on Imaging Sciences, 6(3):1665–1688.
Lebrun, M., Buades, A., and Morel, J.-M. (2013b). Imple-
mentation of the “Non-Local Bayes” (NL-Bayes) Im-
Global Patch Search Boosts Video Denoising
133

age Denoising Algorithm. Image Processing On Line,
3:1–42.
Li, W., Zhang, J., and Dai, Q.-H. (2011). Video denoising
using shape-adaptive sparse representation over simi-
lar spatio-temporal patches. Signal Processing: Image
Communication, 26:250–265.
Liu, C. and Freeman, W. T. (2010a). A high-quality video
denoising algorithm based on reliable motion estima-
tion. In ECCV, pages 706–719.
Liu, C. and Freeman, W. T. (2010b). A high-quality video
denoising algorithm based on reliable motion estima-
tion. In Computer Vision–ECCV 2010, pages 706–
719. Springer.
Maggioni, M., Boracchi, G., Foi, A., and Egiazarian, K.
(2012a). Video denoising, deblocking, and enhance-
ment through separable 4-D nonlocal spatiotemporal
transforms. IEEE Transactions on Image Processing,
21(9):3952–3966.
Maggioni, M., Boracchi, G., Foi, A., and Egiazarian, K.
(2012b). Video denoising, deblocking, and enhance-
ment through separable 4-d nonlocal spatiotemporal
transforms. Image Processing, IEEE Transactions on,
21(9):3952–3966.
Mairal, J., Bach, F., Ponce, J., Sapiro, G., and Zisserman, A.
(2009). Non-local sparse models for image restora-
tion. In Computer Vision, 2009 IEEE 12th Interna-
tional Conference on, pages 2272–2279.
O’Hara, S., Draper, B., et al. (2013). Are you using the right
approximate nearest neighbor algorithm? In Applica-
tions of Computer Vision (WACV), 2013 IEEE Work-
shop on, pages 9–14. IEEE.
Olonetsky, I. and Avidan, S. (2012). TreeCANN - kd-
tree Coherence Approximate Nearest Neighbor algo-
rithm. In Computer Vision–ECCV 2012, pages 602–
615. Springer.
Protter, M. and Elad, M. (2009). Image sequence denois-
ing via sparse and redundant representations. IEEE
Transactions on Image Processing, 18(1):27–35.
Yianilos, P. N. (1993). Data structures and algorithms for
nearest neighbor search in general metric spaces. In
SODA, volume 93, pages 311–321.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
134
