Visual Interactive Creation of Geo-located Networks

Felix Brodkorb

, Manuel Kopp

, Arjan Kuijper

and Tatiana von Landesberger

TU Darmstadt, Darmstadt, Germany

Fraunhofer IGD, Darmstadt, Germany

Keywords:

Geographic Networks, Graph Generators, Graph Editors.

Abstract:

Nodes in real world networks often have a geographic position. In many cases such as for simulation or op-

timization, there is a need for non-trivial synthetic geo-located networks. As synthetic datasets are required

to have speciﬁc properties such as connectivity and geographic distribution, often networks need to be gener-

ated. However, their creation is cumbersome if done purely by hand, and inﬂexible if done fully automated.

Here, we present a framework for creating artiﬁcial geographic located networks in a visually interactive way.

We designed our framework with the what-you-see-is-what-you-get principle in mind, i.e. showing the (in-

termediate) results of the interactive creation process at any time and allowing the user to adjust the network

iteratively. This design allows our system to be also used as a simple viewer for networks that have incomplete

location information. Our approach consists of two steps: (1) Creating the network topology and (2) assigning

locations to its nodes. Our half automatic system enables the user to easily set the location of the nodes to pre-

deﬁned areas like countries, states, and urban regions, while still being able to ﬂexibly and interactively control

the creation process. We show the utility of our system by creating a real-world-like geo-located network.

1 INTRODUCTION

Many networks in real life have a geographic loca-

tion attached to their elements. For example computer

networks like backbones of the companies AT&T and

NTT consists of computers (nodes) that have a phys-

ical location. Other networks with geographic loca-

tion exist, like delivery network, friendship networks,

transportation networks, or collaboration networks.

Such networks are used in business and research and

have a geographic relation that is often abstracted

from.

However, geographic context is relevant as might

inﬂuence rationales and decisions. Additionally, ge-

ographic context is not necessary retrieved directly

from the topology of the network and can be – in the

worst case – entirely independent of it. For exam-

ple, two nodes in a supply chain network can be sepa-

rated by a national border, resulting in additional pro-

cedures such as customs. Many other types of back-

ground knowledge might be relevant (e.g. culture, cli-

mate, or jurisdiction).

Synthetic geo-located network data is necessary

for analysis, simulation or optimization of networks.

Beside general geo-located network data, network

data with use-case dependent geographic properties is

required for testing of algorithms or approaches. Ad-

ditionally, researchers need to create multiple, slightly

similar networks for studies and evaluations. How-

ever, real world data is difﬁcult to obtain, and geo-

based networks are cumbersome to create manually.

Manual creation is especially cumbersome when one

wants to have multiple networks that differ only in

deﬁned parts that can not usually be found in the real

word.

Graphs or networks are a common element used

for visual analytics. In this paper, we use the terms

“graph” and “network” interchangeably. For an

overview of graph visualization possibilities, we re-

fer to (von Landesberger et al., 2011). Visual analyt-

ics approaches visualize the graph structure and de-

tect special parts or sections in a wide range of ap-

plication areas (von Landesberger et al., 2009; von

Landesberger et al., 2013). Here we summarize the

most relevant aspects of geo-located graphs. A graph

G(V, E) consists of vertices V and vdges E. An edge

e ∈ E connects two vertices v

, v

∈ V . A graph whose

edges are directed is called a directed graph. Vertices

and edges can have attributes. If vertices and/or edges

have attributes that represent locations on earth, one

has a geo-located graph. Here, we focus on networks

where only vertices have a geographic location.

In this paper, we present a framework for creat-

Brodkorb F., Kopp M., Kuijper A. and von Landesberger T.

Visual Interactive Creation of Geo-located Networks.

DOI: 10.5220/0006176302830293

In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 283-293

ISBN: 978-989-758-228-8

283

ing geo-located networks or attaching geographic lo-

cation information to an existing network. The frame-

work aims to improve the manual creation process.

With our approach, we cover two generic scenarios:

1. Create a network topology from scratch and add

location information to its nodes.

2. Import a network topology and add location infor-

mation to its nodes.

To reach this goal, we mainly introduce the following

approaches:

• An interactive and iterative visual workﬂow.

• Implementation of the what-you-see-is-what-you-

get (WYSIWYG) principle to show the current

network after each operation.

• Concurrent visualization of mixed networks that

contain nodes with and without geographic infor-

mation at the same time.

• Assign many nodes to hierarchic geographic areas

in the world at any scale.

Using the framework, a user can quickly create geo-

located networks with hundred of nodes while still

having control over the locations of its nodes. We

focus on the interactive visual creation process and

leave techniques that aim at the recreation of statis-

tical features of more speciﬁc types of geo-networks

for future work. While designing our system, we tried

to keep it’s usability as simple and straight forward as

possible by for example avoiding things like multi-

ple views and dialogs. To the best of our knowledge,

there are no approaches by now that generate artiﬁcial

geographic networks in an interactive way. Addition-

ally, we found out that our system is also useful as

a simple viewer for networks that contain nodes with

and nodes without location information at the same

time (mixed networks).

This paper is structured as follows: Section 2

shows related work about geo-located networks and

graph generation. Section 3 presents our approach in

detail. In Section 4, we show a usage example by

trying to mimic a real-world network. Section 5 dis-

cusses the limits of our approach. Finally, Section 6

concludes this paper and outlines future work.

2 RELATED WORK

In research, the creation of synthetic datasets is an

important topic, e.g. for testing algorithms. Man-

ual data creation is very cumbersome, so automatic

and interactive visual systems have been developed.

A number of approaches exist that create data of

a speciﬁc type (e.g. multivariate data (Albuquerque

et al., 2011; Bremm et al., 2012; Wang et al., 2013),

scenario-based data (Whiting et al., 2008), and syn-

dromic surveillance data (Maciejewski et al., 2009)).

We focus on geographic network data.

Geographic data is usually gained by sensor sys-

tems, collected by surveys or generated using spatio-

temporal patterns (Theodoridis et al., 1999; Sak-

shaug and Raghunathan, 2010; Sakshaug and Raghu-

nathan, 2014a). Our previous work (Brodkorb et al.,

2016) shows an rule-based approach that generates

tree-shaped geo-located network data. It focuses on

tree-shaped networks and also has the drawback that

the creation process is controlled by general purpose

graphical user interface (GUI) controls, like list-views

or edit ﬁelds that don’t allow visual parameter manip-

ulation. To the best of our knowledge, all other exist-

ing geographic data generators do not create network

structures, but solely produce data on a predeﬁned

geographic grid (e.g., (Sakshaug and Raghunathan,

2014b)). Some approaches use existing transporta-

tion networks as a basis (Frick, 2011; Cascetta and

Cantarella, 1993; Brinkhoff, 2002), but do not cre-

ate new network structures with geographic locations

in a visually interactive way. SANET (Okabe et al.,

2006a; Okabe et al., 2006b) generates random points

ontop of an existing geo-located network. Further,

there are approaches that focus on the creation of city

structures such as street networks (Parish and M

uller,

2001; Chen et al., 2008). However, these networks

represent a very speciﬁc geographically located net-

work, since they have a quite regular structure when

compared to other types of networks.

Graph generation systems can be categorized

into (1) algorithmic and (2) visualization-based ap-

proaches:

2.1 Algorithmic Approaches

Algorithmic graph generators produce graphs that

are automatically based on input parameters (e.g.,

(Brinkmann and McKay, 2007; Ying and Wu, 2009)).

Parameter-based generation is not well suited to con-

trol graph generation in a visual way and to edit it

interactively. Most close to our work are (Baeza-

Yates et al., 2010) and (

Alvarez-Garc

ıa et al., 2014;

Alvarez-Garcia et al., 2012) which use a set of rules

for generating graphs. However, these approaches

were designed to extract graphs from arbitrary data

and not to generate new graphs without any input

datasets. Moreover, they do not provide the possibil-

ity to generate geo-locations of nodes together with

a graph structure. Beside these generators, the auto-

Poisson model (Grifﬁth, 2002) can be used to gener-

IVAPP 2017 - International Conference on Information Visualization Theory and Applications

284

ate geographic structures. However, it has no visual

way to control the creation process.

2.2 Visualization-based Approaches

Visual graph editors take an interactive approach.

They enable the user to steer the creation process. As

many interactive graph editing projects have shown

(O’Madadhain et al., 2003; YWorks, 2015; Wong

et al., 2006; Benson, 2015; Spritzer and Freitas, 2008;

McGufﬁn and Jurisica, 2009; Gladisch et al., 2014),

techniques for direct and interactive manipulation of

datasets (Baudel, 2006) can be performed on graphs.

In such projects, the user has to edit node and edge

separately. Editing single nodes and edges obviously

do not scale for bigger graphs. yED (YWorks, 2015)

and Illuminations (National Council of Teachers of

Mathematics, 2015) use pre-deﬁned graph templates

to create graphs where the size of the graph can be ad-

justed by the user. However, they only allow creating

complete graphs. Recently, two interactive systems

were presented which allow for iterative graph gen-

eration in a visual interface coupled with automatic

graph generators: The evolutionary graph generation

algorithm developed by (Bach et al., 2013) iteratively

generates multiple graphs, each with different param-

eters. (von Landesberger et al., 2010) proposed an ap-

proach that enables users to create graphs by combin-

ing pre-deﬁned building blocks interactively. In some

systems, the user can specify attributes for individual

nodes and edges. However, to the best our knowledge,

there is no system other than (Brodkorb et al., 2016)

with the possibility to directly create graphs with a

geographic location following a given geographical

structure.

3 APPROACH

In this section, we propose an interactive visual gener-

ator for geo-networks. As the aim is to use it for test-

ing, analysis, simulation or optimization of the net-

work and algorithms on it, we use inspiration from

interactive graph editing projects (see 2.2). We use

a geographic map as background and place a user-

deﬁned network on it that a user can edit incremen-

tally. Our primary focus was to keep the system sim-

ple to be easy to use, and general to apply to a broad

range of different geo-located networks. Except di-

alogs used to set parameters for the network structure

generators, we designed our system to be used from

a single view only, because with growing amount of

data coordinated multiple views are harder to handle

for computers as well as users (Andrienko and An-

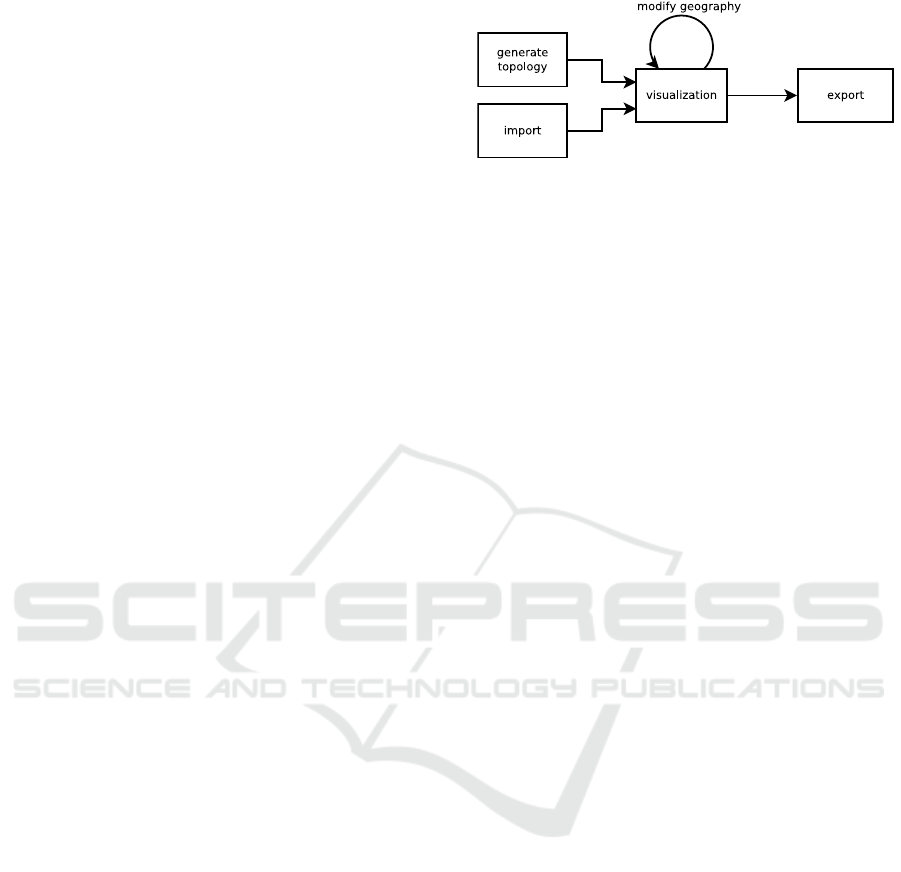
Figure 1: Pipeline showing the workﬂow of creating geo-

based networks.

drienko, 2007). Please see also the attached video for

a demonstration of the most important techniques pre-

sented in our approach.

Issues that we address in our approach are

• workﬂow and interaction,

• topology,

• layout issues,

• visual representation,

• assigning geographic information to nodes.

In this approach, we concentrate on the geography

of the nodes of a network that has been either created

or imported. Geography of a network is deﬁned by

attributes that are attached to its nodes. The geogra-

phy of the edges will be deﬁned by the geography of

its endpoint nodes. Because of this, edges contain no

explicit geographic information themselves, and our

system draws them as straight lines between their end-

point nodes.

3.1 Workﬂow and Interaction

Our pipeline for generating geographic networks con-

sists of two steps (see Figure 1): (1) Generate (or

load) a network topology and (2) assign geographic

information to its nodes.

3.2 Topology

The ﬁrst step is creating the topology of a network, i.e.

a network structure without geo-information. Topol-

ogy of a network describes which nodes are connected

to each other via edges. Many network features can

be deducted from the topology, like reachability of

one node from another node or hop distance between

two nodes. We target two general use-cases:

1. A user needs to create a geo-located network from

scratch including its topology and

2. a user needs to assign geo-location to an existing

topology.

We support case 1 by supplying generators for

the following topologies: Trajectory, tree, directed

Visual Interactive Creation of Geo-located Networks

285

acyclic graph, interconnected star-shaped networks,

Barab

asi scale-free network (Barab

asi and Albert,

1999), Erd

os-R

enyi random graph (Erd

os and R

enyi,

1959), Kleinberg small-world network (Kleinberg,

2000), and Eppstein power-law graph (Eppstein and

Wang, 2002). Alternatively, the user can import an

existing network into the system which targets case 2.

Imported networks may contain (partly) geo-locations

in their nodes. The system does not restrict the type

of network, and there are no restrictions on network

topology for importing graphs. Similar to import-

ing, we support exporting of (partly) geo-located net-

works, too. The focus of our system is assigning geo-

locations to a given network topology. However, we

also provide the user with simple graph editing tech-

niques (i.e. adding, removing and connecting nodes)

that allow modiﬁcation of the topology.

3.3 Layout

The layout of a network deﬁnes the positions of its

nodes on a two-dimensional plane. A large set of lay-

out algorithms has been developed to improve the vi-

sualization of networks (Herman et al., 2000; D

ıaz

et al., 2002). For geo-located networks, the layout

is already given by the geo-information in its nodes.

Assigning geographic information to nodes will indi-

rectly inﬂuence the layout of the network.

In our approach, we pursuit the WYSIWYG prin-

ciple. By making a WYSIWYG-based system, we

intended to vastly speed up the user’s work process

by preserving him from mental context switching be-

tween other dialogs/views, as well as GUI operations

like (re)opening them. The network - once created or

imported - will be displayed on the map. All further

operations will be done directly in this map view. A

user can see the results of each operation immediately

and revoke, improve or alter them.

During editing, the network will contain a mix

of nodes with and without geo-information. We de-

signed our visualization to show both of these types

of nodes on the same network at the same time (see

Figure 2). Besides showing the network in the state of

being edited, this design can also be used as a simple

viewer to visualize partly geo-located networks. This

technique enables users to look at networks in com-

mon cases like when the location information of one

or a few is simply missing.

Map transformations deﬁne the area and scale of

the map that is currently visible for the user. Nodes

with geo-information will be placed on the map at

the corresponding position and directly react to map

transformations. Nodes without geographic informa-

tion don’t have a predeﬁned location. A generic lay-

out algorithm will calculate their locations indepen-

dently of the map transformations. This way, we

can combine a nice looking layout as achieved by

common layout algorithms with a partially ﬁxed geo-

graphic context but still avoiding overplotting.

We also considered other ways of showing mixed

networks: Displaying the nodes without geographic

information at a special location like the screen bor-

der or an off-centered inset makes the layout algo-

rithm inﬂexible and ampliﬁes clutter. Showing them

at another ﬁxed location on the map or leaving them

completely out gives the user a wrong impression of

the data. Using a geographic view for geo-located

nodes and a non-geographic structural view for all

nodes to show different subviews of a network vio-

lates our WYSIWYG principle and requires frequent

mental task switching from the user.

In the examples shown in this paper, we use spring

layout (Eades, 1984) because it is one of the most fa-

mous force-directed layout algorithms. However, any

other layout algorithm can be used, too, and, depend-

ing on the use-case, improve the visual representation

of the network further.

When changing the layout of nodes, one common

effect is a sudden change of the location of one or

multiple nodes. It looks to the user as if the nodes

are jumping and the user can hardly keep track of

this. Jumping of nodes destroys the user’s mental

map forcing him to review the whole graph and thus

increasing the time spent on the editing task and the

chance of making mistakes. This effect happens when

assigning a location to many nodes supported by our

location assigning algorithm (see Section 3.5). As

stated above, our system allows arbitrary layout al-

gorithms for nodes without location. Even though

spring layout that we mentioned above adjusts node

locations smoothly to avoid sudden jumping of nodes,

other layout algorithms will probably cause sudden

changes in node locations and thus triggering jump-

ing effects.

To avoid jumping effects, we use animation effects

for node position changes: Nodes will not be put im-

mediately to their destination locations but moved to-

ward them with limited speed. This effect gives the

impression of a smooth and ﬂuid animation. Using

this kind of animation has shown to have two addi-

tional advantages:

• The sluggish movement of nodes without location

information makes these nodes react slightly dif-

ferent to map transformations and thus to stand

out. This effect is an additional visual clue be-

side the color-based visual clues that we will show

for the presence/absence of location information

of nodes (see Section 3.4).

IVAPP 2017 - International Conference on Information Visualization Theory and Applications

286

Figure 2: After generating a network, we placed 7 nodes in California and 8 nodes in Florida. Blurred nodes yet have to be

assigned to locations and their layout is calculated by a force directed layout algorithm.

Figure 3: A network with nodes being selected. The yel-

low nodes inside the light blue border are selected while the

orange nodes are not selected.

• The sluggish movement of nodes hides wiggling

effects caused by some race conditions or numer-

ical imprecision of a chosen layout algorithm.

For a better impression of this animation effect, we

refer to our video.

3.4 Visual Representation

The visual representation of a network deﬁnes how

nodes and edges are displayed and how their attributes

and properties are visually encoded. In our approach,

we draw nodes as circles. Node color (orange) rep-

resents node degree where darker color means higher

node degree. However, any other information could

be encoded by node color instead (e.g. a given node

attribute). We enable the user to select nodes using a

rectangle tool. Selected nodes are marked by bright

yellow (see Figure 3).

Edges are drawn as straight lines. In the case of

directed edge, an arrow indicates edge direction. We

don’t use edge colors in this context, so this attribute

can be used to visualize other properties.

When a user edits a network there will likely be

the situation where it contains a mix of nodes with

and nodes without location information. Even for a

few nodes, we found out that it is hard for users to

remember which nodes already have location infor-

mation and which do not, especially, when users are

navigating the map. Figure 2 shows a mixed net-

work. Nodes without geo-information will be shown

blurred on the map, while nodes with geo-information

will not be distorted. This way, we intend to create

the impression of unclear location. We distinguish

three types of edges: (1) edges between nodes with

deﬁned locations are solid, (2) edges between nodes

one with and one without deﬁned location are dotted

with thick and long strokes, and (3) edges between

nodes with undeﬁned locations are dotted with light

and short dots. Blurred nodes graphics are precom-

puted in order to speed up visualization. We also in-

tended to blur edges similar to nodes. However, the

edges’ paths (and thus looks) are not static, so a blur-

ring effect has to be computed in real-time for each

edge for each frame. Real-time blurring would have a

bad impact on performance and thus effectively pre-

venting bigger networks from being displayed ﬂuidly.

3.5 Assigning Geographic Information

After a network topology has been created or loaded,

a user can start to attach geography to its nodes.

Assigning locations on a node-by-node basis is

very cumbersome as the time to place the nodes of

a network depends linearly on the number of nodes.

However, pure automatic placement has the disadvan-

tage that the user has no control over the placement of

the nodes. We want to provide the user with a system

that enables the user to place an arbitrary number of

nodes automatically.

In contrast to pure automatic placement, the user

should remain in full control about the area where

nodes will be placed in our system. Further, the sys-

tem should assist by suggesting meaningful areas. On

Visual Interactive Creation of Geo-located Networks

287

the other hand, we want to preserve as much free-

dom as possible, so that our system can be applied

not only to some speciﬁc networks but general geo-

located networks.

To propose meaningful areas, we use a database-

based approach. A database provides a set of areas

that the system will use for placement of nodes. The

database we use in our examples contains the admin-

istrative subdivision of the world because the political

division is commonly known and often implies impor-

tant information when looking at geo-data. This infor-

mation might, for example, indicate a change in ad-

ministrative responsibility or applicable laws in case

of a service-based network. Because of this, the struc-

ture of many networks is inﬂuenced by political bor-

ders.

However, the database is not limited to adminis-

trative subdivision and can deﬁne any subdivision of

the world. Using this exchangeable database-based

approach, we make sure that the system remains ﬂex-

ible in deﬁning what a meaningful area means to the

user.

Depending on the task at hand, it might be nec-

essary to create networks that are on either a big or

small geographic scale. Further, a task might require

the user to create a network that is partly on big and

partly on a small geographic scale at the same time.

Thus, we designed the system to be able to work with

hierarchic area databases. In this kind of database,

the area subdivision forms a tree. We enabled the

user to be able to adjust the active layer of the tree

used for positioning. By changing the active layer,

the user can set the geographic scale of the subdivi-

sion of the world. In the case of our example database,

this means navigating from the subdivision into coun-

tries up to subdivision into cities. Adjusting the geo-

graphic scale will work only if the database contains

hierarchic data. This semi-automated approach helps

to keep the balance between placing nodes in a par-

ticular region and saving the overhead of caring about

details of placement.

Nodes can be assigned to an area using a drag-

and-drop operation. Figure 4 shows how a single node

is dragged by the mouse cursor and dropped to a city

to set its location. While dragging multiple nodes, the

predeﬁned geographic area under the cursor will be

highlighted by an animated dashed border (see Fig-

ure 5a). An animated red border highlights the shape

of the area notably without cluttering the view. High-

lighting gives instant feedback about the size of the

area in which the nodes can be placed. Additionally,

a label will display the area’s name. As mentioned

above, the scale of the area is dependent on the chosen

hierarchy level and can be adjusted freely, even while

dragging. Immediate feedback from the area’s bor-

ders and the label enable the user to select the area of

interest quickly and accurately. When the user drops

the nodes into an area, geo-location within this area

will be assigned to each node (see Figure 5b).

Node placement within an area is calculated by a

coordinate generator algorithm. Like for the database,

we want our system to apply to various kind network

generation tasks, so we designed it to be easily exten-

sible to various coordinate generator algorithms. In

the examples presented here, we use a simple random

coordinate generator that draws two random numbers

(x and y) from interval [0 − 1) and transforms them

into the bounding box area of the shape. A hit-test

makes sure that the coordinate is in contained within

the shape before transforming them to geographical

coordinates. However, depending on the use-case, a

more sophisticated algorithm can be used.

Area shapes are stored in a database. For each

area, the database contains three shapes per area:

• A shape of the area in full resolution used for ac-

tual coordinate generation. When the user drops a

set of shapes into an area, these shapes are used as

boundaries in which the coordinates of the nodes

will be generated.

• A low-resolution shape used for efﬁcient visual-

ization of the area’s borders. This shape is used

for efﬁcient displaying of the area’s borders on

the map. Full resolution shapes often have a

much higher resolution as necessary for display-

ing. This might have a negative impact on ren-

dering performance while not increasing the qual-

ity of the visual result. A user can also use low-

resolution shapes for the actual generation of co-

ordinates to speed up the layout process if he

doesn’t care about the exactness of the layout

around the borders.

• A bounding box used to speed up the point-in-

shape test. This, again, speeds up the rendering,

since, on ﬁne-grained administrative levels, the

number of shapes to check for intersection can be-

come very high.

Since area shapes are immutable, low-resolution

shapes and bounding boxes the bounding boxes have

been pre-calculated.

Borders of administrative areas often include

coast regions. To prevent nodes from being placed

into an ocean, we do not use the administrative

area directly but an intersection of the area with the

world’s land mass. Since this intersection is static, it

has been precomputed and already applied to all full

resolution shapes in the database. However, the in-

tersection has not been applied to the low-resolution

IVAPP 2017 - International Conference on Information Visualization Theory and Applications

288

Figure 4: A single node’s location can be assigned directly to a location by dragging it there. The node is selected with the

cursor (left), moved to the intended location (middle), and is dropped there (right) to assign it to this location.

(a)(a)

(b)(b)

Figure 5: (a) Switzerland is highlighted by a dashed border

when the mouse cursor is dragging a set of nodes over it. (b)

After dropping a set of 7 nodes on Switzerland, the system

assigns random coordinates to the nodes within the area of

Switzerland.

shapes used for displaying the borders on the map.

We decided so because many small islands at the coast

lead to visualization artifacts of the marker borders.

4 USAGE EXAMPLE

In this section, we show a concrete example of our

approach by imitating a real network. The exam-

ple we use here is an academic computer network

named “LitNet” located in Lithuania. The dataset was

obtained from http://topology-zoo.org and resembled

the networks in 2009. The network consists of 43

nodes and 43 edges. Figure 6a shows the network

visualized by our tool.

We notice that location information of 4 nodes

in the dataset is missing since our tool shows them

blurred.

Looking at the network, we see that there are 5

nodes (hub nodes) that are forming a cycle. The re-

maining nodes (we call them child nodes) connect

mostly to their nearest hub node, but not to any other

nodes.

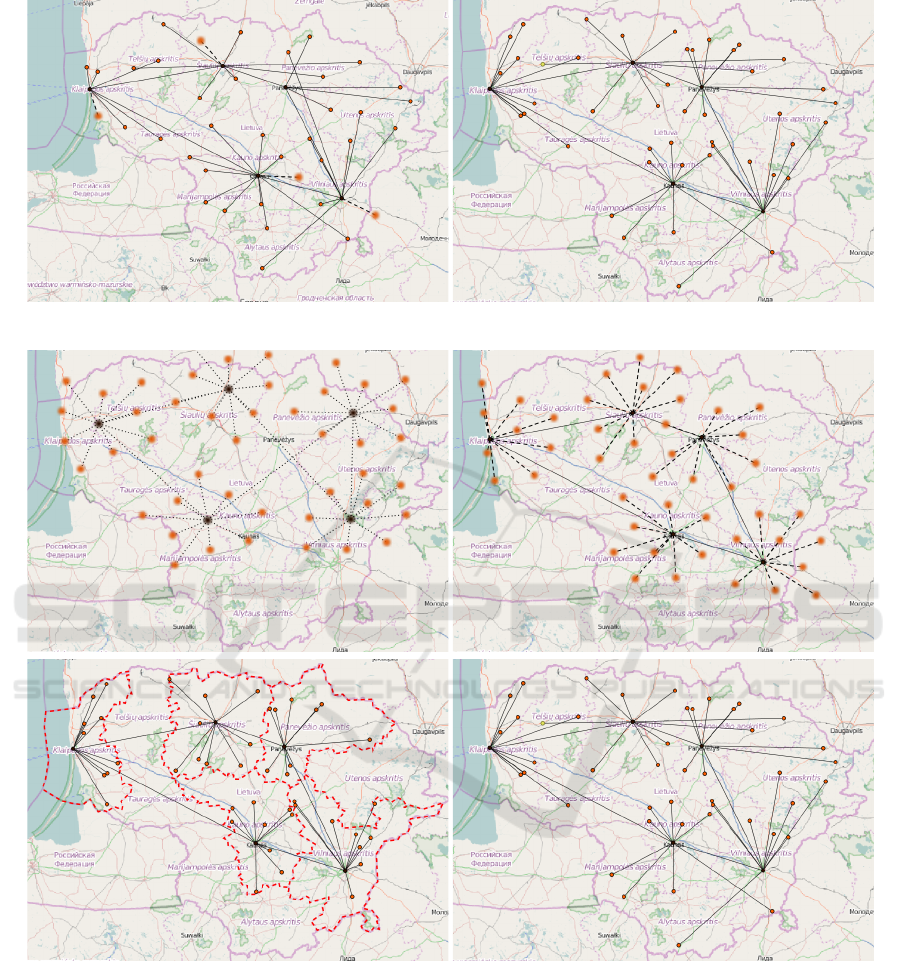
To imitate LitNet, we start by creating its topol-

ogy. We use the generator for inter-connected star

networks with 5 hub nodes and 9 nodes per hub (50

nodes in total). Figure 7a shows the resulting net-

work.

Force directed layouting places child nodes near

to their associated hubs. One by one, we drag the

hubs to the rough locations where the real LitNet also

shows hubs. This results in Figure 7b. Next, we con-

tinue by assigning locations to the child nodes of the

hubs, so that they are roughly located near to their

hubs. To do so, we select the child nodes and drag

the selected nodes to the area around the hub node.

The county around the hub node gets highlighted. As

we drop the selected nodes, they will be placed ran-

domly within the county. Figure 7c shows the result

of assigning locations to all child nodes. We edited

the graphic of Figure 7c to be able to show all county

borders in which we placed nodes. In the original data

of LitNet, a few nodes stand out that are unusually far

away from their associated hub. To imitate this aspect,

we drag some random child nodes around the corre-

sponding hub to the positions we see in the original

data. Figure 7d shows the ﬁnal result of our synthetic

network. We can now export this network and use it

for testing or analysis.

Figure 6 shows the original LitNet and our gen-

erated network side-by-side. We can see how simi-

lar the result looks to the original network. In total,

we used 16 placement operations to imitate LitNet (5

for hubs + 5 for hubs’ child nodes + 6 for individual

nodes). Without our tool, it would have been neces-

sary to adjust each single node resulting in at least 43

operations. By using semi-automated operations, we

could balance between speed and geographic accu-

Visual Interactive Creation of Geo-located Networks

289

(a) Original LitNet(a) Original LitNet (b) Our Imitation(b) Our Imitation

Figure 6: (a) Original LitNet and (b) the network we created with our tool to imitate LitNet.

(a) No geo-location(a) No geo-location (b) Hubs assigned(b) Hubs assigned

(c)(c)

Child nodeChild node

assignedassigned

(d)(d)

Single nodesSingle nodes

adjustedadjusted

Figure 7: Process of creating a network that resembles LitNet (see Figure 6). (a) The topology of a hub network with star like

topology has been created. (b) Hub nodes of the network have been assigned to locations. (c) Child nodes have been assigned

to the area around their hub node. Their exact location was generated randomly. (Note that the graphic was edited with an

image processor to show the red borders of all the counties in one graphic.) (d) Single nodes have been relocated manually to

make the generated network have similar anomalies like the original network.

racy and incrementally increase the (task dependent)

data quality.

We refer to our attached video for a better visual

demonstration of recreating “LitNet”.

5 DISCUSSION

We have shown how our framework can be used to

attach location information to nodes of a network.

Since we provide a ﬂexible way of assigning a loca-

tion to nodes, our approach can be efﬁciently used

IVAPP 2017 - International Conference on Information Visualization Theory and Applications

290

not only for small, but also for bigger networks with

hundreds of nodes. However, as the visualization

uses node-link representation, the approach can not be

used effectively to edit large networks with ten thou-

sands or hundred thousands of nodes.

Our algorithm assigns locations to nodes within a

shape in a random way. This behavior is sufﬁcient

if one only wants to create a roughly geographic bal-

anced network. However, depending on the use-case,

one can extend the framework by a custom plug-in for

custom layout calculation within a shape.

As mentioned in Section 3, we used a pre-

calculated intersection of the area shapes with the

landmass for geography generation. This calculation

can be easily extended to include lakes, rivers or un-

populated areas in this operation if required by the use

case.

While all actions can be performed via descrip-

tive menu items, the primary focus of the system is to

perform all actions with mouse and keyboard only to

speed up the editing process once a user got used to

this.

The examples shown in this paper used the recur-

sive administrative division of the world for assign-

ing locations to multiple nodes because they are com-

monly known and accepted, and for many real world

problems, administrative borders are relevant. How-

ever, our approach can be used for any other type of

division of the earth, regardless of whether it is recur-

sive or not. Examples include biospheres of animals

or nautical zones.

All operations in our framework except for layout

calculation operate in O (n) (n = node count). Perfor-

mance mainly depends on the layout algorithm used.

Here, we used a force-directed algorithm that runs

in approximately polynomial time. Assigning geo-

graphic location depends on the number of nodes to

be processed. However, a custom algorithm might

have a different performance depending on the time

complexity of the algorithm used.

Intersection tests on the database of areas test in-

tersection with all shapes of a given hierarchy level.

Since there are many cities and suburbs, we used

bounding boxes to speed up the tests and observed

no noticeable delay anymore. This intersection test

performance can be further improved by using space

subdividing techniques.

Depending on the number of shapes and edges per

shape (data quality), assigning locations to a set of

nodes within an area can be slow. Our system can

speed up the assigning process using simpliﬁed ver-

sions of shapes in exchange for accuracy at the bor-

ders. Whether this is acceptable or not depends on

the concrete use-case.

6 CONCLUSION AND OUTLOOK

We presented a framework to create networks with

geolocated nodes. Our approach can be used to eas-

ily and fast create custom geo-located networks. The

framework works interactively and supports incre-

mental reﬁnement following the WYSIWYG princi-

ple. It allows the user to place nodes in an arbitrary

area at any scale by using semi-automated placement

algorithms. Still, a user can edit details such as single

nodes or small groups of nodes. Finally, we showed

that our system could be used to mimic existing geo-

located networks easily by recreating a real network.

At the moment, topology creation and location as-

signment are two separate processes in our system. In

the future, it might be necessary connect these two

processes together to create topology dependent on

the geography, e.g. exploiting the effect that many

geo-located networks representing human infrastruc-

ture rarely have edge crossings and thus are nearly

planar. Since manual creation has a high risk of re-

sulting in datasets that do not satisfy statistical proper-

ties for a given use-case, another improvement could

restrict the user to place nodes only in predeﬁned ar-

eas like buildings for node assignment. Node snap-

ping could be used to advise such areas but still leave

freedom to place nodes at unusual places. Other fu-

ture work includes creating the geography of edges

by street network information. Beside this, future

work should investigate how other visual representa-

tions than node-link diagrams can be used to enable

the system to be more scalable. Finally, a user-study

can compare the creation of geo-located networks by

hand with this approach and similar approaches from

related work regarding speed of the creation process

and accuracy.

ACKNOWLEDGEMENTS

We gratefully thank Sebastian Bremm for his many

useful comments and suggestions.

This research was partially carried out and

supported by a Software Campus project (BMBF

01IS12054) funded by the German Ministry of Ed-

ucation and Research.

REFERENCES

Albuquerque, G., Lowe, T., and Magnor, M. (2011). Syn-

thetic generation of high-dimensional datasets. IEEE

transactions on visualization and computer graphics,

17(12):2317–2324.

Visual Interactive Creation of Geo-located Networks

291

Alvarez-Garcia, S., Baeza-Yates, R., Brisaboa, N. R.,

Larriba-Pey, J., and Pedreira, O. (2012). Graphgen:

A tool for automatic generation of multipartite graphs

from arbitrary data. In Web Congress (LA-WEB), 2012

Eighth Latin American, pages 87–94. IEEE.

Alvarez-Garc

ıa, S., Baeza-Yates, R., Brisaboa, N. R.,

Larriba-Pey, J.-L., and Pedreira, O. (2014). Auto-

matic multi-partite graph generation from arbitrary

data. Journal of Systems and Software, 94:72–86.

Andrienko, G. and Andrienko, N. (2007). Coordinated

multiple views: a critical view. In Coordinated and

Multiple Views in Exploratory Visualization, 2007.

CMV’07. Fifth International Conference on, pages

72–74. IEEE.

Bach, B., Spritzer, A., Lutton, E., and Fekete, J.-D. (2013).

Interactive random graph generation with evolution-

ary algorithms. In Graph Drawing, pages 541–552.

Springer.

Baeza-Yates, R., Brisaboa, N., and Larriba-Pey, J. (2010). A

model for automatic generation of multi-partite graphs

from arbitrary data. In Web-Age Information Manage-

ment, pages 49–60. Springer.

Barab

asi, A.-L. and Albert, R. (1999). Emergence of scal-

ing in random networks. science, 286(5439):509–512.

Baudel, T. (2006). From information visualization to di-

rect manipulation: Extending a generic visualization

framework for the interactive editing of large datasets.

In Proceedings of the 19th Annual ACM Symposium

on User Interface Software and Technology, UIST

’06, pages 67–76, New York, NY, USA. ACM.

Benson, D. (2015). Draw. https://www.draw.io/.

Bremm, S., von Landesberger, T., Heß, M., and Fellner, D.

(2012). Pcdc-on the highway to data-a tool for the

fast generation of large synthetic data sets. In EuroVis

Workshop on Visual Analytics, pages 7–11.

Brinkhoff, T. (2002). A framework for generating network-

based moving objects. GeoInformatica, 6(2):153–

180.

Brinkmann, G. and McKay, B. D. (2007). Fast generation

of planar graphs. MATCH Commun. Math. Comput.

Chem, 58(2):323–357.

Brodkorb, F., Kopp, M., Kuijper, A., and von Landesberger,

T. (2016). A modular rule-based visual interactive cre-

ation of tree-shaped geo-located networks. In 2016

12th International Conference on Signal-image Tech-

nology & Internet-based Systems (sitis), pages 397–

403. IEEE Computer Society Press.

Cascetta, E. and Cantarella, G. E. (1993). Modelling dy-

namics in transportation networks: state of the art and

future developments. Simulation practice and theory,

1(2):65–91.

Chen, G., Esch, G., Wonka, P., M

uller, P., and Zhang, E.

(2008). Interactive procedural street modeling. In

ACM transactions on graphics (TOG), volume 27,

page 103. ACM.

ıaz, J., Petit, J., and Serna, M. (2002). A survey of graph

layout problems. ACM Comput. Surv., 34(3):313–356.

Eades, P. (1984). A heuristics for graph drawing. Congres-

sus Numerantium, 42:146–160.

Eppstein, D. and Wang, J. (2002). A steady state model for

graph power laws. arXiv preprint cs/0204001.

Erd

os, P. and R

enyi, A. (1959). On random graphs, i. Pub-

licationes Mathematicae (Debrecen), 6:290–297.

Frick, R. (2011). Simulation of transportation networks. In

Proceedings of the 2011 Summer Computer Simula-

tion Conference, pages 188–193. Society for Model-

ing & Simulation International.

Gladisch, S., Schumann, H., Ernst, M., F

ullen, G., and

Tominski, C. (2014). Semi-automatic editing of

graphs with customized layouts. In Computer Graph-

ics Forum, volume 33, pages 381–390. Wiley Online

Library.

Grifﬁth, D. A. (2002). A spatial ﬁltering speciﬁcation for

the auto-poisson model. Statistics & probability let-

ters, 58(3):245–251.

Herman, I., Melancon, G., and Marshall, M. S. (2000).

Graph visualization and navigation in information vi-

sualization: A survey. IEEE Transactions on Visual-

ization and Computer Graphics, 6(1):24–43.

Kleinberg, J. M. (2000). Navigation in a small world. Na-

ture, 406(6798):845–845.

Maciejewski, R., Hafen, R., Rudolph, S., Tebbetts, G.,

Cleveland, W. S., Grannis, S. J., and Ebert, D. S.

(2009). Generating synthetic syndromic-surveillance

data for evaluating visual-analytics techniques. IEEE

Computer Graphics and Applications, 29(3):18–28.

McGufﬁn, M. J. and Jurisica, I. (2009). Interaction tech-

niques for selecting and manipulating subgraphs in

network visualizations. IEEE Transactions on Visu-

alization and Computer Graphics, 15(6):937–944.

National Council of Teachers of Mathematics (2015). Illu-

minations. http://illuminations.nctm.org.

Okabe, A., Okunuki, K.-i., and Shiode, S. (2006a). Sanet: a

toolbox for spatial analysis on a network. Geographi-

cal Analysis, 38(1):57–66.

Okabe, A., Okunuki, K.-I., and Shiode, S. (2006b). The

sanet toolbox: new methods for network spatial anal-

ysis. Transactions in GIS, 10(4):535–550.

O’Madadhain, J., Fisher, D., White, S., and Boey, Y. (2003).

The jung (java universal network/graph) framework.

University of California, Irvine, California.

Parish, Y. I. and M

uller, P. (2001). Procedural modeling

of cities. In Proceedings of the 28th annual con-

ference on Computer graphics and interactive tech-

niques, pages 301–308. ACM.

Sakshaug, J. W. and Raghunathan, T. E. (2010). Synthetic

data for small area estimation. In Privacy in Statistical

Databases, pages 162–173. Springer.

Sakshaug, J. W. and Raghunathan, T. E. (2014a). Gen-

erating synthetic data to produce public-use micro-

data for small geographic areas based on complex

sample survey data with application to the national

health interview survey. Journal of Applied Statistics,

41(10):2103–2122.

Sakshaug, J. W. and Raghunathan, T. E. (2014b). Non-

parametric generation of synthetic data for small ge-

ographic areas. In Privacy in Statistical Databases,

pages 213–231. Springer.

IVAPP 2017 - International Conference on Information Visualization Theory and Applications

292

Spritzer, A. S. and Freitas, C. M. (2008). A physics-based

approach for interactive manipulation of graph visual-

izations. In Proceedings of the working conference on

Advanced visual interfaces, pages 271–278. ACM.

Theodoridis, Y., Silva, J. R., and Nascimento, M. A.

(1999). On the generation of spatiotemporal datasets.

In Advances in Spatial Databases, pages 147–164.

Springer.

von Landesberger, T., Bremm, S., Bernard, J., and Schreck,

T. (2010). Smart query deﬁnition for content-

based search in large sets of graphs. In EuroVAST

2010, pages 7–12. European Association for Com-

puter Graphics (Eurographics), Eurographics Associ-

ation, Goslar.

von Landesberger, T., Bremm, S., Kirschner, M., Wesarg,

S., and Kuijper, A. (2013). Visual analytics for model-

based medical image segmentation: Opportunities and

challenges. Expert Syst. Appl., 40(12):4934–4943.

von Landesberger, T., G

orner, M., Rehner, R., and Schreck,

T. (2009). A system for interactive visual analysis of

large graphs using motifs in graph editing and aggre-

gation. In Vision Modeling Visualization Workshop,

pages 331–339. DNB.

von Landesberger, T., Kuijper, A., Schreck, T., Kohlham-

mer, J., van Wijk, J. J., Fekete, J.-D., and Fellner,

D. W. (2011). Visual analysis of large graphs: State-

of-the-art and future challenges. Computer Graphics

Forum, pages 1719–1749.

Wang, B., Ruchikachorn, P., and Mueller, K. (2013).

Sketchpadn-d: Wydiwyg sculpting and editing in

high-dimensional space. Visualization and Computer

Graphics, IEEE Transactions on, 19(12):2060–2069.

Whiting, M. A., Haack, J., and Varley, C. (2008). Creat-

ing realistic, scenario-based synthetic data for test and

evaluation of information analytics software. In Pro-

ceedings of the 2008 Workshop on BEyond time and

errors: novel evaLuation methods for Information Vi-

sualization, page 8. ACM.

Wong, P., Foote, H., Mackey, P., Perrine, K., and Chin, G.

(2006). Generating graphs for visual analytics through

interactive sketching. IEEE Transactions on Visual-

ization and Computer Graphics, 12(6):1386–1398.

Ying, X. and Wu, X. (2009). Graph generation with pre-

scribed feature constraints. In SDM, volume 9, pages

966–977. SIAM.

YWorks (2015). Yed graph editor. http://www.yworks.com/

en/products/yﬁles/yed/.

Visual Interactive Creation of Geo-located Networks

293