ε-Strong Privacy Preserving Multiagent Planner by Computational
Tractability
Jan To
ˇ
zi
ˇ
cka, Anton
´
ın Komenda and Michal
ˇ
Stolba
Department of Computer Science, Czech Technical University in Prague,
Karlovo n
´
am
ˇ
est
´
ı 13, 121 35, Prague, Czech Republic
Keywords:
Automated Planning, Multiagent Systems, Privacy, Security.
Abstract:
Classical planning can solve large and real-world problems, even when multiple entities, such as robots, trucks
or companies, are concerned. But when the interested parties, such as cooperating companies, are interested
in maintaining their privacy while planning, classical planning cannot be used. Although, privacy is one of
the crucial aspects of multi-agent planning, studies of privacy are underepresented in the literature. A strong
privacy property, necessary to leak no information at all, has not been achieved by any planner in general yet.
In this contribution, we propose a multiagent planner which can get arbitrarily close to the general strong
privacy preserving planner for the price of decreased planning efficiency. The strong privacy assurances are
under computational tractability assumptions commonly used in secure computation research.
1 INTRODUCTION
A multiagent planning problem is a problem of find-
ing coordinated sequeces of actions of a set of enti-
ties (or agents), so that a set of goals is fulfilled. If
the environment and actions are deterministic (that is
their outcome is unambiguously defined by the state
they are applied in), the problem is a deterministic
multiagent planning problem (Brafman and Domsh-
lak, 2008). Furhtemore, if the set of goals is com-
mon to all agents and the agents cooperate in order
to achieve the goals, the problem is a cooperative
multiagent planning problem. The reason the agents
cannot simply feed their problem descriptions into a
centralized planner typically lies in that although the
agents cooperate, they want to share only the infor-
mation necessary for their cooperation, but not the in-
formation about their inner processes. Such privacy
constraints are respected by privacy preserving multi-
agent planners.
A number of privacy preserving multiagent plan-
ners has been proposed in recent years, such as
MAFS (Nissim and Brafman, 2014), FMAP (Torre
˜
no
et al., 2014), PSM (To
ˇ
zi
ˇ
cka et al., 2015) and
GPPP (Maliah et al., 2016b). Although all of the
mentioned planners claim to be privacy-preserving,
proving such claims was rather scarce. The privacy
of MAFS is discussed in (Nissim and Brafman, 2014)
and expanded upon in (Brafman, 2015), proposing
Secure-MAFS, a version of MAFS with stronger pri-
vacy guarantees. This approach was recently gener-
alized in the form of Macro-MAFS (Maliah et al.,
2016a).
Apart from a specialized privacy leakage quantifi-
cation by (Van Der Krogt, 2009) (which is not prac-
tical as it is based on enumeration of all plans and
also is not applicable to MA-STRIPS in general), the
only rigorous definition of privacy so far was pro-
posed in (Nissim and Brafman, 2014) and extended
in (Brafman, 2015). The authors present two notions,
weak and strong privacy preservation. Weak privacy
preservation forbids only explicit communication of
the private information, which is trivial to achieve and
provides no security guarantees. The strong privacy
preservation forbids leakage of any information al-
lowing other agents to deduce any private information
at all.
2 MULTI-AGENT PLANNING
The most common model for multiagent planning is
MA-STRIPS (Brafman and Domshlak, 2008) and de-
rived models (such as MA-MPT (Nissim and Braf-
man, 2014) using multi-valued variables). We refor-
mulate the MA-STRIPS definition and we also gen-
eralize the definition to multi-valued variables. For-
mally, for a set of agents A , a problem M = {Π
i
}
|A|
i=1
ToÅ¿iÄ ka J., Komenda A. and Å
˘
atolba M.
θt-Strong Privacy Preserving Multiagent Planner by Computational Tractability.
DOI: 10.5220/0006176400510057
In Proceedings of the 9th International Conference on Agents and Artificial Intelligence (ICAART 2017), pages 51-57
ISBN: 978-989-758-219-6
Copyright
c
 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
51

is a set of agent problems. An agent problem of agent
α
i
∈ A is defined as
Π
i
=
D
V
i
= V
pub
∪ V
priv
i
,O
i
= O
pub
i
∪ O
priv
i
∪ O
proj
,s
I
,s
?
E
,
where V
i
is a set of variables s.t. each V ∈ V
i
has
a finite domain dom(V ), if all variables are binary
(i.e. |dom(V )| = 2), the formalism corresponds to
MA-STRIPS. The set of variables is partitioned into
the set V
pub
of public variables (with all values pub-
lic), common to all agents and the set V
priv
i
of vari-
ables private to α
i
(with all values private), such that
V
pub
∩ V
priv
i
=
/
0. A complete assignment over V is
a state, partial assignment over V is a partial state.
We denote s[V ] as the value of V in a (partial) state s
and vars(s) as the set of variables defined in s. The
state s
I
is the initial state and s
?
is a partial state rep-
resenting the goal condition, that is if for all variables
V ∈ vars(s
?
), s
?
[V ] = s[V ], s is a goal state.
The set O
i
of actions comprises of a set O
priv
i
of
private actions of α
i
, a set O
pub
i
of public actions of α
i
and a set O
proj
of public projections of other agents’
actions. O
pub
i
, O
priv
i
, and O
proj
are pairwise disjoint.
An action is defined as a tuple a =
h
pre(a),eff(a)
i
,
where pre(a) and eff(a) are partial states representing
the precondition and effect respectively. An action
a is applicable in state s if s[V ] = pre(a)[V ] for all
V ∈ vars(pre(a)) and the application of a in s, denoted
a ◦ s, results in a state s
0
s.t. s
0
[V ] = eff(a)[V ] if V ∈
vars(eff(a)) and s
0
[V ] = s[V ] otherwise. As we often
consider the planning problem from the perspective
of agent α
i
, we omit the index i.
We model all “other” agents as a single agent
(the adversary), as all the agents can collude and
combine their information in order to infer more.
The public part of the problem Π which can be
shared with the adversary is denoted as a public
projection. The public projection of a (partial) state
s is s
B
, restricted only to variables in V
pub
, that
is vars(s
B
) = vars(s) ∩ V
pub
. We say that s,s
0
are
publicly equivalent states if s
B
= s
0B
. The public pro-
jection of action a ∈ O
pub
is a
B
=
h
pre(a)
B
,eff(a)
B
i
and of action a
0
∈ O
priv
is an empty (no-op) action ε.
The public projection of Π is
Π
B
=

V
pub
,{a
B
|a ∈ O
pub
},s
B
I
,s
B
?

.
Finally, we define the solution to Π and M . A
sequence π = (a
1
,...,a
k
) of actions from O , s.t. a
1
is applicable in s
I
= s
0
and for each 1 ≤ i ≤ k, a
i
is
applicable in s
i−1
and s
i
= a
i
◦ s
i−1
, is a local s
k
-plan,
where s
k
is the resulting state. If s
k
is a goal state, π
is a local plan, that is a local solution to Π. Such π
does not have to be the global solution to M , as the
actions of other agents (O
proj
) are used only as public
projections and are missing private preconditions and
effects of other agents. The public projection of π is
defined as π
B
= (a
B
1
,...,a
B
k
) with ε actions omitted.
From the global perspective of M a public plan
π
B
= (a
B
1
,...,a
B
k
) is a sequence of public projections
of actions of various agents from A such that the ac-
tions are sequentially applicable with respect to V
pub
starting in s
B
I
and the resulting state satisfies s
B
?
. A
public plan is α
i
-extensible, if by replacing a
B
k
0
s.t.
a
k
0
∈ O
pub
i
by the respective a
k
0
and adding a
k
00
∈ O
priv
to required places we obtain a local plan (solution) to
Π
i
. According to (To
ˇ
zi
ˇ
cka et al., 2015), a public plan
π
B
α
i
-extensible by all α
i
∈ A is a global solution to
M .
2.1 Privacy
We say that an algorithm is weak privacy-preserving
if, during the whole run of the algorithm, the agent
does not openly communicate private parts of the
states, private actions and private parts of the public
actions. In other words, the agent openly communi-
cates only the information in Π
B
. Even if not commu-
nicated, the adversary may deduce the existence and
values of private variables, preconditions and effects
from the (public) information communicated.
An algorithm is strong privacy-preserving if the
adversary can deduce no information about a pri-
vate variable and its values and private precondi-
tions/effect of an action, beyond what can be deduced
from the public projection Π
B
and the public projec-
tion of the solution plan π
B
.
2.2 Secure Computation
In general any function can be computed securely
(Ben-Or et al., 1988; Yao, 1982; Yao, 1986). In this
contribution, we focus on more narrow problem of
private set intersection (PSI), where each agent has
a private set of numbers and they want to securely
compute the intersection of their private sets while not
disclosing any numbers which are not in the intersec-
tion. The ideal PSI supposes that no knowledge is
transfered between the agents (Pinkas et al., 2015).
Ideal PSI can be solved with trusted third party
which receives both private sets, computes the inter-
section, and sends it back to agent. As long as the
third party is honest, the computation is correct and
no information leaks.
In literature (e.g., (Pinkas et al., 2015; Jarecki
and Liu, 2010), we can find several approaches how
the ideal PSI can be solved without trusted third
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
52

party. Presented solutions are based on several
computational hardness assumptions, e.g., intractable
large number factorization, DiffieHellman assump-
tion (Diffie and Hellman, 1976), etc. All these as-
sumptions break when an agent has access to unlim-
ited computation power, therefore all the results hold
under the assumption that P 6= NP, in other words by
computational intractability of breaking PSI.
3 STRONG PRIVACY
PRESERVING MULTIAGENT
PLANNER
Multiagent planner fulfilling the strong privacy re-
quirement forms the lower bound of knowledge ex-
changed between the agents. Agents do not leak
any knowledge about their internal problems and thus
their cooperation cannot be effective, nevertheless, a
strong privacy preserving multiagent planner is an im-
portant theoretical result that could lead to better un-
derstanding of privacy preserving during multiagent
planning and consequentially also to creation of more
privacy preserving planners.
In this contribution, we present a planner that is
not strong privacy preserving but can be arbitrarily
close to it. We focus on planning using coordina-
tion space
1
search (Stolba et al., 2016) and thus we
will define the terms in that respect. In the following
definitions and proofs we suppose that there are two
honest agents α
1
and α
2
. We will consider the per-
spective of a curious agent α
1
trying to detect the pri-
vate knowledge of α
2
for the simplicity of the presen-
tation, but all holds for both curious agents and also
for a larger group of agents. Similarly to (Brafman,
2015), we also assume that O
priv
=
/
0. This assump-
tion can be stated WLOG as each sequence of private
actions followed by a public action can be compiled
as a single public action.
Definition 1 (Public plan acceptance). Public plan
acceptance φ(π) is a probability known to agent α
1
whether plan π is α
2
-extensible.
When the algorithm starts, α
1
has some a priori
knowledge φ
0
(π) about the acceptance of plan π by
agent α
2
(e. g. 50 % probability of acceptance of each
plan in the case when α
1
knows nothing about α
2
).
At the end of the algorithm execution this knowledge
changes to φ
⊥
(π). Obviously, every agent knows that
the solution π
∗
agents agreed on is extensible and thus
it is accepted by every agent, i.e. φ
⊥
(π
∗
) = 1. The dif-
ference between the α
1
’s a priori knowledge and the
1
Coordination space contains all the solutions of public
problem Π
B
.
final knowledge represents knowledge which leaked
from α
2
during their communication.
Definition 2 (Leaked knowledge). Leaked knowl-
edge during the execution of a multiagent planner
leading to a solution π
∗
received by agent α
1
is
λ =
∑
π6=π
∗



φ
⊥
(π) − φ
0
(π)



.
Definition of algorithm’s leaked knowledge allows
us to formally define strong privacy of coordination
space algorithm.
Definition 3 (Strong privacy). Coordination space al-
gorithm is strong privacy preserving if λ = 0.
Definition 4 (ε-strong privacy preserving planner).
For any given ε > 0 the algorithm can be tuned to
leak less then ε knowledge, i.e. λ < ε.
Our proposed algorithm (Algorithm 1) is based
on the generate-and-test principle. All agents se-
quentially generate solutions to their problems at Line
4. How to generate new solutions of Π
i
to achieve
desired properties is discussed in respective proofs.
Then the agents create public plans by making public
projections of their solutions. Created public plans
are then stored in a set Φ
i
of α
i
-extensible public
plans. Agents need to continuously check whether
there are some plans in the intersection of these sets.
It is important to compute the intersection without
disclosing any information about plans which do not
belong to this intersection. Plans in the intersection
are guaranteed to be extensible and thus the agents
can extend them to local solutions. If the intersection
is empty, no agent can infer any knowledge about the
acceptance of proposed plans since it is possible that
the other agent just did not generated the correspond-
ing plans yet.
Algorithm 1: ε-Strong privacy preserving multiagent
planner.
1 Function SecureMAPlanner(Π
i
) is
2 Φ
i
←
/
0;
3 loop
4 π ← generate new solution of Π
i
;
5 Φ
i
← Φ
i
∪ {π
B
};
6 Φ ← secure
T
α
j
∈A
Φ
j
!
;
7 if Φ 6=
/
0 then
8 return Φ;
9 end
10 end
11 end
θt-Strong Privacy Preserving Multiagent Planner by Computational Tractability
53

Theorem 1 (Soundness and completeness). Algo-
rithm SecureMAPlanner() is sound and complete.
Proof. Every public plan returned by the algorithm is
extensible, because it is α
i
-extensible by every agent,
and thus it can be extended to valid local solutions.
A new plan is added to the plan set Φ
i
under as-
sumption that underlying planner generating new lo-
cal solutions is complete. Let us suppose that π is a
solution of length l of agent’s local problem Π
i
, such
that π
B
is extensible. If the underlying planner is sys-
tematic, preferring shorter plans, (e.g. breadth-first
search (BFS)) then it has to generate π
B
in finite time
since there is only finite number of different plans of
length at most l. Thus SecureMAPlanner() with sys-
tematic local planner ends in finite time when M has
some solution.
Theorem 2 (ε-strong privacy). Algorithm
SecureMAPlanner() is ε-strong privacy preserving
private when ideal PSI is used.
Proof. Agents have to communicate only when com-
puting the intersection of their plan sets.
Firstly, both agents encode public projections of
their plans into a set of numbers using the same en-
coding. Then, they just need to compare two sets
of numbers representing their sets of plausible pub-
lic plans, in other words they need to compute ideal
PSI (Pinkas et al., 2015; Jarecki and Liu, 2010).
No private knowledge leaks during ideal PSI in
a single iteration. Nevertheless, there can be pri-
vate knowledge leakage when the algorithm continues
several for iterations when the agent uses systematic
plan generation (which is in the completeness require-
ment).
Let us suppose both agents use BFS to solve local
planning problem, but similar reasoning can be used
for any systematic solver of Π
1
. Agent α
1
adds its
local solution π
1
to the Φ
1
in the first iteration. Agent
α
2
also provides some Φ
2
, but α
1
knows only that the
intersection is empty. Then α
1
adds longer plan π
0
1
to its Φ
1
. Let us suppose that after few iterations the
intersection is non-empty and contains π
0
1
only. Then
α
1
knows that agent α
2
does not accept π
1
, because it
would had to add it to Φ
2
before adding π
0
1
.
Agent α
2
could decrease the certainty of α
1
about
the infeasibility of π
1
by interleaving the plans gen-
erated by BFS with other (possibly randomly) gener-
ated local solutions. Certainly, this would not breach
the completeness as it would at most double the
number of iterations before non-empty intersection is
found. From the privacy perspective, α
1
cannot be
sure which of the following cases happened: either
(i) π
0
1
has been generated by BFS and then, similarly
to the previous case, α
2
does not accept π
1
, or (ii)
π
0
1
has been generated by another unsystematic solver
and it is still possible that α
2
would generate π
1
at
some time in future and thus α
1
cannot deduce any-
thing. Although α
1
cannot be sure which is the case,
this information still changes the probabilities of pos-
sible private structures of α
2
problem and thus some
information leaks.
Obviously, α
2
could further decrease the amount
of leaked information by adding more (but still just
finitely many) unsystematically generated plans be-
tween the plans generated systematically. This way
the leaked information can be arbitrarily decreased
and thus we just need to compute how many plans
should be inserted to ensure that the total leakage is
less than ε.
Having Θ
REF
α
2
(l) representing a set of plans of
length l proposed by α
1
and provably refused by α
2
2
,
we can estimate the leakage of the algorithm before
finding a solution π
∗
as follows:
λ ≤
∑
1≤l<|π
∗
|
|Θ
REF
α
2
(l)|
k + 1
,
where k is number of unsystematically generated
plans between two plans generated by BFS. There are
two reasons why the agent α
2
cannot use this formula
to calculate k to keep: λ < ε. Firstly, Θ
REF
α
2
(l) is not
known to α
2
as it cannot know how many plans of
length l are acceptable for α
1
. α
2
can overestimate
this value as the number of all possible public plans
of length l minus plans that are acceptable by itself,
or further overestimate it by number of public plans
of length l: |Θ
ALL
(l)| − |Θ
ACC
α
1
(l)| ≤ |Θ
ALL
(l)|. Sec-
ondly, the length of the solution |π
∗
| is also not known
in advance. This problem can be easily avoided by al-
lowing ε/2 leakage for the plans of length 1, ε/4 for
plans of length 2, ..., ε/2
l
for plans of length l, which
certainly yields in total leakage bellow ε.
λ < ε
∑
1≤l<|π
∗
|
|Θ
REF
α
2
(l)|
k + 1
<
∑
l<|π
∗
|
ε
2
l
∀l :
|Θ
ALL
(l)|
k + 1
<
ε
2
l
∀l : 2
l
·
|Θ
ALL
(l)|
ε
≤ k
Therefore, if there are at least 2
l
·
|Θ
ALL
(l)|
ε
unsystem-
atically generated plans between two systematically
generated plans of length l, the total leakage will be
less then ε and thus Algorithm 1 is ε-strong privacy
preserving.
2
Provably refused plans are those that are guaranteed to
be generated by systematic generation of plans.
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
54

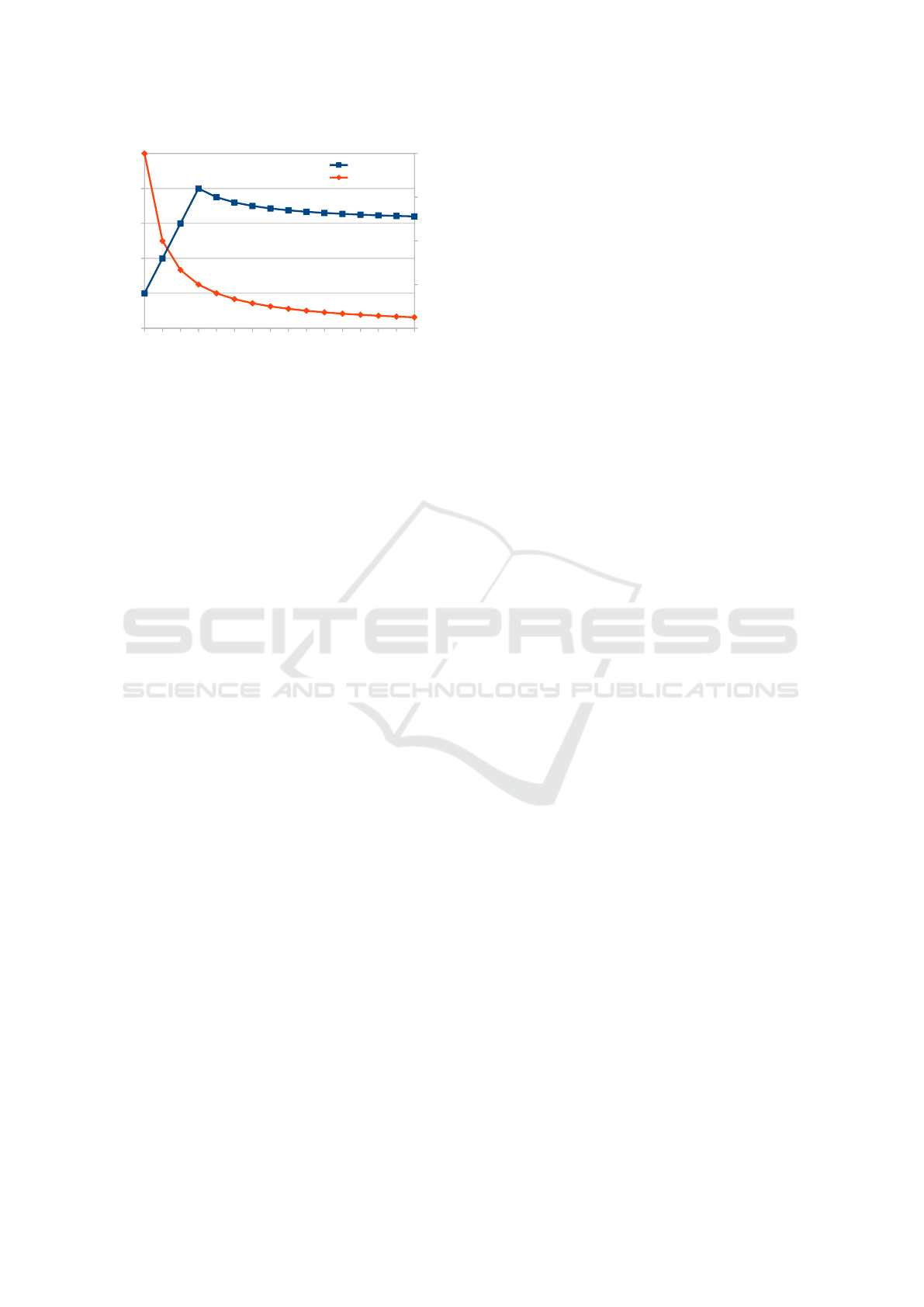
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
0
It(BFS)
It(U)
0=λ(U)
λ(BFS)
Iterations
Leakage
Itera tions
Leakage
k
Figure 1: Trade-off between leaked knowledge λ(BFS/U)
and number of iterations It(BFS/U) required to solve a prob-
lem with different numbers of unsystematically (U) gener-
ated plans inserted between two systematically generated
plans (BFS).
The ε, and consequentially also k, acts as a trade-
off parameter between security and efficiency. If α
2
generates all plans unsystematically, then no knowl-
edge about not yet generated public plans could be
deduced and thus it would imply the strong privacy.
Nevertheless, this would breach the completeness of
the algorithm SecureMAPlanner(), as only the sys-
tematically generated plans ensure complete search
of all possible plans. This trade-off is illustrated by
Figure 1 showing knowledge leakage λ(BFS/U) and
number of iterations It(BFS/U) required to solve a
problem for different values k. We can see, that in
this particular case, this problem is solved by diluted
BFS to up to three unsystematically generated plans
inserted between plans generated by BFS. Then, un-
systematical plan generator finds the solution faster
than BFS, and from this point more unsystematically
generated plans imply both increased efficiency and
reduced knowledge leakage. Obviously, in different
cases, both curves would cross at different k value.
In PSM planner (To
ˇ
zi
ˇ
cka et al., 2015), each agent
stores generated plans in a form of planning state
machines, special version of finite state machines.
(Guanciale et al., 2014) presents an algorithm for se-
cure intersection of finite state machines which can
be used for secure intersection of planning state ma-
chines too.
In the case of different representation of public
plans, more general approach of generic secure com-
putation can be applied (Ben-Or et al., 1988; Yao,
1982; Yao, 1986).
4 EXAMPLE
Let us consider a simple logistics scenario to demon-
strate how private knowledge can leak for k = 0 and
how it decreases with larger k values.
In this scenario, there are two transport vehi-
cles (plane and truck) operating in three loca-
tions (prague, brno, and ostrava). A plane can
travel from prague to brno and back, while a truck
provides connection between brno and ostrava.
The goal is to transport the crown from prague to
ostrava.
This problem can be expressed using MA-
STRIPS as follows. Actions fly(loc
1
,loc
2
) and
drive(loc
1
,loc
2
) describe movement of plane
and truck respectively. Actions load(veh,loc)
and unload(veh,loc) describe loading and unload-
ing of crown by a given vehicle at a given location.
We define two agents Plane and Truck. The
agents are defined by sets of executable actions as fol-
lows.
Plane = {
fly(prague,brno),fly(brno,prague),
load(plane,prague),load(plane,brno),
unload(plane,prague),unload(plane,brno) }
Truck = {
drive(brno,ostrava),drive(ostrava,brno),
load(truck,brno),load(truck,ostrava),
unload(truck,brno),unload(truck,ostrava) }
Aforementioned actions are defined using facts
at(veh,loc) to describe possible vehicle locations,
and facts in(crown,loc) and in(crown,veh) to de-
scribe positions of crown. We omit action ids in ex-
amples when no confusion can arise. For example,
we have the following.
fly(loc
1
,loc
2
) =h
{at(plane,loc
1
)},
{at(plane,loc
2
)},
{at(plane,loc
1
)}i
load(veh,loc) = h
{at(veh,loc),in(crown,loc)},
{in(crown,veh)},
{in(crown,loc)}i
The initial state and the goal are given as follows.
I = { at(plane,prague), at(truck, brno),
in(crown,prague)}
G = { in(crown,ostrava)}
In our running example, the only fact shared by
the two agents is in(crown,brno). As we require
G ⊆ V
pub
we have the following facts classification.
V
pub
= {in(crown,brno),
in(crown,ostrava)}
V
priv
Plane
= {at(plane,prague),at(plane,brno),
in(crown,prague),in(crown,plane)}
θt-Strong Privacy Preserving Multiagent Planner by Computational Tractability
55

load(truck,brno)
B
=
h{in(crown,brno)},
/
0,{in(crown,brno)}i
unload(truck,ostrava)
B
=
h
/
0,{in(crown,ostrava)},
/
0i
All the actions arranging vehicle movements
are internal. Public are only the actions provid-
ing package treatment at public locations (brno,
ostrava). Hence the set O
pub
plane
contains only actions
load(plane,brno) and unload(plane,brno) while
O
pub
Truck
is as follows.
{ load(truck,brno),unload(truck,brno),
load(truck,ostrava),unload(truck,ostrava) }
Agent plane systematically generates possible
plans using BFS and thus it sequentially generates fol-
lowing public plans:
π
plane
1
= h unload(truck, ostrava) i
π
plane
2
= h unload(plane, brno),
unload(truck,ostrava) i
π
plane
3
= h unload(truck, brno),
unload(truck,ostrava) i
π
plane
4
= h unload(plane, brno),
unload(truck,ostrava) i
...
π
plane
i
= h unload(plane, brno), load(truck,brno),
unload(truck,ostrava) i
Note, that actually any locally valid sequence
of action containing action unload(truck,ostrava)
seems to be a valid solution to plane agent. In this
example,π
plane
i
is the first extensible plan generated
by plane and it is generated in i-th iteration of the
algorithm.
Similarly, agent truck sequentially generates fol-
lowing public plans:
π
truck
1
= h unload(plane, brno), load(truck,brno),
unload(truck,ostrava) i
π
truck
2
= hunload(plane,brno), unload(plane,brno),
load(truck,brno), unload(truck,ostrava) i
...
We can see that truck generates an extensible
plan as the first one and plane generated equiva-
lent solution at i-th iteration. Thus, once both agents
agree on a solution, agent plane can try to deduce
something about truck private knowledge. Since all
plans π
plane
1
,... , π
plane
4
are strictly shorter than the ac-
cepted solution π
plane
i
and there were not generated
by truck, that implies that these plans are not ac-
ceptable by truck, i. e. for example φ
⊥
(π
plane
1
) = 0.
More specifically, plane can deduce following about
truck’s private knowledge:
• unload(truck, ostrava) has to contain some
private precondition, otherwise π
plane
1
would be
generated also by truck before π
truck
1
because it
is shorter.
• Private precondition of unload(truck,ostrava)
certainly depends on private fact (possibly indi-
rectly) generated by load(truck,brno), other-
wise π
plane
2
would be generated before π
truck
1
.
In this example, we have shown how systematic
generation of plans can cause private knowledge leak-
age. Let us now consider a case when both agents
add one unsystematically generated plan after each
systematically generated one, i. e. k = 1. For
the simplicity, we will consider previous sequence of
plans, where π
plane
i
is unsystematically generated af-
ter π
plane
3
. In this case, the amount of leaked knowl-
edge is much smaller. plane can still deduce that
φ
⊥
(π
plane
1
) = 0 but cannot deduce the same about
other plans. plane could deduce that truck accepts
no plan of length 2, only once it is sure that all of
them have been systematically generated. But thanks
to the adding of unsystematically generated plans, this
would take twice as long and there is also some proba-
bility that the solution is found using unsystematically
generated plans.
Obviously k = 1 decreases the leaked knowledge
only minimally. To decrease the private knowledge
leakage significantly, k has to grow exponentially with
the length systematically generated solutions as we
showed in proof of Theorem 2.
5 CONCLUSIONS
We have proposed a straightforward application of the
private set intersection (PSI) algorithm to privacy pre-
serving multiagent planning using intersection of sets
of plans. As the plans are generated as extensible to
a global solution provided that all agents agree on a
selection of such local plans, the soundness of the
planning approach is ensured. The intersection pro-
cess can be secure in one iteration by PSI, but some
private knowledge can leak during iterative genera-
tion of the local plans, which is the only practical
way how to solve generally intractable planning prob-
lems. In more iterations, plans which are extensible
by some agents but not extensible by all agents can
leak private information about private dependencies
of actions within the plans. In other words if an agent
says the proposed solution can be from its perspective
used as a solution to the planning problem, but it can-
not be used as a solution by another agent, the first one
learns, that the other one needs to use some private ac-
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
56

tions which obviate usage (extensibility) of the plan
to a global solution. We have shown that this privacy
leakage can be arbitrarily “diluted” by randomly gen-
erated local plans, however never fully averted pro-
vided the completeness of the planning process has to
be ensured.
ACKNOWLEDGEMENTS
This research was supported by the Czech Science
Foundation (no. 15-20433Y).
REFERENCES
Ben-Or, M., Goldwasser, S., and Wigderson, A. (1988).
Completeness theorems for non-cryptographic fault-
tolerant distributed computation. In Proceedings of
the Twentieth Annual ACM Symposium on Theory of
Computing, STOC ’88, pages 1–10, New York, NY,
USA. ACM.
Brafman, R. I. (2015). A privacy preserving algorithm for
multi-agent planning and search. In Yang, Q. and
Wooldridge, M., editors, Proceedings of the Twenty-
Fourth International Joint Conference on Artificial In-
telligence, IJCAI 2015, Buenos Aires, Argentina, July
25-31, 2015, pages 1530–1536. AAAI Press.
Brafman, R. I. and Domshlak, C. (2008). From one to
many: Planning for loosely coupled multi-agent sys-
tems. In Procs. of the ICAPS’08, pages 28–35.
Diffie, W. and Hellman, M. (1976). New directions in cryp-
tography. IEEE Trans. Inf. Theor., 22(6):644–654.
Guanciale, R., Gurov, D., and Laud, P. (2014). Private inter-
section of regular languages. In Miri, A., Hengartner,
U., Huang, N., Jøsang, A., and Garc
´
ıa-Alfaro, J., ed-
itors, 2014 Twelfth Annual International Conference
on Privacy, Security and Trust, Toronto, ON, Canada,
July 23-24, 2014, pages 112–120. IEEE.
Jarecki, S. and Liu, X. (2010). Fast secure computation
of set intersection. In Garay, J. A. and Prisco, R. D.,
editors, Security and Cryptography for Networks, 7th
International Conference, SCN 2010, Amalfi, Italy,
September 13-15, 2010. Proceedings, volume 6280 of
Lecture Notes in Computer Science, pages 418–435.
Springer.
Maliah, S., Shani, G., and Brafman, R. (2016a). Online
macro generation for privacy preserving planning. In
Proceedings of the 26th International Conference on
Automated Planning and Scheduling, ICAPS’16.
Maliah, S., Shani, G., and Stern, R. (2016b). Collaborative
privacy preserving multi-agent planning. Procs. of the
AAMAS’16, pages 1–38.
Nissim, R. and Brafman, R. I. (2014). Distributed heuris-
tic forward search for multi-agent planning. JAIR,
51:293–332.
Pinkas, B., Schneider, T., Segev, G., and Zohner, M. (2015).
Phasing: Private set intersection using permutation-
based hashing. In 24th USENIX Security Symposium
(USENIX Security 15), pages 515–530, Washington,
D.C. USENIX Association.
Stolba, M., Tozicka, J., and Komenda, A. (2016). Secure
multi-agent planning algorithms. In ECAI 2016, pages
1714–1715.
Torre
˜
no, A., Onaindia, E., and Sapena, O. (2014). FMAP:
distributed cooperative multi-agent planning. AI,
41(2):606–626.
To
ˇ
zi
ˇ
cka, J., Jakub
˚
uv, J., Komenda, A., and P
ˇ
echou
ˇ
cek,
M. (2015). Privacy-concerned multiagent planning.
KAIS, pages 1–38.
Van Der Krogt, R. (2009). Quantifying privacy in mul-
tiagent planning. Multiagent and Grid Systems,
5(4):451–469.
Yao, A. C. (1982). Protocols for secure computations. In
Proceedings of the 23rd Annual Symposium on Foun-
dations of Computer Science, SFCS ’82, pages 160–
164, Washington, DC, USA. IEEE Computer Society.
Yao, A. C.-C. (1986). How to generate and exchange se-
crets. In Proceedings of the 27th Annual Sympo-
sium on Foundations of Computer Science, SFCS ’86,
pages 162–167, Washington, DC, USA. IEEE Com-
puter Society.
θt-Strong Privacy Preserving Multiagent Planner by Computational Tractability
57