Access Controlled Temporal Networks

Carlo Combi

, Roberto Posenato

, Luca Vigan

and Matteo Zavatteri

Department of Computer Science, University of Verona, Verona, Italy

Department of Informatics, King’s College London, London, U.K.

Keywords:

Access Control, Temporal Networks, Temporal Authorization, Dynamic Controllability, UPPAAL-TIGA.

Abstract:

We deﬁne Access-Controlled Temporal Networks (ACTNs) as an extension of Conditional Simple Temporal

Networks with Uncertainty (CSTNUs). CSTNUs are able to handle features such as contingent durations and

conditional constraints, and have thus been used to model the temporal constraints of workﬂows underlying

business processes. However, CSTNUs are unable to model users and authorization constraints, and thus can-

not model “who can do what, when”. ACTNs solve this problem by adding users and authorization constraints

that must be considered together with temporal constraints. Dynamic controllability (DC) of ACTNs ensures

the existence of an execution strategy, able to assign tasks to authorized users dynamically, satisfying all the

relevant authorization constraints no matter what contingent durations turn out to be or what conditional con-

straints have to be considered. We show that the DC checking can be done via Timed Game Automata and

provide experimental results using UPPAAL-TIGA on a concrete real-world case study.

1 INTRODUCTION

Context and Motivation. Workﬂow technology has

emerged as one of the leading technologies for mod-

eling, (re)designing, and executing business processes

in several different application domains. For instance,

workﬂows have been used to model processes for

industrial R&D, manufacturing, energy distribution,

banking processes, critical infrastructures and health-

care (Lenz and Reichert, 2007; Combi et al., 2014a).

The formal modeling of workﬂows has been in-

vestigated in quite some detail and, depending on

the characteristics the designers want to focus on,

different formal models have been employed to ver-

ify interesting properties of workﬂow instances. Re-

cent research has in particular investigated the model-

ing of temporal workﬂows by means of Conditional

Simple Temporal Networks with Uncertainty (CST-

NUs, (Combi et al., 2014a; Hunsberger et al., 2012)),

which can handle temporal plans subject to both con-

ditional constraints and contingencies simultaneously.

Time points (modeling the occurrence of the

events upon their “execution”) and constraints be-

tween pairs of time points are labeled by a conjunc-

tion of propositions saying when they must be consid-

ered. Each proposition is associated to an observation

time point, a special type of time point that assigns ei-

ther true or false to the proposition upon its execution.

Instead, a contingent duration between two time

points A and C represents a range (i.e., a real interval)

of allowed durations between A and C that cannot be

ﬁxed by the executing agent (i.e., the controller). A is

the activation time point and it is under the control of

this agent, whereas C is the contingent time point, and

it is not. That is, whatever the duration turns out to

be, the time instant in which the uncontrollable event

modeled by the contingent link ends (i.e., C executes)

is only observed in real time.

CSTNUs can handle temporal plans subject to

both conditional constraints and contingencies. In a

CSTNU, the truth values of propositions and the con-

tingent durations are observed in real time as the net-

work executes. That is, before executing the network,

we do not know what constraints and time points will

be considered nor how long the contingent durations

will last. Hence, to deal with both contingent dura-

tions and truth value assignments, which are uncon-

trollable, the assignment of a task to a user must be

done in real time as different behaviors of such un-

controllable parts might (and most of the time do) en-

tail different assignments. If we pre-computed such

an assignment before starting, we would risk violat-

ing some constraint. The analysis must thus be boiled

down to controllability and not to mere consistency in

which scheduling tasks and deciding which users will

carry them out before the start of the execution would

be sufﬁcient.

For these reasons, the “temporal networks” com-

118

Combi C., Posenato R., ViganÃš L. and Zavatteri M.

Access Controlled Temporal Networks.

DOI: 10.5220/0006185701180131

In Proceedings of the 9th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2017), pages 118-131

ISBN: 978-989-758-220-2

munity has devoted considerable interest to the anal-

ysis of dynamic controllability (DC): a CSTNU is

dynamically controllable if there exists an execution

strategy that executes all the parts under control of the

network by making decisions in real time depending

on how the uncontrollable parts behave. The aim of

this strategy is that of eventually satisfying all rele-

vant constraints. DC analysis is done by either dedi-

cated network-based algorithms (Combi et al., 2013;

Combi et al., 2014b) or translation to Timed Game

Automata (TGAs) (Cimatti et al., 2016).

However, CSTNUs fail to model access-

controlled workﬂows as they do not deal with

users and authorization constraints. To address this

problem, CSTNUs need to be extended by ﬁrst

injecting users and authorization constraints and then

adapting the DC checking to answer to the workﬂow

satisﬁability problem (WSP). WSP is the problem

of ﬁnding an assignment of tasks to users so that

the execution gets to the end without violating any

authorization constraint (Wang and Li, 2010). In a

temporal context we must also say when such an

assignment takes place.

Such an extension allows one to deal with situ-

ations in which users, authorization constraints and

temporal constraints must be considered all together

and not as disjoint at all. In fact, workﬂows and access

control have traditionally been approached as orthog-

onal, independent formalisms, but there are a large

number of relevant cases in which they cannot be con-

sidered so. For example, a surgeon, who has just car-

ried out a 4-hour intervention, is allowed to do another

one only after resting from 2 to 4 hours. Likewise, a

truck driver must rest for at least 45 minutes after a

driving shift of 4.5 hours. These temporal constraints

must be considered in conjunction with access control

as there is a mutual inﬂuence.

Contributions. Our contributions are three-fold.

First, we deﬁne Access-Controlled Temporal Net-

works (ACTNs) as an extension of CSTNUs by the

injection of users and authorization constraints, mo-

tivated by the need of handling workﬂows subject to

both temporal constraints and access control simul-

taneously. Each authorization constraint expresses a

temporal range, a label modeling the conditional part,

and an authorization policy expressing which the au-

thorized users are.

Second, we extend the encoding for CSTNUs into

TGAs and use sound and complete reachability al-

gorithms provided for TGAs by the UPPAAL-TIGA

software (Behrmann et al., 2007) to check whether an

ACTN is DC. The encoding we deﬁne is fully auto-

mated and generates the TGA in polynomial time.

Third, we discuss our approach by means of a con-

PatEv

[5,25]

EmergencyDoctor

SurInt

[60,210]

Surgeon

ICUStayM

[2,4]

Surgeon

FibTh

[60,65]

Cardiologist

ThAst

[2,10]

Cardiologist

LTTh

[5,10]

Cardiologist

[1,3]

urgent

(intervention)

[1,5]

[3 + ε,6]

[1,3] :6=

[2 + ε,5]

[1,2] :=

¬urgent

(therapy)

[1,5]

[1,6]

[1,3]

S[0, 30]S

S[0, ∞]S :6=

S[0, ∞]S :6= ∧¬Relatives

Figure 1: Ofﬁcial STEMI guidelines (excerpt). We model

TSoD as [1, 3] :6=, TBoD as [1,2] :=. Ranges [x, y] and

[x + ε, y] model all durations t s.t. x ≤ t ≤ y and x < t ≤ y,

respectively.

crete, real-world case study from the e-health domain

implemented in UPPAAL-TIGA.

Organization. § 2 introduces our case study. § 3 re-

views essential background on CSTNUs and the en-

coding into TGAs. § 4 deﬁnes ACTNs along with

their execution semantics. § 5 extends the encoding

into TGAs given for CSTNUs. § 6 discusses related

work. § 7 sums up and discusses future work.

2 THE STEMI GUIDELINES

As a simple but real-world (thus fully realistic)

case study, we consider a simpliﬁcation of the ofﬁ-

cial guidelines for the treatment of STEMI patients

(i.e., patients with ST-Elevation Myocardial Infarc-

tion), published by the American College of Cardiol-

ogy/American Heart Association (see the discussion

in (Combi et al., 2014a)). As we discuss below, none

of the previous works can handle such a “simple” ex-

ample as they are not expressive (or formal) enough.

Fig. 1 shows the workﬂow; task durations, delays

and temporal ranges are in minutes. The workﬂow

starts with a patient evaluation (PatEv), in which an

EmergencyDoctor establishes if the patient is in need

of immediate medical attention. If the patient is ur-

gent, a surgery intervention (SurInt) takes place. As

soon as the intervention has ﬁnished, a Surgeon has

to manage the patient’s stay in the Intensive Care Unit

(ICUStayM). This task lasts at least 2 minutes and at

most 4. In addition, following the Temporal Sepa-

ration of Duties (TSoD) policy, whenever ICUStayM

starts within 3 minutes since the end of SurInt, the

Surgeons executing the two tasks must be differ-

ent. TSoD does not apply if this temporal distance

is greater than 3.

If the patient is not urgent, a ﬁbrinolytic ther-

apy (FibTh) takes place. This task lasts at least 60

and at most 65 minutes, and according to the guide-

Access Controlled Temporal Networks

119

[]

[u]

[¬u]

[5,25] [1,3],  [1,5],u [60,210]

[1,5], ¬u

[60,65][0,30], ¬u

Figure 2: CSTNU modeling a portion of the workﬂow given

in Fig. 1. (A

,5, 25,C

) models PatEv, (A

,60, 210,C

)

models SurInt and (A

,60, 65,C

) models FibTh. U?

models the conditional split.

lines, it has to start within 30 minutes since PatEv

has started. After FibTh has terminated, a therapy

assessment (ThAst) starts with minimal and maximal

allowed durations 2 and 10 minutes, respectively. Fol-

lowing the Temporal Binding Of Duties (TBoD) pol-

icy, if the start of ThAst is within 2 minutes since the

end of FibTh, then the same Cardiologist must ex-

ecute the two tasks. TBoD does not apply if this tem-

poral distance is greater than 2 minutes.

Regardless of the chosen branch, after the last task

in that branch has ﬁnished, a long term therapy assess-

ment (LTTh) starts. The minimal and maximal dura-

tions for this task are 5 and 10 minutes, respectively.

A security policy requires that the Cardiologist ex-

ecuting LTTh must be (i) different from and not a rel-

ative of the one who executed PatEv, and different

from the one who executed ThAst if the patient was

not urgent.

We will consider a role-based access control en-

vironment in which EmergencyDoctor contains users

John and Lara, Surgeon contains Bob, Tom and Sara,

and Cardiologist contains Lara, Kate and Rick.

3 CSTNUs

In this section, we provide background on CSTNUs

that will be essential to understand our ACTNs.

Given a set P of propositional letters, a label  is

any (possibly empty) conjunction of literals, where a

literal is either a propositional letter p ∈ P or its nega-

tion ¬p. The empty label is denoted by . The label

universe of P , denoted by P

∗

, is the set of all pos-

sible labels representing all possible (ﬁnite) conjunc-

tions of literals we can obtain from P e.g., the label

universe of P = {p, q} is P

∗

= {, p,q, ¬p, ¬q, p ∧

q, p ∧ ¬q, ¬p ∧ q, ¬p ∧ ¬q}. Two labels 

,

∈ P

∗

are consistent if and only if their conjunction 

∧ 

is satisﬁable and a label 

entails a label 

(written



⇒ 

) iff all literals in 

appear in 

too (i.e., if 

is more speciﬁc than 

). Any label  ∈ P

∗

entails both

itself (i.e.,  ⇒ ) and the empty label (i.e.,  ⇒ ).

Deﬁnition 1. A Conditional Simple Temporal Net-

work with Uncertainty (CSTNU, (Hunsberger et al.,

2012)) is a tuple hT , C , L,OT , O, P ,C T ,Li, where:

(1) T is a ﬁnite set of time points.

(2) P is a ﬁnite set of propositional letters.

(3) L : T → P

∗

is a function assigning a label to each

time point in T saying in what scenarios the time

point must be considered.

(4) OT ⊆ T is a set of observation time points, where

each P? ∈ OT is associated to a proposition p,

whose truth value is unknown before P? executes.

(5) O : P → OT is a bijection associating a unique

observation time point to each propositional letter.

(6) CT ⊂ T is a set of contingent time points such

that OT ∩ CT =

(7) L is a set of contingent links each one having

the form (A, x,y,C), where A ∈ T and C ∈ CT

are different time points (written A 6≡ C), x, y ∈ R

(0 < x < y < ∞), and L(A) = L(C). Once A is ex-

ecuted, C is only observed to occur (as it is out of

control). However, C is guaranteed to occur such

that C − A ∈ [x, y]. For any pair (A

) ∈ L, C

6≡ C

(8) C is a set of labeled constraints each one having

the form (Y − X ≤ k, ), where X,Y ∈ T , k ∈ R

and  ∈ P

∗

. Many labeled constraints between

two time points X and Y can be speciﬁed, pro-

vided that their labels are different.

(9)  ⇒ L(Y )∧L(X) for each (Y −X ≤ k,) ∈ C (con-

straint label coherence), and  ⇒ L(O(p)) for

each p or ¬p appearing in  (constraint label hon-

esty) (Hunsberger et al., 2015).

(10) For each X ∈ T , if p or ¬p appears in X ’s la-

bel, then L(X ) ⇒ L(O(p)), and (O(p) − X ≤

−ε,L(X)) ∈ C for some ε > 0 (time point label

honesty) (Hunsberger et al., 2015).

We represent a CSTNU as a directed multi-graph

where the set of nodes coincides with the set of time

points, whereas the set of edges is partitioned in re-

quirement and contingent links. We draw a require-

ment link

as X

[x,y],

−−−→ Y meaning that once X exe-

cutes, Y must execute such that Y − X ∈ [x,y] if 

holds. We draw a contingent link (A, x, y,C) ∈ L

as A

[x,y]

==⇒ C, where the label [x,y] implicitly means

[x, y],  with  = L(A) = L(C).

Fig. 2 shows an example of a CSTNU modeling a

portion of the workﬂow in Fig. 1 without access con-

trol. We mapped PatEv into (A

,5,25,C

), SurInt

into (A

,60,210,C

), FibTh into (A

,60,65,C

), and

the conditional split connector (diamond) into the ob-

servation time point U?. Once executed, U? sets

[x,y],

−−−→ Y models (Y − X ≤ y, ), (X −Y ≤ −x, ) ∈ C.

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

120

the value of the proposition u and, thus, some con-

straints could be disabled (those having label incon-

sistent with u). We point out it is possible to decide

when to execute U? but not the truth value for u.

DC has been recently investigated by using TGAs,

allowing one to work with sound and complete al-

gorithms, and to synthesize memoryless execution

strategies (Cimatti et al., 2016). In particular, DC

is modeled as a game between two players: the con-

troller ctrl executing all non-contingent time points

and the environment env executing the contingent

ones and assigning truth values to propositions. The

purpose of ctrl is to get to the goal location reach-

able as soon as all time points have been executed and

all constraints have been satisﬁed with respect to the

speciﬁc scenario, whereas that of the env is to prevent

ctrl from getting there. If env wins, the network is

not DC, otherwise it is.

Deﬁnition 2. A Timed Automaton (TA) consists of a

ﬁnite set of locations Loc (with l

the initial one), a ﬁ-

nite set of actions Act, a ﬁnite set of real-value clocks

X , a transition relation →⊆ Loc×H (X )×Act×2

Loc, where elements in H (X ) are conjunctions of

clock constraints of the form x  k or y − x  k with

x, y ∈ X , k ∈ Z and ∈ {<, ≤, =, >, ≥}, and a func-

tion Inv : Loc → H (X ) assigning an invariant (i.e., a

conjunction of clock constraints) to each location.

A Timed Game Automaton (TGA) extends a TA by

partitioning the set of transitions in controllable and

uncontrollable transitions.

In any run, all clocks start at zero and evolve uni-

formly. Each transition has the form (l

;G; N; R; l

where l

is the start location, G is a guard made of a

conjunction of atomic constraints x  y over clocks, N

is the name of the transition, R is a (possibly empty)

set of clocks to reset (the update part) and l

is the

end location. A location is urgent when the automa-

ton must not remain in the location.

Encoding CSTNUs into TGAs. In what follows, we

provide the encoding given in (Cimatti et al., 2016)

from a CSTNU into an equivalent TGA. Since we

use UPPAAL-TIGA for checking the resulting TGA,

we use integer and Boolean variables to improve efﬁ-

ciency and readability.

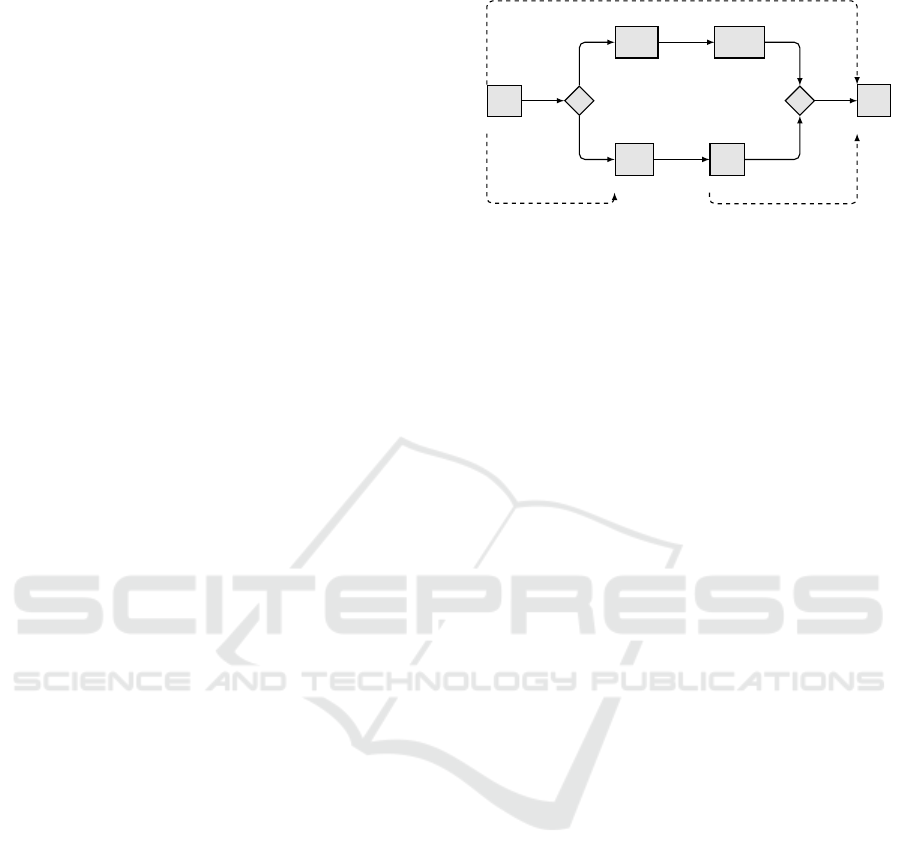
Assume that G in Fig. 3 is the TGA equivalent to

the CSTNU S in Fig. 2. The core of G consists of

three locations:

• ctrl (urgent) modeling the execution of the non

contingent time points,

• env (initial) modeling the occurrence of contin-

gent time points and truth value assignments, and

• goal, which, if reached, implies DC of S.

Differently from the traditional use of TGAs where

env is associated with uncontrollable transitions, here

env is assigned with controllable transitions, whereas

ctrl is assigned with uncontrollable ones. This is

necessary to model the fact that in any CSTNU env

must be able to react instantaneously upon the execu-

tion of a control time point (Cimatti et al., 2016).

We model the interplay of the game between ctrl

and env by means of a clock c

and two transitions,

• (ctrl;>;pass; c

:= 0;env), and

• (env;c

> 0;gain;

0;ctrl)

The ﬁrst transition guarantees that, after an action

of the agent, the environment can react immediately.

The second one guarantees that the agent can react

to an environment action only after a positive delay.

Each control time point X is associated to a clock cX

and a Boolean variable xX (initially set to ⊥). We

model the execution of X as an uncontrollable self-

loop transition

• (ctrl;¬xX; ExX; xX := >, cX := 0; ctrl).

Fig. 3 contains 4 transitions shortened as τ

, τ

modeling the execution A

,U?, A

of Fig. 2.

Clock ˆc represents the global time and it is never

reset. ¬xX (equivalently, cX = ˆc) means that X has not

been executed yet, whereas xX (equivalently, cX < ˆc)

means that X has been executed. Since cX will be

never reset again and clocks never stop, the differ-

ence ˆc−cX represents the execution time instant of X,

when greater than 0, as the run starts at env and gets

to ctrl only after a positive amount of time (gain

transition, c

> 0).

Each propositional letter p associated to an ob-

servation control time point P? has an associated

bounded integer variable p whose value is 0 before

P? executes (i.e., for p unknown), −1 if p is assigned

⊥, and 1 if p is assigned >. To manage the truth value

assignment to p, we have two controllable transitions

• (env;xP?∧p = 0;pTrue; p := 1,c

:= 0; env), and

• (env;xP? ∧ p = 0; pFalse;p := −1, c

:= 0;env)

setting p = 1 and p = −1, respectively. A third un-

controllable transition

• (env;xP? ∧ p = 0 ∧ c

> 0;fail

;

0;goal)

allows ctrl to win the game (i.e., to get to goal) if

env fails or refuses to assign p a value immediately

after P? has been executed. In Fig. 3, we have exactly

3 transitions for u (the unique proposition appearing

in the CSTNU in Fig. 2) shortened as τ

⊥

, τ

(truth

value assignment), and φ

(fail transition).

For each contingent link (A,x, y,C) ∈ L, env has

a controllable self-loop transition

• (env;xA ∧ ¬xC ∧ cA ≥ x ∧ cA ≤ y; ExC; xC :=

>,cC := 0, c

:= 0;env)

to execute C, and ctrl has an uncontrollable one

Access Controlled Temporal Networks

121

• (ctrl;xA ∧ ¬xC ∧cA > y; fail

;

0;goal)

to win the game if env fails or refuses to schedule C

such that C − A ∈ [x, y]. The ﬁrst transition states that

the activation point has been executed (xA), C has not

been yet executed (¬xC) and it is still within the al-

lowed bounds x and y, since cA, representing the time

since the execution of A, is greater-or-equal than x and

lower-or-equal than y. Fail transitions (for any uncer-

tain part) are necessary, otherwise env would always

be able to prevent ctrl from winning the game just

“waiting forever” in its own location. In Fig. 3, we

have 6 transitions shortened as τ

, τ

(contin-

gent point executions), and φ

, φ

(fail).

We model winning conditions as a winning path of

n+1 urgent locations L



→ L



→ · · · → L



(= goal)

going from env to goal, where n is the number of

distinct labels appearing in S. The ﬁrst location in

this path is always L



, reachable as soon as all “un-

labeled” time points have been executed satisfying all

related constraints. Then, the remaining locations are

sequentially connected through sets of transitions.

Each set of transitions between two consecutive

locations represents two cases: (i) the ﬁrst location is

not associated to the current scenario and a transition

allows one to move to the next location, or (ii) the

ﬁrst location is associated to the current scenario and

a transition allows one to move to the next location

only if all the constraints labeled by the label the next

location represents are satisﬁed.

For example, consider the set of transitions going

from L

to goal (i.e., L

¬u

) in Fig. 3. The related con-

ditional constraint to generate this set is: “in the sce-

nario in which U? has been executed and u has been

assigned ⊥, all time points labeled by ¬u must be ex-

ecuted and all constraints labeled by ¬u must be sat-

isﬁed”. This condition is expressed by: (xU? ∧ u =

−1) ⇒ G

¬u

, where G

¬u

def

= xA

∧ xC

∧ cU? − cA

≤

5 ∧ cA

− cU? ≤ −1 ∧ cA

− cA

≤ 30 ∧ cA

− cA

≤

Since TGAs do not allow disjunction nor negation

(of clock constraints) in the guards, we rewrite the

condition as ¬(xU? ∧ u = −1)∨ G

¬u

, which simpliﬁes

to ¬xU? ∨ u = 1 ∨ G

¬u

, and we generate a transition

for each disjunct (Fig. 3, sat

¬u

, skip

¬u

, skip

¬u

). We

proceed similarly to connect L



to L

DC checking is done by model checking the

resulting TGA and seeking a control strategy

for env to win the game. In UPPAAL-TIGA,

this goal is formalized as control: A[] not

tga.goal. If UPPAAL-TIGA answers Property

is NOT satisfied, then the network is DC and a

For each Y − X ≤ k ∈ C, the corresponding guard is

( ˆc − cY) − (ˆc − cX) ≤ k, which simpliﬁes in cX − cY ≤ k as

∀X ∈ T ,( ˆc − cX) is the time in which X was executed.

ctrl

env



goal

¬u

)

h>;pass; c

:= 0i

> 0;gain;

⊥



,sat



hu = −1; skip

;

h!xU?;skip

;

;sat

;

hu = 1; skip

¬u

;

h!xU?;skip

¬u

;

¬u

;sat

¬u

;

Figure 3: TGA equivalent to the CSTNU in Fig. 2.

counter-strategy for ctrl can be printed out.

4 ACTNs

An ACTN extends a CSTNU by adding a set of users

U and turning C into a set of sets each one contain-

ing (possibly several disjunctive) authorization con-

straints. Users are in charge of executing time points,

whereas authorization constraints say which users are

authorized to execute the time points they connect.

Before giving the formal deﬁnition, we introduce a

few useful notions.

A relation over users is denoted by ρ ⊆ U × U,

with the neutral relation ∗

def

= U × U

def

= {(u

) |

∈ U ∧ u

∈ U} and the complement of ρ denoted

by ¬ρ. If (u

) ∈ ρ, then we say that the pair satis-

ﬁes the relation.

Given a ﬁnite set R = {ρ

,. . . , ρ

} of relations, an

authorization policy α is any conjunction of relations

drawn from R , each one appearing as ρ or ¬ρ if dif-

ferent from ∗. If a relation appears as ρ (respectively,

¬ρ), then we say that ρ is positive (respectively, neg-

ative). The neutral authorization policy, i.e., that con-

sisting of ∗ only, is denoted by ~. A pair (u

)

satisﬁes an authorization policy α iff (u

) satis-

ﬁes each ρ ∈ α and does not satisfy each ρ such that

¬ρ ∈ α. An authorization policy α

entails another

authorization policy α

(written α

⇒ α

) iff α

con-

tains all the relations appearing in α

. Two autho-

rization policies α

and α

are consistent if α

∧ α

is satisﬁable, and equivalent if both α

entails α

and

entails α

(i.e., α

⇒ α

and α

⇒ α

For example, suppose that U = {John, Lara, Tom,

Bob, Sara, Rick, Kate} and R = {∗, 6=, Relatives},

with 6=

def

= {(u

) | u

∈ U ∧ u

6= u

} and

Relatives

def

= {(John, Kate), (Kate, John)}. Consider

the policy α

def

= 6= ∧¬Relatives given in Fig. 1 be-

tween PatEv and LTTh saying that the physician giv-

ing the patient the long term therapy must be different

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

122

and not a relative of the physician who did the initial

evaluation. If John carries out the initial PatEv, then

Lara can execute LTTh as (John, Lara) satisﬁes α.

Deﬁnition 3. An Access-Controlled Temporal Net-

work (ACTN) is a tuple hT ,U, UA,C , R ,L, OT , O,P ,

CT , Li, where:

• T , L, OT , O, P , CT ,L are the same as for a

CSTNU along with all assumptions on contingent

links (A,x, y,C).

• U is a non-empty ﬁnite set of users.

• UA ⊆ U × T is the authorization relation.

A(X) = {u | (u,X) ∈ UA} is the set of users au-

thorized for X.

• R is a ﬁnite set of relations ρ ⊆ U × U.

• C is a set of sets such that each set C

∈ C

consists of a (possibly many) authorization con-

straints of the form (x ≤ Y − X ≤ y,  : α)

where

x, y ∈ R ∪ ±∞, Y, X ∈ T ,  ∈ P

∗

, α is an autho-

rization policy.

•  = L(X) ∧ L(Y ) for each (x ≤ Y − X ≤ y, :

α) ∈ C

, and , L(X),L(Y ) entail L(P?) for each

p,¬p ∈ , L(X), L(Y ).

• For each pair (x

≤ Y −X ≤ y

,

: α

),(x

≤ Y −

X ≤ y

,

: α

) belonging to the same set C

, if

] = [x

], then α

6= α

(note that 

= 

• For each (A,x, y,C) ∈ L, we have that A is non-

contingent (i.e., A 6∈ CT ), and A(A) = A(C).

• For each (A

),(A

) ∈ L, we

have that A

6≡ A

and C

6≡ C

The ACTN-graph extends the CSTNU-graph by

labeling requirement links X → Y by (possibly many)

labels of the form [x, y],  : α each one corresponding

to the authorization constraint (x ≤ Y −X ≤ y, : α) ∈

. Fig. 4 gives an example of an ACTN that mod-

els the workﬂow in Fig. 1 considering access con-

trol. Again, we map PatEv to (A

,5,25,C

) and its

authorized users are A(A

) = A(C

) = {John, Lara}

who belong to the role EmergencyDoctor. We

map SurInt and ICUStayM to (A

,60,210,C

) and

,2,4,C

), respectively, and their authorized users

are A(A

) = A(C

) = A(A

) = A(C

) = {Bob, Sara,

Tom}, who belong to the role Surgeon. We

map FibTh, ThAst, and LTTh to (A

,60,65,C

,2,10,C

), and (A

,5,10,C

), respectively, and

their authorized users are A(A

) = A(C

) = A(A

) =

A(C

) = A(A

) = A(C

) = {Lara, Kate, Rick}, who

belong to the role Cardiologist (note that Lara is a

specialist in two medical ﬁelds, so she belongs to two

roles).

(x ≤ Y − X ≤ y, : α) shortens (Y − X ≤ y,  : α) and

(X −Y ≤ −x, : α). We assume C

= C

We model the conditional split and join connec-

tors (shaded diamonds) by means of U ? and E, and

we connect all the components by means of autho-

rization constraints, which also impose relative con-

straints among two non-sequential tasks specifying

authorization policies. For example, we model the

TSoD between tasks SurInt and ICUStayM by means

of the authorization constraint C

[1,3],u:6=

−−−−−→ A

. It says

that once C

has been executed (i.e., SurInt has been

completed), say by Bob at time t = 90 , then either Tom

or Sara can execute A

(i.e., start ICUStayM) from

time 91 to 96. The second authorization constraint

[3+ε,6],u:~

−−−−−−→ A

ensures that TSoD does not apply

otherwise allowing all users to execute A

from time

93 + ε to 96 (we use ε to make sure that no overlap

exists between [1,3] and [3 + ε, 6]).

Execution Semantics. We give the execution seman-

tics of ACTNs in terms of real-time execution deci-

sions (RTEDs). Intuitively, an RTED is a decision

to commit some users(s) to executing a set of time

points, or a decision to wait for something to happen

or an instantaneous reaction.

In what follows, we adapt the RTEDs for CSTNUs

given in (Cimatti et al., 2016) by also renaming a few

symbols and adding details for explanatory purposes.

For an ACTN, the controller (ctrl) seeks a strategy

for committing available users to executing all rele-

vant control time points (i.e., the part under control)

such that all relevant constraints in C will eventually

be satisﬁed no matter what durations the environment

(env) chooses for contingent links and truth values

for propositions. Thus, RTEDs exist for both ctrl

and env. We study the interplay between these two

RTEDs in terms of partial and full outcomes, which

determine how the state of the whole system evolves.

In this paper, we assume that each contingent link

(A,x, y,C) is (i) tied to one range [x, y] only, and (ii)

executed by one user only who, once he has executed

A, remains blocked until the execution of C. We leave

as future work the generalization of the approach to

handling situations in which users are given less (or

more) time for the same task.

The set of all available users is Avail ⊆ U, so that

u ∈ Avail means that u is available and busy otherwise.

The initial state is Avail = U meaning that all users

are available. Blocking users guarantees us that the

same user can be committed for more than one task

in a parallel block ensuring this user will be always

executing one task at a time.

Deﬁnition 4. A partial schedule for an ACTN is a

pair P S = (OccTP, KnownProp), where OccTP is a

set of triples (u, X , k) meaning that user u executed

time point X at time k, and KnownProp is a set of pairs

Access Controlled Temporal Networks

123

(p, b) meaning that p has been assigned b ∈ {>, ⊥}.

We represent the current partial scenario (i.e., the

scenario being generated upon the execution of the

observation time points) by means of the label 

cps

consisting of the conjunction of the already known

literals (i.e., 

cps

= {p | (p, >) ∈ KnownProp}∪ {¬q |

(q,⊥) ∈ KnownProp}).

Executed(OccTP) = {X | (u, X , k) ∈ OccTP} is

the set of executed time points and Instants(OccTP) =

{k | (u, X, k) ∈ OccTP} is the set of time instants in

which the time points in Executed(OccTP) were exe-

cuted. For each X ∈ Executed(OccTP), we represent

the time instant k in which X was executed as time(X)

and the user who executed it as user(X ).

We represent the time instant of the

last executed time point as last(OccTP) =

max{v | v ∈ Instants(OccTP)}; if OccTP =

then last(OccTP) = −∞.

P S is called respectful if all (u, X , k) ∈ OccTP sat-

isfy the constraints in C . The set of all possible partial

schedules is represented by P S

∗

Deﬁnition 5. An RTED for ctrl has two forms:

wait or (t, ControlTP).

• ∆

ctrl

= wait is applicable only if a contingent

time point has been activated (i.e., the activation

time point A has been executed but the related

contingent C has not).

• ∆

ctrl

= (t, ControlTP) represents the conditional

constraints “if env does nothing before time t,

then for each pair (u, X ) ∈ ControlTP, commit

the user u to execute the time point X at time t”.

Such an RTED is applicable iff t > last(OccTP),

ControlTP is a non empty set of pairs of avail-

able users and unexecuted time points. That is, for

each (u, X ) ∈ ControlTP, X 6∈ Executed(OccTP)

and u ∈ Avail. Finally, for each (u

),(u

) ∈

ControlTP, if X

and X

are (different) activation

points, then u

6= u

. If X

is an activation point

and X

is not, then we execute X

ﬁrst. This is

because activation points block users.

An RTED for the environment env (in symbols,

∆

env

) has two forms: wait or (t,ContingentTP).

• ∆

env

= wait is applicable only if no contingent

point C has been activated.

• ∆

env

= (t, ContingentTP) represents the condi-

tional constraints “if ctrl does nothing before

or at time t, then execute the time points in

ContingentTP at time t”. Such a decision is ap-

plicable iff t > last(OccTP), ContingentTP is a

non empty subset of unexecuted contingent points

whose ranges of allowed durations contain t.

The sets of all RTEDs for ctrl and env are rep-

resented by ∆

∗

ctrl

and ∆

∗

env

, respectively.

In other words, ∆

ctrl

deals with the parts under

control: users and non-contingent time points. ∆

env

deals with the parts out of control: contingent time

points and truth value assignments.

Deﬁnition 6. Let PS = (OccTP,KnownProp) be a

partial schedule in which at least one contingent time

point C has been activated and is allowed to be exe-

cuted at last(OccTP). An instantaneous reaction IR

is a decision

(1) to execute a set I

of such time points at time

last(OccTP), or

(2) to assign truth values for each proposition associ-

ated to the observation time points in OccTP that

has not been assigned yet (we model such an as-

signment as a set I

of pairs (p, b) with p ∈ P and

b ∈ {>, ⊥}), or

(3) to do both actions.

We represent an I R as a pair (I

). The set of all

instantaneous reactions is represented by IR

∗

If last(OccTP) happens to be the last possible time

at which a currently-activated contingent time point C

can execute, then the instantaneous reaction must in-

clude C. Similarly, if t is the time in which an obser-

vation time point P? was executed, the instantaneous

reaction must include a truth value assignment for p.

Of course, env can carry out more than one I R .

We now deﬁne how ∆

ctrl

and ∆

env

are handled. Since

both players can either wait or conditionally commit

to executing a set of time points, we have four pos-

sible cases (we point out that a wait decision is not

applicable for both ctrl and env simultaneously).

Deﬁnition 7. We model the partial outcome of ∆

ctrl

and ∆

env

as O

(OccTP,∆

ctrl

,∆

env

) neglecting any

I R . We have four possible cases.

(1) O

(OccTP,wait,(t, ContingentTP)) = OccTP ∪

{(user(A),C,t) | C ∈ ContingentTP} and for each

C ∈ ContingentTP,Avail = Avail∪user(C), where

A is the activation time point that activated C.

(2) O

(OccTP,(t

,ControlTP), (t

,ContingentTP)) =

OccTP ∪ {(user(A),C,t

) | C ∈ ContingentTP} if

< t

and for each C ∈ ContingentTP, Avail =

Avail ∪ user(C), where A is the activation time

point that activated C.

(3) O

(OccTP,(t, ControlTP),wait) = OccTP ∪

{(u,X,t) | (u, X) ∈ ControlTP} and for each

(u,A) ∈ ControlTP, Avail = Avail \ u.

(4) O

(OccTP,(t

,ControlTP), (t

,ContingentTP)) =

OccTP∪{(u, X,t

) | (u, X) ∈ ControlTP} if t

≤ t

and for each (u, A) ∈ ControlTP,Avail = Avail \ u.

For example, O

(OccTP,(0,{(John,A

)}),wait)

= OccTP ∪ {(John, A

,0)}.

(1) says that env can execute the time points in

ContingentTP at time t if ctrl decides to do nothing

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

124

at that time. (2) says that env can execute the time

points in ContingentTP if he decided to do so before

ctrl executes his. (3) is similar to (1) but with respect

to ctrl. (4) says that when ctrl decides to execute a

set of time points before or at the same time of those

env has decided to execute, ctrl moves ﬁrst to allow

env to react instantaneously (Deﬁnition 8).

Deﬁnition 8. We model the full outcome of ∆

ctrl

and ∆

env

as O(OccTP, ∆

ctrl

,∆

env

,I R ) and deﬁne it

as we did for O

(OccTP,wait,(t, ContingentTP)) ex-

cept that in cases (3) and (4) OccTP is augmented with

{(C,t) | C ∈ I

} (applicable if C has been activated),

and KnownProp is augmented with {(p, b) | (p, b) ∈

} (applicable if P? has been executed). Either way

t = last(OccTP).

The full outcome says how the state of the system

(i.e., PS) evolves according to the interplay of ctrl’s

and env’s RTEDs.

Deﬁnition 9. An RTED-based strategy for ctrl is

a mapping σ

ctrl

: P S

∗

→ ∆

∗

ctrl

from respectful par-

tial schedules to RTEDs. An RTED-based strategy for

env is a pair of mappings σ

env

= (µ

∆

env

,µ

), where

∆

env

: PS

∗

→ ∆

∗

ctrl

is a mapping from respectful par-

tial schedules to RTEDs, and µ

: P S

∗

→ I R

∗

is a

mapping from respectful partial schedules to instan-

taneous reactions.

Deﬁnition 10. The one-step outcome of the ga-

me modeling the execution of the network by

ctrl and env is deﬁned as O

(OccTP,σ

ctrl

,σ

env

) =

O(OccTP, σ

ctrl

(OccTP),µ

∆

env

(OccTP),µ

(OccTP

)),

where OccTP

= O

(OccTP,σ

ctrl

(OccTP),

∆

env

(OccTP)).

The terminal outcome O

∗

(σ

ctrl

,σ

env

) is the

complete schedule that results from the re-

cursive deﬁnition: OccTP

0, OccTP

i+1

(OccTP

,σ

ctrl

,σ

env

Deﬁnition 11. An ACTN is DC if there exists

an RTED-based strategy σ

ctrl

such that for all

RTED-based strategies σ

env

, the variable assignments

(u,X, k) in the complete schedule O

∗

(σ

ctrl

,σ

env

) sat-

isfy all constraints in C.

5 DYNAMIC

CONTROLLABILITY OF

ACTNS USING UPPAAL-TIGA

In this section, we extend the mapping given in § 3,

we use UPPAAL-TIGA as an off-the-shelf model

checker and we discuss a few optimizations.

Assume that G in Fig. 5 is the TGA equivalent to

the ACTN S in Fig. 4. The core of the TGA remains

the same as that discussed in § 3.

Internal State. We represent relations, users and

their availability by extending the internal states of

the TGA with a new piece of information. We assign

a unique incremental integer starting from 0 to each

time point, and proceed similarly for each user and

proposition. Mapping time points, users and propo-

sitions to integers allows us to employ them as in-

dexes over array data structures we are going to use

in UPPAAL-TIGA. Without loss of generality, when

intended as indexes, we abuse notation and write u,

X, and p meaning their assigned integer.

We chose to model availability of users as a

Boolean vector Avail indexed on users. Hence,

Avail[u] = > means that u is available and busy other-

wise. The initial state of Avail consists of all elements

set to > meaning that all users are available.

We keep track of who did what by means of a sys-

tem trace vector SysTrace whose index ranges over

time points. If SysTrace[X] = u, then time point X has

been executed by user u. The initial state of SysTrace

consists of all elements set to -1, meaning that all time

points have not been executed yet.

For instance, if John has executed A

, then

SysTrace[A

] = John. We do not need to keep track of

when a time point X has been executed since its value

is given by the difference between global time and its

clock.

We reorganize clocks associated to time points by

means of a vector clk indexed on time points, i.e.,

clk[X] is the clock associated to the time point X .

The vector clk does not contain clocks ˆc (representing

global time) and c

(used in the guards and updates of

the transitions modeling the interplay between ctrl

and env). Likewise, we reorganize Boolean variables

associated to time points by means of a vector xtd in-

dexed on time points whose elements are initialized

to ⊥. Finally, we reorganize propositions by means

of an integer vector prop whose elements are initial-

ized to 0.

Predecessors and Transition Range Limitations.

Before extending the transition guards and updates we

discuss a few optimizations. The mapping given in § 3

generates a transition for each time point. However,

if we only focus on transitions involving control time

points (i.e., those representing the execution of all X

such that X 6∈ CT ), one of the problems is that there

is no partial order for these transitions.

As a results, that approach suffers from a full state

explosion as we can take those transitions to gener-

ate impossible runs. To give an example, consider

the workﬂow in Fig. 1. Assume that the patient is

Access Controlled Temporal Networks

125

{John,Lara}

[]

{John,Lara}

[]

{wf}

[]

{Bob,Tom, Sara}

[u]

{Bob,Tom, Sara}

[u]

{Bob,Tom, Sara}

[u]

{Bob,Tom, Sara}

[u]

{Lara,Kate, Rick}

[¬u]

{Lara,Kate, Rick}

[¬u]

{Lara,Kate, Rick}

[¬u]

{Lara,Kate, Rick}

[¬u]

{wf}

[]

{Lara,Kate, Rick}

[]

{Lara,Kate, Rick}

[]

[5,25] [1,3],  : ~

[1,5], u : ~

[60,210]

[3 + ε,6], u : ~

[1,3], u :6= [2,4]

[1,6], u : ~

[1,5], ¬u : ~

[60,65]

[2 + ε,5], ¬u : ~

[1,2], ¬u := [2, 10]

[1,6], ¬u : ~

[1,3],  : ~ [5,10]

[0,30], ¬u : ~ [0,∞], ¬u :6=

[0,∞],  :6= ∧¬Relatives

Figure 4: ACTN modeling the workﬂow given in Fig. 1.

not urgent (i.e., u = ⊥). In this scenario, we expect

to execute PatEv then SurInt then ICUStayM, and ﬁ-

nally LTTh. However, the transitions for A

(modeling to the start of the tasks just mentioned) also

allow us to explore those runs violating this execu-

tion order (e.g., SurInt before PatEv or LTTh before

SurInt). We enforce the execution order among time

points in the guards of the corresponding transitions

only when we are sure this order is not ambiguous.

Deﬁnition 12. Let Y be a control time point (Y 6∈

CT ). For any X ∈ T different from Y , we say that

X is a predecessor of Y (and write X ∈ Π(Y )) if all

authorization constraints between X and Y have a pos-

itive lower bound (x ≥ 0) and label  identical to that

of Y . Formally:

Π(Y ) = {X | (x ≤ Y − X ≤ y,  : α) ∈ C

∧ x ≥ 0∧

 = L(Y )}

If X ∈ Π(Y ) it follows that Y −X ∈ [x

min

max

], where

• x

min

= min{x | (x ≤ Y − X ≤ y,  : α) ∈ C

}, and

• y

max

= max{y | (x ≤ Y − X ≤ y,  : α) ∈ C

}

That is, if all authorization constraints between X

and Y have a positive lower bound and label equal to

L(Y ) (i.e., we must satisfy at least one of them when-

ever we consider Y ), then Y deﬁnitely executes after

X. Moreover, once we have executed X, we can ex-

ecute Y after at least the minimum among the lower

bounds (x

min

) and within the maximum of the upper

bounds (y

max

) of the authorization constraints in C

to consider all the possible disjunctions.

As an example, consider Fig. 4. Π(A

) = {C

}

since C

= {(1 ≤ A

−C

≤ 3, u :6=), (3 + ε ≤ A

−

≤ 6,u : ~)} and L(A

) = u. Moreover, once env

executes C

, ctrl can execute A

such that A

−C

∈

[1,6] (x

min

= 1 and y

max

= 6). Likewise, Π(A

) =

}, A

−C

∈ [1, 5]. Π(U?) = {C

} and U? −C

∈

[1,3]. Π(A

) = {E, A

}, A

−E ∈ [1, 3] and A

−A

∈

[0,∞]. Π(A

) = {U?} and A

−U? ∈ [1, 5]. Π(A

) =

{U?,A

} and A

−U? ∈ [1, 5], A

− A

∈ [0,30].

Instead, we cannot do much for E, since each con-

straint having E as a target has a label that is not en-

tailed by  (i.e., L(E)). That is, for (1 ≤ E − C

≤

6,u : ~) ∈ C

and (1 ≤ E −C

≤ 6, ¬u : ~) ∈ C

we have that L(E) 6⇒ u nor L(E) 6⇒ ¬u. We recall

that we always execute E since its label, , is entailed

by any scenario. But, if scenario u (respectively, ¬u)

holds, the guard of the transition enforcing the par-

tial order (i.e., that considering Π(E)) would become

conditional depending on the current partial scenario.

For E, we would generate three transitions: one for

 with Π(E) =

0, one for u with Π(E) = {C

} and

−E ∈ [1,6], and another for ¬u with Π(E) = {C

}

and C

− E ∈ [1, 6].

Although such an approach risks making the en-

coding exponential, we should also prove that the

generated transitions do not prevent some scenario

from being explored by the model-checking phase.

For this reason, each Π(Y ) contains a predecessor

only when we are sure that X ∈ Π(Y ) always comes

before Y (similarly, we do not consider the case “C

is before A

”).

Note that activation time points are trivially be-

fore their related contingent and already handled with

a similar approach in the guards of the transitions ex-

ecuting them at env.

Time Point Transitions. For each user authorized for

X (where X 6∈ C T ), we have an uncontrollable self-

loop transition having the form:

(ctrl;Guard(u, X ); uExX; Update(u, X, setBusy); ctrl)

where:

• Guard(u, X)

def

= ¬xtd[X]

p∈L(X)

(prop[p] =

¬q∈L(X)

(prop[q] = −1) ∧ Avail[u]

Y ∈Π(X)

(xtd[Y ] ∧ clk[Y ] ≥ x

min

∧ clk[Y ] ≤ y

max

). This

function formalizes the mandatory part in the

guard: X has not been executed yet, L(X ) is true,

the authorized user u is available, all Y ∈ Π(X )

have been executed and clk[Y ] ∈ [x

min

max

] (as

discussed before).

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

126

• Update(u,X, setBusy)

def

= xtd[X] := >, clk[X] :=

0, SysTrace[X] := u, Avail[u] := ¬setBusy. This

function formalizes the mandatory part in the up-

date: X has been executed by u at time ˆc − clk[X],

and u is now busy (setBusy) if X is an activation

time point.

For concreteness, consider the self loop τ

Kate,A

(ctrl;Guard(Kate, A

);KateExA

;Update(Kate,A

>);ctrli in Fig. 5. It says that if the patient is not

urgent, Kate can start ThAst (i.e., Kate executes A

)

after 1 and within 5 minutes, after FibTh has been

completed (i.e., xtd[C

] ∧ clk[C

] ≥ 1 ∧ clk[C

] ≤ 5).

Kate,A

along with other 18 similar self loops τ

u,X

model the authorized executions of all non contingent

time points.

For each contingent time point, we only extend the

update part of the transition given in § 3 by adding

the two statements SysTrace[C] := SysTrace[A], and

Avail[SysTrace[C]] := >. That is, ﬁrst, we save that

the user executing C is the same of that who executed

A, and second, we release such a user. Note that the

guard does not contain conditions on availability on

purpose. Adding such conditions would result in env

shrinking the range of C.

Game Interplay, Failing Transitions, and Winning

Path Considering Disjunctive Constraints. Failing

transitions and transitions regulating the game inter-

play and assigning the truth values to propositions re-

main the same as those discussed in § 3 (adapted to

the new array-reorganization).

The winning path is extended by adding interme-

diate locations to guarantee that whenever disjunctive

authorization constraints exist, we always take into

consideration one of them. We proceed by ﬁrst intro-

ducing the set of core constraints (i.e., those we must

always consider for the traditional winning path).

Deﬁnition 13. Let  ∈ P

∗

be a label. The set of core

constraints labeled by  is given by:

Core() =

[

∈C

{(x ≤Y −X ≤ y, : α) | |C

| = 1∧

(x ≤ Y − X ≤ y,  : α) ∈ C

∧  = L(X ) ∧ L(Y )}

For our example, Core(u) = {(1 ≤ A

−U? ≤ 5, u :

~),(1 ≤ E −C

≤ 6,u : ~)}. Note that we do not take

into consideration C

= {(1 ≤ C

− C

≤ 3,u :6=

),(3 + ε ≤ C

−C

≤ 6,u : ~)} as |C

| = 2.

in Fig. 5 veriﬁes both that all time points la-

beled by u have been executed and that the core con-

straints and their related authorization policies they

express are satisﬁed. skip

and skip

are the same

as those discussed for classic CSTNUs in § 3.

We now deal with the disjunctive authorization

constraints. We ﬁrst compute the set of non-core con-

straints (dual to the set core), i.e., the set contain-

ing all the disjunctions with respect to a given label

. Then, we generate the locations and transitions to

verify that we satisfy at least one authorization con-

straint for each disjunction avoiding the combinatorial

explosion.

Deﬁnition 14. Let  ∈ P

∗

be a label. The set of non-

core constraints labeled by  for each C

is given by:

NonCore(C

,) = {(x ≤Y −X ≤ y, : α) | |C

| > 1

∧ (x ≤ Y − X ≤ y, : α) ∈ C

∧  = L(X ) ∧ L(Y )}

For our example, NonCore(C

,u) = {(1 ≤

−C

≤ 3,u :6=), (3 +ε ≤ A

−C

≤ 6,u : ~)}. That

is, either A

is executed such that A

− C

∈ [1,3]

and TSoD (6=) must hold, or A

is executed such that

−C

∈ [3 + ε, 6] and any user can do so (~).

To handle the disjunctions with respect to the la-

bel  for each NonCore(C

,), we create an interme-

diate location L

,

to avoid generating an exponen-

tial number of transitions. For each L

,

, we have

a set of transitions containing the same skip tran-

sitions as those for L



and we have a sat transition

for each disjunct in NonCore(C

,). Concretely, for

NonCore(C

,u), we generate L

(shortened

as L

in Fig. 5), sat

(verifying the ﬁrst disjunc-

tion) and sat

(verifying the second one).

Likewise, we generate L

,¬u

(i.e., goal),

sat

,¬u

and sat

,¬u

for NonCore(C

,¬u).

We discuss the complexity and prove the correct-

ness of the encoding in the appendix (Theorem 1 and

Theorem 2-3, respectively).

The ACTN in Fig. 4 is DC. One of the possible

executions is the following. ctrl starts the work-

ﬂow in Fig. 1 by assigning PatEv to John. As soon

as John ﬁnishes (i.e., env executes C

), ctrl com-

mits the workﬂow management system wf to execute

the conditional split connector (modeled by U ?). If

the patient is urgent (i.e., if u is assigned >), then

SurInt is assigned to Tom and exactly 1 minute af-

ter Tom is done, ICUStayM is assigned to Bob (since a

TSoD must hold). If the patient is not urgent, FibTh

and ThAst are both carried out by Lara because the

start of ThAst occurs one minute after FibTh and thus

a TBoD must hold. Regardless of which branch has

been taken, ctrl commits wf to execute the join con-

nector 1 minute after the last task of the chosen branch

terminated. Finally, ctrl commits Rick, who is dif-

ferent from and not related to Lara or John, to exe-

cuting LTTh 1 minute after the join connector ended.

Access Controlled Temporal Networks

127

ctrl

env



¬u

goal

h>;pass; c

:= 0i

> 0; gain;

John,A

Lara,A

wf,U?

Tom,A

Sara,A

Bob,A

Tom,A

Sara,A

Bob,A

Kate,A

Lara,A

Rick,A

Lara,A

Kate,A

Rick,A

wf,E

Lara,A

Kate,A

Rick,A

⊥

hclk[A

] ∧ ¬clk[C

] ∧ clk[A

] > 25; fail

hclk[A

] ∧ ¬clk[C

] ∧ clk[A

] > 210; fail

hclk[A

] ∧ ¬clk[C

] ∧ clk[A

] > 4; fail

hclk[A

] ∧ ¬clk[C

] ∧ clk[A

] > 65; fail

hclk[A

] ∧ ¬clk[C

] ∧ clk[A

] > 10; fail

hclk[A

] ∧ ¬clk[C

] ∧ clk[A

] > 10; fail

hxtd[U?] ∧ prop[u] = 0 ∧ c

> 0; fail



;sat



∧ c

> 0; i

hprop[u] = −1;skip

;

h!xtd[U?]; skip

;

;sat

;

hprop[u] = −1;skip

;

h!xtd[U?]; skip

;

;sat

;

;sat

;

hprop[u] = −1;skip

¬u

;

h!xtd[U?]; skip

¬u

;

¬u

;sat

¬u

;

hprop[u] = −1;skip

¬u

;

h!xtd[U?]; skip

¬u

;

,¬u

;sat

,¬u

;

,¬u

;sat

,¬u

;

Figure 5: TGA equivalent to the ACTN in Fig. 4.

6 RELATED WORK

There exist two main classes of algorithms for check-

ing the DC of a CSTNU: network-based and TGA-

based ones.

The network-based algorithms in (Combi et al.,

2013; Combi et al., 2014b) take as input a CSTNU

and check if the network is DC: they are sound but

not complete.

TGAs allow one to determine a sound and com-

plete DC-checking algorithm. DC of a CSTNU is

implemented by ﬁrst encoding a given CSTNU into

an equivalent TGA (as we discussed) and then, seek-

ing a control strategy for the env—via TCTL model

checking— to prevent ctrl from heading to a special

location called goal. If env succeeds, the network

is not DC, otherwise it is. The correctness of the ap-

proach is proved in (Cimatti et al., 2016).

The structured business process modeling lan-

guage TNest is introduced in (Combi et al., 2014a).

To understand whether a temporal workﬂow is DC,

the TNest speciﬁcation is translated in an equivalent

CSTNU on which DC checking is done. TNest does

not deal with users and authorization constraints.

The work closest to ours is by (Combi et al.,

2016), who used an STNU (Morris et al., 2001) to

model an unconditional temporal role-based access-

controlled workﬂow. They translated a fragment of

a TRBAC (Bertino et al., 2001) into a temporal net-

work, and the workﬂow into another. Then, they con-

nected the resulting networks in order to check if the

temporal constraints of the workﬂow and those of the

access-control model are contradictory. Finally, they

derived for each task the set of authorized users and

gave a formalization of security constraints (SCs) and

Security Constraints Propagation Rules (SCPR) to en-

force authorization constraints at execution time. DC

analysis in the WSP sense is left as future work. In

contrast, in this paper we directly inject users and

authorization constraints in the formalization of the

ACTN itself, and we do not only deal with TSoD and

TBoD, but also with other security policies expressed

by means of relations over users.

(Wang and Li, 2010) and (Crampton et al., 2014)

(to name a few) have addressed the WSP. If an ACTN

modeling a workﬂow is DC, then the temporal WSP is

automatically answered. The execution strategy pro-

vides us with information about who and when has to

execute which time points depending on what is going

on. This assignment is generated in real time.

Finally, approaches such as those proposed by

(Barth et al., 2007) and (Barletta et al., 2011) are not

really suitable to model temporal workﬂows as we are

doing. First, we do not need to use messages, and sec-

ond, we have to know exactly when each transition is

taken (with respect to when we started) in order to

propagate the effect (which means to run algorithms

on the network to update the allowed temporal ranges

of the unexecuted time points. Timed computation

tree logic (TCTL) is able to deal with this problem

(recall that we use dense time, rather than discrete ap-

proximations). The logics in (Barth et al., 2007) and

(Barletta et al., 2011) have no dense time representa-

tion (clocks) and they do not allow for computation

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

128

over real-valued temporal constraints.

7 CONCLUDING REMARKS

We deﬁned ACTNs as an extension of CSTNUs in

order to take into consideration users and authoriza-

tion constraints, and we used them to analyze the of-

ﬁcial STEMI guidelines as a concrete example. We

similarly extended the execution semantics for CST-

NUs given in terms of RTEDs. After that, we pro-

vided an encoding from ACTNs to TGAs discussing

a few optimizations to speed up the model-checking

phase. We proved that our encoding is polynomial,

fully automated, and we also showed the correctness

(see the appendix). As a result, we provided a sound

and complete approach for the temporal WSP. As a ﬁ-

nal contribution, we discussed our experimental eval-

uation using the UPPAAL-TIGA software tool. We

are currently implementing the encoder from ACTNs

into TGAs and an executor for executing the ACTN

following the synthesized strategy.

As future work we will investigate two main di-

rections, distinguished by the use, or not, of TGAs.

In the ﬁrst case, we plan to address the workﬂow re-

siliency problem, which is a reﬁnement of the WSP

when a subset of the authorized user may become

absent before or during the execution (again, a new

kind of uncertainty that needs a controllability ap-

proach). In the second, we plan to devise a network-

based constraint-propagation algorithm for ACTN

DC-checking. These algorithms might be more com-

plex but are typically faster than TCTL model check-

ing as they tighten the network by ruling out all im-

possible execution strategies.

Finally, we plan to provide a structured modeling

language for designing access-controlled workﬂows

to be mapped into ACTNs for the DC checking.

REFERENCES

Barletta, M., Ranise, S., and Vigan

o, L. (2011). A

declarative two-level framework to specify and

verify workﬂow and authorization policies in

service-oriented architectures. SOCA, 5(2):105–137,

http://dx.doi.org/10.1007/s11761-010-0073-4.

Barth, A., Mitchell, J., Datta, A., and Sundaram,

S. (2007). Privacy and utility in business

processes. In CSF ’07, pages 279–294.

http://dx.doi.org/10.1109/CSF.2007.26.

Behrmann, G., Cougnard, A., David, A., Fleury, E.,

Larsen, K. G., and Lime, D. (2007). Uppaal-tiga:

Time for playing games! In Damm, W. and Her-

manns, H., editors, CAV 2007, LNCS, pages 121–125.

http://dx.doi.org/10.1007/978-3-540-73368-3 14.

Bertino, E., Bonatti, P. A., and Ferrari, E. (2001). TRBAC:

A temporal role-based access control model. ACM

Trans. Inf. Syst. Secur., 4(3).

Cimatti, A., Hunsberger, L., Micheli, A., Posenato, R., and

Roveri, M. (2016). Dynamic controllability via timed

game automata. Acta Informatica, 53(6–8):681–722,

http://dx.doi.org/10.1007/s00236-016-0257-2.

Combi, C., Gambini, M., Migliorini, S., and Pose-

nato, R. (2014a). Representing business pro-

cesses through a temporal data-centric workﬂow

modeling language: An application to the man-

agement of clinical pathways. IEEE Trans.

Syst., Man, Cybern., Syst., 44(9):1182–1203,

http://dx.doi.org/10.1109/TSMC.2014.2300055.

Combi, C., Hunsberger, L., and Posenato, R. (2013). An

algorithm for checking the dynamic controllability of

a conditional simple temporal network with uncer-

tainty. In ICAART 2013, volume 2, pages 144–156.

http://dx.doi.org/10.5220/0004256101440156.

Combi, C., Hunsberger, L., and Posenato, R. (2014b).

An algorithm for checking the dynamic controllabil-

ity of a conditional simple temporal network with

uncertainty - revisited. In Agents and Artiﬁcial In-

telligence, volume 449 of CCIS, pages 314–331.

http://dx.doi.org/10.1007/978-3-662-44440-5 19.

Combi, C., Vigan

o, L., and Zavatteri, M. (2016).

Security constraints in temporal role-based

access-controlled workﬂows. In CODASPY.

http://dx.doi.org/10.1145/2857705.2857716.

Crampton, J., Huth, M., and Kuo, J. H.-P. (2014).

Authorized workﬂow schemas: deciding re-

alizability through LTL model checking. Int

J Softw Tools Technol Transfer, 16(1):31–48,

http://dx.doi.org/10.1007/s10009-012-0269-3.

Hunsberger, L., Posenato, R., and Combi, C. (2012). The

Dynamic Controllability of Conditional STNs with

Uncertainty. In PlanEx at ICAPS 2012, pages 1–8.

http://arxiv.org/abs/1212.2005.

Hunsberger, L., Posenato, R., and Combi, C. (2015). A

sound-and-complete propagation-based algorithm for

checking the dynamic consistency of conditional sim-

ple temporal networks. In TIME 2015, pages 4–18.

http://dx.doi.org/10.1109/TIME.2015.26.

Lenz, R. and Reichert, M. (2007). It support

for healthcare processes - premises, challenges,

perspectives. Data Knowl. Eng., 61(1):39–58,

http://dx.doi.org/10.1016/j.datak.2006.04.007.

Morris, P. H., Muscettola, N., and Vidal, T. (2001). Dy-

namic control of plans with temporal uncertainty. In

IJCAI 2001, pages 494–502.

Wang, Q. and Li, N. (2010). Satisﬁability and resiliency

in workﬂow authorization systems. ACM Trans. Inf.

Syst. Secur., 13(4).

APPENDIX

Theorem 1. Encoding ACTNs into TGAs has

polynomial-time complexity.

Proof. The main components having a role in the

complexity analysis of the encoding of an ACTN are:

Access Controlled Temporal Networks

129

(i) time points, (ii) authorized users for each control

time point, (iii) authorization constraints, and (iv) dif-

ferent labels in the ACTN.

For each control time point, there is a self-loop

transition for any authorized user. These transitions

contain in their guard the scenario in which the time

point has to be executed and may contain additional

conditions about the predecessors. From § 4, the com-

plexity of ﬁnding the predecessors for a time point

X is linear in the number of all authorization con-

straints. Thus, the generation of these transitions is

a polynomial-time task.

Transitions modeling the execution of the contin-

gent time points and assigning truth values are the

same as those given for CSTNUs (we just extend the

update part), and they are not even replicated for the

authorized users. Fail transitions and the transitions

regulating the game interplay remain exactly the same

as well. Thus, the time complexity of the generation

of this set of transitions remains polynomial.

We are left to prove that the generation of the win-

ning path is a polynomial-time task too. The main

problem is that such a path consists of intermediate

locations that must allow one to consider all possi-

ble combinations of the disjunctions expressed as au-

thorization constraints. The generation of the win-

ning path is the same of that for CSTNUs (augmented

with the checks for the authorization policies) when

we consider the set of core constraints (polynomial).

When considering the non core authorization con-

straints we create as many intermediate locations as

the number of disjunctions. However, we remark that

our encoding does not generate any combination of

the sat transitions nor a combination of the locations.

The model-checking phase will take care of exploring

them all. Thus, the generation of the winning path

has linear complexity in the number of the different

labels with respect to the number of the possible dis-

junctions.

Since all operations have polynomial complexity,

the overall complexity is polynomial as well.

Theorem 2. Encoding ACTNs into TGAs correctly

captures the execution semantics given in § 4.

Proof. We show that any sequence of partial sched-

ules that can be generated for any ACTN according to

the execution semantics given in § 4 corresponds to a

run for the equivalent TGA that can be generated by

following its transitions according to the classic TGA

semantics. We extend the proof of correctness given

in (Cimatti et al., 2016) to accommodate users and

authorization constraints. The proof is by induction.

Each respectful partial schedule that can be gener-

ated for the ACTN corresponds to a state of the TGA

in which: the location is env, c

= 0, last(OccTP) =

ˆc, and for each executed time point X, time(X) = ˆc −

clk[X], xtd[X ] = >, user(X) = SysTrace[X], whereas

time(X) = ˆc, xtd[X ] = ⊥ and user(X) if X hasn’t

been executed yet. If P? is an observation time point,

then KnownProp contains (p, b) for b ∈ {>,⊥} if

P? has been executed, and doesn’t contain it other-

wise. Also, if some activation point has been exe-

cuted by the user u and the related contingent has

not, then Avail[u] = ⊥, else Avail[u] = >. Note that

Avail[u] = > and Avail[u] = ⊥ (in the TGA) mean

u ∈ Avail and u 6∈ Avail in the execution semantics

given in § 4 (where Avail is a set).

Base Case. The initial P S corresponds to the

initial state of the TGA in which the location is

env, ˆc = 0 all clocks clk[X] = 0, all xtd[X] = ⊥, all

SysTrace[X] = −1, all prop[p] = 0, and Avail[u] = >.

This partial schedule is trivially respectful.

Inductive Step. Suppose that PS is a respectful

partial schedule that can be generated according to the

execution semantics for ACTNs, and that PS satisﬁes

the invariant that we required of each respectful par-

tial schedule at the beginning of this proof.

Let θ be the corresponding state of the TGA. Since

= 0, the only transitions that are immediately en-

abled are those handling contingent time point execu-

tions and truth value assignments. These transitions,

if taken, correspond to env’s instantaneous reactions,

in which a set of one or more contingent time-points

can be executed simultaneously or some propositions

can be assigned a value. Suppose that env doesn’t

take any transition when c

= 0. As soon as c

> 0,

both ctrl and env have transitions that they could

take at any time with respect to the enforced condi-

tion over the predecessors. For example, env might

decide to execute one or more contingent time-points

,. . . ,C

when c

= 3. That would correspond to

∆

env

= (k, {C

,. . . ,C

}), where k = last(OccTP) + 3.

Since each time env takes a transition c

is re-

set to 0, ctrl is unable to interrupt env while env is

executing contingent time points and assigning truth

values to propositions. Thus, at those time instants

∆

ctrl

= wait and the resulting outcomes are exactly

the cases 1-2 of Deﬁnition 7. The guard of env’s

transition, enforcing the duration bounds for a con-

tingent link (A,x, y,C), ensures that the resulting par-

tial schedule is respectful as C can only be executed

such that C − A ∈ [x, y] (analogous to predecessors).

Likewise, for a truth value assignment the fail transi-

tion that ctrl can take (if δ > 0) ensures that env can

assign a truth value to a proposition instantaneously

after the execution of the observation time point (oth-

erwise, ctrl could trivially move to goal).

Also, when env’s sequence of “simultaneous”

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

130

transitions completes, ˆc equals the time of the most

recent execution (e.g., last(OccTP) + 3). In addi-

tion, for each newly executed time-point C, the clock

clk[C] is reset xtd[C] is set to >, SysTrace[C] is set to

SysTrace[A] and Avail[SysTrace[C]] = >. Since clk[C]

is reset only once, ˆc − clk[C] remains ﬁxed forever.

Instead, suppose that ctrl has decided to commit

a set of users to execute a set of control time points

before env executes his, say at time last(OccTP) + 2.

This situation results in ctrl taking the gain tran-

sition to take back control and then, once in its lo-

cation, instantaneously commit the users to execute

the time points at that time, blocking all users exe-

cuting an activation time point, and immediately re-

turning to the env location by means of the pass

transition. Since the location of ctrl is urgent, ˆc =

last(OccTP) + 2 when the pass transition is taken.

This sequence of transitions corresponds to the par-

tial outcome in Deﬁnition 7 (cases 3-4) where ∆

ctrl

(t, {(u

),.. . , (u

)}), t = last(OccTP) + 2, and

for each (u,X) ∈ ControlTP (of ∆

ctrl

), u ∈ A(X).

Moreover, if env chooses to instantaneously exe-

cute some contingent time point at the same time

last(OccTP) + 2, that will correspond to an instanta-

neous reaction.

Finally, if at time last(OccTP), ctrl and env

both decide to execute some time points at time

last(OccTP) + 1, then the ACTN semantics (inherit-

ing the CSTNU semantics) ensures that ctrl’s time

points are executed ﬁrst, and that env is able to in-

stantaneously react if it decides to do so (equivalent

to ctrl’s transitions having priority over env’s). As

soon as the execution returns to the location of env,

the ˆc will still be last(OccTP) + 1 (because, again,

time has not elapsed at ctrl). Since, in all cases, the

resulting state of the TGA satisﬁes the desired invari-

ant property, the result is proven.

Theorem 3. Let S be any ACTN, G be the encoding

of S , and σ

be a winning TGA counter-strategy for

ctrl. Then there is an equivalent RTED-based strat-

egy σ

ctrl

for ctrl that will ensure the satisfaction of

all authorization constraints in S whatever the contin-

gent durations and truth value assignments.

Proof. If S, G, σ

are as assumed, then σ

: Loc ×

V → Act ∪ wait, with Act the set of ctrl’s actions

(equivalently the set of uncontrollable transitions) and

V abstracts the internal state of the TGA.

Suppose the TGA has just got into the state

(env,V ). As we have already noted, for any time

point X, associated clock clk[X] and Boolean vari-

able xtd[X], we have: xtd[X] = ⊥, clk[X] = ˆc, and

SysTrace[X] = −1 before X executes, and xtd[X] = >,

clk[X] < ˆc, and SysTrace[X] = u after X executed. For

each observation time point P?, the associated propo-

sition modeled by prop[p] is 0 (i.e., unknown) before

P? executes, and either 1 (i.e., >) or −1 (i.e., ⊥) after

P? executed. Thus, V speciﬁes a partial schedule.

Now, suppose that last(OccTP) < ˆc (i.e., that

some positive time has elapsed since the last execu-

tion event in P S). If nothing has happened, it means

that there has been a sequence of gain and pass

transitions going back and forth between env’s and

ctrl’s locations. In such a loop, ctrl has not ex-

ecuted any control point, and env has just waited.

Let (env,V

) be the state immediately preceding such

loop. Then, for some positive ε > 0, all the clocks

in V equal those in V

plus ε, and by construction,

last(OccTP) refers to the clocks in V

. We abuse no-

tation and write V + k meaning that all values of the

clocks in V are augmented by k. Next, let d = min{d |

(env,V

+ d) 6= wait ∧ σ

(env,V

+ d) 6= pass}

be the minimum time that can elapse from V be-

fore the strategy σ

recommends a transition dif-

ferent from gain and pass, and let V

= V

+ d.

The unique sequence of execution transitions at ctrl

is τ

= σ

(ctrl,V

),.. . , τ

= σ

(ctrl,V

), where

each V

i+1

= V

, except for the clk[X] with X the time

point executed by τ

. The termination of this sequence

of transitions is guaranteed since time points are ﬁnite

and can only be executed once. If τ

is the last execu-

tion transition, then pass = σ

(ctrl,V

). That tran-

sition leads back to the state (env,V

), where V

is the

same as V

, except that the clocks for the time points

executed by the transitions, τ

,. . . , τ

, are all 0 in V

Next, let t be the time at which σ

recommends

ctrl a non-trivial transition, and ControlTP be the

set of time-points corresponding to the execution tran-

sitions, τ

,. . . , τ

. Then (t, ControlTP) is a ∆

ctrl

corresponding to what the strategy recommends at

(env,V

). Note that env may decide to instanta-

neously react by executing some contingent points at

time t too, an outcome that is prevented by the exe-

cution semantics for ACTNs (Deﬁnition 7, cases 3-

4). Finally, env may decide to intervene before time

t arrives, by executing one or more contingent time-

points and effectively generating a new partial sched-

ule P S

. In that case, the same procedure could be ap-

plied to PS

to generate an appropriate ∆

ctrl

. Since

the guard on the transition from env to ctrl requires

a positive time delay, that ∆

ctrl

is properly prohibited

from any kind of instantaneous reaction (by ctrl).

This procedure gives a mapping from any (env,V )

state that is reachable following σ

. The sequences

of partial schedules generated by following the RT-

EDs correspond to runs that can be produced by σ

Thus, the complete schedules generated by the RT-

EDs satisfy all authorization constraints.

Access Controlled Temporal Networks

131