Principles and Experiments of a Multi-Agent Approach for Large

Co-Simulation Networks Initialization

emy Boes, Tom Jorquera and Guy Camilleri

University of Toulouse, IRIT/Team SMAC, 118 route de Narbonne, Toulouse, France

Keywords:

Multi-Agent Systems, Self-Adaptive Systems, Co-Simulation.

Abstract:

Simulating large systems, such as smart grids, often requires to build a network of speciﬁc simulators. Making

heterogeneous simulators work together is a challenge in itself, but recent advances in the ﬁeld of co-simulation

are providing answers. However, one key problem arises, and has not been sufﬁciently addressed: the initial-

ization of such networks. Many simulators need to have proper input values to start. But in the network, each

input is another simulator’s output. One has to ﬁnd the initial input values of all simulators such as their com-

puted output is equal to the initial input value of the connected simulators. Given that simulators often contain

differential equations, this is hard to solve even with a small number of simulators, and nearly impossible with

a large number of them. In this paper, we present a mutli-agent system designed to solve the co-simulation

initialization problem, and show preliminary results on large networks.

1 INTRODUCTION

Alternatives to nuclear power, renewable energy like

solar panels or wind power, often involves producing

electricity near the consumers. This radically changes

the topology of the electric grid and makes it way

more difﬁcult to manage and control. Smart grids are

a very active research ﬁeld. Simulating smart grids

enables the validation of network control methods and

various network properties, that are as important as

the (simulated) physical properties of the power sys-

tem (Liberatore and Al-Hammouri, 2011). Neverthe-

less, designing a simulator and building a model for

large networks is a difﬁcult task due to the complex-

ity of the considered systems. Co-simulation over-

comes this difﬁculty by running several models and

simulators together, one for each subsystem. In this

approach, simulators exchange data with each other,

in a ”black box” way. Models are then easier to ob-

tain since they only focus on a smaller part of the grid.

However, new problems arise, such as time synchro-

nization (Bouchhima et al., 2006). Most of them are

handled by existing co-simulation frameworks, but

the mutual and interdependent initialization of each

simulator is not.

Indeed, simulators in a co-simulation network re-

quire coherent initial values for their inputs. These in-

puts are connected to the outputs of other simulators.

To preserve the coherence in the network and prevent

simulators from crashing, the initial values that are set

have to be equal (or within a given accuracy limit) to

the values of the connected outputs of the other sim-

ulators. These output values are computed from the

other initial input values, that have been set under the

same constraints. Since each input is connected to an

output in the network, there is no ”ﬁrst input” that is

free to go back to set an arbitrary value and solve the

whole problem.

Due to the large scale of co-simulations net-

works, the heterogeneity and the intrication of the

models involved, co-simulation initialization (or co-

initialization) is a difﬁcult challenge. It requires a

lot of expertise and domain speciﬁc knowledge about

the models. Our approach aims at developping a co-

initialization method that does not rely on such exper-

tise, by considering each simulator as a black-box and

exploring the solutions. In this paper, co-initialization

is viewed as a ﬁxed-point problem. We use a multi-

agent approach to ﬁnd X such as F(X) = X, where F

is the function that transforms the inputs of all sim-

ulators into their outputs. The distributed and de-

centralised decision process of multi-agent systems

should allow our system to scale up to an increasing

number of simulators in the co-simulation network.

Section 2 presents the problem of co-initilization,

while our multi-agent system is described in section

3. Section 4 shows results before we conclude in the

last section.

Boes J., Jorquera T. and Camilleri G.

Principles and Experiments of a Multi-Agent Approach for Large Co-Simulation Networks Initialization.

DOI: 10.5220/0006186300580066

In Proceedings of the 9th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2017), pages 58-66

ISBN: 978-989-758-219-6

2 CO-INITIALIZATION

Co-initialization is the problem of ﬁnding adequate

initial values simultaneously for all the inputs of all

the simulators in a co-simulation network. This sec-

tion explains how we see this problem as a ﬁxed-point

problem.

2.1 Co-Simulation

A co-simulation network is a network of possibly het-

erogeneous simulators running together to simulate

several parts or several scales of a large system. This

method enables to model huge systems that would be

otherwise too complex to handle with a single model,

and to reuse well-established and specialized model

with only minor modiﬁcations. For instance, to simu-

late an emergency brake maneuver for wind turbines,

Sicklinger et al. combine several models (blades,

gearbox, control system, etc) and achieve a more re-

alistic result than monolithic approaches (Sicklinger

et al., 2015).

Co-simulation has been of growing interest these

past years, but despite its efﬁciency, it does raise a

number of challenges. The development of a standard

for model exchange, called Functional Mock-up In-

terface (FMI), brings answers to the problem of mod-

els interoperability (Blochwitz et al., 2011). Other

tools deal with time coherence in co-simulation net-

works, such as MECSYCO which relies on the multi-

agent paradigm (Vaubourg et al., 2015).

2.2 Co-Initialization as a Fixed-Point

Problem

This paper addresses the issue of co-initialization, that

arises when simulators and models have constraints

on their input. For instance, some models can be un-

stable if their input changes too widely between two

timesteps, or crash if the inputs goes outside a given

range. In a co-simulation network, all simulators in-

puts are usually connected to an output from another

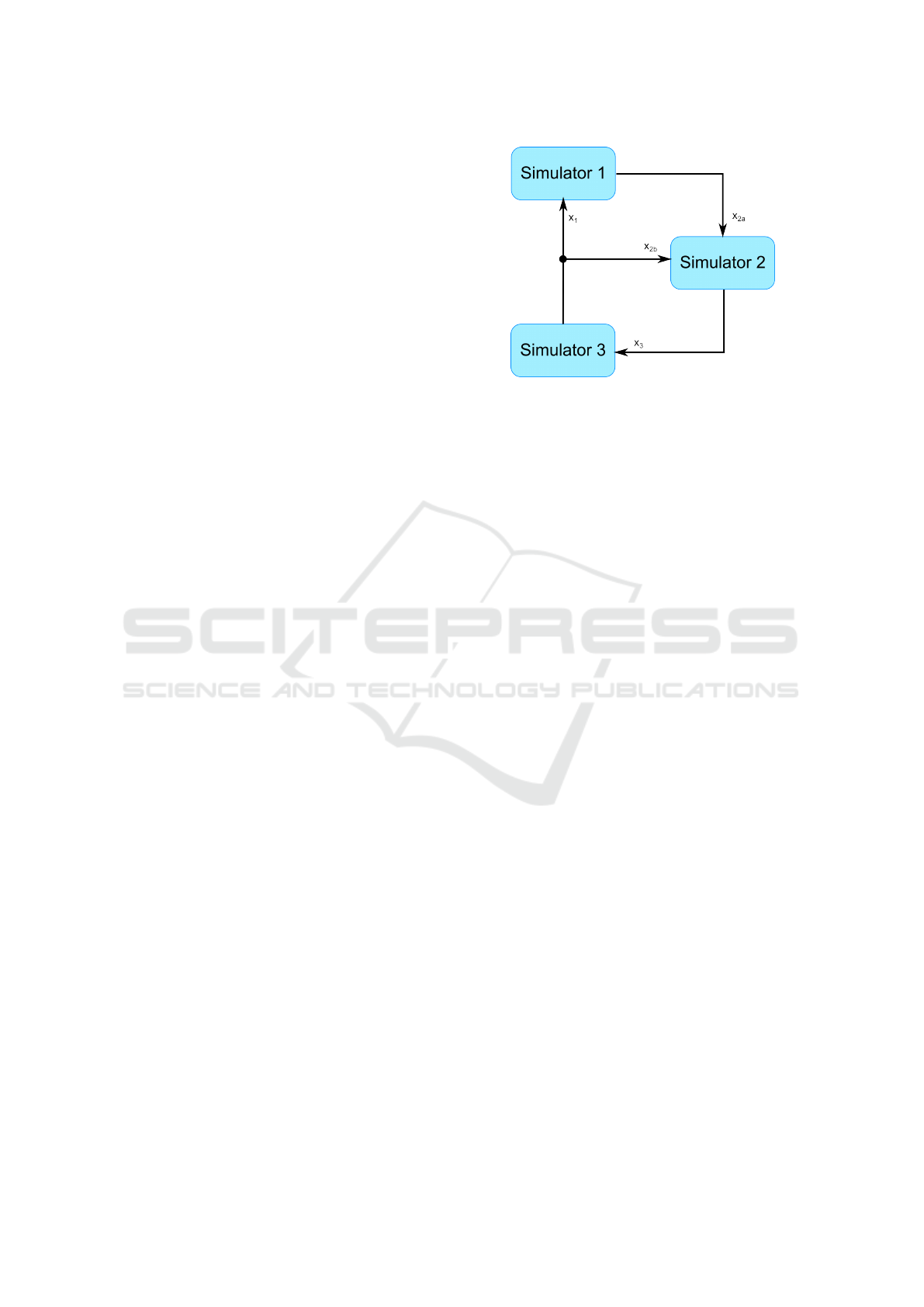
simulator. For instance, in ﬁgure 1, this means that

the initial value of the input of simulator 1 should be

equal or close to the output of simulator 3, which de-

pdends on the initial value of the input of simulator 3,

and so on with simulator 2.

If we consider simulators as functions, we can

express the co-initialization problem as a ﬁxed-point

problem. For instance, with simulator 1 as function

f , simulator 2 function g, and simulator 3 function h,

the initialization problem is to ﬁnd x

, x

, and x

Figure 1: A Co-Simulation Network with 3 Simulators.

such as:











f (x

) = x

g(x

, x

) = x

h(x

) = x

= x

It is a ﬁxed-point problem where we want to solve

X = F(X ) with X = (x

, x

) and F(X ) =

(h(x

), f (x

), h(x

), g(x

, x

)). In our case, we do

not know the models used by the simulators ( f , g, and

h are unknown). But we have access to their jacobian,

so we can know what variation would be caused on

an output by a modiﬁcation of an input for a given

simulator.

2.3 Fixed-Point Solvers

The ﬁxed-point problem is a challenging issue that

have many applications in ﬁelds where the notion

of stability can be expressed as a ﬁxed-point, such

as economics and game theory (Border, 1989), pro-

gram analysis and code optimization (Costan et al.,

2005), or phase transition in physics (Schaefer and

Wambach, 2005).

The most common and proven approaches to solve

ﬁxed-point problems are iterative methods (Alber

et al., 2003), (Yao et al., 2011). For instance, the

Newton-Raphson method (Bonnans et al., 2013) uses

the ﬁrst terms of a Taylor series to approximate a

function for which we want to solve an equation.

While their formal deﬁnition is sound, this type of

approaches tends to suffer from combinatory explo-

sion when faced with a large number of dimensions.

This is why we work on an alternative solution with a

bottom-up multi-agent approach.

Principles and Experiments of a Multi-Agent Approach for Large Co-Simulation Networks Initialization

3 A SELF-ADAPTIVE

MULTI-AGENT SYSTEM FOR

CO-INITIALIZATION

This section details our multi-agent system and ex-

plains how agents help their neighborhood so the

whole system converge towards a solution.

3.1 Adapative Multi-Agent Systems

Our approach is inspired by the AMAS (Adaptive

Multi-Agent Systems) theory, a vision of multi-agent

systems where cooperation is the engine of self-

organization (Georg

e et al., 2011). The AMAS theory

is a basis for the design of multi-agent systems, where

cooperation drives local agents in a self-organizing

process which provides adaptiveness and learning

skills to the whole system. As cooperative entities,

AMAS agents seek to reach their own local goals as

well as they seek to help other agents achieving their

own local goals. Thus, an agent modiﬁes its behavior

if it thinks that its actions are useless or detrimental to

its environment (including other agents).

The AMAS theory has proved useful and efﬁcient

to tackle various problems where scaling up is a key

challenge, such as big data analytics (Belghache et al.,

2016), multi-satellite mission planning (Bonnet et al.,

2015), or air trafﬁc simulation (Rantrua et al., 2015).

This is why we considered applying this approach to

the problem of large co-simulation initialization. The

system presented in this paper is homogeneous (all

agents have the same decision rules) and agents are

reactive, but it is not always the case with AMASs.

3.2 Agents Description

The key problem in co-simulation initialization lies in

the link between simulators. Thus, there is one agent

per link in the network, i.e. one agent for each out-

put of each simulator. In other words, there is only

one type of agent in our system, instanciated at each

output of each simulator.

3.2.1 Environment and Neighborhood

The environment of an agent is composed of all the

simulators and all the other agents. But agents per-

ceive their environment only partially. Each agent has

one input and one output. The value of its input is per-

ceived in the environment, it is the output of the cor-

responding simulator. The value of the agent’s output

is decided by the agent itself, on its own. This output

is connected to one or several simulators, depending

on the co-simulation network.

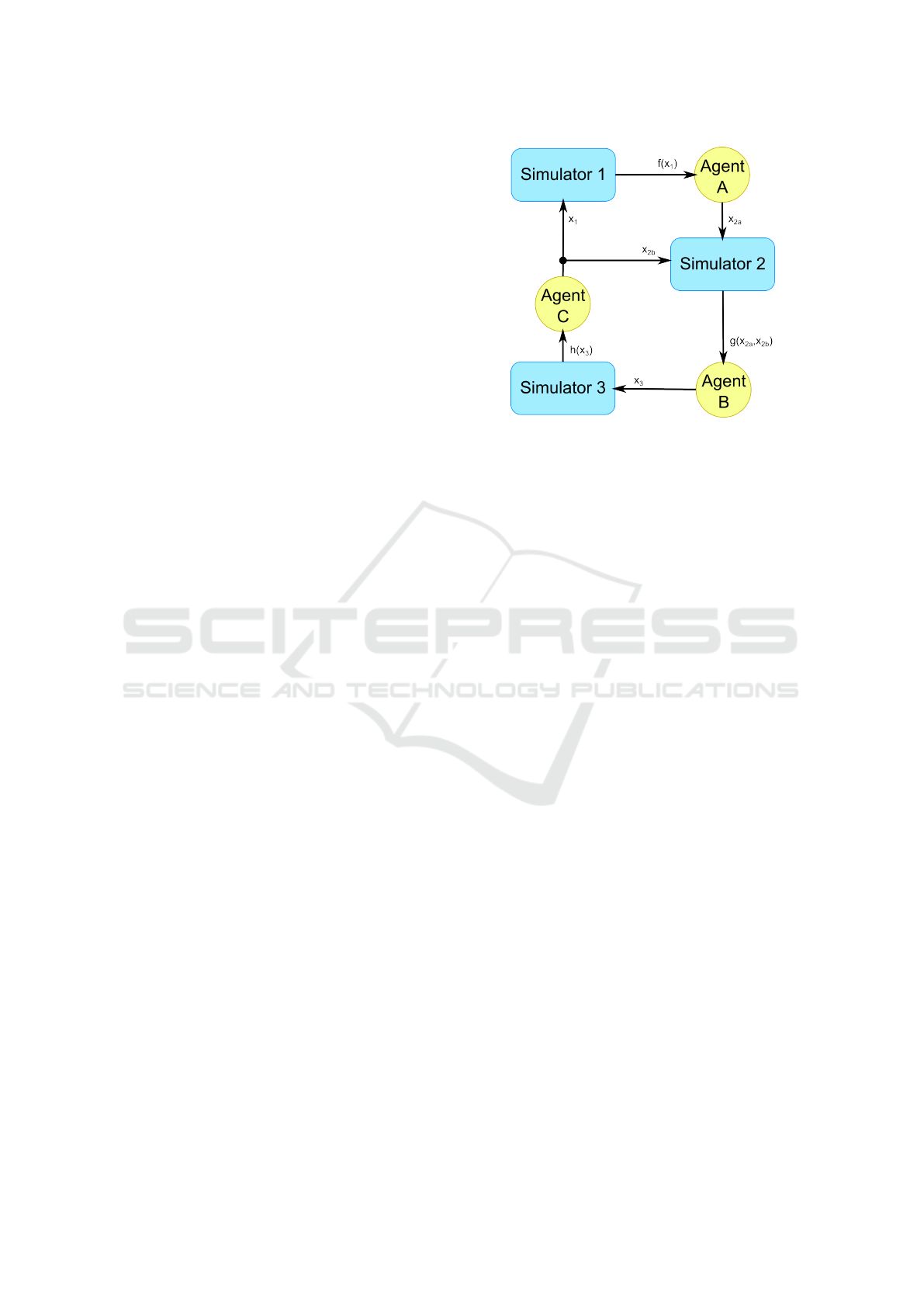
Figure 2: A Co-Simulation Network with 3 Simulators and

our Agents.

The neighborhood of an agent A is deﬁned as the

agents that are directly affected by the output of agent

A, including itself. Hence, the neighborhood of agent

A is composed of agent A and all the agents at the

output of the simulators connected to the output of

agent A. For instance, in ﬁgure 2, the neighborhood

of agent A is composed of agent A and agent B.

The global goal of the system is to reach a state in

which each agent perceives on its input the same value

it had written on its output at the previous timestep.

This would mean the network is correctly initialized

since the computed outputs of the simulators are sta-

ble.

3.2.2 Criticality of an Agent

Each agent seeks to meet the condition |x

−y

t−1

| = 0,

where x is the input of the agent, y its output, and t the

timestep. It is a reformulation of the ﬁxed point prob-

lem for the network, but centered on the links rather

than on the nodes. The value c = |x

− y

t−1

| is called

the criticality of the agent. The higher its critical-

ity, the less satisﬁed an agent is. We deﬁne C

sys

the

global criticality of the system as the highest critical-

ity among the agents. By deﬁnition, the problem is

solved when C

sys

= 0. It is a mere reformulation of

the ﬁxed-point problem expressed in 2.2 that is more

suitable for our approach.

At each timestep, each agent computes its critical-

ity, watches the criticalities in its neighborhood, and

tries to correlate their variation to the variation of its

own output. The agents adjust their output value in

order to lower their neighbors’ criticality. The next

section explains how they decide their output value.

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

3.3 Agents Behavior

Each agent has to decide its next action: whether to

increase or decrease its value, and by what amount,

in order to lower the criticality of its neighborhood as

quickly as possible. Its output y at timestep t is:

= y

t−1

+ a

Where a

is the decided action. The decision is based

on two dynamically adjusted internal variables:

• δ ∈ R

, with δ

min

≤ δ ≤ δ

max

is the amplitude of

the action, δ

min

and δ

max

are user-deﬁned parame-

ters, which will be discussed later ;

• σ ∈ N with −n ≤ σ ≤ n indicates the sign of the

action, n is a user-deﬁned parameter of the agent,

which will be discussed later.

These two variables directly deﬁne a:

a :=

(

δ ×

|σ|

if σ 6= 0

random(−δ, δ) otherwise

The sign of σ is the sign of the action, and the abso-

lute value of σ reﬂects how much the agent is con-

vinced that the sign is correct. If σ = 0, the decision

is a coin ﬂip between −δ and δ. We introduced ran-

domness here because all agents perceive and decide

simultaneously, thus falling into the El Farol bar prob-

lem (Whitehead, 2008).

3.3.1 Adaptation

Each agent dynamically manages its own internal δ

and σ variables, and decide how to adapt them. This

section explains how an agent adjusts its δ and σ.

Thanks to the jacobians provided by the simula-

tors connected on its output, the agent computes a

criticality jacobian, giving him an estimation of the

variations of the criticalities of its neighborhood. The

agent splits its neighbors into two groups, regarding

their criticality jacobian:

• the most critical group contains the most critical

neighbor (i.e. the neighbor with the highest crit-

icality) and all the neighbors whose criticality ja-

cobian has the same sign as the criticality jacobian

of the most critical neighbor. This means that if

the agent helps its most critical neighbor, its ac-

tion will also help all the other neighbors of this

group.

• the opposite group contains all the neighbors

whose criticality jacobian are of opposite sign

with the criticality jacobian of the most critical

neighbor. This means that if the agent helps its

most critical neighbor, its action will aslo hurt all

the neighbors of this group.

We call worst neighbor the most critical neighbor,

and opposite worst neighbor the most critical neigh-

bor from the opposite group. The goal for the agent

is then to help its worst neighbor while preventing its

opposite worst neighbor to become the worst neigh-

bor.

The agent observes four indicators in its environ-

ment to decide how to adjust its δ and σ:

• the direction of variation of the criticality of its

worst neighbor,

• the direction of variation of the criticality of its

opposite worst neighbor,

• the direction of variation of the difference be-

tween the worst neighbor’s criticality and the op-

posite worst neighbor’s criticality,

• the correlation between the sign of σ and the sign

of the criticality jacobian of the worst neighbor,

which indicates if the action of the agent is cur-

rently helping the worst neighbor or the opposite

worst neighbor.

Before computing its action, the agent adapts its δ

and σ according to a small set of rules conditioned

by these four indicators. These rules are presented in

table 1.

”Strengthen σ” means its absolute value is in-

creased without changing its sign: if σ is positive then

σ is incremented by one (decremented by one other-

wise). Likewise, ”weaken σ” means its absolute value

of σ is decreased without changing its sign: if σ is

positive then σ is decremented by one (incremented

by one otherwise). Finally, ”increase δ” means δ is

multiplied by α > 1 and ”decrease δ” means it is di-

vided by β > 1. α and β are user-deﬁned parameters.

The idea underlying this set of rules is to decrease

as fast as possible the criticality of all the neighbors.

The agent seeks to maximize its δ while reducing the

difference between the criticality of the worst neigh-

bor and the criticality of the opposite worst neighbor.

The worst case for an agent is when the condi-

tions of line 1 occur: the criticality of both the worst

neighbor and the opposite worst neighbor are increas-

ing, the highest criticality faster than the other. In

this case, the agent adjusts σ and δ in order to give

more help to its worst neighbor and less to the oppo-

site worst neighbor.

The best case is in line 8, when the criticality of

both the worst neighbor and the opposite worst neigh-

bor are decreasing, and the highest criticality is de-

creasing faster. This is an ideal situation if σ = n or

σ = −n, meaning that the agent is certain about its

current action.

Principles and Experiments of a Multi-Agent Approach for Large Co-Simulation Networks Initialization

Table 1: Rules of Adaptation.

Variation

of the criticality

of the worst neighbor

Variation

of the criticality

of the opposite

worst neighbor

Variation

of the difference

between these

two neighbors

Decision of an agent

currently helping

its worst neighbor

Decision of an agent

currently helping

its opposite worst neighbor

1 ↑ ↑ ↑

strengthen σ,

increase δ

weaken σ,

decrease δ

2 ↑ ↑ ↓ decrease δ

weaken σ,

decrease δ

3 ↑ ↓ ↑

strengthen σ,

increase δ

weaken σ,

decrease δ

4 ↑ ↓ ↓

impossible impossible

5 ↓ ↑ ↑ impossible impossible

6 ↓ ↑ ↓ strengthen σ

strengthen σ,

increase δ

7 ↓ ↓ ↑

strengthen σ,

increase δ

strengthen σ,

decrease δ

8 ↓ ↓ ↓ strengthen σ strengthen σ

3.3.2 Parameters

There are six parameters for the agents:

• n - deﬁnes the boundaries of σ, that varies be-

tween −n and n.

• δ

init

- since δ is adjusted in real time, the system

is able to converge for any initial value of δ but a

proper δ

init

may help for a quicker convergence.

• δ

min

- the minimal value for δ has to be strictly

positive, because δ

min

= 0 often leads to dead-

locks.

• δ

max

- the maximal value for δ is merely a safety

guard to avoid too big variations. If δ

min

= δ

max

the system works with a constant δ.

• α - the ”increase factor” by which δ is multiplied

when it needs to increase,

• β - the ”decrease factor” by which δ is divided

when it needs to decrease.

α and β both have to be strictly greater than one. They

are the only really sensitive parameters as the stabi-

lization of the system depends on them. α should be

small comparatively to β. Although a thorough study

of their impact is needed, in our experiments we never

had good results when α was greater than

β. For

some experiments, the best results were obtained with

β worths 100 times α.

Generally, the lower δ

min

and δ

max

the more pre-

cise the solution, but at the cost of more timesteps to

reach it. A greater β makes δ more frequently close

to δ

min

, hence gaining precision and loosing speed of

convergence, and vice versa for α. A big α tends to

harm the stability of the system, provoking big oscil-

lations around the solution instead of smoothly con-

verging towards it. Finally, n impacts the inertia of

the system: if it is high, an agent will be slower to

change direction after having strengthened σ several

times consecutively.

Except for δ

init

all the parameters can be interac-

tively modiﬁed at runtime, the system will self-adapt

according to the new values.

Figure 3: Neighborhood Graph of a 3 Nodes Test Case.

4 RESULTS

This section shows results of various experiments

on generated networks with polynomial nodes. We

used a generator to create random topologies of net-

works of polynomial nodes. Nodes are of the form of

+ bx + c with random a, b and c. For these ex-

periments, our system is implemented in Java 1.7 and

runs on an HP Elitebook laptop with an Intel Core i7

processor and 16GB of RAM. The parameters were

set as follows:

• n = 3

• δ

init

= 1.0

• δ

min

= 0.001

• δ

max

= 1.0

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

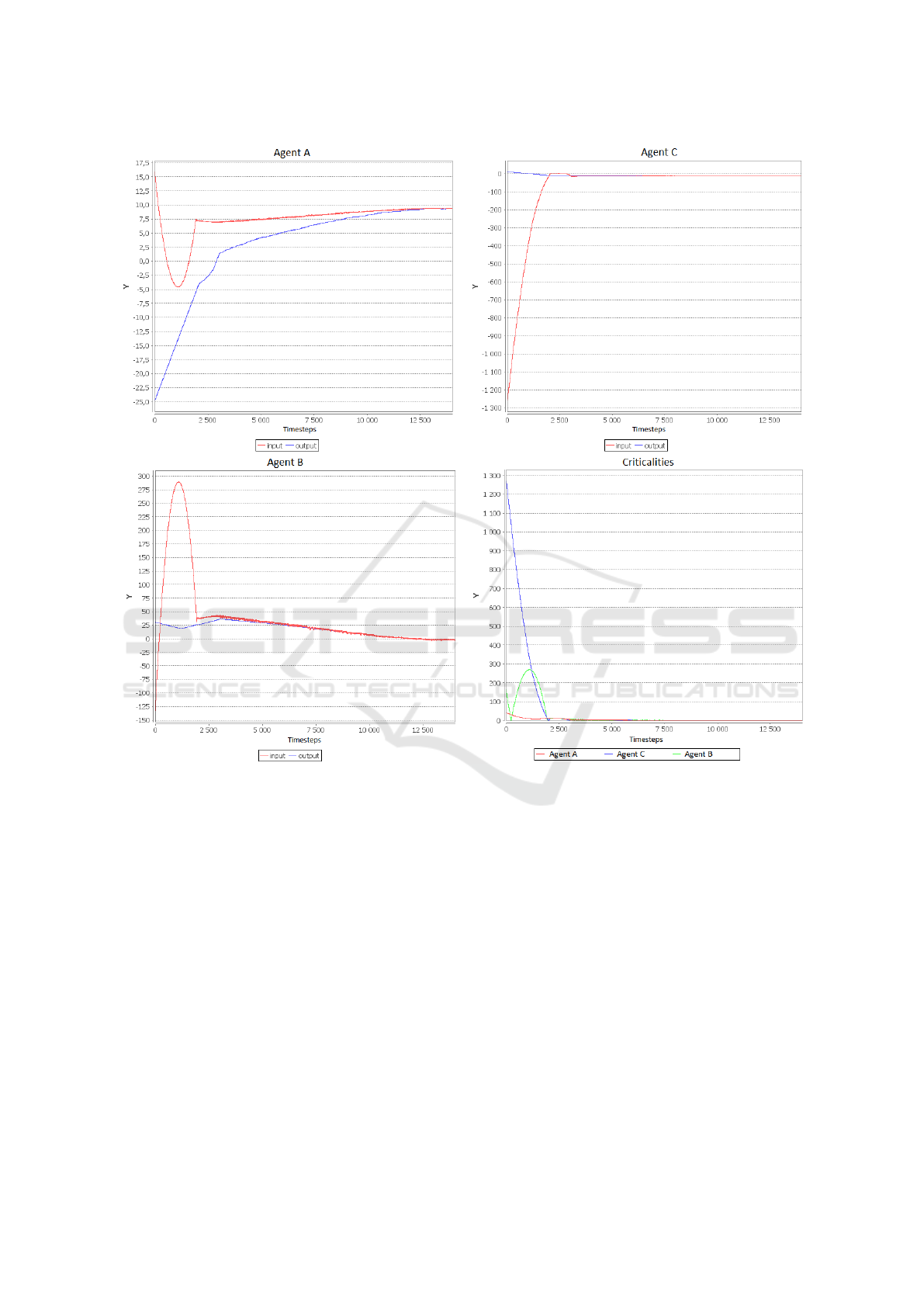
Figure 4: Convergence with a 3 Nodes Network.

• α = 1.2

• β = 100

These values were obtained empirically through ex-

tensive testing and proved to be efﬁcient for all our ex-

perimentations with networks of second degree poly-

nomial nodes, regardless of the topology.

4.1 3 Polynomial Nodes

Our ﬁrst experiment involves a simple 3 nodes net-

work. Figure 3 shows the neighborhood graph of this

simple case. It is a representation of the network of in-

ﬂuence of the agents. An edge from A to B means that

the neighborhood of A includes B, in other words A

directly impacts B via a simulator. Here agent A has

two neighbors including itself, agent B has two neigh-

bors including itself, and agent C has three neighbors

including itself.

Figure 4 shows the input and output of each agent

during the resolution, along with their criticalities (the

difference between their input and their output). We

see that at the beginning, the most critical agent is

C. Since it is in the neighborhood of both A and B,

these agents tend to help C more, even if it increases

their own criticality. Around timestep 1500, agent B

is on the verge to become the most critical agent. The

agents (including B itself) react and ﬁnd a way to de-

crease both C and B’s criticalities, at the expense of

A. In the end, they all have converged toward a stable

state where their criticality is less than δ

min

(presently

−3

). It took approximatively 10000 timesteps (3

seconds).

Principles and Experiments of a Multi-Agent Approach for Large Co-Simulation Networks Initialization

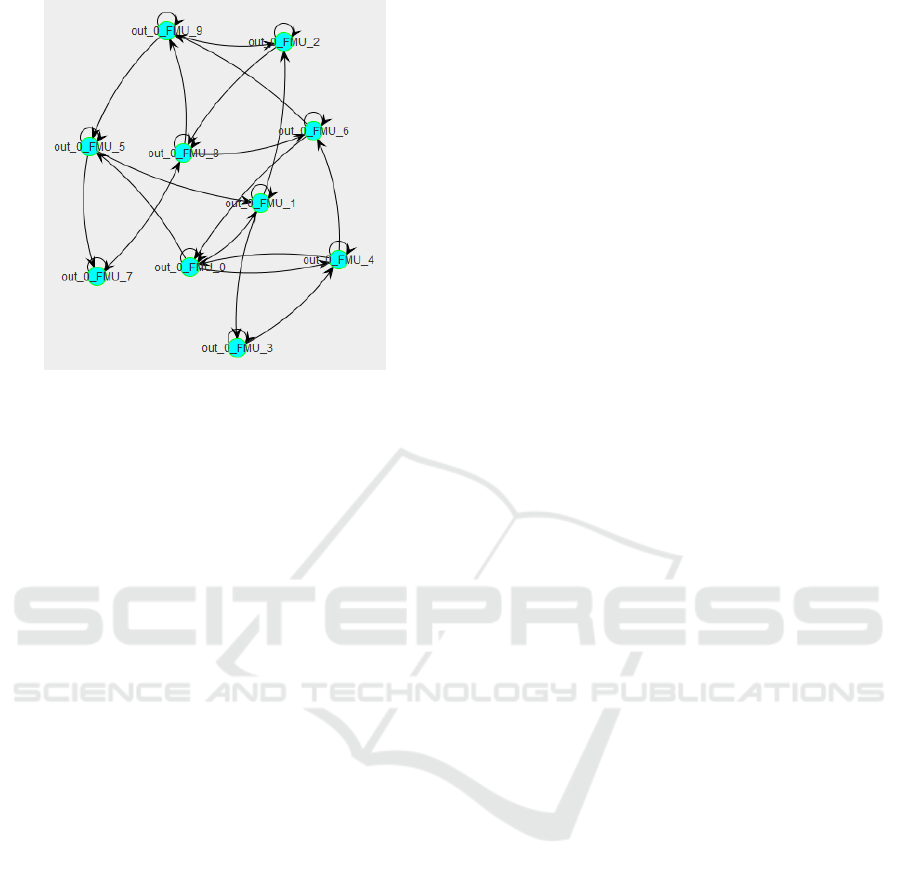
Figure 5: Neighborhood Graph of a 10 Nodes Test Case.

4.2 10 Polynomial Nodes

In this experiment, we test our system with a bigger

network. Figure 5 shows the neighborhood graph of

our MAS for this case. For the sake of concision and

readability, we do not show here the input and output

curves of each agents, but only their criticalities (6).

We can see that the agents immediately ﬁnd a way

to decrease the worst criticalities, but then struggle

to make the residual criticalities disappear. However,

they end up ﬁnding a way to reach a state where each

criticality is less than δ

min

. It took approximatively

14000 timesteps (30 seconds).

With the same parameters, for a network more

than three times the size of the previous one, the num-

ber of timesteps to converge is only 40% greater than

the previous case. Unfortunately, the duration is about

7 times longer.

4.3 100 Polynomial Nodes

This experiments show how the MAS scales up to a

network of 100 polynomial nodes. We do not present

the neighborhood graph because it is unreadable. Fig-

ure 7 shows the criticalities of all agents. We see that

the systems converge in about 18500 timesteps. This

is only 1.32 times more timesteps, while the network

is ten time bigger. However, this time the computa-

tion took 90 minutes to complete (180 times longer

than the 10 nodes network).

4.4 Discussion

The main result of these experiments is that the num-

ber of timesteps to ﬁnd a solution does not increase

with the size of the network. In other words, the sys-

tem scales up to the size of the network in term of

the the total number of actions needed for each agent.

However, the duration of the computation increases

with the size of the network. This is mainly due to the

fact that our prototype is single-threaded: the compu-

tation of each node has to be done sequentially. Co-

simulations can be distributed, sometimes even phys-

ically distributed, enabling to compute each node of

the network in parallel. Moreover, our agents take

completely local decisions and do not need sophisti-

cated synchronization. This is why our future work

will focus on the parallelization of our implementa-

tion. This should signiﬁcantly improve time of com-

putation, making the system also scalable in terms of

duration of computation.

5 CONCLUSION AND FUTURE

WORKS

Co-initialization, the problem of properly initializ-

ing interdependent simulators in a co-simulation is

challenging, especially when simulators are numer-

ous. This problem can be reinterpreted as a ﬁxed-

point problem, for which current methods suffer from

a lack of scalability. This paper presented a multi-

agent approach where each output of each simula-

tor is an agent trying to ﬁnd an initial value for the

simulators that are connected to it. Agents seek to

help their neighborhood as well as themselves, and

together converge towards a stable solution.

Results show that this approach is efﬁcient and

scales up to the number of simulators regarding the

number of timesteps required to reach a solution. It

takes only 1.85 times more timesteps to initialize a

network of 100 simulators than a network of 3 sim-

ulators. However, our current single-threaded Java

implementation does not scale: because their execu-

tion is sequential, the higher the number of simula-

tors, the longer a timestep is. Future work will fo-

cus on a multi-threaded parallelized implementation

to make the system also scalable in terms duration of

computation. Our intention is also to get rid of the

jacobians. The less the agents need to know about the

models, the more generic our approach will be. This

could be achieved by enhancing the learning abilities

of the agents, so they improve their understanding of

the simulators with each action they make. Finally, a

better formalization of the system and a more theoret-

ical analysis are needed before moving forward with

extensive comparisons with other ﬁxed-point solvers.

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

Figure 6: Convergence with a 10 Nodes Network.

Figure 7: Convergence with a 100 Nodes Network.

REFERENCES

Alber, Y., Reich, S., and Yao, J.-C. (2003). Iterative meth-

ods for solving ﬁxed-point problems with nonself-

mappings in banach spaces. Abstract and Applied

Analysis, 2003(4):193–216.

Belghache, E., Georg

e, J.-P., and Gleizes, M.-P. (2016). To-

wards an Adaptive Multi-Agent System for Dynamic

Big Data Analytics. In The IEEE International Con-

ference on Cloud and Big Data Computing (CBD-

Com), Toulouse, France. IEEE Computer Society -

Conference Publishing Services.

Blochwitz, T., Otter, M., Arnold, M., Bausch, C., Clauß, C.,

Elmqvist, H., Junghanns, A., Mauss, J., Monteiro, M.,

Neidhold, T., et al. (2011). The functional mockup

interface for tool independent exchange of simulation

models. In 8th International Modelica Conference,

pages 105–114, Dresden.

Bonnans, J.-F., Gilbert, J. C., Lemar

echal, C., and Sagas-

tiz

abal, C. A. (2013). Numerical optimization: the-

oretical and practical aspects. Springer Science &

Business Media.

Bonnet, J., Gleizes, M.-P., Kaddoum, E., Rainjonneau, S.,

and Flandin, G. (2015). Multi-satellite mission plan-

ning using a self-adaptive multi-agent system. In

IEEE International Conference on Self-Adaptive and

Self-Organizing Systems (SASO), Cambridge, MA,

USA, pages 11–20. IEEE Computer Society - Confer-

ence Publishing Services.

Border, K. C. (1989). Fixed point theorems with applica-

tions to economics and game theory. Cambridge Uni-

versity Press.

Principles and Experiments of a Multi-Agent Approach for Large Co-Simulation Networks Initialization

Bouchhima, F., Briere, M., Nicolescu, G., Abid, M., and

Aboulhamid, E. M. (2006). A systemc/simulink co-

simulation framework for continuous/discrete-events

simulation. In Behavioral Modeling and Simulation

Workshop, Proceedings of the 2006 IEEE Interna-

tional, pages 1–6.

Costan, A., Gaubert, S., Goubault, E., Martel, M., and

Putot, S. (2005). A policy iteration algorithm for

computing ﬁxed points in static analysis of programs.

In Etessami, K. and Rajamani, S. K., editors, Com-

puter Aided Veriﬁcation: 17th International Confer-

ence, CAV 2005, Edinburgh, Scotland, UK, July 6-10,

2005. Proceedings, pages 462–475. Springer Berlin

Heidelberg, Berlin, Heidelberg.

Georg

e, J.-P., Gleizes, M.-P., and Camps, V. (2011). Co-

operation. In Di Marzo Serugendo, G., Gleizes,

M.-P., and Karageogos, A., editors, Self-organising

Software, Natural Computing Series, pages 7–32.

Springer Berlin Heidelberg.

Liberatore, V. and Al-Hammouri, A. (2011). Smart grid

communication and co-simulation. In Energytech,

2011 IEEE, pages 1–5.

Rantrua, A., Maesen, E., Chabrier, S., and Gleizes, M.-P.

(2015). Learning Aircraft Behavior from Real Air

Trafﬁc. The Journal of Air Trafﬁc Control, 57(4):10–

14.

Schaefer, B.-J. and Wambach, J. (2005). The phase dia-

gram of the quark–meson model. Nuclear Physics A,

757(3):479–492.

Sicklinger, S., Lerch, C., W

uchner, R., and Bletzinger, K.-

U. (2015). Fully coupled co-simulation of a wind

turbine emergency brake maneuver. Journal of Wind

Engineering and Industrial Aerodynamics, 144:134–

145.

Vaubourg, J., Presse, Y., Camus, B., Bourjot, C., Ciar-

letta, L., Chevrier, V., Tavella, J.-P., and Morais, H.

(2015). Multi-agent multi-model simulation of smart

grids in the ms4sg project. In International Confer-

ence on Practical Applications of Agents and Multi-

Agent Systems (PAAMS 2015), pages 240–251, Sala-

manca, Spain. Springer.

Whitehead, D. (2008). The el farol bar problem revisited:

Reinforcement learning in a potential game. ESE Dis-

cussion Papers, 186.

Yao, Y., Cho, Y. J., and Liou, Y.-C. (2011). Algorithms

of common solutions for variational inclusions, mixed

equilibrium problems and ﬁxed point problems. Eu-

ropean Journal of Operational Research, 212(2):242

– 250.

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence