
The Possibilistic Reward Method and a Dynamic Extension for the
Multi-armed Bandit Problem: A Numerical Study
Miguel Mart
´
ın, Antonio Jim
´
enez-Mart
´
ın and Alfonso Mateos
Decision Analysis and Statistics Group, Universidad Polit
´
ecnica de Madrid,
Campus de Montegancedo S/N, Boadilla del Monte, Spain
Keywords:
Multi-armed Bandit Problem, Possibilistic Reward, Numerical Study.
Abstract:
Different allocation strategies can be found in the literature to deal with the multi-armed bandit problem under
a frequentist view or from a Bayesian perspective. In this paper, we propose a novel allocation strategy, the
possibilistic reward method. First, possibilistic reward distributions are used to model the uncertainty about
the arm expected rewards, which are then converted into probability distributions using a pignistic probability
transformation. Finally, a simulation experiment is carried out to find out the one with the highest expected
reward, which is then pulled. A parametric probability transformation of the proposed is then introduced
together with a dynamic optimization, which implies that neither previous knowledge nor a simulation of the
arm distributions is required. A numerical study proves that the proposed method outperforms other policies
in the literature in five scenarios: a Bernoulli distribution with very low success probabilities, with success
probabilities close to 0.5 and with success probabilities close to 0.5 and Gaussian rewards; and truncated in
[0,10] Poisson and exponential distributions.
1 INTRODUCTION
The multi-armed bandit problem has been at great
depth studied in statistics (Berry and Fristedt, 1985),
becoming fundamental in different areas of eco-
nomics, statistics or artificial intelligence, such as re-
inforcement learning (Sutton and Barto, 1998) and
evolutionary programming (Holland, 1992) .
The name bandit comes from imagining a gam-
bler playing with K slot machines. The gambler can
pull the arm of any of the machines, which produces a
reward payoff. Since the reward distributions are ini-
tially unknown, the gambler must use exploratory ac-
tions to learn the utility of the individual arms. How-
ever, exploration has to be controlled since excessive
exploration may lead to unnecessary losses. Thus, the
gambler must carefully balance exploration and ex-
ploitation.
In its most basic formulation, a K-armed ban-
dit problem is defined by random variables X
i,n
for
1 ≤ i ≤ K and n ≥ 1, where each i is the index of
an arm of a bandit. Successive plays of arm i yield
rewards X
i,1
,X
i,2
,... which are independent and iden-
tically distributed according to an unknown law with
unknown expectation µ
i
. Independence also holds for
rewards across arms; i.e., X
i,s
and X
j,t
are indepen-
dent (and usually not identically distributed) for each
1 ≤ i < j ≤ K and each s,t ≥ 1.
A gambler learning the distributions of the arms’
rewards can use all past information to decide about
his next action. A policy, or allocation strategy, A is
then an algorithm that chooses the next arm to play
based on the sequence of previous plays and obtained
rewards. Let n
i
be the number of times arm i has been
played by A during the first n plays.
The goal is to maximize the sum of the rewards re-
ceived, or equivalently, to minimize the regret, which
is defined as the loss compared to the total reward that
can be achieved given full knowledge of the problem,
i.e., when the arm giving the highest expected reward
is pulled/played all the time. The regret of A after n
plays can be computed as
µ
∗
n −
K
∑
i=1
µ
i
E[n
i
], where µ
∗
= max
1≤i≤K
{µ
i
}, (1)
and E[·] denotes expectation.
In this paper, we propose two allocation strategies,
the possibilistic reward (PR) method and a dynamic
extension (DPR), in which the uncertainty about the
arm expected rewards are first modelled by means
of possibilistic reward distributions. Then, a pig-
nistic probability transformation from decision the-
Martin M., JimÃl’nez-Martà n A. and Mateos A.
The Possibilistic Reward Method and a Dynamic Extension for the Multi-armed Bandit Problem: A Numerical Study.
DOI: 10.5220/0006186400750084
In Proceedings of the 6th International Conference on Operations Research and Enterprise Systems (ICORES 2017), pages 75-84
ISBN: 978-989-758-218-9
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
75

ory and transferable belief model is used to convert
these possibilistic functions into probability distribu-
tions following the insufficient reason principle. Fi-
nally, a simulation experiment is carried out by sam-
pling from each arm according to the corresponding
probability distribution to identify the arm with the
higher expected reward and play that arm.
The paper is structured as follows. In Section 2
we briefly review the allocation strategies in the litera-
ture. In Section 3, we describe the possibilistic reward
method and its dynamic extension. A numeric study
is carried out in Section 4 to compare the performance
of the proposed policies against the best ones in the
literature on the basis of five scenarios for reward dis-
tributions. Finally, some conclusions are provided in
Section 5.
2 ALLOCATION STRATEGY
REVIEW
As pointed out in (Garivier and Capp
´
e, 2011), two
families of bandit settings can be distinguished. In
the first, the distribution of X
it
is assumed to belong
to a family of probability distributions {p
θ
,θ ∈ Θ
i
},
whereas in the second, the rewards are only assumed
to be bounded (say, between 0 and 1), and policies
rely directly on the estimates of the expected rewards
for each arm.
Almost all the policies or allocation strategies in
the literature focus on the first family and they can
be separated, as cited in (Kaufmann et al., 2012), in
two distinct approaches: the frequentist view and the
Bayesian approach. In the frequentist view, the ex-
pected mean rewards corresponding to all arms are
considered as unknown deterministic quantities and
the aim of the algorithm is to reach the best parameter-
dependent performance. In the Bayesian approach
each arm is characterized by a parameter which is en-
dowed with a prior distribution.
Under the frequentist view, Lai and Robbins (Lai
and Robbins, 1985) first constructed a theoretical
framework for determining optimal policies. For spe-
cific families of reward distributions (indexed by a
single real parameter), they found that the optimal
arm is played exponentially more often than any other
arm, at least asymptotically. They also proved that
this regret is the best one. Burnetas and Katehakis
(Burnetas and Katehakis, 1996) extended their result
to multiparameter or non-parametric models.
Later, (Agrawal, 1995) introduced a generic class
of index policies termed upper confidence bounds
(UCB), where the index can be expressed as simple
function of the total reward obtained so far from the
arm. These policies are thus much easier to compute
than Lai and Robbins’, yet their regret retains the op-
timal logarithmic behavior.
From then, different policies based on UCB can be
found in the literature. First, Auer et al. (Auer et al.,
2002) strengthen previous results by showing simple
to implement and computationally efficient policies
(UCB1, UCB2 and UCB-Tuned) that achieve loga-
rithmic regret uniformly over time, rather than only
asymptotically.
Specifically, policy UCB1 is derived from the
index-based policy of (Agrawal, 1995). The index of
this policy is the sum of two terms. The first term
is simply the current average reward, ¯x
i
, whereas the
second is related to the size of the one-sided confi-
dence interval for the average reward within which the
true expected reward falls with overwhelming proba-
bility. In UCB2, the plays are divided in epochs. In
each new epoch an arm i is picked and then played
τ(r
i
+1)−τ(r
i
) times, where τ is an exponential func-
tion and r
i
is the number of epochs played by that arm
so far.
In the same paper, UCB1 was extended for the
case of normally distributed rewards, which achieves
logarithmic regret uniformly over n without knowing
means and variances of the reward distributions. Fi-
nally, UCB1-Tuned was proposed to more finely tune
the expected regret bound for UCB1.
Later, Audibert et al. (Audibert et al., 2009) pro-
posed the UCB-V policy, which is also based on upper
confidence bounds but taking into account the vari-
ance of the different arms. It uses an empirical ver-
sion of the Bernstein bound to obtain refined upper
confidence bounds. They proved that the regret con-
centrates only at a polynomial rate in UCB-V and that
it outperformed UCB1.
In (Auer and Ortner, 2010) the UCB method of
Auer et al. (Auer et al., 2002) was modified, leading
to the improved-UCB method. An improved bound
on the regret with respect to the optimal reward was
also given.
An improved UCB1 algorithm, termed minimax
optimal strategy in the stochastic case (MOSS),
was proposed by Audibert & Bubeck (Audibert and
Bubeck, 2010), which achieved the distribution-
free optimal rate while still having a distribution-
dependent rate logarithmic in the number of plays.
Another class of policies under the frequentist
perspective are the Kullback-Leibler (KL)-based al-
gorithms, including DMED, K
in f
, KL-UCB and kl-
UCB.
The deterministic minimum empirical divergence
(DMED) policy was proposed by Honda & Take-
mura (Honda and Takemura, 2010) motivated by
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
76

a Bayesian viewpoint for the problem (although a
Bayesian framework is not used for theoretical anal-
yses). This algorithm, which maintains a list of arms
that are close enough to the best one (and which thus
must be played), is inspired by large deviations ideas
and relies on the availability of the rate function asso-
ciated to the reward distribution.
In (Maillard et al., 2011), the K
in f
-based algorithm
was analyzed by Maillard et al. It is inspired by the
ones studied in (Lai and Robbins, 1985; Burnetas and
Katehakis, 1996), taking also into account the full
empirical distribution of the observed rewards. The
analysis accounted for Bernoulli distributions over the
arms and less explicit but finite-time bounds were ob-
tained in the case of finitely supported distributions
(whose supports do not need to be known in advance).
These results improve on DMED, since finite-time
bounds (implying their asymptotic results) are ob-
tained, UCB1, UCB1-Tuned, and UCB-V.
Later, the KL-UCB algorithm and its variant KL-
UCB+ were introduced by Garivier & Capp
´
e (Gariv-
ier and Capp
´
e, 2011). KL-UCB satisfied a uniformly
better regret bound than UCB and its variants for arbi-
trary bounded rewards, whereas it reached the lower
bound of Lai and Robbins when Bernoulli rewards are
considered. Besides, simple adaptations of the KL-
UCB algorithm were also optimal for rewards gener-
ated from exponential families of distributions. Fur-
thermore, a large-scale numerical study comparing
KL-UCB with UCB, MOSS, UCB-Tuned, UCB-V,
DMED was performed, showing that KL-UCB was
remarkably efficient and stable, including for short
time horizons.
New algorithms were proposed by Capp
´
e et al.
(Capp
´
e et al., 2013) based on upper confidence
bounds of the arm rewards computed using differ-
ent divergence functions. The kl-UCB uses the
Kullback-Leibler divergence; whereas the kl-poisson-
UCB and the kl-exp-UCB account for families of
Poisson and Exponential distributions, respectively.
A unified finite-time analysis of the regret of these
algorithms shows that they asymptotically match the
lower bounds of Lai and Robbins, and Burnetas and
Katehakis. Moreover, they provide significant im-
provements over the state-of-the-art when used with
general bounded rewards.
Finally, the best empirical sampled average
(BESA) algorithm was proposed by Baransi et al.
(Baransi et al., 2014). It is not based on the compu-
tation of an empirical confidence bounds, nor can it
be classified as a KL-based algorithm. BESA is fully
non-parametric. As shown in (Baransi et al., 2014),
BESA outperforms TS (a Bayesian approach intro-
duced in the next section) and KL-UCB in several
scenarios with different types of reward distributions.
Stochastic bandit problems have been analyzed
from a Bayesian perspective, i.e. the parameter is
drawn from a prior distribution instead of considering
a deterministic unknown quantity. The Bayesian per-
formance is then defined as the average performance
over all possible problem instances weighted by the
prior on the parameters.
The origin of this perspective is in the work by
Gittins (Gittins, 1979). Gittins’ index based policies
are a family of Bayesian-optimal policies based on
indices that fully characterize each arm given the cur-
rent history of the game, and at each time step the arm
with the highest index will be pulled.
Later, Gittins proposed the Bayes-optimal ap-
proach (Gittins, 1989) that directly maximizes ex-
pected cumulative rewards with respect to a given
prior distribution.
A lesser known family of algorithms to solve ban-
dit problems is the so-called probability matching or
Thompson sampling (TS). The idea of TS is to ran-
domly draw each arm according to its probability of
being optimal. In contrast to Gittins’ index, TS can
often be efficiently implemented (Chapelle and Li,
2001). Despite its simplicity, TS achieved state-of-
the-art results, and in some cases significantly outper-
formed other alternatives, like UCB methods.
Finally, Bayes-UCB was proposed by Kaufmann
et al. (Kaufmann et al., 2012) inspired by the
Bayesian interpretation of the problem but retaining
the simplicity of UCB-like algorithms. It constitutes
a unifying framework for several UCB variants ad-
dressing different bandit problems.
3 POSSIBILISTIC REWARD
METHOD
The allocation strategy we propose accounts for the
frequentist view but they cannot be classified as either
a UCB method nor a Kullback-Leibler (KL)-based al-
gorithm. The basic idea is as follows: the uncertainty
about the arm expected rewards are first modelled
by means of possibilistic reward distributions de-
rived from a set of infinite nested confidence intervals
around the expected value on the basis of Chernoff-
Hoeffding inequality. Then, we follow the pignistic
probability transformation from decision theory and
transferable belief model (Smets, 2000), that estab-
lishes that when we have a plausibility function, such
as a possibility function, and any further information
in order to make a decision, we can convert this func-
tion into an probability distribution following the in-
The Possibilistic Reward Method and a Dynamic Extension for the Multi-armed Bandit Problem: A Numerical Study
77
sufficient reason principle.
Once we have a probability distribution for the re-
ward in each arm, then a simulation experiment is car-
ried out by sampling from each arm according to their
probability distributions to find out the one with the
highest expected reward higher. Finally, the picked
arm is played and a real reward is output.
We shall first introduce the algorithm for rewards
bounded between [0,1] in the real line for simplicity
and then, we will extend it for any real interval. The
starting point of the method we propose is Chernoff-
Hoeffding inequality (Hoeffding, 1963), which pro-
vides an upper bound on the probability that the sum
of random variables deviates from its expected value,
which for [0,1] bounded rewards leads to:
P
1
n
∑
n
t=1
X
t
− E[X]
> ε
≤ 2e
−2nε
2
⇒
P
1
n
∑
n
t=1
X
t
− E[X]
≤ ε
≥ 1 − 2e
−2nε
2
⇒
P
E[X] ∈
1
n
∑
n
t=1
X
t
− ε,
1
n
∑
n
t=1
X
t
+ ε
≥ 1 − 2e
−2nε
2
.
It can be used for building an infinite set of
nested confidence intervals, where the confidence
level of the expected reward (E[X]) in the interval
I = [
1
n
∑
n
t=1
X
t
− ε,
1
n
∑
n
t=1
X
t
+ ε] is 1 − 2e
−2nε
2
.
Besides, a fuzzy function representing a possi-
bilistic distribution can be implemented from nested
confidence intervals (Dubois et al., 2004):
π(x) = sup
{
1 − P(I),x ∈ I
}
.
Consequently, in our approach for confidence in-
tervals based on Hoeffding inequality, the sup of each
x will be the bound of minimum interval around the
mean (
1
n
∑
n
t=1
X
t
) where x is included. That is, the in-
terval with ε =
1
n
∑
n
t=1
X
t
− x
.
If we consider ˆµ
n
=
1
n
∑
n
t=1
X
t
, for simplicity, then
we have:
π(x) =
min{1,2e
−2n
i
×(ˆµ
n
−x)
2
}, if 0 ≤ x ≤ 1
0, otherwise
.
Note that π(x) is truncated in [0,1] both in the x
axis, due to the bounded rewards, and the y axis, since
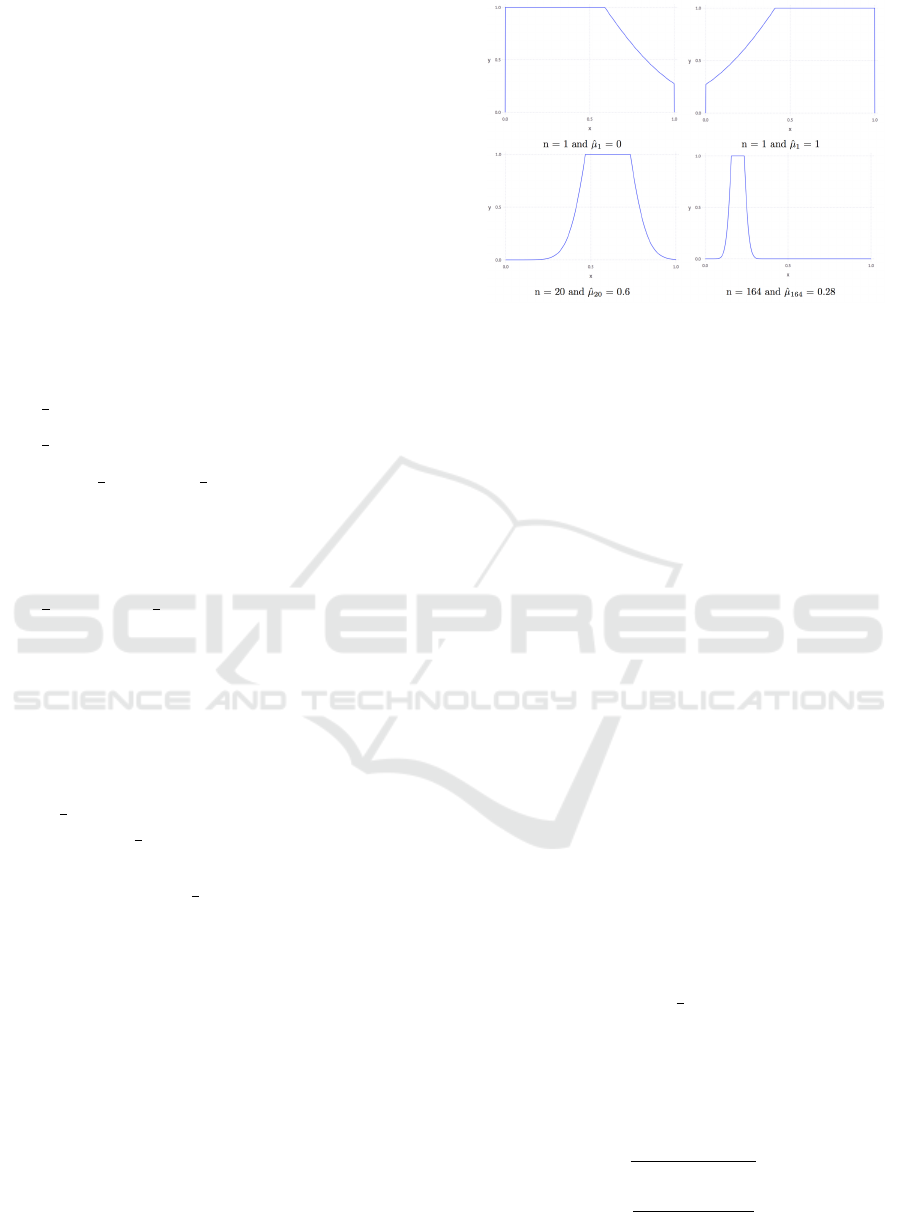
a possibility measure cannot be greater than 1. Fig. 1
shows several examples of possibilistic rewards dis-
tributions.
3.1 A Pignistic Probability
Transformation
Once the arm expected rewards are modelled by
means of possibilistic functions, next step consists of
Figure 1: Possibilistic rewards distributions.
picking the arm to pull on the basis of that uncertainty.
For this, we follow the pignistic probability transfor-
mation from decision theory and transferable belief
model (Smets, 2000), which, in summary, establishes
that when we have a plausibility function, such as a
possibility function, and any further information in or-
der to make a decision, we can convert this function
into an probability distribution following the insuf-
ficient reason principle (Dupont, 1978), or consider
equipossible the same thing that equiprobable. In our
case, it can be performed by dividing π(x) function by
R
1
0
min{1,1 − e
−2n
i
×(ˆµ
n
−x)
2
}dx.
However, further information is available in form
of restrictions that allow us to model a better approx-
imation of the probability functions. Since a proba-
bility density function must be continuous and inte-
grable, we have to smooth the gaps that appear be-
tween points close to 0 and 1. Besides, we know
that the probability distribution should be a unimodal
distribution around the sampling average ˆµ
n
. Thus,
the function must be monotonic strictly increasing in
[0, ˆµ
n
) and monotonic strictly decreasing in (ˆµ
n
,1].
We propose the following approximation to incorpo-
rate the above restrictions:
1. π(x) is transformed into an intermediate function
π
r
(x) as follows:
(a) Multiply the not truncated original function,
2e
−2n
i
×(ˆµ
n
−x)
2
, by
1
2
in order to reach a maxi-
mum value 1.
(b) Fit the resulting function in order to have π
r
(0)
= 0 and π
r
(1) = 0:
∆
low
= e
−2n
i
×(ˆµ
n
)
2
, ∆
up
= e
−2n
i
×(ˆµ
n
−1)
2
,
π
r
(x) =
e
−2n
i
×(ˆµ
n
−x)
2
−∆
low
1−∆
low
, if x ≤ ˆµ
n
e
−2n
i
×(ˆµ
n
−x)
2
−∆
up
1−∆
up
, if x > ˆµ
n
0, otherswise
.
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
78

Figure 2: Pignistic probability transformation examples.
Two exceptions have to be considered. When
all the rewards of past plays are 0 or 1, then the
transformations to reach π
r
(0) = 0 or π
r
(1) = 0
are not applied, respectively.
2. The pignistic transformation is applied to π
r
(x) by
dividing by
R
1
0
π
r
(x)dx, leading to the probability
distribution
P(x) = π
r
(x)/C, with C =
Z
1
0
π
r
(x)dx.
Fig. 2 shows the application of the pignistic prob-
ability transformation to derive a probability distribu-
tion (in green) from the π(x) functions (in blue) in
Fig. 1.
The next step is similar to Thompson sampling
(TS) (Chapelle and Li, 2001). Once we have built the
pignistic probabilities for all the arms, we pick the
arm with the highest expected reward. For this, we
carry out a simulation experiment by sampling from
each arm according to their probability distributions.
Finally, the picked arm is pulled/played and a real re-
ward is output. Then, the possibilistic function cor-
responding to the picked arm is updated and started
again.
3.2 Parametric Probability
Transformation and Dynamic
Optimization
In the previous section, rewards were bound to the in-
terval [0,1] and the most used possibility-probability
transformation according to pignistic or maximal en-
tropy methods (Smets, 2000) was implemented. Now,
we extend rewards to any real interval [a, b] and in-
terpret the possibility distribution π
r
(x) as a proba-
bility distribution set that encloses any distribution
P(x) such as ∀A = [a,b] → π
r
(x ∈ A) ≤ P(x ∈ A) ≤
1 − π
r
(x /∈ A). Consequently, another distribution en-
closed by π
r
(x) that minimizes the expected regret for
any particular reward distribution could be used.
In order to trade off performance and computa-
tional cost issues, we were able to modify our previ-
ous probabilistic-possibilistic transformation to create
a family of probabilities just adding an α parameter as
follows:
P(x) = π
α
(x)/C with C =
Z
b
a
π
α
(x)dx
and
π
α
(x) =
e
−2n
i
×α(
ˆµ
n
−x
b−a
)
2
−∆
α
low
1−∆
α
low
, if x ≤ ˆµ
n
e
−2n
i
×α(
ˆµ
n
−x
b−a
)
2
−∆
α
up
1−∆
α
up
, if x > ˆµ
n
0, otherwise
,
where
∆
α
low
= e
−2n
i
×α(
ˆµ
n
b−a
)
2
,∆
α
up
= e
−2n
i
×α(
ˆµ
n
−1
b−a
)
2
,and α > 1.
By adding parameter α, it is possible to adjust the
transformation for any particular reward distribution
to minimize the expected regret. For this, an opti-
mization process for parameter α will be required.
Alternatively to manually tuning parameter α, we
propose modifying the PR algorithm to dynamically
tune it while bearing in mind the minimization of the
expected regret. Thus, the advantage of the new dy-
namic possibilistic reward (DPR) is that it requires
neither previous knowledge nor a simulation of the
arm distributions. In fact, the reward distributions are
not known in the majority of the cases. Besides, the
performance of the DPR against PR and other poli-
cies in terms of expected regrets will be analyzed in
the next section.
Several experiments have shown that the scale pa-
rameter α is correlated with the inverse of the vari-
ance of the reward distribution shown by the experi-
ment. As such, analogously to Auer et al. (Auer et al.,
2002), for practical purposes we can fix parameter α
as
α = 0.5 ×
(b − a)
2
˜var
, (2)
where ˜var is the sample variance of the rewards
seen by the agent and [a,b] the reward interval.
4 NUMERICAL STUDY
In this section, we show the results of a numerical
study in which we have compared the performance of
The Possibilistic Reward Method and a Dynamic Extension for the Multi-armed Bandit Problem: A Numerical Study
79
PR and DPR methods against other allocation strate-
gies in the literature. Specifically, we have cho-
sen KL-UCB, DMED+, BESA, TS and Bayes-UCB,
since they are the most recent proposals and they out-
perform other allocation strategies (Chapelle and Li,
2001; Capp
´
e et al., 2013; Baransi et al., 2014). Ad-
ditionally, we have also considered the UCB1 policy,
since it was one of the first proposals in the literature
that accounts for the uncertainty about the expected
reward.
We have selected five different scenarios for com-
parison. For this, we have reviewed numerical stud-
ies in the literature to find out the most difficult and
representative scenarios. An experiment consisting
on 50,000 simulations with 20,000 iterations each
was carried out in the five scenarios. The Python
code available at http://mloss.org/software/view/415
was used for simulations, whereas those policies not
implemented in that library have been developed by
the authors, including DMED+, BESA, PR and DPR.
4.1 Scenario 1: Bernoulli Distribution
and Very Low Expected Rewards
This scenario is a simplification of a real situation
in on-line marketing and digital advertising. Specif-
ically, advertising is displayed in banner spaces and
in case the customer clicks on the banner then s/he is
redirected to the page that offers the product. This is
considered a success with a prize of value 1. The suc-
cess ratios in these campaigns are usually quite low,
being about 1%. For this, ten arms will be used with a
Bernoulli distribution and the following parameters:
[0.1, 0.05, 0.05, 0.05, 0.02, 0.02, 0.02, 0.01, 0.01,
0.01].
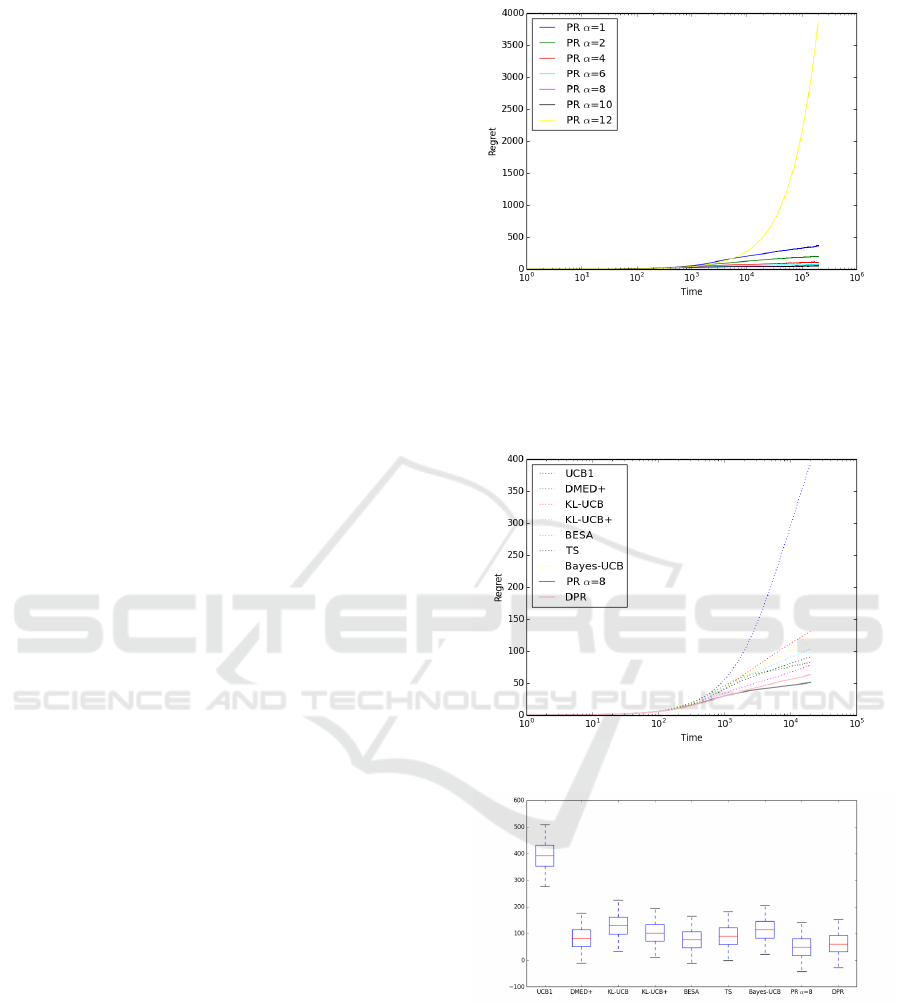
First, a simulation is carried out to find out the best
value for parameter α to be used in the PR method,
see Fig. 3. α = 8 is identified as the best value and
used for this scenario 1. Note that in DPR, no previ-
ous knowledge regarding the scenario is required.
Now, the 50,000 simulations with 20,000 itera-
tions each are carried out. Fig. 4 shows the evolu-
tion of the regret for the different allocation strate-
gies under comparison along the 20,000 iterations
corresponding to one simulation (using a logarithmic
scale), whereas Fig. 5 shows the multiple boxplot cor-
responding to regrets throughout the 50,000 simula-
tions.
The first two columns in Table 1 show the mean
regrets and standard deviations for the policies. The
three with lowest mean regrets are highlighted in bold,
corresponding to DPR, PR and BESA, respectively.
The variance is similar for all the policies under con-
sideration. It is important to note that although PR
Figure 3: Selecting parameter α for PR in scenario 1.
(α = 8) slightly outperforms DPR, DPR requires nei-
ther previous knowledge nor a simulation regarding
the arm distributions, which makes DPR more suit-
able in a real environment.
Figure 4: Policies in one simulation for scenario 1,
Figure 5: Multiple boxplot for policies in scenario 1.
Note that in the above multiple boxplots negative
regret values are displayed. It could be considered
an error at first sight. The explanation is as follows:
the optimum expected reward µ
∗
used to compute re-
grets is the theoretic value from the distribution, see
Eq. (1). For instance, in an arm with Bernoulli distri-
bution with parameter 0.1, µ
∗
after n plays is 0.1 × n.
However, in the simulation the number of success if
the arm is played n times may be higher than this
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
80
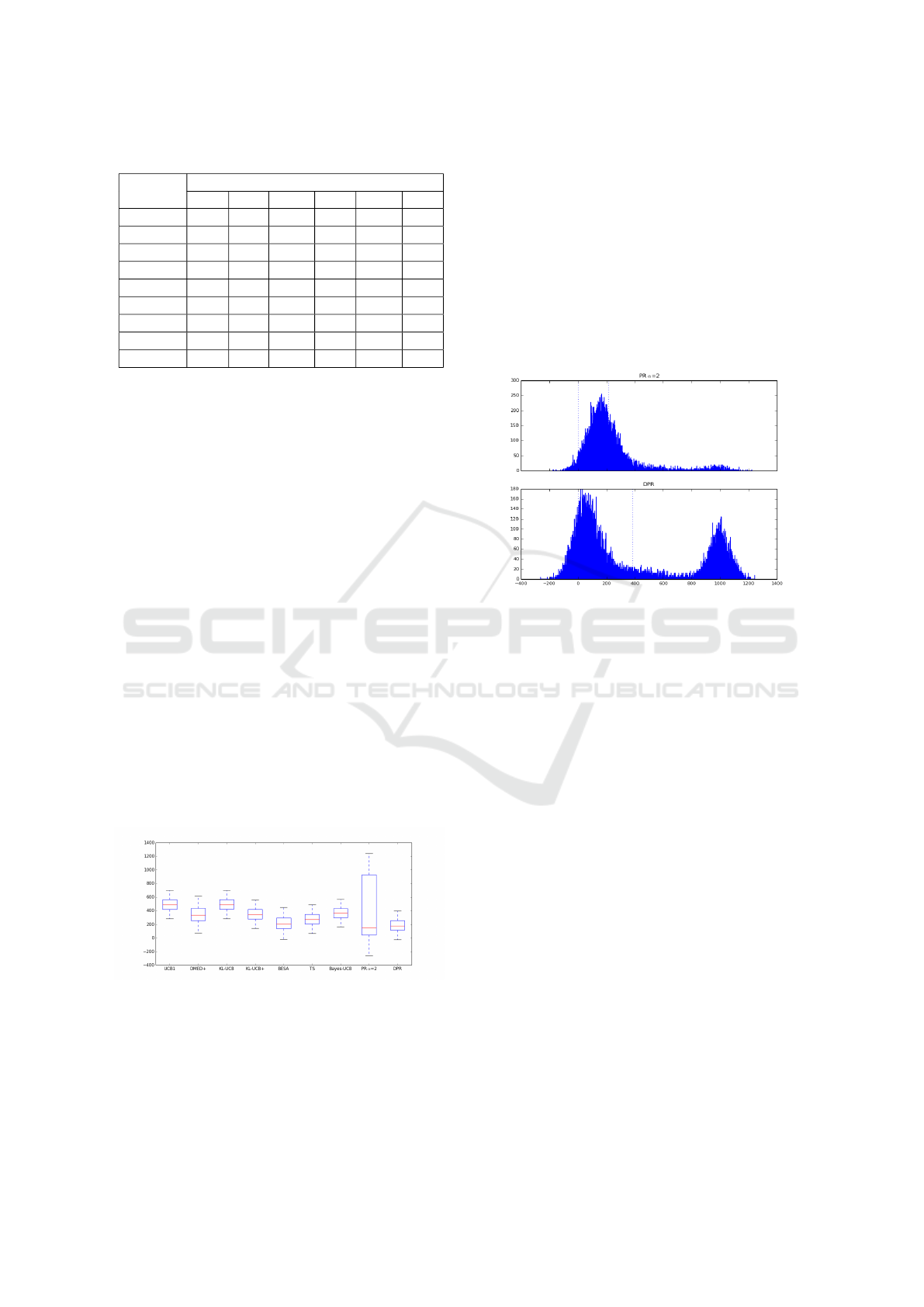
Table 1: Statistics in scenarios 1, 2 and 3.
Bernoulli (low) Bernoulli (med) Bernoulli (G)
Mean σ Mean σ Mean σ
UCB1 393.7 57.6 490.9 104.9 2029.1 125.9
DMED+ 83.1 46.1 356.8 151.5 889.8 313.2
KL-UCB 130.7 47.9 491.5 104.3 1169.6 233.2
KL-UCB+ 103.3 46.0 349.7 104.7 879.7 254.5
BESA 78.1 53.9 281.6 260.9 768.75 399.2
TS 91.1 45.6 284.2 125.1 - -
Bayes-UCB 115.1 46.6 366.3 104.5 - -
PR 51.1
∗
49.2 380.5 426.2 431.0
∗
383.5
DPR 63.6 49.1 214.6
∗
185.1 643.0 387.1
amount, overall in the first iterations, leading to nega-
tive regret values.
4.2 Scenario 2: Bernoulli Distribution
and Medium Expected Rewards
In this scenario, we still consider a Bernoulli distri-
bution but now parameters are very similar in the 10
arms and close to 0.5. This leads to the greatest vari-
ances in the distributions, where in almost all arms in
half of the cases they have a value 1 and 0 in the other
half. Thus, it becomes harder for algorithms to reach
the optimal solution. Moreover, if an intensive search
is not carried out along a sufficient number of iter-
ations, we could easily reach sub-optimal solutions.
The parameters for the 10 arms under consideration
are: [0.5, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45,
0.45].
First, a simulation was carried out again to find
out the best value for parameter α to be used in the
PR method in this scenario and α = 2 was selected.
In Fig. 6 the regrets throughout the 50,000 simula-
tions corresponding to the different policies are shown
by means of a multiple boxplot.
Figure 6: Multiple boxplot for policies in scenario 2.
It draws to attention the high variability on the re-
gret values for the PR method (α = 2). Fig. 7 shows
the histograms corresponding to PR (α = 2) and DPR.
As expected, regret values are mainly concentrated
close to value 0 and around value 1000. Note that
the success probability is 0.45 in 9 out of the 10 arms,
whereas it is 0.5 for the other one. The probability
difference is then 0.05 and as the reward is 1 (if suc-
cessful) and 20,000 iterations are carried out, we ex-
pect regret values around value 1000.
The dotted vertical lines in the histograms repre-
sent the regret value 0 and the mean regret throughout
the 50,000 simulations. Note that the mean regret for
PR is not representative. The number of regret obser-
vations around the value 1000 is considerably higher
for PR than DPR, which explains the higher standard
deviation in PR and demonstrates that DPR outper-
forms PR in this scenario.
Figure 7: Histograms for PR (α = 2) and DPR in scenario
2.
The three allocation strategies with lowest aver-
age regrets, highlighted in bold in the third and fourth
columns in Table 1, corresponds to DPR, BESA and
TS, respectively. However, DPR outperforms BESA
and TS, whose performances are very similar but
BESA has a higher variability.
4.3 Scenario 3: Bernoulli Distribution
and Gaussian Rewards
In this scenario, Bernoulli distributions with very low
expected rewards (about 1% success ratios) are again
considered but now rewards are not 0 or 1, they are
normally distributed. This scenario has never been
considered in the literature but we consider it inter-
esting for analysis. We can also face this scenario in
on-line marketing and digital advertising. As in sce-
nario 1, advertising is displayed in banner spaces and
in case the customer clicks on the banner then s/he is
redirected to the page that offers the product. How-
ever, in this new scenario the customer may buy more
than one product, the number of which is modeled by
a normal distribution.
The success ratios in these campaigns are usually
quite low, as in scenario 1, being about 1%. For this,
the ten arms will be used with a Bernoulli distribution
The Possibilistic Reward Method and a Dynamic Extension for the Multi-armed Bandit Problem: A Numerical Study
81
and the following parameters: [0.1, 0.05, 0.05, 0.05,
0.02, 0.02, 0.02, 0.01, 0.01, 0.01]. Besides, the same
σ = 0.5 is used for the normal distributions, whereas
the following means (µ) are considered: [1, 2, 1, 3,
5, 1, 10, 1, 8, 1]. Moreover, all rewards are truncated
between 0 and 10. Thus, the expected rewards for the
ten arms are [0.1, 0.1, 0.05, 0.15, 0.1, 0.02, 0.2, 0.01,
0.08, 0.01], and the seventh arm is the one with the
highest expected reward.
TS and Bayes-UCB policies are not analyzed in
this scenario since both cannot be applied. α = 70 will
be used in the PR method. Fig. 8 shows the multiple
boxplot for the regrets throughout the 50,000 simula-
tions, whereas the mean regrets and the standard de-
viations are shown in last two columns of Table 1.
The three policies with lowest mean regrets, high-
lighted in bold in Table 1, correspond to PR, DPR and
BESA, respectively, the three with a similar variabil-
ity. However, PR outperforms DPR and BESA in this
scenario.
Figure 8: Multiple boxplot for policies in scenario 3.
4.4 Scenario 4: Truncated Poisson
Distribution
A truncated in [0,10] Poisson distribution is used in
this scenario. It is useful to model real scenarios
where the reward depends on the number of times
an event happens or is performed in a time unit, for
instance, the number of followers that click on the
”like” button during two days since it is uploaded.
The values for parameter λ in the Poisson distribution
for each arm are: [0.75, 1, 1.25, 1.5, 1.75, 2, 2.25].
The variant kl-poisson-UCB was also considered
for analysis, whereas TS and Bayes-UCB will no
longer be considered since both cannot be applied in
this scenario.
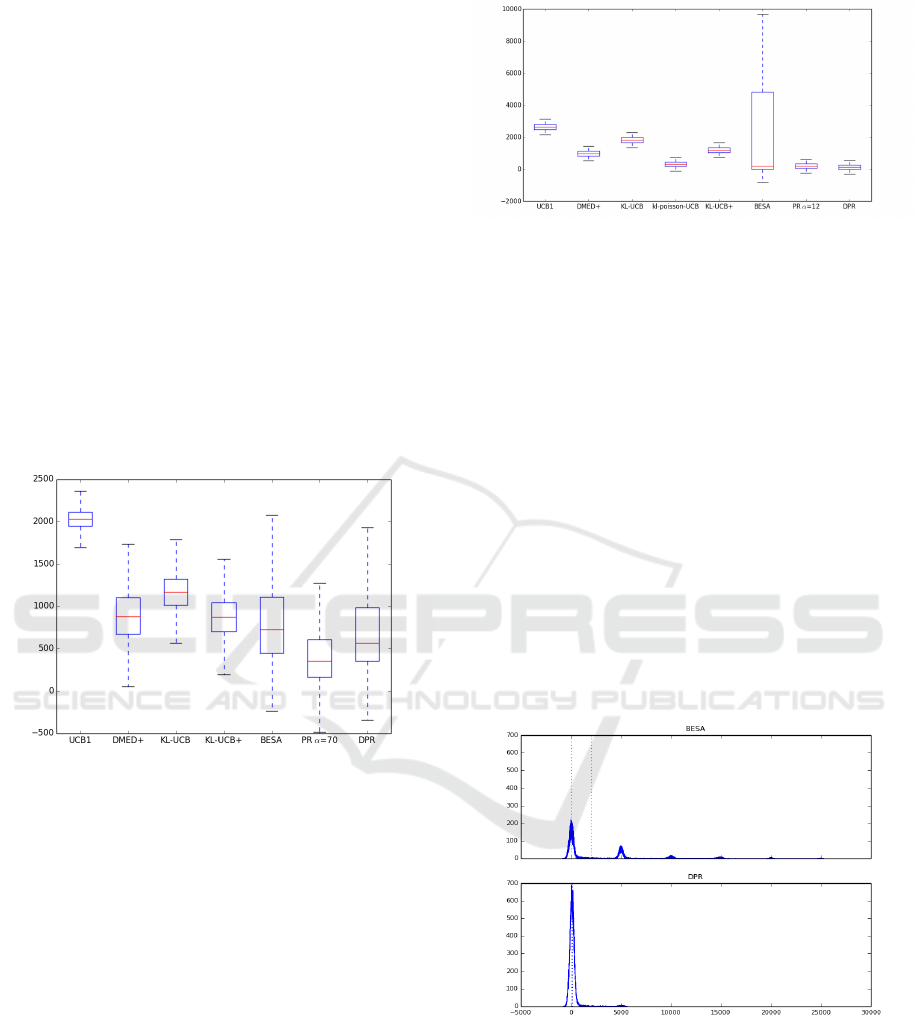
First, the selected value for parameter α to be used
in the PR method in this scenario is 12. Fig. 9 shows
the multiple boxplot for the regrets throughout the
50,000 simulations, whereas the first two columns in
Figure 9: Multiple boxplot in the fourth scenario (Poisson).
Table 2 show the mean regrets and standard devia-
tions.
One should observe the high variability on the re-
gret values in BESA. Fig. 10 shows the histograms
corresponding to BESA and DPR. As expected, re-
gret values are mainly concentrated around 7 values
(0, 5000, 10,000, 15,000, 20,000, 25,000, 30,000),
with the highest number of regret values around 0,
followed by 5000 and so on. Note that the different of
λ values in the 7 arms is 0.25 and 0.25 × 20, 000 iter-
ations carried out in each simulation is 5000, which
matches up with the amount incremented in the 7
points the regrets are concentrated around.
The number of regret observations around the
value 0 regarding the remaining values is consider-
ably higher for DPR than BESA, which explains a
higher standard deviation in BESA and demonstrates
that BESA is outperformed by the other policies in
this scenario.
Figure 10: Histograms for BESA and DPR.
DPR again outperforms the other algorithms on
the basis of the mean regrets, including PR (α = 12),
see Table 2. kl-poisson-UCB Poisson is the only pol-
icy whose results are close to DPR and PR. However,
the variability in DPR is higher than in all the other
policies apart from BESA.
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
82
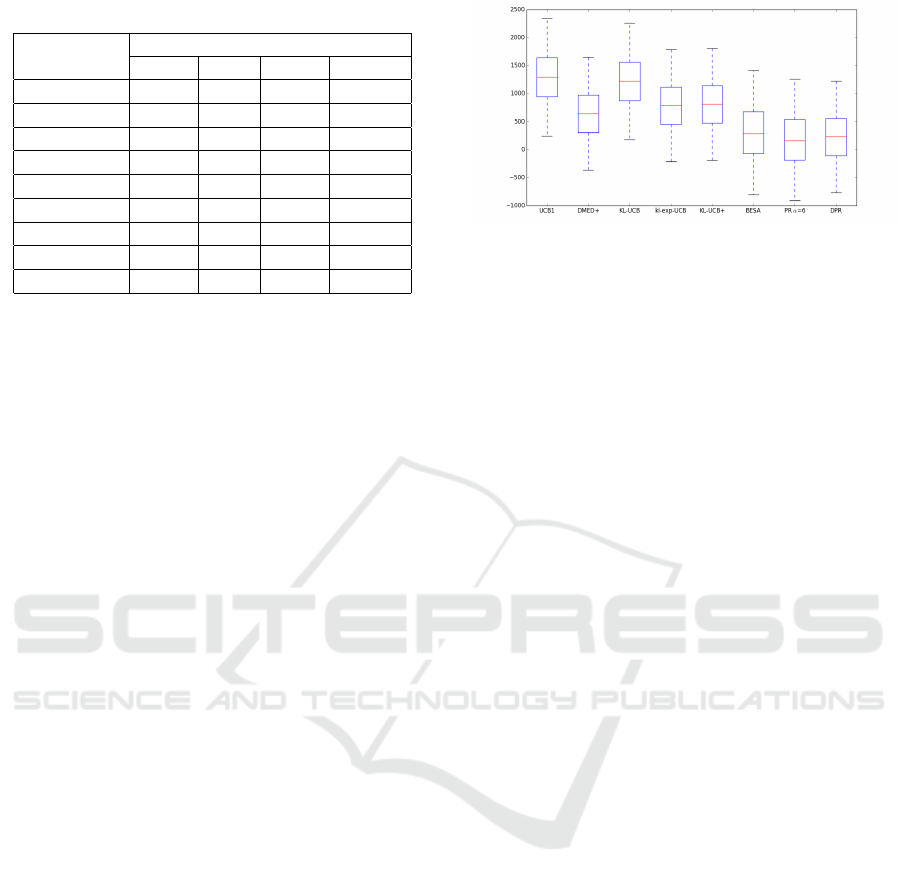
Table 2: Statistics in scenarios 4 and 5.
Truncated Poisson Truncated Exponential
Mean σ Mean σ
UCB1 2632.65 246.03 1295.79 514.03
DMED+ 978.56 225.24 645.70 493.8
KL-UCB 1817.4 236.57 1219.98 510.69
kl-poisson-UCB 314.99 201.79 - -
KL-exp-UCB - - 786.30 498.16
KL-UCB+ 1190.64 225.82 813.45 494.59
BESA 2015.73 3561.5 755.87 2323.22
PR 196.24 212.45 580.31 2182.02
DPR 153.3
∗
409.17 282.83
∗
814.72
4.5 Scenario 5: Truncated Exponential
Distribution
A truncated exponential distribution is selected in this
scenario, since it is usually used to compare alloca-
tion strategies in the literature. It is used to model
continuous rewards, and for scales greater than 1 too.
Moreover, it is appropriate to model real situations
where the reward depends on the time between two
consecutive events, for instance, the time between a
recommendation is offered on-line until the customer
ends up buying. The values for parameter λ in the ex-
ponential distribution for each arm are: [1, 1/2, 1/3,
1/4, 1/5, 1/6].
The variant kl-exp-UCB was incorporated into the
analysis in this scenario, whereas TS and Bayes-UCB
cannot be applied.
The best value for parameter α for the PR method
is 6. Fig. 11 shows the multiple boxplot for the re-
grets throughout the 50,000 simulations. The mean
regret and the standard deviations are shown in last
two columns of Table 2.
PR and DPR again outperform the other policies,
with PDR being very similar to but slightly better than
PR in this scenario. Moreover, DPR requires neither
previously knowledge nor a simulation of the arm dis-
tributions, what makes DPR more suitable in a real
environment. The best four policies are the same as
in scenario 4, with a truncated Poisson, changing the
KL-poisson-UCB with KL-exp-UCB.
5 CONCLUSIONS
In this paper we propose a novel allocation strategy,
the possibilistic reward method, and a dynamic ex-
tension for the multi-armed bandit problem. In both
methods the uncertainty about the arm expected re-
wards are first modelled by means of possibilistic re-
Figure 11: Multiple boxplot for policies in the fifth sce-
nario.
ward distributions derived from a set of infinite nested
confidence intervals around the expected value. Then,
a pignistic probability transformation is used to con-
vert these possibilistic function into probability dis-
tributions. Finally, a simulation experiment is carried
out by sampling from each arm to find out the one
with the highest expected reward and play that arm.
A numerical study suggests that the proposed
method outperforms other policies in the literature.
For this, five complex and representative scenarios
have been selected for analysis: a Bernoulli distribu-
tion with very low success probabilities; a Bernoulli
distribution with success probabilities close to 0.5,
which leads to the greatest variances in the distribu-
tions; a Bernoulli distribution with success probabili-
ties close to 0.5 and Gaussian rewards; a truncated in
[0,10] Poisson distribution; and a truncated in [0,10]
exponential distribution.
In the first three scenarios, in which the Bernoulli
distribution is considered, PR or DPR are the policies
with the lowest mean regret and with similar variabil-
ity regarding the other policies. BESA is the only pol-
icy with results that are close to DPR and PR, mainly
in scenario 1. Besides, DPR and PR clearly outper-
form the other policies in scenarios 4 and 5, in which
a truncated Poisson and exponential are considered,
respectively. In both cases, DPR outperforms PR.
ACKNOWLEDGEMENTS
The paper was supported by the Spanish Ministry
of Economy and Competitiveness MTM2014-56949-
C3-2-R.
REFERENCES
Agrawal, R. (1995). Regret bounds and minimax policies
under partial monitoring. Advances in Applied Prob-
ability, 27(4):1054–1078.
The Possibilistic Reward Method and a Dynamic Extension for the Multi-armed Bandit Problem: A Numerical Study
83

Audibert, J.-Y. and Bubeck, S. (2010). Sample mean based
index policies by o(log n) regret for the multi-armed
bandit problem. Journal of Machine Learning Re-
search, 11:2785–2836.
Audibert, J.-Y., Munos, R., and Szeperv
´
ari, C. (2009).
Exploration-exploitation trade-off using variance esti-
mates in multi-armed bandits. Theoretical Computer
Science, 410:1876–1902.
Auer, P., Cesa-Bianchi, N., and Fischer, P. (2002). Finite-
time analysis of the multiarmed bandit problem. Ma-
chine Learning, 47:235–256.
Auer, P. and Ortner, R. (2010). UCB revisited: Improved
regret bounds for the stochastic multi-armed bandit
problem. Advances in Applied Mathematics, 61:55–
65.
Baransi, A., Maillard, O., and Mannor, S. (2014). Sub-
sampling for multi-armed bandits. In Proceedings
of the European Conference on Machine Learning,
page 13.
Berry, D. A. and Fristedt, B. (1985). Bandit Problems:
Sequential Allocation of Experiments. Chapman and
Hall, London.
Burnetas, A. N. and Katehakis, M. N. (1996). Optimal
adaptive policies for sequential allocation problems.
Advances in Applied Mathematics, 17(2):122 – 142.
Capp
´
e, O., Garivier, A., Maillard, O., Munos, R., and Stoltz,
G. (2013). Kullbackleibler upper confidence bounds
for optimal sequential allocation. Annals of Statistics,
41:1516–1541.
Chapelle, O. and Li, L. (2001). An empirical evaluation of
thompson sampling. In Advances in Neural Informa-
tion Processing Systems, pages 2249–2257.
Dubois, D., Foulloy, L., Mauris, G., and Prade, H.
(2004). Probability-possibility transformations, trian-
gular fuzzy sets, and probabilistic inequalities. Reli-
able Computing, 10:273–297.
Dupont, P. (1978). Laplace and the indifference principle in
the ’essai philosophique des probabilits.’. Rendiconti
del Seminario Matematico Universit e Politecnico di
Torino, 36:125–137.
Garivier, A. and Capp
´
e, O. (2011). The kl-ucb algorithm
for bounded stochastic bandits and beyond. Technical
report, arXiv preprint arXiv:1102.2490.
Gittins, J. (1979). Bandit processes and dynamic alloca-
tion indices. Journal of the Royal Statistical Society,
41:148–177.
Gittins, J. (1989). Multi-armed Bandit Allocation Indices.
Wiley Interscience Series in Systems and Optimiza-
tion. John Wiley and Sons Inc., New York, USA.
Hoeffding, W. (1963). Probability inequalities for sums
of bounded random variables. Advances in Applied
Mathematics, 58:13–30.
Holland, J. (1992). Adaptation in Natural and Artificial Sys-
tems. MIT Press/Bradford Books, Cambridge, MA,
USA.
Honda, J. and Takemura, A. (2010). An asymptotically op-
timal bandit algorithm for bounded support models. In
Proceedings of the 24th annual Conference on Learn-
ing Theory, pages 67–79.
Kaufmann, E., Capp
´
e, O., and Garivier, A. (2012). On
bayesian upper confidence bounds for bandit prob-
lems. In International Conference on Artificial Intel-
ligence and Statistics, pages 592–600.
Lai, T. and Robbins, H. (1985). Asymptotically efficient
adaptive allocation rules. Advances in Applied Math-
ematics, 6:4–22.
Maillard, O., Munos, R., and Stoltz, G. (2011). Finite-
time analysis of multi-armed bandits problems with
kullback-leibler divergences. In Proceedings of the
24th Annual Conference on Learning Theory, pages
497–514.
Smets, P. (2000). Data fusion in the transferable belief
model. In Proceedings of the Third International Con-
ference on Information Fusion, volume 1, pages 21–
33.
Sutton, R. S. and Barto, A. G. (1998). Introduction to Re-
inforcement Learning. MIT Press, Cambridge, MA,
USA, 1st edition.
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
84
