Multi-agent Polygon Formation using Reinforcement Learning
B. K. Swathi Prasad
1
, Aditya G. Manjunath
2
and Hariharan Ramasangu
3
1
Department of Electrical Engineering, M. S. Ramaiah University of Applied Sciences,
Peenya, Bangalore, India
2
Department of Computer Science and Engineering, M. S. Ramaiah University of Applied Sciences,
Peenya, Bangalore, India
3
Department of Electronics and Communication Engineering, M. S. Ramaiah University of Applied Sciences,
Peenya, Bangalore, India
Keywords:
Formation, Pattern, Q-learning, Algorithm, Episode.
Abstract:
This work provides details a simulation experiment and analysis of Q-learning applied to multi-agent systems.
Six agents interact within the environment to form hexagon, square and triangle, by reaching their specific
goal states. In the proposed approach, the agents form a hexagon and the maximum dimension of this pattern
is be reduced to form patterns with smaller dimensions. A decentralised approach of controlling the agents via
Q-Learning was adopted which reduced complexity. The agents will be able to either move forward, backward
and sideways based on the decision taken. Finally, the Q-Learning action-reward system was designed such
that the agents could exploit the system which meant that they would earn high rewards for correct actions and
negative rewards so the opposite.
1 INTRODUCTION
With ever increasing applications of Multi-Agent Sy-
stems (MAS), a transferable learning method is a ne-
cessity so as to increase efficiency in the duration of
adoption of such systems into a particular environ-
ment. These specifically includ e swarm-robot sys-
tems for surveillance, agriculture harvesting and res-
cue opera tions. Multi-Agent formation control confi-
gurations include centralized and decentralized pat-
tern formations. The former entails no interaction
among agents, whereas the opposite applies to the lat-
ter which utilizes a ll agents in the learnin g process.
This part of the work focuses on decentralized reinfor-
cement le a rning for Multi-Agent pattern formation.
Control algorithms are adopted to perform pattern of
agents, thereby achieving formation.
Popular control algorithms adopted for attaining
desired geometric pattern are decentralized control
algorithm (Cheng and Savkin, 2011), synchroniza-
tion control (I. Sanhoury and Husain, 2012), pre-
dictive control (A. Guillet and Martinet, 2014) and
Neural Network Controller and finite time controller
(C. Zhang and Pan, 2014). The geom etric pattern in-
cludes triangle (J. Desai and Kumar, 2001), rectangle
(J. Desai and Kumar, 2001) (Cheng and Savkin, 2011)
(I. Sanhoury and Husain, 2012), ellipse ( A . Guillet
and Martinet, 2014) (I. Sanhoury and Husain , 2012).
However it is necessary to track the leaders pose (po-
sition and direction angle) while achieving the desired
geometric pattern (C. Zhang and Pan, 2014) (Buso-
niu et al., 2006) (Gifford and Agah, 2007) (J. Alonso-
Mora and Beardsley, 2011) (Ren, 2015).
The problem in formation con trol for a group of
agents is dynam ic assignment of geo metric pattern.
Many formation control strategies have been propo-
sed - leaderfollower, behavioural and virtu al struc-
ture/virtua l leader approach (Ren, 2015) (Karimod-
dini et al., 2014) (Dong et al., 2015) (Rego et al.,
2014) for preserving formation among agents. The
control algorithms developed for pattern formation
(Cheng and Savkin, 2011) (B. Dafflon and Koukam,
2013) (Ren, 2015) does not accou nt for decentralized
control configuration. Hence a ny pattern cannot be
formed, where only few formations can be achieved.
Decentralized controller (Smith et al., 2006) (Du-
ran and Gazi, 201 0) (Kric k et al., 2009) was develo-
ped to make ag ents form a desired geometric pattern.
The pattern formations were ach ieved using agents’
ID compared with coordinated variable (Ch e ng and
Savkin, 2011), maintaining relative angle between the
agents’ position (Rezaee and Abdo llahi, 2015), by ad-
justment of distance (Smith et al. , 2006) and visuali-
sing each robot through the sensor and minimizing
Prasad B., Manjunath A. and Ramasangu H.
Multi-agent Polygon Formation using Reinforcement Learning.
DOI: 10.5220/0006187001590165
In Proceedings of the 9th International Conference on Agents and Artificial Intelligence (ICAART 2017), pages 159-165
ISBN: 978-989-758-219-6
Copyright
c
 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
159

the control signal of actual sensor value with desired
value (Krick et al., 2009). Also these patterns are re-
stricted to only directed graph. Pattern formations is
of two f orms: artistic formation (J. Alonso-Mora and
Beardsley, 2011) and precise formation (Gifford and
Agah, 2007). These form ations are required when the
placement of sensors in the unstru ctured environment
becomes inadequate. Thus learning is required suc h
that agents can adapt and accomplish the task in the
unstructured environment where high precision is re-
quired. Learning is evaluated for manipulator link
control (Busoniu et al., 2006) using fuzzy value ite-
ration method. However this method does not lead to
any pattern formation as it focuses only on the motion
control.
The focus of this work is pattern formation for a
dynamic multi-agent system using decentralized ma-
chine learning algorithm. In this paper, 6 agents for m
pattern on cer tain quantity of interest u sin g reinfo r-
cement learning. The learning process utilizes agents
initial position scattered in the defined space. The le-
arning curve utilizes the policy for action to be ta-
ken to move to next step a nd gets highest reward for
reaching correct position . The agents are p e nalized
for moving away from the desired position. The pa-
per is structured as follows: Section 2 delves into th e
learning process. Results are discussed in Section
3. Section 4 describes the conclusion b y giving the
glimpse of the work carried out.
2 DECENTRALIZED LEARNING
FOR MULTI-AGENTS
In this work, Q learning is ad opted where each agent
individually learns thro ugh the set of actions,
′
A
′
for
the given environmen tal state,
′
S
′
. In the proposed
work, as the position of each agent is defined in 2D,
learning problem is defined to operate pa rallel in both
x and y coordinates. With this configur ation, the agent
can explore the state space independently. T he propo-
sed approach contributes to attain poly gonal forma-
tion.
2.1 Proposed Structure for Learning
The decentralized structure utilizes Q learning for
training ag e nts to reach its coordinates. Policy is ba-
sed on exploitation, where an action,
′
Act
′
is perfor-
med using maximum Q value and is given in Eq.1.
Act = argmax
aεA
{Q(States − Space
ID, a)} (1)
where A = [−1, 1]
Initially first agent starts to explore the states-
space from States − Space
ID : 1 till it reach e s the
specified target and lock, 0. Here lock indicates whet-
her the age nt should continue with the learning pro-
cess or not. The current state of the agent is updated
based on the specified condition as in line 19 of Alg o-
rithm 1. Once the state of the agen t gets updated, the
computation of Q matrix is re peated using line 34 in
Algorithm 1, to pre-compute the policy adopted until
the specified target is r eached. For the next agent, th e
target position of previous agent is taken as the ini-
tial state of the states-space and lea rns through the Q-
learning u ntil it reaches the specified target.
2.2 Algorithm to Compute Reward of
the Agent
This section focuses on the computation of reward
of the agent for the defined state space. An agent
is given maximum reward if it performs some action
and is penalized if the agent performs action even af-
ter reaching the target. In Section 2 .2.1 and Section
2.2.2, the assignment of rewards for x-coordinate and
y-coordinate are derived fro m the specific target as-
signed to each agent respectively.
2.2.1 Algorithm for Computing Reward of
x-coordinate of Agent
The next state of each agent is computed and updated
based on the action taken from the o ptimum Q value.
The next state of each agent ID is updated till it rea -
ches the goal state of x-coordinate and lies within the
goal states space of [−2, 2]. The agent gets maximum
reward when it perfo rms c orrect action, gets penalty
when the agent reaches goal state of −1, 0, 1, 2, 1, 0
and also if neither of the case then the agen t is facili-
tated with lesser negative reward. The complete struc-
ture of algorithm for computing next state of each
agent ID is described in Algorithm 2.
2.2.2 Algorithm for Computing Reward of
y-coordinate of Agent
The next state of each agent is com puted and upda-
ted based on the action taken from the optim um Q
value. The next state of each ag e nt ID is updated
till it reaches the goal state of y-coordinate and lies
within the goal states space of [−1, 1]. The agent
gets maximum reward when the agent p erforms cer-
tain action, gets p enalty when the agent reaches goal
state of 0, 1, 1, 0, −1, −1 and also if neither of the case
then the agent is facilitated with lesser n egative re-
ward. The complete structure of algorithm for comp-
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
160

Algorithm 1: Proposed Structure for Learning.
Require: States − Space, Action, Q
Require: Learning Rate and Discount Factor
1: States − Space = −2 : 3
2: Action= [move down (−1), move up (1)]
3: Learning Rate, al pha = 0.5
4: Discount Rate, gamma = 0.5
5: Q = zeros(length (States-Space), length (Action))
6: States − Space
ID = Index of States − Space
7: N = Total no. of agents
8: M = Total no. of iterations
9: x = Current State
10: y = Next State
11: Next State
ID = Index of agent for its next position
in the States − Space
12: lock = To indicate whether to restrict the movement
or not
13: Target = Goal position of the agent
14: repeat
15: for i ← 1, N do
16: States − Space
ID = 1
17: repeat
18: for k ← 1, M do
19: Action
ID = f ind(Action ==
max(Q(States − Space
ID, :))
20: x(i) = States − Space(States −
Space
ID)
21: Comment: Based on current action
and i, next state y is computed
22: if x ≤ max(States − Space)&&x ≥
min(States − Space) then
23: y(i) = x(i) + Action(Action ID)
24: else
25: y(i) = x(i)
26: end if
27: Comment: Based on Current State
and Action, Assign Reward
28: if y == Target then
29: lock = 1
30: else
31: lock = 0
32: end if
33: if y == −3 then
34: y = −2
35: end if
36: Next State
ID = f ind(States −
Space == y)
37: Update Q using Q-Learning Rule
38: Q(States − Space
ID, Action ID)
= (States − Space
ID, Action ID) +
al pha(Reward + gamma ∗ max(Q(Next State ID, :
)))− Q(States − Space
ID, Action ID))
39: States − Space
ID = Next State ID
40: end for
41: until y == Target
42: end for
43: until lock==1
Algorithm 2: Computation of Reward for x- coordinate of
Each Agent.
Require: Current State, Action, Reward
1: x = Current State
2: u = Action
3: r = Reward
4: N = Total no. of agents
5: t = Target
6: for i ← 1, N do
7: if i == 1 then
8: Target = −1
9: else if i == 2 | i == 6 then
10: Target = 0
11: else if i == 3 | i == 5 then
12: Target = 1
13: else
14: Target = 2
15: end if
16: if x == t − 1&& u == 1 then
17: r = 10
18: else if x == t + 1&&u == −1 then
19: r = 10
20: else if x == t&&u == 1 k u == −1 then
21: r = −10
22: else
23: r = −1
24: end if
25: end for
uting next state of each agent ID is describe d in Alg o-
rithm 3.
2.2.3 Algorithm for Plotting Agents Learning
Process
The Alg orithm 4 briefs about the updated state of each
agent for a given episode. This is required to know
whether the agent has reached its goal state or not.
3 RESULTS AND DISCUSSION
This section details agents learning to reach their tar-
get along x and y coo rdinates, and the episodes they
have undergone to achieve the same. With the next
state history o f each agent along x and y coordinates,
the desired pattern of hexagon is achieved.
3.1 Transition Along x Coordinate to
Reach Target
The agents after undergoing the phase of algo rithm
described in Section 2.2.1, it traverses several episo-
Multi-agent Polygon Formation using Reinforcement Learning
161

Algorithm 3: Computation of Reward for y-coordinate
of E ach Agent.
Require: Current State, Action, Reward
1: x = Current State
2: u = Action
3: r = Reward
4: N = Total no. of a gents
5: t = Target
6: for i ← 1, N do
7: if i == 1 | i == 4 then
8: Target = 0
9: else if i == 2 | i == 3 then
10: Target = 1
11: else
12: Target = −1
13: end if
14: if x == t − 1&&u == 1 then
15: r = 10
16: else if x == t + 1&&u == −1 then
17: r = 10
18: else if x == t&&u == 1 k u == −1 then
19: r = −10
20: else
21: r = −1
22: end if
23: end for
Algorithm 4: Plot of Learning of agents to reach target
with episodes incurred by each agent.
Require: next state history
1: P
x
= Positions of x coordinate
2: P
y
= Positions of y coo rdinate
3: R
x
= next state
x
4: R
y
= next state
y
5: E = Episode of Agent ID
6: P
x
=

R
x
, E]
7: P
y
=

R
y
, E]
8: N = Total no. of a gents
9: for i ← 1, N do
10: s1 = f ind(R
x
) == i
11: s2 = f ind(R
y
) == i
12: j j1 = max(s1)
13: j j2 = max(s2)
14: plot(i, R
x
( j j1, 1)
15: plot(i, R
y
( j j2, 1)
16: end for
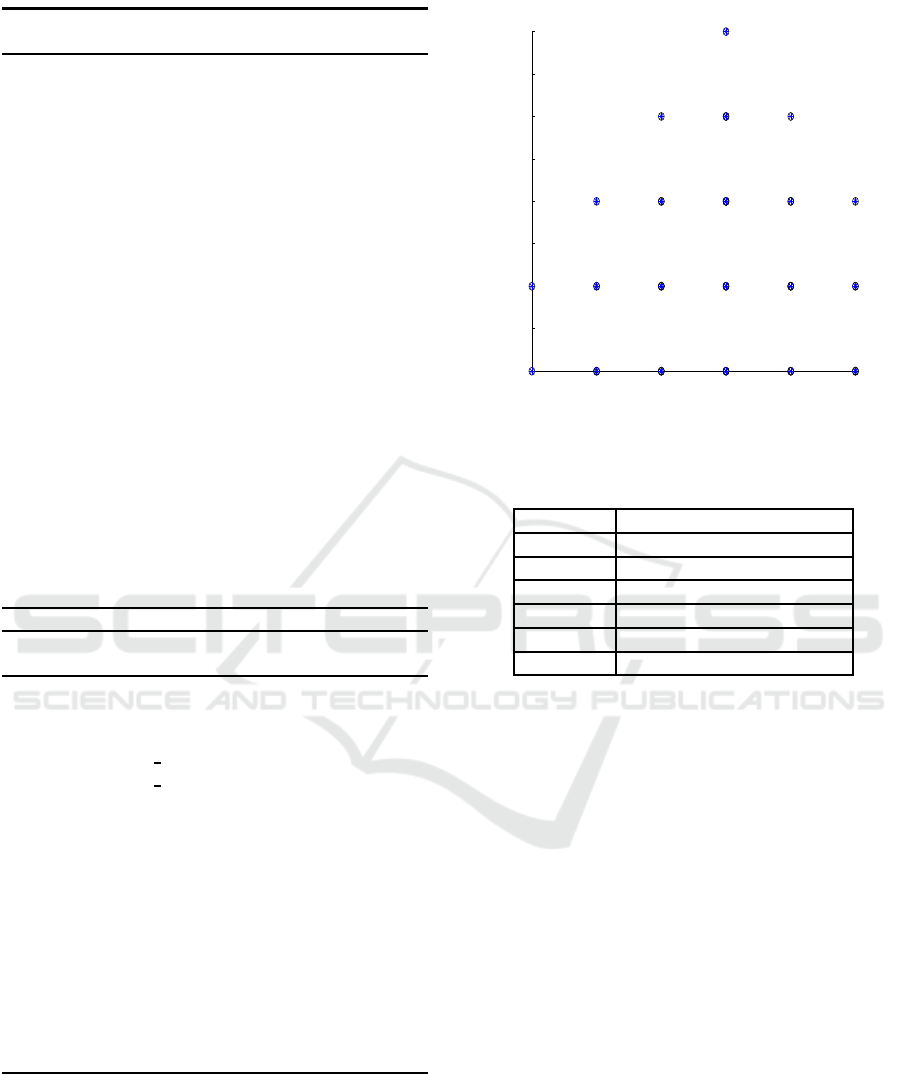
des defined in the state space. This transition of agents
from one state to the other is shown in Fig. 1. It is
seen that agents reach to the goa l state as indicated in
Algorithm 2 of Section 2.2.1. The episodes for tran-
sition is indicated in Table 1.
1 2 3 4 5 6
−2
−1.5
−1
−0.5
0
0.5
1
1.5
2
11
22
11
22
3344
55
66
11
22
3344
55
66
77
88
99
11
22
3344
55
66
77
88
99
1010
1111
1212
11
22
3344
55
66
77
88
99
11
22
3344
55
66
Agent ID
No. of steps taken to reach target
Episode of X− Coordinate
Figure 1: Transition of Agents x coordinate to r each target.
Table 1: Episode incurred by each agents x coordinate.
Agent ID No. of Episodes Incurred
1 2
2 6
3 9
4 12
5 9
6 6
3.1.1 Learning x Coordinate to Reach Target
The agent reaches its target from the initial position
of each agent in x coordinate as shown in Fig.2
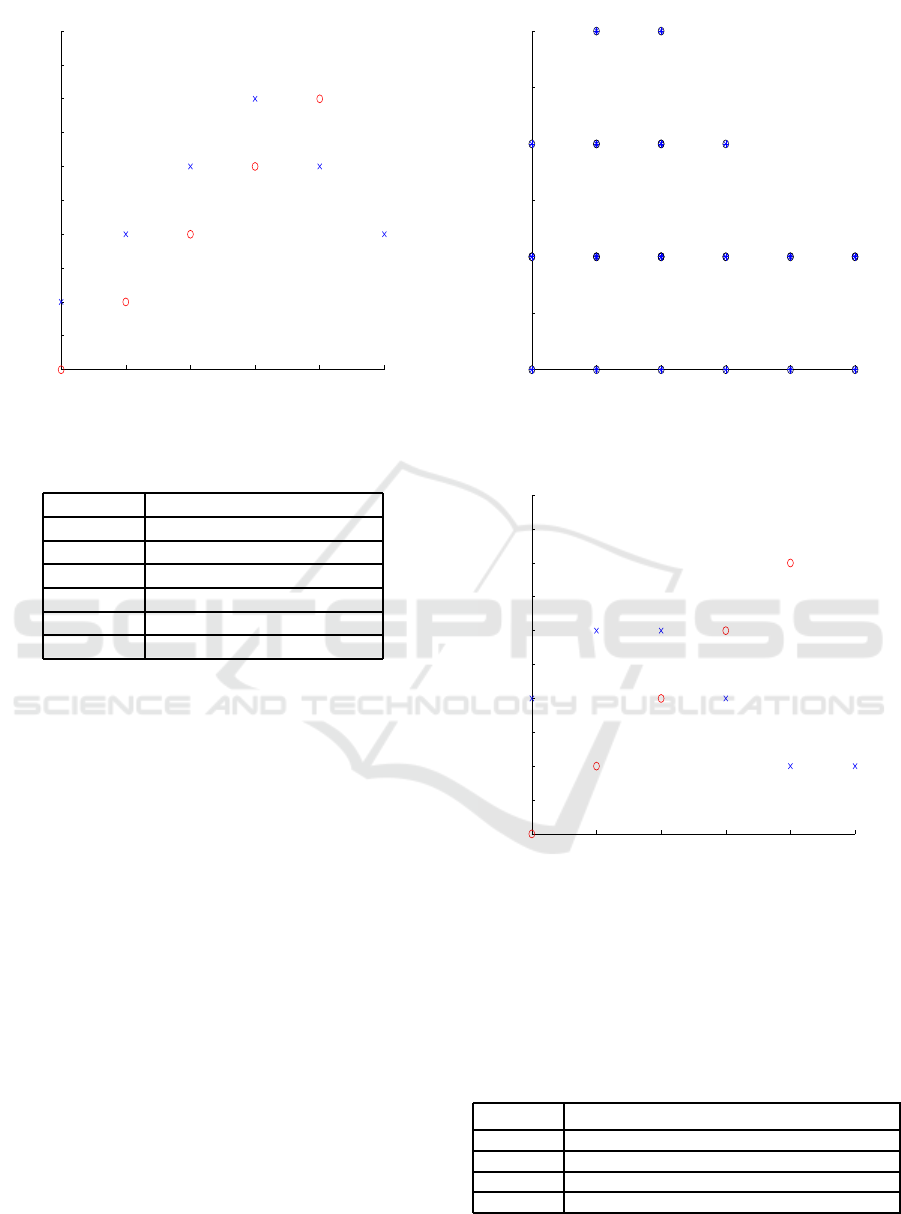
3.1.2 Transition Along y Coordinate to Reach
Target
The agents after undergoing the phase of algo rithm
described in Section 2.2.2, it traverse through several
episodes defined in the state space. This transition of
agents from one state to the other is shown in Fig. 3.
It is seen tha t agents reach to th e goal state as indica-
ted in Algorithm 3 of Section 2.2.2. The episodes for
transition is indicated in Table 2. The critical analysis
was executed for a test data to check the variation of
number of episodes incurred for different initial posi-
tion and target for the same. It is observed that when
the agent needs to travel from lower negative value to
higher negative value or lower positive value to hig-
her positive value, more number of episodes are taken
by the a gent to reach its target. However if the agent
traverses from higher negative value to lower negative
value and higher positive value to lower positive va-
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
162

1 2 3 4 5 6
−2
−1.5
−1
−0.5
0
0.5
1
1.5
2
2.5
3
Learning of agents (x coordinate−position) to reach target
Agent ID
Target
Figure 2: Learning of agents x coordinate.
Table 2: Episode incurred by each agents x coordinate.
Agent ID No. of Episodes Incurred
1 4
2 7
3 7
4 4
5 3
6 3
lue, agents takes lesser episodes comparatively. This
analysis signifies the computational time incurred by
each agent to reach its target.
3.1.3 Learning Along y Coordinate to Reach
Target
The agent reaches its target from the initial position
of each agent in y coordinate as shown in Fig. 4
3.2 Pattern Formation
Patterns from maximum dimension (6 / hexagon) to
reduced polygon d imensions of the size three, four
and five were achieved in this work. To suit all achie-
vable patterns, the target assignm e nt defined in Algo-
rithm 2 of Section 2.2.1 and Algorithm 3 of Section
2.2.2 utilized to obtain the desired pattern. Before
forming pattern , the a gent utilizes initial p osition as
the target position of previous agent position and rea-
ches the specified target through learning. He nce the
agents are connected and cooperative to form the spe-
cified pattern.
While forming the pattern, certain agents cannot
sense or fail to perceive the informatio n about the pre-
1 2 3 4 5 6
−2
−1.5
−1
−0.5
0
0.5
1
11
22
33
44
11
22
33
44
55
66
77
11
22
33
44
55
66
77
11
22
33
44
11
22
33 11
22
33
Agent ID
No. of steps taken to reach target
Episode of Y − Coordinate
Figure 3: Transition of Agents y coordinate to r each target.
1 2 3 4 5 6
−2
−1.5
−1
−0.5
0
0.5
1
1.5
2
2.5
3
Learning of agents (y coordinate−position) to reach target
Target
Agent ID
Figure 4: Learning of agents y coordinate.
sence of other agen ts. Such agen ts are eliminated to
form patterns of smaller d imensions. The elimination
of certain agents for obtaining the desired pattern is
shown in Table 3.
Table 3: Elimination of Agents to Obtain the Desired Pat-
tern.
Pattern Cases to Perform Different Patterns
Hexagon No agents are eliminated
Pentagon Agent 4 is eliminated
Square Agent 1 and Agent 4 is eliminated
Triangle Agent 3, Agent 4 and Agent 5 is eliminated
The patterns of hexagon, pentagon, square and tri-
Multi-agent Polygon Formation using Reinforcement Learning
163

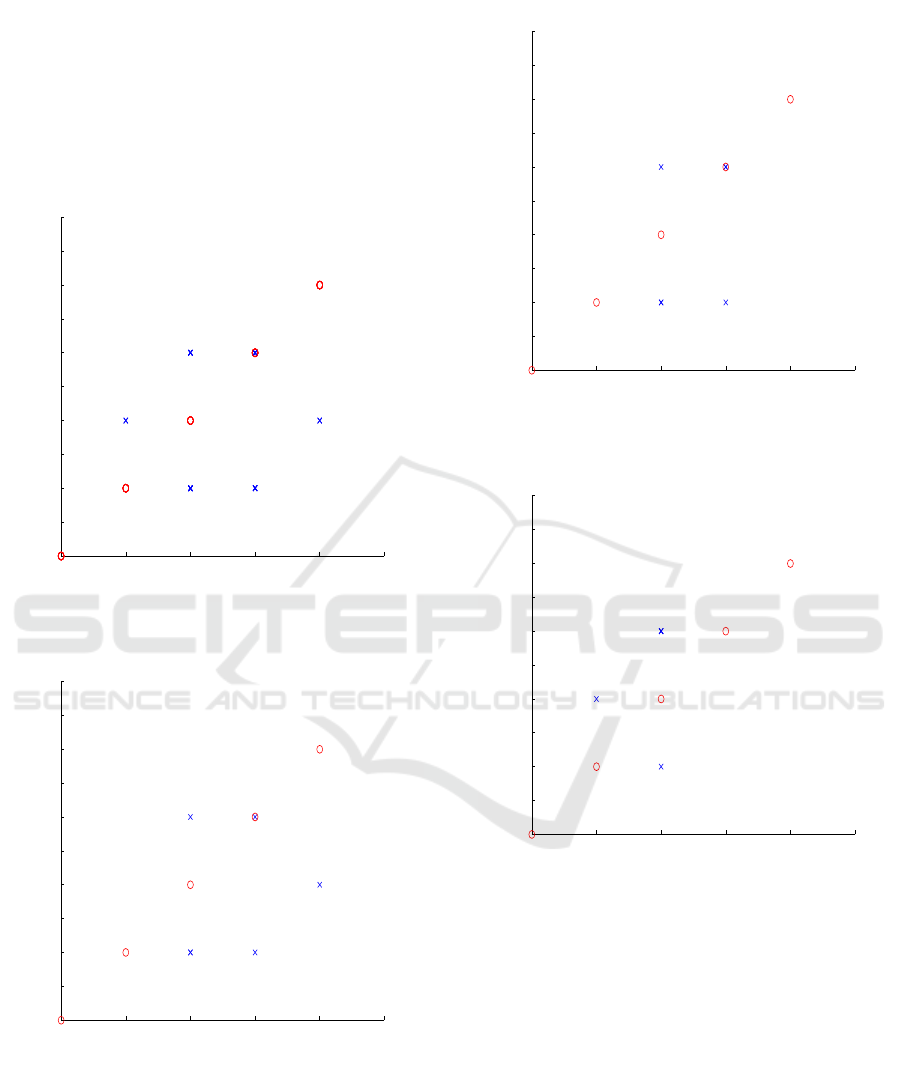
angle are shown in Fig. 5, Fig. 6, Fig. 7 and Fig. 8
respectively. The notations for initial and desired po-
sitions are represented by
′
o
′
and
′
x
′
respectively.
With this propo sed design, patterns of various redu-
ced dimensionality (from the m a ximum o f that of a
hexagon) can be d emonstrated and not just restricted
to the patterns shown in this pap er.
−2 −1 0 1 2 3
−2
−1.5
−1
−0.5
0
0.5
1
1.5
2
2.5
3
X − Axis
Y − Axis
Desired Pattern− Hexagon
Figure 5: Desired Pattern: Hexagon.
−2 −1 0 1 2 3
−2
−1.5
−1
−0.5
0
0.5
1
1.5
2
2.5
3
X − Axis
Y − Axis
Desired Pattern − Pentagon
Figure 6: Desired Pattern: Pentagon.
−2 −1 0 1 2 3
−2
−1.5
−1
−0.5
0
0.5
1
1.5
2
2.5
3
X − Axis
Y − Axis
Desired Plot− Square
Figure 7: Desired Pattern: Square.
−2 −1 0 1 2 3
−2
−1.5
−1
−0.5
0
0.5
1
1.5
2
2.5
3
X − Axis
Y − Axis
Desired Pattern − Triangle
Figure 8: Desired Pattern: Triangle.
4 CONCLUSION AND FUTURE
WORK
This work demonstrates a practical method for pat-
tern formations in MAS. The action-reward system of
Q-learning is ideal choice for formation of patterns in
a behavioural based system (such as the one demon-
strated in this work), as it allows for a rigid control on
the movements through exploitation. Longer learning
periods are a consequence o f freedom to explore the
environment, which means reducing the number of
possibilities of selecting the correct action (higher re-
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
164

ward) is not beneficial for formation of patterns. The
method demonstrated here is best suited for a kn own
environment. Applicatio ns o f MAS patterns are vast,
and this method demonstrated in this paper is highly
adaptable and user frien dly to account for any pat-
terns as desired. Proof of concept of this research is
presented over the formation of po lygons from maxi-
mum hexagonal dimension to minimum dimen sio na-
lity of triang ular. In this work, the control of agents to
reach the specified target is controlled independently
for both x and y position of agent. This can be ad-
vantageous in both computational efforts an d time.
To validate with other methods, the pattern formation
was tested using neural network. The drawback is
each agent should be specified with its initial position
and target. States-Space search cann ot be obtained b y
using this approach.
Future work includes comb ining leader-follower
(Prasad et al., 2016a) (Pr asad et al., 2016b) trajectory
tracking with pattern formation. We would like to
keep pattern selection and formation under the con-
trol of the leader. Coupling this system with le-
ader election would also be interesting and would
help counter any loss of conne ctivity during trajecto ry
tracking.
REFERENCES
A. Guillet, R. Lenain, B. T. and Martinet, P. (2014). Adapta-
ble robot formation control: Adaptive and predictive
formation control of autonomous vehicles. In IEEE
Robotics and Automation Magazine. IEEE.
B. Dafflon, F. Gechter, P. G. and Koukam, A. (2013). A lay-
ered multi-agent model for multi-configuration pla-
toon control. pages pp.33–40. International Confe-
rence on Informatics in Control, Automation and R o-
botics.
Busoniu, L., Schutter, B. D., and Babuska, R. (2006). De-
centralized rei nforcement learning control of a robotic
manipulator. In 2006 9th International Conference on
Control, Automation, Robotics and Vision, pages 1–6.
C. Zhang, T. S. and Pan, Y. (2014). Neural network
observer-based finite-time formation control of mo-
bile robots. pages pp. 1–9. Mathematical Problems
in Engineering.
Cheng, T. and Savkin, A. (2011). Decentralized control of
multi-agent systems for swarming with a given geo-
metric pattern. pages 61(4), pp.731–744. Computers
and Mathematics with Applications.
Dong, X., Yu, B., Shi, Z., and Zhong, Y. (2015). Time-
varying formation control for unmanned aerial vehi-
cles: theories and applications. IEEE Transactions on
Control Systems Technology, 23(1):340–348.
Duran, S. and Gazi, V. (2010). Adaptive formation control
and target tracking in a class of multi-agent systems.
In Proceedings of the 2010 American Control Confe-
rence, pages 75–80.
Gifford, C. M. and Agah, A. (2007). Precise formation of
multi-robot systems. I n 2007 IEEE International Con-
ference on System of Systems Engineering, pages 1–6.
I. Sanhoury, S. A. and Husain, A. (2012). Synchronizing
multi-robots in switching between different formati-
ons tasks while t racking a line. pages pp.28–36. Com-
munications in Computer and Information Science.
J. Alonso-Mora, A. Breitenmoser, M. R. R. S. and Beards-
ley, P. (2011). Multi-robot system for artistic pattern
formation. pages pp. 4512–4517. Robotics and Auto-
mation (ICRA), IEEE International Conference.
J. Desai, J. O. and Kumar, V. (2001). Modeling and control
of formations of nonholonomic mobile robots. pages
17(6), pp.905–908. IEEE Trans. R obot. Automat.
Karimoddini, A., Karimadini, M., and Lin, H. (2014). De-
centralized hybrid formation control of unmanned ae-
rial vehicles. In 2014 American Control Conference,
pages 3887–3892. IEEE.
Krick, L., Broucke, M. E., and Francis, B. A. (2009). Sta-
bilisation of infinitesimally rigid formations of multi-
robot networks. International Journal of Control,
82(3):423–439.
Prasad, B. K. S., Aditya, M., and Ramasangu, H.
(2016a). Flocking t r aj ectory control under faulty le-
ader: Energy-level based election of leader. pages
3752–3757. IEEE.
Prasad, B. K. S., A dit ya, M., and Ramasangu, H. (2016b).
Multi-agent trajectory control under faulty leader:
Energy-level based leader election under constant
velocity. pages 2151–2156. IEEE.
Rego, F., Soares, J. M., Pascoal, A., Aguiar, A. P., and Jo-
nes, C. (2014). Flexible triangular formation keeping
of marine robotic vehicles using range measurements
1. IFAC Proceedings Volumes, 47(3):5145–5150.
Ren, W. (2015). Consensus strategies for cooperative cont-
rol of vehicle formations. In Control Theory and Ap-
plications, pages pp.505 – 512. I ET.
Rezaee, H. and Abdollahi, F. (2015). Pursuit formation of
double-integrator dynamics using consensus control
approach. IEEE Transactions on Industrial Electro-
nics, 62(7):4249–4256.
Smith, S. L., Br oucke, M. E., and Francis, B . A. (2006).
Stabilizing a multi-agent system to an equilateral po-
lygon formation. In Proceedings of the 17th internati-
onal symposium on mathematical theory of networks
and systems, pages 2415–2424.
Multi-agent Polygon Formation using Reinforcement Learning
165