
Reactive Agent-based Model for Convergence of Autonomous Vehicles to
Parallel Formations Heading to Predefined Directions of Motion
Vander L. S. Freitas
1
and Elbert E. N. Macau
2
1
National Institute for Space Research - INPE, 12227-010, S
˜
ao Jos
´
e dos Campos, Brazil
2
Laboratory of Computing and Applied Mathematics, National Institute for Space Research - INPE, 12227-010,
S
˜
ao Jos
´
e dos Campos, Brazil
Keywords:
Reactive Agents, Parallel Formation, Collective Motion.
Abstract:
In this work we introduce a reactive agent-based model for convergence of autonomous vehicles to parallel
formations heading to predefined directions of motion. They interact via rules of repulsion, alignment and
attraction. There is also an abstraction of the desired path of motion, represented by a virtual guiding vehicle,
which shows the desired direction to be followed by the formation. We performed simulations with different
combinations of interaction rules and studied the parameter space. Additionally, we simulate the occurrence
of communication failure among agents and the presence of noise. The resulting formations are evaluated by
three quantifiers.
1 INTRODUCTION
Nature exhibits many emergent motions in collections
of living beings. These emergent order behaviors
are the result of local interactions among the agents.
Common situations of the emergence of collective
motion are in predator escaping, food search or hunt-
ing, for example.
Collective motion is a phenomenon that occurs
in collections of agents, similar or not, who interact
with each other, resulting in ordered motion (Vicsek
and Zafeiris, 2012). Those interactions can be among
close neighbors or in the context of a more evolved
framework. Collective motion is present everywhere,
from colonies of bacteria to schools of fish (Paley
et al., 2007). There are about 1 million species of
known insects in the world (Chapman et al., 2009)
and despite most of them live lonely, many others are
famous because of their organized behavior (Vicsek
and Zafeiris, 2012).
The motivation for the study of collective motion
is to understand the interaction rules among the units.
These rules may be applied to artificial vehicles so
they can work collaboratively in some tasks. Then it
is possible to establish a link between control theory
and applications of collective like robot swarms.
Studies on collective motion have resulted on
models that attempt to recreate the observed collec-
tive arrangements of agents (Reynolds, 1987; Vicsek
et al., 1995; Czir
´
ok et al., 1999; Couzin et al., 2002;
Paley, 2007; Cucker and Smale, 2007; Veerman et al.,
2005; Dafflon et al., 2013). They are used in many
applications like satellites in flight formation (Salazar,
2012), unmanned aerial vehicles (Klein, 2005) (Park
et al., 2015), unmanned subaquatic vehicles (Leonard
et al., 2007), aquatic surface robots (Duarte et al.,
2016) and others.
In this work we propose a reactive agent-based
model for convergence of autonomous vehicles to
moving formations. The aim is to group the vehi-
cles inside a moving bounded area heading to a prede-
fined direction. The agents interact via rules of repul-
sion, alignment and attraction, similar to the works
of Reynolds (Reynolds, 1987). The main difference
is that here there is an individual called virtual agent
(VA), i.e., a “virtual vehicle” that represents the de-
sired path we want to be followed by the formation.
It is not a real vehicle of the model but an abstrac-
tion. The individuals begin at random positions inside
an area and after a transient of interactions they con-
verge to a moving formation that heads in parallel to
the same direction of motion of the VA.
The behavior of the virtual agent is similar to a
leader, or the stakeholder agents of (Kerman et al.,
2012), which have privileged information about the
desired direction of the motion. The main difference
is that, as mentioned before, it is not a real vehicle but
an abstraction.
166
L. S. Freitas V. and E. N. Macau E.
Reactive Agent-based Model for Convergence of Autonomous Vehicles to Parallel Formations Heading to Predefined Directions of Motion.
DOI: 10.5220/0006187201660173
In Proceedings of the 9th International Conference on Agents and Artificial Intelligence (ICAART 2017), pages 166-173
ISBN: 978-989-758-219-6
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

One possible usage of the VA would be to consider
it as a moving GPS signal. In this case, one should
expect the agents to converge in a parallel formation
around its signal coordinates. Considering a scenario
in which the vehicles are disperse in an environment
and doing some work, e.g., measuring temperature, if
one wants them to head to another geographic loca-
tion, our model would be a good choice since VA dic-
tates the path for the flock. Additionally, the model
has the advantage of making the individuals getting
together, which is useful to group disperse agents.
(Duarte et al., 2016) presented controls using neu-
ral networks and one of the tasks their aquatic robots
can do is to go towards a geographic location. The
role of our virtual agent is also to point out coordi-
nates to be followed, but with the difference that these
coordinates change through time.
The interaction rules have biological inspiration,
derived from fishes and birds. (Herbert-Read et al.,
2011) analyzed 2D trajectories of birds and observed
rules of attraction and repulsion between close neigh-
bors. In a similar work, (Katz et al., 2011) found out
that fishes change their trajectories depending on the
neighbors in front of them. In this work we present
strategies for attraction and repulsion usage in the
context of ordered motion.
We performed experiments in parameter space to
seek for formations according to specific objectives.
Besides, we simulated communication problems, by
adding a probability distribution of individuals not re-
sponding to the environment stimuli on each time in-
stant. Lastly, we verified the model behavior in the
presence of a random noise. Both noise and com-
munication failures have to be considered when de-
signing real systems of this kind (Duarte et al., 2016),
because the individuals have sensors with limited pre-
cision. Also, there are environmental issues like the
presence of wind, for aquatic robots, or terrain irreg-
ularities for terrestrial vehicles, etc.
The paper is organized as follows. Section 2 de-
tails the reactive model, Section 3 presents implemen-
tation details, Section 4 reports some simulation re-
sults and Section 5 shows our conclusions.
2 REACTIVE MODEL
This model is called reactive because it uses the ar-
chitecture of reactive agents, in which the individuals
do not keep information of the past, but only respond
to the current state of the system (Russell and Norvig,
2003).
The components of our proposed model are the
so-called virtual agent, with its interaction radius, and
Figure 1: Model components: Virtual agent is in blue,
agents are in red and VAIR is in green.
the reactive agents, as follows (Figure 1):
• Virtual Agent: Its role is to point out the desired
motion direction and the moving region in which
we want that the agents to form a parallel forma-
tion. Despite its interaction with agents, it is not a
real agent but an abstraction.
• Virtual Agent Interaction Radius (VAIR): Cir-
cular region centered in VA, inside which the par-
allel formation will converge.
• Reactive Agents: The agents of the model. They
model autonomous vehicles. Their main charac-
teristic is that they do not keep memory of previ-
ous interactions, i.e., they respond to the current
system state according to simple rules.
The aim here is to make the agents to enter the
VAIR and follow the VA in a parallel formation. For
this purpose they interact via adjustments in their ve-
locity module (speed) and rules (interaction strengths)
based on repulsion, alignment and attraction. We call
these interaction rules as “virtual forces”. Here the
concept of force is related to how the presence of the
neighbors of an agent i can impose changes on its
heading angle θ
i
= θ
i
(t).
The speed adjustment is performed according to
the position of the agent in relation to the VAIR.
When an agent is outside the VAIR its speed is higher
than when it is inside, because it needs to reach the
VA. When an agent is entering the VAIR it suffers a
deceleration according to Eq 1, so it can move along
with the VA. The idea is to guarantee that the parallel
formation will occur inside the VAIR.
|v
i
| = |v
a
| −
(|v
ini
| − |v
a
|)(t −t
f
)
∆t
i
(1)
so that v
i
is the velocity of agent i, v
a
is the velocity
of the VA, v
ini
is the velocity of agent i at the moment
it started entering the VAIR, t is the current time, t
f
is
the time instant in which the acceleration will finish
and ∆t
i
is the total time of this procedure.
In this equation ∆t
i
= t +rnd, in which t represents
the approximate time for the agent to move from the
Reactive Agent-based Model for Convergence of Autonomous Vehicles to Parallel Formations Heading to Predefined Directions of Motion
167

VAIR boundary to the VA’s position, and rnd is a ran-
dom number in the interval rnd ∈ (−γ, γ). Here we
used γ
.
= t to guarantee a homogeneous distribution
of agents inside the VAIR.
When an agent is leaving the VAIR, its speed in-
creases according to Eq 2. In this case, |v
out
| repre-
sents the maximum speed outside the VAIR.
|v
i
| = |v
a
| −
(|v
out
| − |v
ini
|)(t −t
f
)
∆t
i
(2)
We use five interaction rules to achieve the paral-
lel formation in the desired direction of motion. The
rules are written in the form of imposed control ac-
tions, or “forces”, as follows (Figure 2):
• F
a
(Alignment): Orders the agent to align with the
average heading angles of its neighbors.
• F
c
(Cohesion): Orders the agent to go to the center
of mass of its neighbors.
• F
av
(Alignment with virtual agent): Orders the
agent to align with the VA heading angle.
• F
cv
(Cohesion with virtual agent): Orders the
agent to move towards the VA.
• F
s
(Separation): Orders the agent to move apart
from its nearest neighbor.
All of those control actions are applied to the
agent as the angular velocity control input, acting di-
rectly on the heading angle of the agents at discrete
time. Their maximum value is 1.00 decimal degree
per time unit to account for limitations that may be
present in the heading angle changes of real robots.
For example, if agent 1 has θ
1
= 150.00 as its head-
ing angle, and VA θ
a
= 160.00, when F
a
is applied
it will result in F
a
= 1.00 and θ
1
= 151.00. How-
ever, if θ
1
= 159.50 and θ
a
= 160.00 and F
a
is ap-
plied, the result would be F
a
= 0.50 and consequently
θ
1
= 160.00. Each time unit (tu) corresponds to a
travel of 1.00 bl (body length of an agent) of VA, i.e.,
the VA’s speed is |v
a
| = 1 bl/tu.
F
a
and F
c
do the same than alignment and co-
hesion rules defined by Reynolds (Reynolds, 1987).
Each isolated force produces an effect but we are in-
terested on the combinations of them. For this case
the resulting force F is calculated as a linear combi-
nation of the five forces, according to Eq 3.
F(t) =
α
a
F
a
(t) + α
c
F
c
(t) + α
av
F
av
(t) + α
cv
F
cv
(t)
α
a
+ α
c
+ α
av
+ α
cv
(3)
in which α
a
, α
c
, α
av
, α
cv
are control coefficients and
each force is unitary. The separation force does not
appear here because it is used isolated when a colli-
sion between two individuals is about to happen. In
this case, we use Eq 4.
(a) F
s
(b) F
a
(c) F
c
(d) F
av
(e) F
cv
Figure 2: Interaction rules. The dotted circumferences rep-
resent the interaction area (vision radius) of one agent (in
black). At (d) and (e) the blue agent is the virtual agent.
F(t) = F
s
(t) (4)
The dynamics of an agent is given by Eq 5.
˙x
i
= |v
i
|. cos(θ
i
)
˙y
i
= |v
i
|. sin(θ
i
)
˙
θ
i
= F
(5)
where [x
i
, y
i
]
T
∈ R
2
is the ith agent’s position, ex-
pressed in terms of polar coordinates.
The virtual agent represents the desired trajectory
for the parallel formation, i.e., the position over time
that we want our formation to follow. Its dynamics
works as an ordinary agent but with fixed heading an-
gle θ
i
, velocity |v
i
| = |v
a
|.
3 IMPLEMENTATION
The simulations were implemented using the Python
language and some libraries like matplotlib
1
and
numpy
2
, for ploting, random number generation, etc.
The simulation scenario works as a torus. When
the agents reach the outskirts of the environment, they
appear at the opposite side, heading to the same direc-
tion as before. For example, when they are heading to
the left and cross the limits they appear at right.
Agents begin in a bounded rectangular area be-
hind the VA, with random coordinates and heading
angles as shown in Figure 1. The coordinate system
is given by the size of the agent. We assumed that the
VA is able to move the distance of one body length
(bl) per time unit (tu). Considering that particles have
a circular shape, this bl is their diameter.
The implementation has basically three classes:
Agent, Model and Simulation. Agent represents each
1
http://matplotlib.org/
2
http://www.numpy.org/
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
168

(a) C-1 (b) C-2
Figure 3: Calculation of forces: S-1) Considering the entire
agent vision radius equally; and S-2) Considering zones of
perception (ZS - Zone of separation, ZA - Zone of align-
ment and ZC - Zone of cohesion). The black agent is an
ordinary agent of the model and the dotted region corre-
sponds to its vision region (perception region). Agents in
red are its neighbors.
agent of the simulation, with its coordinates and
speed. When the agent enters or leaves the VAIR, its
speed changes through Eqs. 1 and 2. The class Model
has a list of agents and is responsible for evolving the
model, according to the Eq. 5, parameters like neigh-
borhood radius, control coefficients α
a
, α
c
, α
av
, α
cv
,
and the chosen strategy. The strategies are presented
in the next section. The class Simulation is respon-
sible for setting up the parameters of the model and
running the simulations.
4 RESULTS
There are two approaches to deal with the neighbor-
hood of each agent. In the first (S-1) the agent consid-
ers a neighborhood radius in which every neighbor is
treated similarly, i.e., the control actions (forces) are
applied without distinction, regarding their position
(Figure 3a).
The second approach (S-2) takes into account the
distances between the agent and its neighbors through
perception zones (Figure 3b). In this case, when a
neighbor is in the first radius, closer to the agent, only
F
s
is calculated. Following the same logic, when the
neighbor is in the second zone (ZA), only the force of
alignment F
a
is computed, and in the third zone (ZC),
only F
c
is considered. This approach is inspired in
an observed behavior that occurs in schools of fish.
(Katz et al., 2011) showed that some species of fish
increase their speed when a neighbor is far ahead (at-
traction), while decreases when it is too close (sepa-
ration). (Kerman et al., 2012) has implemented these
three perception zones but the outer region (ZC) con-
tains the other two inside, and ZA contains ZS. Here
we consider them as rings, i.e., they do not overlap,
similar to the works of (Couzin et al., 2002).
We test four strategies (combinations of forces) as
shown in Table 1. The application of forces depends
on whether the agent is inside or outside the VAIR.
Despite there are only four strategies, the table shows
eight possibilities because of the two approaches of
neighborhood calculation, S-1 and S-2.
Table 1: Strategies (combinations of control actions) used
when the agents are inside or outside the VAIR.
Strategy
Outside the VAIR Inside the VAIR
S-1.1 (S-2.1)
F
a
, F
cv
F
av
S-1.2 (S-2.2) F
cv
F
av
, F
a
S-1.3 (S-2.3)
F
cv
, F
c
F
av
, F
a
S-1.4 (S-2.4)
F
cv
, F
c
, F
av
, F
a
F
av
, F
a
Definition 1 If all agents are moving in a parallel
formation inside the VAIR and have the same speed of
the virtual agent, then they are in a Desired Formation
(DF).
We consider they are in parallel if the higher dif-
ference between the VA heading angle θ
a
and each
agent heading angle θ
i
is smaller than an imposed tol-
erance β
lim
. In other words, they are in parallel if
|θ
a
− θ
i
| < β
lim
, for i ∈ {1, 2, · · · ,N}.
We define three quantifiers to measure what kind
of parallel formations we can get with different com-
binations of control actions:
1. Temporal index (τ): time units (tu) from the be-
ginning of the simulation until the DF.
2. Angular uniformity index (φ): The relative angles
between the position of each agent and the VA
is calculated. Then the order parameter (Eq 6 -
(Strogatz, 2000)) is evaluated with those angles.
p
Θ
.
=
1
N
N
∑
j=1
e
iΘ
j
(6)
with e
iΘ
k
= cos Θ
j
+ i sin Θ
j
.
In this case, φ = |p
Θ
|. When φ = 0 the agents
are uniformly distributed around the VA. On the
other hand, if φ = 1 then the agents are at the same
position.
3. Radial uniformity index (ρ): The mean of the dis-
tances between each agent and the VA.
The first index (τ) computes the total time for the
model convergence, and the two others, φ and ρ, are
related to the distribution of the formation. If the
agents are very close to each other, they have small ρ.
For the case in which the agents converge to straight
lines, following the VA, φ is near 1. On the other
hand, when the agents converge to some sort of cir-
cular shape, centered in VA, φ is close to zero.
Reactive Agent-based Model for Convergence of Autonomous Vehicles to Parallel Formations Heading to Predefined Directions of Motion
169

We evaluated the strategies with all combinations
of α
a
, α
c
, α
av
, α
cv
∈ {1, 2, ··· , 10}. Each configura-
tion is simulated 10 times using random initial posi-
tions and heading angles θ
θ
θ = (θ
i
(t))
i=1,2,···,N
.
Initial conditions:
• Population of N = 12 agents randomly positioned
inside a rectangle of dimensions 36 x 76 bl, as
shown in Figure 1.
• Vision radius of each agent: 5.5 bl.
• Minimum separation: 2.5 bl.
• F
s
: 2 decimal degrees.
• F
a
= F
c
= F
av
= F
cv
: 1 decimal degree.
• Heading angles θ
θ
θ: Random.
• |v
a
| = 1 bl/tu , |v
out
| = 1.4 bl/tu.
• VAIR: 25 bl.
• Virtual agent heading angle: 180 decimal degrees.
• β
lim
: 5 decimal degrees.
Only cases that reach the DF for all 10 attempts
and obeying τ ≤ 3000 tu are considered. Simulations
are limited to this temporal limit of 3000 tu due to
the large number of combinations in parameter space.
Also, this value is set because the agents usually con-
verge in less than 2000 tu, according to experimental
observations.
We calculate the three indexes for each combina-
tion of control coefficients. Figure 4 depicts the de-
sired formations achieved in terms of the maximum
and minimum values of τ, φ and ρ.
(a) min(τ) =
871: S-2.2
(b) max(τ) =
1971: S-1.1
(c) min(φ) =
0.09: S-1.3
(d) max(φ) =
0.36: S-1.4
(e) min(ρ) =
5.20: S-1.2
(f) max(ρ) =
13.88: S-2.4
Figure 4: Desired formations for the simulated config-
urations in terms of the maximum and minimum values
achieved for τ, φ and ρ. Configurations: (a) S-2.2: α
a
= 8,
α
av
= 9 and α
cv
= 4; (b) S-1.1: α
a
= 7, α
av
= 1 and α
cv
= 3;
(c) S-1.3: α
a
= 1, α
c
= 4, α
av
= 4 and α
cv
= 9; (d) S-1.4:
α
a
= 3, α
c
= 5, α
av
= 7 and α
cv
= 9; (e) S-1.2: α
a
= 3,
α
av
= 10 and α
cv
= 10; (f) S-2.4: α
a
= 2, α
c
= 3, α
av
= 6
and α
cv
= 9.
If one wants agents to converge as fast as possi-
ble, a good choice would be strategy S-2.2 with the
configuration of Figure 4a. An example of simulation
with this configuration is shown in Figure 5. Other-
wise, if the aim is to get them very close to each other
the best option is the configuration of strategy S-1.2 of
Figure 4e. The resulting formations depends on both
the chosen strategy and configuration. In this sense,
some strategies are more suitable for some objectives
than others.
In a situation in which one desires the agents to
spread uniformly inside the VAIR, φ would be near
zero and ρ around the half of VAIR size. Consider-
ing an application in which surveillance vehicles are
monitoring an area it is expected that they travel far
from each other, so they can explore a bigger area.
For this purpose, ρ should be as large as possible.
Certain combinations of parameters α do not lead
to the expected convergence. If one sets the α
a
value
much higher than α
av
, it is possible that the agents
never follow the VA because they are more likelly to
converge to a parallel motion heading elsewere. Fig-
ure 6 shows the dependence between α
a
and α
av
for
strategy S-2.2, in which the colors correspond to the
rate of DF convergence. The agents are more likely to
reach the DF when α
av
≥ α
a
, for S-2.2.
We simulate failures on communication, emulat-
ing what would happen case an agent lost the feed-
back from its neighbors during a time unit. In our
setup, this problem does not last until the end of the
simulation, but it is calculated each time unit. Also,
we add a random noise to the dynamics of their head-
ing angles, to simulate external interferences from the
environment (wind, terrain irregularities, etc) and sen-
sor imprecisions.
The random noise ε ∈ [−δ, δ] is applied according
to Eq. 7, with δ representing the noise strength. There
is also a probability p of the agent to ignore its neigh-
bors stimuli. We simulate both noise and communica-
tion failure for each agent, independently, to account
for what would happen in a real world system.
˙
θ = F + ε (7)
We have chosen strategy S-2.2 with the configu-
ration of Figure 4a to simulate noise and communi-
cation failures, because it converges faster than the
others.
We varied p ∈ [0, 0.9] and δ ∈ [0, 0.9], with steps
of ∆p = ∆δ = 0.1, and calculated the average of 50
simulations for each pair (p, δ) since initial conditions
are random. Figure 7a shows the results. Seems like
for p ∈ [0, 0.8] there is no change in the colors, be-
cause of the abrupt difference between p = 0.8 and
p = 0.9. Figure 7b presents this region in more de-
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
170
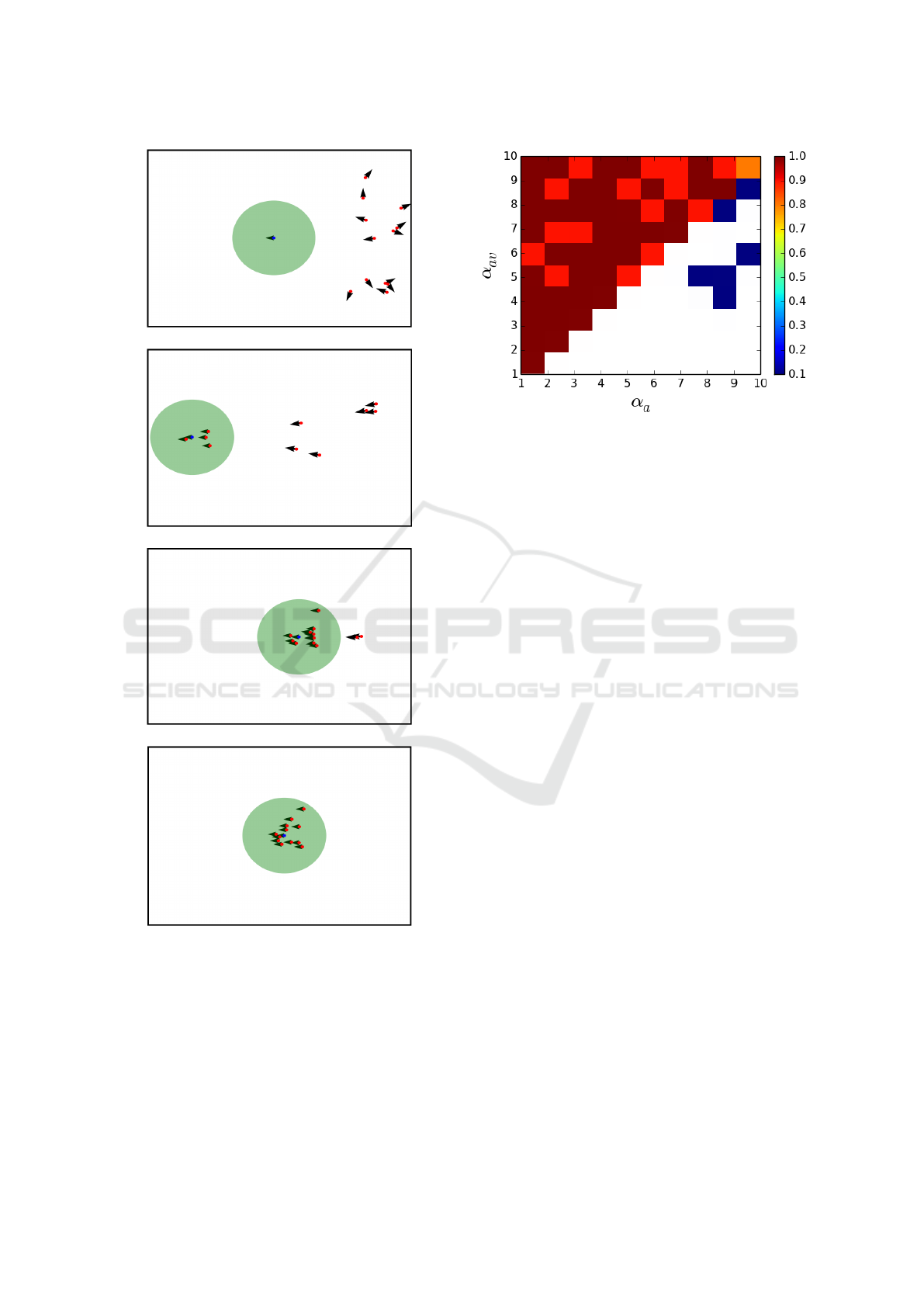
(a) t = 2 tu
(b) t = 383 tu
(c) t = 650 tu
(d) t = 870 tu
Figure 5: Simulation of strategy S-2.2 with configuration
α
a
= 8, α
av
= 9 and α
cv
= 4.
tails. As expected, the higher the value of p the longer
it takes to reach the desired formation, with τ increas-
ing smoothly for p ∈ [0, 0.8]. When p = 0.9 it sud-
denly jumps to a very high value. It probably hap-
pened because for S-2.2 the only force acting outside
the VAIR is F
cv
. If the agents ignore it with a proba-
bility of p = 0.9, than they will only try to go towards
Figure 6: Convergence ratio when varying control coeffi-
cients α
a
and α
av
for strategy S-2.2. Colors represent the
convergence ratio and white regions represent the cases in
which DF was not achieved. The agents are more likely to
reach the DF when α
av
≥ α
a
.
VA 10% of the cases, resulting in a very high τ.
The values of ε were proportional to
˙
θ and it seems
like ε does not affect the convergence of formations,
according to Figure 7.
Results have shown that this model is quite re-
silient to communication failures, and the presence
of noise, since their impact was small, specially for
noise.
5 CONCLUSIONS
We presented a reactive agent-based model whose
aim is to make agents converge to parallel formations
heading to a desired direction. We introduced the so-
called virtual agent, whose role is to indicate the for-
mations direction of motion and also to evaluate their
shapes. The agents interact via five rules depending
on a chosen strategy (combination of rules) and a con-
figuration (weight of each rule).
Four strategies were evaluated and analyzed for
about 44,000 configurations, considering two neigh-
borhood approaches to calculate the virtual forces:
one taking into account the presence of neighbors
likewise, and the other using non-overlapping inter-
action zones.
The last simulations were focused on communi-
cation failures, in which the agents had a probability
of ignoring the external stimuli from neighbors, each
time unit. This represents failures on the wireless net-
work, or even the GPS signal. Besides, we added a
random additive noise to the agents heading angle, to
account for the sensors imprecision, and environmen-
Reactive Agent-based Model for Convergence of Autonomous Vehicles to Parallel Formations Heading to Predefined Directions of Motion
171
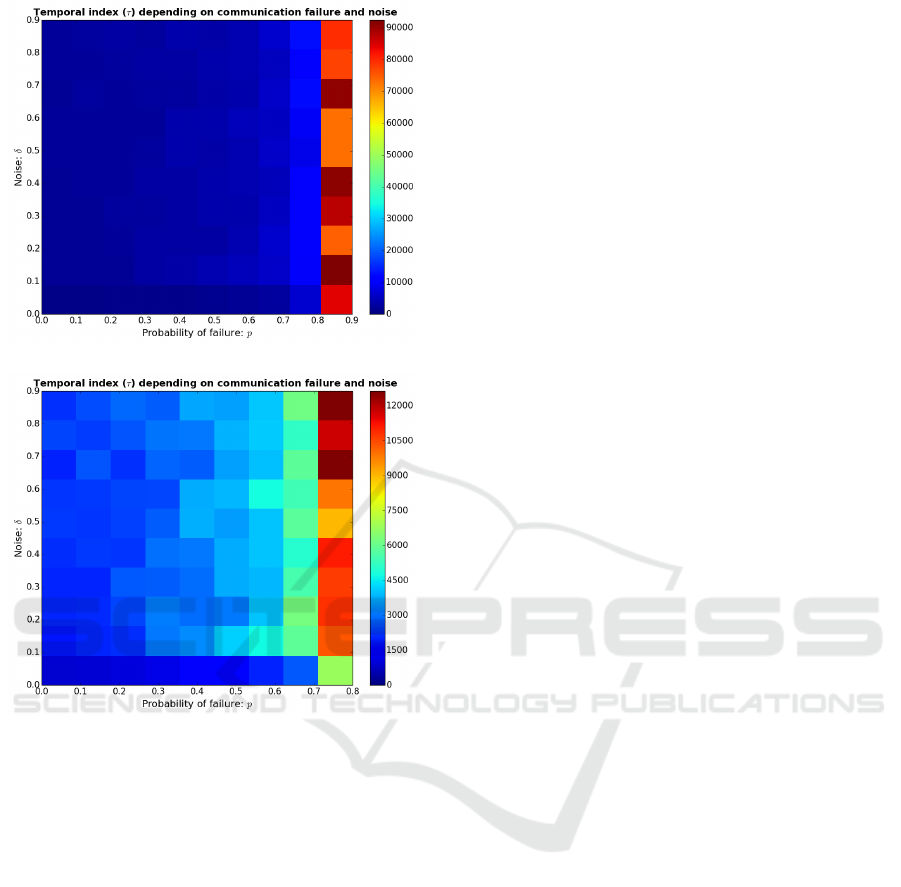
(a)
(b)
Figure 7: Temporal index (τ) depending on the probability
of communication failure p and a random noise ε ∈ [−δ, δ],
for S-2.2, with α
a
= 8, α
av
= 9 and α
cv
= 4. (a) communi-
cation failure with p ∈ [0, 0.9], (b) Zooming to p ∈ [0, 0.8].
Color represents τ.
tal issues as the presence of wind or terrain irregu-
larities. Results have shown that our model is quite
resilient to communication failures, and the presence
of noise, since their impact was small, specially for
noise.
Considering that agents have sensory limitations,
one can use this model as a pre-step before switching
to another model with more controls, since its princi-
ple is to group agents into a bounded region.
ACKNOWLEDGEMENTS
The authors would like to thank the Conselho Na-
cional de Desenvolvimento Cientifico e Tecnologico
- CNPq, and the Coordenacao de Aperfeicoamento
de Pessoal de Nivel Superior - CAPES, for the fi-
nancial support. EENM thanks FAPESP, processes
2011/50151-0 and 2015/50122-0, and CNPq, process
458070/2014-9, for their support.
REFERENCES
Chapman, A. D., Study., A. B. R., and Australia. (2009).
Numbers of living species in Australia and the world /
Arthur D. Chapman. Department of the Environment,
Water, Heritage and the Arts [Canberra, ACT].
Couzin, I. D., Krause, J., James, R., Ruxton, G. D., and
Franks, N. R. (2002). Collective memory and spatial
sorting in animal groups. Journal of Theoretical Biol-
ogy, 218(1):1 – 11.
Cucker, F. and Smale, S. (2007). Emergent behavior in
flocks. IEEE Transactions on Automatic Control,
pages 852–862.
Czir
´
ok, A., Barab
´
asi, A.-L., and Vicsek, T. (1999). Collec-
tive motion of self-propelled particles: Kinetic phase
transition in one dimension. Phys. Rev. Lett., 82:209–
212.
Dafflon, B., Gechter, F., Gruer, P., and Koukam, A. (2013).
Vehicle platoon and obstacle avoidance: A reactive
agent approach. IET Intelligent Transport Systems,
7(3):257–264.
Duarte, M., Costa, V., Gomes, J., Rodrigues, T., Silva, F.,
Oliveira, S. M., and Christensen, A. L. (2016). Evolu-
tion of collective behaviors for a real swarm of aquatic
surface robots. PLOS ONE, 11(3):1–25.
Herbert-Read, J. E., Perna, A., Mann, R. P., Schaerf, T. M.,
Sumpter, D. J. T., and Ward, A. J. W. (2011). Inferring
the rules of interaction of shoaling fish. Proceedings
of the National Academy of Sciences, 108(46):18726–
18731.
Katz, Y., Tunstrom, K., Ioannou, C. C., Huepe, C., and
Couzin, I. D. (2011). Inferring the structure and dy-
namics of interactions in schooling fish. Proceedings
of the National Academy of Sciences, 108(46):18720–
18725.
Kerman, S., Brown, D., and Goodrich, M. A. (2012). Sup-
porting human interaction with robust robot swarms.
In Resilient Control Systems (ISRCS), 2012 5th Inter-
national Symposium on, pages 197–202.
Klein, J. K. (2005). Controlled Collective Motion for Mul-
tivehicle Trajectory Tracking. Master’s thesis, Univer-
sity of Washington, USA.
Leonard, N., Paley, D., Lekien, F., Sepulchre, R., Fratan-
toni, D., and Davis, R. (2007). Collective motion, sen-
sor networks, and ocean sampling. Proceedings of the
IEEE, 95(1):48–74.
Paley, D., Leonard, N. E., Sepulchre, R., Gr
¨
unbaum, D.,
and Parrish, J. K. (2007). Oscillator models and col-
lective motion: Spatial patterns in the dynamics of en-
gineered and biological networks. IEEE Control Sys-
tems Magazine, 27(4):89–105.
Paley, D. A. (2007). Cooperative control of collective mo-
tion for ocean sampling with autonomous vehicles.
PhD thesis, Princeton University.
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
172

Park, C., Cho, N., Lee, K., and Kim, Y. (2015). Formation
flight of multiple uavs via onboard sensor information
sharing. Sensors, 15:17397–17419.
Reynolds, C. W. (1987). Flocks, herds and schools: A
distributed behavioral model. SIGGRAPH Comput.
Graph., 21(4):25–34.
Russell, S. J. and Norvig, P. (2003). Artificial Intelligence.
Pearson Education, 2 edition.
Salazar, F. J. T. (2012). Deployment and maintenance of a
satellite formation flight around L4 and L5 lagrangian
points in the earth-moon system based on low cost
strategies. PhD thesis, Instituto Nacional de Pesquisas
Espaciais.
Strogatz, S. H. (2000). From kuramoto to crawford: Ex-
ploring the onset of synchronization in populations of
coupled oscillators. Phys. D, 143(1-4):1–20.
Veerman, J. J. P., Lafferriere, G., Caughman, J. S., and
Williams, A. (2005). Flocks and formations. Journal
of Statistical Physics, 121(5):901–936.
Vicsek, T., Czir
´
ok, A., Ben-Jacob, E., Cohen, I., and
Shochet, O. (1995). Novel type of phase transition
in a system of self-driven particles. Phys. Rev. Lett.,
75:1226–1229.
Vicsek, T. and Zafeiris, A. (2012). Collective motion.
Physics Reports, 517(3-4):71 – 140. Collective mo-
tion.
Reactive Agent-based Model for Convergence of Autonomous Vehicles to Parallel Formations Heading to Predefined Directions of Motion
173
