
Non-interactive Privacy-preserving k-NN Classifier
Hilder V. L. Pereira and Diego F. Aranha
Institute of Computing, University of Campinas, Campinas, SP, Brazil
{hilder.vitor, dfaranha}@gmail.com
Keywords:
Privacy-preserving Classification, Order-preserving Encryption, Homomorphic Encryption.
Abstract:
Machine learning tasks typically require large amounts of sensitive data to be shared, which is notoriously
intrusive in terms of privacy. Outsourcing this computation to the cloud requires the server to be trusted,
introducing a non-realistic security assumption and high risk of abuse or data breaches. In this paper, we pro-
pose privacy-preserving versions of the k-NN classifier which operate over encrypted data, combining order-
preserving encryption and homomorphic encryption. According to our experiments, the privacy-preserving
variant achieves the same accuracy as the conventional k-NN classifier, but considerably impacts the original
performance. However, the performance penalty is still viable for practical use in sensitive applications when
the additional security properties provided by the approach are considered. In particular, the cloud server does
not need to be trusted beyond correct execution of the protocol and computes the algorithm over encrypted
data and encrypted classes. As a result, the cloud server never learns the real dataset values, the number of
classes, the query vectors or their classification.
1 INTRODUCTION
With corporations and governments becoming more
intrusive in their data collection and surveillance ef-
forts, and the recurrent data breaches observed in the
last years, the cloud paradigm faces multiple chal-
lenges to remain as the computing model of choice
for privacy-sensitive applications. The low operat-
ing costs and high availability of storage capacity and
computational power may not look as attractive after
the risks of outsourcing computation and data storage
are considered. There are no formal guarantees that
the cloud provider is not behaving in abusive or intru-
sive ways, or even that the infrastructure is protected
against external attacks. Different legal regimes and
governmental influence introduce further complica-
tions to the problem and may shift responsibilities
in unclear ways. After the Snowden revelations, the
long-term financial impact from the current crisis in
cloud provider trust is estimated between 35 and 180
billion dollars in 2016 in the US only (Miller, 2014).
A solution proposed to reconcile these issues con-
sists in computing over encrypted data. In this
model, data is encrypted with a property-preserving
transformation (originally called a privacy homomor-
phism (Rivest et al., 1978) that still allows some op-
erations to be performed in the encrypted domain.
Constructions which provide this feature and support
an arbitrary number and type of operations (additions
and multiplications) are called fully homomorphic en-
cryption schemes and usually introduce a massive
performance penalty. The more restricted partial or
somewhat homomorphic encryption schemes impose
an upper bound in the number and type of operations,
with much improved performance figures. However,
they require a redesign of the high-level algorithms to
satisfy the restrictions and conserve most of the orig-
inal performance and effectiveness, when compared
to distributed approaches based on secure multiparty
computation (Xiong et al., 2007).
Classically, computing over encrypted data was
applied to tallying secret votes in electronic elec-
tions (Hirt and Sako, 2000), but modern homomor-
phic encryption schemes may soon enable a host
of interesting privacy-preserving applications in the
fields of genomics, healthcare and intelligence gath-
ering (Naehrig et al., 2011). Natural applications ex-
tend to data mining (Lindell and Pinkas, 2009) and
machine learning (Gilad-Bachrach et al., 2016) which
involve considerable amounts of data to be shared
and manipulated in untrusted platforms. Following
this trend, some previous works in the literature have
experimented with performing the task of classifica-
tion over encrypted data. The problem is fundamental
in itself and as a building block for several machine
learning algorithms, and amounts to identify to which
of a set of categories a new sample belongs, based on
previous observations whose membership is known
362
Pereira, H. and Aranha, D.
Non-interactive Privacy-preserving k-NN Classifier.
DOI: 10.5220/0006187703620371
In Proceedings of the 3rd International Conference on Information Systems Security and Privacy (ICISSP 2017), pages 362-371
ISBN: 978-989-758-209-7
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

(called training set). Graepel et al. adapted simple
classification algorithms to work on encrypted data
using somewhat homomorphic encryption (Graepel
et al., 2012), while Bost et al. considered more com-
plex classifiers such as decision trees and Bayesian
inference for medical applications (Bost et al., 2015).
Other authors designed protocols for clustering en-
crypted data in the two-party setting (Jha et al., 2005).
The main contributions of this paper are privacy-
preserving variants of the k-NN classifier, both
unweighted and distance-weighted, combining two
main building blocks: homomorphic encryption and
order-preserving encryption. The protocols are non-
interactive and ideally suited to cloud computing en-
vironments, where storage and computation are del-
egated from a low-power device to powerful cloud
servers. Experimental results demonstrate that there
is no substantial accuracy loss in performing the clas-
sification task in a privacy-preserving way. Our secu-
rity analysis claims security in the semi-honest (also
called honest-but-curious) threat model, although the
drawbacks from adopting order-preserving encryp-
tion for efficiency restrict the application scenarios to
computing over private encrypted databases with no
publicly available knowledge about the distribution of
data. To the best of our knowledge, this is the first
proposal in the scientific literature for non-interactive
cloud-based k-NN classification over encrypted data.
The paper is organized as follows. In Section 2,
we recall the conventional k-NN classifier and de-
fine the problem of privacy-preserving classification.
Section 3 presents the basic building blocks of our
approach: order-preserving encryption (OPE) and
homomorphic encryption (HE). The proposed algo-
rithms are discussed in Section 4, through descrip-
tions of the initialization, querying, processing and re-
sponse procedures. Section 5 presents the experimen-
tal results of evaluating the plain k-NN and privacy-
preserving versions over 6 different datasets. In Sec-
tion 6, we briefly enumerate the security properties
offered by the scheme and corresponding security as-
sumptions. Related work is discussed in 7 and con-
clusions can be found at the final section.
2 PROBLEM STATEMENT
In this section, we define the classification problem
the k-NN algorithm was designed to solve and discuss
a privacy-preserving variant of the problem, compati-
ble with a cloud-based centralized processing model.
2.1 The k-NN classifier
The k-Nearest Neighbor (k-NN) classifier is a well-
known non-parametric supervised method to classify
an instance based on the classes of its nearest neigh-
bors (Altman, 1992; Alpaydin, 2004). Each instance
is represented by a vector in R
p
and an associated la-
bel, called the instance’s class. A query vector is an
unlabeled instance to be classified.
The k-NN classifier has a positive integer param-
eter k, which is the number of neighbors taken in ac-
count when classifying a new instance, and a function
d from R
p
× R
p
to R, which determines the distance
between two instances (the Euclidean distance is of-
ten used).
In order to classify a query vector x ∈ R
p
, the k-
NN algorithm works as follows:
1. Find the k nearest neighbors: among all the clas-
sified instances u
1
,u
2
,...,u
n
, select the k instances
whose distances d(u
i
,x) are the smallest.
2. Assign a class: select the most frequent class
among the k nearest neighbors and assign it to x.
There is also a k-NN variant known as distance-
weighted k-NN, or simply weighted k-NN. In this
version, instead of assigning the most frequent class
among the k nearest neighbors, the inverse of the dis-
tance to the query vector is used as the vote’s weight
for each of the k neighbors.
2.2 Privacy-preserving k-NN in the
Cloud
The privacy-preserving k-NN problem can be defined
as the problem of computing the k-NN on an untrusted
platform without revealing sensitive information such
as the data instances, their classes, the query vectors,
and the classification results. By untrusted platform
we mean a third party that holds the data in some form
but is not trusted by the data owner. In our scenario,
we assume a client-server model, in which the data
owner is the client and the server is the cloud service.
The client intends to store data in the cloud and pro-
cess it in a non-interactive way, which means that the
cloud will interact with the client only to receive the
data and the query vectors to be classified, but will
not communicate with the client during the process-
ing. In some applications, it may be the case that data
is already collected in the cloud in encrypted form, on
behalf of the client. It is also assumed that the client
is constrained in terms of computation and storage ca-
pabilities, but is capable of managing cryptographic
keys in a secure way.
Non-interactive Privacy-preserving k-NN Classifier
363

The other possible scenario is distributed process-
ing: the client collaborates with the cloud (or the
other parties involved) by receiving and processing
data during the training phase or the classification.
We stress that the centralized model is more conve-
nient to the client and is the expected model when
referring to cloud services.
3 BASIC CONCEPTS
In this section, we present the two encryption schemes
used as building blocks to guarantee the privacy-
preserving property of our k-NN classifier:
3.1 Order-preserving Encryption
“Order-preserving symmetric encryption (OPE) is a
deterministic encryption scheme which encryption
function preserves numerical ordering of the plain-
texts.” (Boldyreva et al., 2011) In other words, given
two plaintexts m
1
and m
2
, and their corresponding ci-
phertexts c
1
and c
2
encrypted with an OPE scheme,
the following implication is true:
m
1
≤ m
2
⇒ c
1
≤ c
2
.
Because this class of schemes works over finite
sets of numerical values, it is sufficient to describe
it using the set D = {1,2,...,M} as the message space
(or domain) and the set R = {1, 2, ..., N} as the cipher-
text space (also called range). OPE schemes are thus
parametrized by two positive integer values M and N,
that represent the number of possible plaintexts and
the number of possible ciphertexts, respectively. We
define the OPE scheme as follows:
OPE.KEYGEN(M, N, s) is a probabilistic algorithm
that receives a secret string s and the parameters
M, N ∈ N such that 1 ≤ M ≤ N; and returns the
secret key K.
OPE.ENC(K, m) is an algorithm that encrypts a
plaintext m ∈ D using the key K and returns a ci-
phertext c ∈ R. When it is clear from the context,
we may omit the encryption key and write simply
OPE.ENC(m) for short.
OPE.DEC(K, c) is an algorithm that decrypts a ci-
phertext c ∈ R using the key K and returns the
corresponding plaintext m ∈ D. We may omit the
decryption key and write simply OPE.DEC(m).
For a vector w = (w
1
,...,w
p
), we define the
component-wise encryption as a vector whose each
component is encrypted with the same key:
OPE.ENC(w) = (OPE.ENC(w
1
),..., OPE.ENC(w
p
)).
We define component-wise decryption similarly,
and refer to the space formed by the encrypted vectors
as encrypted space. If OPE is used to encrypt vectors,
then the order is maintained for each axis. Therefore,
it is very likely that each vector will have the same
neighborhood in the encrypted space. This fact is ex-
ploited to make it possible for the cloud to find the
nearest neighbors of a given encrypted vector.
3.2 Homomorphic Encryption
A criptographic scheme is homomorphic for an opera-
tion if it is equivalent to perform this operation over
plaintexts or over ciphertexts. For instance, consid-
ering the multiplication operation, the product of two
ciphertexts encrypted by a cryptosystem with homo-
morphic properties generates a third ciphertext that
has to be decrypted to the product of the two corre-
spondent plaintexts.
In this work, we employed the Paillier cryptosys-
tem (Paillier, 1999). The plaintext message space of
this scheme is Z
n
, where n the product of two large
primes p and q. The Pailler cryptosystem is also
additively homomorphic, which means that given ci-
phertexts c
0
and c
1
, corresponding to encryption of
two messages m
0
and m
1
, it is possible to calculate a
third ciphertext c that decrypts to m
0
+ m
1
. Further-
more, the cryptosystem offers efficient multiplication
between ciphertext and plaintext. More specifically,
given a ciphertext c
0
, corresponding to the encryp-
tion of m
0
, and a plaintext message m
1
, it is possible
to efficiently compute a ciphertext c that decrypts to
m
0
· m
1
∈ Z
n
.
The scheme can be described using the following
procedures:
HE.KEYGEN(λ): choose two random primes p and q
with equivalent bit lengths such that they ensure λ
bits of security. Set n = pq, g = n + 1, = (p −
1)(q − 1), and y =
−1
∈ Z
n
. Return the private
key SK = (, y) and the public key PK = (n, g).
HE.ENC(PK, m): to encrypt m ∈ Z
n
, sample a ran-
dom r from Z
∗
n
, compute c = g
m
r
n
mod n
2
, and
return c.
HE.DEC(SK, c): to decrypt c ∈ Z
n
2
, calculate x =
c
mod n
2
, divide (x − 1) by n, obtaining x
0
and
then return (x
0
· y ∈ Z
n
).
HE.ADD(c
1
,c
2
): to add two ciphertexts homomor-
phically, return (c
1
· c
2
mod n
2
).
HE.PROD(c
1
,m
2
): to multiply a ciphertext c
1
by
a plaintext m
2
homomorphically, return (c
m
2
1
mod n
2
).
ICISSP 2017 - 3rd International Conference on Information Systems Security and Privacy
364

4 NON-INTERACTIVE k-NN
OVER ENCRYPTED DATA
In this section we present our constructions for the
privacy-preserving k-NN classifier operating over en-
crypted data stored in the cloud. We start by
proposing our unweighted privacy-preserving classi-
fier, which is divided in five subroutines: Encoding,
Initialization, Querying, Processing and Response.
4.1 Unweighted k-NN
The conventional unweighted k-NN classifier can be
described in terms of the following subroutines:
• Encoding: this procedure takes the class ∈ N of
an instance and a positive integer ∆, and returns
the integer 2
·∆
. For instance, fixing ∆ = 64, class
0 is mapped to 2
0
= 1, class 1 is mapped to 2
64
,
class 2 is mapped to 2
128
, and so on.
• Initialization: the client has n vectors u
1
,...,u
n
∈
R
n×p
classified with the corresponding classes
1
,...,
n
∈ N. Thus, each vector u
i
is labeled
with a non-negative integer
i
. This subroutine
encrypts the vectors u
i
using the component-wise
encryption of OPE and encodes each class for en-
cryption using the HE scheme. Note that this ini-
tialization step is executed by the client, as shown
in Algorithm 1.
Algorithm 1: Initialization.
1: Input: (u
1
,...,u
n
) ∈ R
n×p
, (
1
,...,
n
) ∈ N
n
2: K = OPE.KEYGEN(M,N, s)
3: (SK, PK) = HE.KEYGEN(λ)
4: for i ← 1 to n do
5: v
i
← OPE.ENC(K, u
i
)
6: Encoding and encryption.
7: c
i
← HE.ENC(PK, 2
i
·∆
)
8: end for
9: Send (v
1
,...,v
n
) and (c
1
,...,c
n
) to the cloud.
• Querying: the client has a query vector w ∈ R
p
to
be classified. This vector is encrypted using the
OPE scheme and then submitted to the cloud.
Algorithm 2: Querying.
1: Input: w ∈ R
p
2: y ← OPE.ENC(w)
3: Choose number of neighbors k ∈ N
∗
and submit
(y, k) to the cloud.
• Processing: the cloud classifies the encrypted
query vector y using the encrypted vectors
v
1
,...,v
n
and the encrypted classes c
1
,...,c
n
by
running Algorithm 3.
Algorithm 3: Processing.
1: Input: Encrypted query vector y, k ∈ N
∗
2: for j ← 1 to n do
3: d
j
←k v
j
− y k
4: end for
5: Compute the indexes (i
1
,...,i
k
) of the k smallest
distances among (d
1
,...,d
n
).
6: class
y
← c
i
1
7: for j ← 2 to k do
8: class
y
← HE.ADD(class, c
i
j
)
9: end for
10: Return class
y
to the client.
Line 5 of the algorithm returns the indexes of the
k smallest distances. For instance, if the 1st, the
3rd and the 7th vectors were the three nearest vec-
tors of y, then d
1
,d
3
, and d
7
would be the smallest
distances and this function would return (1,3,7).
• Response: the client receives a ciphertext class
y
,
decrypts it and extracts the class of the query vec-
tor w, as in Algorithm 4.
Algorithm 4: Response.
1: Input: Encrypted class class
y
2: c ← HE.DEC(SK, class
y
)
3: Compute maximum coefficient a
from c as a
polynomial in base 2
∆
.
4: Assign class to the query vector.
The algorithm works correctly because when the
server adds the encrypted classes in Algorithm 4, it is
in fact accumulating how many times each class ap-
peared among the k nearest vectors. Since the i-th
class is represented by an integer 2
i·∆
, the sum of the
classes results in an integer a
0
+a
1
2
∆
+a
2
2
2·∆
+. . . +
a
s
2
s·∆
, where each coefficient a
i
represents the num-
ber of times that the i-th class appeared. Furthermore,
since the classes are encrypted with an HE scheme,
the cloud can add the ciphertexts of those classes and
the resulting ciphertext will be decrypted to the ex-
pected addition of the classes. To extract the class,
only shifting and reducing the decrypted sum c mod-
ulo 2
∆
are required to obtain the largest coefficent.
A problem might arise if some of the a
i
coeffi-
cients were larger than 2
∆
, because in this case, the
value of a
i
2
i·∆
would be mixed with the other coeffi-
cients. However, notice that the number of neighbours
Non-interactive Privacy-preserving k-NN Classifier
365

k is an upper bound to each a
i
, and k is typically small.
Therefore, it is sufficient to choose a value for ∆ such
that 2
∆
> k.
4.2 Distance-weighted k-NN
Our proposal also allows a distance-weighted version
of the k-NN classifier over encrypted data. The main
differences between this version and the previous un-
weighted one is the way the encrypted classes are ac-
cumulated in the cloud.
• Initialization and Querying: Identical to the un-
weighted version.
• Processing: To classify an encrypted query vector
y, using the encrypted vectors v
1
,...,v
n
and the
encrypted classes c
1
,...,c
n
, the cloud finds the k
nearest neighbours, encodes the inverse of their
distances into valid plaintexts and combine them
to generate the encrypted assigned class. This
procedure is shown in Algorithm 5.
Algorithm 5: (Weighted) Processing.
1: Input: Encrypted query vector y, k ∈ N
∗
2: for j ← 1 to n do
3: d
j
←k v
j
− y k
4: end for
5: Compute the indexes (i
1
,...,i
k
) of the k smallest
distances among (d
1
,...,d
n
).
6: W ←
1
d
i
1
+
1
d
i
2
+ ... +
1
d
i
k
7: class
y
← HE.ENC(PK, 0)
8: for j ← 1 to k do
9: l ← i
j
10: w ←
1
d
l
·W
11: Accumulation of encoded class w.
12: z ← HE.PROD(c
l
,2
w·∆
)
13: class
y
= HE.ADD(class
y
,z)
14: end for
15: Return class
y
to the client.
• Response: The client receives the encrypted as-
signed class class
y
, decrypts it and extracts the
class, just like in the unweighted version.
This procedure works because each encrypted
class c
l
is the encryption of some integer 2
i·∆
.
In Algorithm 5, when we multiply homomorphi-
cally by the weight w of the neighbor, we obtain
an encryption of w · 2
i·∆
. Since we add all those
k classes homomorphically, we have an encryp-
tion of some integer with the format a
0
+ a
1
2
∆
+
a
2
2
2·∆
+ ... + a
s
2
s·∆
where each a
i
represents the
sum of the weights of all the neighbors with class
i among the k nearest neighbors.
5 EXPERIMENTAL RESULTS
We implemented our versions of k-NN using the state-
less OPE scheme presented in (Boldyreva et al., 2011)
and the Paillier homomorphic cryptosystem (Paillier,
1999).
1
. The Paillier cryptosystem was instantiated at
the 80-bit security level by choosing n to have 1024
bits (Giry, 2015). The approach and implementation
were evaluated using datasets from the UCI Machine
Learning Repository
2
. The datasets are described in
Table 1.
We executed all the tests in a machine equipped
with a 2.6GHz Intel Xeon CPU, 30GB of RAM and
the GNU/Linux Debian 8.0 operating system. We
remark that memory consumption was below 1GB
during the entire collection of experimental results.
Our k-NN version was implemented in C++ and
compiled using GCC 4.9.2 provided by the oper-
ating system with the -O3 optimization flag. For
comparison, we employed the k-NN classifier imple-
mented in the Python Scikit Learn lib
3
as the conven-
tional k-NN implementation. We used the parameter
algorithm=brute to select a compatible approach
for computing distances.
Table 1: Datasets used in the evaluation. The dataset WFR
refers to WALL-FOLLOWING ROBOT.
DATASET INSTANCES ATTRIBUTES
IRIS 150 4
WINE 178 13
CLIMATE MODEL 540 18
CREDIT APPROVAL 690 15
ABALONE 4177 8
WFR 5456 24
The experiments consisted in processing the
datasets using the conventional plaintext k-NN classi-
fier and our non-interactive privacy-preserving k-NN
over encrypted data, and collecting the results of two
metrics: comparison of the resulting accuracies (rate
of query vectors correctly classified) and the compat-
ibility of the privacy-preserving version compared to
the plaintext one (rate of query vectors that our k-NN
over encrypted data classified with the same class as
the conventional k-NN).
The results are summarized in Tables 2, 3, and 4.
The tables have five columns representing the number
of nearest neighbors considered (k ∈ {1, 3, 5, 7, 9}) to
1
The source code is available on the repository
https://github.com/hilder-vitor/encrypted-k-NN.
2
UCI: https://archive.ics.uci.edu/ml/
3
Python Scikit Learn lib: http://scikit-learn.org
ICISSP 2017 - 3rd International Conference on Information Systems Security and Privacy
366
take into account how this number affects the ac-
curacy of the classifier. In order to verify how the
OPE instantiation parameters might influence the ac-
curacy of the privacy-preserving k-NN, we encrypted
the datasets using several pairs of values (M, N) (re-
call that M and N determine the size of the plain-
text and the ciphertext spaces, respectively). Since
no significant differences were observed for the sev-
eral combinations of parameters, we only present the
results of the executions for (M, N) = (2
32
,2
40
). As
expected, the privacy-preserving versions conserved
the original classification accuracy for almost all of
the samples.
A comparison of the running times to classify a
single instance, using k = 3, is shown in Table 5. We
stress that changing the value of k has little effect on
the execution times. We split each dataset into a train-
ing set containing
2
3
of the data and a testing set with
the remaining
1
3
. Afterwards, the plaintext version
was executed 10 times and the average time to classify
the whole set was computed. We performed the same
experiment in the privacy-preserving versions. The
plaintext version of k-NN was about 15 times faster
than the versions over encrypted data. Nevertheless,
our proposal may still be considered viable because,
in the cloud scenario, the client spends most of the
time performing requests to the server and sending
data to it, and this communication time will proba-
bly dominate the time the cloud takes to perform the
classification.
In order to study how the classification time re-
lates with the dataset size, we ran the experiments us-
ing reduced versions of the WFR dataset. First, we
considered only subsets of the dataset by limiting the
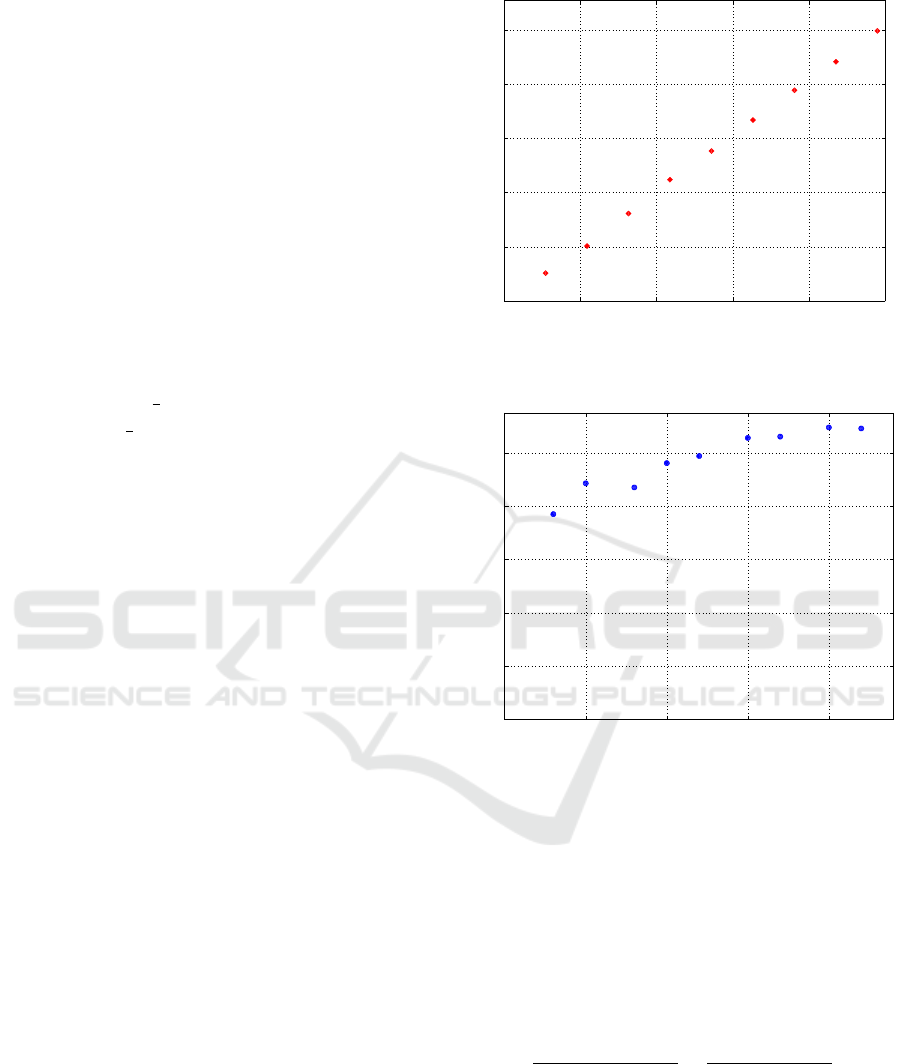
number of instances. As shown in Figure 1, the execu-
tion time grows linearly with the number of instances.
Then we performed the same experiment, but limiting
the number of variables. Figure 2 shows that the exe-
cution time also grows linearly on this scenario. This
is expected, because execution time is dominated by
computation of distances between the query vector
and the other neighbors in the dataset. The time for
computing each distance also grows linearly with the
dimension of the involved vectors.
Table 6 presents the execution times to encrypt the
entire datasets, including the training and the testing
data. It corresponds to the execution of the Initializa-
tion and the Querying procedures, without consider-
ing the cost of submitting the instance and query vec-
tors to the cloud. Encrypting the testing set is many
times faster because in this step we do not need to use
the HE scheme, which is slower than OPE.
The encrypted vectors are represented by vectors
of integers in which the bit lengths of the components
0 1000 2000 3000 4000 5000
0
0.2
0.4
0.6
0.8
1
Number of instances
Classification time (ms)
Figure 1: Execution time for query processing as the num-
ber of instances grow (subsets of WFR dataset).
0 5 10 15 20
0
0.2
0.4
0.6
0.8
1
Number of variables
Classification time (ms)
Figure 2: Execution time for query processing as the num-
ber of variables grow (subsets of WFR dataset).
are up to log
2
(N) and, due to our choice of parame-
ters, the encrypted classes are represented by integers
of 2048 bits. The bit lengths of the plaintext compo-
nents are log
2
(M) and the classes are represented by
32-bit integers. Therefore, considering a data set con-
sisting of n vectors with p dimensions each, the data
expansion, defined as the maximum size in bits of the
encrypted data over the maximum size in bits of the
plaintext data is:
np log
2
N + 2048n
np log
2
M +32n
=
plog
2
N + 2048
plog
2
M +32
.
Notice that the number of instances does not af-
fect the data expansion and the values M and N have
little impact in that expansion because they contribute
in a logarithmic scale. As the number of dimensions
grows, the quotient becomes close to one, which is
the best possible value. A high value to the data ex-
pansion means that client has to upload and download
Non-interactive Privacy-preserving k-NN Classifier
367
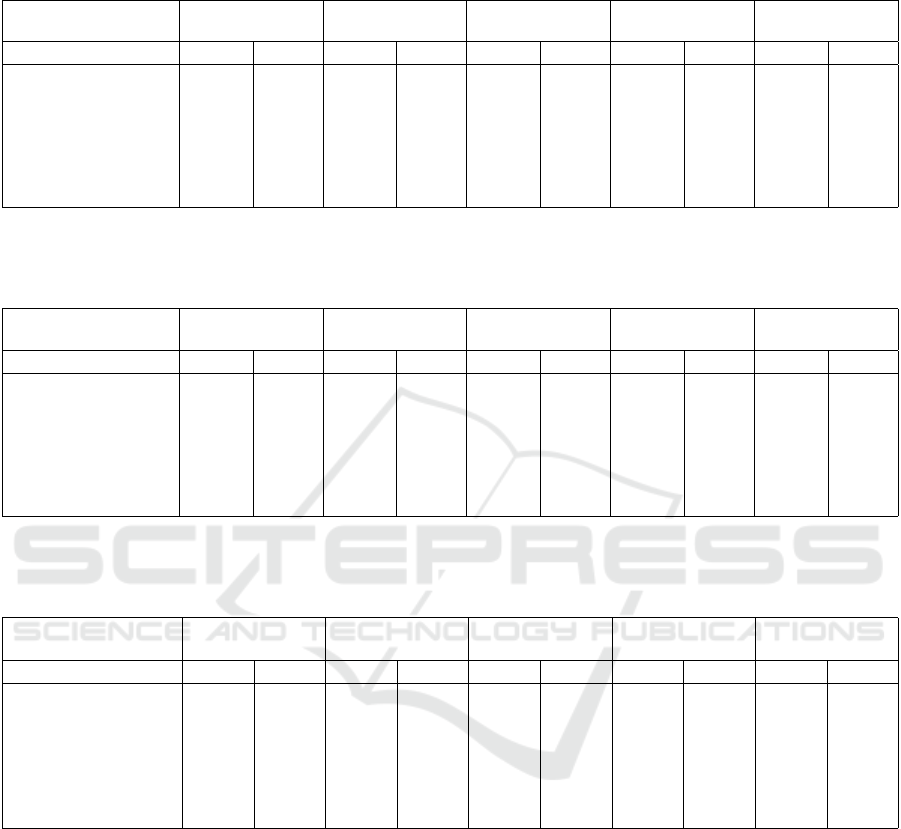
Table 2: Comparison of the accuracies between the conventional unweighted k-NN (PLAIN) and privacy-preserving one
(ENC) instantiated using the OPE parameters (M, N) = (2
32
,2
40
) as the OPE parameters. Values in bold represent a difference
of at least 0.01. No significant classification accuracy is lost with our privacy-preserving approach.
k = 1 k = 3 k = 5 k = 7 k = 9
PLAIN ENC PLAIN ENC PLAIN ENC PLAIN ENC PLAIN ENC
IRIS 0.960 0.960 0.980 0.980 0.960 0.961 0.960 0.960 0.960 0.970
WINE 0.847 0.830 0.796 0.796 0.779 0.779 0.796 0.780 0.745 0.730
CLIMATE MODEL 0.895 0.896 0.928 0.928 0.934 0.934 0.923 0.923 0.917 0.913
CREDIT APPROVAL 0.633 0.619 0.685 0.685 0.680 0.680 0.746 0.746 0.746 0.737
ABALONE 0.591 0.583 0.612 0.618 0.621 0.620 0.628 0.630 0.628 0.627
WFR 0.883 0.882 0.875 0.875 0.868 0.869 0.855 0.855 0.837 0.837
Table 3: Comparison of the accuracies between the conventional weighted k-NN (PLAIN) and privacy-preserving one (ENC)
instantiated using the OPE parameters (M, N) = (2
32
,2
40
). Values in bold represent a difference of at least 0.01. Again, no
significant classification accuracy is lost with our privacy-preserving approach.
k = 1 k = 3 k = 5 k = 7 k = 9
PLAIN ENC PLAIN ENC PLAIN ENC PLAIN ENC PLAIN ENC
IRIS 0.960 0.940 0.980 0.970 0.960 0.960 0.960 0.960 0.960 0.960
WINE 0.847 0.847 0.830 0.813 0.830 0.823 0.830 0.823 0.796 0.800
CLIMATE MODEL 0.895 0.891 0.928 0.928 0.934 0.934 0.923 0.923 0.917 0.918
CREDIT APPROVAL 0.633 0.630 0.671 0.671 0.690 0.680 0.710 0.706 0.737 0.721
ABALONE 0.590 0.590 0.618 0.618 0.627 0.622 0.634 0.629 0.629 0.618
WFR 0.883 0.885 0.882 0.882 0.887 0.888 0.882 0.881 0.880 0.887
Table 4: Compatibility of unweighted (UNW) and distance-weighted (WEI) versions of privacy-preserving k-NN with ref-
erence implementation from Python Scikit. Compatibility numbers are computed as the rate of query vectors classified
identically to the classification from the reference implementation.
k = 1 k = 3 k = 5 k = 7 k = 9
UNW WEI UNW WEI UNW WEI UNW WEI UNW WEI
IRIS 0.98 0.96 0.96 0.96 0.94 0.94 0.94 0.96 0.94 0.96
WINE 0.983 1.00 1.00 0.983 1.00 0.983 0.983 0.983 0.983 0.932
CLIMATE MODEL 1.00 0.994 1.00 0.994 1.00 1.00 1.00 1.00 1.00 1.00
CREDIT APPROVAL 0.978 0.982 0.956 0.964 0.939 0.926 0.917 0.893 0.963 0.900
ABALONE 0.962 0.975 0.964 0.948 0.977 0.948 0.968 0.953 0.970 0.965
WFR 0.998 0.998 0.999 0.987 0.995 0.983 0.994 0.984 0.997 0.972
much more data than what it would be necessary if
plaintext data was sent to the cloud. Figure 3 shows
the effect of varying p after fixing (M, N) = (2
32
,2
40
).
6 SECURITY ANALYSIS
We assume that the cloud satisfies the threat-model
commonly called honest-but-curious (Graepel et al.,
2012), which means that the cloud will follow the pro-
tocol and execute the k-NN procedure as expected, re-
turning the right answer, although it may try to learn
information during the execution or later extract in-
formation from the encrypted data stored.
In our approach, the server does not learn what
are the values of any component of any of the vec-
tors it receives, including the query vectors. It also
does not learn the classes associated with the vec-
tors. And since the homomorphic encryption scheme
used to encrypt the classes is probabilistic, the server
cannot know even how many different classes there
are among the encrypted classes. Since adding ci-
phertexts results in another well-formed ciphertext,
the class assigned to the query vector cannot be dis-
covered by the cloud server. On the other hand, the
cloud can always discover the number of vectors in
the database and the number of components that each
vector has by simply examining the ciphertext sizes.
ICISSP 2017 - 3rd International Conference on Information Systems Security and Privacy
368

Table 5: Comparison of running times in milliseconds to
classify a single instance using k = 3.
DATASET PLAIN
ENCRYPTED
UNWEIGHTED WEIGHTED
IRIS 0.009 0.0196 0.1351
WINE 0.012 0.0315 0.1427
CLIMATE 0.033 0.0924 0.2497
CREDIT 0.044 0.1105 0.2328
ABALONE 0.168 0.8001 0.9142
WFR 0.180 1.1586 1.2313
Table 6: Comparison of running times in seconds to encrypt
the test and training datasets.
DATASET TEST
TRAINING
UNWEIGHTED WEIGHTED
IRIS 0.028 0.177 0.183
WINE 0.129 0.540 0.493
CLIMATE 0.565 2.137 1.812
CREDIT 0.538 1.768 1.856
ABALONE 1.310 8.329 7.971
WFR 6.383 16.780 17.315
Figure 3: Data expansion as a function of the number of
dimensions for the OPE parameters (M, N) = (2
32
,2
40
).
Moreover, the OPE building block is deterministic
and introduces a drawback. If the cloud has informa-
tion about the semantic of the dimensions (what vari-
able is represented by each vector component), and
if it also possesses a dataset that is strongly corre-
lated to the encrypted data, the scheme may be vul-
nerable to inference attacks based on frequency anal-
ysis (Naveed et al., 2015). Hence, our scheme is ap-
propriate only for running k-NN queries over private
databases, with no public information about the data
distribution that can be correlated with ciphertexts.
7 RELATED WORKS
Several works in the literature already studied prob-
lems related to privacy-preserving k-NN classifica-
tion. However, solutions were provided for differ-
ent scenarios involving distributed servers with equiv-
alent computing power; or simpler versions of the
problem, only requiring computation of the k near-
est neighbors and ignoring the classification step. As
a result, our proposal qualitatively improves on these
works by providing additional functionality and cor-
responding privacy guarantees.
The authors of (Zhan et al., 2005) considered a
scenario known as vertically partitioned data, where
each of several parties holds a set of attributes of the
same instances and they want to perform the k-NN
classification on the concatenation of their datasets.
An interactive privacy-preserving protocol was pro-
posed in which the parties have to compute the dis-
tances between the instances in their own partition
and a query vector; and combine those distances using
an additively homomorphic encryption scheme with
random perturbation techniques to find the k near-
est neighbours. The classification step is finally per-
formed locally by each party.
In (Xiong et al., 2006; Xiong et al., 2007) the au-
thors assume that several data owners, each one with
a private database, will collaborate by executing a dis-
tributed protocol to perform privacy-preserving k-NN
classification. The classification of a new instance is
performed by each user in his or her own database
and then a secure distributed protocol is used to clas-
sify the instance based on the k nearest neighbors of
each database, without revealing those neighbors to
the other data owners. It means that the query vector
is revealed and the process is interactive, with heavy
processing load for each involved party.
In the article (Choi et al., 2014), the authors
present three methods to find the k nearest neighbors
preserving the privacy of the data, but they do not
address the classification problem. Furthermore, the
three methods are interactive. It is worth noting that
even if finding the k nearest neighbors is the main step
involved in k-NN classification, this is not compatible
with a cloud computing scenario, implying that the
client has to store at least a table relating the vectors
on the dataset and their classification, and also that the
query vector must be locally classified after the client
receives the k nearest neighbors.
The authors of (Zhu et al., 2013) propose a sce-
nario in which the data owner encrypts the data and
sends them to the cloud, where other users can sub-
mit query vectors to obtain the nearest neighbors in
a privacy-preserving way. The scheme ensures the
Non-interactive Privacy-preserving k-NN Classifier
369

privacy-preserving property thanks to an interactive
protocol executed between any trusted user that wants
to send query vectors and the data owner: this proto-
col generates a key that is used to encrypt the query
vectors and it is not possible to use this key to decrypt
the encrypted instances stored in the cloud. The data
owner must participate on the processing, even if it is
only to generate keys, therefore this protocol cannot
be classified as a non-interactive protocol. Moreover,
the protocol only finds the nearest neighbours and the
classification step is not performed.
The works (Elmehdwi et al., 2014) consider a dif-
ferent scenario: the data owner encrypts the data and
submits them to a first server, sending the secret key
to a second server. Thereby, any authorized person is
able to send a query vector to the first server, which
runs a distributed interactive protocol with the second
server (this sever may decrypt some data in this pro-
cess), and finally the first server returns the k nearest
neighbors. Even if the client does not have to pro-
cess the data, that method requires a trusted server to
store the private key, and this trusted server acts as the
client in the distributed processing scenario. Relying
on a trusted third party naturally introduces additional
substantial risk. Later, the same authors extended the
idea to the classification problem (Samanthula et al.,
2015), but the same risk of collusion remains.
Another approach is proposed in (Wong et al.,
2009), where a new cryptographic scheme called
asymmetric scalar-product-preserving encryption
(ASPE) is also proposed. The scheme preserves a
special type of scalar product, allowing the k nearest
vectors to be found without requiring an interactive
process. The scheme allows the server to calculate
inner products between dataset vectors by calculating
the inner product of encrypted vectors, determining
the vectors that are closer to the query vector. How-
ever, the authors were again only concerned with the
task of finding the nearest neighbors, not with the
classification problem. Also, a cryptographic scheme
created ad hoc for this task lacks extensive security
analysis that more general and well-established
cryptographic schemes already have. In comparison,
the building blocks in our proposal have well-known
properties and limitations.
8 CONCLUSIONS
We presented non-interactive privacy-preserving vari-
ants of the k-NN classifier for both the unweighted
and the weighted versions, and established by ex-
tensive experiments that they are sufficiently effi-
cient and accurate to be viable in practice. The pro-
posed protocol combines homomorphic encryption
and order-preserving encryption and is applicable for
running queries against private databases stored into
the cloud. To the best of our knowledge, this is the
first proposal for performing k-NN classification over
encrypted data in a non-interactive way.
If a client and a cloud already employ any joint
protocol to find nearest neighbours (for instance, by
using other cryptographic primitives instead of OPE,
or by running some interactive algorithm) then they
can use an HE scheme and the techniques presented
here to derive a class from the other classes.
As future work, possible improvements to the k-
NN presented here might involve data obfuscation
and perturbation techniques to achieve stronger se-
curity properties against inference attacks, while pre-
serving accuracy and efficiency.
ACKNOWLEDGMENTS
We thank Google Inc. for the financial support
through the Latin America Research Awards “Ma-
chine learning over encrypted data using Homomor-
phic Encryption” and “Efficient homomorphic en-
cryption for private computation in the cloud”.
REFERENCES
Alpaydin, E. (2004). Introduction to Machine Learning.
The MIT Press.
Altman, N. S. (1992). An introduction to kernel and nearest-
neighbor nonparametric regression. The American
Statistician, 46(3):175–185.
Boldyreva, A., Chenette, N., and O’Neill, A. (2011). Order-
preserving encryption revisited: Improved security
analysis and alternative solutions. In CRYPTO, vol-
ume 6841 of Lecture Notes in Computer Science,
pages 578–595. Springer.
Bost, R., Popa, R. A., Tu, S., and Goldwasser, S. (2015).
Machine learning classification over encrypted data.
In NDSS. The Internet Society.
Choi, S., Ghinita, G., Lim, H., and Bertino, E. (2014). Se-
cure knn query processing in untrusted cloud environ-
ments. IEEE Trans. Knowl. Data Eng., 26(11):2818–
2831.
Elmehdwi, Y., Samanthula, B. K., and Jiang, W. (2014).
Secure k-nearest neighbor query over encrypted data
in outsourced environments. In ICDE, pages 664–675.
IEEE Computer Society.
Gilad-Bachrach, R., Dowlin, N., Laine, K., Lauter, K. E.,
Naehrig, M., and Wernsing, J. (2016). Cryptonets:
Applying neural networks to encrypted data with high
throughput and accuracy. In ICML, volume 48 of
JMLR Workshop and Conference Proceedings, pages
201–210. JMLR.org.
ICISSP 2017 - 3rd International Conference on Information Systems Security and Privacy
370

Giry, D. (2015). Cryptographic key length recomendation.
https://www.keylength.com/ (Acessed December 16,
2016).
Graepel, T., Lauter, K. E., and Naehrig, M. (2012). ML
confidential: Machine learning on encrypted data. In
ICISC, volume 7839 of Lecture Notes in Computer
Science, pages 1–21. Springer.
Hirt, M. and Sako, K. (2000). Efficient receipt-free voting
based on homomorphic encryption. In EUROCRYPT,
volume 1807 of Lecture Notes in Computer Science,
pages 539–556. Springer.
Jha, S., Kruger, L., and McDaniel, P. D. (2005). Privacy
preserving clustering. In ESORICS, volume 3679 of
Lecture Notes in Computer Science, pages 397–417.
Springer.
Lindell, Y. and Pinkas, B. (2009). Secure multiparty com-
putation for privacy-preserving data mining. Journal
of Privacy and Confidentiality, 1(1):5.
Miller, C. C. (2014). Revelations of
N.S.A. spying cost U.S. tech companies.
http://www.nytimes.com/2014/03/22/business/fallout-
from-snowden-hurting-bottom -line-of-tech-
companies.html (Acessed December 16, 2016).
Naehrig, M., Lauter, K. E., and Vaikuntanathan, V. (2011).
Can homomorphic encryption be practical? In CCSW,
pages 113–124. ACM.
Naveed, M., Kamara, S., and Wright, C. V. (2015).
Inference attacks on property-preserving encrypted
databases. In ACM Conference on Computer and
Communications Security, pages 644–655. ACM.
Paillier, P. (1999). Public-key cryptosystems based on com-
posite degree residuosity classes. In EUROCRYPT,
volume 1592 of Lecture Notes in Computer Science,
pages 223–238. Springer.
Rivest, R. L., Adleman, L., and Dertouzos, M. L. (1978).
On data banks and privacy homomorphisms. Founda-
tions of secure computation, 4(11):169–180.
Samanthula, B. K., Elmehdwi, Y., and Jiang, W. (2015). k-
nearest neighbor classification over semantically se-
cure encrypted relational data. IEEE Trans. Knowl.
Data Eng., 27(5):1261–1273.
Wong, W. K., Cheung, D. W., Kao, B., and Mamoulis,
N. (2009). Secure knn computation on encrypted
databases. In SIGMOD Conference, pages 139–152.
ACM.
Xiong, L., Chitti, S., and Liu, L. (2006). k nearest neigh-
bor classification across multiple private databases. In
CIKM, pages 840–841. ACM.
Xiong, L., Chitti, S., and Liu, L. (2007). Mining multiple
private databases using a knn classifier. In SAC, pages
435–440. ACM.
Zhan, J. Z., Chang, L., and Matwin, S. (2005). Privacy pre-
serving k-nearest neighbor classification. I. J. Network
Security, 1(1):46–51.
Zhu, Y., Xu, R., and Takagi, T. (2013). Secure k-nn query
on encrypted cloud database without key-sharing.
IJESDF, 5(3/4):201–217.
Non-interactive Privacy-preserving k-NN Classifier
371
