
Random Projections with Control Variates
Keegan Kang and Giles Hooker
Department of Statistical Science, Cornell University, Ithaca 14850, New York, U.S.A.
{tk528, gjh27}@cornell.edu
Keywords:
Control Variates, Random Projections.
Abstract:
Random projections are used to estimate parameters of interest in large scale data sets by projecting data into a
lower dimensional space. Some parameters of interest between pairs of vectors are the Euclidean distance and
the inner product, while parameters of interest for the whole data set could be its singular values or singular
vectors. We show how we can borrow an idea from Monte Carlo integration by using control variates to reduce
the variance of the estimates of Euclidean distances and inner products by storing marginal information of our
data set. We demonstrate this variance reduction through experiments on synthetic data as well as the colon
and kos datasets. We hope that this inspires future work which incorporates control variates in further random
projection applications.
1 INTRODUCTION
Random projection is one of the methods used in di-
mension reduction, in which data in high dimensions
is projected to a lower dimension using a random ma-
trix R. The entries r
i j
in the matrix R can either be
i.i.d. with mean µ = 0 and second moment µ
2
= 1, or
correlated with each other. Some examples of random
projection matrices with i.i.d. entries are those with
binary entries (Achlioptas, 2003), or sparse random
projections (Li et al., 2006b). Random matrices with
correlated entries range from those constructed by the
Lean Walsh Transform (Liberty et al., 2008) to the
Fast Johnson Lindenstrauss Transform (FJLT) (Ailon
and Chazelle, 2009) and the Subsampled Randomized
Hadamard Transform (SRHT) (Boutsidis and Gittens,
2012).
We can think of vectors x
i
∈R
p
mapped to a lower
dimensional vector
˜
x
i
∈R
k
using a random projection
matrix R under the identity
˜
x
T
= x
T
R. Distance prop-
erties of these vectors x
i
,x
j
are preserved in expecta-
tions in
˜
x
i
,
˜
x
j
. If we wanted to compute a property of
x
i
,x
j
given by some f (x
i
,x
j
), then the goal is to find
some function g(·), such that E[g(
˜
x
i
,
˜
x
j
)] = f (x
i
,x
j
).
If we want the Euclidean distance between two vec-
tors x
i
and x
j
, then f (a,b) = g(a,b) = ka −bk
2
.
The methods used in construction and application
of the random projection matrix R to the vectors x
i
s
have tradeoffs. Very sparse random projections, FJLT,
and the SRHT are fast methods with a tradeoff in ac-
curacy. The former uses extremely sparse R for quick
matrix multiplication (optimal R has about
√
p−1
√
p
zero
entries), and the latter two uses the recursive property
of the Hadamard matrix for quick matrix vector mul-
tiplication. Dense R with entries generated from the
Normal or the Rademacher distribution gives more
accurate estimates and desparsifies data but at a cost
of speed.
The resultant estimates from a chosen random
matrix R have probability bounds on accuracy plus
bounds on their run time, and it is up to the user to
choose a random projection matrix which will suit
their purposes.
In this paper, we propose a method Random Pro-
jections with Control Variates (RPCV), which is used
in conjunction with the above types of different ran-
dom projection matrices. Our approach leads to a
variance reduction in the estimation of Euclidean dis-
tances and inner products between pairs of vectors
x
i
,x
j
with a negligible extra cost in speed and storage
space. These measures of distances are commonly
used in clustering (Fern and Brodley, 2003), (Bout-
sidis et al., 2010), classification (Paul et al., 2012),
and set resemblance problems (Li et al., 2006a).
The paper is structured as follows: We first ex-
press our notation differently from the ordinary ran-
dom projection notation to give intuition on how we
can use control variates. We then briefly discuss
control variates, before describing RPCV. Lastly, we
demonstrate RPCV on both synthetic and experimen-
tal data and show that we can use RPCV together with
any random projection method to gain variance reduc-
138
Kang, K. and Hooker, G.
Random Projections with Control Variates.
DOI: 10.5220/0006188801380147
In Proceedings of the 6th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2017), pages 138-147
ISBN: 978-989-758-222-6
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

tion in our estimates.
1.1 Notation and Intuition
With classical random projections, we denote R ∈
R
p×k
to be a random projection matrix. We let X ∈
R
n×p
to be our data matrix, where each row x
T
i
∈ R
p
is a p dimensional observation. The random projec-
tion equation is then given by
V =
1
√
k
XR (1)
However, we will use
V = XR (2)
without the scaling factor. Consider the random ma-
trix R written as
R = [r
1
| r
2
| ... |r
k
] (3)
where each r
i
is a column vector with i.i.d. entries.
Then for a fixed row x
T
i
, we have that for all j, v
i j
=
x
T
i
r
j
is a random variable from the same distribution.
Here, we focus on each v
i j
as a single element, rather
than seeing v
i1
,...,v
ik
comprising the row vector v
T
i.
.
1.2 Control Variates
Given the notion of each v
i j
as a random variable, we
introduce control variates. Control variates are a tech-
nique in Monte Carlo simulation using random vari-
ables for variance reduction. A more thorough expla-
nation found in Ross, 2006.
The method of control variates assumes we use the
same random inputs to estimate E[A] = µ
A
, for which
we know B with E[B] = µ
B
. We call B our control
variate. Then to estimate E[A] = µ
A
from some dis-
tribution A, we can instead compute the expectation
of
E[A +c(B −µ
B
)] = E[A]+cE[B −µ
B
] = µ
A
(4)
which is an unbiased estimator of µ
A
for some con-
stant c. This value of c which minimizes the variance
is given by
ˆc = −
Cov(A,B)
Var(B)
(5)
and thus we write
Var[A + c(B −µ
B
)] = Var(A) −
(Cov(A,B))
2
Var(B)
(6)
In our random projection scenario for a fixed i, we
can think of a random variable from A as some v
i j
,
where
E[v
i.
] =
1
k
k
∑
m=1
v
im
=
1
k
k
∑
m=1
p
∑
n=1
x
i,n
r
nm
!
(7)
under the law of large numbers.
Intuitively, we then need to find some distribution
B where the variables b
i
are correlated with v
i j
to get
good variance reduction. To do this, B necessarily
needs to fulfill two conditions.
Condition 1: Since each realization v
i j
is the sum
of p random variables r
1 j
,r
2 j
,...,r
p j
, we need to have
y
i
constructed from these same random variables and
also correlated with each x
i1
,...,x
ip
in order to get a
variance reduction.
Condition 2: We need to know the actual value of
µ
B
, the mean of B.
This seems like a chicken and egg problem since
any µ
B
that is related to both x
i.
, r
. j
would be of
some form of either the Euclidean distance or the in-
ner product, both of which we want to estimate in the
first place.
We solve this problem by considering an expres-
sion that relates both the Euclidean distance and the
inner product simultaneously.
1.3 Related Work
We draw inspiration from the works of Li and Church,
2007, Li et al., 2006a, and Li et al., 2006b. In
these papers, marginal information such as margin
counts or margin norms from data is pre-computed
and stored. This extra information is then used with
asymptotic maximum likelihood estimators to esti-
mate parameters of interests.
We also store marginal information from our ma-
trix X, but instead use this information to determine a
control variate, rather than a maximum likelihood es-
timator. We compute and store all the n norms kx
i
k
2
from our X. Computing all these norms are cheap as
they are of order O(np), and can be done when read-
ing in the data at the same time.
Furthermore if the data is normalized (normaliz-
ing is also of order O(np) which we usually take for
granted), we get the norms kx
i
k
2
2
= 1 for free.
1.4 Our Contributions
We propose Random Projections with Control Vari-
ates in this paper which reduces the variance of the es-
timates of the Euclidean distances and the inner prod-
uct between pairs of vectors for a choice of random
projection matrix R. In particular
• We describe the process of RPCV, which keeps to
the same order of runtime as the particular random
projection matrix we use RPCV with.
• We give the first and second moments of A +
c(B −µ
B
) for matrices R with i.i.d. entries, which
Random Projections with Control Variates
139

can then be used to bound the errors in our esti-
mates.
• We demonstrate empirically that RPCV works
well with current random projection methods on
synthetically generated data and the colon and
kos datasets.
2 PROCESS OF RPCV
We describe and illustrate the process of RPCV in this
section.
Without loss of generality, suppose we had
x
1
,x
2
∈ R
p
. Consider v given by Xr. As an illus-
trative example in the case where p = 2, we would
have
V =
v
1
v
2
=
x
11
x
12
x
21
x
22
r
1
r
2
= X r (8)
for one column of R. We do matrix multiplication Xr
and get v
1
,v
2
.
In the next two sections, we will give the control
variate to estimate the Euclidean distance and the in-
ner product. We will also give the respective optimal
control variate correction c, and the respective first
and second moments of the expression A+c(B −µ
B
).
This allows us to compute a more accurate estimate
for the Euclidean distance and the inner product, as
well as place probability bounds on the errors of our
estimates.
2.1 RPCV for the Euclidean Distance
Suppose we computed V as above. The following the-
orem shows us how to estimate the Euclidean distance
with our control variate.
Theorem 2.1. Let one realization of A = (v
1
−v
2
)
2
,
which is our Euclidean distance in expectation. Let
one realization of B to be (v
1
−v
2
)
2
+2v
1
v
2
= v
2
1
+v
2
2
with mean µ
B
= kx
1
k
2
+ kx
2
k
2
2
. The Euclidean dis-
tance (in expectation) between these two vectors is
given by E[A + c(B −µ
B
)], and we can compute c :=
Cov(A,B)/Var(B) from our matrix V directly, using
the empirical covariance Cov(A,B) and empirical
variance Var(B).
Proof. We have
E[(v
1
−v
2
)
2
] + 2E[v
1
v
2
]
= kx
1
−x
2
k
2
+ 2hx
1
x
2
i (9)
= kx
1
k
2
+ kx
2
k
2
−2hx
1
,x
2
i+ 2hx
1
,x
2
i (10)
= kx
1
k
2
+ kx
2
k
2
(11)
We derive the following lemma to help us com-
pute the first and second moments required.
Lemma 2.1. Suppose we assume that our matrix R
has i.i.d. entries, where each r
i j
has mean µ = 0, sec-
ond moment µ
2
= 1, and fourth moment µ
4
. Then un-
der this set up for Euclidean distances in Theorem 2.1,
we have
E[A
2
] = µ
4
p
∑
j=1
(x
1 j
−x
2 j
)
4
+ 6
p−1
∑
u=1
p
∑
v=u+1
(x
1u
−x
2u
)
2
(x
1v
−x
2v
)
2
(12)
E[B
2
] = µ
4
p
∑
j=1
(x
4
1 j
+ x
4
2 j
) + 6
p−1
∑
u=1
p
∑
v=u+1
(x
2
1u
x
2
1v
+ x
2
2u
x
2
2v
)
+ 4
p−1
∑
u=1
p
∑
v=u+1
(x
1u
x
1v
x
2u
x
2v
) + µ
4
p
∑
j=1
x
2
1 j
x
2
2 j
+
p
∑
i6= j
x
2
1i
y
p
2 j
(13)
E[AB] = 4
p−1
∑
u=1
p
∑
v=u+1
(x
1u
−x
2u
)(x
1v
−x
2v
)(x
1u
x
1v
+ x
2u
x
2v
)
+ µ
4
p
∑
j=1
(x
1 j
−x
2 j
)
2
(x
2
1 j
+ x
2
2 j
)
+
∑
i6= j
(x
1i
−x
2i
)
2
(x
2
1i
+ x
2
2 j
)
(14)
Proof. We repeatedly apply Lemma 4.1 in the Ap-
pendix.
Thus, by following Lemma 2.1, we are able to de-
rive expressions for the optimal control variate cor-
rection c in our procedure as follows.
Theorem 2.2. The optimal value c is given by
c =
Cov(A,B)
Var[B]
(15)
where we have
Cov(A,B) = E[AB −Aµ
B
−Bµ
A
+ µ
A
µ
B
] (16)
and
Var[B] = E[B
2
] −(E[B])
2
(17)
They expand to
Cov(A,B) = 4
p−1
∑
u=1
p
∑
v=u+1
(x
1u
−x
2u
)(x
1v
−x
2v
)(x
1u
x
1v
+ x
2u
x
2v
)
+ (µ
4
−1)
p
∑
j=1
(x
1 j
−x
2 j
)
2
(x
2
1 j
+ x
2
2 j
)
(18)
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
140

and
Var[B] = (µ
4
−1)
p
∑
j=1
(x
4
1 j
+ x
4
2 j
) + 4
p−1
∑
u=1
p
∑
v=u+1
(x
2
1u
x
2
1v
+ x
2
2u
x
2
2v
) + 4
p−1
∑
u=1
p
∑
v=u+1
x
1u
x
1v
x
2u
x
2v
+ (µ
4
−2)
p
∑
j=1
x
2
1 j
x
2
2 j
−
∑
i6= j
x
2
1i
x
2
2 j
(19)
We are also able to derive the first and second mo-
ments of A + c(B −µ
B
) for Euclidean distances.
Theorem 2.3. The first and second moments are
E[A + c(B −µ
B
)] = E[A] + cE[B −µ
B
] = 0 (20)
and
E[(A + c(B −µ
B
))
2
]
= E[A
2
+ 2cAB −2cµ
B
A + c
2
B
2
−2c
2
µ
B
B + c
2
µ
2
B
]
(21)
where we substitute in the values of E[A
2
],E[AB],
E[B
2
] from Lemma 2.1.
2.1.1 Motivation for c in Euclidean Distance
To give some motivation for the meaning of c, we sim-
plify the general case and consider what the ratio tells
us when we have normalized vectors, i.e. kx
i
k
2
2
= 1
and when µ
4
= 1 (eg, where we generate r
i j
∼ {±1}
with equal probability). In this case, we have
Cov(A,B) = 4
p−1
∑
u=1
p
∑
v=u+1
(x
1u
−x
2u
)(x
1v
−x
2v
)
× (x
1u
x
1v
+ x
2u
x
2v
) (22)
Var[B] = 4
p−1
∑
u=1
p
∑
v=u+1
(x
2
1u
x
2
1v
+ x
2
2u
x
2
2v
)
+ 4
p−1
∑
u=1
p
∑
v=u+1
x
1u
x
1v
x
2u
x
2v
−
p
∑
j=1
x
2
1 j
x
2
2 j
−
∑
i6= j
x
2
1i
x
2
2 j
(23)
Consider the expansion of
∑
p
i=1
u
i
∑
p
i=1
v
i
, and
consider u
i
v
i
as diagonal terms, and u
i
v
j
, i 6= j as off
diagonal terms for some expressions u
i
,v
i
.
Then c can be seen as some weighted ratio of
the sum of off-diagonal terms of the “Euclidean dis-
tance vector” u
i
:= (x
1i
−x
2i
) weighted by off diago-
nal terms of x
1i
,x
2i
to the sum of off diagonal terms
of the norms.
Intuitively, this implies that if the Euclidean dis-
tance between two vectors is high, then we would get
greater variance reduction (c is large).
2.2 RPCV for the Inner Product
Suppose we computed V as above. The following the-
orem shows us how to estimate the inner product with
our control variate.
Theorem 2.4. Let one realization of A = v
1
v
2
, which
is our inner product in expectation. Let one realiza-
tion of B to be (v
1
−v
2
)
2
+2v
1
v
2
= v
2
1
+v
2
2
with mean
µ
B
= kx
1
k
2
+kx
2
k
2
2
. The inner product between these
two vectors is given by E[A + c(B −µ
B
)], and we can
compute c := Cov(A,B)/Var(B) from our matrix V di-
rectly, using the empirical covariance Cov(A,B) and
empirical variance Var(B).
The optimal control variate c in this procedure is
given by the next theorem.
Theorem 2.5. The optimal value of c is given by
c =
Cov(A,B)
Var[B]
(24)
where
Cov(A,B) = E[AB −Aµ
B
−Bµ
A
+ µ
A
µ
B
]
= (µ
4
−1)
p
∑
j=1
x
1 j
x
2 j
(x
2
1 j
+ x
2
2 j
)
+
∑
i6= j
x
1i
x
2 j
(x
1i
x
1 j
+ x
2i
x
2 j
) (25)
and the value of Var[B] taken from the result in Theo-
rem 2.2.
However, we should not just stop there at our es-
timate of the inner product using RPCV. Li et al.,
2006a describes a more accurate estimator for the in-
ner product using the marginal information kx
1
k
2
and
kx
2
k
2
, where the estimate of the inner product is the
root of the equation
f (a) = a
3
−a
2
hv
1
,v
2
i+ a(−kx
1
k
2
kx
2
k
2
kx
1
k
2
kv
2
k
2
+ kx
2
k
2
kvk
2
1
) −kx
1
k
2
kx
2
k
2
hv
1
,v
2
i (26)
Since we stored and used kx
1
k
2
and kx
2
k
2
in or-
der to get better estimates of the Euclidean distance
and the inner product, we should use Li’s method to
get a better estimate of our inner product, by using
RPCV’s estimated value of hv
1
,v
2
i and kv
i
k
2
in the
cubic equation instead.
In practice, since the control variate method gives
results with similar accuracy to Li’s method for inner
products, one could use our control variate method for
Euclidean distances to complement Li’s method for
inner products, as both methods make use of storing
the norms of each observation.
Random Projections with Control Variates
141
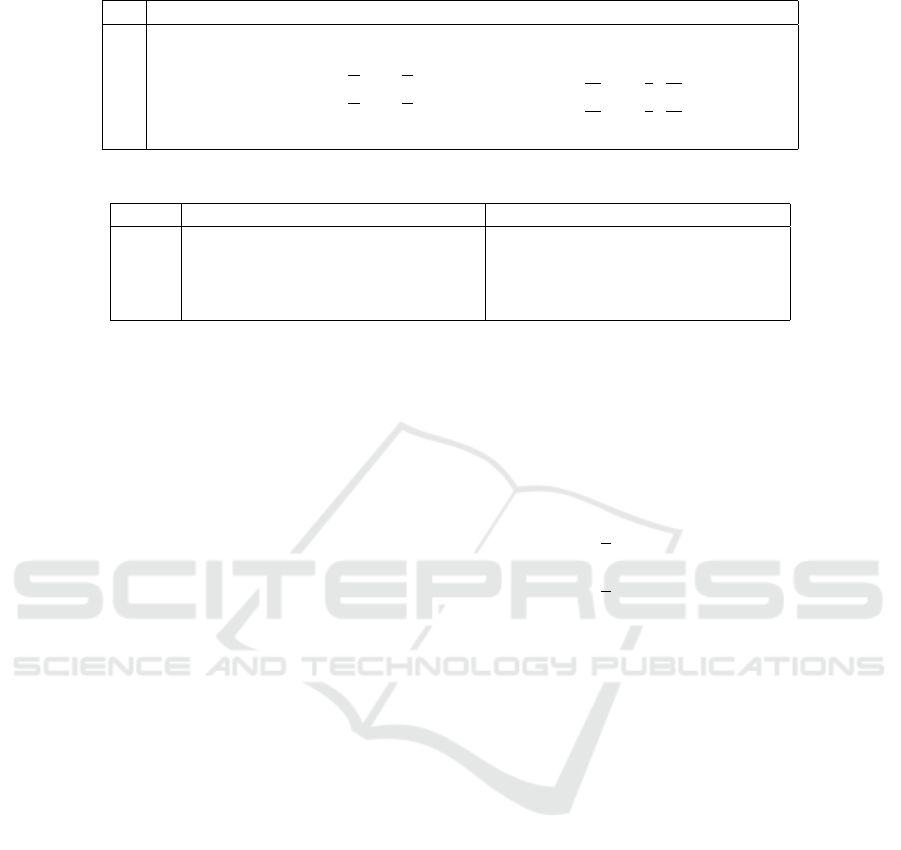
Table 1: Random projection matrices.
R Type
R
1
Entries i.i.d. from N(0,1)
R
2
Entries i.i.d. from {−1,1} with equal probability
R
3
Entries i.i.d. from {−
√
p,0,
√
p} with probabilities {
1
2p
,1 −
1
p
,
1
2p
} for p = 5
R
4
Entries i.i.d. from {−
√
p,0,
√
p} with probabilities {
1
2p
,1 −
1
p
,
1
2p
} for p = 10
R
5
Constructed using the Subsampled Randomized Hadamard Transform (SRHT)
Table 2: Generated Data x
1
, x
2
.
Pairs x
1
x
2
Pair 1 Entries i.i.d. from N(0,1) Entries i.i.d. from N(0,1)
Pair 2 Entries i.i.d. from standard Cauchy Entries i.i.d. from standard Cauchy
Pair 3 Entries i.i.d. from Bernoulli(0.05) Entries i.i.d. from Bernoulli(0.05)
Pair 4 Vector [(1)
p/2
,(0)
p/2
] Vector [(0)
p/2
,(1)
p/2
]
2.2.1 Motivation for c in Inner Product
To give some motivation for this meaning of c, we
again simplify the general case and consider what the
ratio tells us when we have normalized vectors and
when µ
4
= 1. In this case, we have
Cov(A,B) =
∑
u6=v
x
1u
x
2v
(x
1u
x
1v
+ x
2u
x
2v
) (27)
Compared to what we have seen for Euclidean
distances (recall that the denominator Var[B] is un-
changed), the magnitude of c for inner products is
comparatively smaller compared to c for Euclidean
distances (expand both Cov(A,B) for the Euclidean
distance (Equation 22), and Cov(A,B) (Equation 27)
for the inner product and compare terms). We would
then expect the variance reduction for inner product
to not be as substantial as the variance reduction for
the Euclidean distance.
2.3 Motivation for Computing First and
Second Moments
The probability bounds of the errors in our estimate
(where entries of R are i.i.d.) are of the form
P[kvk ≤ (1 −ε)kxk] ≤ f
1
(k, ε) (28)
P[kvk ≥ (1 + ε)kxk] ≤ f
2
(k, ε) (29)
where k is the number of columns of the random
projection matrix. The Markov inequality is used to
bound kvk by the first and second moments together
with the Taylor’s expansion. A full description of
these results can be found in Vempala, 2004.
If we construct R with i.i.d. r
i j
∼ N(0,1), or
r
i j
∼ {±1}, then we can easily find similar proba-
bility bounds for the Euclidean distance by setting
kvk = kv
1
−v
2
k. In the RPCV case, each element
v
1i
−v
2i
in kv
1
−v
2
k now corresponds to
(v
1i
−v
2i
)
2
+ c(v
2
1i
+ v
2
2i
−kxk
2
−kx
2
k
2
) (30)
and thus we need to find probability bounds for this
expression.
For the inner product, we note that
hv
i
,v
j
i =
1
4
kv
i
+ v
j
k
2
−kv
i
−v
j
k
2
(31)
=
1
4
kv
i
−v
j
k
2
−kv
i
+ v
j
k
2
(32)
and by rearranging expressions (31) and (32) together
with (28) and (29), we get
P[v
T
1
v
2
≤ (1 −ε)x
T
1
x
2
] ≤ f
1
(k, ε) + f
2
(k, ε) (33)
P[v
T
1
v
2
≥ (1 + ε)x
T
1
x
2
] ≤ f
1
(k, ε) + f
2
(k, ε) (34)
Thus, computing the first and second moments
for the expression A + c(B −µ
B
) for A = (v
1
−v
2
)
2
,
B = kv
1
k
2
2
+ kv
2
k
2
2
for Euclidean distances suffices,
provided we compute ˆc for the Euclidean distance,
and ˜c for the inner product. We necessarily need to
substitute the value of ˆc (or ˜c) to get the first and sec-
ond moments of A + c(B −µ
B
) for the Euclidean dis-
tance (or inner product).
For R constructed with r
i j
from other distributions,
computing these bounds are a bit more involved.
2.4 Overall Computational Time
We need to compute the empirical covariance be-
tween all pairs A and B as well as the variance of B,
which takes an additional O(k) time. Since the vec-
tors we need to compute this covariance are the ele-
ments of V , we do not need to do further computation
to get them. Furthermore, computing the covariance
takes the same order of time as finding the Euclidean
distance (or inner product) between the vectors v
i
, v
j
.
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
142

If we want a more accurate estimate of the inner
product using Li’s method, we can either use a root
finding method to find a where f (a) = 0, or use the
cubic formula to get the root(s) of a degree 3 poly-
nomial. The time for these methods are are bounded
above by some constant number of operations.
3 OUR EXPERIMENTS
Throughout our experiments, we use five different
types of random projection matrices as shown in Ta-
ble 1. We pick these five types of random projection
matrices as they are commonly used random projec-
tion matrices.
We use N(0, 1) to denote the Normal distribution
with mean µ = 0 and σ
2
= 1. We denote (1)
p
to be the
length p vector with all entries being 1, and (0)
p
to be
the length p vector with all entries being 0. We denote
the baseline estimates to be the respective estimates
given by using the type of random projection matrix
R
i
.
We run our simulations for 10000 iterations for
every experiment.
3.1 Generating Vectors from Synthetic
Data
We first perform our experiments on a wide range of
synthetic data. We look at normalized pairs of vectors
x
1
, x
2
∈ R
5000
generated from the following distribu-
tions in Table 2. In short, we look at data that can
be Normal, heavy tailed (Cauchy), sparse (Bernoulli),
and an adversarial scenario where the inner product is
zero.
We look at the plots of the ratio ρ defined by
ρ =
Variance using control variate with R
i
Variance using baseline with R
i
(35)
in Figure 1 for the Euclidean distance. ρ is a measure
of the reduction in variance using RPCV with the ma-
trix R
i
rather than just using R
i
alone. For this ratio, a
fraction less than 1 means RPCV performs better than
the baseline.
For all pairs x
i
,x
j
except Cauchy, the reduction
of variance of the estimates of the Euclidean distance
using different R
i
s with RPCV converge quickly to
around the same ratio. However, when data is heavy
tailed, the choice of random projection matrix R
i
with
RPCV affects the reduction of variance in the esti-
mates of the Euclidean distance, and sparse matrices
R
i
have a greater variance reduction for the estimates
of the Euclidean distance.
We next look at the estimates of the inner prod-
uct. In our experiments, we use Li et al., 2006a’s
method as the baseline for computing the estimates of
the inner product. Our rationale for doing this is that
both Li’s method and our method stores the marginal
norms of X, thus we should compare our method with
Li’s method for a fair comparison. The ratio of vari-
ance reduction is shown in Figure 2.
As the number of columns k of the random pro-
jection matrix R increases, the variance reduction in
our estimate of the inner product decreases, but then
increases again up to a ratio just below 1. Since Li’s
method uses an asymptotic maximum likelihood es-
timate of the inner product, then as the number of
columns of R increases, the estimate of the inner prod-
uct would be more accurate.
Thus, it is reasonable to use RPCV for Euclidean
distances, and Li’s method for inner products.
3.2 Estimating the Euclidean distance
of vectors with real data sets
We now demonstrate RPCV on two datasets, the
colon dataset from Alon et al., 1999 and the kos
dataset from Lichman, 2013.
The colon dataset is an example of a dense dataset
consisting of 62 gene expression levels with 2000 fea-
tures, and thus we have x
i
∈ R
2000
, 1 ≤ i ≤ 62.
The kos dataset is an example of a sparse
dataset consisting of 3430 documents and 6906 words
from the KOS blog entries, and thus we have x
i
∈
R
3430
, 1 ≤ i ≤ 6906.
We normalize each dataset such that every obser-
vation kx
i
k
2
2
= 1.
For each dataset, we consider the pairwise Eu-
clidean distances of all observations {x
i
,x
j
}, ∀ i 6= j,
and compute the estimates of the Euclidean distance
with RPCV of the pairs {x
i
,x
j
} which give the 20th,
30th, ..., 90th percentile of Euclidean distances.
We pick a pair in the 50th percentile for both the
colon and kos datasets (Figure 3 and Figure 4), and
show that for every different R
i
, the bias quickly con-
verges to zero, and that the variance reduction for the
R
i
s are around the same range. Since the bias con-
verges to zero, this implies that our control variates
work. i.e., we do not get extremely biased estimates
with lower variance.
We now look at the variance reduction for pairs
from the 20th to 90th percentile of Euclidean dis-
tances from both datasets for R
1
(where r
i j
∼N(0,1)).
This is shown in Figure 5. We omit plots of the biases,
as well as plots of ρ varying for different random ma-
trices R
2
to R
5
since the variance reduction follows a
similar trend.
Random Projections with Control Variates
143
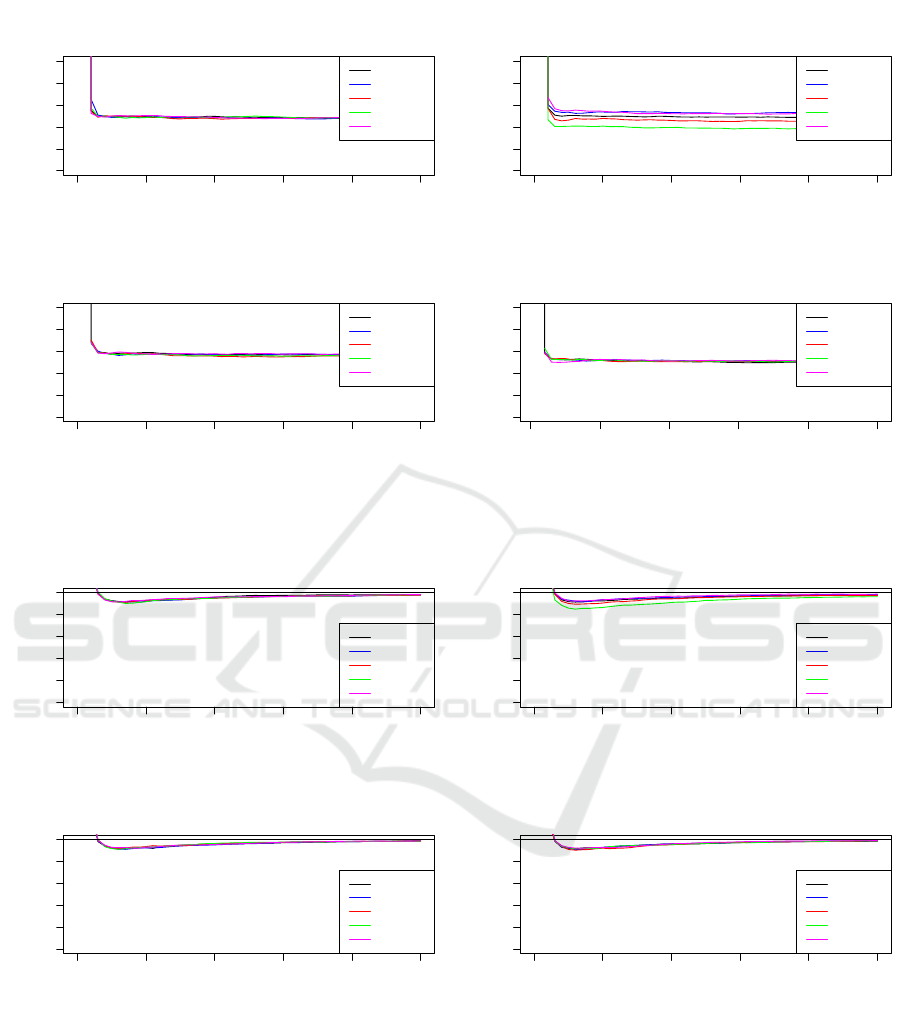
0 20 40 60 80 100
0.0 0.4 0.8
Plot of Ratio ρ for Pair 1 (both vectors Normal)
Number of columns k
Ratio
ρ with R1
ρ with R2
ρ with R3
ρ with R4
ρ with R5
0 20 40 60 80 100
0.0 0.4 0.8
Plot of Ratio ρ for Pair 2 (both vectors Cauchy)
Number of columns k
Ratio
ρ with R1
ρ with R2
ρ with R3
ρ with R4
ρ with R5
0 20 40 60 80 100
0.0 0.4 0.8
Plot of Ratio ρ for Pair 3 (both vectors Bernoulli)
Number of columns k
Ratio
ρ with R1
ρ with R2
ρ with R3
ρ with R4
ρ with R5
0 20 40 60 80 100
0.0 0.4 0.8
Plot of Ratio ρ for Pair 4 (IP 0)
Number of columns k
Ratio
ρ with R1
ρ with R2
ρ with R3
ρ with R4
ρ with R5
Figure 1: Plots of ρ for Euclidean Distances against number of columns in R
i
for each pair of vectors.
0 20 40 60 80 100
0.0 0.4 0.8
Plot of Ratio ρ for Pair 1 (both vectors Normal)
Number of columns k
Ratio
ρ with R1
ρ with R2
ρ with R3
ρ with R4
ρ with R5
0 20 40 60 80 100
0.0 0.4 0.8
Plot of Ratio ρ for Pair 2 (both vectors Cauchy)
Number of columns k
Ratio
ρ with R1
ρ with R2
ρ with R3
ρ with R4
ρ with R5
0 20 40 60 80 100
0.0 0.4 0.8
Plot of Ratio ρ for Pair 3 (both vectors Bernoulli)
Number of columns k
Ratio
ρ with R1
ρ with R2
ρ with R3
ρ with R4
ρ with R5
0 20 40 60 80 100
0.0 0.4 0.8
Plot of Ratio ρ for Pair 4 (IP 0)
Number of columns k
Ratio
ρ with R1
ρ with R2
ρ with R3
ρ with R4
ρ with R5
Figure 2: Plots of ρ for inner product against number of columns in R
i
for each pair of vectors.
We also see that as the Euclidean distances be-
tween vectors increases (percentile increases), we get
more variance reduction in our estimates. This in-
crease in variance reduction is strongly seen in our
dense colon dataset. Furthermore, both datasets
show substantial variance reduction regardless of the
percentile values.
4 CONCLUSION AND FUTURE
WORK
We have presented a new method RPCV which works
well in conjunction with different random projection
matrices to reduce the variance of the estimates of
the Euclidean distance and inner products on differ-
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
144

0 20 40 60 80 100
0.00 0.02 0.04 0.06 0.08 0.10
Bias using Control Variates (Colon)
Number of columns k
Bias
Bias with R1
Bias with R2
Bias with R3
Bias with R4
Bias with R5
0 20 40 60 80 100
0.0 0.2 0.4 0.6 0.8 1.0
Plot of ρ (Colon)
Number of columns k
Ratio
ρ with R1
ρ with R2
ρ with R3
ρ with R4
ρ with R5
Figure 3: Plots of bias and variance reduction of Euclidean distances at 50th percentile against number of columns in R
i
for
colon data.
0 20 40 60 80 100
0.00 0.02 0.04 0.06 0.08 0.10
Bias using Control Variates (Kos)
Number of columns k
Bias
Bias with R1
Bias with R2
Bias with R3
Bias with R4
Bias with R5
0 20 40 60 80 100
0.0 0.2 0.4 0.6 0.8 1.0
Plot of ρ (Kos)
Number of columns k
Ratio
ρ with R1
ρ with R2
ρ with R3
ρ with R4
ρ with R5
Figure 4: Plots of bias and variance reduction of Euclidean distances at 50th percentile against number of columns in R
i
for
kos data.
ent types of vectors x
i
, x
j
. This allows for more accu-
rate estimates of the Euclidean distance. As the Eu-
clidean distance between two vectors increases, we
expect greater variance reduction. In essence, we
have shown that it is possible to juxtapose statistical
variance reduction methods with random projections
to give better results.
While RPCV gives a variance reduction for the es-
timates of the inner products, the ratio of variance re-
duction becomes minimal as the number of columns
increases when compared to Li’s method. This is not
surprising since Li’s method for estimating the inner
products is an asymptotic maximum likelihood esti-
mator, and is extremely accurate as the number of
Random Projections with Control Variates
145

0 20 40 60 80 100
0.0 0.2 0.4 0.6 0.8 1.0
Plot of ρ for percentiles with R_1 (Colon)
Number of columns k
Ratio
ρ at 20th percentile
ρ at 30th percentile
ρ at 40th percentile
ρ at 50th percentile
ρ at 60th percentile
ρ at 70th percentile
ρ at 80th percentile
0 20 40 60 80 100
0.0 0.2 0.4 0.6 0.8 1.0
Plot of ρ for percentiles with R_1 (Kos)
Number of columns k
Ratio
ρ at 20th percentile
ρ at 30th percentile
ρ at 40th percentile
ρ at 50th percentile
ρ at 60th percentile
ρ at 70th percentile
ρ at 80th percentile
Figure 5: Plots of ρ for percentiles of Euclidean distance for R
1
in both colon and kos data.
columns increases.
Although RPCV requires storing marginal norms
and computing the covariance between two p dimen-
sional vectors, the cost of doing so is negligible when
compared to matrix multiplication. Furthermore, the
computation of marginal norms is unnecessary when
the data is already normalized.
In fact, RPCV can be seen as a method that nicely
complements Li’s method since both methods require
storing marginal norms. RPCV substantially reduces
the errors of the estimates of the Euclidean distance,
while Li’s method substantially reduces the errors of
the estimates of the inner product.
We note that different applications may require a
certain type of random projection matrix. Thus if we
want to reduce the errors in our estimates, we can-
not just switch to a different random projection matrix
where the entries allow us to place sharper probability
bounds on our errors. If we want data to be invari-
ant under rotations, then a Normal random projection
matrix would be best suited (Mardia et al., 1979). If
we wanted to desparsify data, then a random projec-
tion matrix with i.i.d. entries from {−
√
p,0,
√
p}, p
small might be preferred (Achlioptas, 2003). If we
are focused on speed and quick information retrieval,
then very sparse random projections (Li et al., 2006b)
or random projection matrices formed by the SHRT
(Boutsidis and Gittens, 2012) would be more prefer-
able. RPCV allows us to reduce the error in all these
estimates.
While we have demonstrated good empirical re-
sults in the variance reduction for Euclidean distances
for RPCV, we still need an expression for the first and
second moments of A + c(B −µ
B
) when the elements
in the random projection matrix R are correlated in
order to theoretically show that RPCV does achieve
this reduction in variance. We are currently working
on this.
Finally, we want look forward to extending this
method of control variates to other applications of
random projections.
REFERENCES
Achlioptas, D. (2003). Database-friendly Random Projec-
tions: Johnson-Lindenstrauss with Binary Coins. J.
Comput. Syst. Sci., 66(4):671–687.
Ailon, N. and Chazelle, B. (2009). The Fast Johnson-
Lindenstrauss Transform and Approximate Nearest
Neighbors. SIAM J. Comput., 39(1):302–322.
Alon, U., Barkai, N., Notterman, D., Gish, K., Ybarra, S.,
Mack, D., and Levine, A. (1999). Broad patterns
of gene expression revealed by clustering analysis of
tumor and normal colon tissues probed by oligonu-
cleotide arrays. Proceedings of the National Academy
of Sciences, 96(12):6745–6750.
Boutsidis, C. and Gittens, A. (2012). Improved matrix al-
gorithms via the subsampled randomized hadamard
transform. CoRR, abs/1204.0062.
Boutsidis, C., Zouzias, A., and Drineas, P. (2010). Random
projections for k-means clustering. In Lafferty, J. D.,
Williams, C. K. I., Shawe-Taylor, J., Zemel, R. S., and
Culotta, A., editors, Advances in Neural Information
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
146

Processing Systems 23, pages 298–306. Curran Asso-
ciates, Inc.
Fern, X. Z. and Brodley, C. E. (2003). Random projection
for high dimensional data clustering: A cluster ensem-
ble approach. pages 186–193.
Li, P. and Church, K. W. (2007). A Sketch Algorithm for
Estimating Two-Way and Multi-Way Associations.
Comput. Linguist., 33(3):305–354.
Li, P., Hastie, T., and Church, K. W. (2006a). Improving
Random Projections Using Marginal Information. In
Lugosi, G. and Simon, H.-U., editors, COLT, volume
4005 of Lecture Notes in Computer Science, pages
635–649. Springer.
Li, P., Hastie, T. J., and Church, K. W. (2006b). Very Sparse
Random Projections. In Proceedings of the 12th
ACM SIGKDD International Conference on Knowl-
edge Discovery and Data Mining, KDD ’06, pages
287–296, New York, NY, USA. ACM.
Liberty, E., Ailon, N., and Singer, A. (2008). Dense fast ran-
dom projections and lean walsh transforms. In Goel,
A., Jansen, K., Rolim, J. D. P., and Rubinfeld, R.,
editors, APPROX-RANDOM, volume 5171 of Lecture
Notes in Computer Science, pages 512–522. Springer.
Lichman, M. (2013). UCI machine learning repository.
Mardia, K. V., Kent, J. T., and Bibby, J. M. (1979). Multi-
variate Analysis. Academic Press.
Paul, S., Boutsidis, C., Magdon-Ismail, M., and Drineas, P.
(2012). Random Projections for Support Vector Ma-
chines. CoRR, abs/1211.6085.
Ross, S. M. (2006). Simulation, Fourth Edition. Academic
Press, Inc., Orlando, FL, USA.
Vempala, S. S. (2004). The Random Projection Method,
volume 65 of DIMACS series in discrete mathematics
and theoretical computer science. Providence, R.I.
American Mathematical Society. Appendice p.101-
105.
APPENDIX
While computing first and second moments neces-
sarily require lots of algebra, we use the following
lemma for ease of computation.
Lemma 4.1. Suppose we have a sequence of terms
{t
i
}
p
i=1
= {a
i
r
i
}
p
i=1
for a = (a
1
,a
2
,...,a
p
), {s
i
}
p
i=1
=
{b
i
r
i
}
p
i=1
for b = (b
1
,b
2
,...,b
p
) and r
i
i.i.d. random
variables with E[r
i
] = 0, E[r
2
i
] = 1 and finite third, and
fourth moments, denoted by µ
3
,µ
4
respectively.
Then:
E
p
∑
i=1
t
i
!
2
=
p
∑
i=1
a
2
i
= kak
2
2
(36)
E
p
∑
i=1
t
i
!
4
= µ
4
p
∑
i=1
a
4
i
+ 6
p−1
∑
u=1
p
∑
v=u+1
a
2
u
a
2
v
(37)
E
"
p
∑
i=1
s
i
!
p
∑
i=1
t
i
!#
=
p
∑
i=1
a
i
b
i
= ha, bi (38)
E
p
∑
i=1
s
i
!
2
p
∑
i=1
t
i
!
2
=
p
∑
i=1
a
2
i
b
2
i
+
∑
i6= j
a
2
i
b
2
j
+ 4
p−1
∑
u=1
p
∑
v=u+1
a
u
b
u
a
v
b
v
(39)
The motivation for this lemma is that we do ex-
pansion of terms of the above four forms to prove our
theorems.
Random Projections with Control Variates
147
