Real-Time Gesture Recognition using a Particle Filtering Approach
Fr
´
ed
´
eric Li
1
, Lukas K
¨
oping
1
, Sebastian Schmitz
2
and Marcin Grzegorzek
1,3
1
Research Group for Pattern Recognition, University of Siegen, Siegen, Germany
2
Fraunhofer SCAI, St. Augustin, Germany
3
University of Economics in Katowice, Faculty of Informatics and Communication, Katowice, Poland
Keywords:
Gesture Recognition, Particle Filter, Gesture Spotting, Dynamic Time Warping, DTW Barycenter Averaging.
Abstract:
In this paper we present an approach for real-time gesture recognition using exclusively 1D sensor data, based
on the use of Particle Filters and Dynamic Time Warping Barycenter Averaging (DBA). In a training phase,
sensor records of users performing different gestures are acquired. For each gesture, the associated sensor
records are then processed by the DBA method to produce one average record called template gesture. Once
trained, our system classifies one gesture performed in real-time, by computing -using particle filters- an
estimation of its probability of belonging to each class, based on the comparison of the sensor values acquired
in real-time to those of the template gestures. Our method is tested on the accelerometer data of the Multimodal
Human Activities Dataset (MHAD) using the Leave-One-Out cross validation, and compared with state-of-
the-art approaches (SVM, Neural Networks) adapted for real-time gesture recognition. It manages to achieve
a 85.30% average accuracy and outperform the others, without the need to define hyper-parameters whose
choice could be restrained by real-time implementation considerations.
1 INTRODUCTION
Gesture recognition is the problem of finding mean-
ing in the movement of humans’ hands, arms, face,
head and/or body in order to enable an interaction
between humans and machines (Mitra and Acharya,
2007). The main purpose of gesture recognition
systems (GRS) is to offer a natural interaction be-
tween humans and machines. An example for this
are today’s Virtual Reality applications where gesture
recognition plays a major role in order to produce an
immersive feeling. Systems that are based on addi-
tional input devices often destroy this immersive feel-
ing since they require the user to act in an unnatural
way. For example, grabbing an object should not be
performed by pushing a button on some external de-
vice. Instead, the natural way would be to put forth
one’s hand and perform a grabbing gesture. How-
ever, the problem of gesture recognition is a difficult
one since it requires to satisfy several different con-
straints:
• User Independent Performance: GRS must
work for people who are not included in the ini-
tial training set. The alternative is to introduce
some sort of calibration phase to fit the system’s
algorithm to the user. However, such a calibra-
tion phase might discourage people from using the
system if it takes too much effort.
• Naturalness of Gestures: Even the same individ-
ual user does not always perform every gesture in
the same way. Instead, gestures have some free
parameters to them like the speed or the intensity
in which they are performed. Gesture recognition
systems should be able to acknowledge these vari-
ations and maybe even react to them.
• Separation from Relevant and Irrelevant Data:
Not all of a user’s movements are particular ges-
tures. The GRS should be able to distinguish be-
tween gestures and random user movements (ges-
ture spotting). Forcing the user to notify the sys-
tem of the beginning and end of a gesture would
again provide an unnatural feeling.
• Realtime Performance: The delay between the
performance of a gesture and its recognition
should be minimal. This is especially needed in
applications that are using Virtual or Augmented
Reality since big delays disturb the interactiveness
of these systems. An early detection of gestures is
only possible if the algorithm is able to process
the data in realtime.
In this work we propose a method that accounts for
394
Li, F., Köping, L., Schmitz, S. and Grzegorzek, M.
Real-Time Gesture Recognition using a Particle Filtering Approach.
DOI: 10.5220/0006189603940401
In Proceedings of the 6th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2017), pages 394-401
ISBN: 978-989-758-222-6
Copyright
c
 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

all the aforementioned difficulties. For this, we are
formulating gesture recognition as a location track-
ing problem that can be solved using recursive state
estimation methods. Our approach uses particle fil-
tering in particular, and takes multi-modal data input
in form of time series gathered by accelerometer sig-
nals. It can recognize gestures of different lengths,
without needing input from the user at the start or end
of a gesture.
The paper is structured as follows. In section 2
we give an overview of related work. Section 3 in-
troduces our method which is evaluated in section 4.
Finally, section 5 summarises our results and gives an
outlook to future work.
2 RELATED WORK
The literature offers a variety of approaches to gesture
recognition (Mitra and Acharya, 2007). To narrow
down the existing work we exclude papers that focus
on video data as input and instead focus on gesture
recognition algorithms that are based on time series
data, e.g. accelerometer. uWave (Liu et al., 2009) is
a gesture recognition system that uses a three-axis ac-
celerometer as input data. Templates of the gestures
that should be recognised by the system are stored in
a database, where for each template gesture one or
two examples exist. uWave determines which gesture
is performed by the user by using the best match be-
tween the input data and the template gestures based
on Dynamic Time Warping (DTW) as similarity mea-
sure. However, this procedure delivers wrong results
if the input gesture is totally different from any of the
template gestures. To avoid these kinds of misclassi-
fications the authors introduce a threshold for the sim-
ilarity. If the similarity between the input gesture and
all other template gestures is below this threshold, the
gesture is recognised as unknown. uWave achieves
strong results in the classification of user dependent
gestures. However, the system requires the user to
press and hold a button during the execution of a ges-
ture.
In (Akl et al., 2011) the authors use DTW as sim-
ilarity measure for clustering with the Affinity Propa-
gation algorithm. This offline training phase returns a
set of exemplars for the gestures of the system. In the
recognition phase firstly those exemplars are chosen
that are closest to the input. In a second step the data
is projected into a lower dimensional space where the
final classification takes place. For the user-dependent
case a recognition rate of 96.84% on the same dataset
as uWave is reported.
The authors of (Chudgar et al., 2014) focus on the
problems of gesture spotting and the identification of
the intensity of a gesture. Gesture spotting describes
the problem of finding the beginning and the end of a
gesture without explicitly marking it, e.g. by pressing
a button. On the other hand, identifying the intensity
of a gesture can help making gesture recognition sys-
tems more convenient, e.g. a fast gesture increases the
TV volume more than a slow gesture. To incorporate
gesture spotting (Chudgar et al., 2014) use a thresh-
old that is based on the variance of the accelerome-
ter signal. For recognition they match the input with
the available training gestures by DTW similarity and
identify the intensity of a gesture with the help of sig-
nal variance.
The topic of finding the intensity of a gesture can
also be found in (Caramiaux et al., 2014). The pro-
posed Gesture Variation Follower (GVF) does not
only classify gestures but also has the ability to es-
timate its speed, scale and rotation. For this, they
extend the work of (Black and Jepson, 1998), where
drawings on a whiteboard are classified and simulta-
neously the speed and scaling of the gesture is esti-
mated. Both approaches are based on the CONDEN-
SATION algorithm which is also known as particle
filtering or Sequential Monte Carlo (see (Isard and
Blake, 1998), (Gordon et al., 1993), (Arulampalam
et al., 2002) for a detailed explanation). Particle fil-
ters are a method to approximate over time the proba-
bility density of a hidden state by integrating a series
of observations. Each particle represents one partic-
ular state and has an associated weighting. The hid-
den state of the GFV consists of a discrete variable
for the class label and some real-valued variables for
the speed, scale and rotation of a gesture. Observa-
tions are simply the incoming accelerometer data val-
ues. When the user performs a gesture with an arbi-
trary speed and rotation, the weightings of the parti-
cles increase that represent exactly this particular ges-
ture class label and that also match with the speed,
scale and rotation. The weighting of all the other par-
ticles will decrease over time. Our work is mostly
motivated by this approach and follows its main prin-
ciples. We formulate gesture recognition in the same
way as (Caramiaux et al., 2014) using particle filter-
ing. However, we change the way that our system
evolves over time and the way observations are inte-
grated into the probability estimation. In addition, we
calculate average gestures in the training phase that
serve as templates for the testing phase.
One point to be noted is the lack of recent similar
approaches in the literature. To some extend related
to our study, a survey presenting an overview of ex-
isting online and offline activity recognition methods
by mobile phones (Shoaib et al., 2015) highlights the
Real-Time Gesture Recognition using a Particle Filtering Approach
395

Figure 1: Example of DTW applied to two 1D time se-
quences. The warping path (in red) can be found after the
computation of the cost matrix C. The DTW associations
between the elements of the two sequences (to the right)
can be deduced from its coordinates.
dominance of approaches like decision trees, SVM,
KNN and naive Bayes, and the rarity of particle filter-
ing for real-time gesture recognition problems.
3 METHOD DESCRIPTION
3.1 DTW Barycentric Averaging (DBA)
DBA is a method of time sequences averaging, which
relies on the use of the Dynamic Time Warping al-
gorithm (DTW) to compute similarities between time
sequences while taking the time dimension into ac-
count. It also provides information about the match-
ing between the elements of two different times se-
quences.
Given two sequences a and b (of lengths m and
n ∈ N
∗
not necessarily equal, with values in R), and
a distance function d : R ×R → R, the DTW method
provides a cost matrix C ∈ M
m×n
(R) containing the
DTW distances between all pairs of elements (a
i
, b
j
),
recursively computed by the relations given in (Petit-
jean and Ganc¸arski, 2012). A few interesting prop-
erties of this cost matrix C have been highlighted as
well in (Petitjean and Ganc¸arski, 2012). In particular,
the cost matrix provides the associations between the
respective elements of the two time series related to
it, by considering the coordinates of the warping path
(Petitjean and Ganc¸arski, 2012) (i.e. path of mini-
mal cost linking C(1, 1) and C(m, n)). The value in
C(m, n) also provides the DTW distance between the
two sequences compared.
Finding those time series element associations
forms the basis of the DBA method: for a set of time
series S = (s
1
, s
2
, ..., s
M
) (with M ∈ N
∗
) of not nec-
essarily equal lengths, the DBA algorithm computes
s
avg
, an estimation of the average time sequence of all
the s
i
, by the following process:
1. Initialize at random s
avg
, of length ”well chosen”.
2. For every sequence s
i
in S, compute the DTW be-
tween s
i
and s
avg
to find the coordinates associa-
tions.
3. For every element s
avg
(i) in s
avg
, replace s
avg
(i)
by the mean value of all coordinates across all s
i
in S, associated with s
avg
(i) at step 2.
4. Repeat steps 2 and 3 until s
avg
converges.
In the scope of our project, we decided to apply
the DBA algorithm M times during the training phase,
by initializing s
avg
to each sequence of the set S, and
in the end select the resulting average sequence mini-
mizing the average DTW distance between itself and
the other sequences of the set S.
3.2 Velocity Factor and Template
Gestures
A dataset of temporal sensor readings from A different
sensors, and for G gestures, acquired from U differ-
ent users, who each performed R different repetitions
of each gesture, is available for the training phase of
our system (with (A, G,U, R) ∈ (N
∗
)
4
). The times-
tamps (real time values in seconds, corresponding to
each sampling moment) are also available for all sen-
sor readings.
Since the number of readings in the training
dataset could vary and result in large datasets, a way
to guarantee the scalability of our system by com-
pressing the information contained in those time se-
quences has to be employed. Furthermore, this com-
pression of the information has to take into account
the multi-sensor aspect of the dataset. To achieve both
goals, we compute for each gesture g ∈ {1, ..., G} a
template gesture using DBA on the sensor readings
of the dataset. However, we decide to use a variation
of the DBA method described previously, by apply-
ing it on the set of multi-sensor time sequences re-
lated to the gesture g (vector of A vectors of sensor
values). The distance function d, necessary to com-
pute the DTW cost matrix, is chosen in this case as
the Euclidean distance in R
A
. The averaging function
of elements of sequences, needed to update the ele-
ments of the average sequence during the iterations
of the DBA process, is also extended to the multidi-
mensional case: for s
1
, s
2
, ..., s
n
n ∈ N
∗
multi-sensor
coordinates (in R
A
), we define the average of the (s
i
)
i
,
avg
A
, by
avg
A
(s
1
, ..., s
n
) =



avg(s
1
(1), s
2
(1), ..., s
n
(1))
avg(s
1
(2), s
2
(2), ..., s
n
(2))
...
avg(s
1
(A), s
2
(A), ..., s
n
(A))



∈ R
A
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
396

We denote S
g
= {M
g
u,r
| u ∈ {1, ...,U }, r ∈
{1, ..., R}} the set of multi-sensor time series related
to gesture g. Each element M
g
u,r
of this set is the con-
catenation of sensor readings related to the r
th
per-
formance of gesture g by user u. M
g
u,r
is therefore a
matrix of size l
u,r
×A, with l
g
u,r
∈ N
∗
number of data
points acquired for this recording of the gesture. DBA
is applied on all sets S
g
, by considering each M
g
u,r
as a
vector of multi-sensor coordinates (i.e. vectors of size
A), to obtain an average multi-sensor time sequence
T
g
∈ M
l
g
×A
(R) (with l
g
∈ N
∗
length of the average
sequence determined by the DBA algorithm), called
template gesture.
DBA provides an average sequence based on the
values of the elements of the sequences used for the
averaging process. However, it does not perform any
matching on the timestamps associated to those el-
ements, which is needed in our model. To address
this issue, we introduce a new value called veloc-
ity factor, giving a partial information on the relative
speeds of how the average and training gestures are
performed, and using the fact that multi-sensor se-
quences and template gestures can be seen as vectors
of multi-sensor coordinates (vectors of R
A
). Given a
set of multi-sensor time sequences related to gesture
g S
g
= {S
g,1
, S
g,2
, ..., S
g,M
} and their associated tem-
plate obtained with DBA T
g
, of size l
g
×A, we define
M
assoc
∈M
l
g
×M
(R) as the association matrix between
T
g
and S
g
by:
for all 1 6 i 6 l
g
and 1 6 j 6 M,
M
assoc
(i, j) = number of multi-sensor coordinates
of sequence S
g, j
associated to the i
th
multi-sensor
element of T
g
by DTW
and the velocity factor vector v
g
∈ R
l
g
associated
to T
g
as:
for 1 6 i 6 l
g
, v
g
(i) =
1
N
M
∑
j=1
M
assoc
(i, j) (1)
The i
th
element of the vector v
g
is the average
number of coordinates of the sequences of S
g
associ-
ated to the i
th
element of its average sequence T
g
. In-
tuitively, each element of v
g
indicates how fast the av-
erage time sequence T
g
is compared to the sequences
of S
g
. In particular, having v
g
(i) < 1 indicates that the
sequence T
g
is slower on average than the ones in S
g
,
at time i, whereas v
g
(i) > 1 denotes the contrary.
Denoting ∆t ∈ R
∗
+
the time gap between two con-
secutive sampling moments (in seconds), we are then
able to define the timestamps (t
g
k
)
16k6l
g
, associated
to the average sequence T
g
by:
Figure 2: Example of one template (in blue) obtained for
one gesture and one sensor, and its standard deviation at all
timestamps (in gray). In red : the ”temporal position” of the
particles within the template gesture. The abscissa of each
particle is its estimated timestamp.
t
g
k
=
(
0 if k = 0
t
g
k−1
+ v
g
(k) ∆t ∀1 6 k 6 l
g
(2)
Note that for convenience purposes, we define an
indexation of template gestures by timestamps (in-
stead of regular indices), by T
g
(t, a) = T
g
(k, a), with
1 6 k 6 l
g
so that t = t
g
k
, for t ∈ R
+
timestamp com-
puted at the previous step, g ∈ {1, ..., G} and a ∈
{1, ..., A}
Finally, given one gesture g, we keep in memory
for all sensors a ∈ {1, ..., A} the standard deviation of
sensor values at all timestamps of the template ges-
ture T
g
, computed -for each timestamp- on the set of
values related to sensor a from the sequences of the
training set, linked by the DBA algorithm to the coor-
dinate of T
g
associated to this timestamp. We denote
the G ×A vectors that we obtain σ
g,a
(∈ R
l
g
):
∀g ∈ {1, ..., G}, ∀a ∈ {1, ..., A}, ∀1 6 k 6 l
g
,
σ
g,a
(k) =
s
1
|S
k
|
∑
c∈S
k
(c(a) −T
g
(k, a))
2
(3)
where S
k
is the set of multi-sensor coordinates (el-
ements of R
A
) of the sequences of the training set, as-
sociated with the k
th
multi-sensor coordinate of T
g
,
and |S
k
| is the cardinality of S
k
.
3.3 Transition Model
Once the template gestures (T
g
)
16g6G
and associ-
ated velocity vectors (v
g
)
16g6G
are obtained after the
training phase, we can define the model of our parti-
cle filter for temporal tracking. Given an input ges-
ture performed in real-time providing real-time sensor
data, we propose to classify it by trying to estimate its
”temporal position” within each template gesture, or
in other words, to find to which of the G templates the
input gesture is the closest, and to which part of it it
corresponds to.
Real-Time Gesture Recognition using a Particle Filtering Approach
397

Given a set of N ∈ N
∗
particles, we define x
i
k
the
i
th
particle (i ∈ {1, 2, ..., N}) at sampling time k ∈ N
by:
x
i
k
=

g
i
t
i
k

(4)
where g
i
∈ {1, 2, ..., G} is the index linking the
particle to the gesture g
i
, and t
i
k
∈R, called timestamp,
is an estimation of the temporal position of the parti-
cle within the template gesture T
g
(in seconds)
In our definition of the model, all particles, from
birth to death, are assigned with one of the G different
gestures, i.e. ∀k ∈N, ∀i ∈{1, 2, ..., N}, x
i
k
(1) = x
i
0
(1).
The timestamp x
i
k
(2) evolves according to the follow-
ing relation:
∀k ∈ N
∗
, t
i
k
= t
i
k−1
+ α
i
k
∆t (5)
with ∆t duration (in seconds) between two consec-
utive sampling steps, and α
i
k
∈R value drawn follow-
ing a stationary process, given by the Gaussian distri-
bution N (µ, σ) of parameters µ and σ set manually.
3.4 Observation Model
The observation model of a particle filter is used to
compute the weight associated to each particle, at all
sampling times. This weight should be proportional
to the likelihood of the particle state regarding the
sensor observations obtained at the current sampling
time. Given e
k
= (e
k,1
, e
k,2
, ..., e
k,A
) the A sensor ob-
servations obtained in real time from the input gesture
at sampling step k ∈ N, and a particle x
i
k
= (g
i
,t
i
k
), we
therefore define the model as follows:
w
i
k
=
A
∏
a=1
α
a
(e
k,a
) (6)
with α
a
(e
k,a
) =
1
√
2π σ
a
(t
i
k
)
e
−
(e
k,a
−T
g
i
(t
i
k
,a))
2
σ
a
(t
i
k
)
2
(7)
and σ
a
(t) =
1
G
G
∑
g=1
σ
g,a
(t) (8)
Considering that the timestamp t
i
k
of one particle
x
i
k
= (g
i
,t
i
k
) can take any value in R
+
and might not be
one of the values computed using the velocity vector
during the training phase, the sensor value T
g
i
(t
i
k
, a)
and sensor standard deviation σ
g
i
,a
(t
i
k
) might not be
defined. We therefore define those values by comput-
ing a simple linear interpolation using the two closest
timestamps stored in memory after the training, and
their associated sensor values: given t
1
, t
2
timestamps
in memory so that t
1
< t
i
k
< t
2
:
T
g
i
(t
i
k
, a) = T
g
i
(t
1
, a) +
t
i
k
−t
1
t
2
−t
1
(T
g
i
(t
2
, a) −T
g
i
(t
1
, a))
(9)
σ
g
i
,a
(t
i
k
, a) = σ
g
i
,a
(t
1
, a)+
t
i
k
−t
1
t
2
−t
1
(σ
g
i
,a
(t
2
, a) −σ
g
i
,a
(t
1
, a)) (10)
One important point to understand the way we
built our model: we could observe very different or-
ders of magnitude in the values of σ
g,a
(t) depending
on the gesture g ∈ {1, ..., G} considered in our dataset
(for all sensor a and timestamp t). The use of an aver-
aged standard deviation across all gestures (9), instead
of the standard deviation of sensor values related to
the gesture x
i
k
(1) = g
i
for the Gaussian distribution,
prevents our model from giving more influence to ges-
tures with low standard deviations on the computation
of w
k
.
All weights obtained at sampling step k ∈ N are
then normalized in [0, 1], as follows:
∀i ∈ {1, 2, ..., N}, w
i
norm,k
=
w
i
k
∑
N
j=1
w
j
k
(11)
3.5 Resampling
Particle filtering approaches are subject to degener-
acy problems, highlighted in (Doucet et al., 2000):
the particles of the system can evolve in a way that
drives them further from sensor observation acquired
in real time, therefore making the values of the as-
sociated weights drop to a point where no particle
can be considered as significant anymore. In order to
address this issue, particles are resampled when this
phenomenon occurs, i.e. the N particles of the sys-
tem are re-initialized with equal weights, after being
drawn with a probability proportional to their former
weights.
In order to determine when to resample, we define
the effective number of particles N
eff,k
at time k ∈ N,
introduced in (Liu and Chen, 1998), by:
N
eff,k
=
1
∑
N
i=1
(w
i
norm,k
)
2
(12)
The resampling occurs when N
eff
falls below a
threshold N
threshold
∈R : N
eff
6 N
threshold
, whose value
is empirically determined.
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
398

One particular case where this system degener-
acy can be observed with the model we defined oc-
curs when the particles keep evolving, whereas the
performance of the input gesture has not actually be-
gun yet, or when the user started to perform a ges-
ture some time after the particles started to evolve. In
those situations, resampling cannot address this issue
alone, considering that all current particles provide
wrong estimations of the timestamp. For this reason,
we perform an additional step, called interspersing,
which consists of adding N
intersperse
∈ N
∗
new parti-
cles, spread across all G gestures, with timestamps
taken randomly between 0 and the maximum duration
of each gesture (i.e. timestamp associated with the
last coordinate of the corresponding template), before
the actual resampling. Associated weights to these
new particles are computed using (6) and (11). Re-
sampling on the N + N
intersperse
is then performed to
draw N new particles.
3.6 Gesture Classification
The classification of an input gesture performed in
real time is done at any sampling step k ∈ N by com-
puting its probability p
g
k
to belong to the class of ges-
ture g ∈ {1, ..., G}, which can be obtained by sum-
ming the weights of all particles associated to this ges-
ture:
∀k ∈ N, ∀g ∈ {1, ..., G}, p
g
k
=
∑
i∈{1,...,N}
with x
i
k
(1)=g
w
i
norm,k
(13)
The class of the input gesture at time k ∈ N,
g
estimated
k
∈ {1, ..., G} , is determined by checking the
highest probability of belonging to one class:
∀k ∈ N, g
estimated
k
= argmax
g∈{1,...,G}
(p
g
k
) (14)
In order to consider only classification results
which would be meaningful (e.g. by not starting to
classify until the input gesture is actually performed),
we also decide to compute g
estimated
k
for k ∈ N only
if the estimated probability of the most likely ges-
ture is ”high enough”, i.e. p
g
estimated
k
k
> p
threshold
with
p
threshold
∈ [0, 1].
To summarize, the following steps are performed
to achieve gesture recognition in our system:
At each sampling step k > 0 :
1. At k = 0, assign N particles to all gestures (
N
G
per
gesture)
2. Move particles following the transition model (5)
3. Acquire real-time data e
k
of the input gesture, and
compute the weights w
k
using (6)
4. Normalize weights using (11)
5. Predict the class using (14) if the certainty on the
result is high enough
6. If N
eff,k
6 N
threshold
, intersperse new particles and
resample
7. k ← k + 1, and loop to step 2
4 EXPERIMENTAL RESULTS
4.1 MHAD Dataset
The performances of our system have been tested on
the Multimodal Human Action Database (MHAD)
from Berkeley University (Ofli et al., 2013), which
features a wide range of different sensor data acqui-
sitions (RGB and Kinect cameras, 3D accelerometers
and audio sensors), acquired from 12 different sub-
jects (7 male, 5 female), who were asked to perform
G = 11 different actions basic enough to be consid-
ered as gestures (1 : jumping in place, 2 : jumping
packs, 3 : bending, 4 : punching, 5 : waving with two
hands, 6 : waving with the right hand, 7 : clapping
hands, 8 : throwing a ball with the right hand, 9 : sit-
ting down then standing up, 10 : sitting down, 12 :
standing up), R = 5 times each.
Considering that we are limiting the scope of our
project to the problem of real time recognition of ges-
tures, using continuous time series data, we decided
to use only the data from the 3D accelerometers (2 on
the subjects’ wrists, 2 on ankles and 2 on hips), result-
ing in A = 6 ×3 = 18 different sensors. The sampling
frequency of those sensors is f = 30 Hz.
4.2 Results
After some manual tuning of our model, we set the
parameters of our transition model to µ = 1, σ = 0.2,
the total number of particles to N = 120, the num-
ber of interspersed particles after resampling to N
i
=
60, the resampling threshold to N
threshold
= 0.2N =
30, and the probability threshold for classifying to
p
threshold
= 0.7. We achieve an average accuracy of
85.30% across all gestures, over the 12 different folds
of the Leave-One-Out cross validation, with a maxi-
mum accuracy of 91.90%, a minimum of 72.73% and
a standard-deviation of 7.29%.
After a look at the averaged confusion matrix over
the 12 folds of the cross-validation (c.f. figure 3),
it can be noted that most of the misclassifications
Real-Time Gesture Recognition using a Particle Filtering Approach
399

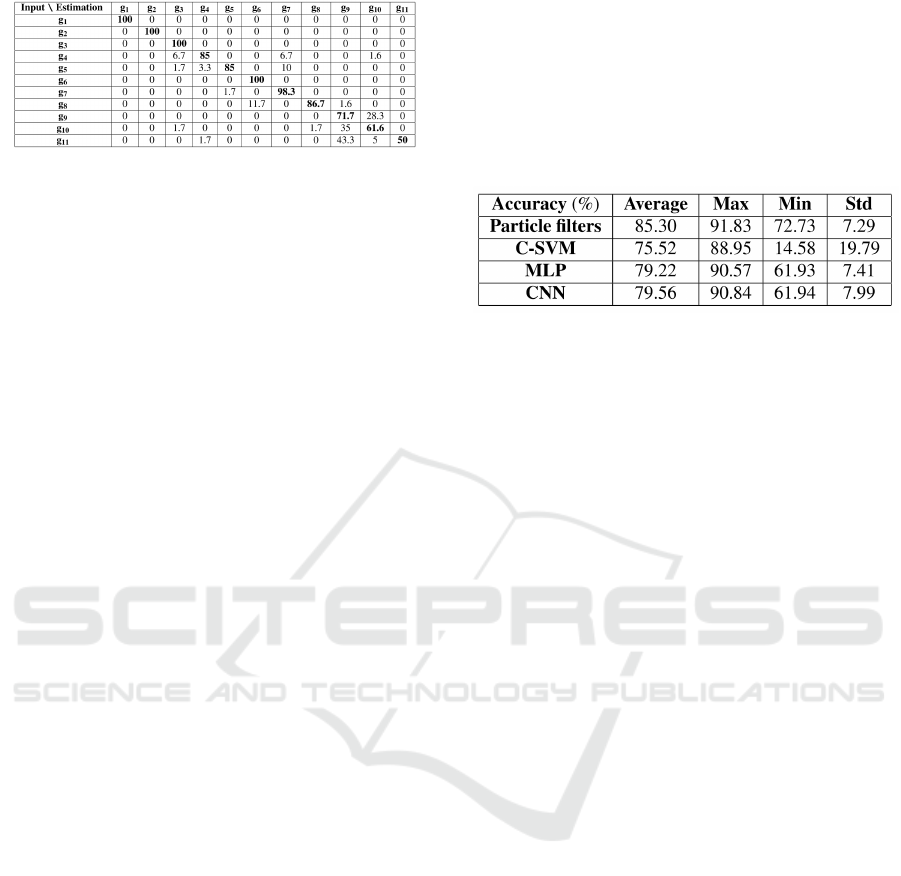
Figure 3: Confusion matrix for the classification of the 11
gestures of the MHAD dataset, using our particle filtering
approach. The results (in percentages) are the accuracies
averaged over the 12 subjects of the dataset.
concern some gestures which share some common
submovements, and therefore are similar in terms of
sensor values and variations. Our method is espe-
cially bad at making a distinction between g
9
, g
10
and
g
11
(respectively sitting down then standing up, sit-
ting down, standing up). On the opposite, our model
achieves very high classification rates for some of the
other gestures of the dataset, regardless of the subject
tested (g
1
, g
2
, g
3
, g
6
and g
7
).
4.3 Comparison to the State-of-the-Art
In order to compare our method’s performances to
the performances of the state-of-the-art ones, we also
tested the following methods for real time gesture
classification:
• Soft-Margin SVM (C-SVM): the sensor data
from all A sensors, comprised within a sliding
time window of T ∈N
∗
sampling times, is directly
used as input features of the model (dimension of
T ×A). The sliding step is set to 1. The kernel
used is the RBF.
• Multi-Layer Perceptron (MLP): classic feed-
forward neural network with one input, output and
hidden layers, trained using mini-batch gradient
descent. Similarly to the previous C-SVM solu-
tion, the sensor data contained within a time win-
dow T ∈ N
∗
is taken as input of the network (vec-
tors of size T ×A), with the same sliding step of
1.
• Convolution Neural Network (CNN): deep neu-
ral network adapted to time series processing,
with two pairs of convolutional + pooling layers,
and a MLP performing classification on the fea-
tures computed at the end of the CNN. The sen-
sor data comprised within a time window T ∈ N
∗
(with a sliding window of 1) is taken as input
(therefore making input ”images” of dimension
T ×A). The training is performed using mini-
batch gradient descent.
All models also have been tested using Leave-
One-Out cross-validation on the 12 subjects of the
dataset. The hyper-parameters of each model have
been determined by grid-search for the C-SVM ap-
proach, and trial and error experiments for both neu-
ral networks approaches (MLP and CNN). The dif-
ferent models have been coded using Python, and the
LibSVM and Theano libraries for C-SVM and neural
networks respectively. The following table summa-
rizes the best results obtained for each of them :
Figure 4: Comparative accuracies of the different classifica-
tion models tested, using Leave-One-Out cross validation.
Our method achieves a better accuracy averaged
over the 12 folds of the MHAD dataset than both neu-
ral network approaches and C-SVM without feature
extraction. It also has the advantage of not having the
need to set an input time window hyper-parameter,
which could be constrained by the requirements on
the performances of an actual implementation in real-
time of the system, or prevent the processing of short
input sequences with length lower than the time win-
dow. The lower average accuracy obtained with Neu-
ral Network approaches and C-SVM can be explained
by the low performances obtained by those models for
some of the subjects of the dataset. We suppose that
while the poor performances of C-SVM can be at-
tributed to the fact that the raw input data comprised
within a time window is not relevant enough to be
used as input features of the model, the accelerome-
ter training data used from the MHAD set might not
be large and diverse enough to obtain optimal results
after the training of both Neural Network models.
5 CONCLUSION AND FUTURE
WORKS
In this paper, we presented a method for real time ges-
ture recognition using 1D temporal sensor data. In a
preliminary phase (training), the sensor readings from
the training set are averaged to obtain one template
gesture. The process is repeated for all of the differ-
ent gestures of the set. In a secondary phase (recog-
nition), a particle filter model is defined for the ges-
ture classification. The sensor data of an input ges-
ture performed by a user is acquired in real time, and
compared to the gesture templates obtained after the
training phase to determine an estimation of the ”tem-
poral position” of the input gesture. The classification
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
400

of the latter is performed by determining the closest
template gesture.
Our method has been tested with the accelerome-
ter data of the MHAD dataset (Ofli et al., 2013) using
the Leave-One-Out cross validation on the 12 sub-
jects of the set, and compared to other state-of-the-
art classification approaches (SVM, MLP and CNN).
It achieves a 85.30% average accuracy, and outper-
forms other real-time gesture classification models,
without having any need -unlike the other approaches-
to set a time-window parameter which could be con-
strained by the constraints of an actual real-time im-
plementation, or not be suitable for the recognition
of very short gestures. The results obtained show
that most misclassifications of our method concern
gestures which share common submovements (e.g.
sitting-down, standing-up). The high accuracies ob-
tained for the other gestures of the dataset, no mat-
ter the subject performing them, or the way they are
performed, indicate that our method is robust to vari-
ations in execution of the gestures.
There are still some points on which our method
could be improved or developed further though. Pre-
liminary experiments carried out on a dataset of hand
gestures using accelerometers (uWave, (Liu et al.,
2009)) seem to confirm the fact that our method
struggles to differenciate gestures similar in terms of
sensor values and variations, as it provides accura-
cies much lower than other tested state-of-the-art ap-
proaches (SVM and Neural Networks) there. Future
works will focus on finding axis of improvements to
address this issue: in particular finding more rele-
vant state features to be tracked by the particle filter,
testing the classification problem with additional 1D
temporal sensor data, and analyze the possibility to
attribute an importance weight to each sensor in our
observation model to favour the recognition of some
gestures.
ACKNOWLEDGEMENTS
Research and development activities leading to this
article have been supported by the German Research
Foundation (DFG) as part of the research training
group GRK 1564 ”Imaging New Modalities”, and
the German Federal Ministry of Education and Re-
search (BMBF) within the project ELISE (grant num-
ber: 16SV7512, www.elise-lernen.de).
REFERENCES
Akl, A., Feng, C., and Valaee, S. (2011). A
novel accelerometer-based gesture recognition sys-
tem. IEEE Transactions on Signal Processing,
59(12):6197–6205.
Arulampalam, M. S., Maskell, S., Gordon, N., and Clapp,
T. (2002). A tutorial on particle filters for on-
line nonlinear/non-gaussian bayesian tracking. IEEE
Transactions on Signal Processing, 50(2):174–188.
Black, M. J. and Jepson, A. D. (1998). A probabilis-
tic framework for matching temporal trajectories:
Condensation-based recognition of gestures and ex-
pressions. In Computer Vision — ECCV’98: 5th Euro-
pean Conference on Computer Vision Freiburg, Ger-
many, June, 2–6, 1998 Proceedings, Volume I”, pages
909–924.
Caramiaux, B., Montecchio, N., Tanaka, A., and Bevilac-
qua, F. (2014). Adaptive gesture recognition with vari-
ation estimation for interactive systems. ACM Trans.
Interact. Intell. Syst., 4(4):18:1–18:34.
Chudgar, H. S., Mukherjee, S., and Sharma, K. (2014). S
control: Accelerometer-based gesture recognition for
media control. In Advances in Electronics, Computers
and Communications (ICAECC), 2014 International
Conference on, pages 1–6.
Doucet, A., Godsill, S., and Andrieu, C. (2000). On se-
quential monte carlo sampling methods for bayesian
filtering. Statistics and Computing, 10(3):197–208.
Gordon, N. J., Salmond, D. J., and Smith, A. F. M. (1993).
Novel approach to nonlinear/non-gaussian bayesian
state estimation. volume 140, pages 107–113.
Isard, M. and Blake, A. (1998). Condensation - conditional
density propagation for visual tracking. International
Journal of Computer Vision, 29(1):5–28.
Liu, J., Zhong, L., Wickramasuriya, J., and Vasudevan, V.
(2009). uwave: Accelerometer-based personalized
gesture recognition and its applications. Pervasive and
Mobile Computing, 5(6):657 – 675. PerCom 2009.
Liu, J. S. and Chen, R. (1998). Sequential monte carlo
methods for dynamic systems. Journal of the Ameri-
can statistical association, 93(443):1032–1044.
Mitra, S. and Acharya, T. (2007). Gesture recognition:
A survey. IEEE Transactions on Systems, Man,
and Cybernetics, Part C (Applications and Reviews),
37(3):311–324.
Ofli, F., Chaudhry, R., Kurillo, G., Vidal, R., and Bajcsy, R.
(2013). Berkeley mhad: A comprehensive multimodal
human action database. In Applications of Computer
Vision (WACV), 2013 IEEE Workshop on, pages 53–
60.
Petitjean, F. and Ganc¸arski, P. (2012). Summarizing a set
of time series by averaging: From steiner sequence to
compact multiple alignment. Theoretical Computer
Science, 414(1):76–91.
Shoaib, M., Bosch, S., Incel, O., H.Scholten, and Havinga,
P. (2015). A survey of online activity recognition us-
ing mobile phones. Sensors, 15:2059–2085.
Real-Time Gesture Recognition using a Particle Filtering Approach
401