
Estimating Coarse 3D Shape and Pose from the Bounding Contour
Paria Mehrani and James H. Elder
Department of Electrical Engineering and Computer Science, York University, 4700 Keele Street, Toronto, Canada
paria@cse.yorku.ca, jelder@yorku.ca
Keywords:
Shape Estimation, 3D Shape Reconstruction, Single-view Reconstruction, Shape-from-contour.
Abstract:
Single-view reconstruction of a smooth 3D object is an ill-posed problem. Surface cues such as shading and
texture provide local constraints on shape, but these cues can be weak, making it a challenge to recover globally
correct models. The bounding contour can play an important role in constraining this global integration. Here
we focus in particular on information afforded by the overall elongation (aspect ratio) of the bounding contour.
We hypothesize that the tendency of objects to be relatively compact and the generic view assumption together
induce a statistical dependency between the observed elongation of the object boundary and the coarse 3D
shape of the solid object, a dependency that could potentially be exploited by single-view methods. To test
this hypothesis we assemble a new dataset of solid 3D shapes and study the joint statistics of ellipsoidal
approximations to these shapes and elliptical approximations of their orthographically projected boundaries.
Optimal estimators derived from these statistics confirm our hypothesis, and we show that these estimators
can be used to generate coarse 3D shape-pose estimates from the bounding contour that are significantly and
substantially superior to competing methods.
1 INTRODUCTION
To be clear on terminology, we follow (Koenderink,
1984) and refer to the set of surface points grazed by
the view vector as the rim of the object, and the pro-
jection of these points into the image as the occluding
contour.
It is well known that the occluding contour
strongly constrains surface shape at the rim (Koen-
derink, 1984). Indeed, human judgement of sur-
face shape is strongly influenced by the shape of the
occluding contour (Todd and Reichel, 1989; Todd,
2004), and often even the occluding contour alone
provides a compelling sense of volumetric shape (Tse,
2002; Elder, 2014) (Fig. 1). Understanding the infor-
Figure 1: Volumetric shape from the bounding contour.
mation provided by the occluding contour is impor-
tant not only for this limiting case, but also for devis-
ing algorithms that effectively exploit contour cues in
conjunction with (possibly weak) surface cues such as
shading and texture (Karsch et al., 2013).
While the computer vision literature on shape
from contour is relatively small, there have been a
few interesting studies in recent years exploring the
degree to which solid shape can be reconstructed
from occluding contours alone (Igarashi et al., 1999;
Twarog et al., 2012; Karsch et al., 2013). These stud-
ies have tended to focus on extracting a complete, de-
tailed model of the 3D shape from the boundary, with-
out considering whether the solution will be close to
correct at a global scale. Here we take the opposite
view, and ask whether the bounding contour can tell
us anything about the global shape of the object at the
coarsest scale and its 3D pose. If this global informa-
tion can be estimated from the bounding contour, it
could then be used to help constrain algorithms that
recover more detailed 3D structure so that reconstruc-
tions are correct at both local and global scales.
Most computer vision work in this area exploits
the bounding contour in conjunction with surface cues
within an optimization framework. Typically, user in-
teraction and/or some inflation term in the objective
function are required to avoid a trivial (flat) solution.
Users were required to specify depth of some sur-
face points in (Prasad et al., 2006), or a fixed volume
that the shape must fill in (Toppe et al., 2011). Os-
wald (Oswald et al., 2009) used an inflation term.
More recent studies has avoided user interaction
Mehrani P. and Elder J.
Estimating Coarse 3D Shape and Pose from the Bounding Contour.
DOI: 10.5220/0006190306030610
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 603-610
ISBN: 978-989-758-225-7
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
603

and arbitrary inflation terms and instead have com-
bined local surface shading cues with contour infor-
mation to estimate surface shape. Cole (Cole et al.,
2012) estimate local surface normals within an MRF
framework and fit a final 3D surface to the estimated
normals using a thin plate spline. Barron and Ma-
lik (Barron and Malik, 2015) assume a probabilis-
tic framework, imposing a prior over the variation in
mean surface curvature. While both of these systems
fuse shading and contour cues to determine the re-
construction, Karsch (Karsch et al., 2013) have shown
that internal contour cues appear to be stronger cues
to shape than shading.
A very different strategy for single-view es-
timation of smooth solid shapes was first intro-
duced in the interactive sketching interface dubbed
Teddy (Igarashi et al., 1999) and later studied by
Twarog (Twarog et al., 2012) under the pseudonym
Puffball. (We will use the latter term as an evocative
label for this class of methods.) In this approach, the
solid shape is defined as the envelope of spheres cen-
tred on the interior skeleton (Blum, 1973) of the shape
in the image, and bi-tangent to the occluding contour
(Fig. 2). The method is simple and can produce sur-
prisingly reasonable results in many cases.
Figure 2: Puffball reconstruction (Twarog et al., 2012).
One limitation of all of these prior algorithms is
that they are typically constrained or at least strongly
biased to return a planar or near-planar and fronto-
parallel rim (i.e., a frontal pose), whereas in the real
world under general viewing the probability of this is
vanishing. A second potential problem is that these
methods impose strong constraints or priors on the
overall depth of the objects. For example, by defin-
ing solid shape as an envelope of spheres, Puffball
makes a very strong local symmetry assumption: at
every point on the skeleton, the depth of the object
(dimension in the viewing direction) is equal to twice
the distance of the contour from the skeleton. Are
these assumptions reasonable?
One of the difficulties in answering this question
is that most prior work has been evaluated only qual-
itatively, not quantitatively. Important exceptions are
the work of Karsch (Karsch et al., 2013) and Barron &
Malik (Barron and Malik, 2015), however their eval-
uations do not explicitly test these assumptions.
2 OUR CONTRIBUTIONS
Instead of focusing on detailed shape reconstruction,
our goal in this paper is to understand information af-
forded by the bounding contour on the rough shape
and global 3D pose of the object. In particular, we
wish to understand whether the contour can provide a
cue to the rough length, width and depth of the object,
and how it might be angled out of the fronto-parallel
plane. To address this question we will study the
joint statistics of ellipsoidal approximations of real
scanned objects and their image projections. Here
we confine ourselves to orthographic projection, un-
der which these ellipsoidal approximations generate
elliptical images.
Our specific contributions are:
1. We introduce a new dataset and methodology for
evaluating methods for single-view reconstruction
of smooth solid objects.
2. We show that statistically, even a simple elliptical
approximation of the occluding contour provides
substantial information about the coarse 3D shape
and pose of the object.
3. We show that the assumptions of symmetry in
depth and fronto-parallel pose imposed by prior
work lead to large errors in single-view 3D object
estimation.
3 INTUITION
Why would a simple elliptical approximation to the
occluding contour carry information about 3D shape
and pose? One of our intuitions is rooted in the com-
pactness of real objects. While objects vary widely
in shape, we conjecture that extreme elongations are
relatively rare. This has implications when we ob-
serve an elongated occluding contour in the image
(Fig. 3(a)).
There is an infinite family of solid objects that
could have generated this contour. However, if the
longest dimension of the object is angled away from
fronto-parallel, the object must be even more elon-
gated than the occluding contour. This induces a bias
for elongated occluding contours to project from ob-
jects whose long dimension is close to fronto-parallel,
whereas for less elongated contours the long dimen-
sion is relatively more likely to be angled away from
the image plane.
A second intuition derives from the generic view-
point assumption (Freeman, 1994). Imagine an elon-
gated object with its longest dimension in the view-
ing direction (Fig. 3(b)). A small change in 3D pose
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
604

(a) Ellipsoids of various shapes can give rise to
the same ellipse. The ellipse is viewed from
front while ellipsoids are viewed from top.
(b) Two ellipsoids giving rise to the same ellipse
with and without fronto-parallel poses (left), and
same ellipsoids rotated 15 deg. The projection
of the longer ellipsoids has drastic changes with
small perturbations in pose (right).
Figure 3: Top: An infinite family of shapes can project onto
the same contour. Bottom: Drastic changes in projection of
an elongated ellipsoid with small perturbations in its pose.
will induce a large change in the appearance of the
occluding contour. If, on the other hand, the object is
rotated so that its smallest dimension is in the viewing
direction, the same change in 3D pose will induce a
relatively small change in the occluding contour. This
suggests that the expected extent of the object in depth
may be small relative to the dimensions observed in
the image, counter to the Puffball assumption.
These are only qualitative intuitions. The main
point of this paper is test these intuitions quantita-
tively, using a simple sampling technique.
4 DATASET
At time of writing, we are not aware of any large-scale
public collection of real 3D scanned objects. For the
purposes of this project, we have therefore assembled
a collection from various sources on the internet in-
cluding the BigBIRD dataset (Singh et al., 2014), the
YCB object and model set dataset (C¸ alli et al., 2015),
and various other 3D model sharing websites such as
Sketchfab
1
. Any duplicates were removed. The final
dataset consists of 122 objects, which we randomly
divided into training and test sets of 61 objects each.
Some examples are shown in Fig. 4.
1
https://sketchfab.com.
!
Figure 4: Example 3D objects in our dataset.
5 METHODS
5.1 Priors
We employ ellipsoids as low-order 3D models cap-
turing global shape and pose. We first use an iterative
closest point algorithm (Besl and McKay, 1992) to
determine, for each object in the dataset, the ellipsoid
that minimizes mean squared Euclidean error (Fig-
ures 12 and 13). The size and shape of each ellipsoid
is completely characterized by the length of its three
axes: a ≥ b ≥ c. Since we are not concerned with ab-
solute size, we can collapse these three numbers into
two ratios specifying the length of its two smaller axes
relative to the largest axis: 1 > λ
2
= b/a > λ
3
= c/a >
0 . The collection of ellipsoid fits to our training data
then form our empirical shape prior (Fig. 6(a)).
Figure 5: Ellipsoid shape priors. Left: Empirical prior de-
rived from training objects. Right: Theoretical prior, based
on a uniform distribution of axis lengths.
There are two major limitations of this prior. First,
given the limited size of our dataset, it is of course
quite noisy. Second, since we employed opportunity
sampling to form the dataset, it is certain to contain
bias. For these reasons, we also constructed a theoret-
ical uniform shape prior, formed by sampling triplets
of numbers uniformly on [0, 1], scaling each triplet to
have maximum value 1, and then assigning the middle
and smaller values to b and c. As expected, the result-
ing distribution is uniform on the subspace λ
2
≥ λ
3
.
(The green diagonal stripe reflects the fact that only
half of each bin on the diagonal lies in the feasible
subspace.) Note that the mean of this distribution is
(λ
2
= 2/3,λ
3
= 1/3). In other words, the mean shape
under the uniform prior has axes in the ratio 3 : 2 : 1.
While the limited sample size for the empirical
prior makes detailed comparison with the uniform
prior difficult, we can at least make some qualita-
tive observations. First, the empirical prior seems to
Estimating Coarse 3D Shape and Pose from the Bounding Contour
605

be biased somewhat toward more compact, less elon-
gated ellipsoids, i.e., toward λ
2
= λ
3
= 1. Second,
there appears to be a bias toward the diagonal, i.e., to-
ward λ
2
= λ
3
, which represents the family of prolate
spheroids (cigar shapes).
We assume a uniform prior over 3D pose. The 3D
pose can be characterized by the angle θ
1
and θ
2
of
the two larger ellipsoid axes with respect to the view
vector (Fig 6), as the remaining degree of freedom
induces a rotation in the projected ellipse, but does
not change its shape.
X
Y
Z
λ
1
λ
2
λ
3
θ
1
θ
2
Figure 6: The angles θ
1
and θ
2
characterize the 3D pose of
ellipsoid.
5.2 Likelihoods
To learn the joint statistics of coarse 3D object
shape/pose and occluding contour shape, we sampled
ellipsoids from the 3D shape/pose priors and pro-
jected them (orthographically) as ellipses to the im-
age. For both empirical and uniform priors we ran-
domly sampled 1 million shape/pose combinations.
Again, the ellipse shape is completely characterized
by the ratio 0 < m < 1 of the length of the minor to
the major axis. The result is a five-dimensional joint
ellipsoid-ellipse space (λ
2
,λ
3
,θ
1
,θ
2
,m). To analyze
the joint distribution, we partitioned the space into 20
bins in each dimension, resulting in 3.2 million bins.
With only 1 million samples, this discrete space will
be sparsely populated overall. However in practice
the density is far from uniform, so that most estima-
tors can be calculated with reasonable accuracy.
We consider three estimation problems:
1. Estimation of ellipsoid shape (marginalizing over
pose).
2. Estimation of ellipsoid pose (marginalizing over
shape).
3. Joint estimation of ellipsoid shape and pose.
We will consider three distinct estimators for el-
lipsoid shape and pose given an ellipse shape:
1. Puffball. To represent the strategy employed by
symmetry axis methods, (Igarashi et al., 1999;
Twarog et al., 2012) the ellipsoid is assumed to be
a prolate spheroid with longest axis in the image
plane and matching the major axis of the ellipse
and the other two smaller axes matching the mi-
nor axis of the ellipse (λ
2
= λ
3
= m).
2. Maximum a Posteriori (MAP). The most probable
ellipsoid shape/pose is selected.
3. Minimum Mean Squared Error (MMSE). The
ellipsoid shape/pose minimizing the expected
squared error is selected. We define the error as
the symmetric mean Euclidean distance between
points on estimated and ground truth ellipsoids.
For the joint estimation of ellipsoid shape and
pose, the MMSE solution is computationally expen-
sive to compute and we therefore approximate it with
a Mean estimator, which selects the ellipsoid with
mean shape/pose parameters. We also consider a
Puffball solution that selects a random pose, for rea-
sons explained below.
Recall that all three estimation problems are ill-
posed: each estimator proposes an ellipsoid shape
and/or pose that is consistent with the observed ellipse
(Within some tolerance due to the discrete sampling
of shape and pose parameters.) Differences in the el-
lipsoid estimates may thus reflect only a) knowledge
of the 3D shape/pose prior, b) an understanding of
how projection affects the joint statistics of the ellipse
and generating ellipsoid and/or c) loss function (delta
function for MAP, quadratic for MMSE and Mean).
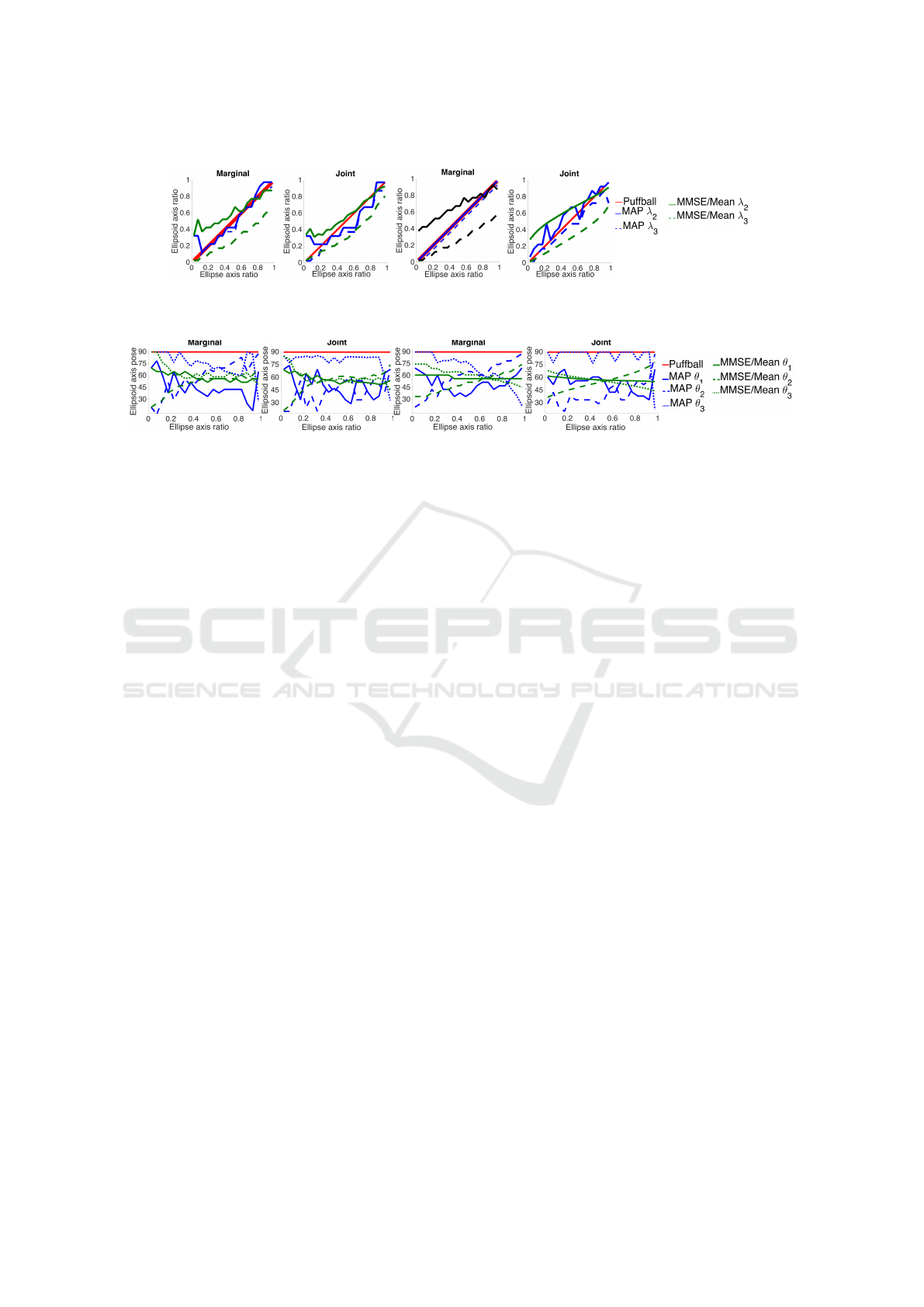
Fig. 7 shows the resulting estimators for shape and
Fig. 8 shows estimators for pose. Note that in the
Puffball solution the largest axis is always in the im-
age plane (θ
1
= 90 deg), and that λ
2
= λ
3
= m.
Consider first the estimation of shape. Regardless
of prior and whether we are doing marginal or joint
estimation, the MAP solution follows Puffball fairly
closely. However, the MAP solution for shape does
deviate slightly from Puffball, and these deviations
are important (see below). A more profound diver-
gence from Puffball is seen in the MMSE and Mean
shape solutions, which in general return a losenge
rather than a cigar for all ellipses, with the two smaller
axes differing substantially in length.
Further insight can be gained by considering the
estimation of pose. Due to sampling error the MAP
solution is noisy, but it can be clearly seen that, un-
like Puffball, the major axis of the ellipsoid is slanted
away from the image plane by between 15 and 75 deg.
Note that, to be consistent with the observed ellipse,
this means that at least one of the smaller ellipsoid
axes must be slightly smaller than the puffball predic-
tion, a condition which can be verified from Fig. 7.
In the case of MMSE/Mean estimators, unlike
Puffball, the major axis of the ellipsoid does not tend
to lie in the image plane (θ
1
= 90 deg), but rather is
angled out of the image plane by roughly 30 deg on
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
606
Empirical Prior Uniform Prior
Figure 7: Estimators for shape.
Empirical Prior Uniform Prior
Figure 8: Estimators for pose.
average (θ
1
= 60 deg). This is not too surprising, as
a uniform pose distribution (not conditioned on the
observation of ellipse) generates an average value for
θ
1
,θ
2
and θ
3
of 1 radian (about 57 deg).
More interesting is the fact that the angle of the
major axis depends upon the ellipse shape: the ma-
jor axis of the ellipsoid is closer to the image plane
for more elongated ellipses. This is consistent with
the intuitions we expressed above. Since the empiri-
cal prior favours compact shapes, a highly elongated
ellipse is more likely to be generated by an ellip-
soid whose major axis is closer to the image plane.
Note, however, that we also see a variation, though
smaller, for the uniform prior. This may be due to
the generic view assumption: when conditioned on an
image measurement (in this case, an ellipse), a highly
elongated ellipsoid with major axis closer to the im-
age plane is favoured as it makes the observation more
stable with respect to angular perturbation, and thus
generates a higher conditional probability density.
There is even larger variation in the angle of the
second and third ellipsoid axes as a function of the
shape of the ellipse. For small ellipse ratios, the third
axis lies closer to the image plane, but for larger el-
lipse ratios the second axis lies closer to the image
plane. This makes sense because highly elongated
ellipses are more likely to be observed if the small-
est ellipsoid axis is close to the image plane, whereas
less elongated ellipses are more likely to be observed
if the second axis is close to the image plane.
6 QUANTITATIVE EVALUATION
We have seen that the MAP, MMSE and Puffball es-
timators make quite distinct predictions of ellipsoid
shape and pose from an observed ellipse. How does
this relate to the perception of more complex objects?
Suppose a more complex occluding contour is ob-
served. To obtain a rough estimate of 3D object shape
and pose, we could first approximate this shape by an
ellipse and then use one of these estimators to infer an
ellipsoidal approximation of the 3D object, and/or its
pose. But which should we use?
To answer this question, we sampled 200 random
3D poses for each of the 61 shapes in our test dataset,
projected each to the image and used an ICP algo-
rithm to compute the best-fitting ellipse to each ob-
served occluding contour. We used each of our meth-
ods to estimate an ellipsoidal approximation of the
original generating object from this observed ellipse.
We evaluated these ellipsoidal approximations by
computing the bidirectional mean-squared Euclidean
error between the estimated ellipsoid and the best-
fitting ellipsoid for the ground truth object.
6.1 Shape Estimators
To evaluate the marginal shape estimators, each esti-
mated ellipsoid was scaled and rotated to minimize
the Euclidean distance from the ground truth ellip-
soid, and the resulting mean symmetric Euclidean dis-
tance was used as a measure of error. Fig. 9 reveals
that both MAP and MMSE shape estimators perform
better than Puffball, with MMSE performing best.
While the overlapping standard error bars in the
top panels of Fig. 9 might call into question the sta-
tistical significance of these differences, these varia-
tions in error are highly correlated across estimators.
This correlated error can be factored out by consider-
ing the average reduction in error for each test shape
for the MAP and MMSE estimators relative to Puff-
Estimating Coarse 3D Shape and Pose from the Bounding Contour
607

Figure 9: Top: Mean Euclidean error for marginal shape
estimation. Bottom: Reduction in error relative to Puffball
(larger is better).
ball (lower panels). From these plots it is easy to see
that the reduction in error is highly significant for both
MAP and MMSE. Table 1 shows the percent reduc-
tion in mean error and also the percentage of shapes
for which error was lower for MAP and MMSE rel-
ative to Puffball. For MAP the improvement is rel-
atively modest (5-9%) but consistent: MAP is better
than Puffball for 75-97% of shapes. For MMSE the
mean improvement is more substantial (24-31%) but
less consistent: MMSE is better than Puffball for only
55-67% of shapes.
6.2 Pose Estimators
To evaluate the marginal pose estimators, we mea-
sured mean symmetric Euclidean error between
ground truth ellipsoid at the correct and estimated
poses. A problem emerges here: in our orthographic
projection framework, for each ellipsoid there are four
3D ’metamer’ poses that generate the same ellipse.
To handle this, when an estimator generates a pose,
we use an oracle to convert this to select from these
four metamers the pose that generates minimal error
relative to ground truth. Unfortunately, this puts Puff-
ball at a disadvantage, since it represents a degenerate
case where the four poses collapse to a single one. To
address this, we add as a baseline a random pose esti-
mator (Random), which selects a random pose, iden-
tifies the four metamers and then selects the optimal
pose of these four using an oracle as described above.
As shown in Fig. 10, both MAP and MMSE pose
estimators perform better than both Puffball and Ran-
dom pose estimators. Since the Random estimator
performs better than Puffball, we evaluate the per-
formance of MAP and MMSE estimators relative to
the latter (Fig. 10, bottom panels and Table 2.) Both
MAP and MMSE generate significantly more accu-
rate pose estimates. While MAP generates slightly
greater mean improvement, improvements are more
consistent across objects for MMSE.
Figure 10: Top: Mean Euclidean error for marginal pose
estimation. Bottom: Reduction in error relative to the Ran-
dom pose estimator (larger is better).
6.3 Joint Configuration Experiments
For the joint estimators, symmetric Euclidean error of
each estimated ellipsoid relative to the ground truth
ellipsoid is computed, with no scaling or rotation.
Again, an oracle is used to select the pose that yields
lowest error, and this does put Puffball at a disadvan-
tage. Unfortunately it is difficult to correct for this
for joint shape-pose estimation, as selecting a random
pose but using the Puffball shape would no longer
be consistent with the observed ellipse. We there-
fore present results without correction, noting that the
marginal shape and pose results presented above con-
firm that our MAP and MMSE estimators outperform
Puffball for both of these dimensions individually.
Fig. 11 shows that for the empirical prior, the
Mean estimator is best, while for the uniform prior,
MAP and Mean are comparable. Table 3 shows that
Figure 11: Mean Euclidean error for joint estimation. Bot-
tom: Reduction in error relative to Puffball (larger is better).
the Mean estimator generates a greater average im-
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
608
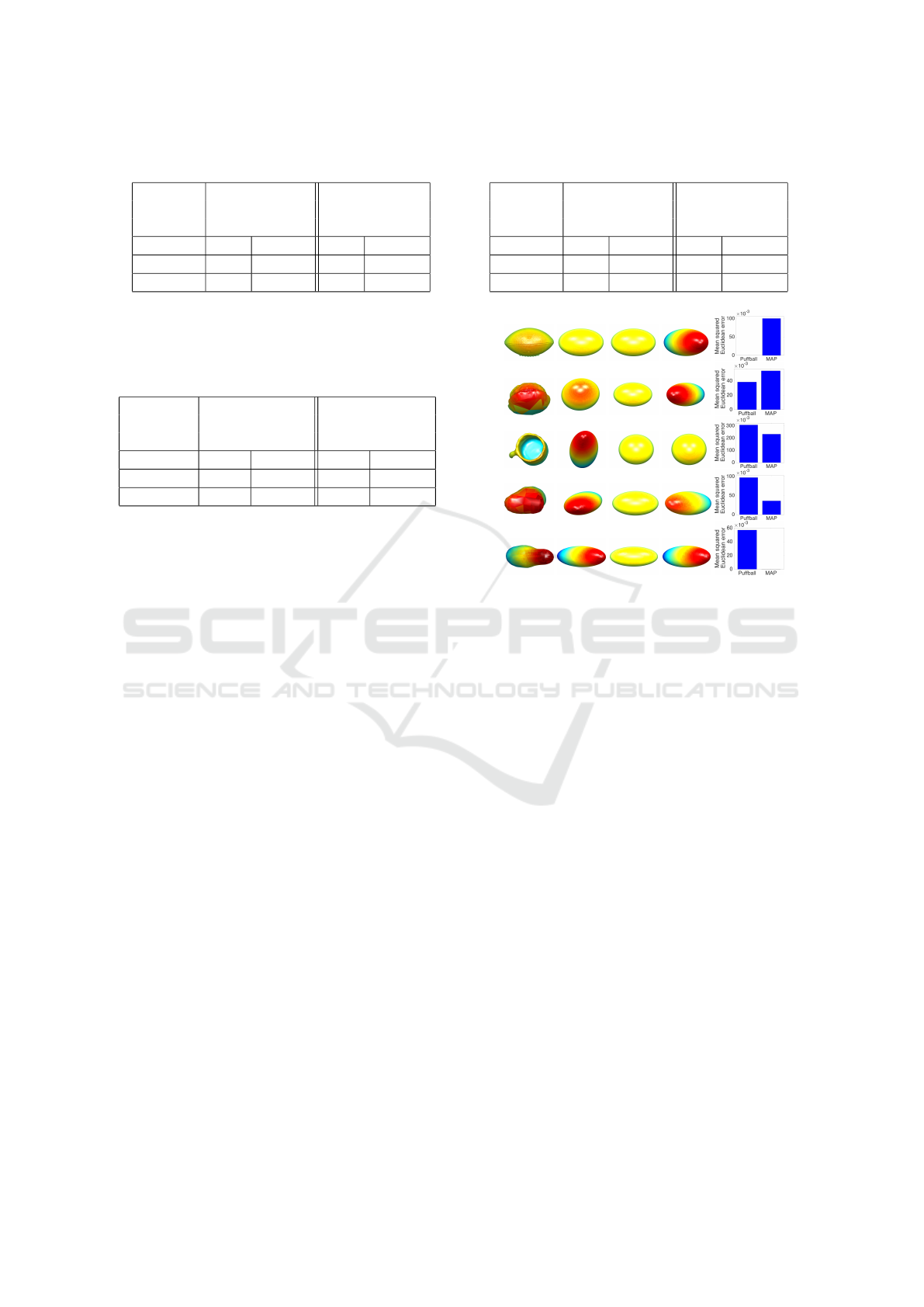
Table 1: Performance of MAP and MMSE shape estimators
relative to Puffball.
Prior Mean reduction % of objects for
in error which error is
reduced
MAP MMSE MAP MMSE
Empirical 5% 31% 75% 67%
Uniform 9% 24% 97% 55%
Table 2: Performance of MAP and MMSE pose estimators
relative to the Random pose estimator.
Prior Mean reduction % of objects for
in error which error is
reduced
MAP MMSE MAP MMSE
Empirical 10% 7% 87% 98%
Uniform 11% 9% 92% 98%
provement for the Empirical prior, but the MAP esti-
mator is more reliable for the uniform prior.
Table 3: Performance of MAP and MMSE joint shape-pose
estimators relative to Puffball.
Prior Mean reduction % of objects for
in error which error is
reduced
MAP Mean MAP Mean
Empirical 9% 23% 70% 70%
Uniform 18% 19% 87% 67%
7 QUALITATIVE EVALUATION
To get a qualitative sense of the performance of our
joint shape-pose estimators, Figs. 12-13 show repre-
sentative results for specific shapes in our test dataset,
using MAP and Mean estimators based on our em-
pirical prior. To generate Fig. 12, we first sorted the
test cases by percent reduction in mean error for MAP
over Puffball, and then show 0th, 25th, 50th, 75th and
100th percentile examples. The first (0th percentile)
case is the shape for which MAP performs worst rel-
ative to Puffball. The last (100th percentile) case is
the shape for which MAP has the largest error reduc-
tion relative to Puffball. The third (50th percentile)
case is the median (representative) example. Simi-
larly, Fig. 13 compares the Mean solution to Puffball.
In these qualitative comparisons, we note the el-
liptical projections of the estimated ellipsoids do not
exactly match, and are sometimes quite different from
the elliptical projections of the ground truth ellip-
soids. This is primarily because the estimated ellip-
soids are conditioned on an ellipse fitted in the image
plane to the projected object, and in general this el-
lipse is different from the elliptical projection of the
ground truth ellipsoid.
In addition, for a given shape there are small vari-
ations between the elliptical projections of the esti-
mated ellipsoids. This is due to the finite sampling of
shape and pose space.
Despite these limitations, the qualitative results
are interesting. It is probably most instructive to con-
sider the median results (third row) as these are repre-
(a)
Object
(b)
Ground
truth
(c) Puff-
ball
(d)
MAP
(e) Error
Figure 12: Examples of joint shape-pose estimation on test
set objects. Objects were ranked according to the percent
reduction in mean error for MAP over Puffball estimator.
From top to bottom: 0, 25, 50, 75, and 100 percentile ob-
jects.
sentative. In both cases of Fig. 12 and 13, the statisti-
cal estimators have smaller errors relative to Puffball.
Interestingly, in Fig. 13, the Mean estimator is able to
capture the greater elongation and out-of-plane rota-
tion of the object that Puffball is unable to capture.
8 CONCLUSIONS AND FUTURE
WORK
In this paper we set out to understand whether coarse
3D shape information could be extracted from object
silhouettes even under orthographic projection. In
particular, we conjectured that the tendency for ob-
jects to be compact and the generic view assumption
should together bias the rough shape and pose when
conditioned on the silhouette. Our experimental re-
sults confirm this hypothesis.
One limitation of this study is the use of an
oracle to distinguish between four metamer poses
in marginal pose and joint shape-pose estimations.
Estimating Coarse 3D Shape and Pose from the Bounding Contour
609

(a)
Object
(b)
Ground
truth
(c) Puff-
ball
(d)
Mean
(e) Error
Figure 13: Examples of joint shape-pose estimation on test
set objects. Objects were ranked according to the percent
reduction in mean error for Mean over Puffball estimator.
From top to bottom: 0, 25, 50, 75, and 100 percentile ob-
jects.
Since this limitation is a direct consequence of or-
thographic projection, an obvious next step is to use
perspective projection, which will disambiguate these
metamers and allow us to do a fairer comparison.
Even with statistically optimal estimators, given
only elliptical approximations, shape and pose esti-
mation is quite unreliable. The value of this work thus
lies not in immediate application, but rather in the in-
tegration of these estimators with additional boundary
shape cues as well as weak surface cues (e.g., shad-
ing, texture) that are usually present in the image but
often insufficient to fully constrain 3D reconstruction.
REFERENCES
Barron, J. T. and Malik, J. (2015). Shape, illumination, and
reflectance from shading. IEEE Transactions on Pat-
tern Analysis and Machine Intelligence, 37(8):1670–
1687.
Besl, P. J. and McKay, H. D. (1992). A method for regis-
tration of 3-d shapes. IEEE Transactions on Pattern
Analysis and Machine Intelligence, 14(2):239–256.
Blum, H. (1973). Biological shape and visual science (Part
I). J. Theor. Biol., 38:205–287.
C¸ alli, B., Walsman, A., Singh, A., Srinivasa, S., Abbeel, P.,
and Dollar, A. M. (2015). Benchmarking in manip-
ulation research: The YCB object and model set and
benchmarking protocols. ArXiv e-prints.
Cole, F., Isola, P., Freeman, W., Durand, F., and Adelson,
E. (2012). Shapecollage: Occlusion-aware, example-
based shape interpretation. In Fitzgibbon, A., Lazeb-
nik, S., Perona, P., Sato, Y., and Schmid, C., edi-
tors, Computer Vision ECCV 2012, volume 7574 of
Lecture Notes in Computer Science, pages 665–678.
Springer Berlin Heidelberg.
Elder, J. H. (2014). Bridging the dimensional gap: Per-
ceptual organization of contour into two-dimensional
shape. In Wagemans, J., editor, Oxford Handbook of
Perceptual Organization, Oxford, UK. Oxford Uni-
versity Press.
Freeman, W. T. (1994). The generic viewpoint assump-
tion in a framework for visual perception. Nature,
368(6471):542–545.
Igarashi, T., Matsuoka, S., and Tanaka, H. (1999). Teddy:
a sketching interface for 3D freeform design. In Pro-
ceedings of the 26th annual conference on computer
graphics and interactive techniques, SIGGRAPH
’99, pages 409–416, New York, NY, USA. ACM
Press/Addison-Wesley Publishing Co.
Karsch, K., Liao, Z., Rock, J., Barron, J. T., and Hoiem,
D. (2013). Boundary Cues for 3D Object Shape Re-
covery. In Computer Vision and Pattern Recogni-
tion (CVPR), 2013 IEEE Conference on, pages 2163–
2170.
Koenderink, J. (1984). What does the occluding contour tell
us about solid shape? Perception, 13(321-330).
Oswald, M., Toppe, E., Kolev, K., and Cremers, D. (2009).
Non-parametric single view reconstruction of curved
objects using convex optimization. In Denzler, J.,
Notni, G., and S
¨
ue, H., editors, Pattern Recognition,
volume 5748 of Lecture Notes in Computer Science,
pages 171–180. Springer Berlin Heidelberg.
Prasad, M., Zisserman, A., and Fitzgibbon, A. W. (2006).
Single view reconstruction of curved surfaces. In
Computer Vision and Pattern Recognition, 2006 IEEE
Computer Society Conference on, volume 2, pages
1345–1354.
Singh, A., Sha, J., Narayan, K. S., Achim, T., and Abbeel, P.
(2014). Bigbird: A large-scale 3D database of object
instances. In 2014 IEEE International Conference on
Robotics and Automation (ICRA), pages 509–516.
Todd, J. (2004). The visual perception of 3D shape. Trends
in Cognitive Sciences, 8(3):115–121.
Todd, J. T. and Reichel, F. D. (1989). Ordinal structure
in the visual perception and cognition of smoothly
curved surfaces. Psychological Review, 96(4):643–
657.
Toppe, E., Oswald, M. R., Cremers, D., and Rother, C.
(2011). Image-based 3D Modeling via Cheeger Sets.
In Proceedings of the 10th Asian Conference on Com-
puter Vision - Volume Part I, ACCV’10, pages 53–64,
Berlin, Heidelberg. Springer-Verlag.
Tse, P. (2002). A contour propagation approach to surface
filling-in and volume formation. Psychological Re-
view, 109(1):91–115.
Twarog, N. R., Tappen, M. F., and Adelson, E. H. (2012).
Playing with Puffball: Simple scale-invariant infla-
tion for use in vision and graphics. In Proceedings
of the ACM Symposium on Applied Perception, SAP
’12, pages 47–54, New York, NY, USA. ACM.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
610
