On the Impact of using Mixed Integer Programming Techniques on

Real-world Offshore Wind Parks

Martina Fischetti

1,2

and David Pisinger

Vattenfall BA Wind, Jupitervej 6, 6000 Kolding, Denmark

Technical University of Denmark, Operations Research, DTU Management,

Produktionstorvet, 424 DK-2800 Kgs. Lyngby, Denmark

Keywords:

Optimization, Mixed Integer Linear Programming, Wind Energy, Routing, Offshore Cables, Green Energy.

Abstract:

Wind power is a leading technology in the transition to sustainable energy. Being a new and still more compet-

itive ﬁeld, it is of major interest to investigate new techniques to solve the design challenges involved. In this

paper, we consider optimization of the inter-array cable routing for offshore wind farms, taking power losses

into account. Since energy losses in a cable depend on the load (i.e. wind), cable losses are estimated by con-

sidering a possibly large number wind scenarios. In order to deal with different wind scenarios efﬁciently we

used a precomputing strategy. The resulting optimization problem considers two objectives: minimizing im-

mediate costs (CAPEX) and minimizing costs due to power losses. This makes it possible to perform various

what-if analyses to evaluate the impact of different preferences to CAPEX versus reduction of power losses.

Thanks to the close collaboration with a leading energy company, we have been able to report results on a

set of real-world instances, based on six existing wind parks, studying the economical impact of considering

power losses in the cable routing design phase.

1 INTRODUCTION

With a total global capacity of more than 400 GW

by the end of 2015, wind power is a leading technol-

ogy in the transition away from fossil fuels. Having

a yearly market growth of 15-20%, it is however nec-

essary to face new challenges on a market that is al-

ways more competitive. According to [Gonzlez et al.,

2014] the expenses for electrical infrastructure of a

offshore wind farm account for 15-30% of the over-

all initial costs. Therefore, high-level optimization in

this area is a key factor. In this work we focus on the

cable routing between offshore wind turbines (the so

called inter-array optimization).

The power production of offshore turbines is col-

lected through one or more substations and then con-

veyed to the coast. The cabling will therefore con-

stitute a tree of cables from each substation to the

connected turbines. Different cables with different

costs, capacities and resistances are available on the

market and the task is therefore not only to connect

the turbines in the cheapest possible way, but also to

choose appropriate dimensions of the cables to mini-

mize losses.

Thanks to the collaboration with a leading energy

company it has been possible to build a detailed model

including nearly all the constraints arising in practical

applications, and to evaluate the savings of optimized

layouts on real cases. The resulting optimization tool

has been validated by company experts, and is now

routinely used by the planners.

Wind park cable routing optimization has ob-

tained considerable attention in the last years. Due to

the large number of constraints and the intrinsic com-

plexity of the problem, many studies (i.e. [Dutta and

Overbye, 2011, Gonzlez-Longatt and Wall, 2012, Li

et al., 2008, Zhao et al., 2009]) preferred to use ad-

hoc heuristics. Only a few papers used Mixed Inte-

ger Linear Programming (MILP), notably [Bauer and

Lysgaard, 2015, Fagerfjall, 2010, Dutta, 2012, Berzan

et al., 2011,Hertz et al., 2012,Cerveira et al., 2016,Pil-

lai et al., 2015]. A MILP approach boosted with

heuristics (a so-called mat-heuristic approach) to deal

with large-scale wind parks in an acceptable time

has been recently proposed in [Fischetti and Pisinger,

2016]. The present work is based on [Fischetti and

Pisinger, 2016] but focuses more on real applications

of the optimization model and on its economical im-

pact. Several variants of the problem have been pro-

posed in the literature. To the best of our knowledge

108

Fischetti M. and Pisinger D.

On the Impact of using Mixed Integer Programming Techniques on Real-world Offshore Wind Parks.

DOI: 10.5220/0006190701080118

In Proceedings of the 6th International Conference on Operations Research and Enterprise Systems (ICORES 2017), pages 108-118

ISBN: 978-989-758-218-9

only [Cerveira et al., 2016] has considered power loss

in cables. However, [Cerveira et al., 2016] does not

take into account variable cable loads due to ﬂuc-

tuating wind. [Bauer and Lysgaard, 2015] proposes

an Open Vehicle Routing approach for this problem

adding the planarity constraints on the ﬂy. In this

Open Vehicle Routing version of the problem, only

one cable can enter a turbine, even if this is often

not the case in the reality. In [Bauer and Lysgaard,

2015], the possibility of branching cables in the tur-

bines (as we are doing), is mentioned as a future work.

However, the substation limits, that could be a major

constraint in practical applications, are not considered

in [Bauer and Lysgaard, 2015]. Different approaches

for the cable network design are provided in [Berzan

et al., 2011]. The suggested approach is a divide-and-

conquer heuristic based on the idea of dividing the

big circuit problem into smaller circuit problems. The

proposed MILP model cannot deal with more than 11

turbines. In [Hertz et al., 2012] the cable layout prob-

lem for onshore cases is studied. The onshore cable

problem is similar to the offshore one with the fol-

lowing differences. First of all, the cable can be of

two types: underground cables (connecting turbines

to other turbines or to the above-ground level), and

above-ground cables. In the ﬁrst case, the cables need

to be dug in the ground. Due to the fact that parallel

lines can use the same dug hole, parallel structures are

preferred (until a ﬁxed number). The above-ground

level cables need to follow existing roads. Such con-

straints do not exist in the offshore case.

The main contribution of this paper is to anal-

yse how the inter-array cable routing of real-world

wind farms can be improved by using modern opti-

mization techniques. A particularly challenging as-

pect in the cable routing design, is to understand if

one could limit power losses by optimizing cable rout-

ing. As a general rule, cables with less resistance are

also more expensive, therefore we would like here to

make a proper trade-off between investments and ca-

ble losses. We formulate the optimization problem

with immediate costs (CAPEX) and losses-related

costs as two separate goals. The two objectives can be

merged into a single objective by proper weighing of

the two parts. The weighing factor can be considered

ﬁxed or can vary: this makes it possible to perform

various what-if analyses to evaluate the impact of dif-

ferent preferences (i.e. of different weighing factors).

The latter approach is important in cases where a pos-

itive pay-back is demanded within a short time hori-

zon, or where liquidity problems hinder choosing the

best long-term solution. We report a study of both

approaches on a set of real-world instances.

In order to perform the above analysis, we devel-

oped a MIP approach to optimize the routing. In the

computation of power losses, it is shown that wind

scenarios can be handled efﬁciently as part of data

preprocessing, resulting in a MIP model of tractable

size. Tests on a library of real-life instances proved

that substantial savings can be achieved.

The rest of the paper is organized as follows: Sec-

tion 2 describes our MILP model, ﬁrst presenting a

basic model and then improving and extending the

formulation. In particular, we show how to model

power losses, and propose a precomputing strategy

that is able to handle this non-linearity efﬁciently, thus

avoiding sophisticated quadratic models that would

make our approach impractical. Section 3 compares

our optimized solutions with an existing cable layout

for a real wind farm (Horns Rev 1), showing that mil-

lions of euro can be saved. Section 4 is dedicated to

various what-if analyses. Subsection 4.1 describes the

real-world wind farms that we considered in our tests

while Subsection 4.2 shows the results of our opti-

mization on a testbed of real-world cases, reporting

the impact of considering power losses for all the in-

stances. Subsection 4.3 is dedicated to the Pareto opti-

mality study. Some conclusions are ﬁnally addressed

in Section 5.

2 MATHEMATICAL MODEL FOR

CABLE ROUTING

OPTIMIZATION

2.1 Basic Model

In the present paper we assume that the location of the

turbines has already been deﬁned. We wish to ﬁnd an

optimal cable connection between all turbines and the

given substation(s), minimizing the total cable costs.

The optimization problem considers that:

• the energy ﬂow leaving a turbine must be sup-

ported by a single cable;

• the maximum energy ﬂow (when all the turbines

produce their maximum) in each connection can-

not exceed the capacity of the installed cable;

• different cables, with different capacities, costs

and impedances, can be installed;

• cable crossing should be avoided;

• a given maximum number of cables can be con-

nected to each substation;

• cable losses (dependent on the cable type, the ca-

ble length and the current ﬂow through the cable)

must be considered in the optimization.

On the Impact of using Mixed Integer Programming Techniques on Real-world Offshore Wind Parks

109

We will ﬁrst model the problem without cable

losses and then discuss in Subsection 2.2 how to efﬁ-

ciently express these constraints. We model turbine

positions as nodes of a complete and loop-free di-

rected graph G = (V, A) and all possible connections

between them as directed arcs. Some nodes corre-

spond to the substations that are considered as the

roots of the trees, being the only nodes that collect

energy. Let P

be the power production at node h. We

distinguish between two different types of node:

h ∈



if the h-th node correspond to a turbine

if the h-th node correspond to a substation

Let T denote the set of different cable types that

can be used. Each cable type t has a given capacity k

and unit cost u

, representing the cost per meter of the

cable (CAPEX). Arc costs can therefore be deﬁned as

i, j

= dist(i, j)u

for each arc (i, j) and for each type

t ∈ T , where dist(i, j) is the distance between turbine

i and turbine j. In our model we use the continuous

variables f

i, j

≥ 0 for the maximum ﬂow on arc (i, j).

The binary variables x

i, j

deﬁne cable connections as

i, j

(

1 if arc (i, j) with cable type t is selected

0 otherwise

Finally, variables y

i, j

indicate whether turbines

i and j are connected (with any type of cable).

Note that variables y

i, j

are related to variables x

i, j

∑

t∈T

i, j

= y

i, j

. The overall model becomes:

min

∑

i, j∈V

∑

t∈T

i, j

(1)

s.t.

∑

t∈T

i, j

= y

i, j

i, j ∈ V : j 6= i (2)

∑

i:i6=h

( f

h,i

− f

i,h

) = P

h ∈ V

(3)

∑

t∈T

i, j

≥ f

i, j

i, j ∈ V : j 6= i, (4)

∑

j: j6=h

h, j

= 1 h ∈ V

(5)

∑

j: j6=h

h, j

= 0 h ∈ V

(6)

∑

i6=h

i,h

≤ C h ∈ V

(7)

i, j

∈ {0, 1} i, j ∈ V, t ∈ T (8)

i, j

∈ {0, 1} i, j ∈ V (9)

i, j

≥ 0 i, j ∈ V, j 6= i (10)

The objective function (1) minimizes the total cable

layout cost. Constraints (2) impose that only one type

of cable can be selected for each built arc, and deﬁnes

the y

i, j

variables. Constraints (3) are ﬂow conserva-

tion constraints: the energy (ﬂow) exiting each node h

is equal to the ﬂow entering h plus the power produc-

tion of that node (except if the node is a substation).

Constraints (4) ensure that the ﬂow does not exceed

the capacity of the installed cable, while constraints

(5) and (6) impose that only one cable can exit a tur-

bine and none can exit the substations (tree structure

with root in the substations). Finally, constraints (7)

impose the maximum number of cables (C) that can

enter each substation.

In order to model no-crossing constraints we need

a constraint for each pair of crossings arcs, i.e. a

huge number of constraints. We have, therefore, de-

cided to generate them on the ﬂy, as also suggested

in [Bauer and Lysgaard, 2015]. In other words, the

optimizer considers model (1) - (10) and adds the

following new constraints whenever two established

connections (i, j) and (h, k) cross

i, j

+ y

j,i

+ y

h,k

+ y

k,h

≤ 1. (11)

The reader is referred to [Fischetti and Pisinger, 2016]

for stronger versions of those constraints. Using

this approach, the number of non-crossing constraints

actually added to the model decreases dramatically,

making the model faster to solve. As presented,

the model is able to deal with small size instances

only. In order to produce high quality solutions in

an acceptable amount of time also for big instances

a “matheuristic” framework (as the one proposed in

[Fischetti and Pisinger, 2016]) should be used on top

of this basic model.

2.2 Cable Losses

In this section we propose an extension of the previ-

ous model taking cable losses into account. Let us

consider a generic cable (i, j) of type t, supporting a

current g

i, j

. Power losses increase with the square of

the current, according to the formula:

· dist(i, j)(g

i, j

)

(12)

where R

is the electrical resistance of the 3-phase

cable of type t, in Ω/m. The current g

i, j

obviously

depends on the considered wind scenario. As a con-

sequence, dealing with equation (12) directly in the

model, would imply dealing with non-linearities over

multiple scenarios. Nevertheless, (12) can be sim-

pliﬁed if we assume that all the turbines in the park

have the same power production under the same wind

scenario. This is a fair assumptions since typical

parks are constructed by using only one turbine model

and wake effect is not usually considered in electrical

studies. Under this assumption, the current I

passing

through a generic cable (i, j) of type t under scenario

s, can be expressed as a function of the number f of

turbines supported by the cable as:

PLoss

t, f ,s

= ( f I

)

dist(i, j). (13)

The value f = 1, ...F is limited by the capacity of the

cables. By introducing the dependency on f in our

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems

110

main binary variables (now x

t, f

i, j

) we can re-write our

two objectives as:

min

∑

i, j∈V

∑

t∈T

∑

f ∈F

∑

s∈S

PLoss

t, f ,s

t, f

i, j

(14)

and

min

∑

i, j∈V

∑

t∈T

∑

f ∈F

i, j

t, f

i, j

(15)

where π

is the probability of scenario s. As we have

discussed earlier, minimizing losses can imply an in-

crease of the CAPEX cost, therefore the two objective

must be properly balanced. In some cases (e.g., when

there is no limit on the CAPEX) they can be merged,

by using a converting factor for the loss-related term:

this is the estimated cost for each MW of production

lost over the wind farm lifetime (Net Present Value).

This value (denoted as K) is an input value, that the

designer can set to the desired project-speciﬁc value.

The merged objective function, now expressed in e,

is then:

min

∑

i, j∈V

∑

t∈T

∑

f ∈F

i, j

t, f

i, j

∑

i, j∈V

∑

t∈T

∑

f ∈F

∑

s∈S

PLoss

t, f ,s

t, f

i, j

(16)

We notice that (16) can be rewritten as:

min

∑

i, j∈V

∑

t∈T

∑

f ∈F

dist(i, j)x

t, f

i, j

∑

i, j∈V

∑

t∈T

∑

f ∈F

∑

s∈S

3π

( f I

)

dist(i, j)x

t, f

i, j

min

∑

i, j∈V

∑

t∈T

∑

f ∈F

+ K

∑

s∈S

3π

( f I

)

)dist(i, j)x

t, f

i, j

(17)

The non-linear expressions in the objective func-

tion (17) can actually be handled implicitly in a

pre-processing phase, without changing the original

model (1)-(10) at all, according to the following idea.

We consider the basic model (1)–(10) without cable

losses on a modiﬁed instance where each cable type

is replaced by a series of “subcables” with discretized

capacity and modiﬁed cable cost taking both CAPEX

and revenue losses due to cable losses into account.

Nearly all wind farms are designed for only one

turbine type, hence the maximum power production

of each turbine can be assumed to be 1, meaning

that we can express the cable capacity as the maxi-

mum number of turbines supported. Consider a cer-

tain cable type t that can support up to k

turbines. We

replace it by k

“subcable” types of capacity f = 1, 2,

..., k

whose unit cost is computed by adding both ca-

ble/installation unit costs (u

) and loss costs (denoted

as loss

t, f

) considering the current produced by exactly

f turbines. Note that such unit costs increase with f ,

so the optimal solution will always select the subca-

ble type f supporting exactly the number of turbines

connected, hence the approach is correct.

The above approach allows us to easily consider

multiple wind scenarios without affecting the model

size. This is obtained by precomputing the subcable

costs by just considering a weighted average of the

loss cost under different wind scenarios (and hence

different current productions). To be more speciﬁc, if

we look again at formula (17), we can now precom-

pute the value

loss

t, f

= K

∑

s∈S

3π

( f I

)

(18)

where π

is the probability of scenario s and I

is the

current produced by a single turbine under wind sce-

nario s, assuming negligible wake effect, i.e., all tur-

bines are producing the same amount of energy under

a given wind scenario s. We refer to the next subsec-

tion for a more detailed example of how cable costs

are pre-processed when considering losses. As said,

K is a factor to estimate the value (in e) of the MW

loss, and can be computed as K = K

euro

· 8760 where

euro

is the NPV for a MW/h production over the park

lifetime, and 8760 is the number of hours in a year.

Notice that K

euro

acts as a weighting factor between

the two objectives: minimize CAPEX costs versus

minimize losses.

2.3 Loss Pre-computation

In this section we elaborate on our pre-computing

strategy proposed in the previous session, using a con-

crete example from the real wind park Horns Rev 1.

The park consists of 80 2MW turbines and is located

about 15 km from the Danish shore. This park will be

used as one of our test cases both in Section 3 and 4.

Fixed the turbine layout, one could consider dif-

ferent sets of cables to be used. Different sets can

differ in cable cross section or in voltage (33kV or

66kV generally), which reﬂects in different capacities

and resistances. The set of most adequate cables is se-

lected by the electrical specialists in the company. Of

course, different cables can lead to different solutions,

as we will see in Section 4.

We will now focus on one cable set only, in order

to better illustrate how different wind scenarios are

handled in the pre-processing phase. Changing the

cable data, the process is analogous.

Let us suppose that we are given a set of two ca-

bles: the cheapest one can support ten 2MW turbines

and the most expensive fourteen turbines. This set

of cables will be indicated as cb05 in Section 4. We

are provided with the following table, that reports the

characteristics of the two cable types.

If we want to optimize on CAPEX costs only, we

just need to input to the model the capacity of each

On the Impact of using Mixed Integer Programming Techniques on Real-world Offshore Wind Parks

111

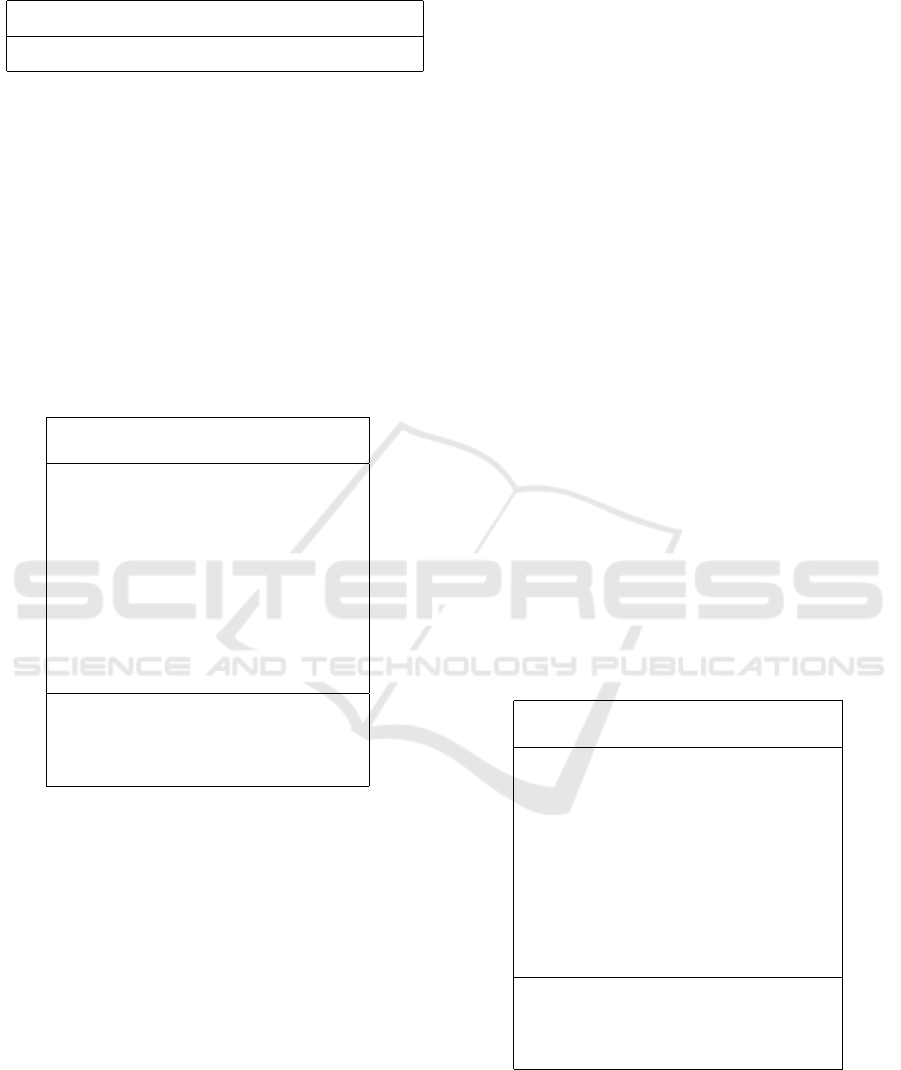
Table 1: Cable information for cb05.

n. of resistance price install. price

cables type 2MW turb. [Ohm/km] [e/m] [e/m]

cb05

1 10 0.13 180 260

2 14 0.04 360 260

cable type and its overall cost (cable price plus instal-

lation cost). In this case, for example, this would be:

• type 1: supports up to 10 turbines with a unit cost

of 440 e/m

• type 2: supports up to 14 turbines with a unit cost

of 620 e/m

Table 2 shows how the model will compute the unit

price (CAPEX only) depending on the number of tur-

bines connected.

Table 2: CAPEX costs for cb05, depending on the number

of turbines connected.

n. of 2MW price

cable type turb. supported [e/m]

1 440

2 440

3 440

4 440

5 440

6 440

7 440

8 440

9 440

10 440

11 620

12 620

13 620

14 620

Notice that, considering CAPEX costs only, the

cost to use one type of cable is independent of how

many turbines it is connected to (up to the capacity

limit).

Let us now consider the losses in our optimization

using the strategy of Subsection 2.2. As we discussed

earlier, the power loss in a cable depends on the cur-

rent passing through it. Since only a discrete number

of turbines can be connected to each cable path, we

can express the current as a function of the number f

of turbines connected (as shown equation (18)) with-

out any loss of precision in the result.

Still referring to equation (18), the losses depend

also on the wind statistics in the site. We can deﬁne a

wind scenario (s) as a wind speed and its probability

to occur (π

). At a given wind speed, a given turbine

will produce a speciﬁc current (I

Wind scenarios can be deﬁned in different ways.

In this paper we used both real measurements and sce-

narios derived from Weibull distributions for the spe-

ciﬁc sites. For the Horns Rev 1 case we are consid-

ering, we had real measurements from the site, i.e., a

wind speed sample each 10 minutes for 10 years. We

grouped all these samples in wind-speed bins of 1m/s,

obtaining 25 wind scenarios (from 1 m/s to 25 m/s).

The probability of each scenario was obtained looking

at the frequency of the speciﬁc wind speed over all the

samples. In our tests we decided to bin our data ev-

ery 1 m/s, following the practice in electrical losses

computations. However this should not be considered

a limit: since the wind scenarios are handled in the

pre-processing phase, the number of scenarios does

not affect the size of the ﬁnal optimization model.

Having computed I

and π

according to the sce-

nario deﬁnition, power losses can now be calculated.

Parameter K

euro

= 690 e/MWh was computed by the

company experts for a wind park lifetime of 25 years,

while resistance R

is deﬁned according to Table 1.

Using equation (18), power loss costs loss

t, f

can be

now precomputed. As shown in (17), the cost con-

sidered in the objective for each cable connection will

need to include the CAPEX costs (u

) and the contri-

bution from losses (loss

t, f

). Therefore the ﬁnal imput

to the optimization tool for Horns Rev 1 with cb05,

will be as shown in Table 3.

Table 3: Precomputed cable prices for cable cb05 (including

installation costs) precomputed considering ﬁxed costs and

power losses for Horns Rev 1.

n. of 2MW price

cable type turb. supported [e/m]

1 441.16

2 442.71

3 445.27

4 448.87

5 453.50

6 459.15

7 465.83

8 473.54

9 482.28

10 492.04

11 639.77

12 643.41

13 647.36

14 651.63

A comparison between Tables 2 and 3 shows the

impact of considering losses on cable prices. While

from a installation perspective the cost for each cable

type is ﬁxed, it now varies depending on how many

turbines are connected. As we will see, this can have

an impact on the optimal cable routing.

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems

112

3 COMPARISON WITH AN

EXISTING LAYOUT

We report in this section a comparison between our

optimized solutions (considering and not considering

losses) and the existing cable routing for Horns Rev 1,

a real-world offshore park located in Denmark. Fig-

ure 1 shows the actual design for Horns Rev 1 (from

[Kristoffersen and Christiansen, 2003]).

Figure 1: Existing cable routing for Horns Rev 1.

Three different types of cables are used: the

thinnest cable supports one turbine only, the medium

supports 8 turbines, and the thickest 16. We estimated

the costs and resistances of these cables based on the

cable cross section. The estimated prices are 85 e/m,

125 e/m and 240 e/m, respectively, plus an estimated

260e/m of installation costs (independent of the ca-

ble type). We ran our CAPEX optimization with the

above prices obtaining the layout in Figure 2. The

optimized layout is signiﬁcantly different from the ex-

isting one. Looking at immediate costs, the optimized

layout is over 1.5 Me less expensive. As already said,

this layout is optimized only on immediate costs, nev-

ertheless if we estimate its value in 25 years (consid-

ering losses) this layout is still more proﬁtable than

the existing one: considering both CAPEX and losses

the optimized layout is 1.6 Me more proﬁtable than

the existing one (Net Present Value) .

By optimizing cable losses, one can further in-

crease the value in the long term. Figure 3 shows

the optimized solution considering losses (thus opti-

mizing the value of the cable route in its lifetime).

Compared with the existing layout (Figure 1), this

new layout is about 1.7 Me (NPV) more proﬁtable

in 25years, and still around 1.5 Me cheaper at con-

Figure 2: Optimized layout for Horns Rev 1 (CAPEX costs

only): this layout results more than 1.5M e more proﬁtable

than the existing one.

Figure 3: Optimized layout for Horns Rev 1 (considering

losses): in the wind park lifetime this layout is estimated to

be more than 1.7Me more proﬁtable than the existing one.

struction time.

Table 4 summarizes the savings of the two opti-

mized layouts compared with the existing one, both

from an immediate cost perspective and from a long-

term perspective: values are expressed in Ke.

The test shows that millions of euros can be saved

using our optimization methods on real parks. In the

next section we want to focus on the other great ad-

vantage of using automatic optimization tools: the

possibility of performing a number of what-if anal-

yses. To the best of our knowledge, this is the ﬁrst de-

On the Impact of using Mixed Integer Programming Techniques on Real-world Offshore Wind Parks

113

Table 4: Savings of optimized solutions compared with the

existing cable routing for Horns Rev 1.

Savings [Ke]

opt mode immediate in 25years

CAPEX 1544 1605

lifetime 1511 1687

tailed study on the impact of different design choices

on the cable routing itself and on its impact on imme-

diate costs (CAPEX) and long term costs.

4 WHAT-IF ANALYSIS

We performed a number of what-if analyses on dif-

ferent real-world wind farms. In particular we were

interest in understanding the impact of considering

power losses in the design phase. We will ﬁrst com-

pare solutions optimized only for CAPEX costs, with

solutions optimized looking at the whole lifetime of

the park. We will then study the usage of differ-

ent types of cable (with different resistances) in both

cases, and the long-term savings compared with the

possible higher investments costs. We will also per-

form a multi-criteria analysis where the user can bal-

ance between initial costs and long-term savings: this

could be of interest, for example, when the company

requests that the higher investment must be paid off

in a limited number of years.

4.1 Test Instances

We tested our model on the real-world instances pro-

posed in [Fischetti and Pisinger, 2016]. They consider

ﬁve different real wind farms in operation in United

Kingdom and Denmark, and one new wind farm un-

der construction. These parks are Horns Rev 1, Ken-

tish Flats, Ormonde, Dan Tysk, Thanet and Horns Rev

This dataset includes old and new parks, with dif-

ferent power ratings and different number of turbines

installed, and therefore represents a good benchmark

for our tests. Each park has one substation with its

own maximum number of connections (C).

In details:

• Horns Rev 1 has 80 turbines Vestas 80-2MW and

C = 10

• Kentish Flats has 30 turbines Vestas 90-3MW. It

is a near-shore wind farm, so it is connected to

the onshore electrical grid without any offshore

substation. Nevertheless, only one export cable is

connected to the shore, therefore the starting point

of the export cable is treated as a substation. We

set C = ∞ as there is no physical substation limi-

tation in this case.

• Ormonde has 30 Senvion 5MW and C = 4

• DanTysk has 80 Siemens 3.6MW and C = 10

• Thanet has 100 Vestas 90-3MW and C = 10

• Horns Rev 3 has 50 Vestas 164-8MW and C = 12

The dataset also includes different sets of cables,

indicated as cb01, cb02, cb03, cb04 and cb05.

The cost of the cables considering power losses

has been precomputed following the strategy pro-

posed in Subsection 2.2. We computed the cable-loss

prices using real measured data (for Horns Rev 1 and

3, Ormonde and DanTysk) and estimations based on

Weibull distributions (Kantish Flats and Thanet).

Each combination of site (i.e. wind farm) and fea-

sible cable set represents an instance in the testbed.

4.2 Impact of Considering Power Losses

The aim of this section is to analyse how cable routing

changes when cable losses are taken into account. We

used the real-world instances presented in the previ-

ous section to perform our tests. We ran our optimiza-

tion tool with a time-limit of 10 hours (Intel Xeon

CPU X5550 at 2.67GHz, using Cplex 12.6) in order

to have high quality solutions (for the small instances

these are the proven optimal solutions).

In all our instances thicker cables are more expen-

sive and have lower resistance. This means that if the

designer of the cable routing aims only at minimizing

the initial costs (CAPEX), then he/she would go for

the cheapest cables satisfying the load, and increase

the power losses. On the contrary, focusing only on

minimizing the losses, one would prefer to increase

the initial costs. Using the methods explained in Sec-

tion 2.2 we aim at ﬁnding the optimal balance be-

tween the two objectives, looking at the overall costs

in the life time of the park.

As it can be seen from Table 5, the amount of sav-

ings varies from instance to instance, depending on

the prices, on the restrictions of the speciﬁc wind farm

and on the structure of the layout.

It should be noticed that the layout optimized on

the lifetime always provides some savings in the long

term, but the amount highly varies from case to case.

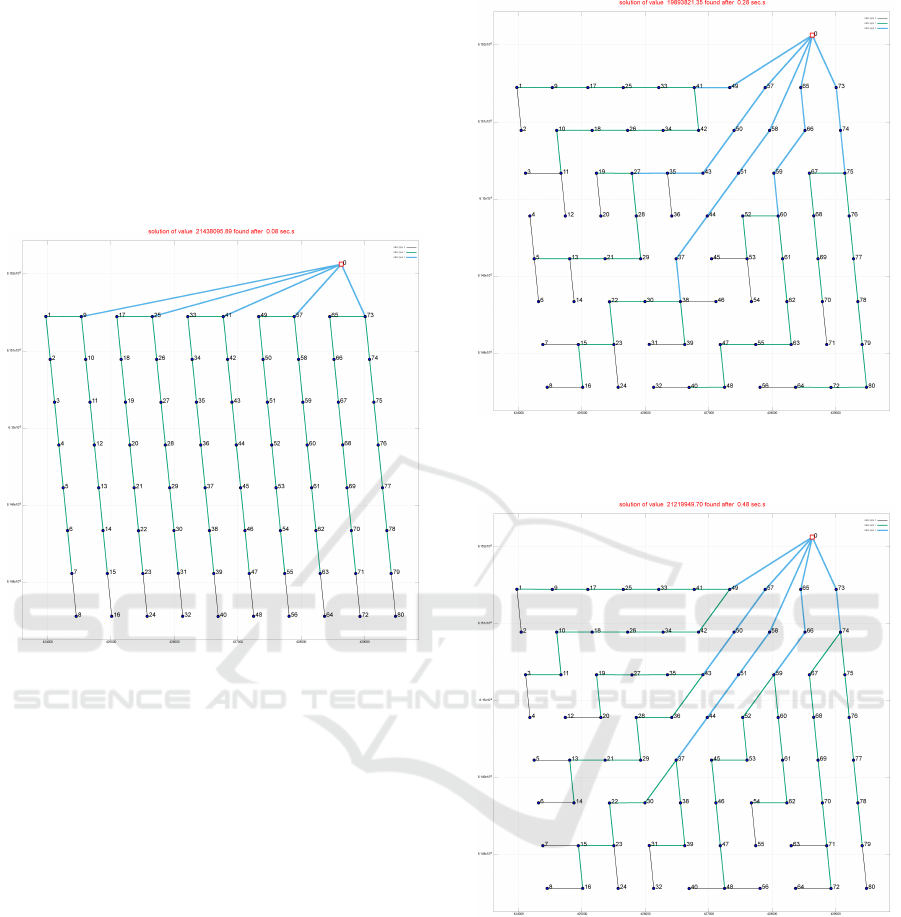
In Figure 4 the case of Horns Rev 3 with cable set

cb04 is shown.

It is seen that both the structure of the

cable routing and the usage of thicker cables (green in

the ﬁgure) increases in the loss-optimized layout.

This is a preliminary layout from Vattenfall, not neces-

sarily reﬂecting the ﬁnal layout.

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems

114

Table 5: Increase in the initial investment and long term

savings for our test instances (Net Present Value). The ﬁrst

two columns denote the wind farm and possible cable types.

The next column shows how much the investment is in-

creased in the layout taking cable losses into account. In all

test cases this amount is paid back in 25 years, and the addi-

tional savings by using the lifetime-optimized cable layout

are shown in the last column.

wind farm cable set increase in savings

initial investment [Ke] in 25y [Ke]

Horns Rev 1 cb01 1 23

cb02 24 60

cb05 103 56

Kentish Flats cb01 2 3

cb02 1 4

cb04 19 8

cb05 5 1

Ormonde cb03 9 0

cb04 19 16

DanTysk cb01 115 21

Thanet cb04 15 92

cb05 1 19

Horns Rev 3 cb04 42 172

cb05 682 208

In this case the loss-optimized layout is 41 Ke

more expensive at construction time (with respect to

the CAPEX optimized layout). Nevertheless, in 25

years, this amount is paid back and another 172 Ke

are saved (NPV).

We now try to investigate how the optimizer is re-

structuring the layout in order to have savings in the

long run. As already noticed, every wind farm is dif-

ferent, so one cannot deﬁne a rule of thumb to design

a good cable routing. Nevertheless, observing our

layouts, we noticed a different proportion in the usage

of the cable types (black and green in the ﬁgures). In

particular, all the CAPEX solutions minimize the use

of the expensive cables: looking only at the immedi-

ate costs, it is always preferable to go for the cheap-

est cable when possible, even creating longer connec-

tions. When optimizing considering losses, instead,

cables with less resistance become more appealing,

even if they are more expensive. In the Horns Rev 1

instance, for example, going from CAPEX optimized

to lifetime-optimized the usage of type 1 cables de-

creases (from 55.5% of the total length to 40.3%) and

the usage of type 2 cables increases (from 44.5 to

59.7%).

In Table 6 we report the cable usage (percentage

of the total cable length) for all our test-bed solutions.

All in all, it can be observed from our results on

real-world instances that in most cases it is convenient

to invest in cables with lower resistance. The cable

route and the type of cable selection for each connec-

tion is not an obvious choice and an optimization tool

is necessary to determine it.

Figure 4: Optimized cable routing for Horns Rev 3, using

cable set cb04. We imposed that cable type 2 can support

5 turbines only twice. The top layout is optimized only on

CAPEX, the second is also considering power losses.

4.3 Bi-objectivity Tests

As discussed in Subsection 2.2, our problem has to

balance between two opposite objectives: minimiz-

ing immediate costs and minimizing revenue losses

in the long run. As we have seen in the previous tests,

these two objectives are not always aligned since the

more expensive cables have lower resistances (so less

losses). The balancing factor between the two objec-

tives is K

euro

, that represents the price of energy (Net

Present Value). Setting K

euro

to zero, for example,

means that there is no revenue from selling energy,

therefore it does not matter to have losses, but it is

On the Impact of using Mixed Integer Programming Techniques on Real-world Offshore Wind Parks

115

Table 6: Analysis on the usage of different types of cables

when optimizing considering or not considering losses. The

last three columns report the usage of the different cable

types as percentage of the total cable length of that layout.

ID wind farm cable set opt mode length per cable type [%]

Type 1 Type 2 Type 3

1 Horns Rev 1 cb01 capex 55.1 40.1 4.8

2 lifetime 53.6 41.7 4.7

3 cb02 capex 57.4 42.6

4 lifetime 44.1 55.9

5 cb05 capex 100.0 0.0

6 lifetime 87.7 12.3

7 Kentish Flats cb01 capex 66.4 33.6 0.0

8 lifetime 66.1 33.9 0.0

9 cb02 capex 66.4 33.6

10 lifetime 60.8 39.2

12 cb04 capex 90.1 9.9

13 lifetime 90.1 9.9

14 cb05 capex 95.6 4.4

15 lifetime 95.6 4.4

16 Ormonde cb03 capex 69.6 30.4

17 lifetime 76.7 23.3

18 cb04 capex 66.9 33.1

19 lifetime 67.4 32.6

20 DanTysk cb01 capex 39.0 19.4 41.7

21 lifetime 38.7 22.5 38.8

26 Thanet cb04 capex 86.3 13.7

27 lifetime 82.7 17.3

28 cb05 capex 71.9 28.1

29 lifetime 71.9 28.1

30 Horns Rev 3 cb04 capex 57.4 42.6

31 lifetime 60.7 39.3

32 cb05 capex 51.8 48.2

33 lifetime 52.6 47.4

instead important only to minimize immediate costs.

This corresponds to the case that we called ”CAPEX

optimized” in the previous tests. On the contrary, set-

ting K

euro

to a high value, implies that big revenue

can be earned selling more energy, so it is very im-

portant to minimize losses (whatever initial costs this

could imply). The balance between the two objec-

tives, in practice, is set by deﬁning the parameter K

euro

for the speciﬁc project of interest. This is a value

known by the designer, and varies from project to

project. A realistic value for K

euro

has been used in

the tests of the previous subsection (this value consid-

ered WACC, subsidies for 10 years of operations and

estimated market price). Nevertheless, one could be

interested in studying how the balance between im-

mediate costs and long term costs varies when vary-

ing K

euro

. As a practical example, one could be in-

terested in optimizing CAPEX and losses at the same

time, but being sure to pay off the extra investment

in a short time. We considered, in this test, Horns

Rev 3 with cable set cb04. For K

euro

= 0 we have our

CAPEX solution of Figure 4 (top), for K

euro

= 690

e/MWh we have our life-time losses optimized so-

lution of Figure 4 (bottom). Company experts es-

timated 690 e/MWh to be a realistic value for the

energy earning over 25 years of operation (expected

lifetime of a wind park). We asked them to recom-

pute this value assuming that we want a return of

investment in a shorter time. They recomputed it

to be K

euro

= 176 for two years, K

euro

= 252 for 3

years, K

euro

= 321 for 4 years, and K

euro

= 386 for

5 years. Setting our balancing factor K

euro

to these

values translates in imposing that extra CAPEX cost

will be paid back in 2, 3, 4 or 5 years, respectively.

We recomputed the cable costs according to these dif-

ferent values of K

euro

and re-optimized the layout ac-

cordingly. Once the optimized layouts were found,

we re-evaluated them with K

euro

= 0 to evaluate their

CAPEX costs and K

euro

= 690 to estimate their cost

in 25 years. Table 7 shows these ﬁgures. For K

euro

higher than 321 e/MWh the layout is not changing

any more. This means that in the lifetime optimized

solution (K

euro

= 690) all the additional CAPEX costs

were actually paid back in 4 years of operation. In

Figure 5 we plot the values from Table 7: the value of

the different layouts is decomposed into its CAPEX

(x axis) and lifetime-cost part (y axis). The ﬁrst point

(the “+” on the leftmost extreme) represents the value

for the CAPEX optimized solution (K

euro

= 0): it has

the lowest immediate cost, but the highest cost on the

long run. Proceeding from left to right, the next “+”s

represent the solutions optimized over 2, 3, 4 and 5

years respectively. From 4 years on, the layout is not

changing any more, and equals the solution optimized

on the park lifetime (K

euro

= 690), therefore all these

layouts are represented at the same coordinates in the

plot in Figure 5.

Table 7: Bi-objective analysis for Horns Rev 3 with cable

set cb04: changing solutions varying the parameter K

euro

immediate cost total lifetime revenue loss due

[ke] cost [ke] to power losses [ke]

0 47283 52663 5379

176 47291 52551 5259

252 47309 52508 5199

321 47325 52490 5165

386 47325 52490 5165

690 47325 52490 5165

5 CONCLUSIONS

In this paper we used a Mixed Integer Linear Pro-

gramming (MILP) approach to optimize inter-array

offshore cable routing considering both the immedi-

ate cost of the cables and their power losses during the

wind farm lifetime. We proved the importance of us-

ing sophisticated optimization tools for this problem.

We compared the optimized solution with an exist-

ing cable layout, proving that millions of euros can be

saved in the given case. We also performed different

what-if analyses taking power losses into considera-

tion. Thanks to our optimization methods, we have

been able, for the ﬁrst time, to quantify the impact of

considering losses when designing the cable connec-

tion of a wind farm. We performed these analyses on

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems

116

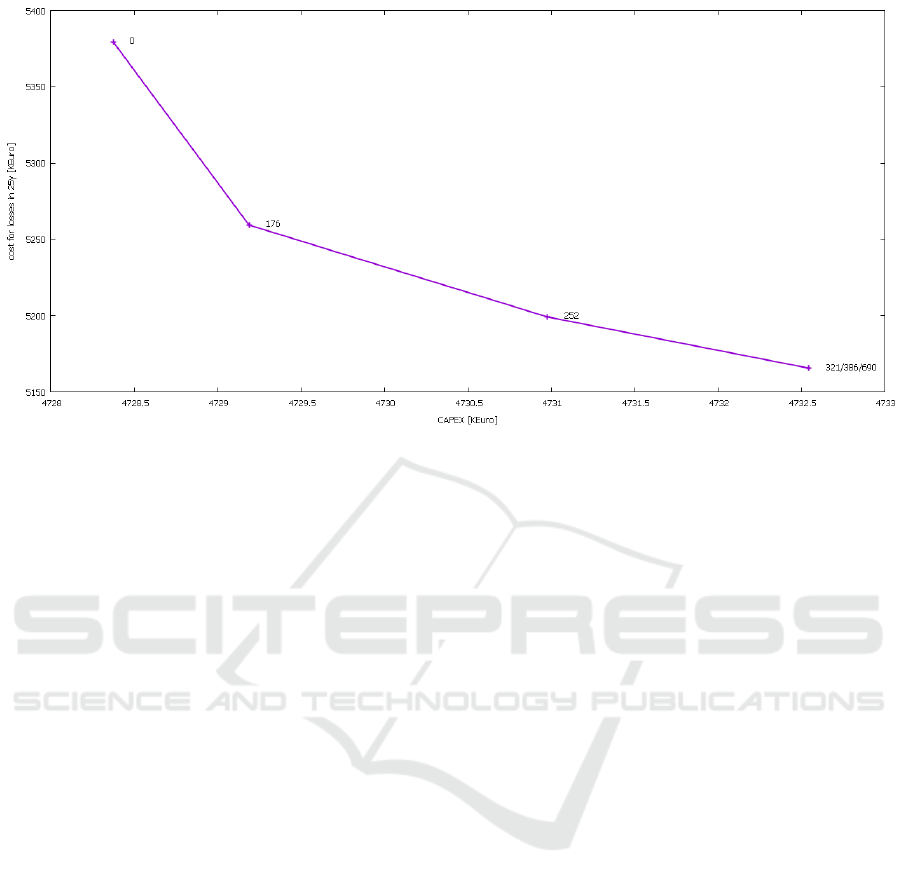
Figure 5: Bi-objective analysis from Table 7. Each “+” corresponds to a layout optimized for a given value of K

euro

(speciﬁed

beside each “+”) and its coordinates correspond to its immediate cost (x axis) and costs in 25years (y axis). The layouts

optimized with K

euro

= 321, 386, and 690 are the same.

a number of real-world instances, analysing the be-

haviour of the solutions. In general, we observed that

it is convenient to invest in cables with less resistance

in order to reduce power losses, even if these cables

are more expensive at construction time. We used our

testbed to evaluate the proﬁtability of the new solu-

tions, both in terms of CAPEX and revenue in the

long term. Finally, we performed a Pareto optimal-

ity analysis by varying the balancing parameter K

euro

This corresponds to giving more or less importance to

power losses in the objective function, and is of great

importance for designers. In this way, indeed, they

can evaluate the return of investment and the impact

of their assumptions on the long-term energy price,

when designing their cable routing.

ACKNOWLEDGEMENTS

This work was supported by Innovation Fund Den-

mark. The authors would like to thank Jesper Runge

Kristoffersen, Kenneth Skaug, Thomas Hjort and Iu-

lian Vranceanu from Vattenfall BA Wind who helped

in deﬁning the cable routing constraints and the cable

losses.

REFERENCES

Bauer, J. and Lysgaard, J. (2015). The offshore wind farm

array cable layout problem: a planar open vehicle

routing problem. Journal of the Operational Research

Society, (66.3):360–368.

Berzan, C., Veeramachaneni, K., McDermott, J., and Reilly,

U. O. (2011). Algorithms for cable network design

on large-scale wind farms. Technical report. Mas-

sachusetts Institute of Technology.

Cerveira, A., Sousa, A. D., Pires, E. J. S., and Baptista,

J. (2016). Optimal cable design of wind farms: The

infrastructure and losses cost minimization case. IEEE

Transactions on Power Systems, (31.6):4319 – 4329.

Dutta, S. (2012). Data Mining and Graph Theory Focused

Solutions to Smart Grid Challenges. PhD thesis, Uni-

versity of Illinois.

Dutta, S. and Overbye, T. J. (2011). A clustering based wind

farm collector system cable layout design. In Power

and Energy Conference at Illinois (PECI), pages 1–6.

Fagerfjall, P. (2010). Optimizing wind farm layout: more

bang for the buck using mixed integer linear program-

ming.

Fischetti, M. and Pisinger, D. (2016). Optimizing wind farm

cable routing considering power losses. Technical re-

port. Danish Technical University.

Gonzlez, J., Payn, M., Santos, J., and Gonzlez-Longatt, F.

(2014). A review and recent developments in the op-

timal wind-turbine micro-siting problem. Renewable

and Sustainable Energy Reviews, (30):133–144.

Gonzlez-Longatt, F. M. and Wall, P. (2012). Optimal

electric network design for a large offshore wind

farm based on a modiﬁed genetic algorithm approach.

IEEE Systems Journal, (6.1):164–172.

Hertz, A., Marcotte, O., Mdimagh, A., Carreau, M., and

Welt, F. (2012). Optimizing the design of a wind farm

collection network. Information Systems and Opera-

tional Research, (50.2):95–104.

Kristoffersen, J. and Christiansen, P. (2003). Horns rev off-

On the Impact of using Mixed Integer Programming Techniques on Real-world Offshore Wind Parks

117

shore windfarm: Its main controller and remote con-

trol system. Wind Engineering, (27.5):351–359.

Li, D., He, C., and Fu, Y. (2008). Optimization of internal

electric connection system of large offshore wind farm

with hybrid genetic and immune algorithm. In Third

International Conference on Electric Utility Dereg-

ulation and Restructuring and Power Technologies

(DRPT2008), pages 2476–2481.

Pillai, A., Chick, J., Johanning, L., and Laleu, M. K. V. D.

(2015). Offshore wind farm electrical cable layout op-

timization. Engineering Optimization, (47.12):1689–

1708.

Zhao, M., Chen, Z., and Blaabjerg, F. (2009). Optimisa-

tion of electrical system for offshore wind farms via

genetic algorithm. IET Renewable Power Generation

3, (3.2):205–216.

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems

118