A Multi-agent Approach to Model and Analyze the Behavior of Vessels in

the Maritime Domain

Mathias Anneken

, Yvonne Fischer

and J

urgen Beyerer

1,2

Vision and Fusion Laboratory, Karlsruhe Institute of Technology (KIT), Karlsruhe, Germany

Fraunhofer Institute of Optronics, System Technologies and Image Exploitation (Fraunhofer IOSB), Karlsruhe, Germany

Keywords:

Multi-agent System, Anomaly Detection, Nash Bargaining Solution, Maritime Domain.

Abstract:

The automatic detection of suspicious behavior is one important part in order to support operators in surveil-

lance tasks. Therefore, an approach to model the behavior of objects by using multi-agent systems is intro-

duced. As each object has its own objectives and desires to fulﬁll, these are modeled as utility functions. The

actions of the objects are estimated by using the Nash bargaining solution. Consequently, it is implied, that

the objects are cooperating in order to achieve an optimal result for themselves. First results for this algorithm

are shown by using examples from the maritime domain. On the one hand, the algorithm is used to calculate

an anomaly score. On the other hand, it is used to predict the movement of vessels.

1 INTRODUCTION

Surveillance tasks, like monitoring and controlling air

or sea trafﬁc, have an increasing importance in times

of terrorist threats, refugee crises, and illegal immi-

gration. In order to prevent disasters, it is crucial to

identify anomalies and suspicious behavior of objects

and vessels in the monitored areas.

The increasing amount of data, captured by a mul-

titude of different sensors, permits the identiﬁcation

of relevant situations. But at the same time, they can

overstrain the operators with too much information.

To counter this information overload, it is important

to support the operators by helping them to focus on

the crucial events. Therefore, an algorithm is intro-

duced to help operators in surveillance tasks to im-

prove their situation awareness, and to support them

during the decision making process.

There are two types of important situations for op-

erators. On the one hand, a speciﬁc situation with im-

portant characteristics can be recognized during the

surveillance tasks (e.g. a pirate attack). On the other

hand, the behavior of some objects deviates from the

expected behavior in the area. The operators have to

react upon both situations and assess their next steps.

The proposed algorithm will model the behavior

of objects by utilizing the Nash bargaining solution

in combination with an agent-based approach. Each

monitored object will be represented by an agent, with

its own utility function and objectives to achieve. As

normal behavior implies, that the agents will cooper-

ate with each other or at least will follow the rules and

laws, a cooperative game theoretic model seems to be

a valid approach to model the behavior.

First, related work with a focus on agent-based

models for surveillance and controlling tasks, and

anomaly detection in particular in the maritime do-

main is described. Then, the proposed algorithm with

the modeling of the bargaining game and the utility

function is introduced. Afterwards, the algorithm is

evaluated by using situations from real sea trafﬁc. Fi-

nally, a conclusion and a forecast on future work are

given.

2 RELATED WORK

One of the ﬁrst applications of multi-agent systems

for control and surveillance tasks is described by

Ljungberg and Lucas (1992) by introducing the Op-

timal Aircraft Sequencing using Intelligent Schedul-

ing (OASIS) system. OASIS is designed to optimize

air trafﬁc and airport capacities by estimating appro-

priate instructions to achieve an efﬁcient sequence of

arriving and departing aircraft. Hence, each aircraft is

modeled as an agent together with ﬁve global agents.

The agents are designed in a believe-desire-intention

architecture.

Yang et al. (2007) describe how agents in a bar-

gaining game can optimize the evasive maneuver of

200

Anneken M., Fischer Y. and Beyerer J.

A Multi-agent Approach to Model and Analyze the Behavior of Vessels in the Maritime Domain.

DOI: 10.5220/0006192002000207

In Proceedings of the 9th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2017), pages 200-207

ISBN: 978-989-758-219-6

ships. For the estimation of the optimal course to

avoid a collision, a negotiation system is used: Each

vessel in a possible collision is modeled as an agent.

Based on a monotonic concession protocol the agents

have to make concessions in order to achieve an

agreement. If they cannot agree on a strategy, a so-

lution based on another algorithm will be used.

A multi-agent system for the maritime surveil-

lance is presented by Mano et al. (2010). Each vessel

in an area is monitored by an individual agent. These

agents estimate the criticality value for the assigned

vessel as a combination of different rules with respect

to the vessel’s state and the area around the vessel. As

the conditions in the monitored area will evolve, it is

designed as an adaptive system.

Agogino and Tumer (2012) introduce a multi-

agent system for managing air trafﬁc ﬂow. Reinforce-

ment learning methods are used in order to reduce

congestion. Each agent is responsible for a speciﬁc

area. For each plane passing the area, the responsi-

ble agent has to chose its action: to change the dis-

tance between airplanes, to order delays, or to reroute

an aircraft. The system is evaluated by using simula-

tions.

Dynamic Bayesian networks are used by Fischer

et al. (2014) in order to model situations of interest,

e.g. smuggling of goods. As a dynamic Bayesian net-

work has several parameters, which domain experts

might not be able to intuitively choose, Fischer et al.

developed an approach to estimate these parameters

by giving only a few more intuitive parameters as in-

put. For the evaluation, a speciﬁc situation is modeled

and results for different sets of parameters are given.

Two different kinds of similarity measures are

analysed by de Vries and van Someren (2014). On

the one hand, alignment measures such as dynamic

time warping, and, on the other hand, measures based

on the integral between two trajectories are used.

Both types of measures are utilized in kernel meth-

ods for clustering and classiﬁcation tasks as well as

for anomaly detection. For the evaluation, a dataset

from the maritime domain is used.

Soleimani et al. (2015) assume, that vessels in the

maritime domain take the shortest possible route be-

tween the start harbor and the destination. Therefore,

they use the A* algorithm to generate a reference tra-

jectory, which is compared to the real path of a vessel.

If the deviation is large, the vessel’s behavior is con-

sidered an anomaly.

As the amount of data processed in surveillance

tasks can be huge, Cazzanti et al. (2015) show how

big data technologies can help to face the arising chal-

lenges. They use these methods to handle incoming

data efﬁciently and to do geospatial analyses on the

stored data.

An algorithm for the identiﬁcation of anomalies in

spatio-temporal data based on b-spline interpolation

is introduced by Anneken et al. (2016). They use the

control points of the b-spline representation of a tra-

jectory as a feature vector for different machine learn-

ing methods. As the training data is annotated, the

machine learning algorithm will be trained to identify

two classes, the normal and abnormal. The whole al-

gorithm is evaluated on a dataset from the maritime

domain.

Milleﬁori et al. (2016) developed a method to pre-

dict the state of vessels under way in open sea. They

use an Ornstein-Uhlenbeck process in order to esti-

mate the long-term state. During their evaluation,

they compare the Ornstein-Uhlenbeck based method,

with a classic approach based on a white noise ran-

dom process on the velocity.

3 ALGORITHM

A bargaining game

B = (N, P, c) (1)

is deﬁned by the set of players N = {1, . . . , n}, the

payoff space P ⊂ R

and the conﬂict or disagreement

point c ∈ P. The conﬂict point represents the payoff c

which will be obtained by the player i, if no agreement

is reached.

Each player i ∈ N has its own strategy space S

. A

strategy for i is denoted by s

∈ S

. The set of possible

strategy combinations is then given by S = S

× ··· ×

. The payoff for a player i ∈ N is given by the utility

function u

: S → R. The whole payoff vector for a

strategy combination s ∈ S is given by u : S → R

3.1 Nash Bargaining Solution

The Nash bargaining solution as introduced by Nash

(1950) satisﬁes the following axioms: pareto optimal-

ity, independece of irrelevant alternatives, symmetry,

and invariance to afﬁne transformations. These ax-

ioms are said to characterize a fair solution of a bar-

gaining game. It can be shown, that for a bargaining

game as given in equation (1) the solution to the opti-

mization problem

max

∏

i=1

− c

) (2)

s.t.: u ∈ P

≥ c

∀i ∈ N

satisﬁes these axioms. The objective function in equa-

tion (2) is called Nash product. Unlike for example

A Multi-agent Approach to Model and Analyze the Behavior of Vessels in the Maritime Domain

201

the Kalai-Smorodinsky bargaining solution, this con-

cept can deal directly with n > 2 players.

Here, the optimization problem is solved by us-

ing the differential evolution algorithm introduced by

Storn and Price (1997). This method does not guar-

antee an optimal solution, but compared to other al-

gorithms, the gradient of the problem is not used for

the optimization process.

3.2 Game Theoretic Model of Sea

Trafﬁc Behavior

The behavior of the players in a game theoretic model

depends mainly on the chosen utility function u and

the solution concept. Here, the Nash bargaining so-

lution is used to identify the optimal strategy for the

players.

The state of a player i ∈ N at the time t is given by

its position p

t,i

= (p

t,i,lon

, p

t,i,lat

), speed v

t,i

and head-

ing φ

t,i

. Here, the heading is counted anti-clockwise.

The speed is limited to v

i,max

Furthermore, each player follows a route consist-

ing of multiple waypoints, and each player wants to

reach a destination p

i,d

. No player desires a collision,

and each player wants to follow its route and reach its

destination as fast as possible.

The position of each player is georeferenced.

Thus, if it is not denoted otherwise, the great-circle

distance will be used for the distance calculations.

The distance between the points a and b is indicated

by d

gcd

(a, b).

3.2.1 Strategies

Each vessel can change its speed and heading during

each timestep. Therefore, a simple motion model is

used, which consists of the change in velocity d

v,i

∈

[−1, 1] and the change of the heading d

φ,i

∈ [−

For the next timestep t + 1 the speed and heading will

be set accordingly to

t+1,i

= d

v,i

· v

i,max

t+1,i

= φ

t,i

+ d

φ,i

The position is estimated by using the great circle

through p

t,i

with φ

t+1,i

and the distance covered by

t+1,i

. Thus, each player i follows a strategy

= (d

φ,i

, d

v,i

3.2.2 Utility Function

The utility function is given by four components,

which deﬁne a desirable behavior of a player. The

total utility is then given by the mean value of the

applicable components, and is shown for an example

constellation in Fig. 1.

Figure 1: The mean of u

, u

, and u

for a player at (50, 50)

on the route (0, 50) → (150, 50) and a stationary player at

(100, 50) with the parameter set to δ

= 20 and δ

= 25.

The gradient from black to white represent the utility of the

player. The euclidean norm is used for the distance calcula-

tions.

Distance to Destination. The utility for reaching

the destination is given by the ratio between the dis-

tance to the destination at the timestep t + 1 and the

distance to the destination at the timestep t

gcd

t+1,i

, p

i,d

)

gcd

t,i

, p

i,d

)

A visual representation of the utility function is shown

in Fig. 2.

Figure 2: u

for a player at (50, 50) on the route (0, 50) →

(150, 50). The gradient from black to white represent the

utility of the player. The euclidean norm is used for the

distance calculations.

Distance to Route. For this utility function, the dis-

tance d

r,i

between the route and p

t+1,i

has to be calcu-

lated. The desire of each player to stay in the proxim-

ity of its route can be conﬁgured by the parameter δ

This results in the following utility function

(

1, if d

r,i

≤ δ

−

· d

r,i

+ 2, otherwise

which is shown in Fig. 3.

Distance to other Players. The utility for a player

i for keeping distance to other players is given by

= min

j∈N, j6=i



min



gcd

t+1,i

, p

t+1, j

)

, 1



ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

202

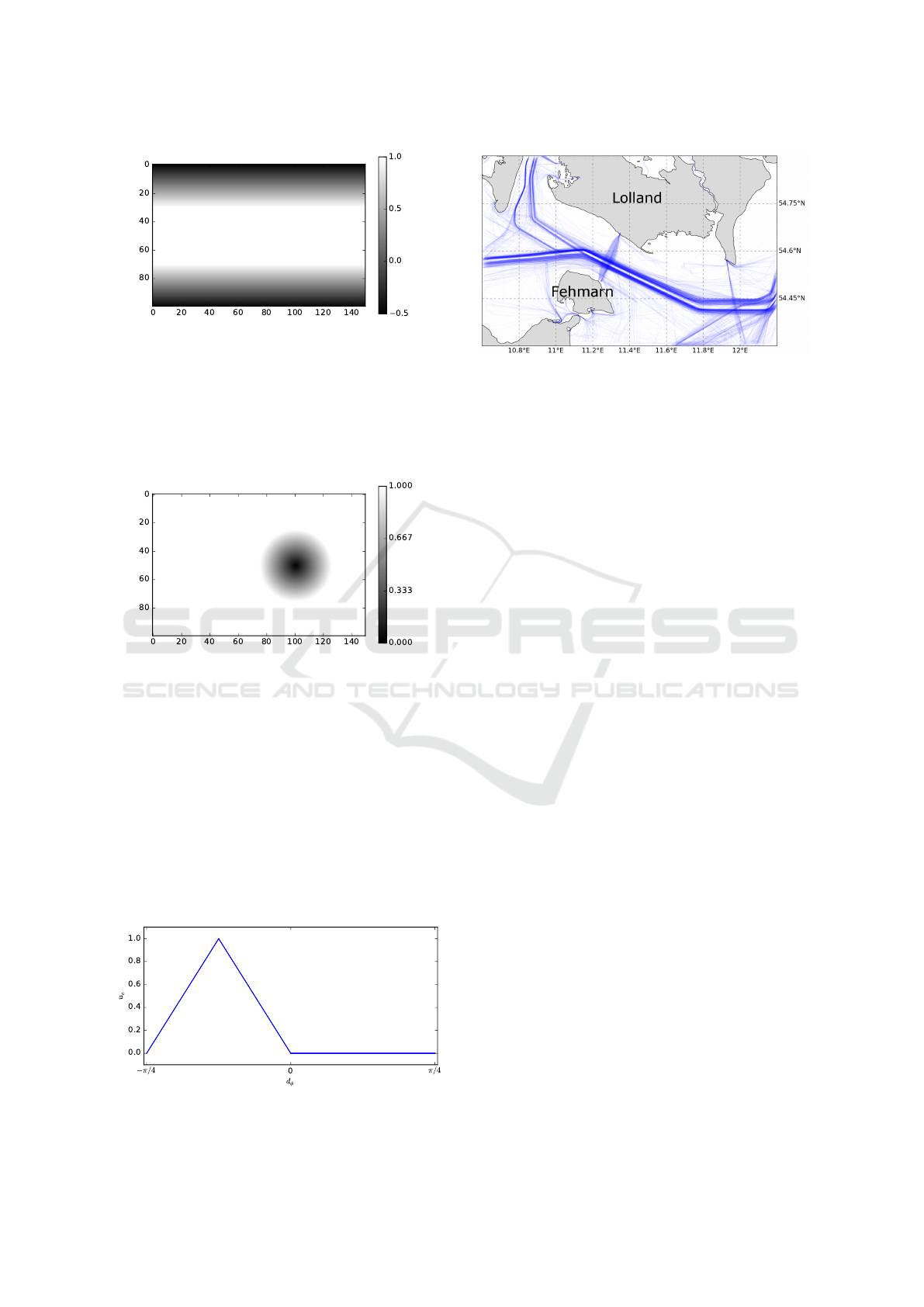
Figure 3: u

for a player at (50, 50) going on the route

(0, 50) → (150, 50) and δ

= 20. The gradient from black

to white represent the utility of the player. The euclidean

norm is used for the distance calculations.

The parameter δ

is used to adjust the distance, a

player likes to keep to the other players. The utility

function is depicted in Fig. 4.

Figure 4: u

for a player at (50, 50) and a stationary player

at (100, 50) and δ

= 25. The gradient from black to white

represent the utility of the player. The euclidean norm is

used for the distance calculations.

Collision Avoidance. As no player with normal be-

havior desires a collision with another player, a mech-

anism has to be implemented to cover this problem by

providing a utility function enforcing the avoidance

of collisions. As the behavior of motorized vessels

is analyzed, the vessels have to avoid a collision by

turning to starboard (right hand side). Therefore, the

utility function u

given in Fig. 5 is used. It will be

applied, if an immediate collision is detected.

Figure 5: u

as a function of d

Figure 6: Sea trafﬁc between Lolland (Denmark) in the

north and Fehmarn (Germany) in the south in a time pe-

riod of one week. The blue lines represent trajectories of

vessels. The grey polygons are landmasses.

4 EVALUATION

For the evaluation, a dataset from the maritime do-

main is used as shown in Fig. 6. The ship trafﬁc

was recorded in a period of 7 days starting from 16th

May 2011 using the Automatic Identiﬁcation System

(AIS). In order to analyze the performance to mimic

the behavior of the vessels, some situations with inter-

esting behavior are selected. In particular, it is the in-

teraction of cargo and tanker vessels with ferries and

passenger ships. Ferries and passenger ships sail, e.g.,

between the islands Lolland (Denmark) and Fehmarn

(Germany). The route of cargo and tanker vessels in-

tersects with the ferry route. Therefore, the vessels

have to avoid collisions with each other.

In the following, some situations are picked from

the dataset for evaluating the prediction capabilities

as well as the suitability as an anomaly detection al-

gorithm.

4.1 Prediction

For the ﬁrst situation same route, two vessels are sail-

ing into the same direction on the same route, but with

different speed. Thus, one vessel overtakes the other.

The simulation results are shown in Fig. 7, Fig. 8, and

Fig. 9. In the ﬁrst two ﬁgures, the results with varying

values for δ

are shown. A low value for δ

means,

that the vessels drive in closer proximity to each other.

In Fig. 9, the utility function for one player is shown.

The blue circle in this ﬁgure is the current position of

the blue vessel, while the green circle represents the

next position of the green vessel.

The inﬂuence of u

and u

can be clearly seen in

Fig. 9, as the route is light grey in the bottom right

corner of the ﬁgure with a gradient to white in the

top left corner. Around the next position of the green

A Multi-agent Approach to Model and Analyze the Behavior of Vessels in the Maritime Domain

203

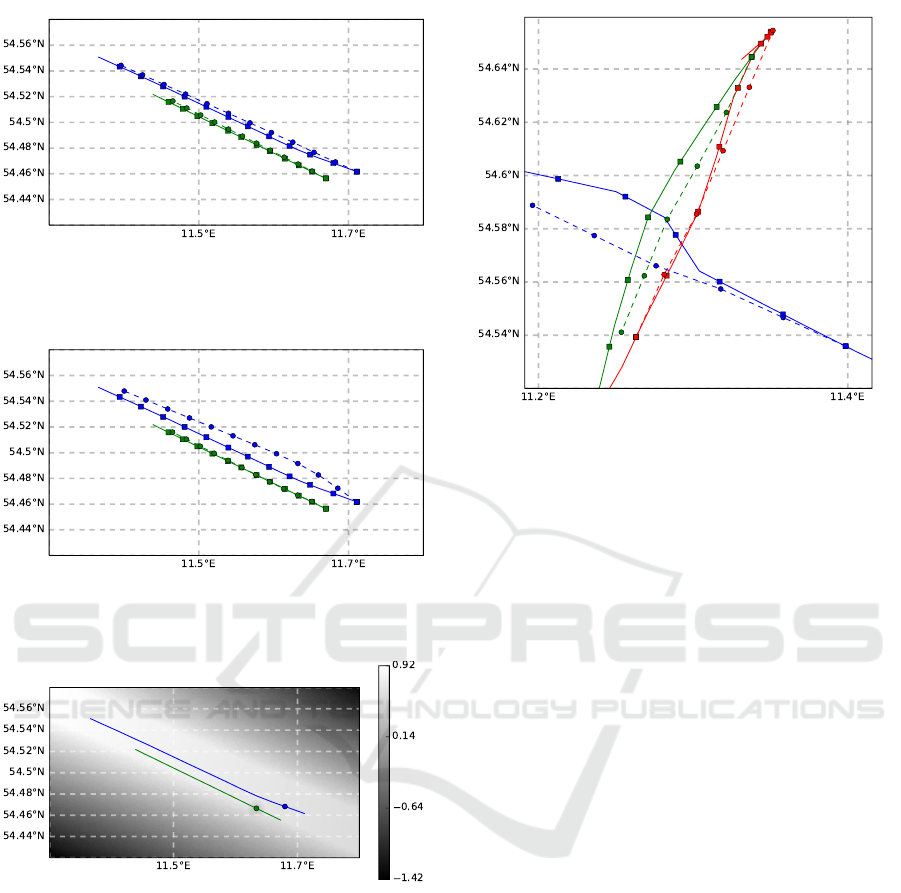
Figure 7: Situation same route. δ

= 1.5. Stroked lines with

squares show the recorded behavior, while dashed lines with

circles show the simulation results.

Figure 8: Situation same route. δ

= 2.5. Stroked lines with

squares show the recorded behavior, while dashed lines with

circles show the simulation results.

Figure 9: Situation same route. δ

= 1.5. Stroked lines

show the recorded behavior. The blue circle represents the

current position of the blue vessel, while the green one rep-

resents the next estimated position of the green vessel. The

backgroundcolor indicates the utility for the blue vessel.

The higher the utility, the brighter the color.

vessel, the inﬂuence of u

can be identiﬁed as a circle

around the green vessel. All in all, the behavior in this

simple situation can be reproduced by the proposed

approach.

For the situation same route, the two vessels do

not need to avoid a direct collision, as both vessels

can sail with enough distance to each other. Thus, for

the next situation, the vessels need to take action in

order to avoid a collision. The situation crossing as

well as the simulation results can be seen in Fig. 10,

Figure 10: Situation crossing, for δ

= 2. Stroked lines with

squares show the recorded behavior, while dashed lines with

circles show the simulation results.

Fig. 11, and Fig. 12. The blue vessel in this situation

sails from right to left, while the green vessels starts

at the top going to the bottom of the ﬁgure and the red

one vice versa.

As different values for δ

are chosen for the simu-

lation, the impact of this parameter is easily visible.

For δ

= 2.5, the simulation closely resembles the

real path of the objects as depicted in Fig. 11, the

other simulations show a different behavior. In Fig.

10, no possible collision is detected. Therefore, the

vessels drive on a straight line without evasive ma-

neuvers. In Fig. 12, the vessels also detect no possible

collision, but the distance each vessel likes to keep be-

tween each other is quite large. Thus, the vessels take

maneuvers in order to maintain their distance. This

results in the red vessel passing the green on the op-

posing side compared to the recorded data.

4.2 Anomaly Detection

Only the situation crossing is used for the anomaly

detection. In order to estimate an anomaly score for

the behavior of the vessels, a new game is started for

each timestep. To give a better insight into the de-

cision process, the utility functions for the different

players at one timestep are depicted in Fig. 13, Fig.

14 and Fig. 15. As the green and blue vessel detect a

possible collision, the starboard of their utility func-

tion yields a greater payoff. In all cases, the utility

gained through keeping on the route is clearly visible.

Further, the higher payoff for decreasing the distance

to the destination as well as the lower payoff in the

proximity of other players is evident.

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

204

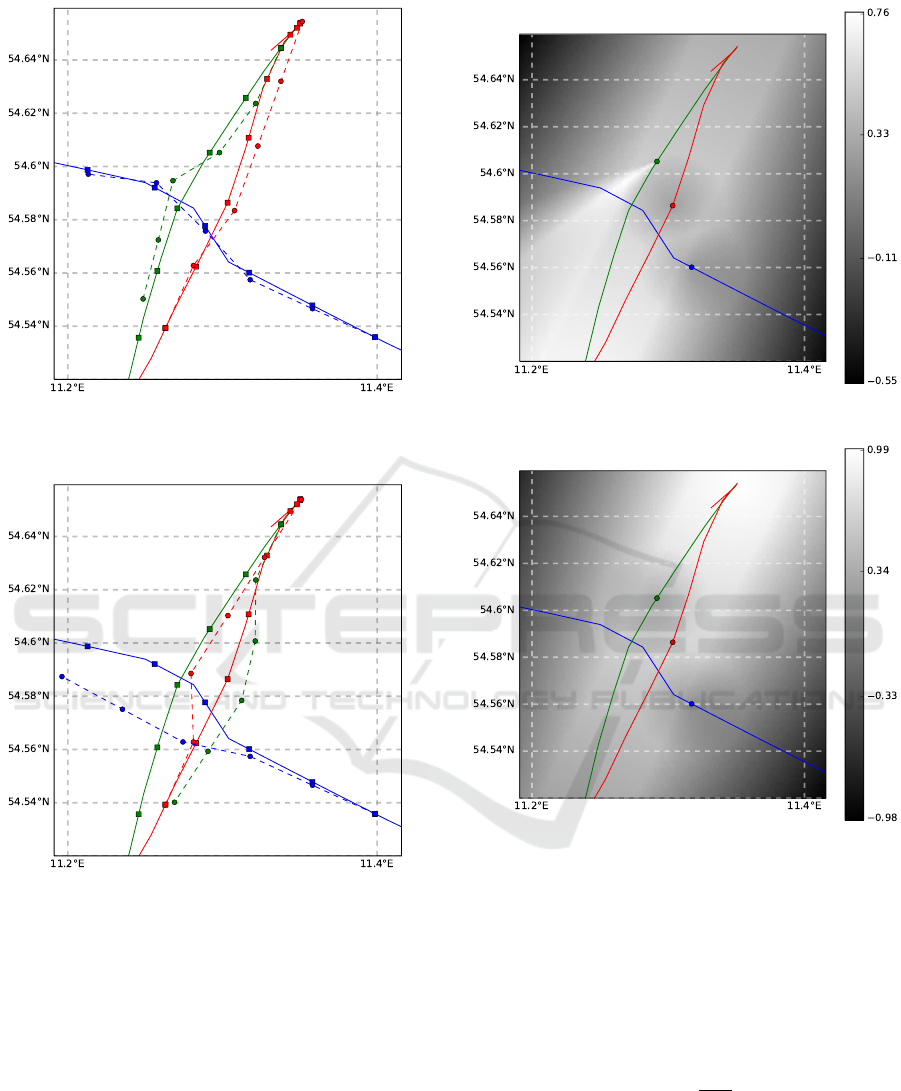
Figure 11: Situation crossing, for δ

= 2.5. Stroked lines

with squares show the recorded behavior, while dashed lines

with circles show the simulation results.

Figure 12: Situation crossing, for δ

= 3. Stroked lines with

squares show the recorded behavior, while dashed lines with

circles show the simulation results.

The simulation results for each timestep are shown

in Fig. 16. In addition, the possible next steps for the

blue player at one timestep are depicted by showing

the utility. For its calculations, the other vessels are

supposed to behave like the Nash bargaining solution

would suggest. Because of an imminent collision in

case of just going straight, the starboard side of the

vessel yields higher payoffs in this timestep.

An anomaly score estimates whether the real be-

havior of the vessels is similar to the simulation.

There are several ways to incorporate different scores

and distance measures into an anomaly score. One is

using the distance between the real position and the

Figure 13: Situation crossing. Utility for the green vessel.

Figure 14: Situation crossing. Utility for the red vessel.

simulated, another is using the payoffs for each indi-

vidual vessel of the real behavior (u

real

) and the simu-

lated one (u

sim

In Fig. 17, the distance between the predicted

position and the real position for each timestep in

the situation crossing is shown, while in Fig. 18,

an anomaly score is given for each vessel at each

timestep by calculating

a = 1 −

real

sim

As seen in Fig. 17, the distance between the simu-

lated and real behavior is always quite large. Compar-

ing the two ﬁgures, it is evident, that the deviation in

the position does not imply, that the simulation or the

real data are actually a better solution for an individ-

ual player: Except for the second timestep, the utility

A Multi-agent Approach to Model and Analyze the Behavior of Vessels in the Maritime Domain

205

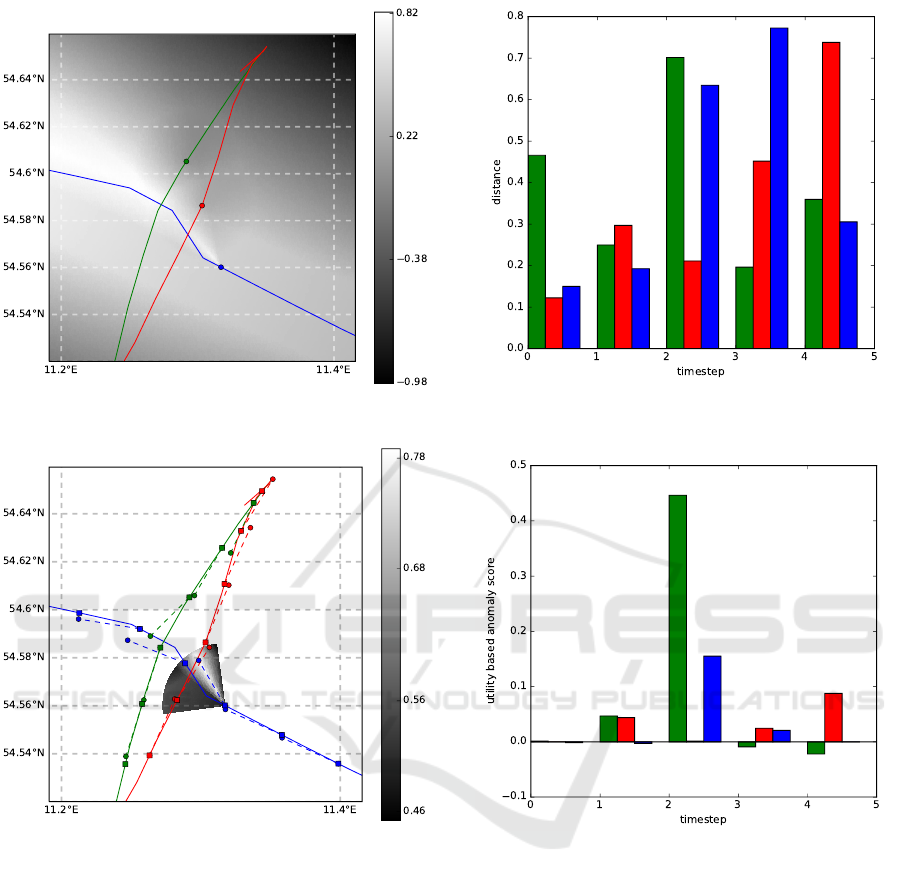
Figure 15: Situation crossing. Utility for the blue vessel.

Figure 16: Situation crossing, δ

= 2.5. Stroked lines with

squares show the recorded behavior, while dashed lines with

circles show the simulation results. The area with the gradi-

ent represents the possible utility for the blue vessel at one

timestep.

ratio is always smaller than 0.1.

Furthermore, the utility gained for the real action

is sometimes greater than the simulated one, because

of the estimated maximal speed. As the Nash bargain-

ing solution estimates a fair payoff distribution for all

players, there might be a strategy for a single player

yielding a greater payoff for this player.

All in all, the utility ratio seems to be a valid

anomaly score. E.g., a high anomaly score for the

green and blue vessel are estimated in the second

timestep in Fig. 18. In Fig. 16, the green and blue

vessel do not keep as much distance in the second

timestep, as they do in the other ones. Therefore, this

Figure 17: Situation crossing. Distance in km between the

simulated and the recorded position for each timestep.

Figure 18: Situation crossing. Utility ratio for each

timestep.

behavior can actually be seen as an anomaly. In the

third timestep the blue vessel also deviates from the

simulation, but the utility deviates only slightly.

5 CONCLUSIONS

It is shown, that the introduced approach can be used

to simulate the behavior of vessels in the maritime do-

main. This is achieved by comparing the simulation

results with the recorded trajectories of up to three

different vessels interacting with each other.

Furthermore, a method to use the simulation for

anomaly detection is given. The ratio between the

gained utility in the simulation and in the recorded

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

206

data seems to be a good measure for the anomaly

score.

6 FUTURE WORK

So far, the algorithm was evaluated by using simula-

tions as well as real data. But only situations with up

to three different vessels are analyzed. As the inter-

action of more vessels can be of interest in areas with

dense trafﬁc, this should be evaluated.

The parameters for the utility function and the

possible strategies are chosen by hand. Therefore,

a system for choosing the parameters automatically

based on recorded data should be developed. Addi-

tionally, a more realistic motion model might increase

the accuracy of the algorithm.

As the algorithm itself does not consider the ap-

plication domain, it should be possible to develop the

utility functions for other domains. Further, the al-

gorithm could be used to model suspicious behavior.

Therefore, another interesting topic is the develop-

ment and evaluation of an utility function describing

a speciﬁc situation of interest.

ACKNOWLEDGEMENTS

The underlying projects to this article are funded by

the WTD 81 of the German Federal Ministry of De-

fense. The authors are responsible for the content of

this article.

REFERENCES

Agogino, A. K. and Tumer, K. (2012). A multiagent ap-

proach to managing air trafﬁc ﬂow. Autonomous

Agents and Multi-Agent Systems, 24(1):1–25.

Anneken, M., Fischer, Y., and Beyerer, J. (2016). Anomaly

detection using b-spline control points as feature

space in annotated trajectory data from the maritime

domain. In Proceedings of the 8th International

Conference on Agents and Artiﬁcial Intelligence, vol-

ume 2, pages 250–257.

Cazzanti, L., Milleﬁori, L. M., and Arcieri, G. (2015). A

document-based data model for large scale computa-

tional maritime situational awareness. In Big Data

(Big Data), 2015 IEEE International Conference on,

pages 1350–1356.

de Vries, G. K. D. and van Someren, M. (2014). An analysis

of alignment and integral based kernels for machine

learning from vessel trajectories. Expert Systems with

Applications, 41(16):7596 – 7607.

Fischer, Y., Reiswich, A., and Beyerer, J. (2014). Model-

ing and recognizing situations of interest in surveil-

lance applications. In Cognitive Methods in Situation

Awareness and Decision Support (CogSIMA), 2014

IEEE International Inter-Disciplinary Conference on,

pages 209–215.

Ljungberg, M. and Lucas, A. (1992). The oasis air trafﬁc

management system. In Proceedings of the Second

Paciﬁc Rim International Conference on Artiﬁcial In-

telligence, PRICAI 92, Seoul, Korea.

Mano, J.-P., Georg

e, J.-P., and Gleizes, M.-P. (2010). Adap-

tive Multi-agent System for Multi-sensor Maritime

Surveillance, pages 285–290. Springer Berlin Heidel-

berg, Berlin, Heidelberg.

Milleﬁori, L. M., Braca, P., Bryan, K., and Willett, P.

(2016). Long-term vessel kinematics prediction ex-

ploiting mean-reverting processes. In 2016 19th In-

ternational Conference on Information Fusion (FU-

SION), pages 232–239.

Nash, J. F. (1950). The bargaining problem. Econometrica,

18(2):155–162.

Soleimani, B. H., Souza, E. N. D., Hilliard, C., and Matwin,

S. (2015). Anomaly detection in maritime data based

on geometrical analysis of trajectories. In Information

Fusion (Fusion), 2015 18th International Conference

on, pages 1100–1105.

Storn, R. and Price, K. (1997). Differential evolution – a

simple and efﬁcient heuristic for global optimization

over continuous spaces. Journal of Global Optimiza-

tion, 11(4):341–359.

Yang, C., Hu, Q., and Shi, C. (2007). Automated colli-

sion resolution for vessel trafﬁc management by us-

ing cooperative multi-agent negotiation. In 2007 7th

International Conference on ITS Telecommunications,

pages 1–6.

A Multi-agent Approach to Model and Analyze the Behavior of Vessels in the Maritime Domain

207