Quantification of De-anonymization Risks in Social Networks
Wei-Han Lee
1
, Changchang Liu
1
, Shouling Ji
2,3
, Prateek Mittal
1
and Ruby Lee
1
1
Princeton University, Princeton, U.S.A
2
Georgia Institute of Technology, Atlanta, U.S.A
3
Zhejiang University, Hangzhou, China
Keywords:
Structure-based De-anonymization Attacks, Anonymization Utility, De-anonymization Capability,
Theoretical Bounds.
Abstract:
The risks of publishing privacy-sensitive data have received considerable attention recently. Several de-
anonymization attacks have been proposed to re-identify individuals even if data anonymization techniques
were applied. However, there is no theoretical quantification for relating the data utility that is preserved by
the anonymization techniques and the data vulnerability against de-anonymization attacks.
In this paper, we theoretically analyze the de-anonymization attacks and provide conditions on the utility
of the anonymized data (denoted by anonymized utility) to achieve successful de-anonymization. To the
best of our knowledge, this is the first work on quantifying the relationships between anonymized util-
ity and de-anonymization capability. Unlike previous work, our quantification analysis requires no as-
sumptions about the graph model, thus providing a general theoretical guide for developing practical de-
anonymization/anonymization techniques.
Furthermore, we evaluate state-of-the-art de-anonymization attacks on a real-world Facebook dataset to show
the limitations of previous work. By comparing these experimental results and the theoretically achievable
de-anonymization capability derived in our analysis, we further demonstrate the ineffectiveness of previous
de-anonymization attacks and the potential of more powerful de-anonymization attacks in the future.
1 INTRODUCTION
Individual users’ data such as social relationships,
medical records and mobility traces are becoming in-
creasingly important for application developers and
data-mining researchers. These data usually contain
sensitive and private information about users. There-
fore, several data anonymization techniques have
been proposed to protect users’ privacy (Hay et al.,
2007), (Liu and Terzi, 2008), (Pedarsani and Gross-
glauser, 2011).
The privacy-sensitive data that are closely re-
lated to individual behavior usually contain rich graph
structural characteristics. For instance, social net-
work data can be modeled as graphs in a straight-
forward manner. Mobility traces can also be mod-
eled as graph topologies according to (Srivatsa and
Hicks, 2012). Many people nowadays have accounts
through various social networks such as Facebook,
Twitter, Google+, Myspace and Flicker. Therefore,
even equipped with advanced anonymization tech-
niques, the privacy of structural data still suffers from
de-anonymization attacks assuming that the adver-
saries have access to rich auxiliary information from
other channels (Backstrom et al., 2007), (Narayanan
and Shmatikov, 2008), (Narayanan and Shmatikov,
2009), (Srivatsa and Hicks, 2012), (Ji et al., 2014),
(Nilizadeh et al., 2014). Narayanan et al. (Narayanan
and Shmatikov, 2009) effectively de-anonymized a
Twitter dataset by utilizing a Flickr dataset as auxil-
iary information based on the inherent cross-site cor-
relations. Nilizadeh et al. (Nilizadeh et al., 2014)
exploited the community structure of graphs to de-
anonymize social networks. Furthermore, Srivatsa
et al. (Srivatsa and Hicks, 2012) proposed to de-
anonymize a set of location traces based on a social
network.
However, to the best of our knowledge, there
is no work on theoretically quantifying the data
anonymization techniques to defend against de-
anonymization attacks. In this paper, we aim to the-
oretically analyze the de-anonymization attacks in
order to provide effective guidelines for evaluating
the threats of future de-anonymization attacks. We
126
Lee, W-H., Liu, C., Ji, S., Mittal, P. and Lee, R.
Quantification of De-anonymization Risks in Social Networks.
DOI: 10.5220/0006192501260135
In Proceedings of the 3rd International Conference on Information Systems Security and Privacy (ICISSP 2017), pages 126-135
ISBN: 978-989-758-209-7
Copyright
c
 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

aim to rigorously evaluate the vulnerabilities of ex-
isting anonymization techniques. For an anonymiza-
tion approach, not only the users’ sensitive informa-
tion should be protected, but also the anonymized
data should remain useful for applications, i.e., the
anonymized utility should be guaranteed. Then, un-
der what range of anonymized utility, is it possible
for the privacy of an individual to be broken? We will
quantify the vulnerabilities of existing anonymization
techniques and establish the inherent relationships
between the application-specific anonymized utility
and the de-anonymization capability. Our quantifi-
cation not only provides theoretical foundations for
existing de-anonymization attacks, but also can serve
as a guide for designing new de-anonymization and
anonymization schemes. For example, the compari-
son between the theoretical de-anonymization capa-
bility and the practical experimental results of current
de-anonymization attacks demonstrates the ineffec-
tiveness of existing de-anonymization attacks. Over-
all, we make the following contributions:
• We theoretically analyze the performance
of structure-based de-anonymization attacks
through formally quantifying the vulnerabilities
of anonymization techniques. Furthermore, we
rigorously quantify the relationships between the
de-anonymization capability and the utility of
anonymized data, which is the first such attempt
to the best of our knowledge. Our quantification
provides theoretical foundations for existing
structure-based de-anonymization attacks, and
can also serve as a guideline for evaluating
the effectiveness of new de-anonymization and
anonymization schemes through comparing their
corresponding de-anonymization performance
with our derived theoretical bounds.
• To demonstrate the ineffectiveness of existing de-
anonymization attacks, we implemented these at-
tacks on a real-world Facebook dataset. Exper-
imental results show that previous methods are
not robust to data perturbations and there is a sig-
nificant gap between their de-anonymization per-
formance and our derived theoretically achiev-
able de-anonymization capability. This analysis
further demonstrates the potential of developing
more powerful de-anonymization attacks in the
future.
2 RELATED WORK
2.1 Challenges for Anonymization
Techniques
Privacy preservation on structural data has been stud-
ied extensively. The naive method is to remove
users’ personal identities (e.g., names, social secu-
rity numbers), which, unfortunately, is rather vul-
nerable to structure-based de-anonymization attacks
(Backstrom et al., 2007), (Narayanan and Shmatikov,
2008), (Narayanan and Shmatikov, 2009), (Hay et al.,
2008), (Liu and Terzi, 2008), (Srivatsa and Hicks,
2012), (Ji et al., 2014), (Sharad and Danezis, 2014),
(Sharad and Danezis, 2013), (Nilizadeh et al., 2014),
(Buccafurri et al., 2015). An advanced mechanism, k-
anonymity, was proposed in (Hay et al., 2008), which
obfuscates the attributes of users so that each user is
indistinguishable from at least k − 1 other users. Al-
though k-anonymity has been well adopted, it still
suffers from severe privacy problems due to the lack
of diversity with respect to the sensitive attributes
as stated in (Machanavajjhala et al., 2007). Differ-
ential privacy (Dwork, 2006), (Liu et al., 2016) is
a popular privacy metric that statistically minimizes
the privacy leakage. Sala et al. in (Sala et al.,
2011) proposed to share a graph in a differentially
private manner. However, to enable the applicabil-
ity of such an anonymized graph, the differential pri-
vate parameter should not be large, which would thus
make their method ineffective in defending against
structure-based de-anonymization attacks (Ji et al.,
2014). Hay et al. in (Hay et al., 2007) proposed a
perturbation algorithm that applies a sequence of r
edge deletions followed by r other random edge in-
sertions. However, their method also suffers from
structure-based de-anonymization attacks as shown in
(Nilizadeh et al., 2014).
In summary, existing anonymization techniques
are subject to two intrinsic limitations: 1) they are
not scalable and thus would fail on high-dimensional
datasets; 2) They are susceptible to adversaries that
leverage the rich amount of auxiliary information to
achieve structure-based de-anonymization attacks.
2.2 De-anonymization Techniques
Structure-based de-anonymization was first intro-
duced in (Backstrom et al., 2007), where both active
and passive attacks were discussed. However, the lim-
itation of scalability reduces the effectiveness of both
attacks.
(Narayanan and Shmatikov, 2008) utilized the
Internet movie database as the source of back-
ground knowledge to successfully identify users’
Quantification of De-anonymization Risks in Social Networks
127

Netflix records, uncovering their political prefer-
ences and other potentially sensitive information. In
(Narayanan and Shmatikov, 2009), the authors fur-
ther de-anonymized a Twitter dataset using a Flickr
dataset as auxiliary information. They proposed the
popular seed identification and mapping propagation
process for de-anonymization. In order to obtain the
seeds, they assume that the attacker has access to a
small number of members of the target network and
can determine if these members are also present in
the auxiliary network (e.g., by matching user names
and other contextual information). The authors in
(Srivatsa and Hicks, 2012) captured the WiFi hotspot
and constructed a contact graph by connecting users
who are likely to utilize the same WiFi hotspot for
a long time. Based on the fact that friends (or peo-
ple with other social relationships) are likely to ap-
pear in the same location, they showed how mobility
traces can be de-anonymized using an auxiliary so-
cial network. However, their de-anonymization ap-
proach is rather time-consuming and may be compu-
tationally infeasible for real applications. In (Sharad
and Danezis, 2013), (Sharad and Danezis, 2014),
Sharad et al. studied the de-anonymization attacks
on ego graphs with graph radius of one or two and
they only studied the linkage of nodes with degree
greater than 5. As shown in previous work (Ji et al.,
2014), nodes with degree less than 5 cannot be ig-
nored since they form a large portion of the original
real-world data. Recently, (Nilizadeh et al., 2014)
proposed a community-enhanced de-anonymization
scheme for social networks. The community-level de-
anonymization is first implemented for finding more
seed information, which would be leveraged for im-
proving the overall de-anonymization performance.
Their method may, however, suffer from the serious
inconsistency problem of community detection algo-
rithms.
Most de-anonymization attacks are based on the
seed-identification scheme, which either relies on the
adversary’s prior knowledge or a seed mapping pro-
cess. Limited work has been proposed that requires
no prior seed knowledge by the adversary (Pedarsani
et al., 2013),(Ji et al., 2014). In (Pedarsani et al.,
2013), the authors proposed a Bayesian-inference ap-
proach for de-anonymization. However, their method
is limited to de-anonymizing sparse graphs. (Ji et al.,
2014) proposed a cold-start optimization-based de-
anonymization attack. However, they only utilized
very limited structural information (degree, neighbor-
hood, top-K reference distance and sampling close-
ness centrality) of the graph topologies.
Ji et al. further made a detailed comparison for the
performance of existing de-anonymization techniques
in (Ji et al., 2015b).
2.3 Theoretical Work for
De-anonymization
Despite these empirical de-anonymization methods,
limited research has provided theoretical analysis for
such attacks. The authors in (Pedarsani and Gross-
glauser, 2011) conducted preliminary analysis for
quantifying the privacy of an anonymized graph G
according to the ER graph model (Erd
˝
os and R
´
enyi,
1976). However, their network model (ER model)
may not be realistic, since the degree distribution of
the ER model (follows the Poisson distribution) is
quite different from the degree distributions of most
observed real-world structural data (Newman, 2010),
(Newman, 2003).
Ji et al. in (Ji et al., 2014) further consid-
ered a configuration model to quantify perfect de-
anonymization and (1−ε)-perfect de-anonymization.
However, their configuration model is also not gen-
eral for many real-world data structures. Furthermore,
their assumption that the anonymized and the aux-
iliary graphs are sampled from a conceptual graph
is not practical since only edge deletions from the
conceptual graph have been considered. In reality,
edge insertions should also be taken into considera-
tion. Besides, neither (Pedarsani and Grossglauser,
2011) nor (Ji et al., 2014) formally analyzed the re-
lationships between the de-anonymization capability
and the anonymization performance (e.g., the utility
performance for the anonymization schemes).
Note that our theoretical analysis in Section 4
takes the application-specific utility definition into
consideration. Such non-linear utility analysis makes
the incorporation of edge insertions to our quantifi-
cation rather nontrivial. Furthermore, our theoretical
quantification does not make any restrictive assump-
tions about the graph model. Therefore, our theo-
retical analysis would provide an important guide for
relating de-anonymization capability and application-
specific anonymizing utility.
Further study on de-anonymization attacks can be
found in (Fabiana et al., 2015), (Ji et al., 2015a), (Ko-
rula and Lattanzi, 2014). These papers provide the-
oretically guaranteed performance bounds for their
de-anonymization algorithms. However, their derived
performance bounds can only be guaranteed under re-
stricted assumptions of the random graph, such as ER
model and power-law model. We will show the ad-
vantage of our analysis over these approaches where
our analysis requires no assumptions or constraints on
the graph model as these approaches required.
ICISSP 2017 - 3rd International Conference on Information Systems Security and Privacy
128

3 SYSTEM MODEL
We model the structural data (e.g., social networks,
mobility traces, etc.) as a graph, where the nodes rep-
resent users who are connected by certain relation-
ships (social relationships, mobility contacts, etc.).
The anonymized graph can be modeled as G
a
=
(V
a
,E
a
), where V
a
= {i|i is an anonymized node} is
the set of users and E
a
= {e
a
(i, j)|e
a
(i, j) is the re-
lationship between i ∈ V
a
and j ∈ V
a
} is the set of
relationships. Here, e
a
(i, j) = 1 represents the exis-
tence of a connecting edge between i and j in G
a
, and
e
a
(i, j) = 0 represents the non-existence of such an
edge. The neighborhood of node i ∈ V
a
is N
a
(i) =
{ j|e
a
(i, j) = 1} and the degree is defined as |N
a
(i)|.
Similarly, the auxiliary structural data can also
be modeled as a graph G
u
= (V
u
,E
u
) where V
u
is
the set of labelled (known) users and E
u
is the set
of relationships between these users. Note that the
auxiliary (background) data can be easily obtained
through various channels, e.g., academic data mining,
online crawling, advertising and third-party applica-
tions (Narayanan and Shmatikov, 2009; Pedarsani and
Grossglauser, 2011; Pham et al., 2013; Srivatsa and
Hicks, 2012).
A de-anonymization process is a mapping σ :
V
a
→ V
u
. ∀i ∈ V
a
, its mapping under σ is
σ(i) ∈ V
u
∪ {⊥}, where ⊥ indicates a non-existent
(null) node. Similarly, ∀e
a
(i, j) ∈ E
a
, σ(e
a
(i, j)) =
e
u
(σ(i),σ( j)) ∈ E
u
∪ {⊥}. Under σ, a successful de-
anonymization on i ∈ V
a
is defined as σ(i) = i, if
i ∈ V
u
or σ(i) =⊥, otherwise. For other cases, the
de-anonymization on i fails.
3.1 Attack Model
We assume that the adversary has access to G
a
=
(V
a
,E
a
) and G
u
= (V
u
,E
u
). G
a
= (V
a
,E
a
) is the
anonymized graph and the adversary can only get ac-
cess to the structural information of G
a
. G
u
= (V
u
,E
u
)
is the auxiliary graph and the adversary already knows
all the identities of the nodes in G
u
. In addition, we do
not assume that the adversary has other prior informa-
tion (e.g., seed information). These assumptions are
more reasonable than most of the state-of-the-art re-
search (Narayanan and Shmatikov, 2009; Srivatsa and
Hicks, 2012; Nilizadeh et al., 2014).
4 THEORETICAL ANALYSIS
In this section, we provide a theoretical analysis for
the structure-based de-anonymization attacks. Un-
der any anonymization technique, the users’ sensi-
tive information should be protected without signif-
icantly affecting the utility of the anonymized data
for real systems or research applications. We aim
to quantify the trade-off between preserving users’
privacy and the utility of anonymized data. Un-
der what range of anonymized utility, is it possible
for the privacy of an individual to be broken (i.e.,
for the success of de-anonymization attacks)? To
answer this, we quantify the limitations of existing
anonymization schemes and establish an inherent re-
lationship between the anonymized utility and de-
anonymization capability. Our theoretical analysis
incorporates an application-specific utility metric for
the anonymized graph, which further makes our rigor-
ous quantification useful for real world scenarios. Our
theoretical analysis can serve as an effective guide-
line for evaluating the performance of practical de-
anonymization/anonymization schemes (will be dis-
cussed in Section 5).
First, we assume that there exists a conceptually
underlying graph G = (V,E) with V = V
a
∪ V
u
and
E is a set of relationships among users in V , where
e(i, j) = 1 ∈ E represents the existence of a connect-
ing edge between i and j, and e(i, j) = 0 ∈ E rep-
resents the non-existence of such an edge. Conse-
quently, G
a
and G
u
could be viewed as observable
versions of G by applying edge insertions or dele-
tions on G according to proper relationships, such
as ‘co-occurrence’ relationships in Gowalla (Pham
et al., 2013). In comparison, previous work (Ji et al.,
2014; Pedarsani and Grossglauser, 2011) only consid-
ers edge deletions which is an unrealistic assumption.
For edge insertions from G to G
a
, the process is:
∀e(i, j) = 0 ∈ E, e(i, j) = 1 appears in E
a
with prob-
ability p
add
a
, i.e., Pr(e
a
(i, j) = 1|e(i, j) = 0) = p
add
a
.
The probability of edge deletion from G to G
a
is p
del
a
,
i.e., Pr(e
a
(i, j) = 0|e(i, j) = 1) = p
del
a
. Similarly, the
insertions and deletions from G to G
u
can be char-
acterized with probabilities p
add
u
and p
del
u
. Further-
more, we assume that both the insertion/deletion re-
lationship of each edge is independent of every other
edge. Furthermore, this model is intuitively reason-
able since the three graphs G, G
a
, G
u
are related
with each other. In addition, our model is more rea-
sonable than the existing models in (Ji et al., 2014;
Pedarsani and Grossglauser, 2011) because we take
both edge deletions and insertions into consideration.
Note that the incorporation of edge insertion is non-
trivial in our quantification of non-linear application-
specific utility analysis. Our quantification analysis
would therefore contribute to relating the real world
application-specific anonymizing utility and the de-
anonymization capability.
Adjacency matrix and transition probability ma-
Quantification of De-anonymization Risks in Social Networks
129

trix are two important descriptions of a graph, and
the graph utility is also closely related to these matri-
ces. The adjacency matrix is a means of representing
which nodes of a graph are adjacent to which other
nodes. We denote the adjacency matrix by A
A
A (resp.
A
A
A
a
and A
A
A
u
) for graph G (resp. G
a
and G
u
), where
the element A
A
A(i, j) = e(i, j) (resp. A
A
A
a
(i, j) = e
a
(i, j)
and A
A
A
u
(i, j) = e
u
(i, j)). Furthermore, the transition
probability matrix is a matrix consisting of the one-
step transition probabilities, which is the probability
of transitioning from one node to another in a sin-
gle step. We denote the transition probability ma-
trix by T
T
T (resp. T
T
T
a
and T
T
T
u
) for graph G (resp. G
a
and G
u
), where the element T
T
T (i, j) = e(i, j)/deg(i)
(resp. T
T
T
a
(i, j) = e
a
(i, j)/deg
a
(i) and T
T
T
u
(i, j) =
e
u
(i, j)/deg
u
(i)), and deg(i),deg
a
(i),deg
u
(i) repre-
sent the degree of node i in G,G
a
,G
u
, respectively.
We now define the smallest (l) and largest (h)
probabilities of an edge existing between two nodes
in the graph G, and the graph density (denoted by R).
For graph G, we denote |V | = N and |E| = M. Let
p(i, j) be the probability of an edge existing between
i, j ∈ V and define l = min{p(i, j)|i, j ∈ V,i 6= j},
h = max{p(i, j)|i, j ∈ V,i 6= j}, the expected num-
ber of edges P
T
=
∑
i, j∈V
p(i, j) and the graph density
R =
P
T
(
N
2
)
.
Then, we start our formal quantification from the
simplest scenario where the anonymized data and
the auxiliary data correspond to the same group of
users i.e., V
a
= V
u
as in (Narayanan and Shmatikov,
2009; Pedarsani and Grossglauser, 2011; Srivatsa
and Hicks, 2012). This assumption does not limit
our theoretical analysis since we can either (a) ap-
ply it to the overlapped users between V
a
and V
u
or
(b) extend the set of users to V
new
a
= V
a
∪ (V
u
\V
a
)
and V
new
u
= V
u
∪ (V
a
\V
u
), and apply the analysis to
G
a
= (V
new
a
,E
a
) and G
u
= (V
new
u
,E
u
). Therefore, in
order to prevent any confusion and without loss of
generality, we assume V
a
= V
u
in our theoretical anal-
ysis. We define σ
k
as a mapping between G
a
and G
u
that contains k incorrectly-mapped pairs.
Given a mapping σ : V
a
→ V
u
, we define the
Difference of Common Neighbors (DCN) on a node
i’s mapping σ(i) as φ
i,σ(i)
= |N
i
a
\N
σ(i)
u
| + |N
σ(i)
u
\N
i
a
|,
which measures the neighborhoods’ difference be-
tween node i in G
a
and node σ(i) in G
u
under the map-
ping σ. Then, we define the overall DCN for all the
nodes under the mapping σ as Φ
σ
=
∑
(i,σ(i))∈σ
φ
i,σ(i)
.
Next, we not only explain why structure-based
de-anonymization attacks work but also quantify the
trade-off between the anonymized utility and the
de-anonymization capability. We first quantify the
relationship between a straightforward utility met-
ric, named local neighborhood utility, and the de-
anonymization capability. Then we carefully analyze
a more general utility metric, named global structure
utility, to accommodate a broad class of real-world
applications.
4.1 Relation between the Local
Neighborhood Utility and
De-anonymization Capability
At the beginning, we explore a straightforward util-
ity metric, local neighborhood utility, which evaluates
the distortion of the anonymized graph G
a
from the
conceptually underlying graph G as
Definition 1. The local neighborhood utility for
the anonymized graph is U
a
= 1 −
||A
A
A
a
−A
A
A||
1
N(N−1)
= 1 −
E[D(G
a
,G)]
N(N−1)
(the denominator is a normalizing factor
to guarantee U
a
∈ [0,1]), where D(·,·) is the ham-
ming distance (Hamming, 1950) of edges between two
graphs, i.e., if e
a
(i, j) 6= e(i, j), D(e
a
(i, j),e(i, j)) =
1 and E[D(G
a
,G)] is the distortion between G
a
and G and E[D(G
a
,G)] = E[
∑
i, j
D(e
a
(i, j),e(i, j))] =
∑
i, j
(p(i, j)p
del
a
+ (1 − p(i, j))p
add
a
).
Thus, we further have
U
a
= 1 −
∑
i, j
(p(i, j)p
del
a
+ (1 − p(i, j))p
add
a
)

N
2

= 1 − (Rp
del
a
+ (1 −R)p
add
a
)
(1)
Similarly, the local neighborhood utility for the aux-
iliary graph is
U
u
= 1 − (Rp
del
u
+ (1 −R)p
add
u
) (2)
Though the utility metric for structural data is
application-dependent, our utility metric can pro-
vide a comprehensive understanding for utility per-
formance by considering both the edge insertions
and deletions, and incorporating the distance between
the anonymized (auxiliary) graph and the concep-
tual underlying graph. Although our utility is one
of the most straightforward definitions, to the best
of our knowledge, it is still the first scientific work
that theoretically analyzes the relationship between
de-anonymization performance and the utility of the
anonymized data.
Based on the local neighborhood utility in Defini-
tion 1, we theoretically analyze the de-anonymization
capability of structure-based attacks and quantify the
anonymized utility for successful de-anonymization.
To improve readability, we defer the proof of Theo-
rem 1 to the Appendix.
ICISSP 2017 - 3rd International Conference on Information Systems Security and Privacy
130

(0,1)
(1, 0)
(0,1)
(1, 0)
(0,1)
(1, 0)
( )
1- l(1- R),1
(0,1)
(1, 0)
u a
R R
Eq. 14: U + 2(1-h) U >1+2(1-h) - R(1-h)
1- R 1- R
u a
1- R 1- R
Eq. 13: U +2l U >1+2l -l(1-R)
R R
1- R
1,1 -
2
æ ö
ç ÷
è ø
R
1,1 -
2
æ ö
ç ÷
è ø
( )
1- R(1 - h),1
( )
1- l(1- R),1
u a
Eq. 11: U +2lU >1+2l - Rl
u a
Eq. 12: U +2(1-h)U >1+2(1-h)-(1-h)(1-R)
1- R
1,1 -
2
æ ö
ç ÷
è ø
1- R
1,1 -
2
æ ö
ç ÷
è ø
( )
1- Rl,1
( )
1- (1 - h)(1 - R),1
u
U
a
U
1- R
1,1 -
2
æ ö
ç ÷
è ø
u
U
1- R
1,1 -
2
æ ö
ç ÷
è ø
( )
1- Rl,1
( )
1- (1 - h)(1 - R),1
a
U
u
U
a
U
( )
1- R(1 - h),1
1- R
1,1 -
2
æ ö
ç ÷
è ø
R
1,1 -
2
æ ö
ç ÷
è ø
u
U
a
U
1- h
(a) R < min 0.5,
1- h + l
ì ü
í ý
î þ
1- h
(b) min 0.5, R < 0.5
1- h + l
ì ü
£
í ý
î þ
l
(c) 0.5 R < max 0.5,
1- h + l
ì ü
£
í ý
î þ
l
(d) max 0.5, R
1- h + l
ì ü
£
í ý
î þ
3
4
5
6
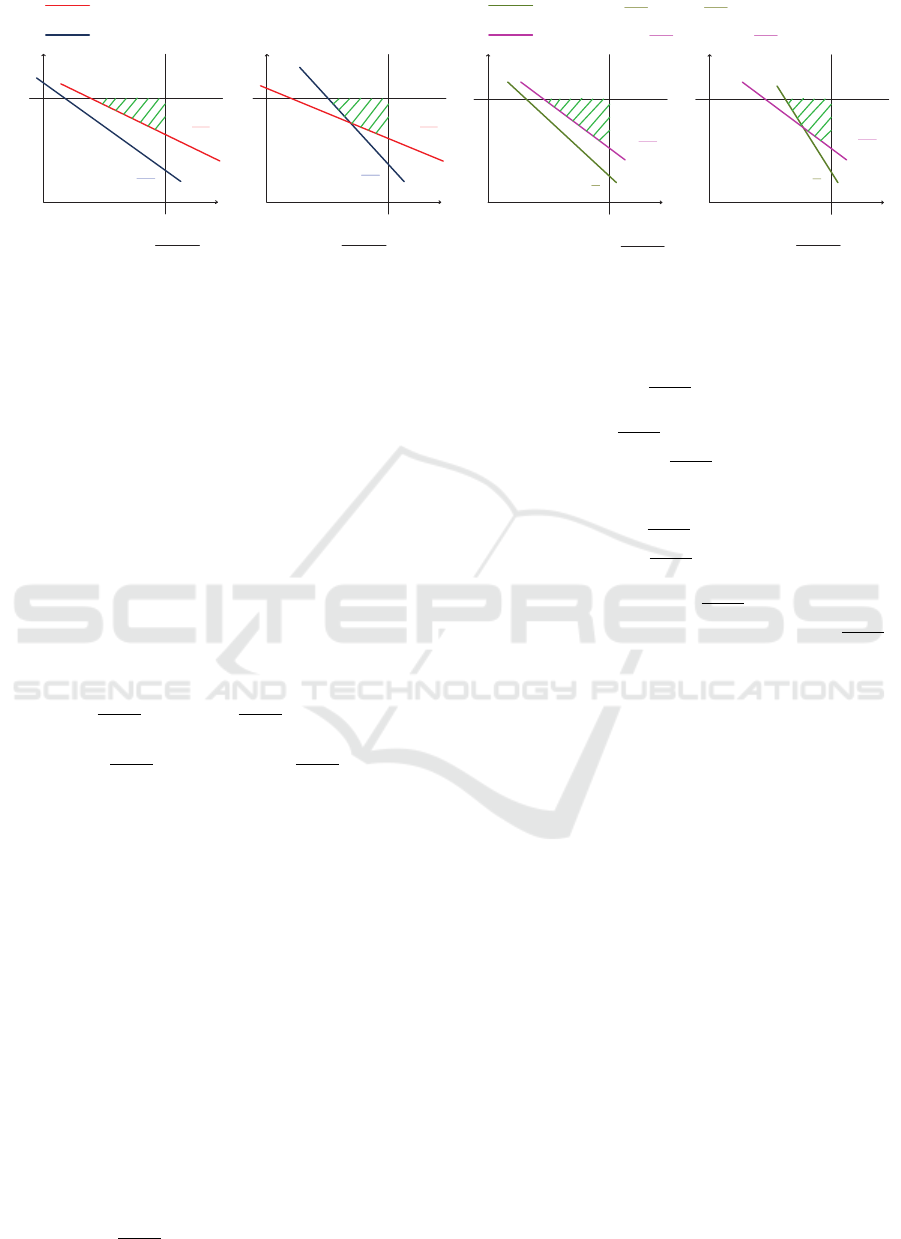
Figure 1: Visualization of utility region (green shaded) for successful de-anonymization under different scenarios. To guar-
antee the applicability of the anonymized data, the anonymized utility should be preserved by the anonymization techniques.
We theoretically demonstrate that successful de-anonymization can be achieved if the anonymized utility locates within these
shaded regions.
Theorem 1 implies that as the number of nodes in
the graphs G
a
and G
u
increase, the probability of suc-
cessful deanonymization approaches 1 when the four
conditions (in Eqs. 3,4,5,6) regarding graph density R,
and the smallest and largest probabilities of the edges
between nodes hold.
Theorem 1. For any σ
k
6= σ
0
, where k is the num-
ber of incorrectly-mapped nodes between G
a
and G
u
,
lim
n→∞
Pr(Φ
σ
k
≥ Φ
σ
0
) = 1 when the following con-
ditions are satisfied.
U
u
+ 2lU
a
> 1 + 2l − Rl (3)
U
u
+2(1 −h)U
a
> 1 +2(1 −h) −(1 −h)(1 −R) (4)
U
u
+ 2l
1 − R
R
U
a
> 1 + 2l
1 − R
R
− l(1 − R) (5)
U
u
+2(1−h)
R
1 − R
U
a
> 1+2(1−h)
R
1 − R
−R(1−h)
(6)
From Theorem 1, we know that when the lo-
cal neighborhood utility for the anonymized graph
and the auxiliary graph satisfies the four condi-
tions in Eqs. 3,4,5,6, we can achieve successful de-
anonymization from a statistical perspective. The rea-
son is that, the attacker can discover the correct map-
ping with high probability by choosing the mapping
with the minimal Difference of Common Neighbors
(DCN), out of all the possible mappings between the
anonymized graph and the auxiliary graph. To the
best of our knowledge, this is the first work to quan-
tify the relationship between anonymized utility and
de-anonymization capability. It also essentially ex-
plains why structure-based de-anonymization attacks
work.
The four conditions in Theorem 1 can be reduced
to one or two conditions under four types of graph
density. Figure 1(a) is the triangular utility region for
R < min{0.5,
1−h
1−h+l
} (where the graph density R is
smaller than 0.5 and
1−h
1−h+l
), which is only bounded
by Eq. 3. Figure 1(b) is the quadrilateral utility re-
gion for min{0.5,
1−h
1−h+l
} ≤ R < 0.5 (where the graph
density R is larger than
1−h
1−h+l
and smaller than 0.5),
which is bounded by Eq. 3 and Eq. 4. Simi-
larly, Figure 1(c) is the triangular utility region for
0.5 ≤ R < max{0.5,
l
1−h+l
} (where the graph den-
sity R is larger than
l
1−h+l
and 0.5), which is only
bounded by Eq. 6. Figure 1(d) is the quadrilateral util-
ity region for R ≥ max{0.5,
l
1−h+l
} (where the graph
density R is larger than 0.5 and smaller than
l
1−h+l
),
which is bounded by Eq. 5 and Eq. 6. Therefore,
we not only analytically explain why the structure-
based de-anonymization works, but also theoretically
provide the bound of anonymized utlity for sucessful
de-anonymization. When the anonymized utility sat-
isfies the conditions in Theorem 1 (or locates within
the green shaded utility regions shown in Figure 1),
successful de-anonymization is theoretically achiev-
able.
4.2 Relation between the Global
Structure Utility and
De-anonymization Capability
In Definition 1, we consider a straightforward local
neighborhood utility metric, which evaluates the dis-
tortion between the adjacency matrices of the two
graphs, i.e., ||A
A
A
a
− A
A
A||
1
. However, the real-world data
utility is application-oriented such that we need to
consider a more general utility metric, to incorporate
more aggregate information of the graph instead of
just the adjacency matrix. Motivated by the general
utility distance in (Mittal et al., 2013a; Liu and Mit-
tal, 2016), we consider to utilize the w-th power of
the transition probability matrix T
w
, which is induced
Quantification of De-anonymization Risks in Social Networks
131

by the w-hop random walk on graph G, to define the
global structure utility as follows:
Definition 2. The global structure utility for the
anonymized graph G
a
is defined as
U
a(w)
= 1 −
||T
T
T
w
a
− T
T
T
w
||
1
2N
(7)
where T
T
T
w
a
,T
T
T
w
are the w-th power of the transition
probability matrix T
T
T
a
,T
T
T , respectively. The denomi-
nator in Eq. 7 is a normalization factor to guarantee
U
a(w)
∈ [0,1]. Similarly, the global structure utility
for the auxiliary graph is
U
u(w)
= 1 −
||T
T
T
w
u
− T
T
T
w
||
1
2N
(8)
Our metric of global structure utility in Defini-
tion 2 is intuitively reasonable for a broad class of
real-world applications, and captures the w-hop ran-
dom walks between the original graph G and the
anonymized graph G
a
. We note that random walks
are closely linked to structural properties of real-
world data. For example, a lot of high-level social
network based applications such as recommendation
systems (Andersen et al., 2008), Sybil defenses (Yu
et al., 2008) and anonymity systems (Mittal et al.,
2013b) directly perform random walks in their proto-
cols. The parameter w is application specific; for ap-
plications that require access to fine-grained commu-
nity structure, such as recommendation systems (An-
dersen et al., 2008), the value of w should be small.
For other applications that utilize coarse and macro
community structure of the data, such as Sybil de-
fense mechanisms (Yu et al., 2008), w can be set to
a larger value (typically around 10). Therefore, our
global structure utility metric can quantify the util-
ity performance of a perturbed graph for various real-
world applications in a general and universal manner.
Based on this general utility metric, we fur-
ther theoretically analyze the de-anonymization ca-
pability of structure-based attacks and quantify the
anonymized utility for successful de-anonymization.
To improve readability, we defer the proof of Theo-
rem 2 to the Appendix.
Theorem 2. For any σ
k
6= σ
0
, where k is the num-
ber of incorrectly-mapped nodes between G
a
and G
u
,
lim
n→∞
Pr(Φ
σ
k
≥ Φ
σ
0
) = 1 when the following con-
ditions are satisfied:
U
u(w)
+ 2lU
a(w)
> 1 + 2l −
wRl(N − 1)
2
(9)
U
u(w)
+ 2(1 − h)U
a(w)
> 1 + 2(1 − h) −
w(N − 1)(1 − h)(1 − R)
2
(10)
U
u(w)
+ 2l
1 − R
R
U
a(w)
> 1 + 2l
1 − R
R
−
wl(1 − R)(N −1)
2
(11)
U
u(w)
+2(1−h)
R
1 − R
U
a(w)
> 1+2(1 −h)
R
1 − R
−
wR(1 − h)(N − 1)
2
(12)
Table 1: De-anonymization Accuracy of State-of-the-Art
Approaches.
Datasets noise = 0.05 noise = 0.15 noise = 0.25
(Ji et al., 2014) 0.95 0.81 0.73
(Nilizadeh et al., 2014) 0.83 0.74 0.68
Similar to Theorem 1, when the global structure
utility for the anonymized graph and the auxiliary
graph satisfies all of the four conditions in Theorem
2, we can achieve successful de-anonymization from
a statistical perspective. With rather high probabil-
ity, the attacker can find out the correct mapping be-
tween the anonymized graph and the auxiliary graph,
by choosing the mapping with the minimal DCN out
of all the potential mappings.
Furthermore, both Theorem 1 and Theorem 2
give meaningful guidelines for future designs of de-
anonymization and anonymization schemes: 1) Since
successful de-anonymization is theoretically achiev-
able when the anonymized utility satisfies the condi-
tions in Theorem 1 (for the local neighborhood utility)
and Theorem 2 (for the global structure utility), the
gap between the practical de-anonymization accuracy
and the theoretically achievable performance can be
utilized to evaluate the effectiveness of a real-world
de-anonymization attack; 2) we can also leverage
Theorem 1 and Theorem 2 for designing future secure
data publishing to defend against de-anonymization
attacks. For instance, a secure data publishing scheme
should provide anonymized utility that locates out of
the theoretical bound (green shaded region) in Fig-
ure 1 while enabling real-world applications. We will
provide a practical analysis for such privacy and util-
ity tradeoffs in Section 5.
5 PRACTICAL PRIVACY AND
UTILITY TRADE-OFF
In this section, we show how the theoretical analy-
sis in Section 4 can be utilized to evaluate the pri-
vacy risks of practical data publishing and the per-
formance of practical de-anonymization attacks. To
enable real-world applications without compromis-
ing the privacy of users, a secure data anonymiza-
tion scheme should provide anonymized utility which
does not locate within the utility region for perfect
de-anonymization shown as the green shaded regions
in Figure 1 (a) (d). From a data publisher’s point of
view, we consider the worst-case attacker who has ac-
cess to perfect auxiliary information, i.e., noise
u
= 0.
Based on Theorem 1, we aim to quantify the amount
of noise that is added to the anonymized data for
achieving successful de-anonymization. After care-
ICISSP 2017 - 3rd International Conference on Information Systems Security and Privacy
132

ful derivations, we know that when the noise of the
anonymized graph is less than 0.25 (note that our
derivation is from a statistical point of view instead
of from the perspective of a concrete graph), success-
ful de-anonymization can be theoretically achieved
(proof is deferred to the Appendix). Therefore, when
the noise added to the anonymized graph is less than
0.25, there would be a serious privacy breach since
successful de-anonymization is theoretically achiev-
able. Note that such a utility bound only conser-
vatively provides the minimum noise that should be
added to the anonymized data. Practically, we sug-
gest a real-world data publisher to add more noise to
protect the privacy of the data. Furthermore, such
privacy-utility trade-off can be leveraged as a guide
for designing new anonymization schemes.
In addition, our derived theoretical analysis can
also be utilized to evaluate the performance of ex-
isting de-anonymization attacks. We first implement
our experiments on the Facebook dataset (Viswanath
et al., 2009) which contains 46,952 nodes (i.e., users)
connected by 876,993 edges (i.e., social relation-
ships). To evaluate the performance of existing de-
anonymization attacks, we consider a popular pertur-
bation method of Hay et al. in (Hay et al., 2007),
which applies a sequence of r edge deletions followed
by r random edge insertions. A similar perturbation
process has been utilized for the de-anonymization at-
tacks in (Nilizadeh et al., 2014). Candidates for edge
deletion are sampled uniformly at random from the
space of the existing edges in graph G, while candi-
dates for edge insertion are sampled uniformly at ran-
dom from the space of edges that are not existing in G.
Here, we define noise (perturbations) as the extent of
edge modification, i.e., the ratio of altered edges r to
the total number of edges, i.e., noise =
r
M
. Note that
we add the same amount of noise to the original graph
of the Facebook dataset to obtain the anonymized
graph and the auxiliary graph, respectively. Then, we
apply the state-of-the-art de-anonymization attacks in
(Ji et al., 2014) and (Nilizadeh et al., 2014) to de-
anonymize the anonymized graph by leveraging the
auxiliary graph.
We utilize Accuracy as an effective evaluation
metric to measure the de-anonymization perfor-
mance. Accuracy is the ratio of the correctly de-
anonymized nodes out of all the overlapped nodes be-
tween the anonymized graph and the auxiliary graph:
Accuracy =
N
cor
|V
a
∩V
u
|
, (13)
where N
cor
is the number of correctly de-anonymized
nodes. The Accuracy of these de-anonymization at-
tacks corresponding to different levels of noise is
shown in Table 1.
From Table 1, we can see that the state-of-the-art
de-anonymization attacks can only achieve less than
75% de-anonymization accuracy when the noise is
0.25, which demonstrates the ineffectiveness of previ-
ous work and the potential of developing more pow-
erful de-anonymization attacks in the future.
6 DISCUSSION
There is a Clear Trade-off between Utility and Pri-
vacy for Data Publishing. In this work, we ana-
lytically quantify the relationships between the util-
ity of anonymized data and the de-anonymization ca-
pability. Our quantification results show that privacy
could be breached if the utility of anonymized data
is high. Hence, striking the balance between utility
and privacy for data publishing is important yet dif-
ficult - providing the high utility for real-world ap-
plications would decrease the data’s resistance to de-
anonymization attacks.
Suggestions for Secure Data Publishing. Secure
data publishing (sharing) is important for companies
(e.g., online social network providers), governments
and researchers. Here, we give several general guide-
lines: (i) Data owners should carefully evaluate the
potential vulnerabilities of the data before publishing.
For example, our quantification result in Section 4 can
be utilized to evaluate the vulnerabilities of the struc-
tural data. (ii) Data owners should develop proper
policies on data collections to defend against adver-
saries who aim to leverage auxiliary information to
launch de-anonymization attacks. To mitigate such
privacy threats, online social network providers, such
as Facebook, Twitter, and Google+, should reason-
ably limit the access to users’ social relationships.
7 CONCLUSION
In this paper, we first address several funda-
mental open problems in the structure-based de-
anonymization research by quantifying the condi-
tions for successful de-anonymization under a gen-
eral graph model. Next, we analyze the capability
of structure-based de-anonymization methods from a
theoretical point of view. We further provided theoret-
ical bounds of the anonymized utility for successful
de-anonymization. Our analysis provides a theoret-
ical foundation for structure-based de-anonymization
attacks, and can serve as a guide for designing new de-
anonymization/anonymization systems in practice.
Future work can include studying our utility versus
privacy trade-offs for more datasets, and designing
Quantification of De-anonymization Risks in Social Networks
133

more powerful anonymization/de-anonymization ap-
proaches.
ACKNOWLEDGEMENTS
This work was supported in part by NSF award num-
bers SaTC-1526493, CNS-1218817, CNS-1553437,
CNS-1409415, CNS-1423139, CCF-1617286, and
faculty research awards from Google, Cisco and In-
tel.
REFERENCES
Andersen, R., Borgs, C., Chayes, J., Feige, U., Flaxman, A.,
Kalai, A., Mirrokni, V., and Tennenholtz, M. (2008).
Trust-based recommendation systems: an axiomatic
approach. In WWW.
Backstrom, L., Dwork, C., and Kleinberg, J. (2007).
Wherefore art thou r3579x?: anonymized social net-
works, hidden patterns, and structural steganography.
In WWW.
Buccafurri, F., Lax, G., Nocera, A., and Ursino, D. (2015).
Discovering missing me edges across social networks.
Information Sciences.
Dwork, C. (2006). Differential privacy. In Encyclopedia of
Cryptography and Security. Springer.
Erd
˝
os, P. and R
´
enyi, A. (1976). On the evolution of random
graphs. Selected Papers of Alfr
´
ed R
´
enyi.
Fabiana, C., Garetto, M., and Leonardi, E. (2015). De-
anonymizing scale-free social networks by percola-
tion graph matching. In INFOCOM.
Hamming, R. W. (1950). Error detecting and error correct-
ing codes. Bell System technical journal.
Hay, M., Miklau, G., Jensen, D., Towsley, D., and Weis,
P. (2008). Resisting structural re-identification in
anonymized social networks. VLDB Endowment.
Hay, M., Miklau, G., Jensen, D., Weis, P., and Srivastava,
S. (2007). Anonymizing social networks. Computer
Science Department Faculty Publication Series.
Ji, S., Li, W., Gong, N. Z., Mittal, P., and Beyah, R. (2015a).
On your social network de-anonymizablity: Quantifi-
cation and large scale evaluation with seed knowledge.
In NDSS.
Ji, S., Li, W., Mittal, P., Hu, X., and Beyah, R. (2015b). Sec-
graph: A uniform and open-source evaluation system
for graph data anonymization and de-anonymization.
In USENIX Security Symposium.
Ji, S., Li, W., Srivatsa, M., and Beyah, R. (2014). Structural
data de-anonymization: Quantification, practice, and
implications. In CCS.
Korula, N. and Lattanzi, S. (2014). An efficient reconcilia-
tion algorithm for social networks. Proceedings of the
VLDB Endowment.
Liu, C., Chakraborty, S., and Mittal, P. (2016). Dependence
makes you vulnerable: Differential privacy under de-
pendent tuples. In NDSS.
Liu, C. and Mittal, P. (2016). Linkmirage: Enabling
privacy-preserving analytics on social relationships.
In NDSS.
Liu, K. and Terzi, E. (2008). Towards identity anonymiza-
tion on graphs. In SIGMOD.
Machanavajjhala, A., Kifer, D., Gehrke, J., and Venkita-
subramaniam, M. (2007). l-diversity: Privacy beyond
k-anonymity. ACM Transactions on Knowledge Dis-
covery from Data.
Mittal, P., Papamanthou, C., and Song, D. (2013a). Preserv-
ing link privacy in social network based systems. In
NDSS.
Mittal, P., Wright, M., and Borisov, N. (2013b). Pisces:
Anonymous communication using social networks.
NDSS.
Narayanan, A. and Shmatikov, V. (2008). Robust de-
anonymization of large sparse datasets. IEEE S&P.
Narayanan, A. and Shmatikov, V. (2009). De-anonymizing
social networks. IEEE S&P.
Newman, M. (2010). Networks: an introduction. Oxford
University Press.
Newman, M. E. (2003). The structure and function of com-
plex networks. SIAM review.
Nilizadeh, S., Kapadia, A., and Ahn, Y.-Y. (2014).
Community-enhanced de-anonymization of online so-
cial networks. In CCS.
Pedarsani, P., Figueiredo, D. R., and Grossglauser, M.
(2013). A bayesian method for matching two similar
graphs without seeds. In Allerton.
Pedarsani, P. and Grossglauser, M. (2011). On the privacy
of anonymized networks. In SIGKDD.
Pham, H., Shahabi, C., and Liu, Y. (2013). Ebm: an
entropy-based model to infer social strength from spa-
tiotemporal data. In SIGMOD.
Sala, A., Zhao, X., Wilson, C., Zheng, H., and Zhao, B. Y.
(2011). Sharing graphs using differentially private
graph models. In IMC.
Sharad, K. and Danezis, G. (2013). De-anonymizing d4d
datasets. In Workshop on Hot Topics in Privacy En-
hancing Technologies.
Sharad, K. and Danezis, G. (2014). An automated social
graph de-anonymization technique. In Proceedings of
the 13th Workshop on Privacy in the Electronic Soci-
ety. ACM.
Srivatsa, M. and Hicks, M. (2012). Deanonymizing mobil-
ity traces: Using social network as a side-channel. In
CCS.
Viswanath, B., Mislove, A., Cha, M., and Gummadi, K. P.
(2009). On the evolution of user interaction in face-
book. In ACM workshop on Online social networks.
Yu, H., Gibbons, P. B., Kaminsky, M., and Xiao, F. (2008).
Sybillimit: A near-optimal social network defense
against sybil attacks. In IEEE S&P.
ICISSP 2017 - 3rd International Conference on Information Systems Security and Privacy
134

APPENDIX
Proof of Theorem 1
Proof Sketch: First, we aim to derive p
add
ua
(i, j) which
is the projection process from G
u
to G
a
and p
del
ua
(i, j)
which is the deletion process from G
u
to G
a
, to
have p
add
ua
(i, j) =
p
add
a
(1−p
add
u
)(1−p(i, j))+(1−p
del
a
)p
del
u
p(i, j)
(1−p
add
u
)(1−p(i, j))+p
del
u
p(i, j)
and p
del
ua
(i, j) =
(1−p
add
a
)p
add
u
(1−p(i, j))+p
del
a
(1−p
del
u
)p(i, j)
p
add
u
(1−p(i, j))+(1−p
del
u
)p(i, j)
.
Then, we want to prove p
add
ua
(i, j) <
1
2
and
p
del
ua
(i, j) <
1
2
. It is easy to show that they are equiv-
alent to (1 − p
add
u
)(1 − 2p
add
a
)(1 − p(i, j)) > p
del
u
(1 −
2p
del
a
)p(i, j) and p
add
u
(1 − 2p
add
a
)(1 − p(i, j)) < (1 −
p
del
u
)(1 − 2p
del
a
)p(i, j). From Eqs. 3,6,5,4, we
have
1
2
> max{p
add
u
, p
del
u
}. Similarly, we have
1
2
>
max{p
add
a
, p
del
a
}. Now, we consider four different sit-
uations (a) p
del
u
≥ p
add
u
and p
del
a
≥ p
add
a
, (b) p
del
u
≥ p
add
u
and p
del
a
≤ p
add
a
, (c) p
del
u
≤ p
add
u
and p
del
a
≥ p
add
a
, and
(d) p
del
u
≤ p
add
u
and p
del
a
≤ p
add
a
to prove p
add
ua
(i, j) <
1
2
and p
del
ua
(i, j) <
1
2
. Under σ
k
, let V
k
u
⊆ V
u
be the set of
incorrectly de-anonymized nodes, E
k
u
= {e
u
(i, j)|i ∈
V
k
u
or j ∈ V
k
u
} be the set of all the possible edges ad-
jacent to at least one user in V
k
u
, E
τ
u
= {e
u
(i, j)|i, j ∈
V
k
u
,(i, j) ∈ E
k
u
, and ( j,i) ∈ E
k
u
} be the set of all the
possible edges corresponding to transposition map-
pings in σ
k
, and E
u
= {e
u
(i, j)|1 ≤ i 6= j ≤ n} be the
set of all the possible links on V . Furthermore, define
m
k
= |E
k
u
| and m
τ
= |E
τ
u
|. Then, we have |V
k
u
| = k,
m
k
=

k
2

+ k(n − k), m
τ
≤
k
2
and |E
u
| =

n
2

.
Now, we quantify Φ
σ
0
from a statistical per-
spective. We define Φ
σ
k
,E
0
as the DCN caused
by the edges in the set E
0
under the mapping
σ
k
. Based on the definition of DCN, we ob-
tain Φ
σ
k
= Φ
σ
k
,E
u
\E
k
u
+ Φ
σ
k
,E
k
u
\E
τ
u
+ Φ
σ
k
,E
τ
u
and
Φ
σ
0
= Φ
σ
0
,E
u
\E
k
u
+ Φ
σ
0
,E
k
u
\E
τ
u
+ Φ
σ
0
,E
τ
u
. Since
Φ
σ
k
,E
u
\E
k
u
= Φ
σ
0
,E
u
\E
k
u
and Φ
σ
k
,E
τ
u
= Φ
σ
0
,E
τ
u
, we can
obtain Pr(Φ
σ
k
≥ Φ
σ
0
) = Pr(Φ
σ
k
,E
k
u
\E
τ
u
≥ Φ
σ
0
,E
k
u
\E
τ
u
).
Considering ∀e
u
(i, j) ∈ E
k
u
\E
τ
u
under σ
k
, we
know Φ
σ
k
,e
u
(i, j)
∼ B(1, p(i, j)
u
(p(σ
k(i)
,σ
k( j)
)
u
×
p
del
ua
(i, j) + (1 − p(σ
k(i)
,σ
k( j)
)
u
) × (1 − p
add
ua
(i, j))) +
(1 − p(i, j)
u
)(p(σ
k(i)
,σ
k( j)
)
u
× (1 − p
del
ua
(i, j)) +
(1 − p(σ
k(i)
,σ
k( j)
)
u
) × p
add
ua
(i, j))). Simi-
larly, under σ
0
∀e
u
(i, j) ∈ E
k
u
\E
τ
u
, we obtain
Φ
σ
0
,e
u
(i, j)
∼ B(1, p(i, j)
u
p
del
ua
+ (1 − p(i, j)
u
)p
add
ua
).
Let λ
σ
0
,e
u
(i, j)
and λ
σ
k
,e
u
(i, j)
be the mean of
Φ
σ
0
,e
u
(i, j)
and Φ
σ
k
,e
u
(i, j)
, respectively. Then, we have
λ
σ
k
,e
u
(i, j)
> p(i, j)
u
p
del
ua
+ (1 − p(i, j)
u
)p
add
ua
=
λ
σ
0
,e
u
(i, j)
then Pr(Φ
σ
k
,e
u
(i, j)
> Φ
σ
0
,e
u
(i, j)
) >
1 − 2 exp

−
(λ
σ
k
,e
u
(i, j)
−λ
σ
0
,e
u
(i, j)
)
2
8λ
σ
k
,e
u
(i, j)
λ
σ
0
,e
u
(i, j)

= 1−
2exp

− f (p(i, j)
u
, p(σ
k
(i),σ
k
( j))
u
m
2

, where f (.,.)
is a function of p(i, j)
u
and p(σ
k
(i),σ
k
( j))
u
. After
further derivations, we obtain lim
n→∞
Pr(Φ
σ
k
,E
k
u
\E
τ
u
≥
Φ
σ
0
,E
k
u
\E
τ
u
) = 1 and have Theorem 1 proved.
Proof of Theorem 2
We first relate the adjacency matrix A
A
A with the tran-
sition probability matrix T
T
T as A
A
A = Λ
Λ
ΛT
T
T , where Λ
Λ
Λ is a
diagonal matrix and Λ
Λ
Λ(i,i) = deg(i). Then we analyze
the utility distance for the anonymized graph. When
w = 1, we can prove ||A
A
A
a
− A
A
A||
1
= ||Λ
Λ
Λ
a
T
T
T
a
− Λ
Λ
ΛT
T
T ||
1
=
||(Λ
Λ
Λ
a
T
T
T
a
−Λ
Λ
Λ
a
T
T
T +Λ
Λ
Λ
a
T
T
T −Λ
Λ
ΛT
T
T )||
1
≥ ||Λ
Λ
Λ
a
||
1
||T
T
T
a
−T
T
T ||
1
.
Since the element in the diagonal of Λ
Λ
Λ
a
is greater than
1, we have ||A
A
A
a
− A
A
A||
1
≥ ||T
T
T
a
− T
T
T ||
1
. Therefore, we
can obtain U
a
≤ U
a(w)
. Similarly, we have U
u
≤ U
u(w)
.
Incorporating these two inequalities into Eqs. 3,4,5,6,
we have Theorem 2 satisfied under w = 1. Next, we
consider w ≥ 1. It is easy to prove that ||T
T
T
w
a
−T
T
T
w
||
1
≤
w||T
T
T
a
− T
T
T ||
1
so ||T
T
T
w
a
− T
T
T
w
||
1
≤ w||A
A
A
a
− A
A
A||
1
. There-
fore, we have U
a
≤ wU
a(w)
+1−w. Similarly, we also
have U
u
≤ wU
u(w)
+ 1 − w for the auxiliary graph. In-
corporating these two inequalities into Eqs. 3,4,5,6,
we have Theorem 2 proved.
Proof of Utility and Privacy Trade-off
For the anonymization method of Hay et al. in (Hay
et al., 2007), we have P
del
a
= k
a
/M
a
and P
add
a
=
k
a
/(

N
2

− M
a
). Similarly, we have P
del
u
= k
u
/M
u
and
P
add
u
= k
u
/(

N
2

− M
u
). Based on our utility metric in
Definition 1, we have U
u
= 1 − 2R × noise
u
and U
a
=
1 − 2R × noise
a
. Considering the sparsity property
in most real-world structural graphs (Narayanan and
Shmatikov, 2008), the utility condition for achieving
successful de-anonymization is restricted by Eq. 3,
which can be represented as noise
u
+ l × noise
a
<
l
2
.
Consider the worst-case attacker who has access to
perfect auxiliary information, i.e., noise
u
= 0. There-
fore, we have noise
a
< 0.25.
Quantification of De-anonymization Risks in Social Networks
135