
A Hierarchical Book Representation of Word Embeddings for
Effective Semantic Clustering and Search
Avi Bleiweiss
BShalem Research, Sunnyvale, U.S.A.
Keywords:
Word Vectors, Deep Learning, Semantic Matching, Multidimensional Scaling, Clustering.
Abstract:
Semantic word embeddings have shown to cluster in space based on linguistic similarities that are quantifiably
captured using simple vector arithmetic. Recently, methods for learning distributed word vectors have pro-
gressively empowered neural language models to compute compositional vector representations for phrases
of variable length. However, they remain limited in expressing more generic relatedness between instances of
a larger and non-uniform sized body-of-text. In this work, we propose a formulation that combines a word
vector set of variable cardinality to represent a verse or a sentence, with an iterative distance metric to eval-
uate similarity in pairs of non-conforming verse matrices. In contrast to baselines characterized by a bag of
features, our model preserves word order and is more sustainable in performing semantic matching at any
of a verse, chapter and book levels. Using our framework to train word vectors, we analyzed the clustering
of bible books exploring multidimensional scaling for visualization, and experimented with book searches
of both contiguous and out-of-order parts of verses. We report robust results that support our intuition for
measuring book-to-book and verse-to-book similarity.
1 INTRODUCTION
The attraction of using vector spaces for analyz-
ing natural language semantics, stems primarily from
providing an instinctive relation mechanism by sub-
scribing to lexical distance and similarity concepts.
In a large corpora of text, the structure of a seman-
tic space is created by evaluating the various con-
texts in which words occur. Thus leading to distribu-
tional models of word meanings with the underlying
assertion that words who transpire in similar contexts
tend to have similar interpretations (Turney and Pan-
tel, 2010). Distributed words, also known as word
embeddings, are each represented with a dense, low-
dimensional real-valued vector, and follow efficient
similarity calculations directly from the known Vec-
tor Space Model (Salton et al., 1975). Word vectors
have been widely used as features in a diverse set of
computational linguistic tasks, including information
retrieval (IR) (Manning et al., 2008), parsing (Socher
et al., 2013), named entity recognition (Guo et al.,
2014), and question answering (Iyyer et al., 2014).
In recent years, neural network architectures have
inspired the deep learning of word embeddings from
large vocabularies to avoid a manual labor-intensive
design of features. The work by Bengio et al. (2003)
introduced a statistical language model formulated by
the conditional probability of the next word given all
its preceding words in a sequence, or a context. How-
ever, the time complexity of the neural model ren-
ders the scheme inefficient due to the non-linear hid-
den layer. The succeeding Word2Vec (Mikolov et al.,
2013a) and GloVe (Pennington et al., 2014) methods,
preserve the probabilistic hypotheses founded in Ben-
gio et al. (2003) approach, and further eliminate the
hyperbolic tangent layer entirely, thus becoming more
effective and feasible tools for language analysis. No-
tably, these methods expand on the input context win-
dow to include the words that both precede and follow
the target word. Word embeddings are typically con-
structed by way of minimizing the distance between
words of similar contexts, and encode various simple
lexical relations as offsets in vector space. Our work
investigates the linguistic structure in raw text, and
explores clustering and search tasks using Word2Vec
to train the underlying word representations.
Applying unsupervised learning (Duda et al.,
2001) of distributed word embeddings to a broader set
of semantic tasks has not yet been fully established
and remains an active research to date. In their recent
work, Fu et al. (2014) utilize word embeddings to dis-
cover hypernym-hyponym type of linguistic relations.
154
Bleiweiss A.
A Hierarchical Book Representation of Word Embeddings for Effective Semantic Clustering and Search.
DOI: 10.5220/0006192701540163
In Proceedings of the 9th International Conference on Agents and Artificial Intelligence (ICAART 2017), pages 154-163
ISBN: 978-989-758-220-2
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Figure 1: Framework overview: on the left, tokens and context from a text corpus are used to train word vectors. A collection
of word vectors is constructed to represent word-for-word the source text of every book. Word vectors are first row bound
into a matrix to represent a verse. Then, verse matrices are concatenated into chapter matrices that are further coalesced into
a hierarchical book matrix. We run all-book-pairs and all-query-book-pairs similarity process on matrices of a non-uniform
row count, and generate a distance matrix that we use for cluster analysis and search ranking, respectively.
Noting that offsets of word pairs distribute into struc-
tured clusters, they modeled fine-grained relations by
estimating projection matrices that map words to their
respective hypernyms, and report a reasonable test
F1-score of 73.74%. Socher et al. (2013) proposed a
recursive neural network to compute distributed vec-
tor representations for phrases and sentences of vari-
able length. Their model outperforms state-of-the-art
baselines on both sentiment classification and accu-
racy metrics, however, its supervised method requires
extensive manual labeling and makes scaling to larger
sized text non trivial. A representation more rooted in
a convolutional neural architecture (Kim, 2014), pro-
duces a feature map for each possible window in a
sentence, and follows with a max-over-time pooling
(Collobert et al., 2011) to capture the most important
features. Pooling has the apparent benefit of naturally
adapting to variable length sentences. At the higher
document level, Le and Mikolov (2014) introduced a
paragraph vector extension to the learning framework
of word vectors. Given their different dimensionality,
paragraph and word vectors are concatenated to yield
fixed sized features, however, unique paragraph vec-
tors constrain context sharing across the document.
For a composition of words, most of the tech-
niques discussed tend to reshape the varying dimen-
sionality of input sentences into uniform feature vec-
tors. Rather, our implementation retains the word vec-
tors as distinct rows in a matrix form to construct any
of the verse, chapter, or book data structures for per-
forming our set of linguistic tasks. The main contribu-
tion of our work is a framework (Figure 1) with a lex-
ical representation that abides word-for-word by the
corpus source sequence, to facilitate a generic evalu-
ation of relationships among entities of non-uniform
text size. The rest of this paper is organized as fol-
lows. In section 2, we briefly review the neural mod-
els to found Word2Vec, and proceed with motivating
our choice for a verse matrix representation that leads
to our chapter and book hierarchies. Section 3 derives
our book similarity measure as it applies to a pair of
non-conforming concatenations of verse embeddings,
whereas Section 4 profiles the compiled format of the
bible corpus we used for evaluation. We then present
our methodology for analyzing clusters of bible sub-
divisions and ranking book searches of unsolicited
keywords, and report extensive quantitative results of
our experiments, in section 5. We conclude with a
discussion and future prospect remarks in section 6.
2 EMBEDDING HIERARCHY
In Word2Vec, Mikolov et al. (2013a) proposed a
shallow neural-network structure for learning useful
word embeddings to support predictions within a lo-
cal bi-directional context-window. Both the skip-
gram and continuous bag-of-words (CBOW) models
offer a simple single-layer architecture based on the
inner product between a pair of word vectors. In the
skip-gram version the objective is to predict the not
necessarily immediate context words given the tar-
get word, and conversely, CBOW estimates the target
word based on its neighboring context. As a context
window scans over the corpus, the models attempt to
maximize the log probability of the generated objec-
tive function, based on their respective multi and sin-
gle output layers, and training word vectors proceeds
in a stochastic manner using back propagation. To im-
prove upon accuracy and training time, Mikolov et al.
(2013b) introduced both randomly discarding of fre-
quent words that exceed a prescribed count threshold,
A Hierarchical Book Representation of Word Embeddings for Effective Semantic Clustering and Search
155

and the concept of negative sampling that measures
how well a word pairs with its context drawn from a
noise distribution of a small sample of tokens. Empir-
ically, neural model performance shown mainly gov-
erned by tunable parameters, including the word vec-
tor dimension, d, the symmetric context-window size,
c
w
, and the number of negative samples, s
n
. Overall,
skip-gram works well with a small amount of training
data, while CBOW is several times faster to train.
The corpus we used for our study comprises a set
of tens of books and to train word embeddings we
first flattened the entire corpus into a linear array of
verses, or sentences. We then proceeded to construct
our basic data structures that culminate in an effective
hierarchical representation of a book object, which is
perceived nameless across subsequent clustering and
search analysis. Let w
(k)
∈ R
d
be the d-dimensional
word vector corresponding to the k-th word in a verse.
A verse S of length n is represented as a matrix
S = w
(1)
⊕ w
(2)
⊕ . . . ⊕ w
(n)
, (1)
where ⊕ is a row-wise binding operator and S ∈ R
n×d
.
S is thus regarded as a vector set and rows of S are
considered atomic. To index a word vector in a verse,
we use the notation s
k
. Similarly, a book chapter C
of m verses becomes a concatenation of verse matri-
ces, C = S
(1)
⊕ S
(2)
. . . ⊕ S
(m)
, where C ∈ R
r
c
×d
and
r
c
=
∑
m
j=1
|S
( j)
|, and a book B comprises l chapter ma-
trices, B = C
(1)
⊕C
(2)
. . . ⊕C
(l)
, where B ∈ R
r
b
×d
and
r
b
=
∑
l
i=1
r
(i)
c
. Respectively, c
j
itemizes a verse ma-
trix in a chapter, and b
i
enumerates a chapter matrix
in a book. Equation 2 provides an alternate matrix
notation for each a verse, chapter, and book.
S =
w
(1)
w
(2)
.
.
.
w
(n)
C =
S
(1)
S
(2)
.
.
.
S
(m)
B =
C
(1)
C
(2)
.
.
.
C
(l)
. (2)
The length of a verse, |S
( j)
|, and the number of verses
per chapter, |C
(i)
|, are varying parameters that we
track and keep in a book map for traversing the book
hierarchy. For book similarity computations, we often
iterate a book matrix and access the entire collection
of word vectors. Conveniently, we use a three dimen-
sional indexing scheme, b
i jk
, where each of i, j, and
k points to a chapter matrix, verse matrix, and word
vector, respectively. Space complexity for book em-
beddings is linear, O (lmn), and for a vocabulary that
permits storing a 16-bit token enumeration instead,
memory area required is reduced by a half. We further
denote the corpus book set T = {B
(1)
, B
(2)
, . . . , B
(N)
},
where N, or cardinality |T |, is the number of books.
3 BOOK SIMILARITY
Measuring similarity and relatedness between dis-
tributed terms is an important problem in lexical se-
mantics (Agirre et al., 2009). Recently, the process of
learning word embeddings transpired compelling lin-
guistic regularities by simply probing the linear dif-
ference between pairs of word vectors. This evalua-
tion scheme exposes relations that are adequately dis-
tributed in a multi-clustering representation (Fu et al.,
2014). However, a single offset term is insufficient to
assess similarity between a pair of books represented
by non-conforming matrices, each potentially retain-
ing many thousands of word vectors. For evaluating
semantic closeness of a pair of books, b
(u)
and b
(v)
,
we explored a similarity concept that expands on the
Chebychev matrix distance and is defined by
d(u, v) =
1
b
(u)
∑
xyz
max
i jk
sim(b
(u)
xyz
, b
(v)
i jk
)
, (3)
where |b
(u)
| is the book cardinality that amounts to
the total number of distributed word vectors for rep-
resenting the book, and |b
(u)
| 6= |b
(v)
|. Whereas sim is
a similarity function that operates on two word vec-
tors and takes either a Euclidean or an angle form.
We chose cosine similarity (Baeza-Yates and Ribeiro-
Neto, 1999) that performs an inner product on a pair
of normalized vectors g and h,
g·h
T
kgk
2
khk
2
, and returns a
scalar value as a measure of proximity. The time com-
plexity of the distance algorithm is roughly quadratic,
as for each word vector in book b
(u)
, we find the clos-
est word vector in book b
(v)
, and then calculate the
mean of all the closest distances derived formerly.
In our system, all possible pairs of the corpus
books, T , are evaluated for similarity in the context
of a |T |-dimensional squared distance-matrix, D. El-
ements of the distance matrix are considered direc-
tional and hence imply d(u, v) 6= d(v, u). Matrix D
facilitates unsupervised learning for clustering books
that apart from knowing their individual representa-
tions, they are perceived as a collection of unlabeled
objects. Following an identical vein, as the distance
metric provided by Equation 3 is generic and assumes
opaque matrix pairs, our framework extends the se-
mantic distance intuition to express a query-book type
of relations for conducting a search. A query, q, com-
prises an unsolicited keyphrase and as such abides by
our verse matrix formulation, S. The distance d(q, u),
where u ∈ {1, 2, . . . , |T |}, thus conveys a distinct rel-
evancy measure for ranking the search of a query in
each of the corpus books, T . Our system reports back
search results as a table of sorted distances paired with
the book enumeration (Cormen et al., 1990).
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
156

4 BIBLE CORPUS
We evaluated the performance of our model on raw
bible text we acquired online from the publicly avail-
able repository provided by Google (2008). Among
the editions offered, we chose the American Stan-
dard version of the Old Testament that is distributed
in constructive book folders, each with a list of chap-
ter files. The bible script comprises three major book
collections termed Torah, Neviim, and Ketuvim, also
known correspondingly as Pentateuch, Prophets, and
Writings. Compactly, we denote the compilation into
three timeline related components with the commonly
used acronym, TNK. Table 1 lists the book names as-
sociated with each of the TNK partitions.
Table 1: Book names for each of the TNK partitions.
Torah Neviim Ketuvim
Genesis Joshua Hosea Psalms
Exodus Judges Joel Proverbs
Leviticus 1 Samuel Amos Job
Numbers 2 Samuel Obadiah Song of Solomon
Deuteronomy 1 Kings Jonah Ruth
2 Kings Micah Lamentations
Isaiah Nahum Ecclesiastes
Jeremiah Habakkuk Esther
Ezekiel Zephaniah Daniel
Haggai Ezra
Zechariah Nehemiah
Malachi 1 Chronicles
2 Chronicles
The bible dataset contains 39 titles, as 5, 21, and
13 books subscribe to each of the TNK groups, re-
spectively. In total, the corpus incorporates 929 chap-
ters and 23,145 verses, with over one and a half mil-
lion tokens. Table 2 provides further TNK summa-
rizations of books-per-partition, chapters-per-book,
and verses-per-chapter, whereas the visualization of
both chapter and stacked verse distribution across all
the TNK books is outlined in Figure 2 and Figure 3,
respectively. To derive our word vectors, we trained
11,319 unique tokens that include stop words and
punctuation marks, with no preprocessing to attend
to any exclusion or exception. Notably, most tokens
are of a low frequency term with 3,536 tokens that oc-
cur only once in the dataset, and 8,254, or about 73%,
come up each under ten incidents. To construct a con-
text window, we randomly select an unlabeled book
enumeration in the [1, 39] range, and traverse our hi-
erarchy top-to-bottom by arbitrarily sampling chapter
and verse indices that are confined to the limits set by
the singled out book. In the chosen verse, a random
target-word position is used to extract from left and
right context words that are delimited by the verse
start and end words. One of our system goals is to
discover semantic relations that closely align learned
book clusters with the handmade TNK partitions.
Table 2: Summarizations of TNK books-per-partition,
chapters-per-book, verses-per-book, and corpus tokens.
Books
Torah Neviim Ketuvim Total
5 21 13 39
Chapters
Min Max Mean Total
1 150 23.8 929
Verses
Min Max Mean Total
21 2,461 593.5 23,145
Tokens
Unique Total
11,319 1,507,790
5 EMPIRICAL EVALUATION
Previously, we discussed vector embedding tech-
niques, such as Word2Vec (Mikolov et al., 2013a)
and GloVe (Pennington et al., 2014), and their role
to transform natural language words into a semantic
vector space. In this section, we proceed to quantita-
tively evaluate the intrinsic quality of the produced set
of latent vector representations, and analyze their im-
pact on the performance of our unsupervised learning
tasks that comprise book clustering and search. As an
aid to tune our system level performance, we explored
varying some of the hyperparameters designed to con-
trol the neural models incorporated in the word em-
bedding methods. In practice, we have implemented
our own Word2Vec technique natively in R (R, 1997)
for better integration with our software framework.
Across all of our experiments we trained word vec-
tors employing mini-batch stochastic gradient descent
(SGD) with an annealed learning rate, and semantic
similarity results we report on both book-to-book and
verse-to-book relations presume anonymous books.
A Hierarchical Book Representation of Word Embeddings for Effective Semantic Clustering and Search
157
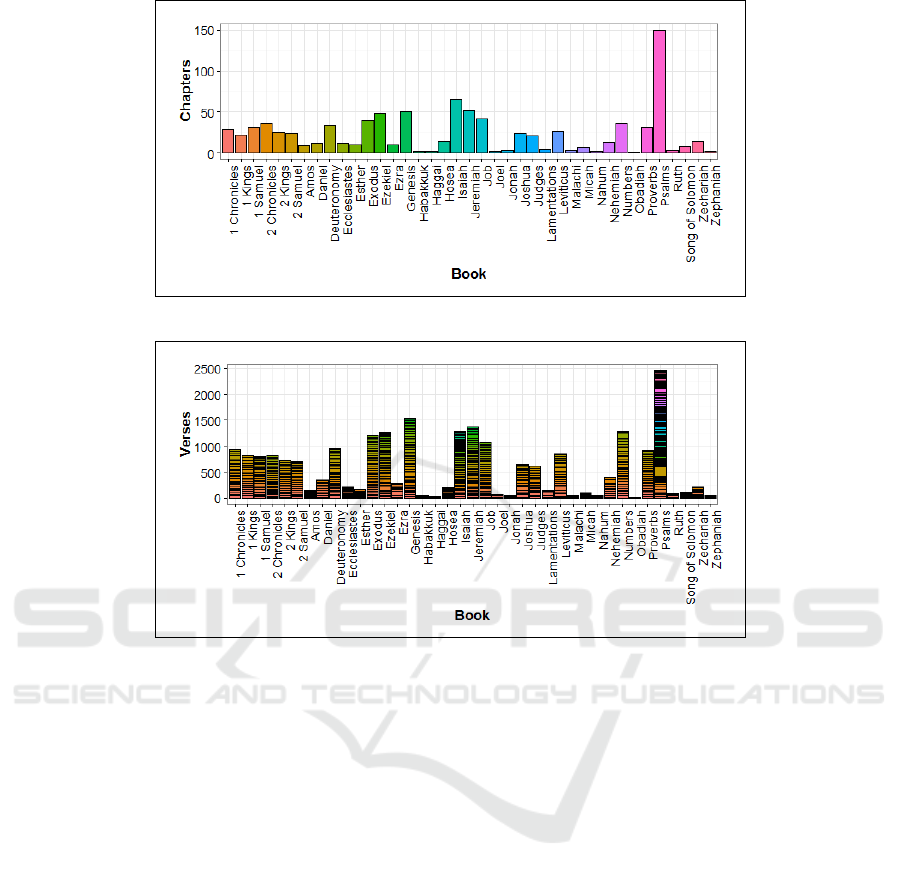
Figure 2: Chapter distribution across the entire TNK book suite.
Figure 3: Stacked verse distribution for chapters across the entire TNK book suite.
5.1 Experimental Setup
The raw bible text (Google, 2008) underwent a data
cleanup preprocess to properly space words from
punctuation marks and introduce a more definite sep-
aration symbol between a verse ID and the verse text.
We then tokenized the corpus using the R tokenizer
and built a maximal vocabulary of size |V | = 11, 319.
Each word in this sparse 1-of-|V | encoding is repre-
sented as a one-hot vector ∈ R
|V |×1
, with all 0s and a
single 1 bit at the word index in the vocabulary, that
is further mapped onto a lower-dimensional seman-
tic vector-space. Projecting onto the denser formula-
tion transpires preceding the hidden layer of the neu-
ral models that underlie the embedding technique.
In the absence of a large supervised training set of
word vectors, the use of pre-trained word vectors ob-
tained from an unsupervised neural model became a
favorable practice to boost system performance (Col-
lobert et al., 2011; Iyyer et al., 2014; Kim, 2014).
While proven useful for word analogy and multi-class
classification tasks, clustering and search over a rather
unique dataset requires however randomly initialized
word-vectors. Hence our model generates distinct in-
put and output sets of word vectors, W and
˜
W , that
only differ as a result of their random initialization.
To help reduce overfitting and noise, we used their
sum, W +
˜
W , as our final vectors and that typically
yields a small performance gain. To better assess the
space complexity of our book representation made of
the trained word embeddings, Figure 4 provides a vi-
sual interpretation of a flattened book hierarchy, out-
lined as a single linear matrix with up to several tens-
of-thousands rows of word vectors, and shown dis-
tributed across the entire TNK book suite.
Recent study by Baroni et al. (2014) alluded
to neural word-embedding models that consistently
outperform the more traditional count-based distribu-
tional methods on many semantic matching tasks and
by a fair margin. Furthermore, much of the achieved
performance gains cited are mostly attributed to a sys-
tem design choice of the configured hyperparameters.
Motivated by these results, we evaluated task perfor-
mance comparing distinct book hierarchies generated
by each skip-gram and CBOW, and choose negative
sampling that typically works better than hierarchical
softmax (Mikolov et al., 2013b). For the learning hy-
perparameters, there seems no single selection for an
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
158
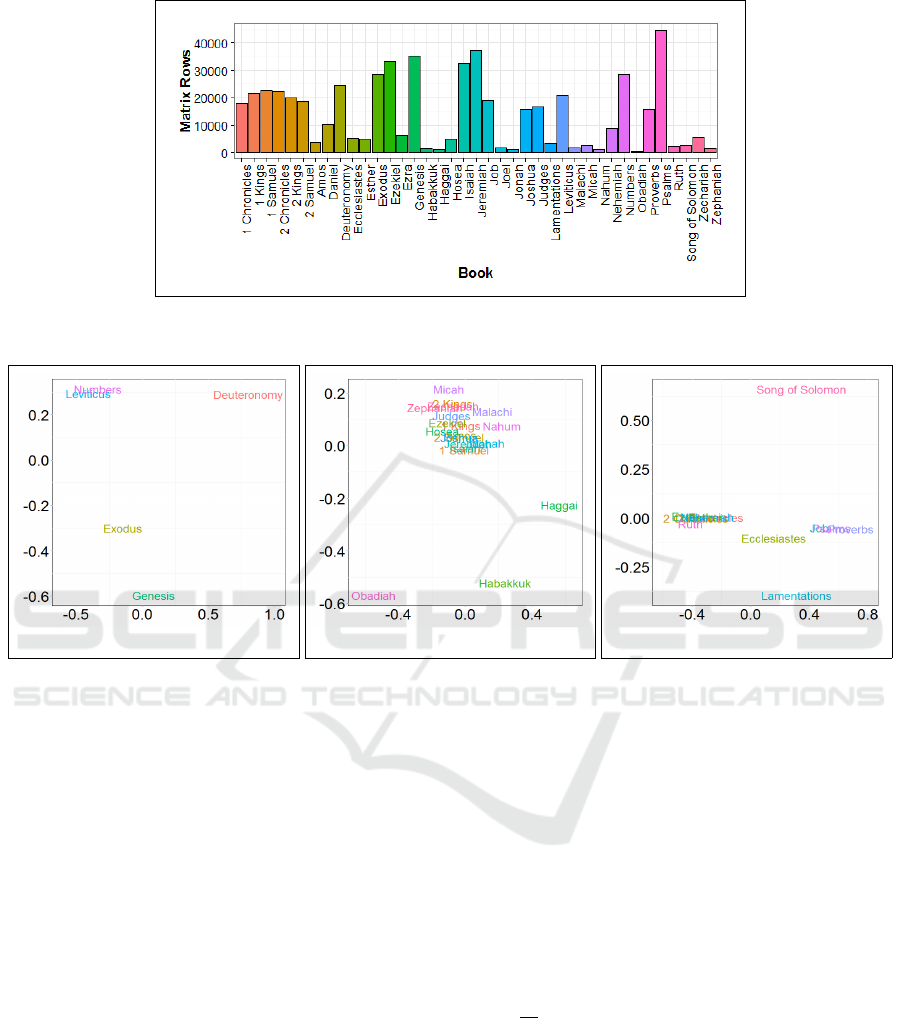
Figure 4: Flattened book hierarchy into a single linear matrix of word vectors w
(k)
∈ R
d
. Showing distribution of matrix row
count across the entire TNK book suite.
(a) Torah. (b) Neviim. (c) Ketuvim.
Figure 5: Visualization of book distance matrices using Multidimensional Scaling, representing the TNK subsets of Torah,
Neviim, and Ketuvim with 5, 21, and 13 books, respectively.
optimal word-vector dimension, d, as it tends to be
highly task dependent and varies from 25 for seman-
tic classification (Socher et al., 2013) up to 300 for
word analogy (Mikolov et al., 2013a). Rather, we set
d = 10 and traded-off word vector dimension to attain
more tractable computation in building the distance
matrix that is inherently of a quadratic time complex-
ity, O (|T |
2
). Whereas, to better assess the impact
of the context window on our system performance,
we varied discretely its size c
w
= {5, 15, 25, 50}, in a
wide range of word counts. Evidently, Word2Vec per-
formance tends to decrease as the number of negative
samples increases beyond about 10 (Pennington et al.,
2014), thereby we used s
n
= 10. For our mini-batch
SGD to train word vectors, we used a batch size of
25 and an initial learning rate α = 0.1, as we ran 100
iterations and updated parameters after each window.
5.2 Experimental Results
We present book clustering results of our own trained
TNK corpus at both the component level and for the
entire suite of |T | = 39 books. To visualize TNK clus-
ters we used Multidimensional Scaling (MDS) (Torg-
erson, 1958; Hofmann and Buhmann, 1995) that ex-
tracts patterns of semantic proximities from our book
distance-matrix representation, D. The distance ma-
trix is composed of a set of pairwise book-similarity
values with O (|T |
2
) scaling that MDS further com-
piles and projects onto an embedding p-dimensional
Euclidean-space. This mapping is intended to faith-
fully preserve the clustering structure of the origi-
nal distance data-points, and often, data visualiza-
tion quality of clusters is directly proportional to the
ratio
p
|T |
. In our experiments, we consistently ren-
dered similarity measures of book pairs onto a two-
dimensional coordinate frame to inspect and analyze
formations of TNK book clustering.
In Figure 5, we provide baseline visualization of
MDS applied to our book distance matrices that repre-
sent each of the TNK components of Torah, Neviim,
and Ketuvim with dimensionality |T | = {5, 21, 13},
respectively. For this experiment, we used the CBOW
neural model to train word vectors, as hyperparame-
A Hierarchical Book Representation of Word Embeddings for Effective Semantic Clustering and Search
159

Table 3: Visualization of clustering the entire TNK book suite using Multidimensional Scaling, as each book is assigned its
formal TNK-subset legend post projecting onto the displayable embedding space. Shown as a function of a non-descending
context window-size, c
w
, for both the skip-gram and CBOW neural models.
Skip-gram
c
w
= 5 c
w
= 15 c
w
= 25 c
w
= 50
CBOW
c
w
= 5 c
w
= 15 c
w
= 25 c
w
= 50
ters were uniformly set to their defaults, using 5 words
for the context window size, c
w
. The Torah collection
shows Leviticus and Numbers semantically closely
related, as Genesis, Exodus, and Deuteronomy are
each of some distance apart. Given the Neviim largest
number of 21 book samples, clusters appear more
statistically sound, with 18 books grouped together
and only leaving the books of Habakkuk, Haggai, and
Obadiah somewhat disjoint. On the other hand, Ketu-
vim formed two major clusters with the book of Ec-
clesiastes close to both, whereas the books of Lamen-
tations and Song of Solomon are notably outliers.
A much broader interest of our work underscores
the cluster analysis of a single distance matrix with di-
mensionality |T | = 39 that represents the entire TNK
book suite. Through this evaluation, our main ob-
jective is to predict unsupervised book clustering and
assess its matching to the TNK formal subdivisions.
Table 3 shows the clustering produced by applying
MDS to the single matrix that captures all-book-pairs
semantic similarities, as each book is assigned its for-
mal TNK-subset legend post projecting onto the dis-
playable embedding space. In these experiments, we
compared unique word-vector sets generated by each
skip-gram and CBOW, as we stepped over the fairly
large extent of discrete values prescribed for the con-
text window size, c
w
. Expanding the context window
scope has a rather mild impact on cluster construc-
tion with word vectors trained by the CBOW neural
model, however for skip-gram, group formations are
considerably susceptible and affected by even a mod-
erate change of c
w
. Furthermore, the book partitions
we generated under CBOW training persistently re-
semble the official subdivision of TNK collections,
although for visualization in a 2D embedding space,
the Torah and Neviim sets do overlap each other.
In our book search experiments, we explored three
types of keyphrase queries including fixed verses
drawn from a known book and chapter, reordered
words of random partial verses distributed uniformly
in each of the books of the TNK suite, and randomly
selected tokens from the TNK vocabulary composed
into a set of keywords that exclude stop words and
punctuation marks. Every search is preceded by con-
verting the query composition into a matrix of word
vectors and then pairing the query matrix with each of
the book hierarchies to compute similarity distances.
Thus resulting in a process of linear time complexity,
O(|T |). Unless otherwise noted, for the search exper-
iments we used CBOW-based trained word-vectors.
In Table 4, we list search queries of fixed verses
and correspondingly enumerate their book origins.
Overall, for each of the five verses searched the pre-
dicted book title matched the expected label and was
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
160
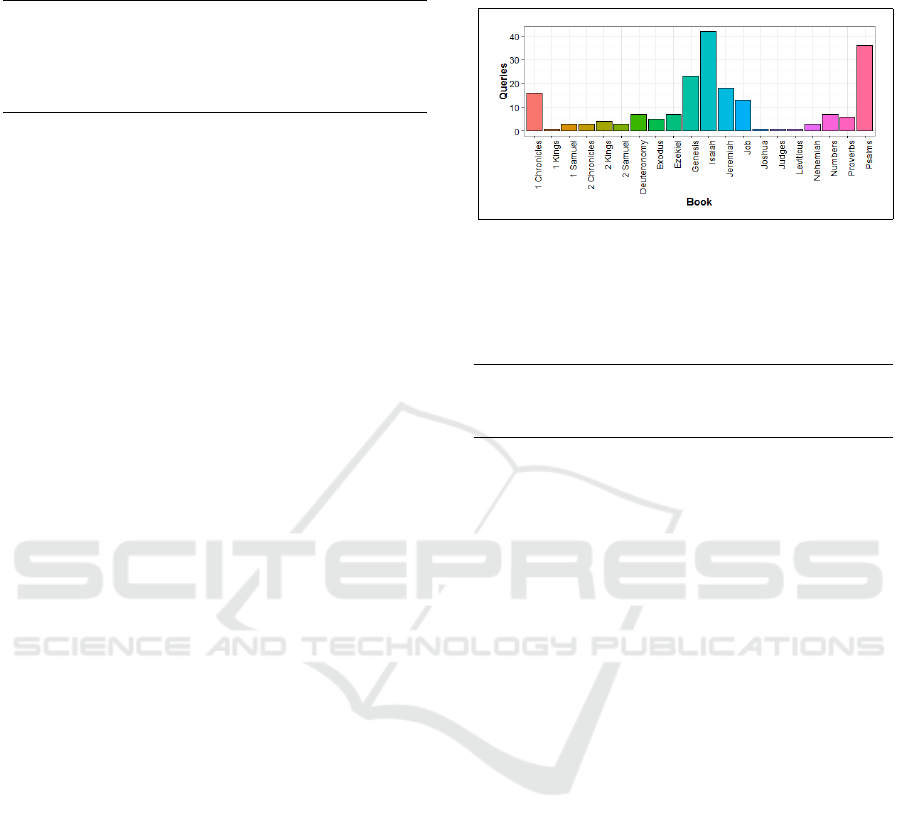
Table 4: Search queries of fixed verses from known books.
Book Search Query
Psalms Fret not thyself because of evil doers
Esther king delight to do honor more than to myself
Genesis his sons buried him in the cave of Machpelah
Jonah go unto Nineveh that great city
Proverbs lips of the wise disperse knowledge
ranked highest with a score of 1.0. Surprisingly, and
without any advanced knowledge, our search uncov-
ered that some of the fixed keyphrases were sourced
by unlisted TNK books that equally claimed the top
rank. For example, the first verse listed from the book
of Psalms, also shows up contiguously and in its en-
tirety to overlap a verse of the Proverbs book (chap-
ter 24, verse 19). Alternately, keyphrase words may
extend over chapters non-adjacently and would still
be ranked high for relevance in the context of a book
search. For instance, the book of Nahum scored high
on the keyphrase from the book of Jonah, while hav-
ing its keywords split to the subsets {Nineveh,great}
and {go,unto,that,city} that appear in chapters 1 and
3, respectively. Figure 7(a) provides visualization to
our fixed-verse search results in the form of a confu-
sion matrix, with actual and predicted books listed at
the bottom and to the left of the grid, respectively.
In the second search experiment, we selected from
each of the TNK books five random samples of partial
verses, each with eight unordered context words. We
ran a total of 5 × 39 = 195 search episodes and con-
structed a search matrix by computing all directional
pairs of query-book distances, and then averaged the
score for multiple queries per book. In Figure 7(b),
we show our results for the random sub-verse search
and demonstrate consistent top ranking for when the
source book of the queries matches the predicted book
along the confusion matrix diagonal.
Our third task deployed cumulatively a total of
200 searches using a query keyphrase that is a com-
posite of randomly selected tokens from our entire vo-
cabulary, and thus implies a weak contextual relation
to any of the TNK books. Distributed non uniformly,
our token based keyphrases are evidently biased to-
wards affiliation with books of the largest content.
Figure 6 shows non-zero query allocations that result
in occupying only a subset of 20 out of 39 books. As a
preprocess step, we iterated over the extended search
matrix of dimensionality 39 × 200 and identified the
book that is closest to a given query. We followed by
averaging the distances in the case of multiple queries
per book, and ended up with a reduced search matrix
of dimensionality 39 × 20. Figure 7(c) shows the re-
sults of random token search as the straddling bright
line along the confusion matrix diagonal highlights
our best ranks. In this experiment, expected diverse
search-scores span a rather wide range of [0.15, 0.86].
Figure 6: Distribution of queries in random token search,
presented across 20 TNK books of the largest content.
Table 5: Running time for key computational tasks in per-
forming clustering and search. Figures shown in seconds.
Task Min Max Mean Total
Hierarchy Formation 0.01 1.25 0.29 11.52
Distance Matrix 1.03 107.68 28.01 1,092.62
Keyphrase Query 6.87 11.91 9.73 379.73
In table 5, we list computational runtime of our
implementation for key tasks in performing linguis-
tic clustering and search. All reported figures are
in seconds and were obtained by running our soft-
ware single-threaded on a Windows 10 mobile de-
vice, with Intel 4th generation Core
TM
processor at
1.8GHz, and 8GB of memory. Book hierarchy con-
struction is linear with the number of verses per book,
and as expected the book of Psalms claimed the slow-
est to generate the data structure at 1.25 seconds.
The distance matrix item shows the time to com-
pute a set of similarities for one book paired with
each of the rest of the books in the TNK collection.
On average, book-to-book distance derivation amor-
tized across T = 39 books takes about 0.72 seconds.
Launching a keyphrase query task typically involves
a verse-to-book similarity operator that is linear in
the total number of verses for the entire book collec-
tion. Query response times are shown for each search
episode and they remain consistent regardless of the
keyphrase originating book, with a small standard de-
viation of two percent of the mean. The total column
of Table 5 further accumulates individual book pro-
cessing times and is roughly the mean column value
multiplied by the number of TNK books, T = 39.
6 CONCLUSIONS
In this study, we have demonstrated the apparent po-
tential in a hierarchical representation of word embed-
dings to conduct effective book level clustering and
A Hierarchical Book Representation of Word Embeddings for Effective Semantic Clustering and Search
161

(a) Fixed full verse search. (b) Random sub-verse search. (c) Random token search.
Figure 7: Visualization of our search results in the form of confusion matrices for each of the experimental classes: fixed full
verse search (a), random sub-verse search (b), and random token search (c).
search. We trained our system on a 39-book bible cor-
pus that comprises a vocabulary of 1.5 million tokens,
and generated our own word vectors for each of our
experimental choices of model-hyperparameter con-
figurations. We showed that the CBOW neural model
outperforms skip-gram for the linguistic tasks we per-
formed, and furthermore, clustering under CBOW
proved sustainable to modifying the context window
size in a fairly large extent. To evaluate any-pair se-
mantic similarity of both book-to-book and query-to-
book, we proposed a simple and generic distance met-
ric between a pair of word vector sets, each of up to
tens of thousands elements, that disambiguates non-
matching matrix dimensionality. We reported robust
empirical results on our tasks for deploying state-of-
the-art unsupervised learning of word representations.
At first observation, our hierarchical representa-
tion of books might appear greedy storage wise, and
rather than a matrix interpretation, we could have re-
sorted to a more compact format by averaging all the
verse word vectors and produce a single verse vector.
While this approach seems plausible for the clustering
tasks to both reduce footprint and streamline compu-
tations, the data loss incurred by doing so adversely
impacted the performance of our search tasks. To ad-
dress this shortcoming, our experimental choice of a
modest 10-dimensional word vector appears as a rea-
sonable system-design trade-off that aids to circum-
vent excessive usage of memory space.
To the best of our knowledge and based on liter-
ature published to date, we are unaware of semantic
analysis systems with similar goals to evenhandedly
contrast our results against. The more recent work
by Yang et al. (2016), proposed a hierarchical at-
tention network for document classification. Their
neural model explores attention mechanisms at both
a word and sentence levels in an attempt to differenti-
ate content importance when constructing a document
vector representation. However, for evaluation their
work focuses primarily on topic classification of short
user-review snippets. Unlike our system that reasons
semantic relatedness between any full length books.
On the other hand, Jiang et al. (2015) skip the sen-
tence level construct altogether and combine a set of
word vectors to directly represent a complete Yelp re-
view. In their report, there is limited exposure to fine-
grained control over the underlying neural models to
show performance impact on business clustering.
Given that the training of word vectors is a one
time process, a natural progression of our work is to
optimize the core computations of constructing the
distance matrix and performing a keyphrase query.
The inherent independence of deriving similarity ma-
trix elements and separating book search rankings,
lets us leverage parallel execution, and we expect to
reduce our runtime complexity markedly. For a larger
number of corpus books, we contend that projecting
the distance matrix onto a three-dimensional embed-
ding space is essential to improve cluster perception
for analysis. Lastly, we seek to apply our book dis-
tance matrix directly to methods that partition objects
around medoids (Kaufman and Rousseeuw, 1990) and
potentially avoid outliers.
ACKNOWLEDGEMENTS
We would like to thank the anonymous reviewers for
their insightful suggestions and feedback.
REFERENCES
Agirre, E., Alfonseca, E., Hall, K., Kravalova, J., Paca, M.,
and Soroa, A. (2009). A study on similarity and re-
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
162

latedness using distributional and WordNet-based ap-
proaches. In Human Language Technologies: North
American Chapter of the Association for Computa-
tional Linguistics (NAACL), pages 19–27, Strouds-
burg, PA.
Baeza-Yates, R. and Ribeiro-Neto, B., editors (1999). Mod-
ern Information Retrieval. ACM Press Series/Addison
Wesley, Essex, UK.
Baroni, M., Dinu, G., and Kruszewski, G. (2014). Don’t
count, predict! a systematic comparison of context-
counting vs. context-predicting semantic vectors. In
Annual Meeting of the Association for Computational
Linguistics (ACL), pages 238–247, Baltimore, MD.
Bengio, Y., Ducharme, R., Vincent, P., and Janvin, C.
(2003). A neural probabilistic language model. Ma-
chine Learning Research (JMLR), 3:1137–1155.
Collobert, R., Weston, J., Bottou, L., Karlen, M.,
Kavukcuoglu, K., and Kuksa, P. (2011). Natural lan-
guage processing (almost) from scratch. Machine
Learning Research (JMLR), 12:2493–2537.
Cormen, T. H., Leiserson, C. H., Rivest, R. L., and
Stein, C. (1990). Introduction to Algorithms. MIT
Press/McGraw-Hill Book Company, Cambridge, MA.
Duda, R. O., Hart, P. E., and Stork, D. G. (2001). Unsu-
pervised learning and clustering. In Pattern Classifi-
cation, pages 517–601. Wiley, New York, NY.
Fu, R., Guo, J., Qin, B., Che, W., Wang, H., and Liu, T.
(2014). Learning semantic hierarchies via word em-
beddings. In Annual Meeting of the Association for
Computational Linguistics (ACL), pages 1199–1209,
Baltimore, MD.
Google (2008). Google Bible Text. https://sites.
google.com/site/ruwach/bibletext.
Guo, J., Che, W., and Wang, H., L. T. (2014). Revisiting
embedding features for simple semi-supervised learn-
ing. In Empirical Methods in Natural Language Pro-
cessing (EMNLP), pages 110–120, Doha, Qatar.
Hofmann, T. and Buhmann, J. (1995). Multidimensional
scaling and data clustering. In Advances in Neural
Information Processing Systems, pages 459–466. MIT
Press, Cambridge, MA.
Iyyer, M., Boyd-Graber, J., Claudino, L., Socher, R., and
Daume, H. (2014). A neural network for factoid ques-
tion answering over paragraphs. In Empirical Meth-
ods in Natural Language Processing (EMNLP), pages
633–644, Doha, Qatar.
Jiang, R., Liu, Y., and Xu, K. (2015). A general
framework for text semantic analysis and clustering
on Yelp reviews. http://cs229.stanford.edu/proj2015/
003 report.pdf.
Kaufman, L. and Rousseeuw, P. J., editors (1990). Finding
Groups in Data: An Introduction to Cluster Analysis.
Wiley, New York, NY.
Kim, Y. (2014). Convolutional neural networks for sentence
classification. In Empirical Methods in Natural Lan-
guage Processing (EMNLP), pages 1746–1751, Doha,
Qatar.
Le, Q. V. and Mikolov, T. (2014). Distributed rep-
resentations of sentences and documents. ArXiv
e-prints, 1405.4053. http://adsabs.harvard.edu/abs/
2014arXiv1405.4053L.
Manning, C. D., Raghavan, P., and Schutze, H. (2008). In-
troduction to Information Retrieval. Cambridge Uni-
versity Press, Cambridge, United Kingdom.
Mikolov, T., Chen, K., Corrado, G., and Dean, J.
(2013a). Efficient estimation of word representa-
tions in vector space. ArXiv e-prints, 1301.3781.
http://adsabs.harvard.edu/abs/2013arXiv1301.3781M.
Mikolov, T., Sutskever, I., Chen, K., Corrado, G. S., and
Dean, J. (2013b). Distributed representations of words
and phrases and their compositionality. In Advances in
Neural Information Processing Systems, pages 3111–
3119. Curran Associates, Inc., Red Hook, NY.
Pennington, J., Socher, R., and Manning, C. D. (2014).
GloVe: Global vectors for word representation. In
Empirical Methods in Natural Language Processing
(EMNLP), pages 1532–1543, Doha, Qatar.
R (1997). R project for statistical computing. http://www.r-
project.org/.
Salton, G., Wong, A., and Yang, C. S. (1975). A vector
space model for automatic indexing. Communications
of the ACM, 18(11):613–620.
Socher, R., Perelygin, A., Wu, J. Y., Chuang, J., Manning,
C. D., Ng, A. Y., and Potts, C. (2013). Recursive deep
models for semantic compositionality over a senti-
ment treebank. In Empirical Methods in Natural Lan-
guage Processing (EMNLP), pages 1631–1642, Seat-
tle, WA.
Torgerson, W. S. (1958). Theory and Methods of Scaling.
John Wiley and Sons, New York, NY.
Turney, P. D. and Pantel, T. (2010). From frequency to
meaning: Vector space models of semantics. Artifi-
cial Intelligence Research (JAIR), 37:141–188.
Yang, Z., Yang, D., Dyer, C., He, X., Smola, A., and
Hovy, E. (2016). Hierarchical attention networks for
document classification. In Human Language Tech-
nologies: North American Chapter of the Association
for Computational Linguistics, pages 1480–1489, San
Diego, California.
A Hierarchical Book Representation of Word Embeddings for Effective Semantic Clustering and Search
163
