
A Fuzzy Chance-constraint Programming Model for a Home Health
Care Routing Problem with Fuzzy Demand
Yong Shi, Toufik Boudouh, Olivier Grunder
IRTES EA 7274, Universit
´
e de Bourgogne Franche-Comt
´
e, UTBM, Rue Thierry Mieg, 90000 Belfort cedex, France
Keywords:
Home Health Care, Fuzzy Chance Constraint Programming, Hybrid Genetic Algorithm, Stochastic
Simulation.
Abstract:
Home Health Care (HHC) companies are widespread in European countries, and aim to serve patients at home
to help them recover from illness and injury in a personal environment. Since transportation costs constitute
one of the largest forms of expenditure in the Home Health Care industry, it is of great significance to research
the optimization of the Home Health Care logistics. This paper considers the Home Health Care Routing
Problem with Fuzzy Demand, which comes from the logistics practice of the home health care company. A
fuzzy chance constraint programming model is proposed based on the fuzzy credibility theory, the hybrid
genetic algorithm and stochastic simulation method are integrated to solve the proposed model. Firstly the
uncertain constraints have been reduced to the deterministic ones, experimental results for the benchmark test
problem show the good efficiency of the proposed algorithm. Then the proposed hybrid algorithm has been
applied to solve the fuzzy model, the influence of the parameters to the objective function has been discussed.
This research will help HHC companies to make appropriate decisions when arranging their vehicle routes.
1 INTRODUCTION
Home health care (HHC) is a growing medical ser-
vice in France and other developed countries. This
service is provided by the Home Health Care compa-
nies, which aim to serve the patients at home to help
them recover from illness or injury in a personal envi-
ronment(Liu et al., 2014). Each day, a HHC company
carries out various logistics activities including the
delivery of drugs or medical instruments from the a
pharmacy to patients, and pickup the biological sam-
ples from patients’ home to the laboratory (Liu et al.,
2013). A large number of patients distributed in a
town or village, a certain quantity of the drugs needed
according to the recovery degree of them. For a HHC
company, the transportation cost is one of the most
important spendings in the company activities, so it is
of great significance to optimize the vehicle routing
problem in home health care companies.
According to a survey (Mankowska et al., 2014;
Harris, 2015) of the home health care companies, the
main operational process of the HHC can be summa-
rized as 3 steps.
(1) The HHC company collects the information from
the patients, this information may include: the
name, address, sex, type of the illness, symptom
and other related information;
(2) The HHC company plan to arrange the visited
routes and assign nurses according to the infor-
mation collected;
(3) The nurses are scheduled to visit the patients.
Each nurse is assigned to a planned route, and
he/she has to carry out all of the service-related
activities for the route. This nurse will drive the
vehicle to visit the patients one by one according
to the designed route. In case of a lack of drugs,
the nurse has to go back to the depot, load more
drugs into the vehicle and continue to attend to
the remaining patients until all the patients are at-
tended to.
It is easy to find that the home health care routing
optimization problem is closely related the Capaci-
tated Vehicle Routing Problem (CVRP) which is one
of the most classical combinatorial optimization prob-
lems (Eksioglu et al., 2009). CVRP is a basic model
in supply chain, and it has been applied into many
filed. However, our problem is neither like the classi-
cal VRP nor like the Open Vehicle Routing problem
(OVRP); all the variations of VRP can be seen in the
literature (Pillac et al., 2013; Toth and Vigo, 2014). In
the classical VRP, each vehicle needs to return to the
depot again, while in the OVRP, each vehicle does not
return to the depot after servicing the last customer on
Shi Y., Boudouh T. and Grunder O.
A Fuzzy Chance-constraint Programming Model for a Home Health Care Routing Problem with Fuzzy Demand.
DOI: 10.5220/0006194703690376
In Proceedings of the 6th International Conference on Operations Research and Enterprise Systems (ICORES 2017), pages 369-376
ISBN: 978-989-758-218-9
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
369

a route, but may end at a different location.
Moreover, demand is one of the most important
parameters in supply chain optimization. However
in previous studies, most researchers have focused on
the deterministic demand. While in the real world, it
is usually very hard to determine the precise demands
of customers and thus they are estimated from histor-
ical data. Given this aspect of VRPs, a consideration
of stochastic vehicle routing problems (SVRP) and
fuzzy vehicle routing problems (FVRP) may be use-
ful (Wen and Iwamura, 2008). In the Vehicle Rout-
ing Problem with Stochastic Demand (Bianchi et al.,
2006), the demand is a stochastic variable, which is
decided by probability distribution parameters, but
the parameters are often obtained from the histori-
cal data. However sometimes, we could not obtain
enough historical data for the new customers or pa-
tients. Although stochastic models can cater for a
variety of cases, they are not sufficient to describe
many other situations, where the probability distribu-
tion of customers demands may be unknown or par-
tially known (Wen and Iwamura, 2008). On the con-
trary, fuzzy language exists everywhere in the health
care domain, such as a doctor may inform us “small
penicillin”, or “you have a little fever ”. So, it is very
appropriate to describe the non-deterministic demand
in HHC domain using fuzzy variables.
This paper contributes to the home health care
routing optimization with fuzzy demand in the fol-
lowing aspects: (1) a fuzzy chance constraint pro-
graming model is proposed based on the fuzzy
credibility theory; (2) hybrid genetic algorithm and
stochastic simulation are integrated to solve the pro-
posed model; (3) Some experiments are carried out on
the deterministic model to validate the efficiency of
the proposed method, and then the heuristic method
has been employed to solve the fuzzy model. The
rest of this paper is organized as follows: in second
section some necessary theory of credibility is intro-
duced, then the home health care problem with fuzzy
demand model is constructed, and a hybrid heuristic
algorithm is proposed to solve the model, at last some
experiments are presented to illustrate the algorithm.
2 SUPPLY CHAIN MODELING
2.1 The Description of Fuzzy Demand
Constraints
Liu (Liu et al., 2003) recently developed credibility
theory, which can be used to measure the chance of
that a fuzzy chance occurs. The law of credibility in
the theory of fuzzy sets plays a role similar to that
played by the law of probability in measurement the-
ory of the ordinary sets. In this section we will first
introduce the credibility theory (Liu et al., 2003), be-
cause it is crucial to describe the fuzzy demand.
In the deterministic VRP, it is straightforward to
describe the capacity constraints: the total demand of
the whole route should not exceed the vehicle capac-
ity. However, in the VRPFD, the capacity constraints
become more complex than the deterministic ones for
the uncertain demand. Now, we have to consider the
relationship between the fuzzy demand and the capac-
ity of the vehicle (Mousavi and Niaki, 2013).
For a vehicle, after serving the j th patient, the
remaining capacity is changed and it becomes a fuzzy
variable named
f
Q
j
, where
f
Q
j
= q −
j
∑
i=1
e
d
i
= (q −
j
∑
i=1
d
3,i
, q −
j
∑
i=1
d
2,i
, q −
j
∑
i=1
d
1,i
)
= (Q
1, j
, Q
2, j
, Q
3, j
)
In the deterministic model, if the remaining ca-
pacity of the vehicle is greater than a customer’s de-
mand, this vehicle has the chance to serve this cus-
tomer. However, facing with a fuzzy variable of de-
mand and remaining capacity, how can we make a de-
cision that whether the vehicle should continue visit-
ing the ( j + 1)th patient or go to the lab directly? It
should be compared with the demand of the ( j + 1)
th patient, of course, which is also a fuzzy variable.
Based the credibility we can derive equation (1) and
equation (2) as follows:
Cr = Cr{
˜
d
j+1
≤
˜
Q
j
}
= Cr{(d
1, j+1
− Q
3, j
, d
2, j+1
− Q
2,k
, d
3,k+1
− Q
1, j
) ≤ 0};
(1)
Cr = Cr{
˜
d
j+1
≤
˜
Q
j
}
=
0, d
1, j+1
≥ Q
3, j
Q
3, j
− d
1, j+1
2(Q
3, j
− d
1, j+1
+ d
2, j+1
− Q
2, j
)
, d
1, j+1
≤ Q
3, j
, d
2, j+1
≥ Q
2, j
d
3, j+1
−Q
1, j
− 2(d
2, j+1
− Q
2, j
)
2(Q
2, j
− d
2, j+1
+ d
3, j+1
− Q
1, j
)
, d
2, j+1
≤ p
2, j
, d
3, j+1
≥ Q
1, j
1 d
3, j+1
≤ Q
1, j
(2)
There is no doubt that if the quantity of remaining
drugs is very high, and the demand of the next pa-
tient is very low, then the chance of the vehicle of be-
ing able to provide the next patient’s service becomes
greater (Cao and Lai, 2010).
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
370

We will describe the preference index by Cr,
which denotes the magnitude of our preference to
drive the vehicle to the next patient after it has served
the current patient according to formulation (2). Note
that Cr ∈[0, 1]. When Cr = 0, we declare that the ve-
hicle does not have the capacity to serve the next pa-
tient and it should terminate service at the current pa-
tient and return to the depot to replenish drugs. When
Cr = 1, we can be completely sure that the vehicle
should serve the next patient. However, in most cases,
Cr is neither 0 nor 1, but Cr ∈ (0, 1).
To describe Cr in a convenient way, let us in-
troduce the dispatcher preference index DPI, where
DPI ∈ [0, 1]. Note that DPI expresses the dispatcher’s
attitude toward risk. When the dispatcher is not a risk-
averse, he/she will choose lower values of parameter
DPI, which indicates that the dispatcher prefers to use
the vehicle available capacity as much as possible, al-
though there is an increase in the number of cases in
which the vehicle arrives at the next customer’s home
and is not able to carry out planned service due to
small available capacity. On the other hand, when
the dispatcher is a risk-averse, he will choose greater
DPI, this may result in a less complete utilization of
vehicle capacity along the planned routes and less ad-
ditional distance to cover due to failures
2.2 Mathematical Model
In order to describe the supply chain by formulation,
we give the assumption as follows.
(1)The vehicles are homogeneous.
(2)Each nurse responds for one route. In the process
of delivery, if the remaining drugs is not enough for
the patients, she must drive back and fill up the drugs,
return to this patient, then she will continue visiting
the remaining patients until all the patients she re-
sponds are served.
(3)Each vehicle starts from the depot, then visits and
attends to patients, and terminates the journey at the
laboratory.
(4)we assume that the drugs have their own volume,
so the vehicle capacity must be taken into considera-
tion. However, the samples are vials of blood, or tem-
perature record sheets, which could be assumed to be
negligible and will not be considered with respect to
the capacity of the vehicle.
(5)In the process of delivery, the demand of the drugs
is described by fuzzy triangle variable. Only if the
nurse arrives the patient’s home, can she know the ex-
act quantity of the drugs.
Now, we give the mathematical notations as fol-
lows:
V : the set of the vehicles.
N: the set of the all the vertex in the graph, including
the depot, patients,and laboratory.
˜
d
i
= (d
1,i
, d
2,i
, d
3,i
): the fuzzy demand of the patient i;
C: the set of the patients.
i, j = 0, 1, 2, . . . , n + 1 is the index of the all the nodes
in the graph. Especially 0 stands for the index of the
depot, n+1 stands for the index of lab, and others are
the patients.
k = 1, 2, . . . , K stands for the index of the vehicle.
q: the capacity of the vehicle.
p: the employee salary for every nurse in this task.
u
i
: it is an artificial variable which is used to construct
the sub-tour constraint.
f
1
: the additional distance caused by failure route.
let us describe the mathematical model with the
most common used 3-index method:
x
i jk
=
(
1 if the kth vehicle traveals from patient i to patient j;
0 otherwise.
The Home Health Care Routing Problem with
Fuzzy Demand (HHCRPFD) model can be mathe-
matically formulated as shown below:
min f =
∑
i∈V
p
∑
i∈C
∑
j∈N
x
i jk
+
∑
k∈V
∑
i∈N
∑
j∈N
c
i j
x
i jk
+ f
1
(3)
subject to,
∑
k∈V
∑
j∈N
x
i jk
= 1 ∀i ∈ C (4)
Cr(
∑
i∈C
˜
d
i
∑
j∈N
x
i jk
− q ≥ 0) ≥ DPI ∀k ∈ V (5)
∑
j∈N
x
0 jk
= 1, ∀k ∈ V (6)
∑
i∈N
x
ihk
−
∑
j∈N
x
h jk
= 0, ∀h ∈ C, ∀k ∈ V (7)
∑
i∈N
x
i(n+1)k
= 1, ∀k ∈ V (8)
x
i jk
∈ {0, 1}, ∀i, j ∈ N, ∀k ∈ V (9)
u
i
− u
j
+ q ∗
K
∑
k=1
x
i jk
≤ q − d
1, j
, ∀i, j = 0, 1, . . . , N + 1, i 6= j;
(10)
The objective function (3) is to minimize the
total cost which includes the nurse employee cost,
planned transportation cost and the additional cost.
The constraints (4) donate that each customer is vis-
ited once and only once, and constraints(5) mean that
no vehicle is loaded with more than its capacity un-
der the fuzzy credibility theory. The constraints (6)
mean each vehicle starts from the depot. Constraints
(7)mean that each vehicle visits the patient and then
A Fuzzy Chance-constraint Programming Model for a Home Health Care Routing Problem with Fuzzy Demand
371
leaves the patient. Constraints (8) means that the ve-
hicle ends at the laboratory. Constraints (9) make the
decision-variable are binary. Constraints (10) are used
to eliminate sub-tours.
Our problem is neither like the classical VRP nor
like the Open Vehicle Routing problem (OVRP); all
the variations of VRP can be seen in the literature (Pil-
lac et al., 2013; Toth and Vigo, 2014). In the classical
VRP, each vehicle needs to return to the depot again,
while in the OVRP, each vehicle does not return to the
depot after servicing the last customer on a route, but
may end at a different location.
Remark 1: The mathematical is a typical Fuzzy
Chance Constraint Programming(FCCP), which is a
new branch in the uncertain programming. What’s
more, if we assume d
1,i
= d
2,i
= d
3,i
, the fuzzy
variable become a determinate variable, and the
HHCRPFD is reduced to a vehicle routing problem.
Considering that VRP has been proved to be the np-
hard problem, so there is no wonder that our model is
also a np-hard problem with fuzzy chance constraints.
Remark 2: If d
1,i
= d
2,i
= d
3,i
, this problem becomes
a deterministic model, and in this situation, the addi-
tional distance f
1
= 0.
3 HYBRID HEURISTIC
ALGORITHM
As mentioned above, the proposed model is a NP-
hard problem, which is difficult to solve by the exact
method when the size of the problem becomes large.
Here, we propose a hybrid heuristic algorithm (HHA)
by integrating the stochastic simulation method and
hybrid genetic algorithm. Generally speaking, in the
first stage, we apply the route construction method to
generate initial feasible solutions, then hybrid genetic
algorithm is employed to improve the initial solution.
To accelerate the convergence, elitism selection and
local search are employed, while to make the solution
escape from the local optima in advance, mutation op-
erators and crossover operators are designed. Consid-
ering that our problem is an instance of Fuzzy Chance
Constraint Programming (FCCP), Stochastic Simula-
tion method is designed to evaluate the each solution
candidate.
The detailed description of the HHA can are de-
scribed in the rest part of this section.
3.1 Individual Representation
In our research, each individual stands for feasible so-
lution, which is a vehicle routing arrangement. Here
we use a List to encode an individual which contains a
lot of routes. The process of the encoding and decod-
ing can be seen in Figure 1. The strength of this en-
code method is that each individual does not need to
be decoded and encoded alternately in the optimiza-
tion process.
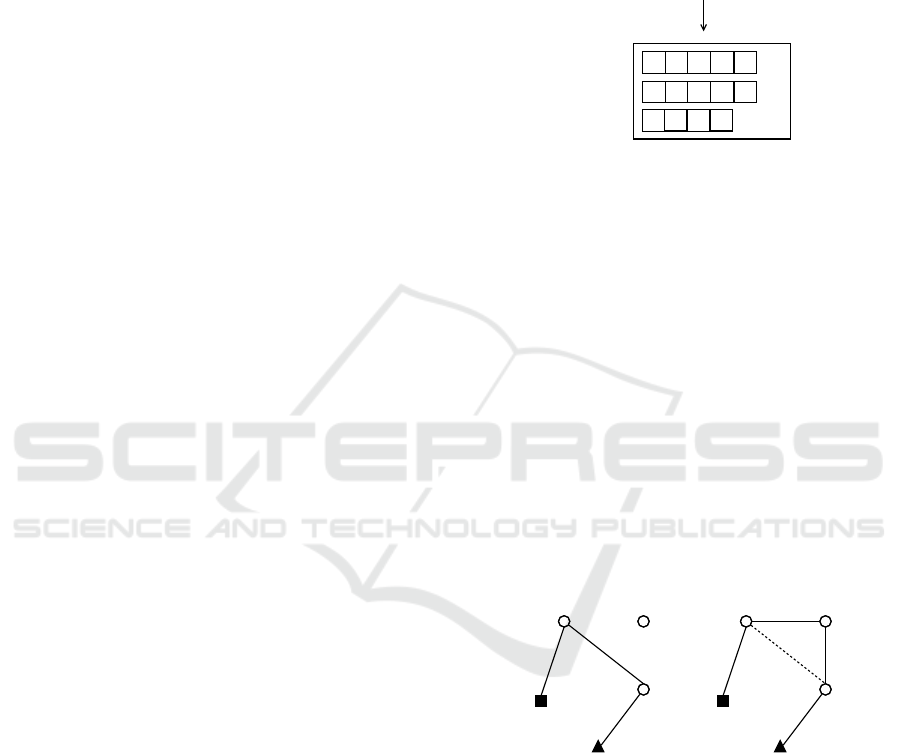
3
5
7
11
14
4
6
8
1
9
10
13
12
2
Depot->2->3->7->5->11->lab
Depot->14->4->6->8->1->lab
Depot->9->10->13->12->lab
Solution
Individual
Figure 1: The representation of a individual.
3.2 Initial Population
The initial population are composed by two kinds,
most of them are ordinary individuals which are gen-
erate randomly, the rest are high-quality ones which
are obtained from the classical heuristic algorithm
called insertion.
Insertion heuristic are widely used to quickly con-
struct a feasible solution (Toth and Vigo, 2014). In
each iteration, a node is selected among all the unvis-
ited nodes, and then insert it in a right position which
makes the new route feasible and least cost, while a
insertion position couldn’t be found, a new route is
started. This insertion process repeated until all the
nodes are visited. Figure 2 illustrates the insertion of
the node k between i and j with the corresponding
insertion cost c
ik
+ c
k j
− c
i j
.
i
depot
lab
j
k
depot
i
k
j
lab
Figure 2: The brief description of the insert method.
3.3 Fitness Evaluation
As mentioned above, the demand of drugs for each
patient is a triangular fuzzy number, so it cannot be
directly considered as a deterministic one.
Regarding the simulation of the phases of the
operation process of the HHC company and related
works, we derive an approximate estimate about ad-
ditional distances ( f
1
) due to route failures using a
stochastic simulation algorithm. We summarize the
stochastic simulation (Cao and Lai, 2010) as follows:
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
372

Step 1: For each patient, estimate the additional dis-
tance by simulating “actual” demand. The
“actual” demands were generated by the fol-
lowing process:
(1) randomly generate a real number of x in the
interval between the left and right bound-
aries of the triangular fuzzy number repre-
senting demand at the patient, and compute
its membership u.
(2) generate a random number a, a ∈ [0, 1];
(3) compare a with u, if a ≤ u, then “actual”
demand at the patient is adopted as being
equal to x; in the opposite case, if a < u, it
is not accepted that demand at the patient
equals x. In this case, random numbers x
and a are generated again and again until
random number x and a are found that sat-
isfy relation a ≤ u;
(4) check and repeat (1)–(3), and terminate the
process when each patient has a simulation
“actual” demand quantity.
Step 2: Move along the route designed by credibil-
ity theory and accumulate the amounts picked
up and calculate the additional distance due
to routes failure in terms of the “actual ” de-
mand..
Step 3: Repeat Step 1 and Step 2 for M times.
Step 4: Compute the average value of additional dis-
tance by M times simulation, and it is re-
garded as the additional distance f
1
.
In the fuzzy demand model, the objective is to
minimize the total cost, so the fitness value here we
choose to use f =
1
AD+PD
. Specially, if d
1,i
= d
2,i
=
d
3,i
,this problem becomes a determinate model, and
in this situation, the additional distance f
1
= 0, the
fitness can be described as f =
1
PD
3.4 Selection
In the evolution process, sometimes the good indi-
viduals may lost due to the crossover and mutation,
which is not favorable to the convergence of fitness
value. To overcome this drawback, we employ the
famous elitism strategy in the selection operator.
Here we pick out the top 2% individuals as elite
which are retained to the next generation directly
without taking part in the crossover, mutation and lo-
cal search operator.
3.5 Crossover
Crossover provides a chance to enhance the commu-
nication between different individuals, and aims to re-
produce new offspring. Ombuki proposed a effective
crossover operator named Best Cost Route Crossover
(BCRC) (Ombuki et al., 2006), the main idea is to
select nodes from one sub-route, and find a best po-
sition to reinsert them into the other individual one
by one. We can call this operator as a global version
of BCRC. Although his operator can perform well, it
takes a long time to find the best position of whole the
potential position. Inspired by his research, we pro-
posed a local version of BCRC. we insert each node
to the best position of a randomly selected route of the
individual. It is obviously that the local version saves
a lot of computing time.
The main steps of the crossover operator an be
found in Figure 3.
Figure 3: the crossover operator.
Specifically, for two individuals, the crossover is
undertaken as follows:
Step 1: For each individual, a route is selected ran-
domly. Before inserting the route into the
other individual, the repeating nodes would
be removed.
Step 2: The nodes selected from P1 (P2) are inserted
in to P2 (P1) one by one. Be attention that,
for the insertion of one node, one route is se-
lected randomly. The length of this route is
m, and the possible position for insertion is
m +1, and this node is inserted to the best po-
sition. This insertion is undertake until all the
selected nodes are inserted to the other indi-
vidual. while a insertion position could not be
found, a new route is started.
3.6 Mutation
Mutation is a divergence operation. It is intended to
occasionally break one or more members of a popu-
A Fuzzy Chance-constraint Programming Model for a Home Health Care Routing Problem with Fuzzy Demand
373

lation out of a local minimum space and potentially
discover a better minimum space. The mutation op-
erator is conducted by bring random, unrelated traits
into the present population and increase the variance
of the population. According to the characteristic of
individuals, two simple mutation operators are intro-
duced in our algorithm.
• inversion: two cut points are generated randomly,
and all the nodes between them will be inversed.
• single-point mutation: two nodes are randomly
generated, then they are swapped.
3.7 Local Search
In this paper, local search operator is employed to
improve the fitness value of the individuals and ob-
tain better solutions. The most commonly-used 2-opt
method, or-opt method and their extension (Br
¨
aysy
and Gendreau, 2005) are used to search the better so-
lution.
Note that the local search operators are quite not
the same with the mutation operator in two aspects:
(1) the aim of the local search operator is to make
an improvement of the solution, while the mutation
is just to make the population diversified which aims
to avoid the trapping into local optimal in advance.
(2) The mutation operator is executed just once in one
iteration, while the local search operators are executed
many times, until a solution deemed optimal is found
or a time bound is elapsed.
4 EXPERIMENTAL RESULTS
Because there was no one does the same work with
us, so it can not compare our work with the exist work
directly to validate the efficiency of the proposed Hy-
brid Heuristic Algorithm (HHA). Here, we firstly re-
duced our problem into the classical CVRP, experi-
mental results are compared with the optimal results.
After ensuring the algorithm is effective, we will use
it to solve the proposed fuzzy model. Here we need
to emphasize that the aim of our research is not to
design a new and efficient algorithm to solve the clas-
sical CVRP, but just to design an efficient algorithm
to solve the fuzzy model.
4.1 Experiments on Determinate Model
The fuzzy model is reduced to CVRP, if we assume
the following 3 points: (1) the fuzzy variables re-
duce to the deterministic ones, namely d
i,1
= di, 2 =
d
i,3
, i = 1, 2, . . . , N; (2) the laboratory is in the same
position with the depot. (3) the cost for each nurse is
0. In this situation, the fuzzy chance constraints be-
come the deterministic ones, additional distance be-
come 0.
Note that, when we apply the HHA to solve
the deterministic model, for there is no chance con-
straints, the additional cost is 0. And in the process of
fitness evaluation, stochastic simulation doesn’t used.
Here we use one of the most famous bench-
mark instances called A series to test the pro-
posed HHA. The instances and the optimal re-
sult can not be downloaded from the web-
site http://neo.lcc.uma.es/vrp/vrp-instances/, and our
computing results and the comparison can be found
in Table 1.
Note that, in Table 1, NO means the ID of the
instance,and the name of instance is composed in 3
parts: for example, the instance named “A-n60-k9”,
“A” means the instance is from A-series, “n60” means
the size of the nodes is 60, and “k9” means that the
number of expected used vehicle is 9. As results
show, TD means the total distance (also called to-
tal cost in some literature), NV means the number
of the used vehicles, CT means the computing time,
and GAP means the percentage of the error between
our result and the optimal result (Juan et al., 2010;
MirHassani and Abolghasemi, 2011).
Table 1: Experimental results for the CVRP model.
HGA optimal result
GAP
No. NV TD CT(s) NV TD
A-n32-k5 5 787.20 10.54 5 784.00 0.41%
A-n33-k5 5 688.11 10.34 5 661.00 4.10%
A-n33-k6 6 745.80 9.56 6 742.00 0.51%
A-n34-k5 5 794.64 10.39 5 778.00 2.14%
A-n36-k5 5 819.93 11.34 5 799.00 2.62%
A-n37-k5 5 673.50 11.98 5 669.00 0.67%
A-n37-k6 6 961.68 19.77 6 949.00 1.34%
A-n38-k5 5 761.40 21.73 5 730.00 4.30%
A-n38-k5 5 845.00 19.84 5 822.00 2.80%
A-n45-k7 7 1216.56 20.47 7 1146.00 6.16%
A-n60-k9 9 1437.48 17.17 9 1408.00 2.09%
B-n31-k5 5 680.96 10.31 5 672.00 1.33%
B-n41-k6 6 875.31 11.02 6 829.00 5.59%
B-n50-k8 8 1373.56 12.09 8 1313.00 4.61%
B-n63-k10 10 1627.00 55.61 10 1537.00 5.86%
B-n78-k10 10 1305.00 66.50 10 1266.00 3.08%
We can conclude that: (1) the number of used ve-
hicle in our results are quite the same with the ex-
pected number; (2) our result is quite close to the op-
timal solution; (3) our result arrives convergence in a
reasonable time even for the big size instance, consid-
ering that CVRP is a NP-hard problem. So there is no
doubt that the proposed hybrid algorithm have a good
performance in solving the CVRP, and we will apply
our heuristic algorithm to the fuzzy chance constraint
programming in the next subsection.
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
374

4.2 Experiments on the Fuzzy Model
In this part, the experiments will be taken on the fuzzy
model. Because there is no corresponding benchmark
for this problem, we adopted the instance from the
exited instance named A-n32-k5, which is a small size
instance. The hybrid heuristic algorithm is encoded in
Matlab 2015b; in the process of computing the fitness
value, the stochastic simulation for every individual is
500 times.
The Value for the Dispatcher’s Preference Index
(DPI) varied with the interval of 0.1 to 1 with the step
of 0.1. The computing results can be seen in Table 2 ,
Figure 4 and Figure 5.
Table 2: Experimental results for HHCRPFD model.
DPI NV TD PD AD
0.1 4 969.17 794.25 174.91
0.2 5 968.11 836.88 131.23
0.3 5 998.85 859.09 139.76
0.4 5 973.45 842.37 131.08
0.5 5 967.03 850.38 116.65
0.6 6 936.16 906.71 29.45
0.7 6 946.87 932.58 14.28
0.8 7 1063.27 1063.27 0.00
0.9 8 1163.66 1163.66 0.00
1 8 1203.94 1203.94 0.00
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
DPI value
0
200
400
600
800
1000
1200
1400
Cost
Total Distance
Planned Distance
Additional Distance
Figure 4: Cost changes for different DPI values.
We can find that, as DPI rose, the planned dis-
tance is increasing. While the additional distance is
strictly decreasing as DPI value increases from 0 to
0.7. However, when DPI ∈ [0.7, 1], the additional dis-
tance becomes 0, that means there’s no failure route.
The total distance is increasing, but not in a very strict
tendency. We can also find that, with the DPI rose,
the number of the needed nurses are increasing. It
concludes that more used nurses can help to decrease
the degree of the failure route.
As a consequence, lower values of parameter DPI
express our desire to use vehicle capacity the best we
can, so less nurses are needed. These values corre-
spond to routes with shorter planned distances. On
the other hand, lower values of parameter DPI in-
crease the number of cases in which vehicles arrive
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
the DPI value
4
4.5
5
5.5
6
6.5
7
7.5
8
the number of the used nurses
Figure 5: Number of the needed nurses changes for differ-
ent DPI values.
at a customer and are unable to service it, thereby in-
creasing the total additional distance they cover due
to the “failure”. Higher values of parameter DPI are
characterized by less utilization of vehicle capacity
along the planned routes and less additional distance
to cover due to failures, so more nurses are needed.
Therefore,when a HHC company makes decision on
this scenes (instance), the selected dispatcher prefer-
ence index should be 0.7 approximate.
5 CONCLUSIONS
Since transportation costs constitute one of the largest
forms of expenditure in the Home Health Care in-
dustry, it is of great significance to research the op-
timization of the Home Health Care logistics. Based
on a survey of the Home Health Care companies,
the basic operational process illustrates that the de-
mand for the required drugs for each patient is non-
deterministic when the HHC company makes a de-
cision to arrange the vehicle routing. In this paper,
vehicle routing problem with fuzzy demand is con-
sidered, and a fuzzy chance constraint is constructed
based on the fuzzy credibility theory. Stochastic sim-
ulation method and hybrid genetic algorithm are inte-
grated to solve the proposed model.
In order to test the proposed model and algo-
rithm, the fuzzy chance constraints were reduced to
the deterministic ones. Hybrid heuristic algorithm
were applied to solve the benchmark instances, re-
sults show that the proposed hybrid heuristic algo-
rithm perform well. Then the algorithms are applied
to the HHCRPFD, the best Dispatcher’s Preference
Index (DPI) is obtained, and the influence of the pa-
rameters to the objective functions are analyzed.
In the future, we will consider some other uncer-
tain information in the routing optimization problem,
such as stochastic traveling time, or fuzzy traveling
time. Some other heuristic method like Simulated
annealing (SA), Tabu search (TS), will also be inte-
grated to solve the related problems.
A Fuzzy Chance-constraint Programming Model for a Home Health Care Routing Problem with Fuzzy Demand
375

REFERENCES
Bianchi, L., Birattari, M., Chiarandini, M., Manfrin, M.,
Mastrolilli, M., Paquete, L., Rossi-Doria, O., and
Schiavinotto, T. (2006). Hybrid metaheuristics for
the vehicle routing problem with stochastic demands.
Journal of Mathematical Modelling and Algorithms,
5(1):91–110.
Br
¨
aysy, O. and Gendreau, M. (2005). Vehicle routing prob-
lem with time windows, part ii: Metaheuristics. Trans-
portation science, 39(1):119–139.
Cao, E. and Lai, M. (2010). The open vehicle routing prob-
lem with fuzzy demands. Expert Systems with Appli-
cations, 37(3):2405–2411.
Eksioglu, B., Vural, A. V., and Reisman, A. (2009). The
vehicle routing problem: A taxonomic review. Com-
puters & Industrial Engineering, 57(4):1472–1483.
Harris, M. D. (2015). Handbook of home health care ad-
ministration. Jones & Bartlett Publishers.
Juan, A. A., Faulin, J., Ruiz, R., Barrios, B., and Caball
´
e,
S. (2010). The sr-gcws hybrid algorithm for solving
the capacitated vehicle routing problem. Applied Soft
Computing, 10(1):215–224.
Liu, B., Zhao, R., and Wang, G. (2003). Uncertain pro-
gramming with applications.
Liu, R., Xie, X., Augusto, V., and Rodriguez, C. (2013).
Heuristic algorithms for a vehicle routing problem
with simultaneous delivery and pickup and time win-
dows in home health care. European Journal of Oper-
ational Research, 230(3):475–486.
Liu, R., Xie, X., and Garaix, T. (2014). Hybridization of
tabu search with feasible and infeasible local searches
for periodic home health care logistics. Omega,
47:17–32.
Mankowska, D. S., Meisel, F., and Bierwirth, C. (2014).
The home health care routing and scheduling problem
with interdependent services. Health care manage-
ment science, 17(1):15–30.
MirHassani, S. and Abolghasemi, N. (2011). A parti-
cle swarm optimization algorithm for open vehicle
routing problem. Expert Systems with Applications,
38(9):11547–11551.
Mousavi, S. M. and Niaki, S. T. A. (2013). Capacitated lo-
cation allocation problem with stochastic location and
fuzzy demand: a hybrid algorithm. Applied Mathe-
matical Modelling, 37(7):5109–5119.
Ombuki, B., Ross, B. J., and Hanshar, F. (2006). Multi-
objective genetic algorithms for vehicle routing prob-
lem with time windows. Applied Intelligence,
24(1):17–30.
Pillac, V., Gendreau, M., Gu
´
eret, C., and Medaglia, A. L.
(2013). A review of dynamic vehicle routing prob-
lems. European Journal of Operational Research,
225(1):1–11.
Toth, P. and Vigo, D. (2014). Vehicle routing: problems,
methods, and applications, volume 18. Siam.
Wen, M. and Iwamura, K. (2008). Fuzzy facility location-
allocation problem under the hurwicz criterion. Eu-
ropean journal of operational research, 184(2):627–
635.
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
376
