Fault Tolerance Analysis for Dependable Autonomous Agents using

Colored Time Petri Nets

Lan Anh Trinh, Baran C¨ur¨ukl¨u and Mikael Ekstr¨om

School of Innovation, Design and Technology, M¨alardalen University, V¨aster˚as, Sweden

Keywords:

Dependability, Fault Tolerance, Colored Time Petri Nets, Autonomous Agents.

Abstract:

Fault tolerance has become more and more important in the development of autonomous systems with the aim

to help the system to recover its normal activities even when some failures happen. Yet, one of the concerns

is how to analyze the reliability of a fault tolerance mechanism with regards to the collaboration of multiple

agents to complete a complicated task. To do so, an approach of fault tolerance analysis with the colored time

Petri net framework is proposed in this work, where a task can be represented by a tree of different concurrent

and dependent subtasks to assign to agents. Different subtasks and agents are modeled by color tokens in

Petri network. The time values are added to evaluate the processing performance of the whole system with

respect to its ability to solve a task with fault tolerance ability. The colored time Petri nets are then tested

with simulation of centralized and distributed systems. Finally the experiments are performed to show the

feasibility of the proposed approach. From the basics of this study, a generalized framework in the future can

be developed to address the fault tolerance analysis for a set of agents working with a sophisticated plan to

achieve a common target.

1 INTRODUCTION

Until recently, robots have played an important role

mainly in controlled processes such as manufactur-

ing. However, nowadays there is a shift which points

in the direction of having various types of (semi-

)autonomous agents, or robots, in our daily activities.

This paradigm shift also means that these agents will

most likely interact with each other, sometimes for

collaboration, in most case without having human su-

pervision. In short this is a shift to replace a conven-

tional automatic system with its autonomous coun-

terpart. Unlike an automatic robot that usually per-

forms repetitive tasks within a well-controlled envi-

ronment, an autonomous robot must perform its tasks

with a very high level of automation and may col-

laborate with other robots and human to complete in-

tended tasks. In this work, it is assumed that building

a trustworthy system of collaboration raises a num-

ber of challenging questions, that could be addressed

with the deﬁnition of dependability. Originally, de-

pendability is devised from software development ar-

eas and can be stated by Aviˇzienis et al. (Aviˇzienis

et al., 2004) as ”the ability to deliver service that can

justiﬁably be trusted”. To realize this idea, the de-

pendability is measured by attributes such as avail-

ability, reliability, safety, integrity, or maintainability.

In general, the dependability of a system is assessed

by one, several, or all above attributes. Within the

scope of this paper, the dependability is implemented

with the reliability which presents the continuity of a

system to provide correct services. It is noted that the

things affecting dependability consist of failures, er-

rors, and faults. The link between the above factors

is known as the fault-error-failure chain: The failure

happens when the service provided by a system does

not comply with its speciﬁcation; The error affects the

services and leads to the failure of the system; The hy-

pothesized cause of an error is a fault. However, the

failures are only detected at the system boundary. As

a system contains a number of interconnected parts,

the system boundary is deﬁned to decide which el-

ements are inside and which are outside the system.

In some cases, the faults cause errors inside the sys-

tem boundary and thus the errors may be not observ-

able immediately but lead to a failure later. There-

fore, the fault is the key that leads to a system fail-

ure and the approach to protect the system’s depend-

ability is to develop means of fault analysis and of

fault removal to prevent failures from the system. For

the sake of simplicity, the concept of agent is used in

this paper to refer to software or hardware (robot) sys-

228

Trinh L., CÃijrÃijklÃij B. and EkstrÃ˝um M.

Fault Tolerance Analysis for Dependable Autonomous Agents using Colored Time Petri Nets.

DOI: 10.5220/0006196002280235

In Proceedings of the 9th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2017), pages 228-235

ISBN: 978-989-758-219-6

tems which perform actions to interact with an envi-

ronment. Extensive literature reviews of conventional

works to deal with the means to remain dependabil-

ity of autonomous agents are presented by Guiochet

(Guiochet, 2015). It is noted that not all the faults

from the system always can be analyzed and removed.

Fault tolerance therefore aims at continuing agent ser-

vices even with the presence of faults during the op-

erational stages of autonomous agents. Usually, fault

tolerance is implemented by using redundant agents,

i.e., once a failure is present, the backup agent is acti-

vated to replace the failed one. One limitation of most

conventional works is that there is a lack of investi-

gation on the analysis of fault tolerance mechanism

within the scope of system dependability. Obviously,

the evaluation on the fault tolerance ability of a sys-

tem could provide valuable information to improve

the system performance. This paper therefore pro-

poses a fault tolerance analysis for autonomousagents

within the context of agent-agent collaboration. By

the means of fault analysis, different methods such as

Petri net (PN), fault tree analysis (FTA), failure modes

effects and criticality analysis (FMECA), and hazard

operability (HAZOP) have been developed (Bernardi

et al., 2013). Yet, the PN framework has received a

lot of attention from research community due to its

wide applications for fault prevention in both devel-

opment and operational stages of an agent architec-

ture. Which also includes support for mitigation of

the implementation progress. With regards to those

advantages, an extended PN with colored time PN

(CTPN) for the analysis of fault tolerance mechanism

of collaborative agents has been chosen.

The rest of the paper is organized as follows. Sec-

tion 2 presents extensive literature reviews related to

this work. The analyses of fault tolerance in both cen-

tralized and decentralized approaches together with

PN background are described in Section 3. Exper-

imental results are illustrated in Section 4. Finally,

Section 5 concludes the paper with discussion of fu-

ture works.

2 RELATED WORKS

As aforementioned,the assessment of system depend-

ability is based on the basic attributes. Depending on

the speciﬁc applications, different attributes are used

to measure the dependability of a system. In the early

developments of software platforms, a multi-level

view of dependable computing was ﬁrst developed by

Parhami (Parhami, 1994), in which most dependabil-

ity attributes were implemented. For robotics, with

regards to the safety to assess the dependability, an

intelligent home care robot to assist elderly people

was introduced by (Graf and Gele, 2001). The pro-

posed home care system was equipped with alterna-

tive levels of safety to prevent accidents caused by a

person being hit by the robot. The safety navigation

system consisted of user interface, path planning, and

obstacle avoidance with extensive sensors for motion

detection. In the work of (Mustapic et al., 2004), a

safe platform for industrial robotics has been devel-

oped. The authors have initialized the architectural

level of how to open a platform for quality constraints

and how to implement fault prevention. Although the

aspect of dependability was of major interest, these

papers did not address issues related to collaborative

robots.

For reliability analysis, PN has been applied as

an effective technique to model dependability (Mal-

hotra and Trivedi, 1995). Recently, reliability assess-

ment was introducedwith time PN and Markov chains

(Kohl´ık, 2009). The analysis of fault tolerance in

manufacturing systems by using PN was developed

by (Miyagi and Riascos, 2004). In their study, the

hierarchical and modular integration of PN was com-

bined to analyze production process, fault detection

process, and fault treatment process. Meanwhile, the

application of the generalized stochastic PN used on

the navigation of a single service agent was presented

by (Kim and Chung, 2007). The coordination of mul-

tiple controllers for agent navigation was then intro-

duced by (Moon and Chung, 2012). Similarly, PN

was used for the control of a group of robotic agents

(Joaquin et al., 2011).

In another aspect, the development of fault toler-

ance aims at increasing the reliability of a system. In

the work of (Troubitsyna and Javed, 2014), adaptive

fault tolerance was developed with regards to the sys-

tem dependability. A research on fault tolerance for

a group of agents in a cooperative environment was

described by (Haddad and Haddad, 2004). In their re-

search, the authors proposed a communication mech-

anism between the agents in a team to coordinate and

allocate the resources. The PN was used to illustrate

the model of the whole system. However, the research

is limited to a scheduling protocol for an agent team.

Close to our study, the fault tolerance analysis with

PN for a coordination of multi agents was developed

by (Acharya et al., 2014). However the approach pro-

posed by Acharya et al. has just initialized a picture

of how the system may look like. The study lacked

experimental setup for validation. Moreover, the non-

colored and non-hierarchy PN structure used in the

approach made the design complicated and unclear.

In this paper, the colored time PN enhanced with a

hierarchy structure is utilized to analyze the depend-

Fault Tolerance Analysis for Dependable Autonomous Agents using Colored Time Petri Nets

229

ability of cooperative autonomous agents. The ef-

fectiveness of color tokens helps to distinguish mul-

tiple agents working together to address a compli-

cated tasks of multiple subtasks. Unlike the origi-

nal Petri nets, the hierarchy structure of colored PN

combined with time value lacks for well-deﬁne math-

ematical tools for analysis. To deal with difﬁculty, the

repeated experiments and recorded data at interested

places and transitions of PN are applied for statistical

analysis. Finally, the proposed approach are exam-

ined with centralized and distributed studies.

3 BACKGROUND AND

PROPOSED APPROACH

3.1 Background of Petri Nets

Petri net (PN)(Yen, 2006) was described as a se-

quence of place-transition-place to move tokens

within a PN network. Well deﬁned mathematic mod-

els with a set of theory and linear algebra have been

developed to analyze the state-transition of PN. Be-

sides, a graphical presentation of PN helps to have a

clear visualization of the modeled system, which may

consist of synchronization, concurrency, and confu-

sion stage within distributed manners.

In mathematical aspect, PN is a bipartite graph de-

ﬁned as a set of three tuples (Γ,Σ,Θ), where Γ and Σ

are the set of ﬁnite places and transitions in such a

way that there is no element belonging to both Γ and

Σ,i.e, Γ and Σ are disjoint sets. Θ is the set of arcs

so that an arc connects from a place to a transition

and vice versa and the connections between places or

between transitions are unacceptable. The arcs go-

ing out from a place to a transition are named input

places of transitions, while the arcs going out from a

place are deﬁned as output places of transitions. An

extension of PN adds the weight on the input and out-

put ﬂows of each transition. With regards to the set

of output weights W

−

and input weights W

, PN is

reﬁned with a set of ﬁve tuples (Γ,Σ,Θ,W

−

A marking M of PN assigns a number of tokens to

each place. Let the marking M be expressed by a vec-

tor [M(p

),M(p

),...,M(p

)], where p

a place, n the number of places in PN, and M(p

)

the number of tokens at the place p

. Let W

−

be a

two dimensional matrix of weights W

−

) from

the place p

to the transition t

. W

is deﬁned in a

similar way with the weight W

, p

) from the tran-

sition t

to the place p

. Note that 1 ≤ j ≤ m, where m

is the number of transition. With regards to the tran-

sition t, the change of the marking vector from M to

′

is expressed by

′

(p) = M(p) + W

(t, p) −W

−

(p,t),∀p. (1)

The tuple (Γ,Σ,Θ,W

−

) of PN is extended to

(Γ,Σ,Θ,W

−

) with M

as the initial mark-

ing. Applying linear algebra based on equation (1),

the reachability from the marking M to M

′

can be

checked. Moreover, a full graph of all markings and

possible transition from one marking to another are

described by state-space analysis. As the number of

vertices and edges of the state-space graph increase

dramatically with regards to the number of places and

transitions, state-space analysis is limited to a small

PN network.

The colored PN (CPN) is an extension of PN,

in the sense that CPN has different types of token

marked with color (Jensen, 2003). The transition ﬁres

separately with respect to each kind of token. The

arc expressions built from operators and functions are

further used to decide the transition behavior of differ-

ent colors. Unlike conventional PN, only backward-

compatible CPN is able to be analyzed with avail-

able mathematical models. Other CPNs must rely on

simulation with statical analysis to reveal the visiting

frequencies of tokens at places and availability of a

marking state.

Another extension is the stochastic PN which adds

a time delay at each transition where the ﬁring rate

is determined by a random variable. The state-space

analysis is performed by probabilistic inference in a

Markov chain. Generalized stochastic PN extended

the stochastic PN with the possibility of immediate

transition to forward to token without any time delay.

In this paper, the generalized framework with colored

time PN (CTPN) is utilized to deal with the time de-

lay of both non-deterministic and deterministic vari-

ables. CPNTools (Jensen, 2003) are used to create

CTPN and perform the analysis.

3.2 Fault Tolerance with Cooperative

Agents

In the proposed system, it is supposed that there is

a pool of agents A = {a

,...,a

}, where N

is the number of agents. A sequence of tasks T =

,...,T

...,T

} are assigned to the set of agents

A to be processed one by one where t is the time

index. For a complicated task, it is convenient to

separate each task into a number of subtasks T

,...,t

}, where iG is the number of subtasks

of the task T

. The subtasks are categorized into inde-

pendent subtasks and dependent subtasks. The inde-

pendent subtasks can be processed independently and

concurrently by different agents. Meanwhile, the de-

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

230

pendent subtasks, like t

→ t

, requires that the sub-

task t

must be completed before t

For fault tolerance, the deﬁnition of peer agent is

introduced. The two agents a

and a

are peer agents

if they are able to solve the common subtask. Thanks

to the availability of multiple peer agents, once an

agent fails to do a subtask, other peer agents with the

similar function are used to continue the tasks. In

this model, the agents {a

} and the subtasks

} are available. Agent a

is assigned with the

subtasks {t

}, agent a

with the subtasks {t

and a

with the subtasks {t

} respectively.

3.3 CPN Models of Agents for Fault

Tolerance Analysis of Centralized

Systems

In this model, all subtasks are managed by a super-

vision module (SM) (Figure 1) with the tokens t(1),

t(2), and t(3). Once the SM receives a request to

perform a set of subtasks from a task management

module (TMM), it will send the subtasks to available

agents according to the description provided in Sec-

tion 3.2. If one of the agents fails to complete the sub-

task, the SM will assign the subtask to another peer

agent. Meanwhile, the SM will collect all ﬁnished

subtasks and send them to the TMM. For each sub-

task tree, the TMM is respectively designed. In this

paper, the design of the TMM for a combined subtask

tree is introduced as an example.

Subtasks

TSK

Completed

subtasks

TSK

Uncompleed

subtasks

TSK

For a(1)

AGxTSK

For a(2)

AGxTSK

For a(3)AGxTSK

Available

a(1)

1`a(1)

Available

a(2)

1`a(2)

Available

a(3)

AG1`a(3)

Agent(1)

Agent

Try

again

Agent(2)

Agent

Agent(3)

Agent

(a1xt1)

(a1xt2)

(a2xt2)

(a2xt3)

(a3xt1)

(a3xt3)

Task

Management

Task Management

(tk,ag)

a(1)

t(1)

(t(1),a(1))

t(2)

a(1)

(t(2),a(1))

t(2)

a(2)

(t(2),a(2))

t(3)

a(2)

(t(3),a(2))

t(1)

t(3)

a(3)

(t(1),a(3))

(t(3),a(3))

Agent

Task Management

Figure 1: Design of a supervision module in centralized sys-

tems.

The agents a

, a

, and a

(Figure 2) share the same

structure. It can be noted that this structure models

the agent modules (AMs) in the SM. If there is an

available agent, that agent will receive a subtask from

the SM. The approximate processing time to ﬁnish the

subtask is assumed to be τ

(value proctime in agent).

Meanwhile, the fail event of an agent is modeled by

a random variable of the exponential distribution with

the rate λ

(value failrate in agent). Once the agent

fails, the failed subtask will be returned to the SM and

it requires a time τ

(value ﬁxtime in agent) to recover

the normal activity of the agent. The tokens a(1),

a(2), and a(3) are used to reveal the availability of

the agents. Obviously, the performance of fault toler-

ance mechanism will depend on the tuples (τ

,λ

,τ

)

and the further analyses are presented in Section 4.

Tasks

AGxTSK

Return

agents

Out

Processing

AGxTSK

Done

AGxTSK

Completed

tasks

Out

TSK

Failures

Locked

Failed

agents

Returned

tasks

Out

TSK

Failed

token

1`f

start

transition

after

finished

failed

move

repair

fire

1`(tk,ag)@+

proctime

1`(tk,ag)

1`tk1`ag

1`f

1`(tk,ag)

1`ag

1`ag@+

fixtime

1`f

1`tk

1`f

1`f@+exp(failrate)

1`(tk,ag)

Out

Figure 2: Design of an agent module in centralized systems.

3.4 CPN Models of Agents for Fault

Tolerance Analysis of Distributed

Systems

For a distributed system, in the SM (Figure 3), each

agent will share the information of which subtasks

have been completed and which subtasks are un-

ﬁnished by broadcasting messages for any updates.

Whenever an agent decides to do a subtask, it will

send a broadcast message to the other agents. If there

are no conﬂicts, the agent will start the subtask and

remove the subtask from an uncompleted subtasks

(USs) place to process. Once the subtask is accom-

plished, the agent broadcasts a message to inform the

others to update and append the list in a completed

subtasks (CSs) place with the new completed subtask.

The agent, while doing a task, is being checked for its

availability and will frequently send an ”alive” mes-

sage. All agents will be noticed of the failures of an

Fault Tolerance Analysis for Dependable Autonomous Agents using Colored Time Petri Nets

231

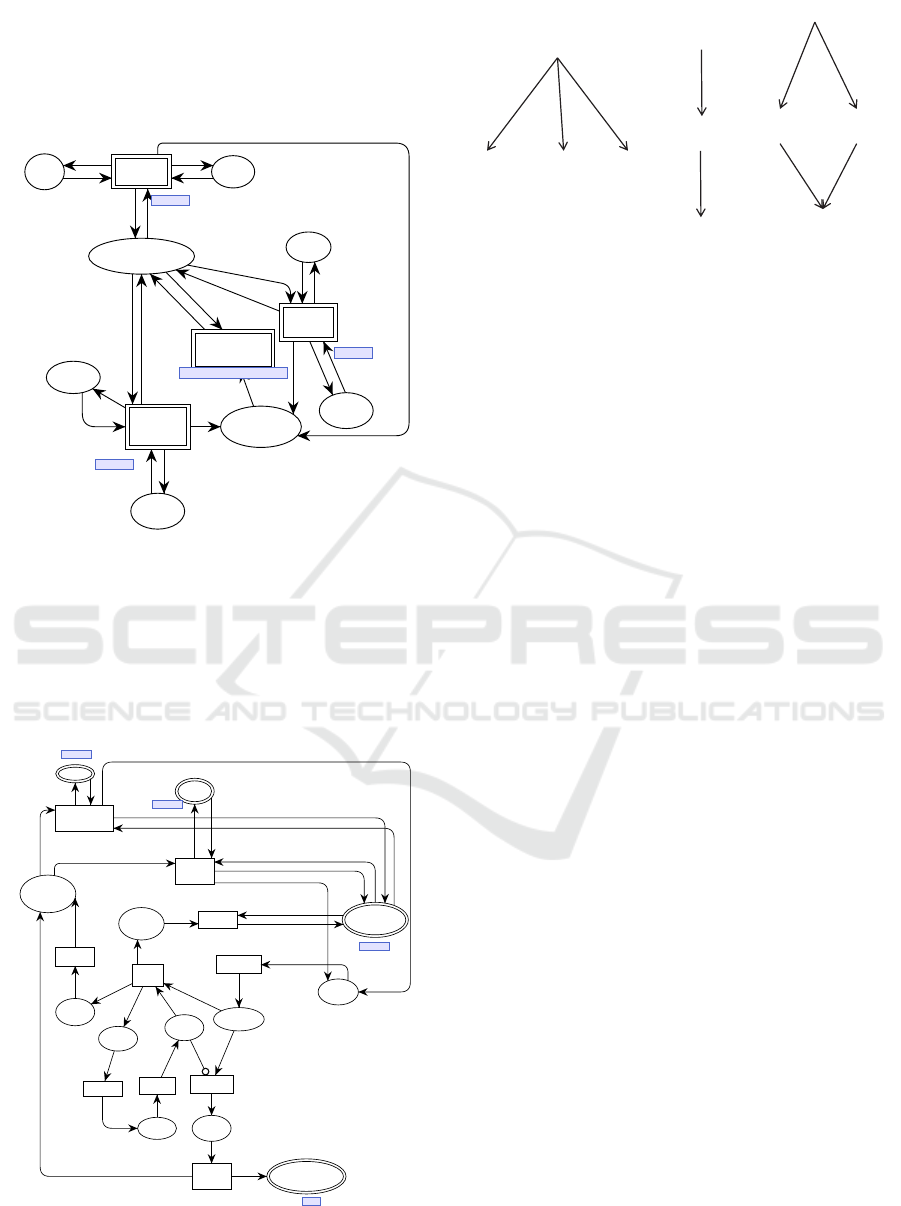
agent and the information is updated in the USs place.

In our system, it is assumed that the copy of the list

USs and CSs are available in the memory of every

agents. The design of an AM (Figure 4) is developed

Uncompleted

subtasks

TSKlist

Completed

subtasks

TSK

t(1)

TSK

1`t(1)

t(2)

TSK

1`t(2)

t(3)

TSK

1`t(3)

t(1) TSK

1`t(1)

t(2)

TSK

1`t(2)

t(3)

TSK

1`t(3)

Agent(1)

Agent

Agent(2)

Agent

Agent(3)

Agent

Task

Management

Task Management

tlist

Agent

Task Management

Agent

Figure 3: Design of a supervision module in distributed sys-

tems.

from the centralized systems. Yet, the module is ad-

vanced with the ability to choose and process the sub-

tasks from the USs by itself. Besides, the time delay

with a variable τ

(value broadcast in agent) is intro-

duced for the broadcast process.

Tasks

AGxTSK

Available

agents

1`a(1)

Processing

AGxTSK

Done AGxTSK

Completed

tasks

Out

TSK

Failures

Locked

Failed

agents

Returned

tasks

TSK

Failed

token

1`f

Uncompleted

tasks

In/Out

TSKlist

Test1

In/Out

TSK

Test2

In/Out

TSK

start

transition

after

finished

@+broadcast

failed

move

repair

fire

add

@+broadcast

check

@+broadcast

[mem tlist tk]

check

@+broadcast

[mem tlist tk]

1`(tk,ag)@+

proctime

1`(tk,ag)

1`tk

1`ag

1`f

1`(tk,ag)

1`ag1`ag

1`ag@+

fixtime

1`f

1`tk

1`f

1`f@+exp(failrate)

1`(tk,ag)

tlist

tlist^^[tk]

tlist

(tk,ag) rm tk tlist

tlist

rm tk tlist

(tk,ag)

In/Out

Out

In/Out

Figure 4: Design of an agent module in distributed systems.

(a) (b) (c)

Figure 5: Subtask trees. (a) Three subtasks t

, t

, and t

are

independent. (b) The order of processing subtasks is t

, t

and then t

. (c) Two subtasks t

and t

must be completed

before the subtask t

is processed.

4 RESULTS

As it is depicted in Figure 5, the differentsubtask trees

including independent subtasks, dependent subtasks,

and the combination of independent and dependent

subtasks are used for testing CPN models for both

centralized and distributed systems.

4.1 Fault Tolerance Analysis of

Centralized Systems

The TMM (Figure 6) is utilized to handle the com-

plicated tasks requiring the subtask t

to follow the

accomplishment of the subtask t

and t

. The TMMs

are designed similarly for the independent subtasks

and dependent subtasks. One hundred tasks are gen-

erated to test the fault tolerance ability of the coop-

erative agents. Each task consists of three concur-

rent subtasks t

, t

, and t

. Once all the subtasks are

completed, the TMM checks the results to conﬁrm

the accomplishment of the task and requires a new

task for the set of agents. The performance of fault

tolerance is evaluated by the average processing time

needed to process each task. The processing time of

each agent for a subtask is assumed τ

= 20. The

longer recovering time τ

needed of each agent after

a fail appears, the more time the whole system will

need to ﬁnish a task in general. Therefore, three cases

/τ

= 0.5, τ

/τ

= 1, and τ

/τ

= 1.5 were evalu-

ated respectively. The fail rate varies from 10 to 100,

(10 ≤ λ

≤ 100).

The results (Figure 7(a)) reﬂect what is expected

that the processing time increases when τ

/τ

in-

creases. Meanwhile, the processing time decreases

when the intervals between two fail events are pro-

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

232

10 20 30 40 50 60 70 80 90 100

Fail rate

1.5

2.5

3.5

Processing time

/τ

=0.5

/τ

=1.5

10 20 30 40 50 60 70 80 90 100

Fail rate

1.5

2.5

3.5

Processing time

/τ

=0.5

/τ

=1.5

10 20 30 40 50 60 70 80 90 100

Fail rate

1.5

2.5

3.5

Processing time

/τ

=0.5

/τ

=1.5

(a) (b) (c)

Figure 7: The average processing time to ﬁnish a task with respect to τ

/τ

in centralized systems. (a) Independent subtasks,

(b) Dependent subtasks, and (c) Mixtures of independent and dependent subtasks.

Generate

tasks

TSKx

100`(t(1),t(2),t(3))

Subtasks

Out

TSK

Finish

1 task

Completed

subtasks

TSK

Finish

tasks

TSKx

Process

1 task

Input

buffer

TSK

Output

buffer

TSK

divide

check

1st

2nd

3rd

done

(t(1),t(2),t(3))

t(3)

t(2)

t(1)

t(2)

t(3)

t(1)

t(2)

t(3)

t(2)

t(3)

t(1)

Out

Figure 6: Design of task management module for mixtures

of independent and dependent subtasks in centralized sys-

tems.

longed. Logarithm scale is utilized to present the pro-

cessing time as it is very high with respect to the low

fail rate λ

. For dependent subtasks, the same con-

ﬁgurations of parameters τ

, τ

, and λ

are used to

perform the simulation results. The similar results

(Figure 7(b)) are obtained that the average processing

time increases according to rising τ

/τ

and the de-

creasing interval between two fail events. However,

there are not many differences between τ

/τ

= 1 and

/τ

= 1.5. This may be due to the similar probabil-

ity of one of all three agents available to take care of

a subtask each time in the two cases. In the case of

combined subtask tree, the similar performance anal-

ysis of the processing time to complete all the tasks

with regards to the ratio τ

/τ

is acquired as given

in Figure 7(c). In conclusion, the dependency of dif-

ferent subtask within a task will require more time to

complete the task. Besides, the processing time in-

creases with respect to the increasing ratio τ

/τ

all the above studies.

4.2 Fault Tolerance Analysis of

Distributed Systems

As there are not many differences in the design of the

TMM between centralized and distributed systems, an

example of the TMM to deal with the complicated

tasks consisting of independent and dependent tasks

is shown in Figure 8. The conﬁguration parameters of

, τ

, and λ

are similar to those used in Section 4.1,

thus τ

= 2 is used in the following experiments.

The evaluation of fault tolerance performance of

distributed agents to process the independent subtasks

is given in Figure 9(a). Similarly, the average pro-

cessing time to complete a task is proportional to the

ratio τ

/τ

. However, due to the delay of broadcast-

ing messages, in overall, the processing time in dis-

tributed system is higher than that in centralized sys-

tem.

The results (Figure 9(b)) show the fault tolerance

performance of the distributed system to deal with

the tasks of dependent subtasks. However, the differ-

ences of the processing time with regards to the ratio

/τ

in the cases 0.5, 1.0, and 1.5 are not signiﬁcant.

Because all agents take time to deliver the broadcast

messages, a failed agent may be recovered before a

new subtask arrives. Therefore, the distributed system

is less dependent on the recovering time rather than

the centralized system. However, more experiments

must be performed to validate this conclusion. The

Fault Tolerance Analysis for Dependable Autonomous Agents using Colored Time Petri Nets

233

10 20 30 40 50 60 70 80 90 100

Fail rate

1.5

2.5

3.5

Processing time

/τ

=0.5

/τ

=1.5

10 20 30 40 50 60 70 80 90 100

Fail rate

1.5

2.5

3.5

4.5

Processing time

/τ

=0.5

/τ

=1.5

10 20 30 40 50 60 70 80 90 100

Fail rate

1.5

2.5

3.5

Processing time

/τ

=0.5

/τ

=1.5

(a) (b) (c)

Figure 9: The average processing time to ﬁnish a task with respect to τ

/τ

in distributed systems systems. (a) Independent

subtasks, (b) Dependent subtasks, and (c) Mixtures of independent and dependent subtasks.

Genere

tasks

TSKx

100`(t(1),t(2),t(3))

Subtasks

In/Out

TSKlist

Finish

1 task

Completed

subtasks

TSK

Finish

tasks

TSKx

Process

1 task

Input

buffer

TSK

Output

buffer

TSK

divide

check

3rd

done

1st&2nd

(t(1),t(2),t(3))

tlist

t(1)

t(2)

t(3)

t(2)

tlist^^[t(3)]

t(2)

t(3)

t(1)

t(2)

t(3)

t(1)

t(2)

[t(1),t(2)]

t(1)

tlist

In/Out

Figure 8: Design of task management module for mixtures

of independent and dependent subtasks in distributed sys-

tems.

last experimental results (Figure 9(c)) present how

the distributed systems process the tasks of mixed in-

dependent and dependent subtasks. There are simi-

lar conclusions to those presented in previous simula-

tions.

Finally, an overall evaluation (Figure 10) is used

to assess the fault tolerance ability of cooperative dis-

tributed agents. It can be seen that the appearances of

more dependent subtasks will prolong the whole pro-

cess to perform the task. Besides, the time required

by communication protocol used in distributed pro-

tocol also affected the fault tolerance performance.

In order to investigate further on this concern, the

processing time is evaluated with regards to the time

0.5 1.0 1.5

Ratio τ

/τ

200

400

600

800

1000

1200

1400

1600

1800

2000

Processing time

Independent subtasks

Dependent subtasks

Combined subtasks

Figure 10: Overall evaluation of distributed systems.

10 20 30 40 50 60 70 80 90 100

Fail rate

1.5

2.5

3.5

4.5

5.5

6.5

Processing time

/τ

=0.25

/τ

=0.5

/τ

=0.75

/τ

=1.25

/τ

=1.5

Figure 11: Correlation of time to deliver broadcast message

with the fault tolerance performance.

needed to broadcast messages among agents. Sim-

ilarly, the ﬁxed ratio is in a range τ

/τ

= 1 and

0.25 ≤ τ

/τ

≤ 1.5. The results in Figure 11 clearly

showthe effects of communicationtime with fault tol-

erance ability of the system.

5 CONCLUSIONS

In this paper, the formulation of CTPN has been in-

troduced for the fault tolerance analysis for a group

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

234

of agents cooperating to solve complicated tasks. The

fault tolerance is performed by replacing a failed

agent to continue the unﬁnished tasks. The CTPN

models have been designed to validate this method

for both centralized and distributed approaches. In

simulations, different trees of independent and depen-

dent subtasks were evaluated. From the experimental

results, the analysis has shown the correlation of the

processing time to ﬁnish a complicated task with the

failure rates of an agent. Besides, the experiments re-

vealed that for distributed agents, the communication

protocol also played an important role on the fault tol-

erance success of the whole system.

In future, the proposed approach will be extended

to deal with a more complicated tree of subtasks.

Other fault tolerance mechanisms for the group of

agents are also concerned. Furthermore, experiments

with real robots will be planned to compare the fault

tolerance analysis provided by PN with that acquired

from realistic setup.

ACKNOWLEDGEMENTS

The research leading to the presented results has

been undertaken within the research proﬁle DPAC -

Dependable Platforms for Autonomous Systems and

Control project, funded by the Swedish Knowledge

Foundation.

REFERENCES

Acharya, S., Upadhyay, P. D., and Dutta, A. (2014). Fault

tolerance multi agent co-ordination: A petri net based

approach. In Proceedings on International Confer-

ence on Recent Advances and future Trends in Infor-

mation Technology.

Aviˇzienis, A., Laprie, J., Randell, B., and Landwehr, C.

(2004). Basic concepts and taxonomy of dependable

and secure computing. IEEE Transactions on Depend-

able and Secure Computing, 1(1).

Bernardi, S., Merseguer, J., and Petriu, D. C. (2013).

Model-Driven Dependability Assessment of Software

Systems. SPRINGER.

Graf, B. and Gele, M. (2001). Dependable interation with

an intelligent home care robot. In In proceedings of

ICRA - Workshop on Technical Challenge for Depend-

able Robots in Human Environments. IEEE.

Guiochet, J. (2015). Trusting robots : Contributions to de-

pendable autonomous collaborative robotic systems.

Technical report, LAAS - Laboratoire d’analyse et

d’architecture des systmes [Toulouse].

Haddad, J. and Haddad, S. (2004). A fault-tolerant commu-

nication mechanism for cooperative robots. Interna-

tional Journal of Production Research, 42(14):2793–

2808.

Jensen, K. (2003). Coloured Petri Nets: Basic Concepts,

Analysis Methods and Practical Use. Springer Verlag.

Joaquin, L., Diego, P., and Eduardo, Z. (2011). A frame-

work for building mobile single and multi-robot ap-

plications. Robotics and Autonomous Systems, 59(3-

4):151–162.

Kim, G. and Chung, W. (2007). Navigation behavior se-

lection using generalized stochastic petri nets for a

service robot. IEEE Transactions on Systems, Man,

and Cybernetics part C: Applicactions and Reviews,

37(4).

Kohl´ık, M. (2009). Dependability models based on petri

nets and markov chains. In Information Science and

Computer Engineering, 1st Class, Full-time study.

Malhotra, M. and Trivedi, K. (1995). Dependability model-

ing using Petri-nets. IEEE Transactions on Reliability,

44(3).

Miyagi, P. and Riascos, L. (2004). Modeling and analy-

sis of fault-tolerant systems for machining operations

based on petri nets. Control Engineering Practice,

14(4):397–408.

Moon, C. and Chung, W. (2012). Coordination of multi-

ple control schemes for mobile robot navigation on

the basis of the generalized stochastic petri-nets. Ad-

vanced Robotics, 26(5-6):581–603.

Mustapic, G., Anderson, J., Norstrom, C., and Wall, A.

(2004). A Dependable Open Platform for Industrial

Robotics - A Case Study. SPRINGER.

Parhami, B. (1994). A multi-level view of dependable

computing. Computers and Electrical Engineering,

20(4):347–368.

Troubitsyna, E. and Javed, K. (2014). Towards systematic

design of adaptive fault tolerant systems. In ADAP-

TIVE 2014, The Sixth International Conference on

Adaptive and Self-Adaptive Systems and Applications.

IARIA.

Yen, H. (2006). Introduction to petri net theory, in recent ad-

vances in formal languages and applications. In Stud-

ies in Computational Intelligence, volume 25, pages

343–373.

Fault Tolerance Analysis for Dependable Autonomous Agents using Colored Time Petri Nets

235