
Orthogonal Neighborhood Preserving Projection using L1-norm
Minimization
Purvi A. Koringa and Suman K. Mitra
Dhirubhai Ambami Institute of Information and Communication Technology, Gandhinagar, Gujarat, India
{201321010, suman mitra}@daiict.ac.in
Keywords:
L1-norm, L2-norm, Outliers, Dimensionality Reduction.
Abstract:
Subspace analysis or dimensionality reduction techniques are becoming very popular for many computer vi-
sion tasks including face recognition or in general image recognition. Most of such techniques deal with
optimizing a cost function using L2-norm. However, recently, due to capability of handling outliers, opti-
mizing such cost function using L1-norm is drawing the attention of researchers. Present work is the first
attempt towards the same goal where Orthogonal Neighbourhood Preserving Projection (ONPP) technique is
optimized using L1-norm. In particular the relation of ONPP and PCA is established in the light of L2-norm
and then ONPP is optimized using an already proposed mechanism of L1-PCA. Extensive experiments are
performed on synthetic as well as real data. It has been observed that L1-ONPP outperforms its counterpart
L2-ONPP.
1 INTRODUCTION
Images are very high dimensional data which poses
many challenges while handling them in fields like
computer vision, machine learning etc. Though, im-
age seems to be high dimensional data, it is observed
that it lies in comparatively very low linear or non-
linear manifold (He et al., 2005), (Kokiopoulou and
Saad, 2007). This leads to the development of data di-
mensionality reduction techniques. The fundamental
idea is to seek a linear or non-linear transformation to
map the high dimensional data to a lower dimensional
subspace which makes the same class of data more
compact. This leads to favorable outcomes for classi-
fication tasks or reduces computational burden. Such
manifold learning based methods have drawn consid-
erable interests in recent years. Some of the exam-
ples are Principal Component Analysis (PCA) (Turk
and Pentland, 1991), Linear Discriminant Analysis
(LDA) (Lu et al., 2003), Locality Preserving Projec-
tion (LPP) (He and Niyogi, 2004), (Shikkenawis and
Mitra, 2012) and Neighborhood Preserving Embed-
ding (NPE) (He et al., 2005), (Koringa et al., 2015).
Techniques such as PCA and LDA preserve global ge-
ometry of data. On the other hand, techniques such as
LPP and NPE tend to preserve local geometry by a
graph structure, based on local neighborhood infor-
mation.
The linear dimensionality reduction method
Orthogonal Neighborhood Preserving Projection
(ONPP) proposed in (Kokiopoulou and Saad, 2007)
preserves global geometry of data as well as captures
innate relationship of local neighborhood. An ex-
tended version of the same is presented in (Koringa
et al., 2015). ONPP is linear extension of Locally
Linear Embedding (LLE) presented in (Roweis and
Saul, 2000) which assumes that the data point ly-
ing on a small patch have linear relationship with its
neighbours. LLE uses a weighted nearest neighbor-
hood graph to represent local geometry by represent-
ing each data point as linear combination of its neigh-
bors and it embeds sample points into lower dimen-
sional space such that the linear relationship is also
preserved in lower dimensional space. Being a non-
linear dimensionality reduction technique, LLE does
not have any mechanism of accommodating out-of-
sample data. ONPP uses the same philosophy as that
of LLE and projects the sample data onto linear sub-
space and thus allows an out-of-sample data point to
be projected in low dimensional space.
All these dimensionality reduction techniques
mainly use cost function in the form of optimizing
error in L2-norm, which are not robust to out-liers
(Chang and Yeung, 2006). L1-norm on other hand, is
known for its robustness to out-liers. In recent times,
L1-norm optimization is employed to dimensionality
reduction techniques. This paper uses one such al-
gorithm used in L1-PCA (Kwak, 2008) to achieve
Koringa, P. and Mitra, S.
Orthogonal Neighborhood Preserving Projection using L1-norm Minimization.
DOI: 10.5220/0006196101650172
In Proceedings of the 6th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2017), pages 165-172
ISBN: 978-989-758-222-6
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
165

L1-ONPP. This article contains the experiments on
synthetic data showing susceptibility of L2-ONPP to-
wards outliers and comparison of the performance of
L2-ONPP and L1-ONPP on data having outliers. The
relationship between PCA and ONPP is established
and proved theoretically, the experiment performed
on synthetic as well as real data supports the claim
that ONPP basis can be obtained using PCA. Experi-
mental results suggest that L1-ONPP outperforms L2-
ONPP while dealing with the outliers.
In the next section, L1-norm based PCA is ex-
plained in detail, following section III establishes
relation between ONPP and PCA. Section IV con-
sists of experimental results followed by conclusion
in Section V.
2 L1-NORM FOR
DIMENSIONALITY
REDUCTION
All conventional Dimensionality reduction tech-
niques employs optimization of cost function in terms
of L2-norms. Conventional ONPP is also based
on L2-norm optimization (Kokiopoulou and Saad,
2007). Although it has been successful in many prob-
lems, it is prone to the presence of outliers because
the effect of the outliers with a large norm is exag-
gerated by the use of the L2-norm. In order to allevi-
ate this problem and achieve robustness, research has
been performed on L1-norm based dimensionality re-
duction techniques. Many works have been done in
PCA based on L1-norm (Ding et al., 2006), (Baccini
et al., 1996), (Ke and Kanade, 2005), (Kwak, 2008).
Not much works has been carried to propose L1-norm
based methods of recently proposed dimensionality
reduction techniques such as LPP and ONPP.
In (Baccini et al., 1996), (Ke and Kanade, 2005),
each component of the error between the original
data point and its projection was assumed to follow a
Laplacian distribution instead of Gaussian and maxi-
mum likelihood estimation was used to formulate L1-
norm PCA (L1- PCA) to the given data. In (Bac-
cini et al., 1996), a heuristic estimation for general
L1 problem was used to obtain a solution of L1-PCA.
While, in (Ke and Kanade, 2005), the weighted me-
dian method and convex programming methods were
proposed for L1-norm PCA. Despite the robustness
of L1-PCA, it has several drawbacks and it is com-
putationally expensive because it is based on linear
or quadratic programming. In (Ding et al., 2006),
R1-PCA was proposed, which combines the merits of
L2-PCA and those of L1-PCA. R1-PCA is rotational
invariant like L2-PCA and it successfully suppresses
the effect of outliers as L1-PCA does. However, these
methods are highly dependent on the dimension d of
a subspace to be found. For example, the projection
vector obtained when d = 1 may not be in a subspace
obtained when d = 2. Moreover, as it is an iterative
algorithm so for a large dimensional input space, it
takes a lot of time to achieve convergence. Let us now
discuss the work on L1-norm based PCA.
2.1 L1-norm PCA
Let X = [x
1
,x
2
,....,x
n
] ∈ R
m×n
be the given data
where m and n denotes dimensions of the original in-
put space and number of data samples, respectively.
Without losing generality, data is assumed to have
zero mean i.e.
¯
x = 0. L2-PCA tries to find a d(<m)
dimensional linear subspace such that the basis vec-
tors capture the direction of maximum variance by
minimizing the error function:
argmaxE(y) = arg max
n
∑
i=1
k y
i
−
¯
y k
2
y
i
= V
T
x
i
argmax E(V) = arg max
n
∑
i=1
k V
T
x
i
− V
T
¯
x k
2
argmax E(V) = arg max
n
∑
i=1
k V
T
x
i
k
2
argmax E(V) = arg max k V
T
X k
2
(1)
subject to V
T
V = I
d
where, V ∈ R
m×d
is the projection matrix whose
columns constitute the bases of the d dimensional lin-
ear subspace.
In (Kwak, 2008), instead of maximizing variance
in original space which is based on the L2-norm, a
method that maximizes the dispersion in L1-norm in
the feature space is presented to achieve robust and
rotational invariant PCA. The approach presented in
(Kwak, 2008) for L1-norm optimization is simple, it-
erative and easy to implement. It is also proven to find
a locally maximal solution. Maximizing dispersion
using L1-norm in the feature space can be presented
as
argmax E(V) = arg max k V
T
X k
1
(2)
The closed form solution is not possible in L1-
norm maximization problem, thus the basis are sought
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
166

iteratively as follows:
For d = 1
v
1
= argmax k v
T
X k
1
= argmax
n
∑
i=1
|v
T
x
i
| (3)
subject to k v k
2
= 1
For d>1
Once the basis in the direction of maximum vari-
ance v
i
(here, v
1
) is found as explained above,
the data is projected on this basis vector. For
rest of the basis vectors the same maximiza-
tion problem given in 2 is solved for projected
samples (X
d
= X
d−1
− v
d−1
(v
T
d−1
X
d−1
)) iteratively,
which essentially means in every iteration, direction
of maximum variance is sought, the data is projected
on this basis and from this projected data the direction
of maximum variance is sought until desirable dimen-
sional space is achieved.
Algorithm to Compute L1-PCA Basis:(Kwak,
2008)
For d = 1:
1. Initialization: Pick any v(0). Set
v(0) ← v(0)/ k v(0) k
2
and t = 0.
2. Polarity Check: For all i ∈ 1,...,n, if v
T
(t)x
i
< 0,
p
i
(t) = −1, otherwise p
i
(t) = 1
3. Flipping and maximization: Set t ← t + 1, and
v(t) =
∑
n
i=1
p
i
(t)x
i
. Set v(t) ← v(t)/ k v(t) k
2
4. Convergence Check:
a. if v(t) 6= v(t − 1), go to Step 2.
b. Else if there exists i such that v
T
(t)x
i
= 0, set
v(t) ← (v(t)+∆v)/ k v(t)+∆v k
2
and go to step
2, Here, ∆v is a small nonzero random vector.
c. Otherwise, set v
∗
= v(t) and stop.
For d>1:
For j = 2 to d,
1. Projecting Data: X
j
= X
j−1
− v
j−1
(v
T
j−1
X
j−1
)
2. Finding L1-PCA basis: in order to find v
j
, apply
L1-PCA procedure to X
j
end
3 ONPP IN TERMS OF PCA OF
RECONSTRUCTION ERRORS
Now coming to ONPP(Kokiopoulou and Saad, 2007),
which is a linear extension of LLE and thus inherits
the sensitivity towards outliers. The degradation in
manifold learning in the presence of outliers inspired
the use of L1-norm minimization of ONPP to tackle
the outliers. In the Section 3.1 traditional L2-ONPP is
explained and then the relationship between L2-PCA
and L2-ONPP established in Section 3.2. Section 3.3
explains how L1-PCA can be used to compute L1-
ONPP bases.
3.1 L2-ONPP and L2-MONPP
LLE is a nonlinear dimensionality reduction tech-
nique that embeds high dimension data samples on
lower dimensional subspace. The drawback of this
embedding is the non-explicit mapping, in the sense
that embedding is data dependent. In LLE, learned
data manifold will change with the inclusion or ex-
clusion of data point. Hence, problem such as recog-
nition or classification of out-of-sample, LLE fails.
ONPP is linear extension of LLE which resolves this
problem and finds the explicit mapping of the data in
lower dimensional subspace through a linear orthog-
onal projection matrix. In presence of this orthogonal
projection matrix, new data point can be embedded
into lower dimensional subspace making classifica-
tion or recognition task of out-of-sample data possi-
ble. However, like LLE, ONPP is also susceptible
to presence of outliers. Another variant of ONPP is
Modified ONPP (Koringa et al., 2015), which consid-
ered local non-linearity in neighbourhood patch and
uses non-linear weight to reconstruct the data point.
ONPP and MONPP both uses L2-norm optimization,
the difference between both dimensionality reduc-
tion algorithm is the mechanism to assign weights to
neighbours of a data points as explained below.
Let X = [x
1
,x
2
,....,x
n
] ∈ R
m×n
be the data ma-
trix such that x
1
,x
2
,....,x
n
are data points from m-
dimensional space. The key task of the subspace
based dimensionality reduction techniques is to find
an orthogonal or non-orthogonal projection matrix
V
m×d
such that Y = V
T
X, where Y ∈ R
d×n
is the em-
bedding of X in lower dimension as d is assumed to
be less than m.
ONPP achieves the projection matrix in two step
algorithm, the first step considers local patches, where
each data point is expressed as a linear combination
of its neighbors. In the second step, ONPP tries to
preserve this linear relationship in neighbourhood and
achieves data compactness through a minimization
problem.
Let N
x
i
be the set of k neighbors x
j
s of data point
x
i
. First, data point x
i
is expressed as linear combi-
nation of its neighbors as
∑
k
j=1
w
i j
x
j
where, x
j
∈ N
x
i
.
The weight w
i j
are computed by minimizing the re-
construction errors i.e. error between x
i
and linear
combination of its neighbours x
j
∈ N
x
i
. The mini-
mization problem can be posed as:
Orthogonal Neighborhood Preserving Projection using L1-norm Minimization
167

argmin E(W) = arg max
1
2
n
∑
i=1
k x
i
−
k
∑
j=1
w
i j
x
j
k
2
(4)
subject to
∑
k
j=1
w
i j
= 1.
The problem corresponding to point x
i
can be
solved as a least square problem. let X
N
i
be a neigh-
bourhood matrix having x
j
as its columns, where
x
j
∈ N
x
i
. Note that X
N
i
includes x
i
as its own neigh-
bor. Hence, dimension of X
N
i
is m × k + 1. Now
equation (4) can be written as a least square problem
(X
N
i
− x
i
e
T
)w
i
= 0 with a constraint e
T
w
i
= 1. Here,
w
i
is a weight vector of dimension k × 1 and e is a
vector of ones. A closed form solution, as shown in
equation (5) is derived for w
i
. Here, e is a vector of
ones having dimension k × 1 same as w
i
.
w
i
=
G
−1
e
e
T
G
−1
e
(5)
where, G is Gramiam matrix of dimension k ×
k. Each element of G is calculated as g
pl
= (x
i
−
x
p
)
T
(x
i
− x
l
), f or ∀x
p
,x
l
∈ N
x
i
On the other hand, MONPP stresses on the fact
that the local neighbourhood patch assumed to be lin-
ear may have some non-linearity and thus uses non-
linear weights incorporating Z-shaped function (Ko-
ringa et al., 2015) to reconstruct a data point using its
neighbours. Equation(6) is used to assign weight to
each neighbor x
j
corresponding to x
i
using Z-shaped
function based on the distance d between them. Note
that this equation is same as equation(5), where G
−1
is replaced by Z. The new weights are
w
i
=
Ze
e
T
Ze
(6)
Next step is dimensionality reduction or finding
the projection matrix V such that the data point x
i
∈
R
m
is projected on lower dimensional space as y
i
∈
R
d
(d << m) with the assumption that the linear com-
bination of neighbors x
j
s which reconstruct the data
point x
i
in higher dimensional space would also re-
construct y
i
in lower dimensional space with corre-
sponding neighbors y
j
s along with same weights w
i j
as in higher dimensional space. Such embedding can
be obtained by solving a minimization problem of re-
construction errors in the lower dimensional space.
Hence, the objective function is given by
argmin E(Y) = arg max
n
∑
i=1
k y
i
−
n
∑
j=1
w
i j
y
j
k
2
(7)
subject to, V
T
V = I
d
(orthogonality constraint).
This optimization problem results in a eigen-value
problem and the closed form solution is eigen-vectors
corresponding to the smallest d eigen values of matrix
X(I−W)(I−W
T
)X
T
. ONPP explicitly maps X to Y,
which is of the form Y = V
T
X, where, each column
of V is an eigen-vector.
3.2 L2-norm ONPP using PCA
Consider the philosophy of ONPP, where each data
point x
i
is reconstructed with its neighbours x
j
∈ N
x
i
.
Let X
0
= [x
0
1
,x
0
2
,....,x
0
n
] ∈ R
m×n
be the reconstructed
data matrix. The same can be written as a product of
data matrix X and weight matrix W = [w
1
,w
2
,...w
n
]
i.e. XW. Thus reconstruction error for each data
point can be denoted as er
i
= x
i
− x
0
i
as shown in
Figure(1) and the reconstruction error matrix is
Er = X − XW such that each column of matrix
Er represents error vector er
i
between x
i
and its
reconstruction x
0
i
.
Figure 1: Illustration of data point x
i
, its reconstruction x
0
i
using neighbors N
x
i
and error vector er
i
.
To establish relationship between PCA and ONPP,
rewrite the equation (7) in a matrix form:
argmin E(Y) = arg max k Y − YW k
2
argmin E(V) = arg max k V
T
X − V
T
XW k
2
argmin E(V) = arg max k V
T
(X − XW) k
2
argmin E(V) = arg max k V
T
Er k
2
(8)
Now comparing the optimization problems for
PCA in Equation(1) and the optimization problem
for ONPP in Equation(8), both are eigen-value prob-
lems and have closed form solution in term of eigen-
vectors. Equation(1) is maximization problem thus
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
168

the desired bases are eigen-vectors corresponding to
largest d eigen-values, where as Equation(8) is min-
imization problem thus the bases vectors are eigen-
vectors corresponding to smallest d eigen-values.
In other word, ONPP is essentially finding bases
vectors V such that it captures the direction in which
the variance of reconstruction error is minimum. Thus
the weakest basis of PCA when performed on the re-
construction errors Er is the strongest ONPP basis.
This result was verified in experiments performed on
the synthetic data and it is observed that the ONPP
bases obtained in using conventional algorithm and
ONPP bases obtained using PCA on reconstruction
error are same. The experiments are documented in
Section 4.
3.3 L1-norm ONPP using PCA on
Reconstruction Error
The relationship established between L2-PCA and
L2-ONPP in Section 3.2 led to the use of L1-PCA
algorithm to solve L1-ONPP optimization problem.
Rewriting ONPP optimization problem in Equation
(7) as a L1-norm minimization problem, we have
argmin F (Y) = argmax
n
∑
i=1
k y
i
−
n
∑
j=1
w
i j
y
j
k
1
(9)
subject to, V
T
V = argmax I (orthogonality con-
straint).
In matrix form,
argmin F (Y) = argmax k Y − YW k
1
argmin F (V) = argmax k V
T
X − V
T
XW k
1
argmin F (V) = argmax k V
T
(X − XW) k
1
argmin F (V) = argmax k V
T
Er k
1
(10)
As established in Section 3.2, the problem stated
in Equation(10) is similar to problem stated in L1-
PCA (Equation(2)), and can be solved using L1-PCA
algorithm performed on reconstruction error matrix
Er.
Comparing equation (10) with equation (2) of
PCA, we can intuitively state that the component in
the direction of minimum variance gives strong ONPP
basis i.e. considering each reconstruction error vector
er
i
as one data point in m-dimensional space, the d-
dimensional space can be sought such that the bases
vectors are in the direction of minimum variances of
the reconstruction error. Such bases can be computed
using L1-PCA algorithm given in Section 2.1 where,
each reconstruction error er
i
is treated as a data point.
4 EXPERIMENTS
To validate the theoretical conclusion on the bases L2-
ONPP and L2-PCA, experiments were performed on
the synthetic as well as real data as documented in this
Section.
4.1 A Toy Problem with Swiss Role
Data
An experiment was performed on Swiss-role data to
observe the effect of outliers on L2-ONPP embed-
dings. Over 2000 3D data points were randomly sam-
pled from a continuous Swiss-role manifold, random
uniform noise was added to nearly 2.5% of these data
points i.e. 50 data points were chosen randomly and
corrupted with uniform noise. As it can be seen from
Figure 2(a), in clean data local as well as global ge-
ometry of data is well preserved. Whereas in case of
noisy data (Figure 2(b)), all neighbours of the clean
data point may not lie on locally linear patch of a man-
ifold, which leads to the biased reconstruction. On the
other hand, the neighbourhood of the outlier compar-
atively very larger and thus does not represent local
geometry very well, as the effect of outliers is exag-
gerated by the use of L2-norm.
4.2 Comparing L2-ONPP Basis and
L1-ONPP Basis on Synthatic Data
This experiment was performed on toy data to vali-
date the relationship between PCA and ONPP as de-
scribed in Section 3.2. 2D data was randomly gen-
erated from 7 clusters which are closely placed and
slightly overlapping, 2 out of 7 were slightly sep-
arated. 100 samples from each cluster were taken
resulting in 700 data points. L2-ONPP bases were
found using conventional method and another set of
bases vectors were computed by performing PCA on
reconstruction error. The bases are same.
L2-norm ONPP basis [Figure 3(a)]
1
st
basis : [0.6361,0.7716]
T
2
nd
basis: [−0.7716,0.6361]
T
PCA basis on Reconstruction errors [Figure 3(b)]
Orthogonal Neighborhood Preserving Projection using L1-norm Minimization
169

(a) (b)
Figure 2: L2-ONPP performed on Swiss role data (a) Continuous manifold (left), sampled 3D data (middle) and its 2D
representation using strongest 2 basis of ONPP(right) (b) Continuous manifold (left), sampled 3D data corrupted with uniform
noise (middle) and its 2D representation using strongest 2 basis of ONPP (right).
1
st
basis : [0.6360,0.7717]
T
2
nd
basis: [−0.7717,0.6360]
T
Figure 3(c) shows that ONPP bases are basi-
cally searching the direction in which the variance
of reconstruction error is minimum. For this data,
L1-ONPP bases were computed using L1-PCA algo-
rithm as can be seen from Figure 3(d) the projection
basis are tilted towards the outlier data.
L1-norm ONPP basis [Figure 3(b)]
1
st
basis : [0.4741,0.8805]
T
2
nd
basis: [−0.8805,0.4741]
T
In this experiment, the residual error was observed
for both, L2-ONPP and L1-ONPP, when data is pro-
jected on lower dimension space. In this case, the
data was projected using only 1 dimension using the
strongest basis vector. The average residual error was
calculated using
e
avg
=
1
n
n
∑
i=1
x
i
− v
1
(v
T
1
x
i
) (11)
The average residual errors of L2-ONPP and L1-
ONPP are 2.3221 and 0.7894, respectively. Thus. it
can be concluded that L1-ONPP is less susceptible to
outliers compared to L2-ONPP.
4.3 Experiment with IRIS Dataset
Iris data form UCI Machine Learning Reposatory
(Fisher, 1999) is used to compare the classification
performance of L1-ONPP and L2-ONPP. The Iris
data set contains 4D data from 150 instances belong-
ing to 3 different classes. Fig 4 shows the residual er-
ror obtained while reconstructing the data using vary-
ing number of dimensions. As shown in Table 1 the
residual error is less in L1-ONPP as compared to L2-
ONPP which significantly improves classification ac-
curacy at lower dimensions. When dimension is 4,
the projection spans entire original space, thus the
reconstruction error drops nearly zero for both, L2-
ONPP and L1-ONPP. As can be seen from Table 1 the
classification error at 4 dimension yields greater than
the lower dimension representation as it includes the
redundant details present in higher dimension. The
same results can be observed in all dimensionality re-
duction techniques at higher dimensions. Here, Near-
est Neighbour (NN) classifier is used.
5 CONCLUSION
Liner dimensionality reduction techniques such as
PCA, LPP and ONPP try to solve an optimization
problem. Usually, the optimization is performed us-
ing L2-norm. However, these techniques based on
L2-norm are susceptible to outliers present. The
present work is first attempt to compute basis vector
for ONPP using L1-norm. In particular, a relation is
established to show that ONPP bases are same as that
of PCA of reconstruction error. These phenomenon
is established both theoretically and experimentally.
An existing technique of finding PCA basis using L1-
norm is utilized to compute the L1-norm ONPP basis.
It has also been shown experimentally that the resid-
ual error after reconstructing data with less number of
dimension is comparatively low in case of L1-norm
ONPP than that of L2-norm ONPP. Experiments are
performed for synthetic as well as real data, and the
same conclusion as mentioned above is observed. As
a future work one can employ L1-norm based ONPP
on face reconstruction problem to observe its suitabil-
ity to handle outliers such as a faces with occluded
areas.
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
170
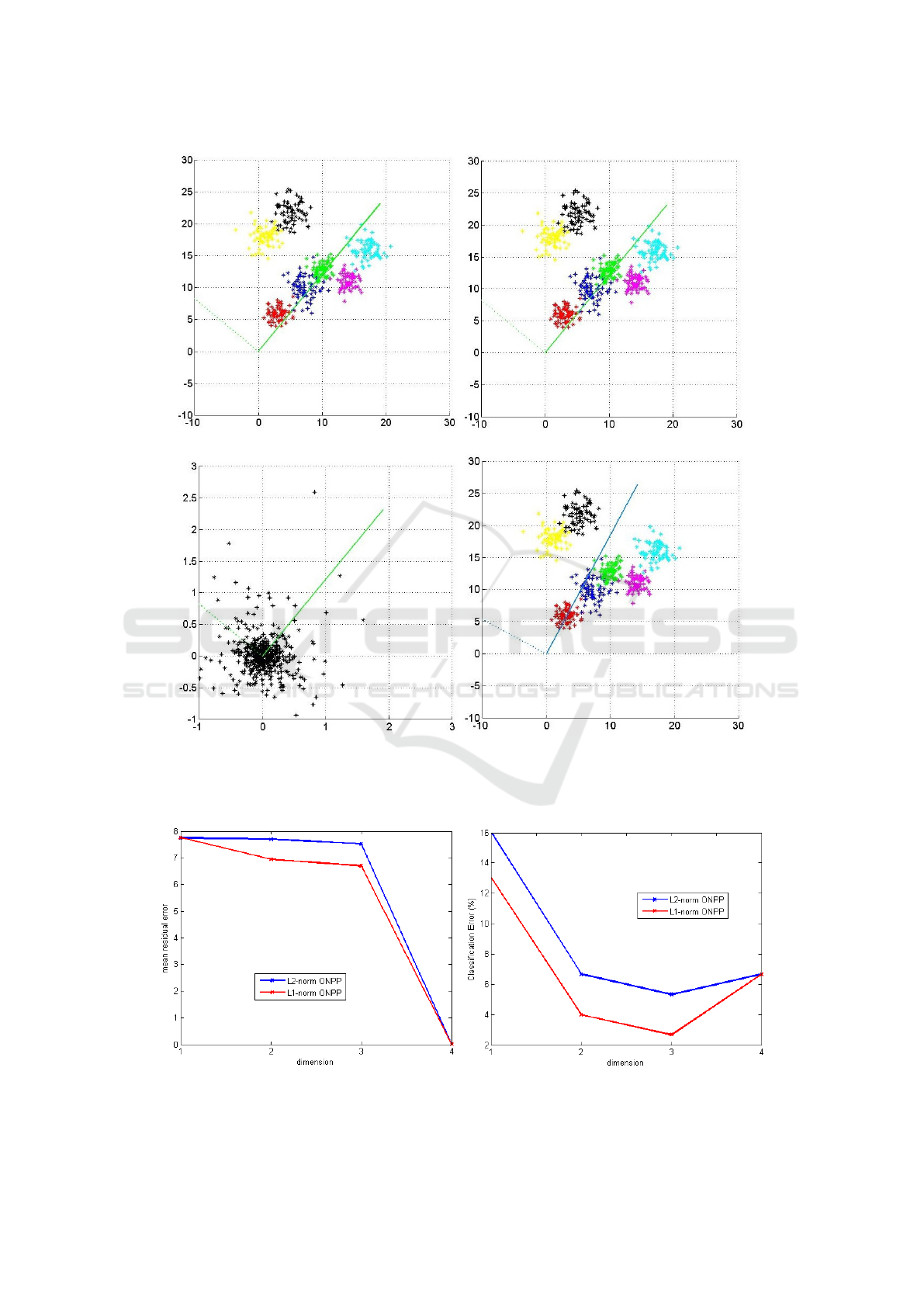
(a) (b)
(c) (d)
Figure 3: A toy example with 700 data samples from 7 clusters. Solid line : first projection basis, Dotted line : second
projection basis (a) Projection basis using ONPP (b) Projection basis using PCA on reconstruction basis (c) Projection basis
overlapped on reconstruction errors (d) Projection basis using L1-norm ONPP.
(a) (b)
Figure 4: Performance comparision of L2-ONPP and L1-ONPP with respect to varying number of dimensions used to recon-
struct the IRIS data in terms of (a) Residual Error (b) Classification Error.
Orthogonal Neighborhood Preserving Projection using L1-norm Minimization
171

Table 1: Comparison of performance in terms of residual error and classification error (in %) of L2-ONPP and L1-ONPP on
IRIS data.
Residual Error Classification Error(%)
Dim L2-ONPP L1-ONPP L2-ONPP L1-ONPP
1 7.8614 7.8546 16.00 13.00
2 7.7450 7.6730 6.67 4.00
3 7.0055 5.6545 5.33 2.67
4 1.44e-15 1.45e-15 6.67 6.67
REFERENCES
Baccini, A., Besse, P., and De Falguerolles, A. (1996). A
l1-norm pca and a heuristic approach.
Chang, H. and Yeung, D.-Y. (2006). Robust locally linear
embedding. Pattern recognition, 39(6):1053–1065.
Ding, C., Zhou, D., He, X., and Zha, H. (2006). R 1-
pca: rotational invariant l 1-norm principal component
analysis for robust subspace factorization. In Proceed-
ings of the 23rd international conference on Machine
learning, pages 281–288. ACM.
Fisher, R. A. (1999). UCI repository of machine learning
databases – iris data set.
He, X., Cai, D., Yan, S., and Zhang, H. J. (2005). Neighbor-
hood preserving embedding. In Tenth IEEE Interna-
tional Conference on Computer Vision, ICCV 2005.,
volume 2, pages 1208–1213. IEEE.
He, X. and Niyogi, P. (2004). Locality preserving projec-
tions. In Advances in Neural Information Processing
Systems, pages 153–160.
Ke, Q. and Kanade, T. (2005). Robust l 1 norm factorization
in the presence of outliers and missing data by alter-
native convex programming. In Computer Vision and
Pattern Recognition, 2005. CVPR 2005. IEEE Com-
puter Society Conference on, volume 1, pages 739–
746. IEEE.
Kokiopoulou, E. and Saad, Y. (2007). Orthogonal neigh-
borhood preserving projections: A projection-based
dimensionality reduction technique. IEEE Transac-
tions on Pattern Analysis and Machine Intelligence,
29(12):2143–2156.
Koringa, P., Shikkenawis, G., Mitra, S. K., and Parulkar,
S. (2015). Modified orthogonal neighborhood pre-
serving projection for face recognition. In Pattern
Recognition and Machine Intelligence, pages 225–
235. Springer.
Kwak, N. (2008). Principal component analysis based on
l1-norm maximization. IEEE transactions on pattern
analysis and machine intelligence, 30(9):1672–1680.
Lu, J., Plataniotis, K. N., and Venetsanopoulos, A. N.
(2003). Face recognition using lda-based algorithms.
Neural Networks, IEEE Transactions on, 14(1):195–
200.
Roweis, S. T. and Saul, L. K. (2000). Nonlinear dimension-
ality reduction by locally linear embedding. Science,
290(5500):2323–2326.
Shikkenawis, G. and Mitra, S. K. (2012). Improving the lo-
cality preserving projection for dimensionality reduc-
tion. In Third International Conference on Emerging
Applications of Information Technology (EAIT), 2012,
pages 161–164. IEEE.
Turk, M. and Pentland, A. (1991). Eigenfaces for recogni-
tion. Journal of cognitive neuroscience, 3(1):71–86.
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
172
