Measuring the Efficiency of the Food Industry in Central and East

European Countries by using the Data Envelopment Analysis

Approach

Zrinka Lukač and Margareta Gardijan

Faculty of Economics and Business, University of Zagreb, Trg J.F. Kennedyja 6, Zagreb, Croatia

Keywords: Efficiency, Competitiveness, Food Industry, Data Envelopment Analysis.

Abstract: The food industry plays an important role in economy of many countries. It is the leading manufacturing

industry in EU in terms of turnover, value added and employment. However, it has been facing a decrease in

competitiveness lately. In this paper we study the competitiveness of very large companies from the food

industry sector in central and east European countries (CEE) by measuring their efficiency within the Data

Envelopment Analysis (DEA) approach. The efficiency analysis is conducted by using the BCC model

where certain financial ratios are used as its inputs and outputs. The study includes more than 200 very large

companies from 13 CEE countries over time period from 2005-2013. The research results have shown that

although some countries were more efficient than the others during the entire research period, no patterns in

the efficiency of the food industry subsectors could be recognised. On the other hand, DEA approach

enabled recognizing sources of inefficiency on a national level.

1 INTRODUCTION

The food industry is a very important component of

the economy of many countries and has a unique

role in expanding their economic opportunities. Its

impact is not limited only to the economic growth

but also affects various aspects of the society.

Together with agriculture it is the main source of

national income for most developing countries. Even

in developed countries its role is of utmost

importance. For example, the food and drink

industry is the first manufacturing industry in the

EU, leading in terms of turnover (€1090 billion or

15.6%), value added (€212 billion or 13%) and

employment (4.25 billion people in direct

employment or 15.2%) (FoodDrink Europe, 2016).

Statistical classification of economic activities in the

European Community, abbreviated as NACE,

classifies food industry as sector C10. Its 9

subsectors are shown in Table 1.

In 2013, the food industry sector in Europe

included 264.1 thousand enterprises that employed

13.6% of the total manufacturing workforce in and

had a wage-adjusted labour productivity ratio of

157.1% (manufacturing ratio average is 148,0%).

Almost 60% of these companies were engaged in

activities classified under C.10.7, followed by

approximately 15% in C.10.1 and 23.3% in C.10.8

(Eurostat 2013).

Table 1: Classification of food industry sector C10.

C10.1 Production, processing, preserving of meat, meat

products

C10.2 Processing and conservation of fish, crustaceans

and molluscs

C10.3 Processing and conservation of fruit and

vegetables

C10.4 Manufacture of vegetable and animal fats and

oils

C10.5 Manufacture of dairy products

C10.6 Manufacture of milling products, starches and

starch products

C10.7 Manufacture of bakery products and pastas

C10.8 Manufacture of other foodstuffs

C10.9 Manufacture of products for animal feed

The leading European countries in the food

industry are Germany, France, UK and Italy, but

certain central and east European (CEE) countries,

such as Bulgaria, Romania and Poland, have one of

the greatest wage-adjusted labour productivity

ratios. However, the EU food and drink industry is

facing a decrease in competitiveness lately. Despite

LukaÄ Z. and Gardijan M.

Measuring the Efﬁciency of the Food Industry in Central and East European Countries by using the Data Envelopment Analysis Approach.

DOI: 10.5220/0006196303850392

In Proceedings of the 6th International Conference on Operations Research and Enterprise Systems (ICORES 2017), pages 385-392

ISBN: 978-989-758-218-9

385

that fact, no analysis of the food sector in CEE has

been made recently.

In this paper, we study the competitiveness of

large companies from food industry sector in 13

CEE countries (Bosnia and Herzegovina, Bulgaria,

Croatia, Czech Republic, Hungary, Latvia,

Lithuania, Montenegro, Poland, Romania, Serbia,

Slovakia and Slovenia). The study includes all very

large companies from food sector for which data

was provided by AMADEUS database, that is over

200 very large companies during the time period

from 2005-2013. We investigated their relative

efficiency using the BCC model from the Data

Envelopment Analysis (DEA). DEA is a

nonparametric method for measuring the relative

performance of decision making units (DMU’s) and

identifying efficient production frontiers in presence

of multiple inputs and outputs. The method was

developed by Charnes, Cooper and Rhodes

(Charnes, Cooper and Rhodes, 1978). In our

analysis, DMUs are particular companies, while

inputs and outputs of the BCC model are their

financial ratios. Based on the efficiency scores of

companies, we draw conclusions about the

efficiency of the food industry subsectors as well as

the efficiency of food industries of particular

countries. Also, we were able to identify sources of

inefficiency of certain countries, which might assist

policy makers in developing strategies which might

improve competitiveness of their food industry

sectors and thus affect their economic growth.

2 LITERATURE REVIEW

Given the role the food industry plays in the

economy of many countries as well as in global

economy there are many publications issued by

official governmental and non-governmental

organizations, such as Food and Agriculture

Organization of the United Nations (FAO) or

European Commission (EC), that deal with the

agribusiness, its role in economic development and

its competitiveness. Each year FAO publishes The

State of Food and Agriculture report. In its 1997

issue special chapter was devoted to the subject of

agro-processing industry and economic development

(FAO, 1997). In 2009, FAO has published another

document on key factors affecting the development

and competitiveness of agro-industries (FAO, 2009).

Given the decrease in the relative

competitiveness of EU food and drink industry

compared to other world food producers in terms of

slower growth in labour productivity and added

value, EC is actively taking efforts to come up with

the policy measures which would support the

competitiveness of that sector. It also publishes

studies which assess EU food and drink industry

competitive positions. Some of such recent studies

on the competitive position of the European food

and drink industry commissioned by EC are

(Wijnands and Verhoog, 2016) and (European

Commission, 2016).

Verschlede et al. (2014) conducted a general

study to obtain insight into firm-level

competitiveness across all sectors in Europe,

including the food industry, by using a

semiparametric stochastic metafrontier approach.

Many studies have used DEA approach to measure

efficiency and competitiveness of the food industry.

Charles and Zegarra (2014) have developed a

regional competitiveness index by using the

methodology based on DEA to measure and rank the

competitiveness of all the regions of Peru.

Rodmanee and Huang (2013) have used a relational

two-stage DEA to evaluate the efficiency of 23 food

and beverage companies in Thailand. Shamsudin et

al. (2011) used the DEA approach to evaluate the

market competitiveness of small and medium

enterprises in the food industry in Malaysia. Study

conducted by Tektas and Tosun (2010) benchmarks

the supply and chain performance of Turkish food

and beverage companies by using DEA. The DEA-

efficiency and productivity changes in the food

industry in India during pre and post liberalisation

period were studied by Ali et al. (2009). The former

also identifies the causes of inefficiency across

various sectors. Kocisova (2015) investigates the

relative efficiency of the agricultural sector in the

EU using DEA during the period 2007-2011, where

decision-making units (DMUs) are agricultural

subsectors. The paper by Kocisova (2015) also gives

a good literature review of different approaches to

measuring efficiency in the agricultural sector in

Europe. However, there are no recent studies of the

competitiveness of European food industry by using

the DEA approach.

3 METHODOLOGY

The mathematical formulation of the basic DEA

CCR model (Charnes, Cooper and Rhodes, 1978) is

as follows. We observe N decision making units,

denoted as DMU

, DMU

…,DMU

, that use the

same n inputs in order to produce the same m

outputs. Let x

be an input i for some DMU

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems

386





1, ,in

and y

its output r,





1, ,rm





1, , .

N

Therefore, a particular DMU

described by vectors



,,,

jnj

xxX 

and





,,,

jmj

yyY 

. In order to make the model

stable, it is recommended that









max ,3 .

mn m n For an arbitrary decision

making unit DMU

=DMU





1, , ,

N

a virtual

input

...

onno

ux ux

and a virtual output

...

ommo

vy v y

are formed with (initially) unknown

weights (v

) and (u

). The model can be input or

output oriented, depending on whether DMUs’ aim

is to minimize the inputs for a given level of outputs

or vice versa. In the output oriented approach, these

weights are determined by solving the following

fractional programming model for each

DMU

=DMU



11 2 2

,..., , ,...,

11 2 2

...

max ,

...

subject to

...

1, 1, , ,

...

,0,,,

oo mmo

vvuu

oo nno

jj mmj

jj nnj

vy vy v y

ux ux ux

uy uy u y

vx vx v x

uv ir











(1)

where





is a non-Archimedean element. Using

Charnes-Cooper transformation (Charnes and

Cooper, 1962) this fractional programming model

can be linearized and also written in its envelopment

form (Cooper, Seiford and Zhu, 2011).

Since CCR model assumes constant returns to

scale, Banker, Charnes and Cooper (Banker,

Charnes and Cooper, 1984) developed a generalised

DEA model that assumes variable returns to scale

(VRS). Their significant contribution to the DEA

was the idea to let each DMU use the set of weights

that puts it in the best position regarding the other

DMUs (www.deazone.com [10.7.2013]). In output-

oriented BCC model, the measure of technical

efficiency ϕ is obtained by solving the following

linear program for each DMU

=DMU









max

1, 2 ,

0, ,,

es s

































(2)

where s

, s

are vectors of slack variables and θ is the

solution of the dual problem. If we denote the

optimal solution as

( , , )





 

, then DMU

efficient iff ϕ=1 and







= 0. DMU

is weakly

efficient iff ϕ* = 1 and





≠ 0 or



≠ 0 in some

alternate optima (Cooper, Seiford and Zhu, 2011).

This study uses BCC model for several reasons.

First, it is a relatively simple tool that gives the

needed results. Secondly, it allows assuming

variable returns to scale, and thirdly, it can handle

negative data that is often found in financial analysis

(Pastor and Ruiz, 2007).

4 DATA AND RESULTS

The data sample for our study included all the very

large food manufacturers in CEE countries for which

data were available in AMADEUS database. We

considered the time period from 2005-2013. The

number of companies varies between 235 in 2005

and 284 in years 2007 and 2008 (table A1 in

appendix). There are several reasons why it is

interesting to analyse the segment of very large

companies. On average, very large companies from

this database hold on around 40.2% of total asset

and 37,52% of all the capital in food industry of the

countries observed during the period of analysis.

Also, very large companies have employed 22.28%

of the total workforce (on average) within the CEE

food industry sector. The data shows that during

2005-2013 the average profit margin (PM) of very

large producers in food industry sector was smaller

than the PM of large companies. Compared to

medium sized companies, the profit margin of very

large companies was smaller only in years before

2010. Furthermore, when compared to companies

classified as small, they reaped greater profit margin.

Data shows that the number of very large food

producers has been increasing over the years. The

choice of variables used for evaluating the

companies was determined by the availability of

data. Since the most commonly reported data in

AMADEUS dataset are operating revenue, total

asset, capital and profit margin, these variables were

used to investigate the relative efficiency of the very

large food producers in CEE countries. Given the

fact that DEA cannot deal with missing values

(Smirlis, Maragos and Despotis, 2006), companies

with missing data were excluded from the study.

This reduced the sample by not more than 5% of the

total number of companies in each year. The ratio of

profit/loss before tax to total asset (ROA) and profit

Measuring the Efﬁciency of the Food Industry in Central and East European Countries by using the Data Envelopment Analysis Approach

387

Figure 1: Relative position of countries by years during 2005-2013.

margin were used as indicators of profitability. Since

capital and operating revenue are given in absolute

terms, we introduce their ratio (capital/operating

revenue) as a measure of productivity of capital.

Classification of companies by their subsector is

presented in table A2 in the appendix.

DEA demands that there is at least one variable

considered as input and one variable considered as

output. Since greater values of ROA and profit

margin are preferred, these variables were taken as

outputs, while the productivity of capital was taken

in its inverse form (revenue/capital) and considered

as an input of the BCC model. The minimum and

maximum values of correlation coefficients among

variables for each year during the time period from

2005-2013 are given in Table 2. The correlation

coefficients between input and output variables are

meaningful and indicate that there are no redundant

variables.

Table 2: Minimum and maximum values from the

correlation matrix.

/rev ROA RM

/rev 1

ROA -0,22 / -0,08 1

RM -0,61 / -0,05 0,6 / 0,73 1

For each year, the rankings of companies were

obtained by solving the BCC model. The results

showing the most efficient and 5 least efficient

companies are reported in tables A3 (years 2005-

2009) and A4 (years 2010-2014) in the appendix.

Averaging the efficiency ratios of food

companies from a specific country allows ranking of

countries by their food industry efficiency. Figure 1

shows the relative positions of countries in time

period 2005-2013. It is obvious that Bulgaria,

Poland, Czech Republic and Hungary are the leading

countries in this sector. Bosnia and Herzegovina is

the least efficient country. On the other hand,

averaging the rankings within each food industry

subsector allows recognising the changes in the

relative efficiency over the years. The results

illustrated in Figure A1 in the appendix show that

subsector C10.7 is strongly at the bottom. Also,

C10.9 and C10.2 are in the middle of the range of

relative rankings with respect to other sectors for

each year of the considered period. However, there

are large oscillations of average efficiency ranking

within subsectors during 2005-2013.

DEA also allows recognizing the weaknesses of

a specific DMU. It is given by the percentage

difference of DMUs inputs and outputs compared to

its efficient projection on the efficient frontier. By

averaging these percentage differences within a

single country, we got indicators of competitive

advantages and inefficiency sources, as shown in

tables A5, A6 and A7 in the appendix. These results

show that, on average, efficient countries have small

deviations from their projections in both outputs and

input. On the other hand, the inefficient countries

have large deviations from projections, again in both

outputs and input. Overall, each country has

different sources of strengths and weaknesses, as

shown by table A5, A6 and A7 in the appendix.. The

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems

388

results obtained on a company level, as well as on

the country level, can be used as guidelines for

assisting policy makers in creating policies which

might lead to improving efficiency and

competitiveness, thus also having positive effects on

economic growth.

5 CONCLUSIONS

The food industry plays an important role in the

economy of many countries. Developing its

competitiveness has positive effects on long-term

economic growth. Therefore it is important to assist

the policy makers in identifying sources of

inefficiency and developing strategies which would

improve its competitiveness. In this study we have

conducted efficiency analysis of very large

companies in the food sector of CEE countries using

the DEA approach, namely the BCC model. The

results of the BCC model identified Bulgaria,

Poland, Czech Republic and Hungary as leader CEE

countries in terms of efficiency of very large

companies in the food sector in the period of 2005-

2013. Bosnia and Herzegovina, Montenegro and

Slovakia were relatively inefficient in this dataset.

Croatia and Romania showed to be somewhere in

the top middle, which is rather surprising since

Romanian food industry is considered as more

developed. Moreover, the model detects the ex-post

efficiency/ inefficiency of decision-making units.

The results indicate variables where improvements

can be made. It also indicates the sources of

efficiency which a company/ country should

strengthen as its competitive advantage. The

findings are company/country specific. However, the

analysis does not include any future projections or

effects of the uncertainty. Limitations of this study

are related to the availability of financial data. It

must be noted that small and medium enterprises are

poorly covered in AMADEUS database. This

restricts the number of companies in the sample,

leading to conclusions that cannot be generalized.

As for further research, in order to derive the

generalized results, the analysis should also include

small, medium and large companies within food

industry, but that would require using models which

allow missing data. Also, it would be interesting to

conduct the similar analysis for all European

countries.

ACKNOWLEDGEMENTS

This research has been fully supported by Croatian

Science Foundation under the project The role of

structural reforms in boosting external

competitiveness in European Union countries.

REFERENCES

Ali, J., Singh, S.P., Ekanem, E., 2009. Efficiency and

Productivity Changes in the Indian Food Processing

Industry: Determinants and Policy

Implications.International Food and Agribusiness

Management, Vol. 12 (1), pp 43- 66

Banker, R. D., Charnes, A., Cooper, W. W. 1984. Some

Models for Estimating Technical and Scale

Inefficiencies in Data Envelopment Analysis.

Management Science, Vol. 30 (9), pp 1078–1092

Charles, V., Zegarra, L.F., 2014. Measuring regional

competitiveness through Data Envelopment Analysis:

A Peruvian case. Expert Systems with Applications,

Vol. 41, pp 5371-5381

Charnes, A., Cooper, W.W,. Rhodes, E., 1978. Measuring

the efficiency of decision making units, European

Journal of Operations Research, Vol. 2 (6), pp 429-

444

Charnes, A., Cooper, W.W. 1962. Programming with

linear fractional functionals. Naval Research Logistics,

Vol 9 (3-4), September - December 1962, pp 181–186

Cooper, W.W., Seiford, L.M., Zhu, Joe (eds.) 2011. Data

Envelopment Analysis: History, Models, and

Interpretations, In: Handbook on Data Envelopment

Analysis:International Series in Operations Research

& Management Science Springer 2011, pp. 1-39

European Commission, 2016. The competitive position of

the European food and drink industry, Final report.

Available at: http://edz.bib.uni-mannheim.de

/daten/edz-h/gdb/16/EA0416075ENN.pdf

FAO, 1997. The State of Food and Agriculture 1997

(SOFA):The Agroprocessing Industry and Economic

Development. Available at:

http://www.fao.org/docrep/w5800e/W5800e00.htm

FAO, 2009. Agro-industries for Development. Available

at: http://www.fao.org/docrep/017/i3125e/i3125e00

.pdf

FoodDrink Europe, 2016. A Competitive EU Food and

Drink Industry for Growth and Jobs: Ambitions for

2025. Priorities and policy recommendations.

Available at: http://www.fooddrinkeurope.eu/uploads/

publications_documents/Competitive_food_industry_

growth_jobs_report.pdf

Kocisova, K., 2015. Application of the DEA on

themeasurment of efficiency in the EU

countries.Agricultural Economics – Czech, Vol. 61

(2), pp 51-62

Pastor, J. T., Ruiz, J. L., 2007. Variables With Negative

Values in Dea. In: Modelling Data Irregularities And

Measuring the Efﬁciency of the Food Industry in Central and East European Countries by using the Data Envelopment Analysis Approach

389

Structural Complexities. In Data Envelopment

Analysis, Cook, W., Zhu, J. (eds.). Springer, e–book,

pp 63–84.

Rodmanee, S., Huang, W., 2013. Efficiency Evaluation of

Food and Beverage Companies in Thailand: An

Application of Relational Two-Stage Data

Envelopment Analysis.International Journal of Social

Science and Humanity, Vol. 3 (3), pp 202-205

Shamsudin, M.N., Yodfiatfinda, Mohamed, Z.A., Yusop,

Z., Radam, A., 2011. Evaluation of market

competitiveness of SMEs in the Malaysian Food

Processing Industry. Journal of Agribusiness

Marketing, Vol. 4., pp 1-20

Smirlis, Y. G., Maragos, E. K., Despotis, D. K. 2006. Data

Envelopment Analysis with Missing Values: An

Interval DEA Approach. Applied Mathematics and

Computation, Vol. 177 (1), pp 1–10

STATISTICAL OFFICE OF THE EUROPEAN

COMMUNITIES. (2016). EUROSTAT:

Manufacturing statistics - NACE Rev. 2. Available at:

http://ec.europa.eu/eurostat/statistics-explained/index.

php/Manufacturing_statistics_-_NACE_Rev._2

Tektas, A., Tosun, E.O., 2010. Performance

Benchmarking in Turkish Food and Beverage

Industry. Communications of the IBIMA, Vol. 2010

Verschelde, M., Dumont, M., Rayp, G., Merlevede, B.,

2016. Semiparametric stochastic metafrontier

efficiency of European manufacturing firms. Journal

of Productivity Analysis, Vol. 45, No. 1, pp 53-69

Wijnands, J.H.M., Verhoog, D.,2016. Competitiveness of

the EU food industry; Ex-post assessment of trade

performance embedded in international economic

theory.Wageningen, LEI Wageningen UR (University

& Research centre), LEI Report 2016-018. Available

at: http://edepot.wur.nl/369980

APPENDIX

In this section we bring the figure and tables that we

have referenced in the text.

Table A1: Number of companies per country per year included in the study.

2005 2006 2007 2008 2009 2010 2011 2012 2013

BIH

11 12 15 14 14 12 11 7 8

HUN

11 10 13 13 13 14 15 15 15

CRO

17 17 17 17 17 17 17 17 15

SLV

3 4 4 4 4 4 4 4 4

SER

50 53 54 55 49 48 48 49 43

ROM

40 28 40 42 42 40 43 42 42

CZE

13 11 14 14 16 17 16 17 17

POL

51 65 72 76 86 85 85 84 78

BUL

3 4 5 6 7 6 6 6 7

6 11 10 11 11 11 11 11 11

MNE

3 3 0 0 6 6 7 6 1

LAT

1 1 1 1 1 1 1 2 2

LIT

7 8 8 8 8 8 8 8 8

216 227 253 261 274 269 272 268 251

Table A2: Number of companies per activity (by NACE classification) per year included in the study.

2005 2006 2007 2008 2009 2010 2011 2012 2013

C10.7

5 5 335544 2

C10.7.1

26 26 28 28 27 29 28 25 24

C10.8.2

16 16 17 18 21 21 20 21 20

C10.8.4

1 1 222222 2

C10.6.1

29 29 31 34 33 32 31 33 29

C10.8.6

3 3 333333 3

C10.5.2

1 1 111111 1

C10.7.3

1 1 223333 3

C10.8.9

3 3 567699 8

C10.9.1

22 22 23 23 24 23 25 23 22

C10.9.2

5 5 556666 6

C10.6.2

6 6 677777 7

C10.8.1

14 14 15 15 18 16 17 17 16

C10.5.1

39 39 47 47 49 49 48 48 47

C10.2

7 7 789998 8

C10.1.1

25 25 29 29 27 26 29 27 26

C10.3.1

2 2 222222 2

C10.1.2

9 9 12 12 12 12 11 12 9

C10.1.3

13 13 15 16 18 17 17 17 16

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems

390

Table A3: Efficient and 5 least efficient companies, 2005-2009.

2005 2006 2007 2008 2009

ROM124.C10.1.1 POL145.C10.1.3 ROM160.C10.6.2 POL51.C10.8.2 POL94.C10.9.2

CRO143.C10.1.3 SER169.C10.1.1 POL184.C10.1.3 SER120.C10.1.1 POL150.C10.8.2

POL192.C10.9.1 POL191.C10.9.1 POL206.C10.5.1 BUL194.C10.8.6 BUL157.C10.8.6

POL207.C10.8.1 ROM211.C10.1.1 ROM199.C10.1.1 ROM175.C10.5.1

POL222.C10.9.1 POL228.C10.9.1 ROM177.C10.1.1

ROM240.C10.1.3 ROM188.C10.1.3

POL260.C10.3.1 POL239.C10.9.1

…

BIH133.C10.1.1 BIH1.C10.7 BIH179.C10.1.1 SER72.C10.6.1 SER78.C10.6.1

MNE161.C10.8.4 ROM154.C10.8.2 SER42.C10.7.1 LAT216.C10.2 BIH6.C10.6.1

SER61.C10.6.1 SER37.C10.8.2 SER74.C10.6.1 SER93.C10.6.2 ROM217.C10.6.1

BIH6.C10.6.1 BIH126.C10.1.1 ROM201.C10.6.1 SLK156.C10.8.1 ROM189.C10.1.3

SER59.C10.6.1 BIH4.C10.6.1 SER193.C10.9.1 ROM205.C10.7.1 BIH77.C10.6.1

Table A4: Efficient and 5 least efficient companies, 2010-2014.

2010 2011 2012 2013

ROM139.C10.1.1 SER55.C10.7.1 ROM127.C10.1.1 HUN8.C10.6.2

POL148.C10.1.1 SER110.C10.8.1 ROM159.C10.1.1 ROM78.C10.8.9

POL180.C10.1.3 ROM135.C10.1.1 ROM198.C10.6.1 ROM116.C10.1.1

BUL193.C10.8.6 MNE197.C10.1.1 SER273.C10.6.1 BUL157.C10.8.1

ROM203.C10.1.1 ROM200.C10.1.1 ROM161.C10.1.1

POL227.C10.1.3 POL233.C10.8.2 POL207.C10.8.2

POL233.C10.8.2 POL238.C10.9.1 SER257.C10.6.1

POL238.C10.9.1

POL273.C10.1.2

…

… … …

SER86.C10.6.1 POL219.C10.2 CZE 50.C10.7.1 POL24.C10.6.1

BIH1.C10.7 ROM152.C10.1.3 SER68.C10.8.2 HUN44.C10.1.1

SER85.C10.6.1 ROM180.C10.7.1 ROM38.C10.5.1 ROM38.C10.5.1

ROM211.C10.6.1 ROM206.C10.6.1 ROM171.C10.7.1 SER152.C10.9.1

ROM158.C10.1.3 POL226.C10.1.1 POL232.C10.2 ROM37.C10.5.1

Table A5: Average inefficiency of input (%).

2005 2006 2007 2008 2009 2010 2011 2012 2013

BIH -12.47 -93.43 -54.31 -71.16 -71.55 -68.24 -89.83 -69.37 -61.04 -66.30

HUN 0.00 -51.63 0.00 -6.53 -4.20 -3.30 -44.64 0.00 0.00 -13.79

CRO -4.74 -78.34 -17.33 -29.32 -31.67 -30.31 -62.47 -23.32 -3.32 -34.69

SLV 0.00 -87.01 -1.48 -3.56 -1.79 0.00 -82.84 -1.81 0.00 -22.31

SER -1.74 -88.61 -26.01 -34.22 -36.78 -33.64 -77.00 -18.06 -14.22 -39.51

ROM 0.00 -59.87 -3.49 -19.73 -15.72 -18.17 -56.67 -11.36 -14.91 -23.13

CZE 0.00 -67.09 0.00 -2.42 -6.37 -6.67 -50.13 -4.07 -3.70 -17.09

POL 0.00 -47.32 -3.23 -13.00 -12.57 -8.13 -37.01 -5.59 -7.65 -15.86

BUL 0.00 -42.88 -6.83 0.00 -13.23 0.00 -45.95 -11.62 -4.18 -15.06

0.00 -86.68 -20.31 -27.10 -32.90 -31.38 -72.88 -18.95 -20.80 -36.27

MNE -33.30 -92.81 -61.96 -69.62 -82.42 -74.93 0.00 -69.17

LAT 0.00 -93.18 -13.73 -87.51 -57.19 -32.91 -92.54 -9.04 -16.19 -48.26

LIT 0.00 -75.23 0.00 -5.55 -8.28 -8.30 -66.28 -3.45 -7.47 -20.89

-4.02 -74.16 -12.23 -25.01 -27.25 -23.90 -66.20 -19.35 -11.81

Measuring the Efﬁciency of the Food Industry in Central and East European Countries by using the Data Envelopment Analysis Approach

391

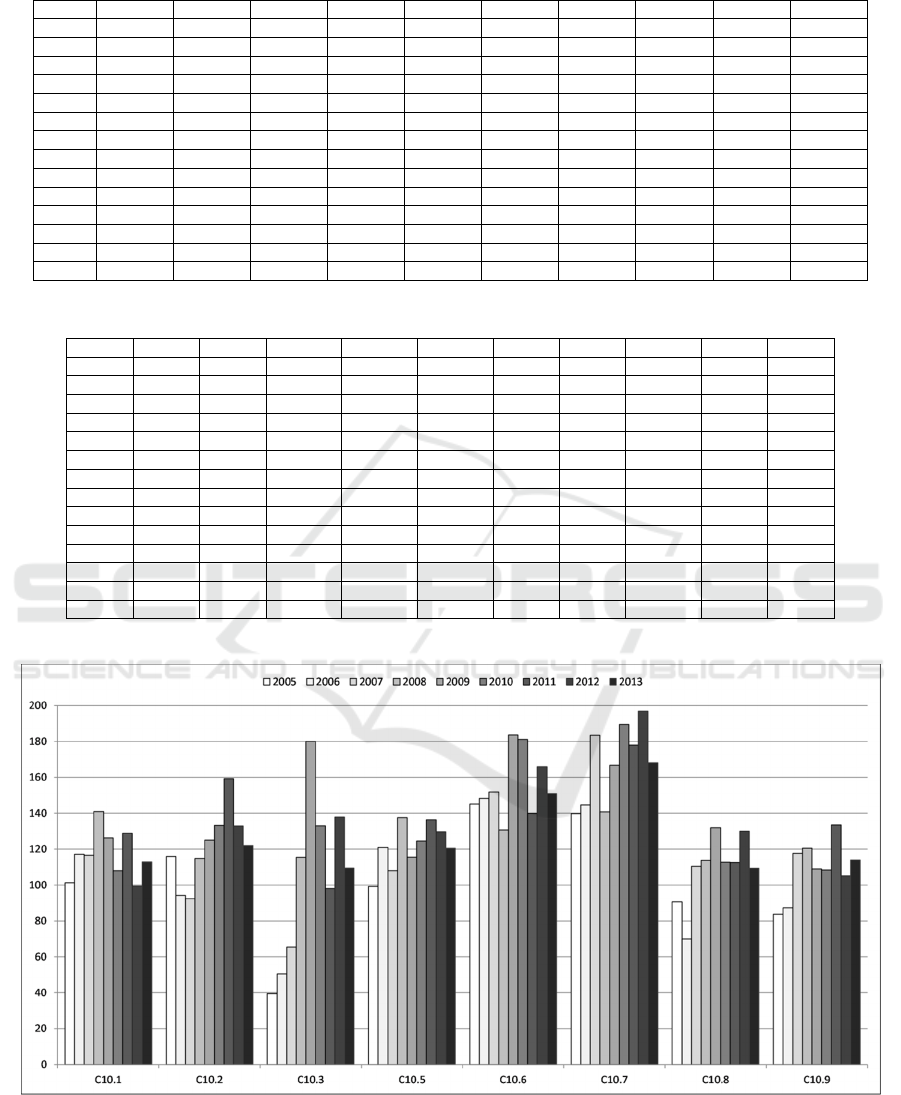
Table A6: Average inefficiency of ROA (%).

2005 2006 2007 2008 2009 2010 2011 2012 2013

BIH 132.62 202.75 95.25 44.51 180.67 87.99 24.95 27.55 57.74 99.53

HUN 61.85 154.15 64.06 30.88 60.27 54.57 23.12 19.33 45.07 58.53

CRO 75.76 117.78 68.16 23.89 57.40 54.77 21.51 24.26 44.97 55.44

SLV 99.31 178.00 78.30 28.39 67.17 64.45 24.76 25.35 52.31 70.72

SER 130.10 210.06 89.24 36.81 73.81 71.13 19.59 24.73 46.22 81.93

ROM 71.17 149.79 67.95 66.78 187.90 74.18 26.33 21.96 50.27 83.26

CZE 64.00 151.69 68.51 27.62 61.50 50.22 18.84 18.45 36.53 57.60

POL 55.45 98.12 50.72 29.10 56.19 39.77 18.95 18.90 34.95 45.90

BUL 60.21 74.20 53.84 24.77 46.49 38.94 18.16 16.70 27.88 41.66

150.02 166.41 79.19 41.93 63.50 61.68 21.65 22.11 45.22 75.81

MNE 135.35 184.93 67.16 88.34 22.23 30.35 48.75 88.06

LAT 99.33 250.19 79.78 0.00 75.48 51.94 22.03 28.03 49.93 75.85

LIT 58.88 118.77 68.26 29.79 57.70 44.91 19.59 19.18 36.39 52.14

91.85 158.22 71.94 32.04 81.17 60.22 21.67 22.84 44.33

Table A7: Average inefficiency of profit margin (%).

2005 2006 2007 2008 2009 2010 2011 2012 2013

BIH 79.26 44.78 281.26 145.80 169.59 87.99 28.68 41.88 85.22 107.16

HUN 27.23 26.89 60.99 29.82 57.04 53.67 24.22 29.04 45.07 39.33

CRO 29.28 19.22 66.83 23.86 55.33 52.77 36.07 37.24 44.97 40.62

SLV 33.85 28.11 78.30 28.39 67.17 64.45 25.54 41.09 52.31 46.58

SER 49.98 33.41 85.23 43.61 72.96 72.64 26.69 53.01 97.32 59.43

ROM 29.35 26.01 72.35 52.22 77.77 88.60 33.93 49.74 53.95 53.77

CZE 26.91 25.99 63.10 26.42 57.31 49.26 20.25 26.69 37.08 37.00

POL 25.25 21.16 50.09 27.23 46.72 38.34 20.23 28.16 34.87 32.45

BUL 23.71 16.48 53.84 24.77 43.70 38.94 18.83 23.00 27.88 30.13

42.78 24.71 79.19 41.93 63.50 61.68 26.38 33.47 45.22 46.54

MNE 76.80 34.08 67.16 65.20 29.64 299.42 48.75 88.72

LAT 33.45 37.07 79.78 131.69 75.48 51.94 23.11 45.77 49.93 58.69

LIT 27.62 23.84 68.26 29.79 57.70 44.91 21.48 28.79 36.39 37.64

38.88 27.83 86.60 50.46 70.11 59.26 25.77 56.71 50.69

Figure A1: Rankings of food industry subsectors by years.

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems

392