
EINCKM: An Enhanced Prototype-based Method for Clustering
Evolving Data Streams in Big Data
Ammar Al Abd Alazeez, Sabah Jassim and Hongbo Du
Department of Applied Computing, The University of Buckingham, Buckingham, U.K.
Keywords: Big Data, Data Stream Clustering, Outliers Detection, Prototype-based Approaches.
Abstract: Data stream clustering is becoming an active research area in big data. It refers to group constantly arriving
new data records in large chunks to enable dynamic analysis/updating of information patterns conveyed by
the existing clusters, the outliers, and the newly arriving data chunk. Prototype-based algorithms for solving
the problem have their promises for simplicity and efficiency. However, existing implementations have
limitations in relation to quality of clusters, ability to discover outliers, and little consideration of possible
new patterns in different chunks. In this paper, a new incremental algorithm called Enhanced Incremental
K-Means (EINCKM) is developed. The algorithm is designed to detect new clusters in an incoming data
chunk, merge new clusters and existing outliers to the currently existing clusters, and generate modified
clusters and outliers ready for the next round. The algorithm applies a heuristic-based method to estimate
the number of clusters (K), a radius-based technique to determine and merge overlapped clusters and a
variance-based mechanism to discover the outliers. The algorithm was evaluated on synthetic and real-life
datasets. The experimental results indicate improved clustering correctness with a comparable time
complexity to existing methods dealing with the same kind of problems.
1 INTRODUCTION
Recent advances in information and networking
technologies have led to a rapidly growing flux of
massive data interaction that has led to the
emergence of Big Data witnessed in almost every
sector of life ranging from the stock market, online
shopping, banking, social media, and healthcare
systems (Liu et al., 2013). Despite numerous
attempts at defining the term, big data fundamentally
refers to a huge volume of data that are generated by
various applications and stored in different sources
and locations. Big data requires frequent updating
and analysis with the aim of the enhanced
competitiveness and improved performance of
organizations (Olshannikova et al., 2014).
Velocity is one of the known characteristics of
big data. It means that data arrive and require
processing at different speeds. While for some
applications, the arrival and processing of data can
be performed in batch analysis style, other analytics
applications require continuous and real-time
analyses of incoming data chunks (Islam, 2013).
Data stream clustering is defined as the grouping of
new data that frequently arrive in chunks with the
objective of gaining understanding about underlying
grouping patterns that may change over time in the
data streams (Yogita and Toshniwal, 2012).
Most existing data stream clustering solutions
follow the path of adapting existing static data
clustering approaches and methods to the dynamic
data stream scenarios, attempting to accommodate
the capability of two-phase processing, i.e. offline-
online or online-offline (Aggarwal et al., 2003)
(Bhatia and Louis, 2004). There are mainly three
schools of thoughts in data stream clustering, i.e.
prototype-based, density-based, and model-based
(Yogita and Toshniwal, 2012; Nguyen et al., 2015;
Silva et al., 2013). Prototype-based algorithms
initially divide data objects into imprecise prototype
clusters and then iteratively refine the prototypes
into final clusters (e.g. K-Means (MacQueen,
1967)). Density-based algorithms look for dense
regions in each of which there is a high
concentration of data points, and then the dense
regions form clusters of similar data objects (e.g.
DBSCAN (Ester et al., 1996)). Model-based
algorithms consider the data points as the results of a
statistical modeling process. Finding clusters of
similar data points is equivalent to finding the
Al Abd Alazeez A., Jassim S. and Du H.
EINCKM: An Enhanced Prototype-based Method for Clustering Evolving Data Streams in Big Data.
DOI: 10.5220/0006196901730183
In Proceedings of the 6th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2017), pages 173-183
ISBN: 978-989-758-222-6
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
173

distributions of the statistical model (e.g.
Expectation Maximization (Dempster et al., 1977)).
Prototype-based methods are favored due to their
promises of simplicity, ease of implementation, and
efficiency. However, most, if not all, prototype-
based methods have their limitations, such as
requiring the advanced setting of a number of
clusters (K), lack of capability in discovering
outliers, etc. The aim of our research is to develop
an efficient dynamic clustering solution that
improves existing prototype-based algorithms.
In this paper, a new algorithm called Enhanced
Incremental K-Means (EINCKM) is presented. At
any incremental round, the inputs of the algorithm
consist of a newly arrived data chunk, summary of
the current set of clusters, and a list of outliers from
the previous iteration. The outputs of the algorithm
include the summary of a set of modified clusters
and a new list of outliers. The EINCKM algorithm
applies a simple heuristic-based method to estimate
the number (K) of new clusters to be constructed
from the new chunk. In addition, a radius-based
technique is used to decide how to merge
overlapping new and existing clusters. Moreover,
the algorithm utilizes a variance-based mechanism
to discover the output outliers. The algorithm was
evaluated on both synthetic and real-life datasets.
The experimental results show that the proposed
algorithm improves clustering correctness with a
comparable time complexity to the existing methods
of the same type. The structure of the algorithm is
designed to be modular for easy accommodation of
any further improvements.
The rest of this paper is organized as follows:
Section 2 presents the state of the art of the related
work on data stream clustering algorithms in the
current literature. Section 3 explains the proposed
algorithm. Section 4 presents a systematic evaluation
of the performance of the algorithm and compares it
with a selected number of existing algorithms
through theoretical analysis and practical
experiments using the synthesized and real-life
datasets. A number of further issues regarding the
proposed algorithm will be discussed in Section 5.
Section 6 concludes the work and outlines the
possible future directions of this research.
2 RELATED WORK
2.1 Existing Approaches for Clustering
Data Streams
From a computation point of view, there are two
approaches for data stream mining: incremental-
learning and two-phase-learning (Nguyen et al.,
2015). Both approaches of mining can be adopted
for clustering purposes. Figure 1 illustrates the
principles of the two approaches. In the incremental-
learning approach, a model of clusters continuously
evolves to fit changes made by incoming data
chunks (Guha et al., 2000). On the other hand, the
basic principle of the two-phase-learning approach is
to split the clustering process into two phases. The
first phase summarizes the data points into “pseudo”
clusters, i.e. not finalized clusters. In the second
phase, i.e. whenever a query about the clustering
results is raised, the pseudo-clusters are modified to
produce the finalized clusters (Aggarwal et al., 2003;
Silva et al., 2013).
2.2 Existing Algorithms
Several prototype-based algorithms using the
traditional K-Means clustering principles have been
developed. The Adapt.KM algorithm (Bhatia and
Louis, 2004) first finds K clusters in an initial
dataset using the K-Means method. It then takes the
minimum distance among the centroids of the
clusters as a threshold. When a new data point
arrives, if the distance between the data point and
the centroid of its closest cluster is below the
threshold, the data point is then added to the cluster.
Figure 1: Computational approaches of data stream clustering (Nguyen et al., 2015).
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
174

The cluster centroid, as well as the threshold, are
subsequently updated. If the distance is greater than
the threshold, a new cluster is created for this new
data point and the two closest existing clusters are
merged followed by updating the centroid of the
merged cluster and the threshold. The main
limitation of this algorithm is its merging strategy. If
there are a lot of outliers then clustering results will
become meaningless.
Chakraborty and Nagwani later suggested an
improvement, known as Inc.KM (Chakraborty and
Nagwani, 2011), that uses the average distance
between centroids as the threshold and ignores the
data point with a distance greater than the threshold
as an outlier. The drawback of this algorithm is that
it ignores the outliers which may create a new
cluster(s).
Guha, et al. (Guha et al., 2000) presented the
STREAM algorithm. In the first phase, the algorithm
evenly divides the stream into D chunks of equal
size, finds S clusters in each chunk using the K-
Median algorithm, and the centroids of the S clusters
are weighted by the number of data points in each.
After that, only the weighted centroids of all clusters
are kept and treated as “data points” when a buffer
of size m prototypes is accumulated. In the second
phase, these m prototypes are further clustered into
K cluster representations. The main shortcoming of
STREAM is that it is unable to adapt to the
evolution concept of data, i.e. merge, split, add, and
delete clusters.
2.3 Merging Strategies for Overlapped
Clusters
Merging overlapped clusters that may emerge during
the updating phase is one of the most important steps
in data stream clustering algorithms. It has an effect
on the correctness of the resulting clusters. There
exist three main strategies of merging clusters:
matching, the conditional probability of intersection
area, and cluster radius.
Spiliopoulou et al. (Ntoutsi et al., 2009)
presented MONIC+ (Modeling and Monitoring
Cluster Transitions) framework that computes the
matching between clusters to capture their evolution.
Clusters are only merged if they share at least a half
of their memberships. Oliveira and Gama (Oliveira
and Gama, 2012) produced MEC (Monitoring
Clusters’ Transitions) framework which relies on the
conditional probability and a predefined merging
threshold of 0.5. Conditional probabilities are
computed for every pair clusters obtained at the
consecutive time. The weakness of (Ntoutsi et al.,
2009) and (Oliveira and Gama, 2012) is that
information about the data points must be kept for
each cluster, which is very expensive to maintain.
Zhang et al. (Zhang et al., 1996) presented
BIRCH (Balanced Iterative Reducing and Clustering
using Hierarchies) algorithm. To decide whether to
add a new data point into the previous clusters or
not, BIRCH depends on the radius (i.e. the average
distance from memberships to the centroid of the
cluster). Cao et al. (Cao et al., 2006) produced
Denstream algorithm which relies on the radius r
avg
,
which is the average distance from the points in a
micro-cluster to the centroid. The radius is then used
to determine the merge of two closest micro-
clusters. Although calculating radius in these two
algorithms gives a very high probability for data
points to belong to a cluster, they may consider
some data points as outliers instead of members.
3 THE PROPOSED ALGORITHM
3.1 The Algorithm Framework
The general framework of the proposed EINCKM
algorithm is depicted in Figure 2. The algorithm
consists of the following main steps. Firstly, the
outliers from the previous iteration are added into
the incoming data chunk (step 1) in order to generate
the K new clusters. The number K of new clusters is
determined by an estimation function (step 2), which
currently uses some heuristic rules to determine the
value of K, but can be improved into a learning
function to learn the best possible number of clusters
for the new chunk. An Enhanced K-Means (EKM)
algorithm is applied to the new data chunk (step 3)
to discover the K new clusters. After that, a merging
strategy is applied to the overlapped new and
existing clusters of the last round using a radius-
based technique to derive a set of modified clusters
(steps 4, 5). Finally, data points that are currently
members of the modified clusters are filtered using a
variance-based mechanism to determine the outliers
among them (step 6).
Figure 3 shows the pseudo-code of the EINCKM
algorithm. The inputs are a data chunk of size M, a
pool of outliers, the minimum number of data points
per cluster, and a set of existing clusters summary.
Each cluster summary is a tuple (N, LS, LSS, µ, R),
where N is a number of data points, LS is the linear
sum of the data points, LSS is the sum of squared
data points, µ is the centroid, R is the radius. The
outputs are K clusters and outliers.
EINCKM: An Enhanced Prototype-based Method for Clustering Evolving Data Streams in Big Data
175

Figure 2: Main steps of the EINCKM algorithm.
EINCKM Algorithm:
Inputs:
: Data chunk of size. Initially CH = {}
: Set of clusters summary //Previous clustering
summary of T clusters. Initially, CF = {}
: Pool of outliers; //Previous Pool of W outliers. Initially, Po = {}.
Minimum number of data points per cluster.
Outputs:
`: Modified ;
`: Modified ;
Algorithm Steps:
1.
2.
//Estimate K and the initial centroids
3.
//cf is a structure contains cf.member as cluster
members & cf.summary as cluster summary.
4. //Find the cluster summary of new clusters.
Calculate
//
is a cluster in cf.
Set
as
from
;
Calculate cluster summary for
//i.e. N, LS, L SS.
5.
//Merge overlapping clusters.
6.
//Filter outliers
Figure 3: Pseudo-code of the proposed algorithm.
3.2 Main Functions of the Algorithm
We intend to keep the Estimate function simple and
hence it determines the number of clusters and
initial centroids using heuristics (see Figure 4).
For the first iteration, the number of clusters is set to
where N is the number of data points in
the new chunk plus the number of outliers in the
previous pool. For the later iterations, is set to the
value of the previous iteration (in Section 4.1 we
will explain why we select K in this way). Parameter
refers to the collection of the initial centroids.
For the first iteration, the initial centroids are
assigned as randomly selected data points in the data
collection, but for later iterations, the centroids of
the clusters of the previous iteration are taken as the
initial centroids for the current round. The EKM
function is an enhanced K-Means method that uses
and determined by the Estimate function. The
intension is to minimize the nondeterministic results
of clustering caused by different random seeds.
Estimate Function:
then//
is the number of clusters in
{
}
{
//
in
}
Figure 4: Pseudo-code for the Estimate Function.
The Merge function (see Figure 5) first creates a
pairwise centroid distance matrix for all clusters.
It then locates a pair of closest clusters with the
minimum distance. If the distance is less than or
equal to the radius of the smaller cluster, then the
two clusters are merged into a single cluster with
updated cluster summary and memberships for the
data points involved. One row and one column of
the matrix need to be updated to modify the
distances of the newly merged cluster with the other
clusters. The process is repeated until this criterion
cannot be satisfied by any pair of clusters in the
matrix .
Merge Function:
1.
2. Calculate the pairwise distance matrix for distances between
in //
3. Repeat
(A) Locate
,
in where
(B) Find
(C)
then
{
(a)
// Merging two clusters and reassigned the
memberships
(b) Calculate
for cluster
in ;
(c) Set
as
from
(d) Modify
(e) Update cluster summary for
}
Until no more merge clusters
Figure 5: Pseudo-code for the Merge Function.
Extracting the outliers from the final clusters is
done by calling the Filter function (see Figure 6)
which uses the variance of each cluster and MinPts
threshold to distinguish outliers. It scans the data
points in each final cluster and compares their
distance to the centroid with the radius of that
cluster. If the distance is greater than the radius, the
data point is considered as an outlier.
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
176

Filter Function:
{
// cf.member
{
// p is a data point in
then
}
then
Update cluster summary for
}
Figure 6: Pseudo-code for the Filter Function.
4 EVALUATION OF EINCKM
4.1 Logical Evaluation
Our evaluation of correctness focuses on the three
main functions of the algorithm. The Estimate
function only approximates the value of K and initial
centroids. Since the number of clusters is normally
smaller than the number of data points, using the
square root of half of the data points as suggested in
(Kodinariya and Makwana, 2013) is sensible as the
initial estimate.
The Merge function depends on the general
characteristics of the normal distribution to calculate
the cluster radius. The cautious merge strategy
ensures that the centroid of the smaller cluster not
only belongs to the big cluster, but also close to the
centroid of the big cluster. The Filter function
extracts the outliers from the final clusters using
their variance. Using the understanding of the
normal distribution, the function excludes some data
points outside the radius as an outlier, ensuring the
high quality of the clusters.
The number of clusters in each iteration is
affected by the Estimate and Merge functions. It
could be increased or decreased at one round of
clustering. In other words, the number of clusters is
determined after each round of clustering.
Regarding completeness, unlike Inc.KM, the
proposed algorithm does not lose any data point
during the clustering process. If a data point does not
belong to any clusters, it will be kept in the pool as
outliers. If the outliers kept in the pool are
considered belonging to a default cluster, the
proposed algorithm is complete.
The time complexity of EINCKM is determined
by the time complexity of its main functions. First,
the time complexity of EKM algorithm is estimated
as O(NKI) where N is the total number of data points
in a chunk plus the outliers in the input pool, K is the
number of clusters, and I is the number of iterations
until the clusters converge. The estimated time
complexity of the Merge function is O((T+k)
2
)
where T is the number of clusters of previous
iteration and k is the number of clusters from a new
chunk. The estimated time complexity of Filter
function is O(N) because each data point within the
chunk and the previous pool is determined as a
cluster member or an outlier. Therefore, the time
complexity of EINCKM is estimated as
O(M(NKI)+(T+k)
2
+N), where M is the chunk size.
The time complexity of the Adapt.KM algorithm
is estimated as O(M(NKI+k(k-1)+N(K+1))). The
time complexity of the Inc.KM algorithm is
estimated as O(M(NKI+k(k-1)+NK)). The time
complexity of STREAM is estimated as
O(M(NKI)+2k+N). Comparing the Big O notations
across the different algorithms shows that STREAM
is the fastest among the algorithms. The proposed
EINCKM algorithm time complexity depends on
(T+k)
2
whereas the Inc.KM and the Adapt.KM
algorithms depend on MK
2
and M(K
2
+1). Since in
most cases, the number of clusters is much fewer
than the number of data points within a chunk, the
proposed algorithm should be marginally faster than
Inc.KM and Adapt.KM but slower than STREAM.
4.2 Empirical Evaluation
Different approaches to evaluate clustering
algorithm performance exist in the literature
(Kremer et al., 2011). In order to evaluate the
correctness of the proposed algorithm, we have
decided to use the evaluation by the reference
method, i.e. to find if the algorithm can return the
known clusters in a given ground truth. To do so, we
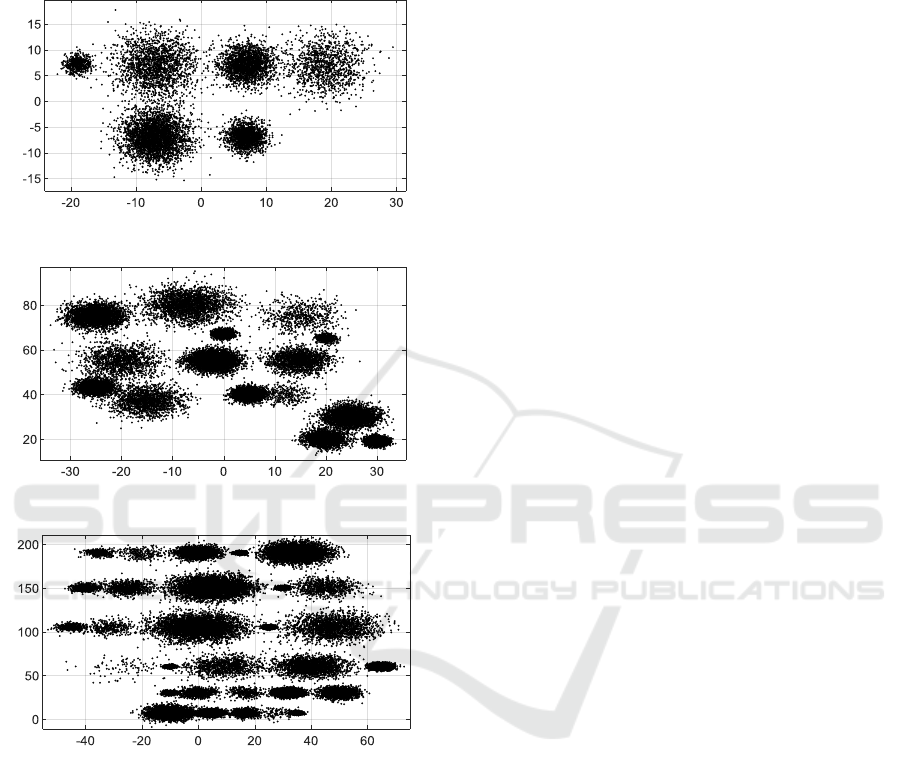
generated three synthetic datasets (DS1, DS2, and
DS3) of 10000, 30000, and 50000 data points
respectively of two dimensions. The DS1 contains
six clusters; DS2 contains fifteen clusters, and DS3
contains thirty clusters. Clusters in each of the three
datasets have different sizes. Each cluster is
generated randomly by following a normal
distribution of a different mean and variance. Figure
7 (a, b, c) shows the scatterplots of the three
datasets. The details of the normal distributions used
for generating the datasets are given in Appendix1.
For real-life dataset, we selected the Network
Intrusion Detection (NID) dataset from the KDD
Cup’99 repository. This dataset contains TCP
connection logs for 14 days of local network traffic
(494,021 data points). Each data point corresponds
to a normal connection or attack. The attacks split
into four main types and 22 more specific classes:
denial-of-service (DOS), unauthorized access from a
EINCKM: An Enhanced Prototype-based Method for Clustering Evolving Data Streams in Big Data
177
remote machine (R2L), unauthorized access to local
user privileges (U2R), and surveillance (PROBING).
We used all 34 continuous attributes as in (Aggarwal
et al., 2003) and (Cao et al., 2006).
(a) Scatterplot of dataset DS1.
(b) Scatterplot for dataset DS2.
(c) Scatterplot for dataset DS3.
Figure 7: Overview of synthesized datasets.
To evaluate correctness, we used three
commonly used evaluators: purity, entropy, and the
sum of squared errors (SSE). Purity was used in
(Cao et al., 2006), entropy in (Karypis and George,
2001), and SSE in (Aggarwal et al., 2003). Purity
refers to the proportion of the data points belonging
to a known cluster that are assigned as members of a
cluster by the algorithm. The higher the proportion
of purity (between [0, 1]) is, the more certain that
the algorithm has found the original clusters and the
better the algorithm is (Silva et al., 2013). Entropy
reflects the number of the data points from different
known clusters in the original dataset that are
assigned to a cluster by the algorithm. The value of
this measure is between [0,
] where N is the
number of known clusters involved. The smaller
value of the entropy is, the fewer members of the
known clusters are mixed in the clusters discovered
by the algorithm, and the better the clustering
algorithm is (Nguyen et al., 2015). SSE is a
commonly used cluster quality measure. It evaluates
the compactness of the resulting clusters. Low
scores of SSE indicates better clustering results as
the clusters contain less internal variations (Silva et
al., 2013). The efficiency of an algorithm was
measured by the amount of time in seconds taken for
the algorithm in completing the clustering task.
MATLAB was used to build an implementation
of the EINCKM algorithm and the experiment
framework. For the Adapt.KM and Inc.KM
algorithms, we split a given dataset into two parts:
the dynamic arriving data chunks of a certain size
and the initial dataset before the arrival of the first
dynamic data chunk. We randomly selected (e.g.
DS1) an initial collection of 1000 data points as the
initial dataset and the remaining 9000 were
randomly selected as data points in the dynamic
chunks. Our proposed algorithm does not treat the
initial dataset and later arrived chunks differently,
and hence an empty set of existing clusters and an
empty set of outliers were assumed as the inputs
when the first chunk is processed. For STREAM and
EINCKM algorithms, we randomly selected all the
chunks with size 100 data points. The idea behind
the random selection of the data points is to
investigate the behavior of the algorithms when
there is no control on the sequence of data points,
i.e. we did not select specific data points from
specific groups in the original datasets. No
assumption was made that the initial data chunk
represents the entire data domain. In order to
minimize the effect of random choice of data points,
the experiments were repeated 100 times, and the
average is calculated.
Figure 8 shows the details of comparison results
between the known clusters and the output clusters
from the Inc.KM, Adapt.KM, STREAM, and
EINCKM algorithms respectively. EINCKM has the
highest purity. This is the result of the stringent
merge strategy deployed and the exclusion of some
data points as outliers. Inc.KM also has good purity
by ignoring the outliers, but this strategy denies the
opportunity for some ignored outliers to become
members of some clusters at a later stage. Adapt.KM
has the poorer purity because of its merging strategy,
i.e. combining two closest clusters could belong to
different clusters in the original dataset. STREAM
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
178
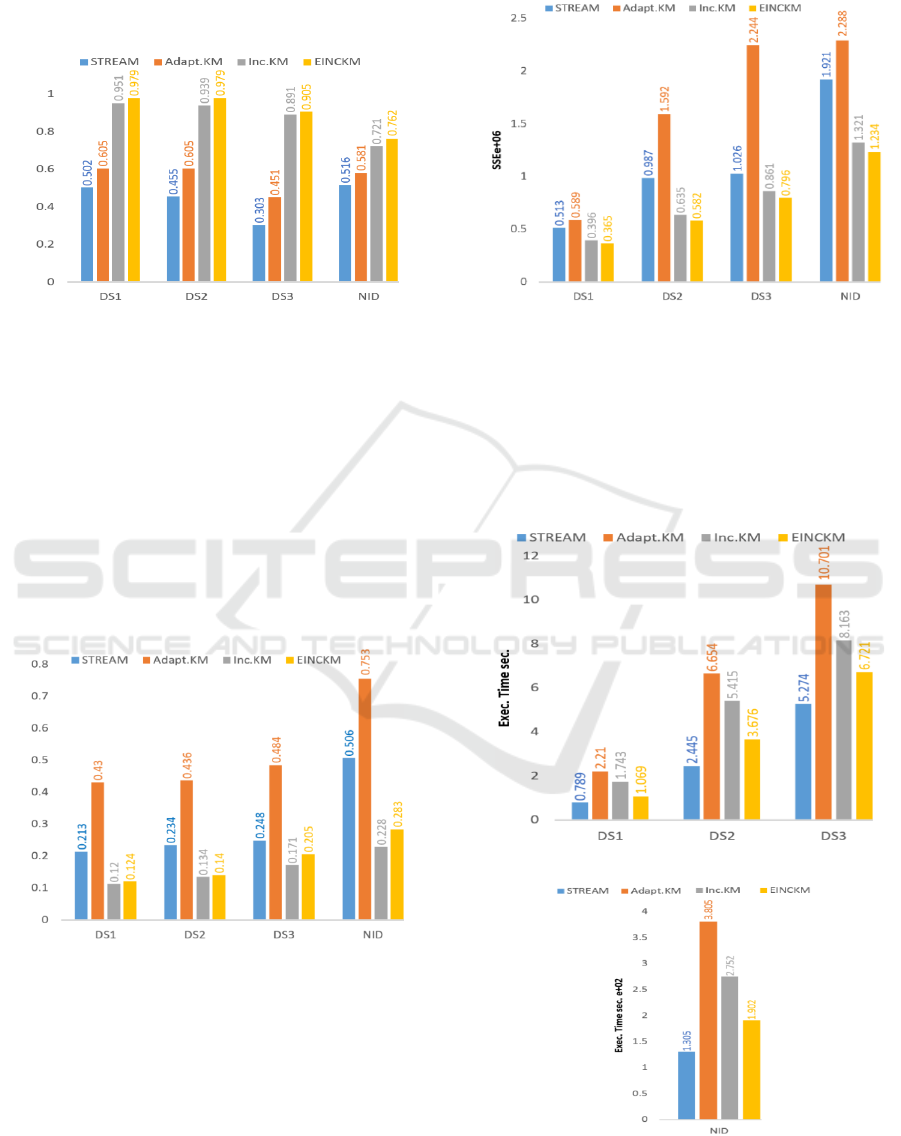
has the lowest purity because it selects randomly
initial centroids as one property of K-Median and
this leads to clusters contain data points belong to
different clusters in the original dataset.
Figure 8: The purity measurement.
As shown by Figure 9, Inc.KM has the lowest
entropy because it deletes all the outliers. EINCKM
has the second lowest level because adding the
outliers to the new data chunk may group them into
different clusters comparing with original dataset.
STREAM has the third level because the random
initial centroids could lead to getting output clusters
including some data points from other clusters.
Adapt.KM has the highest level of entropy because
its merging approach is getting output clusters
contain many data points belong to different clusters
in the original dataset.
Figure 9: The entropy measurement.
The EINCKM has the lowest SSE because it
produces compact and more stable clusters as a
result of merging criterion and keeps the outliers
separately (see Figure 10). In.KM has the second
level because it gives us almost balanced clusters.
STREAM has the third level because it presents
different cluster sizes every time. Adapt.KM has the
highest level because it produces bigger clusters
during the merging process.
Figure 10: The SSE measurement.
Test results are shown in Figure 11 (a, b) confirm
the logical analysis on efficiency: the STREAM
algorithm has the minimum execution time followed
by the EINCKM algorithm which in turn is better
than both Inc.KM and Adapt.KM. The pattern is
consistent across the synthesized and the real-life
datasets.
(a) The efficiency measurement for synthesized dataset.
(b) The efficiency measurement for real-life dataset.
Figure 11: The efficiency measurement.
EINCKM: An Enhanced Prototype-based Method for Clustering Evolving Data Streams in Big Data
179
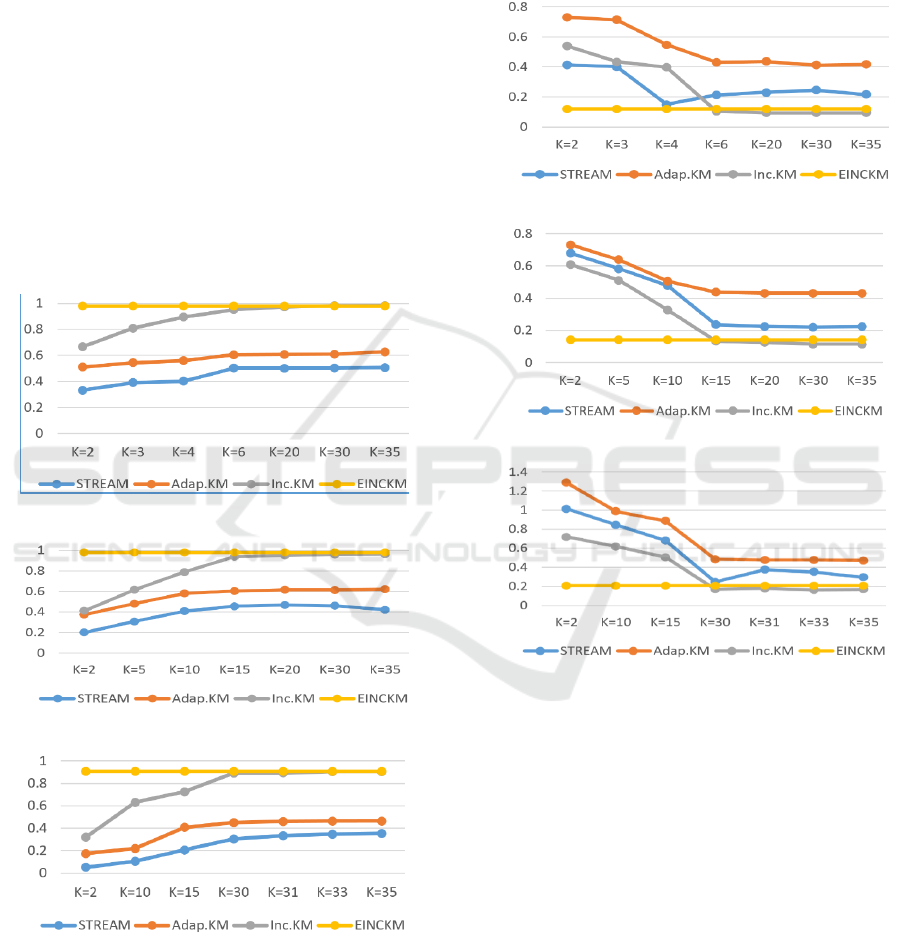
5 DISCUSSIONS
5.1 Adaptive Number of Clusters K by
EINCKM
Our algorithm determines the number of clusters K
automatically whereas the others require a
predefined K. The empirical study results presented
in the previous section compared those algorithms
against the proposed algorithm when they were
using the appropriate K values. However, those
algorithms would have performed much worse if
inappropriate K values were used. Figure 12 (a, b, c)
shows the purity differences of the existing
algorithms from the proposed algorithm when
different K values were chosen. The results clearly
demonstrate that the proposed algorithm outperform
the others.
(a) Different values of K for DS1 dataset.
(b) Different values of K for DS2 dataset.
(c) Different values of K for DS3 dataset.
Figure 12: The purity measurements of the algorithms for
synthesized datasets when different values of K were used.
Figure 13 (a, b, c) shows the differences between
the algorithms for the entropy correctness metric
over the synthesized datasets. We have also tested
the performances on SSE and performances on the
real-life dataset NID, but will not present the results
here due to space constraint. All test results indicate
the same performance gaps between the proposed
algorithm and the existing ones.
(a) Different values of K for DS1 dataset.
(b) Different values of K for DS2 dataset.
(c) Different values of K for DS3 dataset.
Figure 13: The entropy measurements of the algorithms
for synthesized datasets when different values of K were
used.
5.2 Refinements of EINCKM
One advantage of the EINCKM algorithm is its
highly modular structure where the essential
operations of the algorithm, i.e. estimating the value
of K, the K-Means performed on the new data
chunk, the merge operation, and the filter operation,
are designated to functions. This means that we can
continuously improve each function without
changing the structure of the algorithm.
As for the further improvement of each function
within the algorithm, first we do realize that using a
heuristic estimation at the start of the algorithm may
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
180

be too trivial, and may not guarantee optimal results.
We have noted the work presented in (Pio et al.,
2014) that used the principal component analysis
(PCA) to estimate the value of K before the K-
Means clustering is conducted on the newly arrived
data chunk, and consider adopting the method in the
future improved version of the algorithm. Besides,
machine learning solutions may be investigated to
predict a more suitable value for K based on past
clustering history on the previous chunks.
Besides, both the merge strategy and filtering
scheme are currently quite simply in order to limit
the amount of processing time. In fact, both the
merging strategy and the filtering scheme may be
further improved through learning. This is one area
for future research that we intend to investigate.
5.3 Adaptation of EINCKM to Concept
Drift
Concept Drift has been recognized as one major
issue in data stream clustering and classification
(Nguyen et al., 2015). In clustering, concept drift
refers to the evolutionary changes to cluster models
over time. Static data clustering only has one
concept: the global model of clusters whereas data
stream clustering may have multiple concepts that
evolve over time. We identified concept drift at two
levels: the adaptation level and change monitoring
level.
At the adaptation level, our algorithm, by
following the incremental approach of data stream
clustering, always refines the existing model of
clusters in light of the newly arrived data chunk, and
hence always adapts to the changes reflected by new
clusters added into the model or modification to the
existing clusters via merging.
At the change monitoring level, the proposed
algorithm itself does not keep a history trail of the
changed cluster models. In fact, implementation of
the algorithm may use variable parameters to keep a
single copy of the new model of clusters, over-
writing the previous model. However, this problem
can be solved by adding an outer loop in the data
streaming clustering process where the proposed
algorithm can be called when a new chunk arrives,
the refined new model of clusters can be recorded
into a permanent file. Then from time to time, a
monitoring task over the stored versions of the
cluster model can be undertaken to identify the
changes from one version to the next. It can be an
interesting problem to investigate further about how
to mine evolving patterns among the past cluster
models. This task requires developing a new kind of
algorithm for the “second order” discovery.
6 CONCLUSION AND FUTURE
WORK
In this paper, we presented a new algorithm
EINCKM for data stream clustering. The algorithm
emphasizes on simplicity, modularity, and
adaptivity. The key ideas of the algorithm are to
estimate the number of clusters (K) using heuristics,
merge the overlapped clusters using a radius-based
technique based on statistical information, and to
filter outlier using a variance-based mechanism. The
algorithm addressed two significant problems of
prototype-based methods: using a fixed predefined
value of K and produce clusters as well as outliers.
The evaluation on some synthesized datasets and
real dataset has shown that the algorithm produces
correct and good quality clusters with low time
complexity.
Our future work will focus on enhancing the
algorithm. Since the algorithm is modular, those
enhancement efforts can focus on the main functions
within the algorithm. The Estimate function can be
improved with learning capability to more
accurately estimate the value of K for later rounds of
calling the algorithm. A more adaptive strategy
based on learning of mixture models of Gaussians
can be developed for the Merge function, and a
fuzzy and shape based cluster radius could be
embedded into the Filter function to identify real
outliers.
ACKNOWLEDGMENTS
The first author wishes to thank the University of
Mosul and Government of Iraq/Ministry of Higher
Education and Research (MOHESR) for funding
him to conduct this research at the University of
Buckingham.
REFERENCES
Aggarwal, C. , Han, J., Wang, J. and Yu, P., 2003. A
Framework for Clustering Evolving Data Streams.
Proceedings of the 29th VLDB Conference, Germany.
Bhatia, S.K. and Louis, S., 2004. Adaptive K-Means
Clustering. American Association for Artificial Intelli-
gence.
EINCKM: An Enhanced Prototype-based Method for Clustering Evolving Data Streams in Big Data
181
Cao, F., Ester, M., Qian, W. and Zhou, A., 2006. Density-
based clustering over an evolving data stream with
noise. Proceedings of the Sixth SIAM International
Conference on Data Mining, 2006, pp.328–339.
Chakraborty, S. and Nagwani, N.K., 2011. Analysis and
Study of Incremental K-Means. Springer-Verlag
Berlin Heidelberg, pp.338–341.
Dempster, A.P., Laird, N.M. and Rubin, D.B., 1977.
Maximum Likelihood from Incomplete Data via the
EM Algorithm. Journal of the Royal Statistical
Society. Series B (Methodological), 39(1), pp.1–38.
Ester, M., Kriegel, H.-P., Sander, J. and Xu, X., 1996. A
Density-Based Algorithm for Discovering Clusters in
Large Spatial Databases with Noise. the 2nd
International Conference on Know- ledge Discovery
and Data Mining, 2, pp.226–231.
Guha, S., Mishra, N., Motwani, R. and O’Callaghan, L.,
2000. Clustering Data Streams. IEEE FOCS
Conference, pp.359–366.
Islam, M.Z., 2013. A Cloud Based Platform for Big Data
Science. Department of Computer and Information
Science, Linköping University, pp.1–57.
Karypis, Y.Z. and George, 2001. Technical Report
Criterion Functions for Document Clustering:
Experiments and Analysis. , pp.1–30.
Kodinariya, T.M. and Makwana, P.R., 2013. Review on
determining number of Cluster in K-Means Clustering.
International Journal of Advance Research in
Computer Science and Management Studies, 1(6),
pp.2321–7782.
Kremer, H., Kranen, P., Jansen, T., Seidl, T., Bifet, A.,
Holmes, G. and Pfahringer, B., 2011. An effective
evaluation measure for clustering on evolving data
streams. Proceedings of the 17th ACM SIGKDD
International Conference on Knowledge Discovery
and Data Mining - KDD ’11, pp.868–876. Available
at:
http://eprints.pascal-network.org/archive/00008693/.
Liu, C., Ranjan, R., Zhang, X., Yang, C., Georgakopoulos,
D. and Chen, J., 2013. Public Auditing for Big Data
Storage in Cloud Computing - A Survey. 2013 IEEE
16th International Conference on Computational
Science and Engineering, pp.1128–1135. Available at:
http://ieeexplore.ieee.org/lpdocs/epic03/wrapper.htm?
arnumber=6755345.
MacQueen, J., 1967. Some Methods for classification and
Analysis of Multivariate Observations. 5th Berkeley
Symposium on Mathematical Statistics and Probability
1967, 1(233), pp.281–297. Available at:
http://projecteuclid.org/euclid.bsmsp/1200512992.
Nguyen, H.L., Woon, Y.K. and Ng, W.K., 2015. A survey
on data stream clustering and classification.
Knowledge and Information Systems, pp.535–569.
Available at: http://dx.doi.org/10.1007/s10115-014-
0808-1.
Ntoutsi, I., Spiliopoulou, M. and Theodoridis, Y., 2009.
Tracing cluster transitions for different cluster types.
Control and Cybernetics, 38(1), pp.239–259.
Oliveira, M. and Gama, J., 2012. A Framework to Monitor
Clusters’ Evolution Applied to Economy and Finance
Problems. Intell. Data Anal. 16, 1, 93-111.
Olshannikova, E., Ometov, A. and Koucheryavy, Y.,
2014. Towards Big Data Visualization for Augmented
Reality. 2014 IEEE 16th Conference on Business
Informatics, pp.33–37. Available at:
http://ieeexplore.ieee.org/lpdocs/epic03/wrapper.htm?
arnumber=6904299.
Pio, G., Lanotte, P. F., Ceci, M. and Malerba, D., 2014.
Mining Temporal Evolution of Entities in a Stream of
Textual Documents. Springer International Publishing
Switzerland 2014, pp.50–60.
Silva, J., Faria, E., Barros, R., Hruschka, E. and Carvalho,
A., 2013. Data Stream Clustering : A Survey. ACM
Computing Surveys (CSUR), pp.1–37.
Yogita and Toshniwal, D., 2012. Clustering Techniques
for Streaming Data – A Survey. , pp.951–956.
Zhang, T., Ramakrishnan, R. and Livny, M., 1996.
BIRCH: An Efficient Data Clustering Databases
Method for Very Large Databases. ACM SIGMOD
International Conference on Management of Data, 1,
pp.103–114.
APPENDIX 1
The following tables show the details and specify
the distribution of each of the three synthesized
datasets.
Table 1: Parameters details of DS1.
K
Mean
STD
SZ
X
Y
X
Y
K1
5
7
2
2
20000
K2
16
7
3
3
11000
K3
5
-7
1.5
1.5
15000
K4
-5
7
3
3
18000
K5
-16
7
1
1
5000
K6
-5
-7
2.5
2.5
31000
Table 2: Parameters details of DS2.
K
Mean
STD
SZ
X
Y
X
Y
K1
20
20
2
2
2000
K2
5
40
1.5
1.5
2600
K3
30
19
1.1
1.1
3400
K4
12
40
2.5
2.5
300
K5
25
30
2.4
2.4
3100
K6
-15
37
3.5
3.5
1600
K7
-25
43
1.8
1.8
2100
K8
1
67
1.2
1.2
1500
K9
15
55
2.9
2.9
1700
K10
-2
54
2.3
2.3
4000
K11
-20
55
3.9
3.9
1300
K12
15
75
3.8
3.8
600
K13
20
65
0.9
0.9
500
K14
-7
80
4.1
4.1
2300
K15
-25
75
2.7
2.7
3100
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
182

Table 3: Parameters details of DS3.
K
Mean
STD
SZ
X
Y
X
Y
K1
7
7
2.5
2.5
800
K2
30
7
3.5
3.5
110
K3
-11
7
1.9
1.9
3500
K4
-35
7
3.9
3.9
2900
K5
45
7
1.1
1.1
1290
K6
7
30
3.4
3.4
300
K7
32
30
2.2
2.2
5000
K8
-15
30
3.1
3.1
700
K9
-30
30
1.2
1.2
600
K10
50
30
3.3
3.3
1700
K11
-15
60
1.2
1.2
900
K12
45
60
5.9
5.9
2000
K13
10
60
6.4
6.4
1000
K14
-50
60
7.9
7.9
100
K15
75
60
1.7
1.7
4300
K16
1
105
7.5
7.5
4000
K17
25
105
1.3
1.3
1650
K18
-35
105
4.4
4.4
350
K19
-60
105
2.4
2.4
400
K20
60
105
7.7
7.7
1900
K21
5
150
6.4
6.4
5000
K22
30
150
0.9
0.9
1200
K23
-30
150
4.4
4.4
800
K24
-60
150
2.4
2.4
500
K25
60
150
5.5
5.5
800
K26
7
190
3.6
3.6
2500
K27
25
190
0.8
0.8
750
K28
-20
190
4.2
4.2
250
K29
-50
190
2.8
2.8
350
K30
50
190
5.6
5.6
4350
EINCKM: An Enhanced Prototype-based Method for Clustering Evolving Data Streams in Big Data
183
