
Adversarial Reinforcement Learning in a Cyber Security Simulation
Richard Elderman
1
, Leon J. J. Pater
1
, Albert S. Thie
1
, Madalina M. Drugan
2
and Marco A. Wiering
1
1
Institute of Artificial Intelligence and Cognitive Engineering, University of Groningen, Groningen, The Netherlands
2
Mathematics and Computer Science Department, Technical University of Eindhoven, Eindhoven, The Netherlands
Keywords:
Reinforcement Learning, Adversarial Setting, Markov Games, Cyber Security in Networks.
Abstract:
This paper focuses on cyber-security simulations in networks modeled as a Markov game with incomplete
information and stochastic elements. The resulting game is an adversarial sequential decision making problem
played with two agents, the attacker and defender. The two agents pit one reinforcement learning technique,
like neural networks, Monte Carlo learning and Q-learning, against each other and examine their effectiveness
against learning opponents. The results showed that Monte Carlo learning with the Softmax exploration
strategy is most effective in performing the defender role and also for learning attacking strategies.
1 INTRODUCTION
In an ever changing world, providing security to indi-
viduals and institutions is a complex task. Not only is
there a wide diversity of threats and possible attack-
ers, many avenues of attack exist in any target rang-
ing from a web-site to be hacked to a stadium to be
attacked during a major event. The detection of an at-
tack is an important aspect. The authors in (Sharma
et al., 2011) showed that 62% of the incidents in the
study were detected only after attacks have already
damaged the system. Recognizing attacks is there-
fore crucial for improving the system. The balance
between prevention and detection is a delicate one,
which brings unique hurdles with it. Our aim is to
evaluate the effectiveness of reinforcement learning
in a newly developed cyber security simulation with
stochastic elements and incomplete information.
Related Work. Markov games (Littman, 1994)
are played between two adversarial agents with a min-
max version of the popular Q-learning algorithm. Ad-
versarial reinforcement learning (Uther and Veloso,
2003) has been used for playing soccer with two play-
ers using a Q-learning variant. In his book (Tambe,
2011), Tambe describes a variety of methods to best
use limited resources in security scenarios. Some
problems mentioned in that book are: 1) Address-
ing the uncertainty that may arise because of an ad-
versary’s inability to conduct detailed surveillance,
and 2) Addressing the defender’s uncertainty about
attackers payoffs. In this paper, we will address these
problems.
A Novel Cyber-security Game for Networks.
Consider a network consisting of nodes representing a
server or network connected with each other. The at-
tacker attempts to find a way through a network con-
sisting of various locations, to reach and penetrate the
location containing the important asset. The defender
can prevent this by either protecting certain avenues
of attack by raising its defense or choosing to improve
the capability of the location to detect an attack in
progress. The attacker executes previously success-
ful strategies, and in the same time adapts to the de-
fender’s strategies. The environment resembles a dy-
namic network that is constantly changing at the end
of a game due to the opponent’s behavior.
Adversarial Reinforcement Learning Agents.
In our setting, a number of reinforcement learning al-
gorithms (Sutton and Barto, 1998; Wiering and van
Otterlo, 2012) are pitted against each other as the de-
fender and attacker in a simulation of an adversarial
game with partially observable states and incomplete
information. Reinforcement learning techniques for
the attacker that are used are Monte Carlo learning
with some exploration strategies: ε-greedy, Softmax,
Upper Confidence Bound 1 (Auer et al., 2002), and
Discounted Upper Confidence Bound (Garivier and
Moulines, 2008), and backward Q-learning with ε-
greedy exploration (Wang et al., 2013). The defender
uses the same algorithms and two different neural net-
works with back-propagation as extra algorithms.
As the attacker becomes more successful in suc-
cessive games, the defender creates new situations
for the attacker. The same holds true the other way
Elderman R., J. J. Pater L., S. Thie A., M. Drugan M. and M. Wiering M.
Adversarial Reinforcement Learning in a Cyber Security Simulation.
DOI: 10.5220/0006197105590566
In Proceedings of the 9th International Conference on Agents and Artificial Intelligence (ICAART 2017), pages 559-566
ISBN: 978-989-758-220-2
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
559

around. This process becomes more complicated by
the fact that in the beginning the attacker has no
knowledge of the network. The attacker can only gain
access to knowledge about the network by penetrat-
ing the defenses. The defender in turn does know the
internal network, but not the position or type of at-
tack of the attacker. Adapting different strategies to
unobservable opponents is crucial in dealing with the
realities of cyber attacks (Chung et al., 2016).
Outline. In Section 2 the cyber security game is
described and explained. In Section 3 the used rein-
forcement learning techniques and algorithms are de-
scribed. Section 4 explains the experimental setup,
and Section 5 presents the experimental results for
the simulations and discusses these results. Finally,
in Section 6 the main findings are summarized.
2 CYBER SECURITY GAME
In cyber security in the real world, one server with
valuable data gets attacked by many hackers at the
same time, depending on the value of the data con-
tent. It is also often the case that one network contains
more than one location with valuable data. However,
in the simulation made for this study, only one at-
tacker and one defender play against each other, while
there is only one asset. This is chosen for the sake of
little complexity of the ”world”, such that agents do
not have to learn very long before they become aware
of any good strategy.
2.1 Network
In the simulation the attacker and defender play on
a network representing a part of the internet. The
network consists of nodes, which are higher abstrac-
tions of servers in a cyber network, such as login
servers, data servers, internet servers, etc. Nodes can
be connected with each other, which represents a dig-
ital path: it is possible to go from one server to an-
other one, only if they are (in)directly connected. Ev-
ery connection is symmetric. In the network there are
three types of nodes:
1. The starting node, START , is the node in which
the attacker is at the beginning of each game. It
has no asset value. It can be seen as the attacker’s
personal computer.
2. Intermediate nodes. These are nodes without asset
values, in between the start node and the end node.
They must be hacked by the attacker in order to
reach the end node.
3. The end node, DATA, is the node in the network
containing the asset. If the attacker successfully
attacks this node, the game is over and the attacker
has won the game.
An attacker node is defined as n(a
1
, a
2
, ..., a
10
), where
each a is the attack value of an attack type on
the node. A node for the defender is defined as
n(d
1
, d
2
, ..., d
10
, det) where each d is the defense
value of an attack type on the node and det is the
detection value on the node. Each node consists of
10 different attack values, 10 different defense val-
ues, and a detection value. Each value in a node has a
maximal value of 10.
Even the standard network of 4 nodes, see Fig-
ure 1, creates a huge number of possible environmen-
tal states. The attack and defense values are paired,
each pair represents the attack strength and security
level of a particular hacking strategy. The detection
value represents the strength of detection, which rep-
resents the chance that, after a successfully blocked
attack, the hacker can be detected and caught. The en-
vironmental state of the network can be summarized
as a combination of the attack values, defense values
and detection value of each node. Both the attacker
and defender agents have internal states representing
parts of the entire environmental state, on which they
base their actions.
The game is a stochastic game due to the
detection-chance variable. When an attack on a node
fails (which is very likely), a chance equal to the
detection parameter determines if the attacker gets
caught. This resembles a real-life scenario because
attacks can remain unnoticed, and the chance that an
attack is unnoticed decreases if there is more detec-
tion.
2.2 Agents
In the simulation there are two agents, one defender
agent and one attacker agent. Each agent has limited
access to the network, just like in the real world, and it
has only influence on its side of the values in the nodes
(security levels or attack strengths). Both agents have
the goal to win as many games as possible.
The Attacker. Has the goal of hacking the net-
work and get the asset in the network. An attacker
wins the game when it has successfully attacked the
node in the network in which the asset is stored. For
every node n that is accessible by the attacker, only
the values for the attack strengths are known by the
attacker, a
1
, . . . , a
10
. The attacker has access to the
node it is currently in, and knows the nodes directly
accessible from that server. With a particular attacker
action, the attack value of the attacked node n from
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
560

Figure 1: The game from the Attacker’s and Defender’s per-
spective. Arrows indicate possible attacks A with attack
type n from the current node. All initial attack values are
equal to zero. The attacker starts at the start-node. For the
defender, the V values indicate the initial defense values. D
stands for the initial detection-chance if an attack fails.
node m and a specific attack type a
i
is incremented by
one. Per game step, an attacker is allowed to attack
only one of the accessible nodes, for which the value
is not already the maximal value.
The Defender. Has the goal to detect the attack
agent before it has taken the asset in the network. We
assume that the defender has access to every node in
the network, and that the defender only knows the de-
fend and detection values on each node, but not the
attack values. Per game step, the defender is allowed
to increment one detection value on one node in the
network or to increase the defend values of an attack
type in a node. By incrementing a defend value, it be-
comes harder for the attacker to hack the node using
a specific attack type. By incrementing the detection
value, the chance that an unsuccessful attack is de-
tected becomes higher.
2.3 Standard Network
In our simulations, the agents play on the standard
network, consisting of four nodes connected with
each other in a diamond shape. The starting node,
START , is connected with two intermediate nodes,
which are both connected with the end node (see Fig-
ure 1).
All attack and defense values on the start node are
initially zero: both agents need to learn that putting
effort in this node has no positive effect on their win
rate, since the attacker cannot take the asset here and
the defender therefore does not need to defend this
node. By design, both intermediate nodes have a ma-
jor security flaw represented by one attack type hav-
ing an initial security level of zero, leaving the at-
tacker two best actions from the start node. The end
node, DATA, contains data. This node containing the
asset has a similar security flaw as well giving the at-
tacker an easy path towards its goal. The defender
must identify this path and fix the security flaws by
investing in the security level of the attack type with
initially low security on the node.
2.4 Game Procedure
When starting each game, the attacker is in the start
node. The values in all the nodes are initialized as
shown in Table 1. Each game step, both agents choose
an action from their set of possible actions. The ac-
tions are performed in the network, and the outcome
is determined. The node on which the attack value of
an attack type was incremented determines if the at-
tack was successful. If the attack value for the attack
type is higher than the defend value for that attack
type, then the attack overpowers the defense and the
attack was successful. In this case, the attacker moves
to the attacked node. When this node is the end node,
the game ends and the attacker wins. When the attack
value of the attack type is lower than or equal to the
defense value, the attack is blocked. In this case, the
attack is detected with some probability given by the
detection value, a number between 0 and 10, of the
node that was attacked. The chance to be detected is
(detection value * 10)%. If the attack was indeed de-
tected, the game ends and the defender wins. If the
attack was not detected, another game step is played.
At the end of each game, the winner gets a re-
ward with the value 100, and the loser gets a reward
with the value -100. One agent’s gain is equivalent to
another’s loss, and therefore this game is a zero-sum
game (Neumann and Morgenstern, 2007).
An Example Game. An example game on the
standard network is shown in Table 1. In game step 1
the attacker attacks the gap in one of the intermediate
nodes, while the defender fixes the flaw in the other
node. The attacker now moves to the attacked inter-
mediate node. Then the attacker attacks the security
flaw in the end node, while the defender increments
the same value as in the previous game step. Now
the attacker moves to the end node and has won the
game. The agents update the Q-values of the state-
action pairs played in the game, and a new game will
be started. A game on the standard network lasts at
least 1 time step, and at most 400 time steps.
3 REINFORCEMENT LEARNING
The agents in the simulation need to learn to optimize
their behavior, such that they win as many games as
possible. In each game step, an agent needs to choose
Adversarial Reinforcement Learning in a Cyber Security Simulation
561

Table 1: An example game showing the attacker moving to CPU2 and subsequently to the DATA node. The defender performs
two defense actions in CPU1. Therefore, in this example game the attacker wins after two moves.
Gamestep Action Attacker Action Defender Node Attack Values Defense Values
0 - - START [0, 0, 0, 0, 0, 0, 0, 0, 0, 0] [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
CPU1 [0, 0, 0, 0, 0, 0, 0, 0, 0, 0] [0, 2, 2, 2, 2, 2, 2, 2, 2, 2]
CPU2 [0, 0, 0, 0, 0, 0, 0, 0, 0, 0] [2, 0, 2, 2, 2, 2, 2, 2, 2, 2]
DATA [0, 0, 0, 0, 0, 0, 0, 0, 0, 0] [2, 2, 0, 2, 2, 2, 2, 2, 2, 2]
1 CPU2, Attack Type 2 CPU1, Defense Type 1 START [0, 0, 0, 0, 0, 0, 0, 0, 0, 0] [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
CPU1 [0, 0, 0, 0, 0, 0, 0, 0, 0, 0] [1, 2, 2, 2, 2, 2, 2, 2, 2, 2]
CPU2 [0, 1, 0, 0, 0, 0, 0, 0, 0, 0] [2, 0, 2, 2, 2, 2, 2, 2, 2, 2]
DATA [0, 0, 0, 0, 0, 0, 0, 0, 0, 0] [2, 2, 0, 2, 2, 2, 2, 2, 2, 2]
2 DATA, Attack Type 3 CPU1, Defense Type 1 START [0, 0, 0, 0, 0, 0, 0, 0, 0, 0] [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
CPU1 [0, 0, 0, 0, 0, 0, 0, 0, 0, 0] [2, 2, 2, 2, 2, 2, 2, 2, 2, 2]
CPU2 [0, 1, 0, 0, 0, 0, 0, 0, 0, 0] [2, 0, 2, 2, 2, 2, 2, 2, 2, 2]
DATA [0, 0, 1, 0, 0, 0, 0, 0, 0, 0] [2, 2, 0, 2, 2, 2, 2, 2, 2, 2]
an action out of a set of possible actions. Agents
base their decision on the current state of the network.
States are defined differently for both agents, because
the complete state of the network is partially observ-
able for both agents, and they have access to different
kinds of information about the network. The agents
also have different actions to choose from.
The Attacker. States are defined as s(n), where n
is the node the agent is currently in. An action is de-
fined as A(n
0
, a), where n
0
is one of the neighbouring
nodes of node n that is chosen to be attacked and a
an attack type as before. In each state, the number of
possible actions is 10 * the number of neighbours of n
minus the actions that increment any attack value that
is already maximum (has the value 10).
The Defender. For a defender agent, the state is
defined as s(n
1
, n
2
, ..., n
i
), where each n
i
is the i-th
node in the network. An action for a defender is de-
fined as A(n, a), where n is the node in the network
that is chosen to invest in, and a ∈ d
1
, d
2
, ..., d
10
, det
the defend values and detection value. In each state,
the number of possible actions is 11 * the number of
nodes minus the actions that increment the defense
value of an attack type or detection value that is al-
ready maximum (has the value 10).
The Monte-Carlo and Q-learning agents do not
have an internal state representation, but they base
their actions on previous success, regardless of the en-
vironmental state. The neural and linear networks use
the entire observable environmental state as an input.
3.1 Monte Carlo Learning
In the first reinforcement learning technique, agents
learn using Monte Carlo learning (Sutton and Barto,
1998). The agents have a table with possible state-
action pairs, along with estimated reward values.
After each game the agents update the estimated
reward values of the state-action pairs that were se-
lected during the game. Monte Carlo learning up-
dates each state the agent visited with the same reward
value, using:
Q
t+1
(s, a) = Q
t
(s, a) + α ∗ (R − Q
t
(s, a))
where α is the learning rate which is a parameter rang-
ing from 0 to 1 that represents how much the agent
should learn from a new observation. R is the re-
ward obtained at the end of each game. The Q-values
are the estimated reward values. They represent how
much the agent expects to get after performing an ac-
tion. The s is the current state of the world, for the at-
tacker the node it currently is in and for the defender
it is empty: the state s has always the value 0. The
a is a possible action to do in that state (see also the
start of this section). For the defender the state s used
in the learning algorithm has always the value 0, be-
cause using a tabular approach it is unfeasible to store
all possible states. Although the state value is 0, the
environmental state determines which actions can be
selected. The attacker has information of the node it
currently is in, and this forms the state.
A reinforcement learning agent has the dilemma
between choosing the action that is considered best
(exploitation) and choosing some other action, to
see if that action is better (exploration). For Monte
Carlo learning, four different exploration algorithms
are implemented that try to deal with this problem
in the cyber security game. The four algorithms
are ε-greedy, Softmax, Upper Confidence Bound 1
(Auer et al., 2002), and Discounted Upper Confidence
Bound (Garivier and Moulines, 2008), which we will
now shortly describe.
ε-greedy Strategy. The first method is the ε-
greedy exploration strategy. This strategy selects the
best action with probability 1 − ε, and in the other
cases it selects a random action out of the set of pos-
sible actions. ε is here a value between 0 and 1, deter-
mining the amount of exploration.
Softmax. The second exploration strategy is Soft-
max. This strategy gives every action in the set of
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
562

possible actions a chance to be chosen, based on the
estimated reward value of the action. Actions with
higher values will have a bigger chance to be chosen.
A Boltzmann distribution is used in this algorithm to
calculate the action-selection probabilities:
P
t
(a) =
e
Q
t
(s,a)
τ
∑
K
i=1
e
Q
t
(s,i)
τ
where P
t
(a) is the chance that action a will be cho-
sen. K is the total number of possible actions. τ is the
temperature parameter, which indicates the amount of
exploration.
UCB-1. The third exploration strategy is called
Upper Confidence Bound 1 (UCB-1) (Auer et al.,
2002). This algorithm bases its action selection on the
estimated reward values and on the number of previ-
ous tries of the action. The less an action is tried be-
fore, the higher the exploration bonus that is added to
that value for the action selection. At the start of the
simulation, actions will be chosen that have not been
tried before. After no such actions are left, the action
will be chosen that maximizes V
t
(a), computed by:
V
t
(a) = Q
t
(s, a) +
s
c ∗ ln n
n(a)
where n(a) is the number of previous tries of action
a over all previously played games in the simulation.
n is the total number of previous tries for all actions
currently available over all previously played games
in the simulation. c is the exploration rate.
Discounted UCB. The last exploration strategy
is called Discounted Upper Confidence Bound (Dis-
counted UCB), and is a modification of the UCB-1
algorithm (Garivier and Moulines, 2008). It is based
on the same idea, but more recent previous tries have
more influence on the value than tries longer ago.
This algorithm was proposed as an improvement of
the UCB-1 algorithm when used in a non-stationary
environment like the simulation in this study.
Like in UCB-1, at the start of the simulation ac-
tions will be chosen that have not been tried before,
and after no such actions are left the action will be
chosen that maximizes V
t
(a), computed by:
V
t
(a) = Q
t
(s, a) + 2B
s
ξlog n
t
(γ)
N
t
(γ, a)
B is the maximal reward that can be obtained in a
game. ξ is the exploration rate. n
t
(γ) is defined as:
n
t
(γ) =
K
∑
i=1
N
t
(γ, i)
K is the number of possible actions in time step t.
N
t
(γ, i) is defined as:
N
t
(γ, i) =
t
∑
s=1
γ
t−s
1
{a
s
=i}
1
{a
s
=i}
is the condition that the value for time step
s must only be added to the sum if action i was per-
formed in time step s. γ is the discount factor that
determines the influence of previous tries on the ex-
ploration term.
3.2 Q-Learning
Q-learning is a model-free reinforcement learning
technique. In (Watkins and Dayan, 1992) it was
proved that Q-learning converges to an optimal pol-
icy for a finite set of states and actions for a single
agent. The Backward Q-learning algorithm (Wang
et al., 2013) is used here to train the attacker and
defender agents. We combined the (Backward) Q-
learning algorithm only with the ε-greedy exploration
strategy. The ’backward’ here signifies that the up-
date starts at the last visited state, and from thereon
updates each previous action until the first. The
backward Q-learning algorithm can enhance learning
speed and improve final performance over the normal
Q-learning algorithm.
The last action brings the agent in a goal state, and
therefore it has no future states. Hence the last state-
action pair is updated as follows:
Q
t+1
(s, a) = Q
t
(s, a) + α ∗ (R − Q
t
(s, a))
For every other state-action pair but the last one the
learning update is given by:
Q
t+1
(s, a) = Q
t
(s, a) + α ∗ (γ max Q
t
b
(s
0
, b) − Q
t
(s, a))
Normally the reward is also a part of the second for-
mula, but it is omitted here for the reason that only
the last state-action pair gets an immediate reward. γ
is the discount parameter. γ ∈ [0, 1] and serves to find
a balance between future and current rewards.
3.3 Neural Network
The neural network (multi-layer perceptron) is only
implemented for the defender agent and not for the
attacker. Compared to the tabular approaches, the
neural network has the advantage that it can use input
units denoting the observable environmental state.
The neural network uses stochastic gradient de-
scent back-propagation to train its weights. It uses
an input neuron for each defense or detection value
in the network and an output neuron for each possi-
ble action. In the hidden layer the sigmoid activation
Adversarial Reinforcement Learning in a Cyber Security Simulation
563

Table 2: Parameter settings for the attacker agent that result
in the highest win score against the optimized ε-greedy de-
fender (except for the ε-greedy attacker which is optimized
against a defender with random action selection).
Learning technique Learning Rate Parameter(s)
Discounted UCB α = 0.05 ξ = 6, γ = 0.6
ε-greedy α = 0.05 ε = 0.05
Q-learning α = 0.1 γ = 1.0, ε = 0.04
Softmax α = 0.05 τ = 5
UCB-1 α = 0.05 c = 4
function is used. Rewards for the neural network are
calculated after each game as the Monte Carlo algo-
rithm with rewards normalized to 1 for winning and
-1 for losing, using only the selected action (output
neuron) per game step as the basis for the stochas-
tic gradient descent algorithm. Training is done by
way of experience replay (Lin, 1993), using the last n
games t times for updating the network.
In total, there are 44 input and output neurons.
Preliminary testing showed that 6 neurons in the hid-
den layer connected to the 44 input and output neu-
rons provided the best results, using experience replay
parameters n = 10 and t = 2. The 44 output neurons
represent each of the 44 moves available to the de-
fender at any game step. The highest activation value
amongst the output nodes of the network represents
the defensive action that is taken.
3.4 Linear Network
The linear network follows the same approach as well,
but has no hidden layer. It therefore directly calcu-
lates its output based on an input layer of 44 nodes,
again representing each of the defense and detection
values in the network, with weighted connections to
the output layer. Each of the outputs represents a pos-
sible move in the game. Experience replay did not
show to significantly increase the result of the Linear
network, so it is not used in the experiments. The out-
put with the highest activation is selected as the move
to be played.
4 EXPERIMENTAL SETUP
To test the performance of the different reinforcement
learning techniques, simulations are run in which the
attacker and defender agent play the game with dif-
ferent techniques. The attacker plays with six differ-
ent techniques: random action selection, four differ-
ent Monte Carlo learning techniques and Q-learning,
while the defender plays with eight different tech-
niques, the six from the attacker and the two neural
Table 3: Parameter settings for the defender agent that result
in the highest win score against the optimized ε-greedy at-
tacker (except for the ε-greedy defender which is optimized
against an attacker with random action selection).
Learning technique Learning Rate Parameter(s)
Discounted UCB α = 0.05 ξ = 4, γ = 0.6
ε-greedy α = 0.05 ε = 0.1
Linear Network α = 0.1 -
Neural Network α = 0.01 hiddenneurons = 6, n = 10, t = 2
Q-learning α = 0.05 γ = 0.91, ε = 0.07
Softmax α = 0.05 τ = 4
UCB-1 α = 0.05 c = 5
networks.
Every technique is optimized for both agents, by
changing the learning rate and its own parameter(s).
The Monte Carlo learning technique with ε-greedy
exploration is for both agents taken as a basis, this
technique is optimized against an opponent with ran-
dom action selection. All other learning techniques
are optimized against an opponent using this opti-
mized technique. For every parameter setting 10 runs
of 20000 games are simulated, and the one with the
highest total average win score is selected as the opti-
mal parameter setting. The optimal parameter settings
can be seen in Tables 2 and 3.
5 RESULTS
The obtained results can be seen in Table 4, which
displays the average win score over the full 10 sim-
ulations of 20000 games. The average scores come
along with their standard deviations. Each win score
is a value between -1 and 1, -1 indicates the attacker
has won everything, 1 means the defender did always
win. In the bottom row and rightmost column, the
best attacker(A)/defender(D) for that column/row is
displayed.
From the ”average” row and column in the table,
which shows the average score against all opponents,
it can be concluded that for both agents there is not a
single algorithm that always performs best. Softmax
is a good learning algorithm for the defender, against
all opponents it is, if not the best, among the best
performing defenders, but ε-greedy, UCB-1, and Q-
learning are also doing pretty well. For the attacker all
different exploration strategies used for Monte Carlo
learning show good results, with Softmax having a
slight lead over the others.
When we take a look at the individual results of
the algorithms from the attacker’s perspective, it turns
out that the algorithm with random action selection is
by far the worst performing algorithm, with an aver-
age win score of 0.93, which means it only wins about
3 percent of the games. The second worst attacker’s
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
564
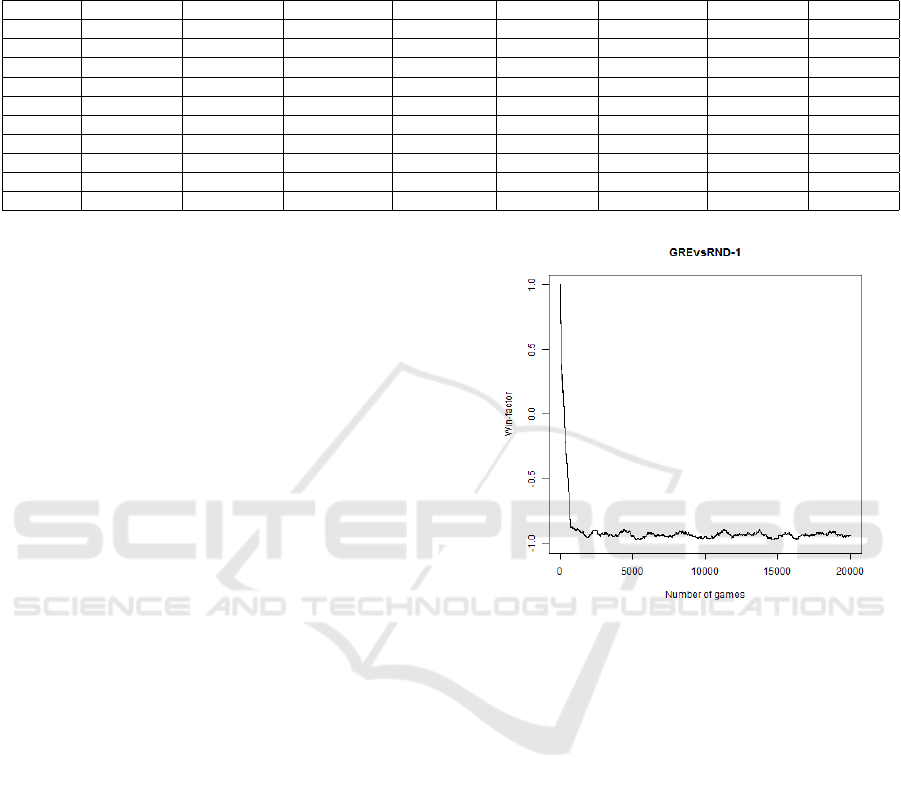
Table 4: Average score of 10 complete simulations of 20000 games for each strategy pair along with the standard deviation.
DUC = discounted UCB, GRE = ε-greedy, LN = linear network, NN = neural network, QL = Q-learning, RND = Random,
SFT = Softmax, UCB = UCB-1. The average row/column shows the total average score for each attacker/defender strategy
against all opponents.
D ↓ A → DUC GRE QL RND SFT UCB average BEST A
DUC -0.26 ± 0.14 -0.26 ± 0.08 -0.14 ± 0.11 0.93 ± 0.02 -0.42 ± 0.13 -0.26 ± 0.09 -0.07 ± 0.46 SFT
GRE -0.13 ± 0.05 -0.15 ± 0.03 0.08 ± 0.07 0.97 ± 0.004 -0.19 ± 0.03 -0.15 ± 0.05 0.07 ± 0.41 SFT
LN -0.95 ± 0.03 -0.87 ± 0.04 0.07 ± 0.66 0.93 ± 0.008 -0.94 ± 0.04 -0.95 ± 0.02 -0.45 ± 0.77 DUC/UCB
NN -0.41 ± 0.17 -0.43 ± 0.24 -0.44 ± 0.18 0.93 ± 0.02 -0.41 ± 0.19 -0.32 ± 0.05 -0.18 ± 0.53 QL
QL -0.15 ± 0.04 -0.16 ± 0.01 0.25 ± 0.05 0.94 ± 0.005 -0.19 ± 0.02 -0.13 ± 0.02 0.09 ± 0.41 SFT
RND -0.96 ± 0.01 -0.91 ± 0.02 -0.91 ± 0.004 0.92 ± 0.002 -0.95 ± 0.05 -0.96 ± 0.007 -0.63 ± 0.69 DUC/UCB
SFT -0.07 ± 0.08 -0.08 ± 0.05 0.35 ± 0.07 0.95 ± 0.02 -0.10 ± 0.06 -0.10 ± 0.07 0.16 ± 0.39 SFT/UCB
UCB -0.16 ± 0.06 -0.15 ± 0.04 0.37 ± 0.17 0.89 ± 0.01 -0.19 ± 0.05 -0.17 ± 0.03 0.10 ± 0.41 SFT
average -0.39 ± 0.35 -0.38 ± 0.33 -0.05 ± 0.48 0.93 ± 0.02 -0.43 ± 0.33 -0.38 ± 0.34 -0.11 ± 0.59 SFT
BEST D SFT SFT UCB GRE SFT SFT SFT
algorithm turns out to be Q-learning, which wins on
average just more than half of its games (win score -
0.05). The remaining four Monte Carlo learning algo-
rithms with each a different exploration strategy per-
form on average almost equally well, with a win score
between -0.38 and -0.43.
The two worst performing algorithms for the de-
fender agent turn out to be random action selection
(average win score = -0.63) and the Linear Network
(average win score = -0.45). The Neural Network per-
forms better, with an average win score of -0.18, but
it is still worse than the learning algorithms that use
tabular representations. Only one of these defender
algorithms has a win score less than zero, and this
is, surprisingly, Monte Carlo learning with discounted
UCB exploration, with an average win score of -0.07.
The four best performing defender algorithms have
an almost equal average win score between 0.07 and
0.16.
There is a huge initial advantage of the defender
agent with respect to the attacker agent when the
game is played: when both agents do not learn, the
defender wins about 95% of the games. This is most
likely caused by the random selection procedure of
the attacker, which makes it highly unlikely that it se-
lects a node more than once (which is required for
most attack types to break through a node).
5.1 Notable Aspects of the Results
An interesting part of the results is that for the de-
fender agent both algorithms based on neural net-
works perform worse than all algorithms based on
tabular representations. This reflects the problem that
neural networks have with adversarial learning. The
network is slower in adapting to a constantly chang-
ing environment than other algorithms, therefore be-
ing consistently beaten by attackers.
Another remarkable result is that Q-learning is
among the best algorithms for the defender agent,
Figure 2: Plot of the running average of the win score over
the previous 500 games for ε-Greedy against Random.
while it is among the worst for the attacker agent. This
is probably the case because the action-chains, or op-
timal policy is less clear for the attacker. Another pos-
sible explanation for the Q-learning attacker under-
performing the Monte Carlo ε-greedy algorithm could
be that Q-learning takes slightly longer to find an op-
timal policy. This also supports the earlier study from
(Szepesv
´
ari, 1997), who found that Q-learning may
suffer from a slow rate of convergence. The last-
mentioned is crucial in an environment with a chang-
ing optimal policy.
A very surprising result is that the Monte Carlo al-
gorithm with Discounted UCB exploration performs
for both agents not better than the same learning al-
gorithm with UCB-1. This seems to contradict with
the argument made in (Garivier and Moulines, 2008),
which states that the Discounted UCB algorithm per-
forms better than UCB-1 in non-stationary environ-
ments like the simulation in this paper.
Adversarial Reinforcement Learning in a Cyber Security Simulation
565

Figure 3: Plot of the running average of the win score over
the previous 500 games for ε-Greedy against ε-Greedy.
5.2 Visual Analysis of Simulations
To get some insight in the adversarial learning effects
during a simulation, plots are made for a simulation
that display the running average of the average win
score over the previous 500 games in the simulation.
These plots can be seen in Figures 2 and 3. Figure 2
shows that the ε-greedy attacker in after only a couple
of hundred games manages to win almost every game
against the random agent, and so it learns very fast
to attack the security flaws in the network. It turns
out that a simulation of any of the learning attackers
against a defender with random action selection re-
sults in a similar plot as in Figure 2.
Figure 3 shows the behavior of the agents when
both learn using ε-greedy. The win rate shows a lot
of fluctuations, which means the agents try to opti-
mize their behavior by adapting to each other, and
overall the attacker optimizes slightly better than the
defender, resulting in an average win rate of around
-0.15. This adversarial learning behavior creates a
non-stationary environment in which the agents are
not able to maintain a good win score over a large
amount of games.
6 CONCLUSION
In this paper we described a cyber security simulation
with two learning agents playing against each other
on a cyber network. The simulation is modelled as a
Markov game with incomplete information in which
the attacker tries to hack the network and the de-
fender tries to protect it and stop the attacker. Monte
Carlo learning with several exploration strategies (ε-
greedy, Softmax, UCB-1 and Discounted UCB) and
Q-learning for the attacker and two additional neu-
ral networks using stochastic gradient descent back-
propagation for the defender (one linear network and
one with a hidden layer) are evaluated. Both agents
needed to use the algorithms to learn a strategy to win
as many games as possible, and due to the compe-
tition the environment became highly non-stationary.
The results showed that the neural networks were not
able to handle with this vey well, but the Monte Carlo
and Q-learning algorithms were able to adapt to the
changes in behavior of the opponent. For the de-
fender, Monte Carlo with Softmax exploration per-
formed best, while the same holds for learning effec-
tive attacking strategies.
REFERENCES
Auer, P., Cesa-Bianchi, N., and Fischer, P. (2002). Finite-
time analysis of the multiarmed bandit problem. Ma-
chine Learning, 47:235–256.
Chung, K., Kamhoua, C., Kwiat, K., Kalbarczyk, Z., and
Iyer, K. (2016). Game theory with learning for cyber
security monitoring. IEEE HASE, pages 1–8.
Garivier, A. and Moulines, E. (2008). On upper-confidence
bound policies for non-stationary bandit problems.
ALT.
Lin, L.-J. (1993). Reinforcement Learning for Robots Us-
ing Neural Networks. PhD thesis, Carnegie Mellon
University.
Littman, M. L. (1994). Markov games as a framework for
multi-agent reinforcement learning. In ICML, pages
157–163.
Neumann, J. V. and Morgenstern, O. (2007). Theory of
games and economic behavior. Princeton University
Press.
Sharma, A., Kalbarczyk, Z., Barlow, J., and Iyer, R. (2011).
Analysis of security data from a large computing or-
ganization. In 2011 IEEE/IFIP DSN, pages 506–517.
Sutton, R. S. and Barto, A. G. (1998). Reinforcement Learn-
ing: An Introduction. The MIT press, Cambridge MA.
Szepesv
´
ari, C. (1997). The asymptotic convergence-rate of
q-learning. In NIPS, pages 1064–1070.
Tambe, M. (2011). Security and Game Theory: Algorithms,
Deployed Systems, Lessons Learned. Cambridge Uni-
versity Press, New York, NY, USA, 1st edition.
Uther, W. and Veloso, M. (2003). Adversarial reinforce-
ment learning. Technical Report CMU-CS-03-107.
Wang, Y., Li, T., and Lin, C. (2013). Backward q-learning:
The combination of sarsa algorithm and q-learning.
Eng. Appl. of AI, 26:2184–2193.
Watkins, C. and Dayan, P. (1992). Q-learning. Machine
Learning, 8:279–292.
Wiering, M. and van Otterlo, M. (2012). Reinforcement
Learning: State of the Art. Springer Verlag.
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
566
