An Evolutionary Traveling Salesman Approach for Multi-Robot Task

Allocation

Muhammad Usman Arif and Sajjad Haider

Faculty of Computer Science, Institute of Business Administration, Karachi, Pakistan

Keywords: Multi-Robot Task Allocation, Evolutionary Algorithms, Robot Operating System, Multi-Agent Systems.

Abstract: Multi-Robot Task Allocation (MRTA) addresses the problems related to an efficient job assignment in a

team of robots. This paper expresses MRTA as a generalization of the Multiple Traveling Salesman

Problem (MTSP) and utilizes evolutionary algorithms (EA) for optimal task assignment. The MTSP version

of the problem is also solved using combinatorial optimization techniques and results are compared to

demonstrate that EA can be effectively used for providing solutions to such problems.

1 INTRODUCTION

Efficient planning is one of the major skills required

to accomplish a complex task by a team of agents,

be it humans or robots. Multi-Robot Task Allocation

(MRTA) deals with the problem of determining the

optimal assignment of a group of tasks to a team of

robots for efficient completion of the jobs at hand. A

group of robots cleaning up an office block, a team

of surveillance bots providing security to a facility,

or a team of firefighting robots unit covering a

disaster situation in a forest fire are all examples of

multi-robot tasks. To make this cooperation of

agents efficient, a plan needs to be formulated on

how a team of robots should approach a set of tasks

for optimum results.

The first and the most fundamental question that

needs to be asked in this case is “which agent

performs what task?” To answer this, an

optimization strategy needs to be executed. The

strategy must keep all the spatial, temporal, and

physical constraints of the team in check and

provide a plan that optimizes the whole operation.

Gerkey and Matarić (2004) proposed a 3 axis

taxonomy for MRTA. Gerkey (2003) proved that

MRTA in its simplest form is a typical

Combinatorial Optimization problem that is of NP-

Hard nature. This implies that for larger problems,

only approximate solutions are possible which

brings heuristic-based optimization schemes into the

picture. This research aims to use Evolutionary

Algorithms (EA) for this purpose. It is worth

mentioning that compared to mathematical modeling

methods, the evolutionary computing paradigm has

proved to be more flexible in real-life dynamic

environments. Especially, since at times, it is

difficult to formulate every real-life scenario

mathematically. Even if it is done, any change in the

environment may make the whole mathematical

model infeasible. The experiments for the EA are

performed on a Robot Operating System (ROS)

(Quigley et al., 2009) based setup, using Gazebo

(Koenig and Howard, 2004) as a simulator. The

selection of ROS for implementation makes the

experiments as close to the real robots as possible. In

addition, the whole setup can be implemented on a

team of real robots with only minor changes.

The results obtained from the optimization are

validated against a mathematical formulation of the

same problem using Multi-Traveling Salesman

Problem (MTSP) approach. The MTSP is modelled

in AMPL (Fourer et al., 1987) and is solved using

CPLEX (“IBM CPLEX CP Optimizer,” n.d.) Solver.

The CPLEX is commercially provided by IBM and

solves linear programming problems using the

simplex technique through primal or dual variants.

Due to computing constraints in AMPL’s student

version, the CPLEX solver provided by the NEOS

server (Gropp and Moré, 1997) was used. NEOS

server hosts a number of free solvers online for

numerical optimization purpose.

The rest of the paper is organized as follows.

Section 2 provides a brief literature review along

with an overview of the key concepts used in this

work. Section 3 provides the details of the

Arif M. and Haider S.

An Evolutionary Traveling Salesman Approach for Multi-Robot Task Allocation.

DOI: 10.5220/0006197305670574

In Proceedings of the 9th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2017), pages 567-574

ISBN: 978-989-758-220-2

567

experimental setup. Section 4 analyses the results

obtained. Finally, Section 5 discusses the findings of

the research and provides future research directions.

2 LITERATURE REVIEW

2.1 Overview of MRTA

MRTA is the study of efficient task allocation for

multi-robot teams. It was classified by Gerkey and

Matarić (2004) on a three axis taxonomy. The

taxonomy differentiates among (a) Type of Robot:

Single Task Robot (ST) and Multiple Task Robots

(MT) (b) Task type: Single Robot Tasks (SR) and

Multiple Robot Tasks (MR) and (c) Arrival Time of

the task: Instantaneous Arrival (IA) and Time

Extended (TE). According to this taxonomy, the

most basic and the most researched distribution is

the Single Task - Single Robot - Instantaneous

Arrival (ST-SR-IA).

In an organizational paradigm, MRTA

techniques could be distributed into two types,

namely, centralized and distributed. Centralized

techniques comprise of a central planning unit which

has the knowledge of the whole environment.

Information about the number of jobs at hand,

positions of every robot, the current task list of every

robot, etc. are available to the central unit. Global

communication is needed for sharing all the

information with the central station. The centralized

techniques have the advantage of providing the

optimal solution all the time. Such systems are

widely used for MRTA (Al-Yafi et al., 2009).

Centralized systems, however, suffer in robustness

and overhead of communication. Distributed

techniques, on the other hand, have no centralized

agent, and the authority of task allocation is

dispersed amongst the agents. Depending upon the

technique used, robots in a distributed system might

act completely independent or occasionally share

some information with other robots for plan

optimization. Distributed planning might not provide

with the optimal solution, but do not need global

communication, and have a high degree of

robustness and scalability (Parker, 1998). All the

MRTA techniques present in the literature can be

distributed into the following four major approaches

which are briefly discussed in the sequel:

(a) Behaviour Based

(b) Market Based

(d) Evolutionary Algorithm Based

2.1.1 Behaviour based Approaches

These are distributed solution approaches which

incorporate some form of mathematical or heuristic

based action selection mechanism in the robot.

Based on a reluctance or willingness like feature, the

mechanism decides if the robot should consider a

particular job or not. ALLIANCE (Parker, 1998),

and BLE (Werger and Matarić, 2000) are good

examples of these schemes. Behavior-based

techniques enjoy the basic advantages of distributed

systems and require no communication at all. Since

the plans executed by robots are local in nature and

lack any interaction at the global level, these

techniques at times fail to provide the best solutions

and usually come up with approximate solutions.

2.1.2 Market-based Approaches

The market-based approach is another distributed

approach which works on an auction-based

mechanism. Usually, a bid is requested from all the

interested robots to attempt an available task. The

bid majorly corresponds to the cost (in terms of the

required resources) the robot expects to incur while

attempting the task. When all the bids have been

received, the task is assigned to the best bidder. It

must be stated that comparative studies (Badreldin et

al., 2013) have found auction based schemes to

struggle in performance when compared with other

approaches. Hybrid schemes have also been

explored that work in combination with techniques

such as reinforcement learning (Kose et al., 2004)

and combinatorial optimization (Hunsberger and

Grosz, 2000) for improved results.

2.1.3 Combinatorial Optimization based

Approaches

Gerkey and Matarić (2003) showed that ST-SR type

MRTA problems are instances of Optimal

Assignment Problem (OAP) (Gale, 1960). This is

the only distribution of the MRTA taxonomy that is

polynomially solvable; all the remaining problems

are NP-hard. Despite the fact that exact solutions of

the ST-SR distribution exist and can be achieved in

finite time, suboptimal techniques have been

proposed in the literature mainly because the

expansibility and efficiency of combinatorial

optimization based approaches are weak. The two

popular techniques that have been used in this case

of MRTA are linear programming (Atay and

Bayazit, 2006) and Optimal Auction Algorithms

(Berhault et al., 2003).

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

568

2.1.4 Evolutionary Algorithm based

Approaches

Evolutionary algorithms are population-based

optimization schemes, inspired by Darwin’s theory

of evolution, that comprise of a population of

solutions optimized using evolutionary operators

such as selection, reproduction, mutation, and

recombination.

The algorithm starts with a population of

randomly initiated solutions. It aims to improve

solution quality over a period of several generations.

A balance is kept in every generation between

exploring and exploiting the solution space through

the crossover and mutation operators. Evolutionary

techniques are quite famous and successful in

solving problems such as MRTA. For example,

(Shea et al., 2003) uses a genetic algorithm to

provide a solution for multiple target tracking by a

group of robots. (Jones et al., 2011) also used a

genetic algorithm for a time extended task

assignment in a disaster situation. This paper uses

EA based optimization for multi-robot task

assignment. There are three major components of an

EA which need to be taken care of while designing

an effective optimization scheme. These three

components are explained below:

Chromosome Encoding

MTSPs are usually encoded for EA using 3 basic

formats: single chromosome technique, two

chromosome technique, and two part chromosome

technique. All three representation are shown in

Figure 1.

Having n jobs at hand to be attempted by m

robots, the single chromosome representation

represents the complete solution using a single

chromosome which is n + m -1 in length. Figure 1a

provides a possible representation of single

chromosome scheme. The solution comprises of m

sub-tours, one for each robot, each of which is

identified by a marker (negative numbers in this

case). All the sub-tours combined should be a

permutation of n jobs. Jobs are visited by the robots

in the order by which they appear in the

chromosome. The second encoding scheme

(Figure 1b) uses two chromosomes of length n to

represent a single solution. The first chromosome

represents a permutation of jobs to be attempted

whereas the second chromosome gives information

regarding the robot attempting a particular job from

chromosome 1. The index of a job represents the

order in which it will be attempted by the robot

responsible for it.

Carter and Ragsdale (2006) highlight the lacking

of these two schemes and propose the two-part

chromosome representation (Figure 1c). The two-

part chromosome has one portion having a

permutation of the jobs to be attempted, and the

other portion representing the number of jobs

assigned to each robot from the first portion. The

chromosome length is n + m, n for the first portion

and m for the second. This representation needs no

markers for isolating the two portions, as it could be

done on the basis of length. This paper uses the two

part chromosome representation for the ST-SR-IA

type of MRTA problem.

Figure 1: Chromosome Representation for MRTA.

Evolutionary Operators

A balanced exploration and exploitation of the

solution space ensure good results in EA. Crossover

and mutation have to be smartly designed and

customized according to the problem, for them to be

effective. (Carter, 2003; Yuan et al., 2013) highlight

the limitations of conventional crossover operators

when applied to the two-part chromosome

representation. Carter (2003) emphasizes the

importance of further exploration whereas (Yuan et

al., 2013) presents a new crossover operator called

the Two-part crossover (TCX), used with mutation,

to achieve better results. TCX shows better results

when compared with conventional crossover

schemes (Yuan et al., 2013). This paper uses the

TCX operator for an effective explorative crossover.

Fitness Function

Fitness function guides the search direction of EA as

it aims to obtain a good solution. The fitness

function judges the effectiveness of the proposed

solution. It helps the EA not only differentiate

between good and bad solutions but also helps in

moving from one generation to another. The

crossover, mutation, and selection operators of an

EA all depend on the fitness function, either directly

or indirectly.

An Evolutionary Traveling Salesman Approach for Multi-Robot Task Allocation

569

3 PROBLEM FORMULATION

It is generally suggested that problem formulation

plays a vital role towards getting desirable results

from an EA. This paper takes advantage of the

similarities the ST-SR-IA problem distribution has

with MTSP by formulating it as a generalization of

MTSP. This section explains the structure of the

representation used for solving the MRTA.

Figure 2: Two-part Chromosome Crossover (TCX).

3.1 Multiple Traveling Salesman

Problem

MTSP is an extension of the famous traveling

salesman problem (TSP). With n cities to be visited,

the MTSP seeks m tours, one for each salesman (n >

m) traveling to each city only once. Even the simple

TSP falls under the NP-complete (Junjie and

Dingwei, 2006) class of problems. Although exact

solution approaches for MTSP exist, but due to its

NP-hard nature, the combinatorial complexity

increases for large sized problems. Heuristic based

methods are a popular choice in such cases.

Amongst heuristic based methods, EA is successful

and widely used. Due to its structure, MTSP could

be generalized to solve a number of similar

problems. Problems such as vehicle routing problem

(Park, 2001) and job scheduling (Carter and

Ragsdale, 2002) provide promising results when

modeled as MTSP. This research uses MTSP for

formulating the structural representation of MRTA

to be optimized by EA. The MTSP based

representation is also later used for validating the

EA results by solving the MTSP through

combinatorial optimization based technique.

3.2 Evolutionary Algorithm

As already discussed in Section 2, chromosome

encoding, evolutionary operators, and fitness

function are the three most important factors of an

EA for achieving effective results.

The two-part chromosome technique is used in

this paper for solving the ST-SR-IA type MRTA

problem. The first part represents a permutation of

all the jobs, while the second part represents the set

of jobs to be executed by each robot. The position of

the job in the permutation represents the order in

which they are to be executed. Figure 1c represents a

solution where the first robot attempts 5 jobs in the

order 1-9-12-3-4, the second robot has 4 jobs to do

in the order 7-8-5-11, and the third robot will

perform 3 jobs in the order 2-6-10.

As already discussed in Section 2, the TCX

(Yuan et al., 2013) shows better results when

compared with conventional crossover scheme for a

two-part chromosome representation. The working

of the TCX is illustrated in Figure 2. TCX is a 5 step

operation that takes 2 parents and produces 2

offspring. The figure represents chromosomes for a

12 task problem with 3 robots.

Mutation is as important as crossover in an EA

because it keeps genetic diversity in the population

alive. The algorithm uses inverse mutation for this

purpose. Inverse mutation picks a sub-tour randomly

from the first portion of the two-part chromosome

and inverts it. No mutation is applied to the second

portion of the chromosome.

The fitness function is concerned with the total

distance the team has to cover in order to complete

all the tasks. Since we are concerned with reducing

the team's efforts to accomplish all the tasks at hand,

this becomes a minimization problem. Hence, the

fitness function comprises of a simple sum of

Euclidean distance calculation for each robot. In

other words, for every robot, the sub-tours presented

by the chromosome are worked through once and

the total distance traveled by all the robots combined

acts as the fitness function.

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

570

4 EXPERIMENTAL

EVALUATION

4.1 Simulation

The experiments were performed on a powerful

open-source simulator, Gazebo, which provides an

accurate simulation environment for population of

robots with a robust physics engine. A team

comprising of three Turtlebots (Garage, 2011) was

used for these experiments. Turtlebot is a low-cost

open-source robot, comprising of (a) depth camera

that allows the robot to see in 3D (b) a mobile base

which has bumper sensors and (c) two differential

drive motors which help the robot move. During the

experiments, each Turtlebot was initiated as an

individual ROS node having its independent

navigation using the depth camera. The navigation

not only planned the robot’s path for stationary goals

but also kept the dynamic obstacles (other robots) in

consideration.

The simulation was carried out on a preloaded

map of 7 x 7 meters. The locations of the jobs were

provided at the start of the algorithm as the paper

only focuses on Instantaneous Arrival (IA) type of

problem. For simplicity, the robot had to just visit

the job location in order to get it counted as

complete. Only one robot had to visit a job location

as the jobs are SR (Single robot) in nature. Random

job locations were generated for this purpose. Any

solution which was unable to complete even a single

job from the job set was considered invalid and was

removed from the population.

4.2 EA Implementation

The TCX operator with a conventional mutation

operator for exploration and exploitation was used.

To further improve the exploration and exploitation

components and to prevent the algorithm from

getting stuck at local minima, an Artificial Immune

System (AIS) (Hunt and Cooke, 1996) type

approach was used in the algorithm. In the (µ + λ)

generational scheme, 30% randomly generated

solutions were inducted in every generation. Figure

3 gives an overview of the scheme.

Figure 3: Overview of the working model.

4.3 Validation

For validation purposes, the job distribution and the

map information was passed to a linear optimization

program written in AMPL for the optimization of

the MTSP based representation of free AMPL the

ST-SR-IA. Due to computing constraints in the

version, the code was run on NEOS online server

using the CPLEX solver. Distance matrix

comprising of distance values from one job to

another was generated using ROS and Gazebo. This

step was repeated for different jobs. The distance

matrices were fed into the CPLEX algorithm for tour

optimization. Figure 4 shows a distance matrix for a

10 job problem. The tours generated through

CPLEX and their lengths were used for validation

purpose. Next, the EA was initiated with a random

initial population. A fix population size of 300

individuals was kept for all the job distributions,

with a crossover probability of 0.4 and a mutation

probability of 0.6.

The EA was terminated whenever the fitness of

our best solution reached in the proximity of 1% of

our exact solution obtained through CPLEX. The

generations taken to reach the solution were also

recorded. It is worth mentioning that EA was able to

match the best solution for all the job distributions

on which it was tested. Table 1 gives the accuracy

comparison of CPLEX and EA and the generations

taken by the EA to achieve the exact solution.

The relation between accuracy of the EA and

generations needed was also plotted. Figure 5

provides this graph for a cluster of 30 job problems.

The average generation values for the graph were

computed by generating random job distributions

multiple times and running the EA over them. As it

can be seen, the better quality we seek the more

An Evolutionary Traveling Salesman Approach for Multi-Robot Task Allocation

571

generations would be needed, and it is exponential in

nature.

A surface plot representing the changes in fitness

value with any changes in the job distribution of the

robots is shown in Figure 6. This provides a deep

insight into the properties of the fitness curve. The

figure shows the surface plot for the 30 job problem.

from the first portion of the chromosome constant

and just altering the number of jobs to be executed

by each robot (that is the second portion of the

chromosome). For easier visual understanding, the

surface plot in Figure 6 represents the inverse of

fitness values. A constant value is assigned to the

combinations that are not possible, that is, for a 30

job problem, this included combinations that have a

sum greater than 30.

As can be seen from the surface plot, there is a

very obvious ridge along the diagonal, indicating not

much difference in fitness values for minor changes

in robots job distribution (keeping the job

permutation in the first part of the chromosome

constant). In addition, there is a very sharp valley

just before the ridge of optimum values indicating

the tricky nature of the fitness function. This sharp

valley just before the maximization ridge explains

the need for AIS like optimization strategy as it

provides a certain portion of randomly generated

solutions in every generation; making the EA fall

out of any local optima when stuck. The

combination of this ridge and valley also explains

why mutation during the EA was not performed in

the second half of the chromosome, as keeping the

job permutation constant and making minor

adjustments to the job distributions of the robot

would either have made minimal changes to the

fitness value (ridge) or had substantially increased

the fitness value (valley). Figure 7 provides the Best

so Far (BSF) and Average so Far (ASF) curves of

EA for different job distributions. The figure

represents a scenario having 30 jobs which are to be

distributed among 3 robots by the EA. The algorithm

takes around 500 generations with a population size

of 300 individuals to reach within 1% of the exact

solution provided by the combinatorial optimization

technique. The gap between ASF and BSF is due to

the 30% random individuals injected every

generation for better diversity.

Table 1: Fitness comparison of CPLEX with EA.

Figure 4: Distance matrix for 10 jobs.

Figure 5: Average number of generations taken by EA

with respect to accuracy.

Figure 6: Surface Plot for 30 Job Optimum Solution.

500

1000

1500

25%

20%

15%

10%

Average#ofGenerations

Takenfor30JobMRTA

Average#of

Generations

Takenfor30

JobMRTA

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

572

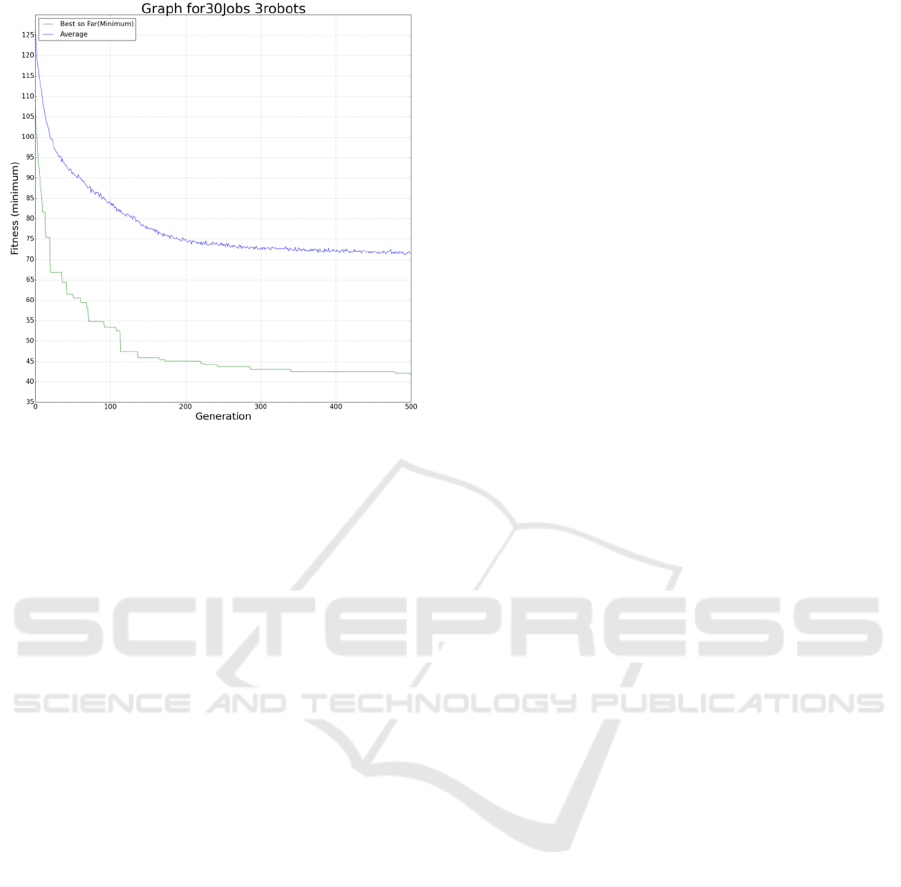
Figure 7: BSF and ASF Curves for a 30 Jobs 3 Robot ST-

SR-IA problem.

5 CONCLUSION AND FUTURE

WORK

The paper used MTSP based chromosome

representation to solve MRTA using EA. The results

were compared with exact mathematical solutions

obtained through CPLEX. EA provided an optimal

solution in each and every case and did it in an

acceptable number of generations. However, the

advantage EA has over combinatorial optimization

based techniques is that for dynamic environments,

such as a robot team executing tasks in real life

scenarios, the problem will not need remodeling if

minor changes occur in the structure of the problem.

Moreover, EA provide the flexibility of restarting

the optimization from the last solution in case the

last solution becomes invalid due to some structural

changes in the problem.

The future work will focus on using this same

MTSP representation for solving more complex

MRTA distributions. This will allow taking

advantage of EA for adjusting to changes made in

problem representation more flexibly as compared to

exact mathematical solutions.

REFERENCES

Al-Yafi, K., Lee, H., Mansouri, A., 2009. Mtap-masim: a

multi-agent simulator for the mobile task allocation

problem, in: Enabling Technologies: Infrastructures

for Collaborative Enterprises, 2009. WETICE’09. 18th

IEEE International Workshops on. IEEE, pp. 25–27.

Atay, N., Bayazit, B., 2006. Mixed-integer linear

programming solution to multi-robot task allocation

problem.

Badreldin, M., Hussein, A., Khamis, A., Badreldin, M.,

Hussein, A., Khamis, A., 2013. A Comparative Study

between Optimization and Market-Based Approaches

to Multi-Robot Task Allocation, A Comparative Study

between Optimization and Market-Based Approaches

to Multi-Robot Task Allocation. Adv. Artif. Intell.

Adv. Artif. Intell. 2013, 2013, e256524.

doi:10.1155/2013/256524, 10.1155/2013/256524

Berhault, M., Huang, H., Keskinocak, P., Koenig, S.,

Elmaghraby, W., Griffin, P., Kleywegt, A., 2003.

Robot exploration with combinatorial auctions, in:

Intelligent Robots and Systems, 2003.(IROS 2003).

Proceedings. 2003 IEEE/RSJ International Conference

on. IEEE, pp. 1957–1962.

Carter, A.E., 2003. Design and application of genetic

algorithms for the multiple traveling salesperson

assignment problem. Virginia Polytechnic Institute

and State University.

Carter, A.E., Ragsdale, C.T., 2006. A new approach to

solving the multiple traveling salesperson problem

using genetic algorithms. Eur. J. Oper. Res. 175, 246–

257.

Carter, A.E., Ragsdale, C.T., 2002. Scheduling pre-printed

newspaper advertising inserts using genetic

algorithms. Omega 30, 415–421.

Coltin, B., Veloso, M., 2010. Mobile robot task allocation

in hybrid wireless sensor networks, in: Intelligent

Robots and Systems (IROS), 2010 IEEE/RSJ

International Conference on. IEEE, pp. 2932–2937.

Czyzyk, J., Mesnier, M.P., Moré, J.J., 1998. The NEOS

server. IEEE Comput. Sci. Eng. 5, 68–75.

Dolan, E.D., 2001. NEOS Server 4.0 administrative guide.

ArXiv Prepr. Cs0107034.

Fourer, R., Gay, D.M., Kernighan, B.W., 1987. AMPL: A

mathematical programming language. Citeseer.

Gale, D., 1960. The theory of linear economic models.

University of Chicago press.

Garage, W., 2011. Turtlebot. Website Httpturtlebot

Comlast Visit. 11–25.

Gerkey, B.P., 2003. On multi-robot task allocation.

University of Southern California.

Gerkey, B.P., Matarić, M.J., 2004. A Formal Analysis and

Taxonomy of Task Allocation in Multi-Robot

Systems. Int. J. Robot. Res. 23, 939–954.

doi:10.1177/0278364904045564

Gerkey, B.P., Matarić, M.J., 2003. On role allocation in

RoboCup, in: Robot Soccer World Cup. Springer, pp.

43–53.

Gropp, W., Moré, J., 1997. Optimization environments

and the NEOS server. Approx. Theory Optim. 167–

182.

Hunsberger, L., Grosz, B.J., 2000. A combinatorial

auction for collaborative planning, in: MultiAgent

An Evolutionary Traveling Salesman Approach for Multi-Robot Task Allocation

573

Systems, 2000. Proceedings. Fourth International

Conference on. IEEE, pp. 151–158.

Hunt, J.E., Cooke, D.E., 1996. Learning using an artificial

immune system. J. Netw. Comput. Appl. 19, 189–212.

IBM CPLEX CP Optimizer [WWW Document], n.d. URL

https://www-

01.ibm.com/software/commerce/optimization/cplex-

cp-optimizer/ (accessed 10.23.16).

Jones, E.G., Dias, M.B., Stentz, A., 2011. Time-extended

multi-robot coordination for domains with intra-path

constraints. Auton. Robots 30, 41–56.

Junjie, P., Dingwei, W., 2006. An ant colony optimization

algorithm for multiple travelling salesman problem, in:

First International Conference on Innovative

Computing, Information and Control-Volume I

(ICICIC’06). IEEE, pp. 210–213.

Koenig, N., Howard, A., 2004. Design and Use Paradigms

for Gazebo, An Open-Source Multi-Robot Simulator,

in: In IEEE/RSJ International Conference on

Intelligent Robots and Systems. pp. 2149–2154.

Kose, H., Tatlidede, U., Meriçli, C., Kaplan, K., Akin,

H.L., 2004. Q-learning based market-driven multi-

agent collaboration in robot soccer, in: Proceedings of

the Turkish Symposium on Artificial Intelligence and

Neural Networks. pp. 219–228.

Martinson, E., Arkin, R.C., 2003. Learning to role-switch

in multi-robot systems, in: Robotics and Automation,

2003. Proceedings. ICRA’03. IEEE International

Conference on. IEEE, pp. 2727–2734.

Park, Y.-B., 2001. A hybrid genetic algorithm for the

vehicle scheduling problem with due times and time

deadlines. Int. J. Prod. Econ. 73, 175–188.

Parker, L.E., 1998. ALLIANCE: An architecture for fault

tolerant multirobot cooperation. IEEE Trans. Robot.

Autom. 14, 220–240.

Quigley, M., Conley, K., Gerkey, B., Faust, J., Foote, T.,

Leibs, J., Wheeler, R., Ng, A.Y., 2009. ROS: an open-

source Robot Operating System, in: ICRA Workshop

on Open Source Software. Kobe, Japan, p. 5.

Shea, P.J., Alexander, K., Peterson, J., 2003. Group

tracking using genetic algorithms. Proc Int. Soc. Inf.

Fusion.

Tang, F., Parker, L.E., 2005. Asymtre: Automated

synthesis of multi-robot task solutions through

software reconfiguration, in: Proceedings of the 2005

IEEE International Conference on Robotics and

Automation. IEEE, pp. 1501–1508.

Werger, B.B., Matarić, M.J., 2000. Broadcast of local

eligibility for multi-target observation, in: Distributed

Autonomous Robotic Systems 4. Springer, pp. 347–

356.

Yuan, S., Skinner, B., Huang, S., Liu, D., 2013. A new

crossover approach for solving the multiple travelling

salesmen problem using genetic algorithms. Eur. J.

Oper. Res. 228, 72–82.

Zlot, R., Stentz, A., 2006. Market-based multirobot

coordination for complex tasks. Int. J. Robot. Res. 25,

73–101.

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

574