
Probabilistic Multi-Agent Plan Recognition
as Planning (P-Maprap): Recognizing Teams, Goals, and Plans from
Action Sequences
Chris Argenta and Jon Doyle
North Carolina State University, Raliegh NC, U.S.A.
Keywords: Multi-Agent Systems, Plan Recognition.
Abstract: We extend Multi-agent Plan Recognition as Planning (MAPRAP) to Probabilistic MAPRAP (P-MAPRAP),
which probabilistically identifies teams and their goals from limited observations of on-going individual
agent actions and a description of actions and their effects. These methods do not rely on plan libraries, as
such are infeasibly large and complex in multi-agent domains. Both MAPRAP and P-MAPRAP synthesize
plans tailored to hypothesized team compositions and previous observations. Where MAPRAP prunes team-
goal interpretations on optimality grounds, P-MAPRAP directs its search base on a likelihood ranking of
interpretations, thus effectively reducing the synthesis effort needed without compromising recognition. We
evaluate performance in scenarios that vary the number of teams, agent counts, initial states, goals, and
observation errors, assuming equal base-rates. We measure accuracy, precision, and recall online to evaluate
early stage recognition. Our results suggest that compared to MAPRAP, P-MAPRAP exhibits improved
speed and recognition accuracy.
1 INTRODUCTION
The focus of Multi-Agent Plan Recognition (MAPR)
research is to observe the actions of individual
agents and from those actions infer which agents are
working together as teams and what these teams are
attempting to accomplish. MAPR is a subset of the
Plan, Activity, and Intent Recognition (PAIR)
research topic (Sukthankar et. at., 2014). Most
current MAPR solutions target recognizing activities
in specific domains, rely on matching observations
to human generated libraries, and/or forensically
analyzing the structures of complete synchronized
traces. Our contributions avoid these simplifications
of the MAPR challenge while focusing on persistent
teams and goal-oriented plans.
In this paper, we describe Probabilistic Multi-
agent Plan Recognition as Planning (P-MAPRAP),
an online recognizer that probabilistically ranks
interpretations of team compositions and goals based
on observed actions. We compare P-MAPRAP with
previous results of discrete versions of MAPRAP by
Argenta and Doyle (2015). Both discreet and
probabilistic implementations extend Ramirez and
Geffner’s (2009, 2010 respectively) Plan
Recognition as Planning (PRAP) approaches into
multi-agent domains by developing methods that
dynamically reduce the exponential search space
that results from all potential partitionings of agents
into teams. We evaluate performance on the well-
established Blocks World domain (e.g., Ramiaz and
Geffner, 2009; Zhou et al., 2012; Banerjee et al.,
2010).
P-MAPRAP is a general plan recognition
technique that does not depend on prior domain
knowledge in the same manner that the General
Game Playing (GPP) community (Genersereth and
Love, 2005) and International Planning Competition
(IPC) provide problem specifications at the time of
testing. The planning domain used by P-MAPRAP
to specify problems is the Plan Domain Description
Language (PDDL) (McDermott et al., 1998)
annotated for multiple agents. This specification is
similar to MA-PDDL (Kovacs, 2012) converted via
(Muise et al., 2014) to support classical planners.
This domain includes a complete initial state, list of
agents, list of potential goals, and action model.
In contrast, most plan recognition techniques
match observables to patterns within a plan library
(often human generated). P-MAPRAP does not
Argenta C. and Doyle J.
Probabilistic Multi-Agent Plan Recognition as Planning (P-Maprap): Recognizing Teams, Goals, and Plans from Action Sequences.
DOI: 10.5220/0006197505750582
In Proceedings of the 9th International Conference on Agents and Artificial Intelligence (ICAART 2017), pages 575-582
ISBN: 978-989-758-220-2
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
575
depend on human expertise to create a plan library
or rely on domain-specific recognition strategies.
Likewise, this approach does not require a training
set of labeled traces or a priori base rates. Instead we
are provided a list of possible goals to recognize.
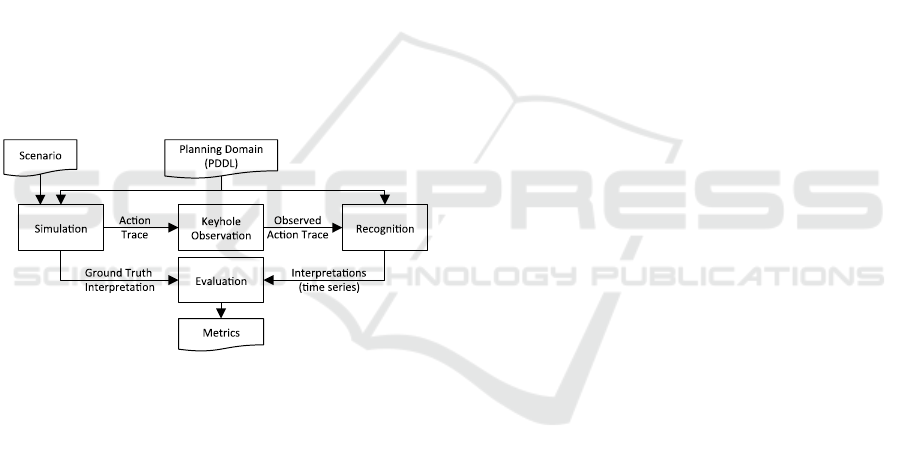
Figure 1 shows our high level architecture for
staging and evaluating recognition problems. We
first simulate a given scenario to produce a full
action trace and ground truth interpretation of goals
and team composition. Under the keyhole observer
model (Cohen, Perrault, and Allen, 1981) used here,
the recognizer has no interaction with the observed
agents, and any observations can be randomly
dropped to simulate errors and hidden actions. P-
MAPRAP is an online recognizer that infers the
team’s agents are affiliated with and that team’s goal
(with a corresponding total-ordered plan). Finally,
we evaluate the performance of recognition using
precision, recall, and accuracy by comparing the
recognizer’s interpretation with the simulator’s
ground truth interpretation. We compare P-
MAPRAP’s results to those of discrete MAPRAP,
and parametrically vary the observation error to
determine sensitivity.
Figure 1: Our evaluation framework allows us to generate
and evaluate many cases, varying key parameters to
achieve reliable evaluation.
In Section 2, we place this work in the context of
related research in plan recognition. We describe our
recognizer in Section 3, and evaluation in Section 4.
Section 5 compares P-MAPRAP results with those
of MAPRAP for efficiency and recognition
performance. This is followed by future work and
conclusions.
2 RELATED RESEARCH
Multi-agent Plan Recognition (MAPR) solutions
attempt to make sense of a temporal stream of
observables generated by a set of agents. The
recognizer’s goal is to infer both the organization of
agents that are collaborating on a plan, and the plan
each team is pursuing. (While not addressed here,
some have also included identifying dynamic teams
that change over time (e.g., Banerjee, Kraemer, and
Lyle 2010; Sukthankar and Sycara, 2006, 2013).) To
accomplish this goal, solutions must address two
challenges noted by Intille and Bobick (2001). First,
the combination of agents significantly inflates state
and feature spaces making exhaustive comparisons
infeasible. Second, detecting coordination patterns in
temporal relationships of actions is critical for
complex multi-agent activities.
One approach is to use domain knowledge to
identify activities indicative of team relationships.
For example, Sadilek and Kautz (2010) recognized
tagging events in a capture-the-flag game by
detecting co-location followed by an expected effect
(tagged player must remain stationary until tagged
again). Sukthankar and Sycara (2006) detected
physical formations in a tactical game domain and
inferred cooperation to prune the search space.
While practical and effective for the given domains,
discovering exploitable characteristics has been a
human process and similar patterns may not exist in
other domains.
Generalized MAPR solutions use domain-
independent recognition algorithms along with a
description of the domain. Most commonly, a plan
library is created that provides patterns for which a
recognizer searches. For example, Banerjee,
Kraemer, and Lyle (2010) matched patterns in
synchronized observables, for all combination of
agents, to a flattened plan library. Sukthankar and
Sycara (2008) detected coordinated actions and used
them to prune the multi-agent plan library using a
hash table that mapped key observerable sequences
for distinguishing sub-plans (i.e., last action of
parent and first of sub-plan). However, it may be
difficult to build a full plan library for complex
domains, so others use a planning domain to guide
the recognizer. Zhuo, Yang, and Kambhampati
(2012) used MAX-SAT to solve hard (observed or
causal) and soft (likelihood of various activities)
constraints derived from the domain (action-model).
In an effort to replicate the spirit of general game
playing and IPC planning competitions where the
algorithm is only given a general description of the
problem at run-time, we use no a priori domain-
specific knowledge or manually tuned libraries.
Plan Recognition as planning (PRAP) was
introduced by Ramirez and Geffner in (2009) as a
generative approach to single agent plan recognition
that uses off-the-shelf planners and does not require
a plan library. They convert observations to interim
subgoals that the observed agent has accomplished.
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
576

They synthesize plans for each goal with and
without the observed subgoals, if the costs are equal
then observations could be interpreted as pursuing
that goal. In (Ramirez and Geffner 2010), they
extended PRAP to probabilistic recognition. In the
case of uniform priors, the most likely goals are
those that minimize the cost difference for achieving
the goal with and without explicitly meeting the
observed subgoals. P-MAPRAP extends discrete
MAPRAP (Argenta, Doyle 2015) in a similar way
but for the MAPR problem.
3 PROBABLISTIC MAPRAP
The primary problem addressed by P-MAPRAP is
correctly inferring both the teams of agents that are
working together towards a common goal, and
identify which goal each team is pursuing. A
recognizer makes this inference given information
about the scenario and a sequence of observations.
3.1 Inputs for Recognizer
Domain Description (D) defines all of the possible
actions, their preconditions, and effects on the
current state. We use Plan Domain Description
Language (PDDL) to describe domains.
Scenario Description (P) details the specific
initial state. In Blocks World P includes the list of
blocks and agents in the scene, and the initial state.
This is a PDDL problem file without goals.
Agents are uniquely identifiable actors capable
of performing actions. For each scenario instance we
are given a set of agents, =
{
,
,…,
}
with >0. The list of agents does not change
within a problem instance. All potential actions are
specified in the domain with each action
parameterized by the performing agent (in our case
the first parameter of any action). Agents can be
differentiated in the domain by type or by predicate
in the initial conditions. Agents are presumed to be
members of some team, but no information is given
as input about the team composition.
Team Goals describe the ultimate objective of
the agents on a team. We are given a set of all
possible goals =
,
,…,
. Each team
is assigned a single unknown goal
∈ and ≥
(usually much larger). In this research, each team
has exactly one goal, and we do not consider goals
that change over time. The recognizer must infer the
goal assigned to each team.
Action Sequence Trace defines the observables
that we pass to the recognizer in an online fashion.
Our simulation component produces a trace file,
which consists of time-stamped observations =
{
,…,
} where each observation includes a
grounded action from parameterized by the acting
agent ∈. All traces start at the initial state
(defined in P) and include all actions required for
each team to achieve its goal.
Actions that can take place concurrently (same )
are randomly ordered in the serial trace. The
observer component interleaves the actions of all
agents while maintaining action dependencies within
teams. This is also where we drop observations to
evaluate sensitivity. We do not introduce “noop”
actions when no action is observed and the online
recognizer is unaware of the length of the trace.
3.2 Outputs of Recognizer
Teams are sets of Agents. is partitioned into a set
of teams ={
,
,…,
} such that each
team has at least one agent
|
|
≥1, and each
is
assigned to one and only one team. Teams can be
identified as the composition of agents assigned to it,
e.g.,
=
,
. We do not consider teams that
change over time. The recognizer must infer the
number of teams and assignment of agents to teams.
Partial Interpretations: The recognizer
identifies the agents on a team and the goal being
pursued by the team. For example the partial
interpretation (
,
:
) indicates that agents
and
are teamed and pursuing goal
. For each
partial interpretation, the recognizer can produce a
total ordered plan that accounts for previous
observations, missed observations, and future
actions required to achieve the goal.
Interpretations: An interpretation (or full
interpretation) is set of partial interpretations that
completely and uniquely assign each agent in . For
example, given =
{
,
,
}
and =
{
,
,
,
}
one interpretation is
{(
,
:
)
,(
:
)
}
. For any given scenario there
are many possible interpretations but only a single
correct interpretation An interpretation is feasible at
a particular time if it explains the actions observed
up to that time.
Feasibility of Interpretations: At each time step,
the recognizer determines from all possible
interpretations, which best explain all the
observations up to that point. In Discrete MAPRAP
the recognizer emitted the set of all feasible
interpretations as positive classifications and others
as negative. In P-MAPRAP the recognizer ranks the
Probabilistic Multi-Agent Plan Recognition as Planning (P-Maprap): Recognizing Teams, Goals, and Plans from Action Sequences
577
interpretation by degree of feasibility. The feasibility
of an interpretation is the mean of the feasibilities of
each partial interpretation. Perfect feasibility (1.0) is
achieved when each partial interpretation is
supported by an optimal plan (cost based on action
count) for a given team achieving its goal while
including every action observed up to that point in
time. The less optimal the plan required for a given
team to realize their goal, the lower the feasibility
score. If the observations made achieving a goal
impossible for a team, its feasibility would be 0.0.
3.3 The P-MAPRAP Recognizer
Probabilistic MAPRAP is a redesign of our discrete
MAPRAP Recognizer based on ranking the
complete set of interpretations by their likelihood of
being correct. Unlike discrete MAPRAP where an
interpretation is either feasible (considered) or not
(pruned), our P-MAPRAP uses the difference
between baseline and plans that include the
appropriate observations (to date) as an indicator of
how well the interpretation explains the
observations. So, agents can be acting sub-optimally
without pruning the correct interpretation. Only the
most likely interpretations are considered for re-
computation at any time step, but if, after being
recomputed with the new observations, their
likelihood decreases interpretations that were
previously less likely resurface and are considered.
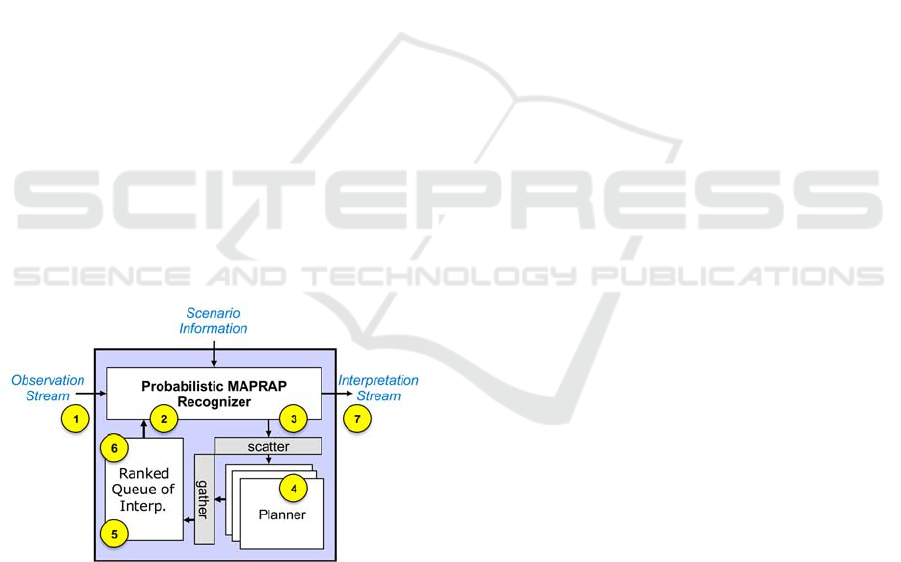
This design is shown in Figure 2.
Figure 2: P-MAPRAP maintains a queue of interpretation
to prioritize testing new observations against the best
explanations first.
The steps of the P-MAPRAP algorithm in
labelled in Figure 2 and described below:
1. Before the first observerable, the baseline plan
cost is established for each interpretation given
no observables (also prunes interpretations that
have impossible combinations of teams/goals).
2. The recognizer checks the top of the priority
queue of interpretations. We decompose the set
of highest likelihood interpretations into a set of
unique partial interpretations.
3. We create new planning instances, to include
hypothesized team/goal, and all observations
that correspond to the team.
4. An off the shelf planner (GraphPlan)
synthesizes plans (potentially in parallel) that
accomplishes the hypothesized goal and
observed actions. We track the plan and cost.
5. The difference between the baseline cost and
the new plan cost (with observations) is used to
calculate a likelihood score. The score doesn’t
change if the observations are consistent with
the baseline plan. If the cost increases, the
likelihood score is reduced.
6. Putting the interpretations back into the priority
queue causes them to be repositioned. If the
new top (most likely) interpretation does not
include the current observations, then we rerun
this process (from step 2) until it is. This allows
interpretations that were previously less likely
to return for consideration once the others have
been deemed less likely than it.
7. The interpretations that have the highest
likelihood are classified as positives and sent for
evaluation. The next observation is read in (go
to step 2) until trace is complete.
3.4 Assumptions and Limitations
Base rates are intentionally not used in our
recognition because low base rate activities are often
the most interesting for our applications. While
using base rates could improve average
performance, it would accomplish this at the cost of
missing unusual activities particularly in early stage
recognition. For applications such as surveillance
and threat detection, low base rate events are
interesting and maintaining high recall is ideal.
Like MAPRAP, P-MAPRAP assumes that team
activities are independent and agents do not interfere
with the execution of plans by other teams. This
assumption is necessary to facilitate synthesizing
plans for hypothesized partial interpretations and
reusing those results in multiple full interpretations.
If the actions of teams were not independent (for
example they were competing for limited resources)
then the cross-team context becomes an important
factor in explaining actions. Eliminating this
assumption would prevent reuse of partial
interpretations, which would increase run time.
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
578

Other PRAP assumptions, such as finite and
enumerable goals, and purposeful actions are also
true of P-MAPRAP.
4 P-MAPRAP EVALUATION
We evaluate P-MAPRAP by comparing it to the
results from discrete MAPRAP (Argenta, Doyle
2015) using same planning domain formulation and
planner. We simulate a set of scenarios to produce
an observation trace consisting of a sequence of
actions, each parameterized with the agent
performing them. Concurrent actions are randomly
ordered (i.e., no turn taking pattern). An observer
model filters observations with a given probability
of dropping each prior to recognition. The
recognizer infers interpretations of the team and
goals while producing a corresponding plan. P-
MAPRAP labels each interpretation with a
likelihood value, and the set of best scoring
interpretations are considered feasible inferences for
evaluation. MAPRAP did not penalize early state
recognition for mis-assigning agents that had not yet
acted to the wrong teams, P-MAPRAP counts all
errors in the interpretation regardless of what has or
has not been observed up to that point.
Blocks World Domain: A multi-agent adaptation
of the Blocks World domain (Team Blocks) is the
most common evaluation domain for MAPR. In this
domain there are a series of lettered blocks randomly
stacked on a table. Each agent operates a robot
gripper that can pick up one block at a time. Teams
are composed of 1 to |A| agents that are planning
together and act collaboratively towards the same
goal. Actions are atomic and include: pickup,
unstack (pickup from atop another block), put down
(on table), stack (put down atop another block); each
action is parameterized by the block(s) acted on and
agent performing the action. The goal of Team
Blocks is for each team to rearrange blocks into a
stack in a specified sequence. Goals are stacks of
random letter sequences of various lengths. Since we
plan teams independently, we partitioned the blocks
and goals to avoid conflicting plans. However, no
information about teams (count or sizes),
partitioning of blocks, or goals assignments are
accessible to the recognizer.
Test Scenarios: We randomly selected 107
different Team Blocks scenarios from (Argenta and
Doyle 2015). These were generated with 1-2 teams
with 1-5 agents. Goals were all permutations of
selected stacking orders of 6-7 blocks (μ=6.5). We
limited the list of possible goals to 20 (the correct
goal for each team plus randomly selected possible
goals) for each scenario. We simulated each scenario
and recorded an action trace. Each trace consists of a
serialized sequence of observerables identifying time
step (1 to t), agent, and action. Traces ranged from 6
to 14 actions (μ=9.6).
5 RESULTS
Efficiency in terms of the number of plans
synthesized drives the run-time performance of
PRAP-based recognition. For comparison of many
examples, we normalized actual counts by number
of goals and time step in the trace to ensure, such
that the worst-case single agent performance would
be 1.0. We previously demonstrated two pruning
approaches for discrete MAPRAP aggressive and
conservative. Aggressive pruning attempted to limit
the interpretations considered by assuming all agents
are on the same team for each goal and removing
members as observations suggested otherwise. This
was very effective (blue in
Figure 3
) but is not
general for all domains. Conservative pruning is
general, but does not scale as well (red in
Figure 3
).
Figure 3: P-MAPRAP (green) effectively prunes the
search space faster than discrete MAPRAP with
conservative pruning (red). Aggressive pruning (blue)
performs better, but has strict domain limitations that P-
MAPRAP does not. The worst-case single agent score is
1.0.
Probabilistic Multi-Agent Plan Recognition as Planning (P-Maprap): Recognizing Teams, Goals, and Plans from Action Sequences
579

P-MAPRAP (green in
Figure 3
) prunes the search
space by prioritizing interpretations and only
pursuing those that are best explaining the
observations at that time step. Similar to MAPRAP
each interpretation further decomposed into the set
of partial interpretations to avoid synthesizing plans
for equivalent hypothesis. As a result of these
enhancements P-MAPRAP performance has a mean
improvement of 25.2% over conservative pruning
(min 19.7% for 1 team / 1 agent and max 30.0% for
2 teams / 5 agents) and while maintaining full
domain generality. Aggressive pruning (which is
valid for the Blocks World domain) still outperforms
P-MAPRAP (mean 48.6%, min 3.9%, max 87.4%).
Recognition: Our evaluation metrics for
recognition are Recall, Precision, and Accuracy
based on the interpretations emitted by the
recognizer for each time step. In P-MAPRAP,
positives classifications are the set of the most
highly ranked interpretations. A True Positive (TP)
is the correct interpretation recognized successfully
(max of 1) and True Negatives (TN) are incorrect
interpretations identified as infeasible/unlikely. In
our formulation, there is only one correct and many
incorrect interpretations. This results in recall values
of either 0 or 1. Our goal is maintain perfect recall
for all time steps, potentially trading precision and
accuracy to accomplish this.
Recall is the ratio of correct interpretations
identified correctly. Recall is used to identify if the
correct interpretation is in the set of interpretations
indicated by the recognizer to be likely or feasible.
High recall is particularly important in online
analysis as it enables us to use early results to limit
the analysis needed for future observations (i.e.,
pruning). Our results for recall were consistently 1,
indicating that the correct answer was always in the
positive set for every timestamp.
Precision is the ratio of true positives to all
positives. Precision indicates how well the analytic
narrows in on the correct interpretation and avoids
giving false positive responses. As indicated under
recall, we would like to use early recognition results
to prune our search space for the future, so a high
number of false positives are expected, particularly
early in the observation trace
As shown in Figure 4, single agent scenarios
again require fewer observations to converge on
interpretations than multi-agent scenarios. Again, we
observed that reduced precision in the multi-agent
cases reflects both fewer observations per individual
agent at any time, and a large number of potential
team compositions. For P-MAPRAP, we have the
ability to provide base rates for both the goals and
teaming arrangements or team counts – however,
since a positive classification is made only for
interpretations with the highest (relative) likelihood,
base rates would also introduce situations where
recall = 0 in early state recognitions because the
scenario did not match the base rates.
We observed that reduced precision in the multi-
agent cases reflects both fewer observations per
individual agent at any time, and a large number of
potential team compositions. In essence, the
explanatory power of each observation is diluted
across the pool of agents. As a result, it takes more
observations to rule out all feasible, but ultimately
incorrect, interpretations. In fact, unlike the single
agent case, most multi-agent traces ended before the
recognizer converged to a single correct
interpretation.
Figure 4: P-MAPRAP (solid lines) shows mixed results
compared to the discrete version (dashed lines). As before,
mean precision shows multi-agent scenarios retain false
positives.
Figure 5: P-MAPRAP (solid lines) improves Accuracy
over discrete version (dashed lines) in all cases except the
single agent scenario. Accuracy shows many true
negatives are eliminated with each observation.
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
580

Accuracy is the ratio of correct classifications to
total classifications. Accuracy is a good measure of
how well we are eliminating (pruning) some of the
many incorrect interpretations. Accuracy is the
metric that is the least impacted by the needle-in-
haystack issues of a single correct interpretation.
This resilience is due to giving credit for identifying
incorrect interpretations.
As shown in Figure 5, the mean accuracy of
MAPRAP trails the single agent per team cases, but
demonstrates correct classifications of potential
interpretations for observerables over time.
5.1 Sensitivity to Missing Observations
Performance of the run time is measured by the
relative quantity of plans synthesized as above.
Dropped observations were modeled as time steps
with no observations (to ensure consistency of
scenarios) so one might expect fewer time plans
synthesized on average. However, some of this
reduction is offset by not reducing the pool of
feasible interpretations. For example, despite 50% of
the time steps not requiring any plan synthesis, the
50% Error cases showed only 21% (2 teams / 5
agents) to 36% (1 team / 1 agent) reduction in plans
synthesized. Overall, the reduced workload from
dropped observations is partially offset by missing
information preventing search space reduction.
Precision measurements were further reduced as
expected due to the reduction in observations. This
essentially reflects more FPs being carried further
into the trace time.
Accuracy measurements clearly capture the
decrease for more dropped observations (Error!
Reference source not found.). Since observation
dropping in random, we ran each scenario four times
for each error level. The results between runs were
not significantly different indicating that recognition
in the Team Blocks domain is not highly sensitive to
detecting specific observations. In part this is
explained by the dependency between the picking up
and putting down actions. It only takes observing
one of these actions to identify the other for the
same block.
6 FUTURE WORK
Space limitations restrict detailing several aspects of
our work in this paper. For example, P-MAPRAP
handles alternative domains and planners, and
suboptimal team activities. These will be addressed
in future papers.
1 Team / 1 Agent
1 Team / 2 Agents
1 Team / 3 Agents
2 Teams / 2 Agents 2 Teams / 3 Agents
2 Teams / 4 Agents 2 Teams / 5 Agents
Figure 6: When some of the actions in the trace are
dropped, recognition must proceed with less information.
This generally results in lower accuracy, but the impact is
less than expected.
We are currently evaluating additional planning
domains for multi-agent plan recognition
benchmarking. For evaluation purposes, these
Probabilistic Multi-Agent Plan Recognition as Planning (P-Maprap): Recognizing Teams, Goals, and Plans from Action Sequences
581

domains must scale from 1 agent on 1 team to
agents on teams with ≤ without artificially
limiting the search space of possible interpretations.
Ramirez and Geffner (2010) also compared that
optimal and satisficing planners, reducing run time
with little cost to PRAP accuracy. We are also
investigating alternative and specialized planners.
Secondly, moving to a probabilistic recognizer
allows for evaluating performance on suboptimal
action traces. While we are primarily interested in
applications that do not use base rates, our
probabilistic approach is very amenable to
introducing base rates, likely improving mean
precision and accuracy provided one is willing to
accept varying recall.
7 CONCLUSIONS
In this paper we introduced P-MAPRAP a
probabilistic version of MAPRAP, our MAPR
system based on an extension to PRAP. This
recognizer uses a multi-agent planning domain vice
a human-generated plan library. Our implementation
enforces generalization and eliminates the
dependency on human expertise in designating what
actions to watch in a domain.
We show that we can recognize team
compositions from an online action sequence,
without domain-specific tricks, and manage the very
large the search space of potential interpretations.
We evaluated the efficiency and performance of P-
MAPRAP a range of Team Blocks scenarios, and
compared these to a previous discrete version given
the same scenarios. Despite tracking all possible
interpretations, we found prioritizing consideration
of interpretations effectively prunes the search space
and this continues to reduce run-time independent of
the planner used. Our results placed P-MAPRAP
We evaluated our recognition performance on a
multi-agent version of the well-known Blocks World
domain. We assessed precision, recall, and accuracy
measures over time and compared those results with
discrete MAPRAP. In both cases we maintained
perfect recall, but observed low precision,
particularly during early stage recognition. Accuracy
was improved over discrete version. This in turn
requires more observations to limit potential
interpretations down to the single correct
interpretation. Our precision and accuracy measures
over time help quantify this difference.
REFERENCES
Argenta C, and Doyle J (2015) “Multi-Agent Plan
Recognition as Planning (MAPRAP),” In Proceedings
of the 8th International Conference on Agents and
Artificial Intelligence (ICAART 2016) - Volume 2,
pages 141-148
Banerjee B, Kraemer L, and Lyle J (2010) “Multi-Agent
Plan Recognition: Formalization and Algorithms,”
AAAI 2010
Banerjee B, Lyle J, and Kraemer L (2011) “New
Algorithms and Hardness Results for Multi-Agent
Plan Recognition,” AAAI 2011
Cohen P R, Perrault C R, and Allen J F (1981) “Beyond
Question Answering,” in Strategies for Natural
Language Processing, NJ: Hillsdale, pp. 245-274.
Genersereth M and Love N (2005) “General Game
Playing: Overview of the AAAI Competition,” AI
Magazine, vol. 26, no. 2
Intille S S and Bobick A F (2001) “Recognizing planned,
multi-person action,” Computer Vision and Image
Understanding, vol. 81, pp. 414-445
Kovacs D (2012) “A Multi-Agent Extension of
PDDL3.1,” WS-IPC 2012:19
McDermott D and AIPS-98 Planning Competition
Committee (1998) “PDDL–the planning domain
definition language”
Muise C, Lipovetzky N, Ramirez M (2014) “MAP-
LAPKT: Omnipotent Multi-Agent Planning via
Compilation to Classical Planning,” Competition of
Distributed and Multi-Agent Planners (CoDMAP-15)
Pellier D (2014) “PDDL4J and GraphPlan open source
implementation,” http://sourceforge.net/projects/pdd4j
Ramirez M and Geffner H, (2009) “Plan recognition as
planning,” in Proceedings of the 21st international
joint conference on Artificial intelligence
Ramirez M and Geffner H (2010) “Probabilistic Plan
Recognition using off-the-shelf Classical Planners,”
Proc. AAAI-10
Sadilek A and Kautz H (2010) “Recognizing Multi-Agent
Activities from GPS Data,” in Twenty-Fourth AAAI
Conference on Artificial Intelligence
Sukthankar G, Goldman R P, Geib C, Pynadath D V, Bui
H H (2014) “Plan, Activity, and Intent Recognition
Theory and Practice.” Morgan Kaufmann
Sukthankar G and Sycara K (2006) “Simultaneous Team
Assignment and Behavior Recognition from Spatio-
temporal Agent Traces,” Proceedings of the Twenty-
First National Conference on Artificial Intelligence
(AAAI-06)
Sukthankar G and Sycara K (2008) “Efficient Plan
Recognition for Dynamic Multi-agent Teams,”
Proceedings of 7th International Conference on
Autonomous Agents and Multi-agent Systems (AAMAS
2008)
Zhuo H H, Yang Q, and Kambhampati S (2012) "Action-
model based multi-agent plan recognition." Advances
in Neural Information Processing Systems 25
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
582
