
Exact Approach to the Scheduling of F-shaped Tasks with Two and
Three Criticality Levels
Antonin Novak
1,2
, Premysl Sucha
1
and Zdenek Hanzalek
1,2
1
Czech Institute of Informatics, Robotics and Cybernetics, Czech Technical University in Prague, Prague, Czech Republic
2
Department of Control Engineering, Faculty of Electrical Engineering, Czech Technical University in Prague,
Prague, Czech Republic
Keywords:
Scheduling, Mixed-criticality, Embedded Systems, Integer Linear Programming.
Abstract:
The communication is an essential part of a fault tolerant and dependable system. Safety-critical systems are
often implemented as time-triggered environments, where the network nodes are synchronized by clocks and
follow a static schedule to ensure determinism and easy certification. The reliability of a communication bus
can be further improved when the message retransmission is permitted to deal with lost messages. However,
constructing static schedules for non-preemptive messages that account for retransmissions while preserving
the efficient use of resources poses a challenging problem. In this paper, we show that the problem can be
modeled using so-called F-shaped tasks. We propose efficient exact algorithms solving the non-preemptive
message scheduling problem with retransmissions. Furthermore, we show a new complexity result, and we
present computational experiments for instances with up to 200 messages.
1 INTRODUCTION
The communication buses in modern vehicles are an
essential part of advanced driver assistants. Those
systems depend on the data gather by sensors, such as
LIDAR, cameras, and radars. The data describing the
surrounding environment are communicated through
communication buses to ECUs (Electronic Control
Units) where they are processed, and appropriate ac-
tions are taken. For example, if an obstacle is detected
in front of the vehicle, the car automatically activates
breaks. Not only driver assistant systems rely on the
communication. Different ECUs are responsible for
running the car as a whole. The fuel is injected ac-
cordingly to the current combustion and outside con-
ditions and cars with the drive-by-wire system steer
via electronic signals.
The modern vehicle is considered as a fault-
tolerant and dependable system. If one part of it
breaks down or does not work as expected, the hu-
man life is in risk. Since the intra-vehicular com-
munication is the key element of the car, it is sub-
ject to a safety certification. The safety certification
is a process, where the manufacturer proves that his
safety-critical systems such as autonomous driving
are working correctly to a high degree of assurance.
If manufacturers are not able to demonstrate the cor-
rect behavior of the central communication bus, then
the whole certification process is not complete. Ac-
cording to SSR Automotive Warranty & Recall Report
2016, the number of software-related recalls in 2015
accounted for 15% of all recalls, marking the impor-
tance of the certification.
Traditionally, event-triggered communication pro-
tocols are commonly used in automotive industry. In
the event-triggered environment, the actions are per-
formed on-demand, i.e. triggered by some events.
Even though, event-triggered protocols are flexible,
their usage in modern cars is limited due to certifica-
tion and verification issues. The response time analy-
sis (i.e. the analysis of the behavior of the system) in
real-life event-triggered communication systems in-
cluding gateways and precedence relations is a very
complex problem, therefore the safety certification of
systems utilizing the event-triggered environment is a
difficult task (Baruah and Fohler, 2011).
An alternative to event-triggered real-time sys-
tems is the time-triggered paradigm. Messages
in time-triggered communication are transferred
through the network at specific times prescribed by
a static pre-computed static schedule. The sched-
ule is constructed usually with tools known from
OR/Mathematical Optimization field (Dvorak and
Hanzalek, 2016; Kopetz et al., 2005) such that it re-
160
Novak A., Sucha P. and Hanzalek Z.
Exact Approach to the Scheduling of F-shaped Tasks with Two and Three Criticality Levels.
DOI: 10.5220/0006198101600170
In Proceedings of the 6th International Conference on Operations Research and Enterprise Systems (ICORES 2017), pages 160-170
ISBN: 978-989-758-218-9
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
criticality levelcriticality level
timetime
T
1
T
1
T
2
T
2
T
3
T
3
T
4
T
4
T
5
T
5
C
max
C
max
execution scenari oexecution scenari o
55
99
00
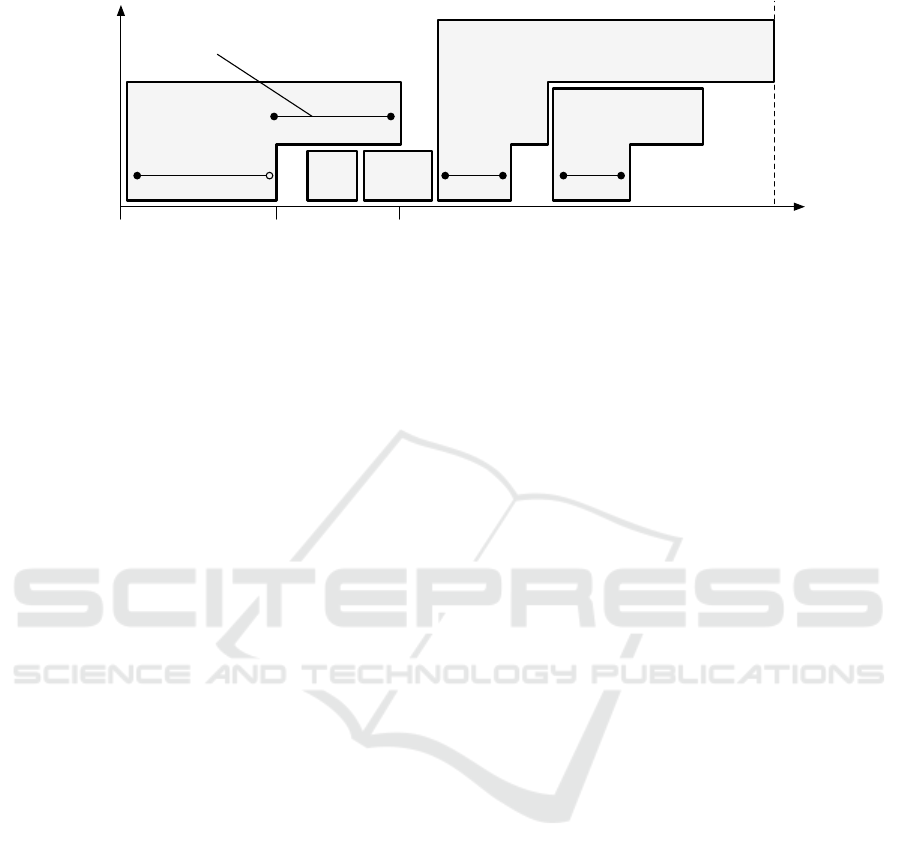
Figure 1: A feasible schedule of F-shaped tasks with a runtime execution scenario denoted by the black line.
spects the problem and safety constraints. Therefore,
the certification of the system is achieved via showing
feasibility of the produced communication schedule.
The determinism and verifiability of time-
triggered communications led to the design of proto-
cols that includes time-triggered communication for
safety-critical systems. For example, FlexRay bus
is used nowadays in the automotive industry (e.g.
Porsche Panamera, Nissan Infinity Q50). One of the
disadvantages of time-triggered protocols is their non-
flexibility. For example, the static schedule does not
take into consideration the message retransmission.
The retransmission occurs when a highly critical mes-
sage is not delivered e.g. due to EM noise. A possi-
ble solution how to enable message retransmissions in
static time-triggered schedules is to allocate more pro-
cessing time for each message to account for possible
retransmissions. If no retransmission occurs during
an actual execution, then the resource is idle until the
start time of the next message. However, since re-
transmissions do not appear as frequently, the average
resource utilization would be poor.
In this paper, we introduce a new solution to this
problem. We build static schedules that allow retrans-
mission of non-preemptive messages to some degree.
An extra time needed for retransmissions is compen-
sated by skipping less critical messages. The trick
we use to solve the problem is to include a part of
the problem solution to its formulation. Instead of
scheduling rectangles, denoting the single exact pro-
cessing time of a message, we schedule so-called F-
shapes. This leads to an interesting combinatorial
problem, where we are given a set of shapes that
are aligned on the left side with the right side that is
jagged (see an example in Fig. 1). The goal is to pack
these shapes as tightly as possible so that they do not
overlap.
The use of F-shapes is a very elegant solution that
achieves efficient resource utilization. It modifies the
traditional scheduling problem into the challenging
one where the schedule has to assume alternatives
based on the observed runtime scenario. Even though
there is an exponential number of possible runtime
scenarios, and for each of them, the static schedule
is well-defined, we will show, that the introduced for-
malism makes the problem computationally tractable
in practice.
1.1 Application to Automotive
Frequently, in the complex systems, functionalities
with different criticality co-exist on a single bus. The
adaptation of IEC 61508 safety standard (Bell, 2006),
the ASIL, defines the application levels with a haz-
ard assessment corresponding to three Safety Integrity
Levels. Therefore the schedules with three criticality
levels arise from the application in the automotive do-
main:
• messages with high criticality (criticality level 3)
are used for safety-related functionalities (their
failure may result in death or serious injury to peo-
ple), such as steering and braking;
• messages with medium criticality (criticality level
2) are used for mission-related functionalities
(their failure may prevent a goal-directed activity
from being successfully completed), such as com-
bustion engine control;
• messages with low criticality (criticality level 1)
are used for infotainment functionalities, such as
audio playback.
For the automotive application we assume, the
criticality of a message corresponds to its maximum
number of possible (re)transmissions and that mes-
sages are non-preemptive since the preemption is
costly in communications. See an example of a static
schedule that accounts for retransmissions in Fig. 1.
The individual shapes correspond to messages sched-
uled on the communication bus. There T
2
and T
3
have
low criticality, and no retransmissions are allowed. T
1
and T
5
correspond to messages with medium critical-
ity; thus they can be retransmitted once. The most
Exact Approach to the Scheduling of F-shaped Tasks with Two and Three Criticality Levels
161

critical message is T
4
, that can be retransmitted twice.
The retransmission of the messages causes a prolon-
gation of the processing time that is depicted in levels
on the vertical axis. The top level of each message
represents its WCET (the worst case execution time),
i.e. the time that it takes to transmit the message un-
der the most pessimistic conditions. The prolonga-
tions are compensated by skipping less critical mes-
sages. With this mechanism, the successful transmis-
sion of highly critical messages is guaranteed while
in the average case runtime scenario the resource (i.e.
communication bus) is efficiently utilized.
Scheduling of safety-critical non-preemptive mes-
sages on this time-triggered network can be modeled
as the scheduling problem 1|mc = L,mu|C
max
(Han-
zalek et al., 2016). It represents the scheduling prob-
lem with one resource (a communication channel in
the network) with non-preemptive mixed-criticality
tasks with maximum L criticality levels, mu stands
for the match-up of the execution scenario. The cri-
terion is to minimize the maximal completion time
C
max
.
A solution of the scheduling problem is given by
a schedule that switches to the higher criticality level
when a prolongation of a task occurs. After its suc-
cessful completion, it matches-up with the original
schedule. The trade-off between the safe and efficient
schedules is achieved by skipping less critical mes-
sages when the prolongation of a more critical one
takes place.
1.2 Paper Contribution and Outline
In this paper, we solve the scheduling problem of
message retransmission in time-triggered environ-
ments. The objective is to find a non-preemptive static
schedule that accounts for unforeseen message re-
transmissions while minimizing the length occupied
by time-triggered communication. The uncertainty
about the processing time is modeled using an ab-
straction based on F-shaped tasks. We show the rela-
tion between F-shaped tasks and the underlying prob-
ability distribution functions. Furthermore, we show
a new complexity result that establishes the member-
ship of the considered problem into AP X complex-
ity class, and we provide an approximation algorithm.
We study the characterization of the set of optimal so-
lutions for the problem with two criticality levels. Fi-
nally, we propose efficient exact algorithms for prob-
lems with two and three criticality levels, which solve
instances with up to 200 tasks, beating the best-known
method by a large margin.
The rest of the paper is organized as follows. In
Sec. 2 we survey the related work. In Sec. 3 we show
the relation between F-shaped tasks and discretization
of cumulative probability distribution functions. In
Sec. 5 we prove approximability of the problem. In
Sec. 6 and 7 we show properties of the problem with
two and three criticality levels and we propose effi-
cient exact algorithms. Finally, in Sec. 8 we present
computational results on the sythetic data as well as
on the data inspired by a real-life embedded system
of our industrial partner.
2 RELATED WORK
The exhaustive survey on mixed-criticality in real-
time systems is presented by (Burns and Davis, 2013).
This research is traditionally concentrated around
event-triggered approach to scheduling. In the sem-
inal paper (Vestal, 2007) proposed a method that as-
sumes different WCETs (the worst case execution
time) obtained for discrete levels of assurance. Apart
from this proposition, the paper presents modified
preemptive fixed priority schedulability analysis al-
gorithms. However, the preemptive model is not suit-
able for communication protocols, and it significantly
changes the scheduling problem. (Baruah et al., 2010)
formulated the basic model of mixed-criticality sys-
tems. They study MC schedulability problem with
two criticality levels under special restrictive cases in
the event-triggered environment. (Theis et al., 2013)
argued that mixed-criticality shall be pursued in time-
triggered systems. (Baruah and Fohler, 2011)’s ap-
proach in the time-triggered environment assumed
preemptive tasks with up to two criticality levels.
It makes it unsuitable for communication protocols
since the preemption would be costly. (Hanzalek
et al., 2016) proposed the problem of non-preemptive
mixed-criticality match-up scheduling motivated by
scheduling messages on a highly used communica-
tion channel. They showed how a schedule with F-
shaped tasks can be used to deal with a task disruption
by skipping less critical tasks. They provide the rela-
tive order MILP model for 1|r
j
,
˜
d
j
,mc = L,mu|C
max
scheduling problem, but it can deal with instances
with only about 20 messages.
The concept of match-up scheduling was intro-
duced by (Bean et al., 1991). In a case of a disruption,
the goal is to construct a new schedule that matches
the original one at some point in the future. This con-
cept is mostly studied in the context of manufacturing
problems (Qi et al., 2006).
Taking broader perspective, the problem can be
viewed as a case of robust and stochastic optimiza-
tion due to uncertainty about transmission times while
satisfying safety requirements. (Bertsimas et al.,
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
162

2011) surveys robust versions of various optimization
problems, but rather continuous than discrete ones.
The field of stochastic optimization is reviewed by
(Sahinidis, 2004). They state that integer variables
introduced to stochastic programming complicate its
solution, yielding suboptimal results even for small-
sized problems.
As in our problem, some of the less critical mes-
sages are allowed to be skipped, the problem is related
to the scheduling with a job rejection. (Shabtay et al.,
2013) reviews offline scheduling with a job rejection.
These approaches consider two criteria, a measure as-
sociated with schedule quality and the cost incurred
by rejected jobs. The solution to this problem is a set
of accepted jobs and a set of rejected jobs. However,
rejected jobs cannot be executed in any execution sce-
nario; thus this model is not suitable for communica-
tion protocols mentioned in our motivation.
To the best of our knowledge, the problem
of offline non-preemptive mixed-criticality match-up
scheduling was addressed by (Hanzalek et al., 2016)
only, but it lacks an efficient solution method which is
suggested in this paper.
3 NON-PREEMPTIVE
MIXED-CRITICALITY
SCHEDULING
We assume that a set of communication messages is
given to be scheduled on a single communication bus
segment. For each message T
i
, the criticality X
i
∈ N is
specified. It denotes the number of allowed transmis-
sions. Each message (task) is specified by its critical-
ity levels. For each criticality level ∈ {1, . .. ,X
i
}, we
define the associated processing time with this level.
See an example in Fig. 1. Here, T
1
has criticality
X
1
= 2; therefore it can be retransmitted once. The
processing time at the first level is given by its BCET
(the best case execution time) while the processing
time at the second level is its WCET (the worst case
execution time). During the run time execution, ex-
actly one processing time of the message is realized;
however, it is not known in advance which it will be.
We can view processing time prolongations as a
retransmission of the whole message content. How-
ever, this mixed-criticality scheduling model is useful
also for scheduling of computational tasks, where the
exact computational time is not known in advance,
but only a probability distribution is known. Let us
consider the processing time of task T
i
to be a ran-
dom variable T
i
. Let us assume an arbitrary probabil-
ity distribution over a discrete set of processing times
from N for a particular task stating Pr[T
i
= t]. The
same information given by the probability distribution
is captured by the CDF (cumulative distribution func-
tion) F
i
giving the probability that processing time
T
i
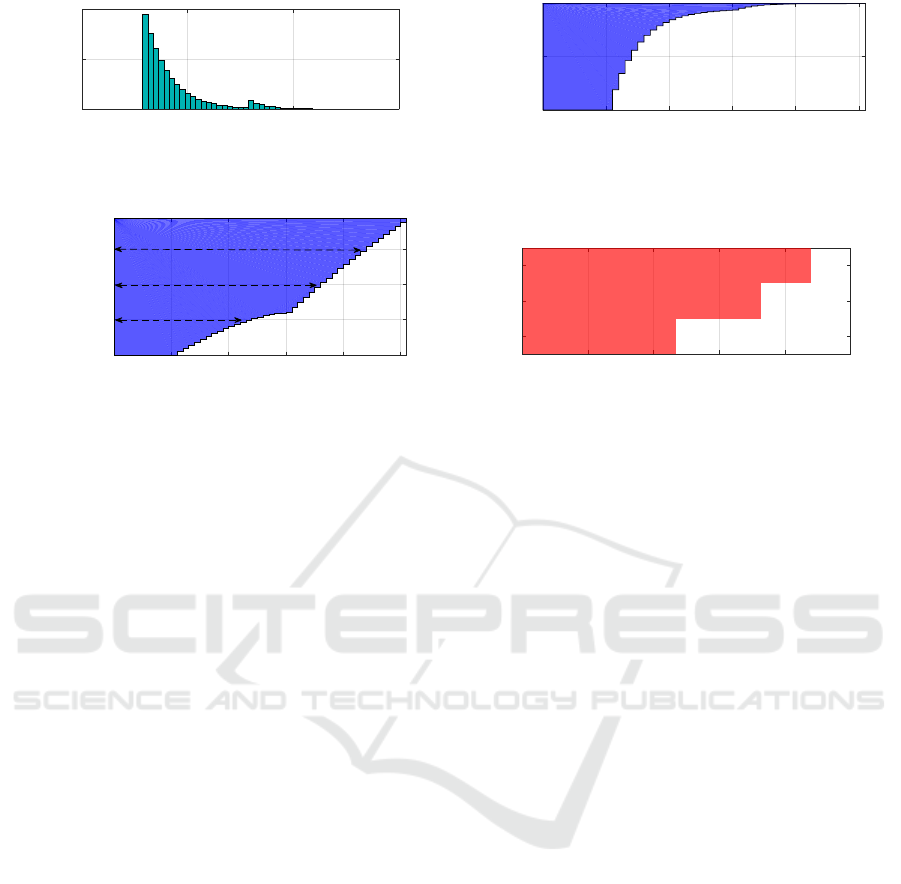
is at most t. See Figs. 2a and 2b for such an ex-
ample. Corresponding processing times p
()
i
for each
criticality level are taken from F
i
as p
()
i
= F
−1
i
(c
),
where F
−1
i
is the quantile function. The criticality of
a task is a user-defined parameter. For example, if we
identify criticality levels with a safety standard IEC
61508 SIL (Safety Integrity Levels) (Bell, 2006), then
the task criticality X
i
is given by the SIL of the func-
tionality carried out by the content and c
is defined
as 1−probability of failure defined by SIL .
Processing times obtained according to criticality
levels then form a single task like the one depicted in
Fig. 2d. Since CDFs are non-decreasing functions, a
set of processing times p
()
i
yields shapes like the F
letter rather than ordinary rectangles, hence the name
F-shape. See an example in Fig 2. There we see dis-
cretization for a task with criticality three at corre-
sponding levels 1, 2 and 3 with the vertical axis on
the logarithmic scale.
The solution to the scheduling problem is a feasi-
ble static schedule of the given set of F-shaped tasks.
Consider a particular example of the schedule with
tasks having up to three levels of criticality that is
shown in Fig. 1. A feasible schedule with F-shaped
tasks describes alternative schedules for any realiza-
tion of the processing time of messages. Observed
prolongations of more critical messages are compen-
sated by skipping execution of less critical messages.
The black line denotes a scenario, where T
1
was
disrupted once. The actual processing time of T
1
was
9 instead of 5 due to a disturbance. When the dis-
ruption occurred, the execution switched to the next
higher criticality level. There, by the assumption, the
execution was successful with a probability given by
the = 2 criticality level. After upon T
1
finished, the
execution matched-up back with the lowest criticality
level. In general, if a task T
i
is prolonged to level ,
then all tasks T
j
for which s
i
+ p
(1)
i
≤ s
j
< s
i
+ p
()
i
are
not executed. Therefore, in this execution scenario,
after T
1
finished, T
4
was up next. Moreover, if we
unify the F-shape from Fig. 2d with task T
4
in Fig. 1,
then we can say that T
5
will be executed with very
high probability of 0.99, but in rare cases, it won’t be
executed since T
4
is more critical and needs more time
to complete. However, here the choice of 0.99 is just
for the illustrative purposes only, since the levels of
the probability are inputs to the problem and they can
be set to any feasible value.
Exact Approach to the Scheduling of F-shaped Tasks with Two and Three Criticality Levels
163
processing time t
0 20 40 60
Pr[T
i
= t]
0
0.1
0.2
(a) A discrete probability distribution over a set of
processing times.
processing time t
0 10 20 30 40 50
Pr[T
i
5 t]
0
0.5
(b) Corresponding cumulative distribution function.
processing time t
0 10 20 30 40 50
Pr[T
i
5 t]
0.9
0.99
0.999
p
(3)
i
p
(2)
i
p
(1)
i
(c) Discretization of a cumulative distribution function
processing time t
0 10 20 30 40 50
criticality level
1
2
3
p
(2)
i
p
(3)
i
p
(1)
i
(d) Resulting F-shaped task with X
i
= 3
Figure 2: Discretized cumulative distribution function forms an F-shaped task.
4 PROBLEM STATEMENT
We assume a set of non-preemptive F-shaped tasks
I
M C
= {T
1
,. .. , T
n
} to be processed on a single ma-
chine. We define an F-shaped task and its criticality
as follows:
Definition 1 (F-shape). The F-shape T
i
is a pair
(X
i
,P
i
) where X
i
∈ {1, . . ., L}, L ∈ N is the task crit-
icality and P
i
∈ N
X
i
, P
i
= (p
(1)
i
, p
(2)
i
,. .. , p
(X
i
)
i
) is the
vector of processing times such that
p
(1)
i
< p
(2)
i
< . .. < p
(X
i
)
i
.
The F-shape is an abstraction for non-preemptive
tasks with multiple different processing times. See
for example T
4
in Fig. 1. It is F-shaped task with crit-
icality X
4
= 3; therefore it has 3 different processing
times. Having a set I
M C
of F-shaped tasks, we define
the feasible schedule as follows:
Definition 2 (Feasible Schedule). By the schedule for
a set of F-shaped tasks I
M C
= {T
1
,T
2
,. .. , T
n
} we re-
fer to an assignment (s
1
,s
2
,. .. , s
n
) ∈ N
n
. We say that
schedule (s
1
,s
2
,. .. , s
n
) for I
M C
is feasible if and only
if ∀i, j ∈ {1,. .. , n}, i 6= j :
(s
i
+ p
(min{X
i
,X
j
})
i
≤ s
j
) ∨ (s
j
+ p
(min{X
i
,X
j
})
j
≤ s
i
).
Feasibility of a schedule with F-shaped tasks re-
quires that tasks do not overlap on any criticality level.
For example in Fig. 1, since T
5
follows after T
4
, it can-
not start earlier than s
4
+ p
(2)
4
, since min{X
4
,X
5
} = 2
is the highest common criticality level of T
4
and T
5
.
We deal with the problem of finding a feasible
schedule for a set of F-shaped tasks with criticality
at most L such that the makespan (i.e. max s
i
+ p
(X
i
)
i
)
is minimized. In the three-field Graham-Blazewicz
notation it is denoted as 1|mc = L, mu|C
max
, where
mc = L stands for the mixed-criticality aspect of tasks
of maximal criticality L and mu stands for the match-
up. This problem is known to be N P -hard in the
strong sense even for mc = 2 (two criticality levels)
as shown by reduction from 3-Partition Problem in
(Hanzalek et al., 2016).
5 GENERAL PROPERTIES
Since the problem 1|mc = 2,mu|C
max
is strongly N P -
hard, it does not admit FPTAS unless P = N P . How-
ever, we show that the problem is polynomial-time
approximable within a constant multiplicative factor.
Proposition 1 (Approximability). For any given fixed
L, the problem 1|mc = L,mu|C
max
is contained in
AP X complexity class.
Proof. Suppose the algorithm LCF (Least Criticality
First) that takes an input instance I
M C
and schedules
tasks in a non-decreasing sequence by their criticali-
ties without waiting. Then the makespan of resulting
schedule is
LCF(I
M C
) =
∑
i|X
i
=1
p
(1)
i
+
∑
i|X
i
=2
p
(2)
i
+ . . . +
∑
i|X
i
=L
p
(L)
i
A sum of processing times on a given criticality level
over a set of tasks is a lower bound on the makespan.
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
164

Therefore we have
max{
∑
i|X
i
≥1
p
(1)
i
,
∑
i|X
i
≥2
p
(2)
i
,. .. ,
∑
i|X
i
≥L
p
(L)
i
} ≤
≤ OPT (I
M C
) ≤ LCF(I
M C
) ≤ L · OPT (I
M C
).
where OPT (I
M C
) denotes the optimal makespan of
I
M C
problem instance.
In fact, this result shows more than that there ex-
ists a polynomial-time algorithm producing schedules
with a constant bounded quality. For example, for
the problem with L = 2 criticality levels, actually any
left-shifted schedule will be at most twice as worse as
the optimal makespan since LCF actually produces
the worst ordering of tasks in terms of the makespan.
In the following sections, we present exact algo-
rithms for the problem with 2 and 3 criticality levels.
Due to the C
max
criterion, it can be shown that the
search for an optimal solution can be reduced to find-
ing a permutation of tasks. Therefore, any optimal
schedule is given by a permutation of tasks π. Hence
we denote the makespan of the left-shifted schedule
of permutation π by C
max
(π). In Sec. 6 we give a
characterization of the set of optimal permutations for
problem 1|mc = 2, mu|C
max
and we introduce a MILP
model utilizing it. In Sec. 7, we introduce an opera-
tor acting on F-shapes, and we show how the optimal
solutions for problems with two and three criticality
levels are related.
6 TWO CRITICALITY LEVELS
We showed that optimal solutions to 1|mc =
L, mu|C
max
are given by a permutation π of tasks. For
the problem with two criticality levels, the optimal
permutations can be characterized more precisely. Let
us refer to tasks with criticality X
i
= 2 as HI-tasks
and tasks with criticality X
j
= 1 as LO-tasks. The
key structure of the optimal permutations are cover-
ing blocks:
Definition 3 (Covering Block). For any given fea-
sible schedule (s
1
,. .. , s
n
), a HI-task T
i
and a LO-
task T
j
we say that T
j
is covered by T
i
, denoted as
T
i
∈ cov(T
j
), if and only if s
i
+ p
(1)
i
≤ s
j
< s
i
+ p
(2)
i
.
The covering block B
i
is then the HI-task T
i
and the
set of all LO-tasks covered by T
i
.
See an example in Fig. 1. There T
1
is covering T
2
and T
3
. All these tasks form a covering block. Al-
though the definition of covering block given above
is meant for the problem with two criticality levels,
the notion of covering can be generalized for more
criticality levels. We assign a length to each covering
block. The length is given as the maximum between
the processing time p
(2)
i
of the HI-task T
i
and the sum
of processing times of tasks covered by T
i
plus the
processing time of T
i
at the first level p
(1)
i
.
Proposition 2 (Covering Block Length). Given the
covering block B
i
, its length defined as
max{p
(1)
i
+
∑
T
j
|T
i
∈cov(T
j
)
p
(1)
j
, p
(2)
i
}
is invariant with respect to the ordering of LO-tasks
T
j
for which T
i
∈ cov(T
j
).
Clearly, the ordering of LO-tasks T
j
for which
T
i
∈ cov(T
j
) does not affect the block length since all
LO-tasks are running without waiting. Furthermore,
we say that task T
j
is fully covered by the block B
i
,
if B
i
= p
(2)
i
and T
i
∈ cov(T
j
). If exists a task cov-
ered by the block B
i
that is not fully covered, then
we say that B
i
is saturated. The makespan C
max
of
the schedule is given by a permutation of covering
blocks. However, actually any permutation of cover-
ing blocks contributes to the makespan by the same
amount; hence it is not subject to optimization.
Proposition 3 (Interchangebility). For every instance
of the problem 1|mc = 2, mu|C
max
there exists an opti-
mal solution that is given by an arbitrary permutation
of covering blocks.
A characterization of optimal solutions for 1|mc =
2,mu|C
max
directly follows from Proposition 2 and 3:
Corollary 1. The optimal solution for 1|mc =
2,mu|C
max
is given by an assignment of LO-tasks to
HI-tasks.
6.1 Covering MILP Model for
1|mc = 2, mu|C
max
The following MILP model relies on Corollary 1.
The model assigns LO-tasks to the HI-tasks in or-
der to form covering blocks such that the sum of their
lengths is the minimum. The decision variable x
i j
in-
dicates whether the LO-task T
j
is covered by the HI-
task T
i
; therefore if T
i
∈ cov(T
j
), then x
i j
= 1. The
makespan is then given by the sum of lengths of cov-
ering blocks and the sum of processing times of all
LO-tasks that are not covered.
min
∑
i|X
i
=2
B
i
+
∑
j|X
j
=1
p
(1)
j
(1 −
∑
i|X
i
=2
x
i j
) (6.1)
s.t.
B
i
≥ p
(1)
i
+
∑
j|X
j
=1
p
(1)
j
x
i j
∀i ∈ I
M C
|
X
i
=2
(6.2)
B
i
≥ p
(2)
i
∀i ∈ I
M C
|
X
i
=2
(6.3)
Exact Approach to the Scheduling of F-shaped Tasks with Two and Three Criticality Levels
165

∑
i|X
i
=2
x
i j
≤ 1 ∀ j ∈ I
M C
|
X
j
=1
(6.4)
where
B
i
∈ Z
+
0
∀i ∈ I
M C
|
X
i
=2
x
i j
∈ {0, 1} ∀i ∈ I
M C
|
X
i
=2
,∀ j ∈ I
M C
|
X
j
=1
The main advantage of this model over the model
proposed by (Hanzalek et al., 2016) is that it has
much stronger linear relaxation. Further in Sec. 8 we
demonstrate its ability to solve an order of magnitude
larger instances.
7 THREE CRITICALITY LEVELS
Although two criticality levels are often sufficient for
safety-critical application and this case is frequently
studied in the field of mixed-critical systems (Burns
and Davis, 2013), sometimes the application natu-
rally contains three or more criticality levels. We cap-
ture the direct relation between problems with differ-
ent maximum criticality levels by introducing a trans-
formation given bellow. It is based on the obser-
vation that omitting some criticality levels provides
an instance of the problem with less criticality level
while maintaining a lower bound property. Further-
more, we introduce the Bottom-up algorithm that uses
this observation. The algorithm is used then together
with Covering MILP model for three criticality levels
(L = 3) shown in Sec. 7.2 to form an efficient solution
method.
The transformation is defined as h
±
restrictions:
Definition 4 (h
±
restrictions). Given the mixed-
criticality instance I
M C
and a positive integer h ∈ N,
let I
h
−
M C
and I
h
+
M C
be sets defined as
I
h
−
M C
={(min{h,X
i
}, (p
(1)
i
,. .. , p
(min{h,X
i
})
i
)) |
∀i ∈ I
M C
}
I
h
+
M C
={(X
i
− h + 1, (p
(h)
i
,. .. , p
(X
i
)
i
)) |
∀i ∈ I
M C
: X
i
≥ h}
We refer to I
h
−
M C
(I
h
+
M C
) as h
−
(h
+
) restriction of the
instance I
M C
.
The h
−
restriction takes an F-shape and cuts off all
criticality levels above level h. Similarly, given the set
of F-shaped tasks, h
+
restriction drops all tasks with
criticality below h, and for the rest, it cuts off criti-
cality levels less than h. Restricting an I
M C
instance
yields to a mixed-criticality instance since omitting
some of the criticality levels for an F-shape gives us
an F-shape. The application of the restriction can be
viewed as a relaxation the problem.
Proposition 4 (Two Lower Bounds on the
Makespan). For the problem 1|mc = 3, mu|C
max
expressions lb
−
, lb
+
defined as
lb
±
= min
π∈Π(I
2
±
M C
)
C
max
(π)
are lower bounds on the makespan, where Π(I
2
+
M C
)
and Π(I
2
−
M C
) denote the set of all permutations of ele-
ments I
2
+
M C
, I
2
−
M C
respectively.
Proof. The lb
−
is a lower bound on the makespan of
1|mc = 3,mu|C
max
since it relaxes on the overlapping
condition at the third criticality level. Similarly, lb
+
is
a lower bound on the makespan since it relaxes on the
overlapping condition at the first criticality level.
7.1 Bottom-up Algorithm
We introduce a heuristic algorithm for the problem
1|mc = 3, mu|C
max
. Let us refer to tasks with X
i
= 3
(i.e. criticality 3) as to GREAT-tasks. The Bottom-
up algorithm is based on the idea of constructing the
schedule in two stages. In the first stage, the relaxed
problem is solved up to the optimality, which mini-
mizes a lower bound on the optimal makespan of the
original problem. The second stage takes the relaxed
solution and constructs a locally optimal solution for
the original problem.
The first stage of the algorithm solves 2
−
restric-
tion of the given problem instance; hence it is an
instance of 1|mc = 2, mu|C
max
problem that can be
solved with the model described in Section 6. It as-
signs LO-tasks to HI-tasks and GREAT-tasks; there-
fore it forms covering blocks. In the second stage,
the algorithm defines a new problem instance I
0
M C
of
the problem 1|mc = 2, mu|C
max
. The instance is con-
structed as follows. It contains LO-tasks with process-
ing time equal to the length of covering blocks from
the stage one. LO-tasks that are not part of any cover-
ing block are assigned to an arbitrary covering block.
The assignment of LO-tasks to 2
−
restricted GREAT-
tasks from the first stage defines HI-tasks in the new
instance I
0
M C
. Then, the I
0
M C
instance is solved once
again as an instance of 1|mc = 2, mu|C
max
problem.
See the complete description of the Bottom-up algo-
rithm in Alg. 1.
In general, the Bottom-up algorithm produces
suboptimal solutions even though they are provably
bounded by a factor of 3 from the optimal solution,
as stated by Proposition 1. However, there are cases
when we can verify if the produced schedule is opti-
mal. This is achieved by the concept of critical paths
that captures the cause of achieved makespan.
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
166

Algorithm 1: Bottom-up.
1: π ← solve I
2
−
M C
restriction by Covering MILP 6.1
2: I
0
M C
←
/
0
3: for each covering block B
i
in the left-shifted so-
lution π do
4: if X
i
= 2 in I
M C
then
5: P
i
← (B
i
)
6: I
0
M C
← I
0
M C
∪ {(1, P
i
)}
7: else if B
i
< p
(3)
i
then
8: P
i
← (B
i
, p
(3)
i
)
9: I
0
M C
← I
0
M C
∪ {(2, P
i
)}
10: else
11: block B
i
is saturated, it contributes by a
constant term to the makespan of I
0
M C
12: end if
13: end for
14: π ← solve I
0
M C
by Covering MILP 6.1
Definition 5 (Critical Path). Given the left-shifted
schedule (s
1
,. .. , s
n
) of the permutation π, the critical
path is CP ⊆ {1,. .. , |
˜
π|}×{1, . . ., L} for some
˜
π ⊆ π
such that ∀(i, ) ∈ C P ,i < |
˜
π| : s
˜
π(i)
+ p
()
˜
π(i)
= s
˜
π(i+1)
where
∑
(i,)∈C P
p
()
˜
π(i)
= C
max
(π) = C
max
(
˜
π).
Essentially, for any given left-shifted schedule, the
critical path is a subset of tasks and their criticality
levels such that ∀(i, ) ∈ C P holds that if the process-
ing time p
()
˜
π(i)
is increased by some ε > 0, then the
makespan of the same schedule is also increased by ε.
Proposition 5 (Sufficient Optimality Conditions). If
one of following conditions holds, then the schedule
produced by the Bottom-up algorithm is optimal for
problem 1|mc = 3,mu|C
max
.
1. There exists a critical path going through the first
and the second levels only.
2. Every LO-task is fully covered by the second crit-
icality level.
When none of the optimality conditions is satis-
fied, e.g. a critical path is coming through every criti-
cality level, we get back to the MILP model 7.2 for the
problem 1|mc = 3, mu|C
max
in order to find an optimal
solution or for the proof that the current solution is the
optimal one. The solver is supplied with the initial so-
lution and a lower bound obtained by the Bottom-up
algorithm. The computational time of Bottom-up al-
gorithm is dominated by lines 1 and 14. The total
computational times are reported in Tab. 2.
7.2 Covering MILP Model for
1|mc = 3, mu|C
max
The Covering MILP model for three criticality lev-
els uses a similar idea as the model for 1|mc =
2,mu|C
max
. It assigns LO-tasks to covering blocks
and covering blocks to the GREAT-tasks. The model
utilizes the idea that optimal solutions are made of
blocks (in this case formed by GREAT-tasks that cover
less critical tasks) whose order is interchangeable
within a solution. It assigns LO-tasks to the HI-tasks
and to 2
−
restriction of GREAT-tasks to form cover-
ing blocks. Blocks are assigned to the GREAT-tasks
in order to create a solution. The big M constant is
as large as the number of LO-tasks contained in the
problem instance.
min
∑
i|X
i
=3
p
i
+
∑
j|X
j
=2
P
j,
/
0
+
∑
k|X
k
=1
p
(1)
k
x
/
0,
/
0,k
(7.1)
s.t.
p
i
≥ p
(3)
i
∀i ∈ I
M C
|
X
i
=3
(7.2)
My
i, j
≥
∑
k|X
k
=1
x
i, j,k
∀i ∈ I
M C
|
X
i
=3
∪
/
0,∀ j ∈ I
M C
|
X
j
=2
(7.3)
P
j,i
≥ p
(2)
j
y
i, j
∀i ∈ I
M C
|
X
i
=3
∪
/
0,∀ j ∈ I
M C
|
X
j
=2
(7.4)
P
j,i
≥ p
(1)
j
y
i, j
+
∑
k|X
k
=1
p
(1)
k
x
i, j,k
∀i ∈ I
M C
|
X
i
=3
∪
/
0,∀ j ∈ I
M C
|
X
j
=2
(7.5)
p
i
≥ p
(2)
i
+
∑
j|X
j
=2
P
j,i
∀i ∈ I
M C
|
X
i
=3
(7.6)
p
i
≥ p
(1)
i
+
∑
j|X
j
=2
P
j,i
+
∑
k|X
k
=1
p
(1)
k
x
i,
/
0,k
∀i ∈ I
M C
|
X
i
=3
(7.7)
∑
i|X
i
=3∪
/
0
∑
j|X
j
=2∪
/
0
x
i, j,k
≥ 1
∀k ∈ I
M C
|
X
k
=1
(7.8)
∑
i|X
i
=3∪
/
0
y
i, j
≥ 1 ∀ j ∈ I
M C
|
X
j
=2
(7.9)
where
y
i, j
∈ {0, 1}∀i ∈ I
M C
|
X
i
=3
∪
/
0,∀ j ∈ I
M C
|
X
j
=2
x
i, j,k
∈ {0, 1}
∀i ∈ I
M C
|
X
i
=3
∪
/
0,∀ j ∈ I
M C
|
X
j
=2
∪
/
0,
∀k ∈ I
M C
|
X
k
=1
∪
/
0 : k 6=
/
0 ∨ (i =
/
0 ∧ j =
/
0)
p
i
∈ Z
+
0
∀i ∈ I
M C
|
X
i
=3
P
j,i
∈ Z
+
0
∀i ∈ I
M C
|
X
i
=3
∪
/
0,∀ j ∈ I
M C
|
X
j
=2
Exact Approach to the Scheduling of F-shaped Tasks with Two and Three Criticality Levels
167

When Bottom-up fails to prove optimality, it goes
back to this model while supplying the lb
−
lower
bound and the initial solution. The reason for exe-
cuting Bottom-up ahead solving MILP model 7.2 is
two-fold. First, we have observed the solver struggles
to prove optimality when the solution is clearly opti-
mal regarding the critical path. The other observation
is that if the problem instance contains the majority of
tasks with criticality one and two, then solving its 2
−
restriction frequently yields optimal solution since the
highest criticality levels are not likely to be utilized.
The same holds for the instances with a large number
of tasks with higher criticality. Furthermore, solving
2
±
restrictions of I
M C
is cheap compared to the solv-
ing the whole MILP model 7.2 as it can be seen in
Tab. 1.
8 COMPUTATIONAL
EXPERIMENTS
For the problem 1|mc = 2, mu|C
max
we have randomly
generated sets of 20 instances with n tasks for each
n ∈ {10, .. ., 200}. Criticalities of tasks were dis-
tributed uniformly. The processing time of a task
at level 1 is sampled from the uniform distribution
U(1,11). For tasks with the criticality of 2, the pro-
longation at level 2 is sampled from uniform distribu-
tion U(1,10).
For the problem 1|mc = 3, mu|C
max
we have ran-
domly generated sets of 20 instances with n tasks
for each n ∈ {10,. .. , 80}. For each n, the set con-
tains instances with different splits of tasks’ critical-
ities and different distributions for prolongation (e.g.
U(1,10) and U(1,7) for the second level, U(1, 10)
and U(1,14) for the third level, etc.) in order to gen-
erate instances of various properties. We have inves-
tigated the impact of different processing time dis-
tributions to the overall performance. We have ob-
served that the the proposed approach is not sensitive
to the choice of particular distributions, but rather to
the difference between combined processing times al-
located to each criticality level. Therefore, in our ex-
periments, we have used uniform distributions with
parameters that represent challenging instances.
The column avg t (max t) in Tab. 1 and 2 de-
notes the average (maximal) computational time for
instances that were solved within the time limit of
300 s. The column unsl contains the percentage of in-
stances that were not solved within the time limit and
avg gap denotes average optimality gap proven by the
solver for the unsolved instances. Results were ob-
tained with two Intel Xeon E5-2620 v2 @ 2.10 GHz
processors using Gurobi Optimizer 6.5 with the algo-
rithms implemented in Python 3.4.
In Tab. 1 it can be seen that our model is able to
solve about an order of the magnitude larger prob-
lem instances. The Relative Order model proposed
by (Hanzalek et al., 2016) consistently fails to narrow
optimality gap for instances with more than 40 tasks.
In Tab. 2 it is shown that the combination of Bottom-
up heuristic and MILP 7.2 is able to solve reliably in-
stances with 60 tasks up to the optimality and almost
all instances with 80 tasks. Moreover, the proven gap
is much smaller than for the Relative Order model;
therefore it shows that our model has stronger linear
relaxation.
To put our algorithms into the another test, we
tested them on data obtained from our automotive in-
dustrial partner. The data comes from a real-life au-
tomotive system consisting of a communication mes-
sages between 23 ECUs. From this instance, we con-
structed a probabilistic model that corresponds to the
given instance. We are interested in scheduling mes-
sages inside the basic period (10 ms); therefore those
are messages occurring in every communication cy-
cle. The aim is to minimize C
max
to maximize re-
maining space for other messages with larger periods.
The instance divides messages into three cate-
gories. The lowest critical are debug and develop-
ment messages which do not use any form of a check-
sum. More critical messages are secured by a par-
ity check. The most critical messages are secured
by CRC8 code. The message criticalities are dis-
tributed according Pr[X
i
= 1] = 0.48, Pr[X
i
= 2] =
0.48, Pr[X
i
= 3] = 0.04. The length of each mes-
sage is drawn from distribution U(8,12). The pro-
longation on the second and the third criticality level
is sampled from U(8, 16) to model the message re-
transmission and an extra overhead.
The real-life industrial dataset was created by gen-
erating 20 instances of the problem 1|mc = 3,mu|C
max
according to distributions mentioned above for each
of n ∈ {50, 100, 150, 200}, where n is the number of
messages. The results are reported in Tab. 3. The
computational times were obtained under the same
circumstances as described above.
The results for real-life industrial data are quanti-
tatively better compared to those obtained in Tab. 2.
The reason is likely that the data contain relatively
a few GREAT-tasks and the range of lengths of LO-
tasks is relatively narrow. Therefore, many of them
are identical, and the solver might be able to exploit
this symmetry even though it was not supplied to it.
With the Covering MILP model, the solver scales well
even for larger instances.
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
168
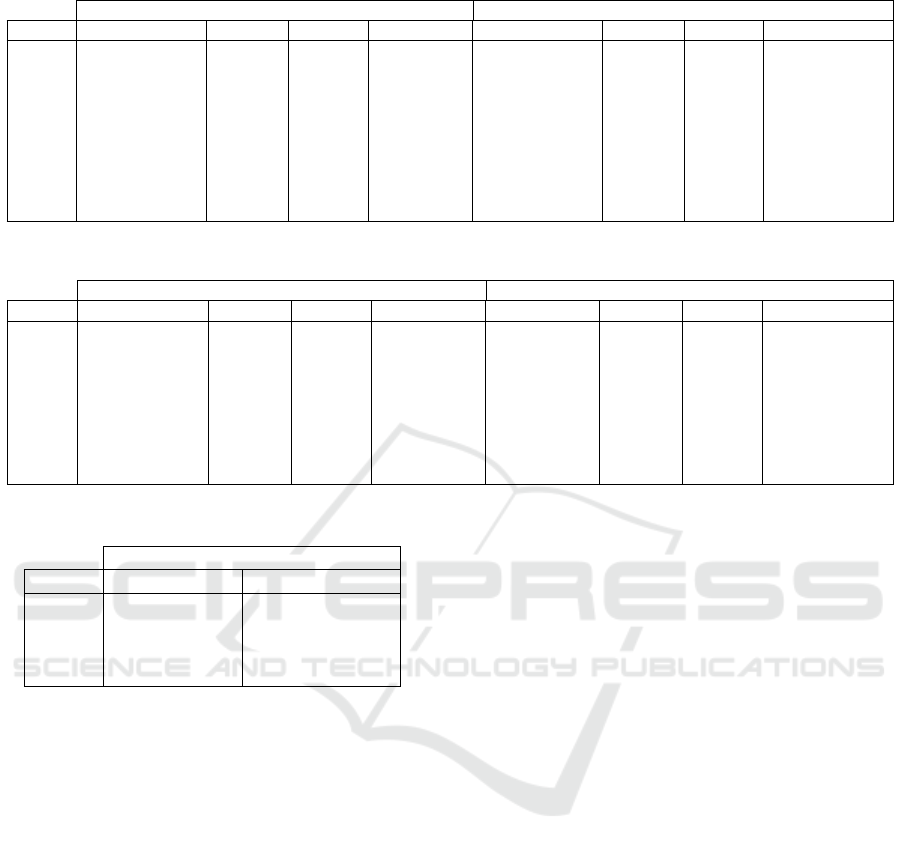
Table 1: Computational results for the problem 1|mc = 2, mu|C
max
.
Covering MILP 6.1 Relative Order MILP (Hanzalek et al., 2016)
n tasks avg t [s] max t [s] unsl [%] avg gap [%] avg t [s] max t [s] unsl [%] avg gap [%]
10 > 0.01 0.03 0 — 13.07 (±44.93) 200.22 0 —
15 > 0.01 0.03 0 — 49.67 (±49.38) 127.09 60 27.32 (±12.54)
20 0.01(±0.01) 0.03 0 — — — 100 40.09 (±15.27)
40 0.09(±0.17) 0.81 0 — — — 100 77.66(±6.23)
60 1.37(±4.33) 19.71 0 — — — 100 84.23(±2.90)
80 0.38(±0.45) 1.94 0 — — — 100 90.72(±1.77)
100 1.28(±1.38) 5.05 0 — — — 100 93.38(±0.76)
150 11.77 (±24.29) 93.01 0 — — — 100 96.02(±0.24)
200 22.69 (±61.24) 281.04 0 — — — 100 97.33 (±0.13)
Table 2: Computational results for the problem 1|mc = 3, mu|C
max
.
Bottom-up w/ Covering MILP 7.2 Relative Order MILP (Hanzalek et al., 2016)
n tasks avg t [s] max t [s] unsl [%] avg gap [%] avg t [s] max t [s] unsl [%] avg gap [%]
10 0.02 (±0.01) 0.04 0 — 0.09 (±0.07) 0.28 0 —
20 0.16 (±0.36) 1.66 0 — — — 100 28.71 (±16.62)
30 0.17 (±0.17) 0.66 0 — — — 100 63.28 (±7.35)
40 0.69 (±1.02) 3.61 0 — — — 100 72.85 (±6.14)
50 2.40 (±7.42) 33.56 0 — — — 100 80.61(±2.96)
60 6.71(±11.97) 44.67 0 — — — 100 84.30 (±2.70)
70 11.30(±22.31) 79.38 10 0.38 (±0.19) — — 100 89.34(±1.43)
80 37.92(±68.82) 224.86 20 0.34 (±0.13) — — 100 91.09(±1.40)
Table 3: Computational results for the real-life instances.
Bottom-up w/ Covering MILP 7.2
n tasks avg t [s] avg gap [%]
50 0.08(±0.14) —
100 1.17(±3.33) —
150 3.67(±7.23) 0.26 (±0.00)
200 5.34(±15.51) —
9 CONCLUSION
In this paper, we have proposed two exact approaches
for the problem of non-preemptive mixed-criticality
match-up scheduling for solving the problem of mes-
sage retransmission in time-triggered communication
protocols. We investigated the fundamental proper-
ties of F-shapes to obtain efficient models of the prob-
lem. Our algorithms outperform recently proposed
approach by a large margin. Furthermore, we showed
the membership of 1|mc = L, mu|C
max
problem in
AP X complexity class for an arbitrary fixed L.
ACKNOWLEDGEMENT
This work was supported by the Grant Agency of
the Czech Republic under the Project GACR P103-
16-23509S. Furthermore, this work was supported
by the US Department of the Navy Grant N62909-
15-1-N094 SALTT issued by Office Naval Research
Global. The United States Government has a royalty-
free license throughout the world in all copyrightable
material contained herein.
REFERENCES
Baruah, S. and Fohler, G. (2011). Certification-cognizant
time-triggered scheduling of mixed-criticality sys-
tems. In Real-Time Systems Symposium (RTSS), 2011
IEEE 32nd, pages 3–12. IEEE.
Baruah, S., Li, H., and Stougie, L. (2010). Towards the
design of certifiable mixed-criticality systems. In
Real-Time and Embedded Technology and Applica-
tions Symposium (RTAS), 2010 16th IEEE, pages 13–
22. IEEE.
Bean, J. C., Birge, J. R., Mittenthal, J., and Noon, C. E.
(1991). Matchup scheduling with multiple resources,
release dates and disruptions. Operations Research,
39(3):470–483.
Bell, R. (2006). Introduction to iec 61508. In Proceedings
of the 10th Australian workshop on Safety critical sys-
tems and software-Volume 55, pages 3–12. Australian
Computer Society, Inc.
Bertsimas, D., Brown, D. B., and Caramanis, C. (2011).
Theory and applications of robust optimization. SIAM
review, 53(3):464–501.
Burns, A. and Davis, R. (2013). Mixed criticality systems-a
review. Department of Computer Science, University
of York, Tech. Rep.
Dvorak, J. and Hanzalek, Z. (2016). Using two indepen-
dent channels with gateway for FlexRay static seg-
Exact Approach to the Scheduling of F-shaped Tasks with Two and Three Criticality Levels
169

ment scheduling. IEEE Transactions on Industrial In-
formatics, article in press.
Hanzalek, Z., Tunys, T., and Sucha, P. (2016). Non-
preemptive mixed-criticality match-up schedul-
ing problem. Journal of Scheduling, doi:
10.1007/s10951-016-0468-y.
Kopetz, H., Ademaj, A., Grillinger, P., and Steinhammer,
K. (2005). The time-triggered ethernet (TTE) design.
In Object-Oriented Real-Time Distributed Computing,
2005. ISORC 2005. Eighth IEEE International Sym-
posium on, pages 22–33. IEEE.
Qi, X., Bard, J. F., and Yu, G. (2006). Disruption manage-
ment for machine scheduling: the case of spt sched-
ules. International Journal of Production Economics,
103(1):166–184.
Sahinidis, N. V. (2004). Optimization under uncertainty:
state-of-the-art and opportunities. Computers &
Chemical Engineering, 28(6):971–983.
Shabtay, D., Gaspar, N., and Kaspi, M. (2013). A survey on
offline scheduling with rejection. Journal of schedul-
ing, 16(1):3–28.
Theis, J., Fohler, G., and Baruah, S. (2013). Schedule ta-
ble generation for time-triggered mixed criticality sys-
tems. Proc. WMC, RTSS, pages 79–84.
Vestal, S. (2007). Preemptive scheduling of multi-criticality
systems with varying degrees of execution time assur-
ance. In Real-Time Systems Symposium, 2007. RTSS
2007. 28th IEEE International, pages 239–243. IEEE.
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
170
