Hierarchical Self-organizing Maps System for Action Classiﬁcation

Zahra Gharaee

, Peter G

ardenfors

and Magnus Johnsson

1,2

Cognitive Science, Lund University, Helgonav

agen 3, Lund, Sweden

Department of Intelligent Cybernetic Systems, NRNU MEPhI, Moscow, Russia

Keywords:

Self-organizing Maps, Neural Networks, Action Perception, Hierarchical Models.

Abstract:

We present a novel action recognition system that is able to learn how to recognize and classify actions. Our

system employs a three-layered neural network hierarchy consisting of two self-organizing maps together

with a supervised neural network for labelling the actions. The system is equipped with a module that pre-

processes the 3D input data before the ﬁrst layer, and a module that transforms the activity elicited over time

in the ﬁrst layer SOM into an ordered vector representation before the second layer, thus achieving a time

invariant representation. We have evaluated our system in an experiment consisting of ten different actions

selected from a publicly available data set with encouraging result.

1 INTRODUCTION

Humans increasingly interact with robotic systems.

Service robots that communicate and collaborate with

people can undertake tasks that stand-alone robots

cannot. In order to realize their full value, robots

will need to interact and work with people ﬂuently.

The design of intelligent collaborative robots in open,

complex and changing environments where they are

expected to communicate, interact and work with pe-

ople presents great scientiﬁc challenges.

The success of the human-robot interaction de-

pends on the development of robust methods that ena-

ble robots to recognize and predict goals and intenti-

ons of other agents. Humans do this, to a large ex-

tent, by interpreting and categorizing the actions they

perceive. Hence, it is central to develop methods for

action categorization that can be employed in robotic

systems. This involves an analysis of on-going events

from visual data captured by cameras to track mo-

vements of humans and to use this analysis to iden-

tify actions. Modelling these tasks is also crucial in

a variety of other domains such as computer games,

surveillance, assisted living, ambient intelligence, and

decision support.

In this article, we present an action categorization

method that, at large, works like the human system.

Results from the cognitive sciences indicate that the

human brain performs a substantial information re-

duction when categorizing actions. In particular, (Jo-

hansson, 1973) patch-light technique for analyzing

biological motion is a source of inspiration for us. He

attached light bulbs to the joints of actors who were

dressed in black and moved in a dark room. The ac-

tors were ﬁlmed performing actions such as walking,

running, and dancing. Watching the ﬁlms - in which

only the dots of light could be seen - subjects recog-

nized the actions within tenths of a second. Further

experiments by (Runesson and Frykholm, 1983), see

also (Runesson, 1994), have shown that subjects ex-

tract subtle details of the actions performed, such as

the gender of the person walking or the weight of ob-

jects lifted (where the objects themselves cannot be

seen). An important lesson to learn from the experi-

ments by Johansson and his followers is that the kine-

matics of a movement contains sufﬁcient information

to identify the underlying dynamic patterns.

From a computational point of view, there are

many challenges that make the action recognition task

difﬁcult to imitate artiﬁcially. For example, the acting

individuals differ in height, weight and bodily propor-

tions. Other important issues to be addressed are the

impact of the camera’s viewing angle and its distance

from the actor and the performance speed of the acti-

ons. In brief, categorizations of actions ought to be

invariant under distance, viewing angle, size of actor,

lighting conditions and temporal variations.

One idea for a model of actions comes from (Marr

and Vaina, 1982) and (Vaina, 1983), who extend

(Marr and Nishihara, 1978) cylinder models of ob-

jects to an analysis of actions. In Marr and Vaina’s

model, an action is described via differential equati-

Gharaee Z., GÃd’rdenfors P. and Johnsson M.

Hierarchical Self-organizing Maps System for Action Classiﬁcation.

DOI: 10.5220/0006199305830590

In Proceedings of the 9th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2017), pages 583-590

ISBN: 978-989-758-220-2

583

ons for movements of the body parts of, for example,

a walking human. What we ﬁnd useful in this model

is that a cylinder ﬁgure can be described as a vector

with a limited number of dimensions. Each cylinder

can be described by two dimensions: length and ra-

dius. Each joining point in the ﬁgure can be described

by a small number of coordinates for point of contact

and angle of joining cylinders. This means that, at a

particular moment, the entire ﬁgure can be written as

a (hierarchical) vector of a fairly small number of di-

mensions. An action then consists of a sequence of

such vectors. In this way, the model involves a consi-

derable reduction of dimensionality in comparison to

the original visual data.

This representation ﬁts well into the general for-

mat of conceptual spaces presented by (G

ardenfors,

2000) and (G

ardenfors, 2007). From that theory we

borrow the idea that a concept, in this case a sequence

of bodily positions, form a convex region in action

space, see (G

ardenfors, 2007), (G

ardenfors, 2000)

and (G

ardenfors and Warglien, 2012).

One may interpret here convexity as the assump-

tion that, given two actions in the region of an action

concept, any linear morph between those actions will

fall under the same concept. One way to support the

analogy between the thesis about properties and the

thesis about actions is to establish that action concepts

share a similar structure with object categories (He-

meren, 2008, p. 25). Indeed, there are strong reasons

to believe that actions exhibit many of the prototype

effects that (Rosch, 1975) presented for object catego-

ries. In a series of experiments, (Hemeren, 2008) sho-

wed that action categories show a similar hierarchical

structure and have similar typicality effects to object

concepts. He demonstrated a strong inverse correla-

tion between judgments of most typical actions and

reaction time in a word/action veriﬁcation task.

We take inspiration from these models in the sense

that we represent actions as sequences of vectors and

aim to categorize an action on the basis of its simila-

rities to other actions. In our model, similarity is mo-

delled as closeness in Self-Organizing Maps, SOMs,

(Kohonen, 1988).

In the current study we have used an approach

similar to the one presented in (Buonamente et al.,

2016) in which we have done experiments employing

hierarchical SOMs for action recognition using 2D

movies as input. In this study instead our system uses

sequences of sets of 3D joint positions extracted from

the depth images captured by a 3D camera similar to

a kinect sensor. By using 3D input data the system

will receive more information from the actor’s spacial

trajectories and thus be able to exploit this informa-

tion for classifying actions with a signiﬁcantly higher

performance as shown in the results. Moreover, in

this study we applied a pre-processing mechanism on

the 3D input data to make it independent of the ac-

tor’s orientation and distance to the camera while ex-

tracting the local interest points from the body of the

actor by applying an attentional mechanism. In this

way the system’s performance is improved.

One of our motivations for a SOM based approach

to action recognition is to achieve an ability to inter-

nally simulate (Hesslow, 2002) the likely continuation

of partly seen actions. This can be done by employing

Associative Self-Organizing Maps, A-SOMs, (Johns-

son et al., 2009), and have been investigated by using

2D movies as input in a number of studies (Johnsson

and Buonamente, 2012; Buonamente et al., 2013a;

Buonamente et al., 2013b; Buonamente et al., 2014;

Buonamente et al., 2015).

In the literature one ﬁnds several systems that can

categorize different sets of actions. Among them is

the one presented by (Li et al., 2010), which was eva-

luated by the MSR Action 3D dataset

. The same

dataset has also been employed by many other resear-

chers ((Xia et al., 2012);(Masood et al., 2013); (Orei-

fej et al., 2013); (Yang et al., 2012); (Wang et al.,

2012a); (Wang et al., 2012b); (Lo Presti et al., 2014)).

In this study, we have evaluated our action recogni-

tion system by actions from the the MSR Action 3D

dataset that are performed by the upper parts of the

body resulting in a more difﬁcult classiﬁcation task

for the system since the similarity between the acti-

ons (e.g, hand catch and high throw) increases. The

implementation of most of the code for the experi-

ments presented in this paper was done in C++ using

the neural modelling framework “Ikaros” (Balkenius

et al., 2010) and some in MatLab.

The rest of the paper is organized as follows: The

proposed architecture is presented in section 2. In

section 3, an experiment evaluating our action recog-

nition system is presented. Finally, section 4 conclu-

des the paper.

2 ARCHITECTURE

In this paper, we focus on the recognition of bodily

actions of one person. The architecture, Fig. 1, is

composed of three neural network layers. The ﬁrst

layer consists of a SOM that develops a compressed

and ordered representation of the preprocessed input

(i.e. parts of the scaled postures in an egocentric

framework). The second layer consists of a second

The repository is available at

http://research.microsoft.com/en-us/um/people/zliu/

ActionRecoRsrc/

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

584

SOM. It receives ordered vectors that are spatialized

representations of the activity patterns elicited in the

ﬁrst-layer SOM during actions. The ordered vector

representation of the sequence of unique activations

in the ﬁrst layer provides a mechanism that makes the

system time invariant. This is possible because si-

milar movements carried out at different performance

speed will elicit similar sequences of unique activa-

tions in the ﬁrst layer SOM. Thus the second layer

that receives these ordered vector representations will

learn to cluster complete actions. The third layer con-

sists of a custom made supervised neural network that

labels the activity in the second layer SOM with the

corresponding actions. The third layer could provide

some independence of the camera’s viewing angle,

but this is done more efﬁciently as a part of the pre-

processing, i.e. by scaling and transforming the sets

of joint positions into an egocentric framework before

they are received by the ﬁrst layer SOM.

To evaluate the architecture, we used input data

composed of sequences of sets of 3D joint positions

obtained by a depth camera similar to the Kinect sen-

sor.

In the following subsections, the different layers

of the architecture will be described.

Figure 1: The three layer action recognition architecture.

The ﬁrst layer consists of a SOM. Layer two consists of a

SOM, and layer 3 of a custom made supervised neural net-

work. The darker arrows in the SOM represent the activity

trace during the performance of an action.

Figure 2: Different sizes of body skeletons due to different

distances.

Figure 3: A sketch of a human body skeleton and the joints

received from the Kinect.

2.1 Preprocessing

Before entering the ﬁrst-layer SOM, the input data

is preprocessed. The distance and the capturing an-

gle between the depth camera and the subjects per-

forming the actions may differ. This can partially

be handled by the three neural network layers in the

architecture, but by re-scaling and transforming the

joint positions into an egocentric coordinate system

the performance of the architecture can be improved.

Thus, ﬁrst the joint positions in each posture frame

from the depth camera is re-scaled, Fig. 2, i.e. made

into a standard size. Then the coordinates of the joint

positions are transformed into a new and egocentric

coordinate system located close to joint number 7 of

the skeleton, Fig. 3.

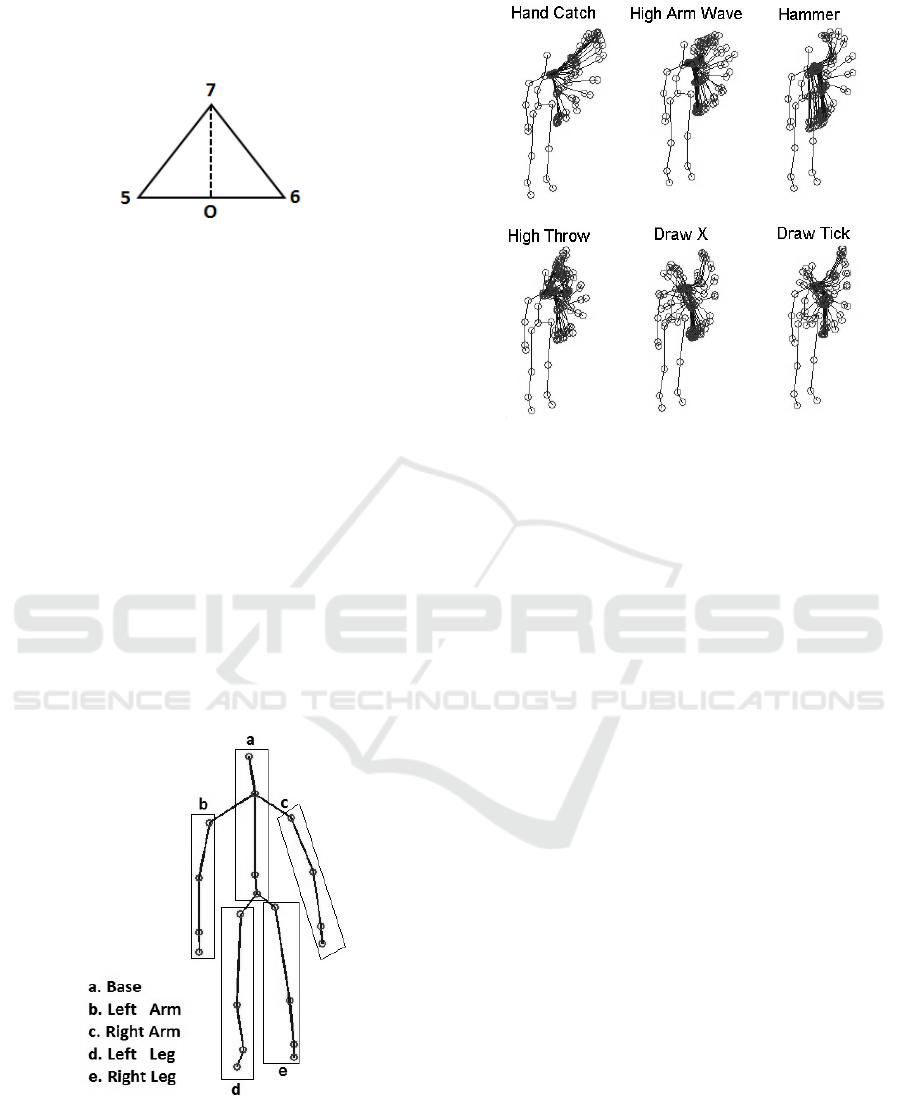
To calculate the axes of the egocentric coordinate

system, joints 5, 6 and 7 are used. As can be seen

in Fig. 4, these joints constitutes the vertices in a tri-

angle and the projection 0 of joint 7 on the side con-

necting joints 5 to 6 can be calculated. Then axes

originating in the point 0 along the line between the

point 0 and joint 7 and along the line between joints 5

and 6 can be selected together with an axis orthogo-

nal to the triangle for the new coordinate system and

Hierarchical Self-organizing Maps System for Action Classiﬁcation

585

a transformation matrix (Craig, 1989) can be calcu-

lated, which enables all the joints to be expressed in

egocentric coordinates.

Figure 4: The joints used to calculate the egocentric coordi-

nate system.

Due to limitations in visual ﬁeld, time, and pro-

cessing capacity, the entire input information cannot

always be processed in real time (Shariatpanahi and

Ahmadabadi, 2007). By using attention mechanisms,

performance can also be improved, e.g. in a driving

task (Gharaee et al., 2014) or in the case of action per-

ception in the current study. We applied an attentio-

nal mechanism to the part of the skeleton that exhibits

the largest movements, the inﬂuence of less relevant

parts of the input data can be decreased whereas the

inﬂuence of more relevant parts of input data in per-

forming an action are increased.

In our experiment, this was achieved by dividing

the skeletons into ﬁve basic parts, Fig. 5. The division

is based on how actions are performed in a human

body. The focus of attention is set to the moving part

which, in this dataset, is the left arm of the subjects.

This can be seen for one subject in Fig. 6.

Figure 5: The division of the skeleton into ﬁve basic parts.

2.2 The First and Second Layer SOMs

The ﬁrst two layers of the architecture consist of

SOMs. The SOMs are trained using unsupervised

Figure 6: A visualization of the series of posture frames for

six of the ten actions performed by the ﬁrst subject in the

ﬁrst event in the dataset we used. The attention is focused

on the left arm of the actor.

learning to produce dimensionality reduced and dis-

cretized representations of their input spaces. These

representations preserve the topology of their corre-

sponding input spaces, which means that nearby parts

of the network will respond to similar input patterns,

reminiscent of the cortical maps found in mammalian

brains. The SOMs will therefore generate a measure

of similarity which is the founding property of a con-

ceptual space (G

ardenfors, 2000). In other words, the

map generated by a SOM can be seen as a conceptual

space that is generated from the training data.

The topology-preserving property of SOMs is a

consequence of the use of a neighbourhood function

in the adaptation of the neuron responses, i.e. the

adaptation strength is a decreasing function of the dis-

tance of the most activated neuron in the network.

This also provides the SOM, and in the extension our

action recognition system, with the ability to genera-

lize learning to novel inputs. This is because similar

inputs elicit similar activities in the SOM. Thus simi-

lar sequences of postures will elicit similar sequences

of activity in the ﬁrst layer SOM, and these will in turn

elicit similar activations in the second layer SOM.

The SOM consists of an I ×J grid of neurons with

a ﬁxed number of neurons and a ﬁxed topology. Each

neuron n

i j

is associated with a weight vector w

i j

∈

with the same dimensionality as the input vectors.

All the elements of the weight vectors are initialized

by real numbers randomly selected from a uniform

distribution between 0 and 1.

At time t each neuron n

i j

receives the input vector

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

586

x(t) ∈ R

. The net input s

i j

(t) at time t is calculated

using the Euclidean metric:

i j

(t) = ||x(t) − w

i j

(t)|| (1)

The activity y

i j

(t) at time t is calculated by using

the exponential function:

i j

(t) = e

−s

i j

(t)

(2)

where σ is the exponential factor set to 10

and

0 ≤ i < I, 0 ≤ j < J, i, j ∈ N. The role of the exponen-

tial function is to normalize and increase the contrast

between highly activated and less activated areas.

The neuron n

with the strongest activation is se-

lected:

c = argmax

i j

(t) (3)

The weights w

i jk

are adapted by

i jk

(t + 1) = w

i jk

(t) + α(t)G

i jc

(t)[x

(t) − w

i jk

(t)]

(4)

where 0 ≤ α(t) ≤ 1 is the adaptation strength,

α(t) → 0 when t → ∞. The neighbourhood function

i jc

(t) = e

−

||r

−r

i j

2σ

(t)

is a Gaussian function with a ra-

dius that decreases with time, and r

∈ R

and r

i j

∈ R

are location vectors of neurons n

and n

i j

respectively.

2.3 Ordered Vector Representation

The activity elicited in the ﬁrst-layer SOM during the

sequence of preprocessed input corresponding to an

action is re-arranged into a spatial representation by a

process we call ordered vector representation before

entering the second-layer SOM. The ordered vector

representation process consists of building a vector

representation of the activity trajectory elicited in the

ﬁrst layer SOM during an action. Since sufﬁciently

similar postures are represented by the same neuron,

a particular movement carried out at various speeds

will elicit an activity trajectory along the same path

in the ﬁrst layer SOM. Since this path, which will be

similar for the same movement carried out at various

speeds by the performing agent (see Fig. 7), is what

is used to build the input vector for the second layer

SOM, time invariance is achieved.

The ordered vector representation in this experi-

ment works as follows. The length of the activity trace

of an action ∆

is calculated by

∆

N−1

∑

i=1

||P

i+1

− P

(5)

Figure 7: The activity trajectory in the ﬁrst layer SOM du-

ring an action carried out at two different speeds.

where N is the total number of centres of activity

for action sequence j and P

is the ith centre of activity

in the same action sequence.

Suitable lengths of segments to divide the activity

trace for action sequence j in the ﬁrst layer SOM are

calculated by

= ∆

Max

(6)

where N

Max

is the longest path in the ﬁrst layer

SOM elicited by the M actions in the training data.

Each activity trace in the ﬁrst layer SOM, elici-

ted by an action, is divided into d

segments, and the

coordinates of the borders of these segments in the

order they appear from the start to the end on the acti-

vity trace are composed into a vector used as input to

the second-layer SOM.

2.4 Output Layer

The output layer receives the activity of the second

layer SOM as input and consists of an I × J grid of a

ﬁxed number of neurons with a ﬁxed topology. Each

neuron n

i j

is associated with a weight vector w

i j

∈ R

All the elements of the weight vector are initialized

by real numbers randomly selected from a uniform

distribution between 0 and 1.

At time t each neuron n

i j

receives an input vector

x(t) ∈ R

The activity y

i j

(t) at time t in the neuron n

i j

calculated using the standard cosine metric:

i j

(t) =

x(t) · w

i j

(t)

||x(t)||||w

i j

(t)||

(7)

During the learning phase the weights w

i jl

are

adapted by

i jl

(t + 1) = w

i jl

(t) + βx

(t)[y

i j

(t) − d

i j

(t)] (8)

where β is the adaptation strength and d

i j

(t) is the

desired activity for the neuron n

i j

. The desired acti-

vity is the activity pattern in the output layer that cor-

responds to the unambiguous recognition of the on-

going action.

Hierarchical Self-organizing Maps System for Action Classiﬁcation

587

3 EXPERIMENT

We have evaluated our action recognition architec-

ture, Fig. 1, in an experiment in which we used joint

positions obtained by a depth camera, similar to a Ki-

nect sensor (Wan, 2015). In this experiment we tes-

ted the ability of the architecture to categorize acti-

ons based on sequences of sets of joint positions. The

employed dataset contains 276 samples with 10 dif-

ferent actions performed by 10 different subjects in 2

to 3 different events. Each action sample is composed

of a sequence of frames where each frame contains

20 joint positions, Fig. 3, expressed in 3D cartesian

coordinates. The actions are: 1. High Arm Wave, 2.

Horizontal Arm Wave, 3. Hammer, 4. Hand Catch, 5.

Forward Punch, 6. High Throw, 7. Draw X, 8. Draw

Tick, 9. Draw Circle, 10. Tennis Swing.

Figure 8: Examples of some of the activity traces in the ﬁrst

layer SOM elicited by the training data for the action for-

ward punch. As can be seen, the activity traces elicited by a

particular action in the ﬁrst layer SOM can be grouped into

subclasses of typical patterns. In the ﬁgure these subclasses

are indicated by numbers. The reason to why there are se-

veral typical patterns is that an action can be carried out in

multiple ways. For example, different subjects might have

different typical ways of carrying out the same action.

Figure 9: Examples of activity traces in the ﬁrst layer SOM

elicited by the test data for the action forward punch. The

numbers indicate what subclass the patterns belong to.

For the experiment, the dataset was split into a

training set containing 80% of the action instances

randomly selected from the original dataset and a test

set containing the remaining 20% of the instances.

Then the architecture was trained with randomly se-

lected instances from the training set in two phases,

the ﬁrst to train the ﬁrst-layer 30 × 30 neurons SOM,

and the second to train the second layer 35 × 35 neu-

rons SOM and the output layer containing 10 neurons.

Fig. 8 shows examples of activity traces in the ﬁrst

layer SOM elicited by the training data for the action

forward punch, and Fig. 9 shows examples of activity

traces in the ﬁrst layer SOM elicited by the test data

for the action forward punch.

The activity traces in the ﬁrst layer SOM are clus-

tered in the second layer SOM. Each action appears

to be mapped into two or three clusters. The result of

the supervised third layer neural network, which la-

bels the clusters in the second layer SOM, is shown

in Fig. 10. As can be seen, 83% of the test actions

are correctly categorized. Fig. 11 shows the categori-

zation result for each of the ten actions. As shown in

Fig. 11 four actions among the ten are classiﬁed com-

pletely correct with 100% accuracy. The performance

of the system decreases when the similarity between

different actions increases, and it occurs when these

actions are performed in a more similar way in most

of the sequences. This case can be seen in the actions

hand catch and high throw or the actions hammer and

forward punch which as a consequence receive lower

performance of classiﬁcation.

As shown in Fig. 10, we improved the action re-

cognition performance of hierarchical SOM system

from around 50% in the (Buonamente et al., 2016),

to 83% in this study. The result also shows a signiﬁ-

cant improvement to the state-of-the-art method in (Li

et al., 2010) from 74.7% recognition accuracy to 83%

. Our system outperforms several other studies inclu-

ding ((Xia et al., 2012);(Masood et al., 2013); (Yang

and Tian, 2012); (Lo Presti et al., 2014)). In our ap-

proach, we use a learning mechanism based on self

organizing neural networks both as a descriptor for

action recognition or unique feature extraction in the

ﬁrst layer and as a classiﬁer in the second layer. It re-

presents the ﬂexibility and robustness of SOM archi-

tecture which can be utilized to satisfy different go-

als. Moreover, by applying SOM in the ﬁrst layer we

could easily build a compact representation of postu-

res into a set of action patterns which help us to face

the problem of high dimensionality of the input data.

By applying ordered vector representation on the pat-

terns we invented a time invariant representation of

actions to deal with another condition in a real situa-

tion in which different actions are composed of diffe-

rent number of posture frames and could elicit diffe-

rent number of activated neurons in SOM.

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

588

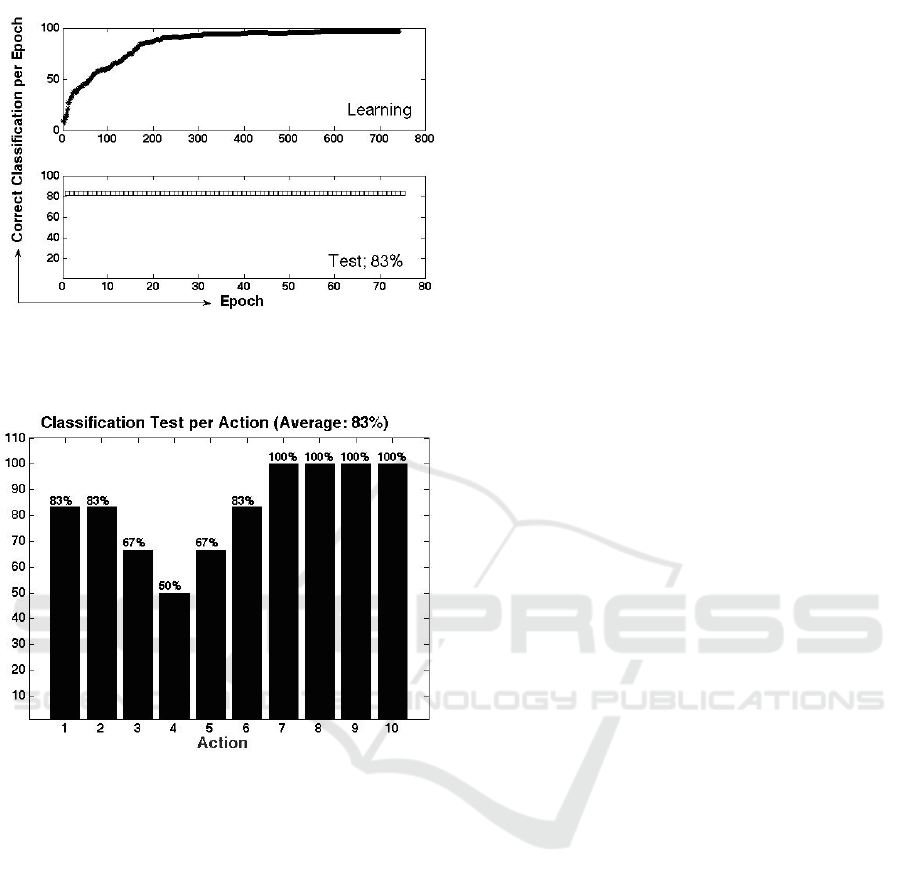
Figure 10: The result of the supervised third layer neural

network in the experiment using sequences of joint positi-

ons as input.

Figure 11: The categorization result for each of the ten acti-

ons in the experiment using sequences of joint positions as

input. The actions are: 1. High Arm Wave, 2. Horizontal

Arm Wave, 3. Hammer, 4. Hand Catch, 5. Forward Punch,

6. High Throw, 7. Draw X, 8. Draw Tick, 9. Draw Circle,

10. Tennis Swing.

4 CONCLUSIONS

In this article we have presented a three layered hier-

archical SOM based architecture for action recogni-

tion. The architecture is inspired by ﬁndings concer-

ning human action perception, in particular those of

(Johansson, 1973). The ﬁrst layer in the architecture

consists of a SOM. The second layer is also a SOM,

and the third layer is a custom made supervised neural

network.

The experiment tested the architecture’s ability to

categorize actions based on input sequences of 3D

joint positions. The primary goal of the architec-

ture is to categorize human actions. As in prototype

theory, the categorization in our system is based on

similarities of actions, and similarity is modelled in

terms of distances in SOMs. In this sense, our cate-

gorization model can be seen as an implementation

of the conceptual space model of actions presented

in (G

ardenfors, 2007) and (G

ardenfors and Warglien,

2012). We believe that attention plays an important

role in selecting what information is most relevant in

the process of action recognition, and our experiment

is a way of testing this hypothesis. The hypothesis

should, however, be tested with further datasets in or-

der to be better evaluated.

We have previously tested our action recognition

architecture when trained to recognize manner and re-

sult actions performed online in real time by a human

performer in front of the system’s Kinect sensor (Gha-

raee et al., 2016) (demo movies are available at the

web site http://magnusjohnsson.se/ar.html).

A model of action categorization based on pat-

terns of forces is presented in (G

ardenfors, 2007) and

ardenfors and Warglien, 2012). Extending the ar-

chitecture to also taking into account forces by consi-

dering the second order dynamics (corresponding to

sequences of joint accelerations) should improve the

performance even more. We will explore this in the

future. The data we have tested comes from human

actions. The generality of the architecture allows it to

be applied to other forms of motion involving animals

and artefacts. This is another area for future work.

REFERENCES

Balkenius, C., Mor

en, J., Johansson, B., and Johnsson, M.

(2010). Ikaros: Building cognitive models for robots.

Advanced Engineering Informatics, 24(1):40–48.

Buonamente, M., Dindo, H., and Johnsson, M. (2013a). Re-

cognizing actions with the associative self-organizing

map. In Information, Communication and Automation

Technologies (ICAT), 2013 XXIV International Sym-

posium on, pages 1–5. IEEE.

Buonamente, M., Dindo, H., and Johnsson, M. (2013b). Si-

mulating actions with the associative self-organizing

map. In Proceedings of the International Workshop

on Artiﬁcial Intelligence and Cognition (AIC 2013).

Buonamente, M., Dindo, H., and Johnsson, M. (2014).

Action recognition based on hierarchical self-

organizing maps. In Proceedings of the Internatio-

nal Workshop on Artiﬁcial Intelligence and Cognition

(AIC 2014).

Buonamente, M., Dindo, H., and Johnsson, M. (2015).

Discriminating and simulating actions with the as-

sociative self-organizing map. Connection Science,

27(2):118–136.

Buonamente, M., Dindo, H., and Johnsson, M. (2016).

Hierarchies of self-organizing maps for action recog-

nition. Cognitive Systems Research, 39:33–41.

Hierarchical Self-organizing Maps System for Action Classiﬁcation

589

Craig, J. J. (1989). Introduction to Robotics: Mechanics

and Control. Addison- Wesley, Longman Publishing

Co, Boston, MA, USA.

ardenfors, P. (2000). Conceptual Spaces: The Geometry

of Thought. Cambridge, Massachussetts: The MIT

Press.

ardenfors, P. (2007). Representing actions and functio-

nal properties in conceptual spaces. In Body, Lan-

guage and Mind, volume 1, pages 167–195. Mouton

de Gruyter, Berlin.

ardenfors, P. and Warglien, M. (2012). Using conceptual

spaces to model actions and events. Journal of Seman-

tics, 29:487–519.

Gharaee, Z., Fatehi, A., Mirian, M. S., and Ahmadabadi,

M. N. (2014). Attention control learning in the deci-

sion space using state estimation. International Jour-

nal of Systems Science (IJSS), pages 1–16. DOI:

10.1080/00207721.2014.945982.

Gharaee, Z., G

ardendors, P., and Johnsson, M. (2016).

Action recognition online with hierarchical self-

organizing maps. In Proceedings of the International

Workshop on Human Tracking and Behaviour Analy-

sis (HTBA2016).

Hemeren, P. E. (2008). Mind in Action. PhD thesis, Lund

University Cognitive Science. Lund University Cog-

nitive Studies 140.

Hesslow, G. (2002). Conscious thought as simulation of be-

haviour and perception. Trends in Cognitive Sciences,

6:242–247.

Johansson, G. (1973). Visual perception of biological mo-

tion and a model for its analysis. Perception & Psy-

chophysics, 14(2):201–211.

Johnsson, M., Balkenius, C., and Hesslow, G. (2009). Asso-

ciative self-organizing map. In Proceedings of IJCCI,

pages 363–370.

Johnsson, M. and Buonamente, M. (2012). Internal simula-

tion of an agent’s intentions. In Proceedings of the Bi-

ologically Inspired Cognitive Architectures 2012, pa-

ges 175–176.

Kohonen, T. (1988). Self-Organization and Associative Me-

mory. Springer Verlag.

Li, W., Zhang, Z., and Liu, Z. (2010). Action recognition

based on a bag of 3d points. In Computer Vision and

Pattern Recognition Workshops (CVPRW), 2010 IEEE

Computer Society Conference on, IEEE, pages 9–14.

Lo Presti, L., La Cascia, M., Sclaroff, S., and Camps, O.

(2014). Gesture modeling by hanklet-based hidden

markov model. In Asian Conference on Computer Vi-

sion (ACCV).

Marr, D. and Nishihara, K. H. (1978). Representation

and recognition of the spatial organization of three-

dimensional shapes. Proceedings of the Royal Society

in London, B, 200:269–294.

Marr, D. and Vaina, L. (1982). Representation and recogni-

tion of the movements of shapes. Proceedings of the

Royal Society in London, B, 214:501–524.

Masood, S., Ellis, C., Tappen, M., LaViola, J., and Sukt-

hankar, R. (2013). Exploring the trade-off between

accuracy and observational latency in action recogni-

tion. International Journal of Computer Vision, 101.

Oreifej, O., Liu, Z., and Redmond, W. (2013). Hon4d: His-

togram of oriented 4d normals for activity recognition

from depth sequences. Computer Vision and Pattern

Recognition.

Rosch, E. (1975). Cognitive representations of semantic

categories. Journal of Experimental Psychology: Ge-

neral, 104:192–233.

Runesson, S. (1994). Perception of biological motion: The

ksd-principle and the implications of a distal versus

proximal approach. In Perceiving Events and Objects,

pages 383–405. Hillsdale, NJ.

Runesson, S. and Frykholm, G. (1983). Kinematic speciﬁ-

cation of dynamics as an informational basis for per-

son and action perception. expectation, gender recog-

nition, and deceptive intention. Journal of Experimen-

tal Psychology: General, 112:585–615.

Shariatpanahi, H. F. and Ahmadabadi, M. N. (2007). Bio-

logically inspired framework for learning and abstract

representation of attention control. Attention in cogni-

tive systems, theories and systems from an interdisci-

plinary viewpoint, 4840:307 – 324.

Vaina, L. (1983). From shapes and movements to objects

and actions. Synthese, 54:3–36.

Wan, Y. W. (accessed 2015). Msr action recognition data-

sets and codes.

Wang, J., Liu, Z., Chorowski, J., Chen, Z., and Wu, Y.

(2012a). Robust 3d action recognition with random

occupancy patterns. In Computer Vision-ECCV, pa-

ges 872–885.

Wang, J., Liu, Z., Wu, Y., and Yuan, J. (2012b). Mining

actionlet ensemble for action recognition with depth

cameras. In Computer Vision and Pattern Recognition

(CVPR) 2012 IEEE Conference on, pages 1290–1297.

Xia, L., Chen, C.-C., and Aggarwal, J. (2012). View in-

variant human action recognition using histograms of

3d joints. In IEEE Computer Society Conference on

Computer Vision and Pattern Recognition Workshops

(CVPRW), pages 20–27.

Yang, X. and Tian, Y. (2012). Eigenjoints-based action re-

cognition using nave-bayes-nearest-neighbor. In IEEE

Computer Society Conference on Computer Vision

and Pattern Recognition Workshops (CVPRW), pages

14–19. DOI: 10.1109/CVPRW.2012.6239232.

Yang, X., Zhang, C., and Tian, Y. (2012). Recognizing

actions using depth motion maps-based histograms of

oriented gradients. In Proceedings of the 20th ACM

international conference on Multimedia, ACM, pages

1057–1060.

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

590