Mathematical Modeling Approaches to Solve the Line Balancing

Problem

Shady Salama

, Alyaa Abdelhalim

and Amr B. Eltawil

Industrial Engineering and Systems Management, Egypt-Japan University of Science and Technology (E-JUST),

New Borg Elarab City, Alexandria 21934, Egypt

Production Engineering Department, Industrial Engineering Division, Alexandria University 21544, Alexandria, Egypt

Keywords: Framework, Review, Survey, Assembly Line, Line Balancing, Mathematical Model.

Abstract: The assembly line balancing problem belongs to the class of NP-hard combinatorial optimisation problem.

For several decades’ line balancing took attention of researchers who are trying to find the solutions for real

world applications. Although tremendous works have been done, the gap still exists between the research and

the real problems. This paper provides analysis of about 50 papers that used mathematical modeling in solving

line balancing problems. Thereafter, a framework is proposed for future work.

1 INTRODUCTION

Assembly lines consist of a number of workstations

that are arranged through a material handling

equipment where tasks are assigned, and the

workpieces are moving from one station to another

until the final product is produced. The workstations

are equipped with all required machines and skilled

operators to perform specific tasks without violating

cycle time, which represents the time between two

consecutive units produced from the assembly line

based on specific production plan. From the first day

that Henry Ford introduced assembly line for a mass

production in this company, the researchers are

seeking for the optimal way to assign all tasks to

workstations that is called Assembly Line Balancing

Problem (ALBP) without violating assignment

constraints (such as precedence constraints). (Dolgui

& Battaı 2013). For instance, when we increase the

balance of workload among workstations that will

lead to increase productivity by removing bottlenecks

and reducing idle time. Each task has a particular time

to perform called processing time and the workstation

time is the sum of all processing times for all assigned

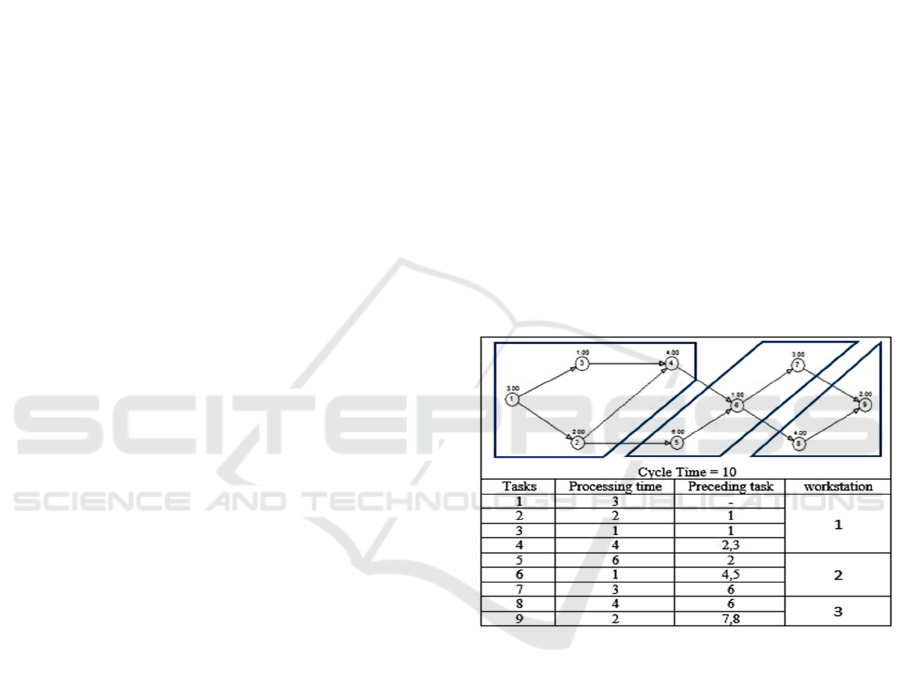
tasks. Figure (1): An illustrative example for

assembly line balancing problem.

Salveson made the first mathematical model

formulation for assembly line balancing problem

(Salveson 1955), and from this day the ALBP has

become an attractive topic for more research.

Figure 1: Assembly line balancing problem.

The ALBP is an NP-hard combinatorial optimisation

problem (Gutjahr & Nemhauser 1964) and the widely

used objective functions are to minimise the number

of workstations with fixed cycle time (SALBP-1),

minimise the cycle time with fixed number of

workstations (SALBP-2) and maximize line

efficiency (SALBP-E). The ALBP can be classified

based on Industrial environment (Machining,

Assembly, Disassembly). Another classification

considers the number of product models in the line

(Single model, Mixed model, Multi-model). The line

layout is also a different theme of classification

(Basic straight line, Straight lines with multiple

workplaces, U-shaped lines, Lines with the circular

transfer, Asymmetric lines). Last but not least the

nature of task times (Deterministic – Stochastic)

Salama S., Abdelhalim A. and B. Eltawil A.

Mathematical Modeling Approaches to Solve the Line Balancing Problem.

DOI: 10.5220/0006199404010408

In Proceedings of the 6th International Conference on Operations Research and Enterprise Systems (ICORES 2017), pages 401-408

ISBN: 978-989-758-218-9

401

(Dolgui & Battaı 2013) (Sivasankaran &

Shahabudeen 2014a).

In the past, the single-model lines were commonly

used for producing large and homogeneous products,

so it was a daunting task to provide any customized

products. Nowadays, due to the increasing demand

and competition for creating customised products, a

large number of traditional lines are replaced by

mixed-model lines to keep up with current market

trends (Vilarinho & Simaria 2002) (Dong et al. 2014).

On the other hand, the multi-model lines produce

batches of different products that requires setup time

to Initialize the machines between different batches.

The difference between single model, mixed-model

and multi-model are illustrated in figure (2).

Figure 2: Different line configurations based on a number

of models.

Additionally, there are many assumptions used to

reduce the level of complexity of the ALBP such as

deterministic processing time, fixed cycle time, etc.

Consequently, the challenges facing researchers is to

reduce these assumptions as possible to simulate the

real-life problems. The U-shaped lines have been

introduced for the first time by the Japanese Factories

where high experience workers were hired to increase

variability and quality of products. However, the

balancing for U-lines is more complicated compared

to traditional lines. Nevertheless, it can provide many

advantages such as; less work-in-process, less worker

movement, increase line efficiency and increase

flexibility in production rate. The straight line and U-

shaped line are illustrated in figure (3).

Figure 3: Different line layouts.

The ALBP has been intensively discussed in the

literature. As a result, many recent reviews have been

published (Boysen et al. 2007), (Battaïa & Dolgui

2013) and (Sivasankaran & Shahabudeen 2014b). In

this paper, we focus on analysing published articles

that formulated mathematical models to solve

different configurations of assembly line balancing

problems. Furthermore, a framework with

improvements in the model formulations is proposed

to tackle ALBP.

The remainder of this paper is organised as follows:

The second section presents the classification of

assembly line balancing problems as well as

reviewing and analysing the articles published in each

category. The third section is dedicated to providing

further research areas and concludes remarks of this

study. The last section explains the proposed

framework.

2 REVIEW ON MATHEMATICAL

MODELS

This section represents a taxonomy of the

mathematical models used in describing a wide range

of different assembly lines configurations:

Figure 4: Assembly Lines Configurations.

2.1 Single-Model and Straight Type

Assembly Lines with Deterministic

Processing Times

The first formulation for SALBP by (Bowman 1960)

used linear programming by using two different linear

program forms. Also, Some modifications were

introduced by (White 1961). Additionally,

(Thangavelu & Shetty 1971) developed an improved

0-1 integer programming version of Bowman-White

model by simplifying certain steps in (Geoffrion

1967) 0-1 integer programming algorithm. Moreover,

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems

402

(Patterson & Albracht 1975) formulated an improved

0-1 integer-programming model draws heavily on the

work done by (Bowman 1960) taking into

consideration to determine feasibility and reduce

computational time by reducing the required number

of variables. Furthermore, (Talbot & Patterson 1984)

presented an integer programming formulation for

defining all feasible assignments for each task to a

workstation with upper and lower bounds. Thereafter,

they solved it by using a modified Balas algorithm

(Balas et al. 1965). In (Vitria 2004) the authors

analysed different ways for modelling precedence

and incompatibility constraints in ALBP to obtain the

best modelling formulation and solving procedure.

(Pastor & Ferrer 2009) used the two efficient models

of (Vitria 2004) for both SALBP-1 and SALBP-2

besides introducing additional constraints based on

the upper bound of the number of workstations or the

cycle time that belongs to the branch and bound

technique. The research carried by (Özcan & Toklu

2009) presented mathematical model used a goal

programming and a fuzzy goal programming for a

two-sided assembly line to minimise the number of

mated workstations at first and then minimise the

number of the workstations as a secondary goal.

(Esmaeilbeigi et al. 2015) presented the mixed integer

programming for maximizing the line efficiency

(SALBP-E) as well as providing secondary objectives

(SALPB-1, SALBP-2, minimizing smoothness

index) for the problem. Their proposed model is

considered as the first MILP model for getting an

exact solution directly in SALBP-E.

2.2 Single-Model and U-type Assembly

Lines with Deterministic Processing

Times

(Miltenburg & Wijngaard 1994) proposed the first

model for the simple U-line balancing and used a

dynamic programming procedure for obtaining the

optimal solution. In (Urban 1998) the authors

formulated an integer programming model for

optimally solving UALBP-1. (Gökçen & Aǧpak

2006) introduced the first multi-criteria for decision-

making technique for U-shaped lines. They

formulated a mathematical model using a goal

programming for a UALBP based on the IP model

proposed by (Urban 1998). Furthermore, their model

was used by (Toklu & özcan 2008) as a base for

formulating the first fuzzy goal programming model

with multi-objectives aiming at optimising the

conflicting goals as well as helping the decision

maker to determine goals in the fuzzy environment.

(Kara et al. 2009) proposed binary fuzzy goal

programming models for each of the traditional and

U-shaped assembly lines. They extended the linear

programming model of (Urban 1998) in developing

their BFGP for balancing U-lines. The improved

version of the previous model in (Urban 1998)

addressed in the work of (Fattahi et al. 2014), They

formulated an integer programming model for

UALBP-1 that was able to reduce the binary variables

to half by increasing the efficiency of LP relaxation.

2.3 Single-Model and Straight Type

Assembly Lines with Stochastic

Processing Times

The processing times in deterministic assembly line

(AL) are assumed to take constant values.

Nonetheless in real life, it takes values based on

probability distribution resulting from machine

breakdowns, the difference in skills between

operators, complex tasks, environment, and so forth.

(Moodie 1964) The first research work that addressed

the stochastic nature to the ALBP. (Carraway 1989)

proposed two dynamic programming approaches for

minimising the number of workstations. The task

times assumed to be independent and normally

distributed. (Aǧpak & Gökçen 2007) formulated a

chance-constrained 0-1 integer programming model

for balancing stochastic traditional assembly line.

Additionally, a goal programming has been proposed

for increasing the reliability of the assembly line.

(Özcan 2010) presented the first study of two-sided

assembly lines with variation in task time and

formulated a chance-constrained, piecewise-linear

and mixed integer programming for solving this

problem. In two-sided assembly lines, the workers are

assigned in both sides of the production line (left and

right) and used in parallel. (Hamta et al. 2013) They

formulated a mixed integer non-linear programming

model. Their model considered multi-objectives to

simultaneously minimise the cycle time, equipment

cost and the smoothness index. Finally, they

developed a solution method based on the

combination of particle swarm optimisation and

variable neighbourhood search to solve the problem

in reasonable time. (Hazır & Dolgui 2013) proposed

robust optimisation models for SALBP-2 considering

uncertainty through operations time and they

developed an exact decomposition algorithm. They

developed two mathematical models in addition to

decomposition based algorithm to find the optimal

solution for large problems. (Ritt et al. 2016) did not

consider the variability in task times rather, they

considered it indirectly by representing the variability

of the workforce due to absenteeism. They proposed

Mathematical Modeling Approaches to Solve the Line Balancing Problem

403

a two-stage mixed integer models to minimise the

cycle time. Furthermore, they presented a local search

heuristic procedure based on simulated annealing for

solving large instances.

2.4 Single-Model and U-type Assembly

Lines with Stochastic Processing

Times

The research done by (Nakade et al. 1997) is

considered the first work in balancing U-lines taking

stochastic nature results from manual work into

consideration. They proposed approximate

formulation for the upper and lower bound of the

expected cycle time. (Guerriero & Miltenburg 2003)

They used dynamic programming in balancing U-

lines and the recursive algorithm for determining the

optimal solution. (Urban & Chiang 2006) formulated

a chance constraint programming model for U-line

balancing problem, then they used piecewise linear,

integer programming for solving the model optimally.

The further investigations are to develop an efficient

heuristic for solving large problems. (Aǧpak &

Gökçen 2007) formulated 0-1 integer programming

model by using a chance-constrained procedure for

balancing stochastic traditional and U-shaped lines.

They used the model of (Urban 1998) as the base for

their work; also they presented two linear

transformations (pure and approximate) to enable the

model to solve large problems. Lastly, they

introduced goal programming for smoothing the

workload among workstations. Most of the researches

done in the U-type assembly line problems focused

on deterministic processing times comparing to the

stochastic time.

2.5 Multi or Mixed Model and Straight

Type Assembly Lines with

Deterministic Processing Times

(Gökċen & Erel 1998) introduced a binary integer

programming model for the Mixed-Model Assembly

Line (MMAL). Flexibility ratio has also been

presented that is used to compute the computational

and storage requirements for solving the problem by

measuring the number of possible sequences for the

precedence diagram. (Vilarinho & Simaria 2002)

developed a mathematical model for balancing

mixed-model assembly lines that gives the decision

maker the ability to define the limit number of parallel

workstations and zoning constraints. (Simaria &

Vilarinho 2009) formulated a mathematical model for

balancing two-sided mixed-model assembly lines.

Moreover, they proposed an ant colony optimisation

algorithm for optimally solving the model. (Fattahi &

Salehi 2009) developed a mixed-integer linear

programming model to minimise the total utility and

idle costs. They tried to solve the problem using

branch and bound method, but it was very time-

consuming so, they used simulated annealing to

resolve this issue. (Mosadegh et al. 2012) formulated

a mixed-integer linear programming model to provide

the exact solution of both balancing and sequencing

problems simultaneously for mixed model assembly

lines. For solving the problem, they developed a

simulated annealing algorithm as well as Taguchi

method for calibrating the algorithm parameters.

(Kucukkoc & Zhang 2014) proposed a mixed integer

programming model to investigate both sequencing

and balancing problems simultaneously in mixed

model parallel two-sided assembly lines. The

objectives of their model were to minimise the

number of workstations, reduce the length of

production lines and maximise workload smoothness.

Furthermore, they presented an agent based ant

colony optimisation algorithm for solving the

problem. (Zhao et al. 2016) formulated a

mathematical model for MMAL focused on the effect

of mental workload and the complexity of the

operations on balancing the line. They concluded that,

the mental workload considered as an essential rule

when minimising cycle time also, the mental

workload was influenced by the level of experience

of the operator.

2.6 Multi or Mixed Model and U-type

Assembly Lines with Deterministic

Processing Times

(Sparling & Miltenburg 1998) are considered the

pioneers in studying MMUL. They presented a model

for U-line balancing problem for assigning a set of

tasks in a minimum number of workstations.

Furthermore, they presented an approximation

algorithm to solve large size problems. (Miltenburg

2002) formulated a mixed, zero-one integer, non-

linear programming model then used a genetic

algorithm for searching for a good solution in a

reasonable computational time. (Kara 2008)

formulated a non-linear mathematical model to solve

balancing and sequencing problem simultaneously

for MMUL. The objective of their model was to

minimise deviation of workloads among

workstations. Due to the complexity so, they

proposed simulated annealing algorithm to solve

large-scale problems. (Kara & Tekin 2009) proposed

a mixed integer linear programming model for

optimally balancing mixed-model U-lines. The goal

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems

404

of their model was to minimise the number of

workstations for a given cycle time. (Kazemi et al.

2011) introduced an integer linear programming

model. The objective of their presented model was to

minimise the number of stations. Furthermore, they

developed a two-stage genetic algorithm approach for

the large-scale problem. (Rabbani et al. 2012)

formulated a multi-objective mixed integer linear

programming model for two-sided Als. Finally, they

introduced a heuristic based on the genetic algorithm

for solving this problem. (Rabbani et al. 2016)

formulated a mixed-integer linear programming

model for robotic mixed-model assembly lines. The

model aimed to minimise the cycle time, robot

purchasing and setup costs.

2.7 Multi or Mixed Model and Straight

Type Assembly Lines with

Stochastic Processing Times

(Paternina-Arboleda & Montoya-Torres 2006)

proposed a mathematical model for balancing and

sequencing MMAL. The model included multi-

objective function aimed to minimise the number of

workstations, increase throughput and find the

appropriate sequence of models to remove

bottlenecks through an assembly line. (Al-e-hashem

2009) formulated a mixed integer robust optimization

model to minimize the total costs that include the cost

of workstations and duplicated tasks.

2.8 Multi or Mixed Model and U-type

Assembly Lines with Stochastic

Processing Times

(Agrawal & Tiwari 2008) proposed a model for

balancing and sequencing mixed-model U-

disassembly lines where the processing times are

different depending on the structure of the products

and the human factor. The objective function was to

minimise the variation of workload and maximise the

line efficiency. They solved this problem by using

collaborative Ant Colony Optimization, and they

tested the results on benchmarks using a design of

experiment and analysis of variance to determine

which factor is significant in the objective. (Dong et

al. 2014) formulated a 0-1 stochastic programming

model to solve balancing and sequencing problem

simultaneously for MMUL with independently and

normally distributed task times. They proposed a

simulated annealing algorithm to resolve the issue

into both situations (Deterministic and stochastic).

3 DISCUSSIONS AND FUTURE

RESEARCH

Although researchers have contributed in various

configurations and application of assembly line

balancing, the gap still exists between research and

real life problems. To the best of our knowledge, only

two papers have been published using a mathematical

model in each branch of MMAL with stochastic

processing times, so the further research may be

carried out in developing multi-objective

mathematical models including more constraints such

as zoning and distance constraints. It is clear that the

majority of authors neglected the use of statistical

methods in comparing the results to clarify the

significant improvement between their proposed

methods and previous research in the literature. Also,

statistical studies are useful in determining the effect

of each variable on the objective function and

calibrating algorithm parameters. It is clear that more

studies are applied in SLs comparing to U-lines.

Thus, further work can be done in a different

configuration of U-lines such as two-sided, multi

lines, disassembly and rebalancing U-lines. Most of

the articles neglect the human factors (skills,

experience, learning effect) and working environment

that directly affects the operator’s performance and

productivity. Consequently, it is very crucial to

enhance existing mathematical models to consider

these aspects in further work. Further work may be

directed to consider other objective functions such as

maximise the line efficiency, minimising smoothness

index and minimise total costs (equipment-

duplication-setup). Enhance current meta-heuristics

such as simulated annealing algorithm, genetic

algorithm, practical swarm optimisation, etc. That

will help in solving large instances of ALBP in less

computational time and provide better results

especially in the case of mixed-models. In MMAL it

is important to handle both ALB and ALS problems

jointly. Formulate a mathematical model for multi-

optimization problems such as the incorporation of

line design and balancing problems.

4 THE PROPOSED SOLUTION

FRAMEWORK

The objective of the ALBP-2 is to minimise the cycle

time as a result of minimising the workload of the

bottleneck workstation. Nevertheless, it is also

important to consider the second heavily loaded

workstation, the third one and so on, to improve the

Mathematical Modeling Approaches to Solve the Line Balancing Problem

405

reliability and the quality of the balance through the

line. The proposed solution approach is to modify the

model formulated by (Kucukkoc et al. 2015) to

include the objective of increasing balance between

and within workstations to ensure that all

workstations through the line have an equal amount

of work also all the workers within the workstations

have the same workload. Moreover, the zoning

constraints will be added to the model to increase the

ability to solve real-life problems with fewer

assumptions as possible. The proposed mathematical

model will be coded using LINGO optimisation

modelling software to solve small-sized problems.

The solution from the solver will be utilised as an

input to a DES model to test the robustness of

solutions when introducing the real-world variability

such as stochastic times, breakdowns, etc. Then a

comparison will be made between the initial solution

and the proposed solution from the model using the

performance indicators of the simulation. Finally,

statistical analysis will be implemented to evaluate

the significant improvement in the assembly line.

5 CONCLUSIONS

The research on ALBP is crucial because it affects the

productivity and the competitiveness of the company.

This paper surveyed studies of ALBP within the area

of mathematical modeling that were published in the

eight branches of ALBP. The goal of this analysis was

to discover the research gaps in line balancing

problems. Furthermore, a proposed framework is

introduced to enhance the solution of the MMAL by

modifying the objective function and adding more

constraints that represent realistic world problems.

ACKNOWLEDGEMENTS

This research project is sponsored by the Mitsubishi

Corporation Graduate Scholarship to the Egypt-Japan

University of Science and Technology (E-JUST) and

support of the Japanese International Cooperation

Agency (JICA).

REFERENCES

Aǧpak, K. & Gökçen, H., 2007. A chance-constrained

approach to stochastic line balancing problem.

European Journal of Operational Research, 180(3),

pp.1098–1115.

Agrawal, S. & Tiwari, M.K., 2008. A collaborative ant

colony algorithm to stochastic mixed-model U-shaped

disassembly line balancing and sequencing problem.

International Journal of Production Research, 46(6),

pp.1405–1429.

Al-e-hashem, S.M., 2009. Mixed model assembly line

balancing problem under uncertainty. , 2009. CIE 2009.

…. Available at: http://ieeexplore.ieee.org/xpls/

abs_all.jsp?arnumber=5223925 [Accessed September

27, 2016].

Balas, E., Glover, F. & Zionts, S., 1965. An Additive

Algorithm for Solving Linear Programs with Zero-One

Variables Author(s): Operations Research, 13(4),

pp.517–549.

Battaïa, O. & Dolgui, A., 2013. A taxonomy of line

balancing problems and their solutionapproaches.

International Journal of Production Economics,

142(2), pp.259–277.

Bowman, E.H., 1960. Assembly-Line Balancing by Linear

Programming. Operations Research, 8(3), pp.385–389.

Boysen, N., Fliedner, M. & Scholl, A., 2007. A

classification of assembly line balancing problems.

European Journal of Operational Research, 183(2),

pp.674–693.

Carraway, R.L., 1989. A Dynamic Programming Approach

to Stochastic Assembly Line Balancing. Management

Science, 35(4), pp.459–471. Available at:

http://pubsonline.informs.org/doi/abs/10.1287/mnsc.3

5.4.459 [Accessed September 24, 2016].

Dolgui, A. & Battaı, O., 2013. Int . J . Production

Economics A taxonomy of line balancing problems and

their solution approaches. , 142, pp.259–277.

Dong, J. et al., 2014. Balancing and sequencing of

stochastic mixed-model assembly U-lines to minimise

the expectation of work overload time. International

Journal of Production Research, 52(24), pp.7529–

7548. Available at: http://www.tandfonline.com/

doi/abs/10.1080/00207543.2014.944280 [Accessed

September 28, 2016].

Esmaeilbeigi, R., Naderi, B. & Charkhgard, P., 2015. The

type E simple assembly line balancing problem: A

mixed integer linear programming formulation.

Computers & Operations Research, 64, pp.168–177.

Available at: http://linkinghub.elsevier.com/retrieve

/pii/S0305054815001446.

Fattahi, A. et al., 2014. A novel integer programming

formulation with logic cuts for the U-shaped assembly

line balancing problem. International Journal of

Production Research, 52(5), pp.1318–1333. Available

at: http://www.tandfonline.com/doi/abs/10.1080/

00207543.2013.832489 [Accessed September 21,

2016].

Fattahi, P. & Salehi, M., 2009. Sequencing the mixed-

model assembly line to minimize the total utility and

idle costs with variable launching interval. The

International Journal of Advanced Manufacturing.

Available at: http://link.springer.com/article/

10.1007/s00170-009-2020-0 [Accessed September 25,

2016].

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems

406

Geoffrion, A.M., 1967. Integer Programming by Implicit

Enumeration and Balas’ Method. SIAM Review, 9(2),

pp.178–190. Available at: http://epubs.siam.org/doi/

abs/10.1137/1009031 [Accessed October 16, 2016].

Gökçen, H. & Aǧpak, K., 2006. A goal programming

approach to simple U-line balancing problem.

European Journal of Operational Research, 171(2),

pp.577–585.

Gökċen, H. & Erel, E., 1998. Binary Integer Formulation

for Mixed-Model Assembly Line Balancing Problem.

Computers & Industrial Engineering, 34(2), pp.451–

461. Available at: http://www.sciencedirect.com/

science/article/pii/S0360835297001423.

Guerriero, F. & Miltenburg, J., 2003. The stochastic U-line

balancing problem. Naval Research Logistics, 50(1),

pp.31–57. Available at: http://doi.wiley.com/10.1002

/nav.10043 [Accessed September 22, 2016].

Gutjahr, A.L. & Nemhauser, G.L., 1964. An Algorithm for

the Line Balancing Problem. , (August 2015).

Hamta, N. et al., 2013. A hybrid PSO algorithm for a multi-

objective assembly line balancing problem with

flexible operation times, sequence-dependent setup

times and learning effect. International Journal of

Production Economics, 141(1), pp.99–111.

Hazır, Ö. & Dolgui, A., 2013. Assembly line balancing

under uncertainty: Robust optimization models and

exact solution method. Computers & Industrial

Engineering, 65(2), pp.261–267. Available at:

http://www.sciencedirect.com/science/article/pii/S036

0835213000934.

Kara, Y., 2008. Line balancing and model sequencing to

reduce work overload in mixed-model U-line

production environments. Engineering Optimization,

40(7), pp.669–684. Available at:

http://www.tandfonline.com/doi/abs/10.1080/0305215

0801982509 [Accessed September 26, 2016].

Kara, Y., Paksoy, T. & Chang, C.-T., 2009. Binary fuzzy

goal programming approach to single model straight

and U-shaped assembly line balancing. European

Journal of Operational Research, 195(2), pp.335–347.

Kara, Y. & Tekin, M., 2009. A mixed integer linear

programming formulation for optimal balancing of

mixed-model U-lines. International Journal of

Production Research, 47(15), pp.4201–4233. Available

at: http://www.tandfonline.com/doi/abs/10.1080/

00207540801905486 [Accessed September 26, 2016].

Kazemi, S.M. et al., 2011. A novel two-stage genetic

algorithm for a mixed-model U-line balancing problem

with duplicated tasks. The International Journal of

Advanced Manufacturing Technology, 55(9–12),

pp.1111–1122. Available at: http://link.springer.com/

10.1007/s00170-010-3120-6 [Accessed September 26,

2016].

Kucukkoc, I. et al., 2015. A mathematical model and

artificial bee colony algorithm for the lexicographic

bottleneck mixed-model assembly line balancing

problem. Journal of Intelligent Manufacturing, pp.1–

13. Available at: http://link.springer.com/10.1007/

s10845-015-1150-5 [Accessed October 24, 2016].

Kucukkoc, I. & Zhang, D.Z., 2014. Mathematical model

and agent based solution approach for the simultaneous

balancing and sequencing of mixed-model parallel two-

sided assembly lines. International Journal of

Production Economics, 158, pp.314–333.

Miltenburg, G.J. & Wijngaard, J., 1994. The U-line Line

Balancing Problem. Management Science, 40(10),

pp.1378–1388. Available at:

http://pubsonline.informs.org/doi/abs/10.1287/mnsc.4

0.10.1378 [Accessed September 21, 2016].

Miltenburg, J., 2002. Balancing and Scheduling Mixed-

Model U-Shaped Production Lines. International

Journal of Flexible Manufacturing Systems, 14(2),

pp.119–151. Available at: http://link.springer.com/

10.1023/A:1014434117888 [Accessed September 26,

2016].

Moodie, C., 1964. A Heuristic Method of Assembly Line

Balancing for Assumptions of Constantor Variable

Work Element Times. Available at:

http://docs.lib.purdue.edu/dissertations/AAI6408691/

[Accessed September 23, 2016].

Mosadegh, H., Zandieh, M. & Ghomi, S.M.T.F., 2012.

Simultaneous solving of balancing and sequencing

problems with station-dependent assembly times for

mixed-model assembly lines. Applied Soft Computing,

12(4), pp.1359–1370.

Nakade, K., Ohno, K. & George Shanthikumar, J., 1997.

Bounds and approximations for cycle times of a U-

shaped production line. Operations Research Letters,

21(4), pp.191–200.

Özcan, U., 2010. Balancing stochastic two-sided assembly

lines: A chance-constrained, piecewise-linear, mixed

integer program and a simulated annealing algorithm.

European Journal of Operational Research, 205(1),

pp.81–97.

Özcan, U. & Toklu, B., 2009. Multiple-criteria decision-

making in two-sided assembly line balancing: A goal

programming and a fuzzy goal programming models.

Computers and Operations Research, 36(6), pp.1955–

1965.

Pastor, R. & Ferrer, L., 2009. An improved mathematical

program to solve the simple assembly line balancing

problem. International Journal of Production

Research, 47(11), pp.2943–2959.

Paternina-Arboleda, C. & Montoya-Torres, J.,

Mathematical formulation for a mixed-model assembly

line balancing problem with stochastic processing

times. laccei.org. Available at: http://www.laccei.org/

LACCEI2006-PuertoRico/Copyright

Pending/IT240_PaterninaArboleda.pdf [Accessed

September 27, 2016].

Patterson, J.H. & Albracht, J.J., 1975. Technical Note--

Assembly-Line Balancing: Zero-One Programming

with Fibonacci Search. Operations Research, 23(1),

pp.166–172.

Rabbani, M., Moghaddam, M. & Manavizadeh, N., 2012.

Balancing of mixed-Model two-Sided assembly lines

with multiple u-Shaped layout. International Journal of

Advanced Manufacturing Technology, 59(9–12),

pp.1191–1210.

Mathematical Modeling Approaches to Solve the Line Balancing Problem

407

Rabbani, M., Mousavi, Z. & Farrokhi-Asl, H., 2016. Multi-

objective metaheuristics for solving a type II robotic

mixed-model assembly line balancing problem.

Journal of Industrial and Production Engineering,

33(7), pp.472–484. Available at:

https://www.tandfonline.com/doi/full/10.1080/216810

15.2015.1126656 [Accessed September 27, 2016].

Ritt, M., Costa, A.M. & Miralles, C., 2016. The assembly

line worker assignment and balancing problem with

stochastic worker availability. International Journal of

Production Research, 54(3), pp.907–922. Available at:

http://www.tandfonline.com/doi/full/10.1080/0020754

3.2015.1108534 [Accessed September 25, 2016].

Salveson, M.E., 1955. The assembly line balancing

problem. Journal of Industrial Engineering, 6(3),

pp.18–25.

Simaria, A.S. & Vilarinho, P.M., 2009. 2-ANTBAL: An ant

colony optimisation algorithm for balancing two-sided

assembly lines. Computers & Industrial Engineering,

56(2), pp.489–506.

Sivasankaran, P. & Shahabudeen, P., 2014a. Literature

review of assembly line balancing problems. The

International Journal of Advanced Manufacturing

Technology, 73(9–12), pp.1665–1694. Available at:

http://link.springer.com/10.1007/s00170-014-5944-y

[Accessed August 20, 2016].

Sivasankaran, P. & Shahabudeen, P., 2014b. Literature

review of assembly line balancing problems. The

International Journal of Advanced Manufacturing

Technology, 73(9–12), pp.1665–1694. Available at:

http://link.springer.com/10.1007/s00170-014-5944-y

[Accessed September 29, 2016].

Sparling, D. & Miltenburg, J., 1998. The mixed-model U-

line balancing problem. International Journal of

Production Research, 36(2), pp.485–501.

Talbot, F.B. & Patterson, J.H., 1984. an Integer

Programming Algorithm With Network Cuts for

Solving the Assembly Line Balancing Problem.

Management Science, 30(1), pp.85–99. Available at:

http://search.ebscohost.com/login.aspx?direct=true&d

b=bth&AN=7357463&site=ehost-live&scope=site.

Thangavelu, S.R. & Shetty, C.M., 1971. Assembly Line

Balancing by Zero-One Integer Programming. AIIE

Transactions, 3(1), pp.61–68.

Toklu, B. & özcan, U., 2008. A fuzzy goal programming

model for the simple U-line balancing problem with

multiple objectives. Engineering Optimization, 40(3),

pp.191–204. Available at:

http://www.tandfonline.com/doi/abs/10.1080/0305215

0701651642 [Accessed September 21, 2016].

Urban, T.L., 1998. Note. Optimal Balancing of U-Shaped

Assembly Lines. Management Science, 44(5), pp.738–

741. Available at: http://pubsonline.informs.org/

doi/abs/10.1287/mnsc.44.5.738 [Accessed September

21, 2016].

Urban, T.L. & Chiang, W.C., 2006. An optimal piecewise-

linear program for the U-line balancing problem with

stochastic task times. European Journal of Operational

Research, 168(3), pp.771–782.

Vilarinho, P.M. & Simaria, A.S., 2002. A two-stage

heuristic method for balancing mixed-model assembly

lines with parallel workstations. International Journal

of Production Research, 40(6), pp.1405–1420.

Available at: http://www.tandfonline.com/doi/abs/

10.1080/00207540110116273 [Accessed September

25, 2016].

Vitria, J., 2004. Different ways of modelling and solving

precedence and incompatibility constraints in the

Assembly Line Balancing Problem. Recent Advances in

Artificial Intelligence Research. Available at:

https://www.google.com/books?hl=en&lr=&id=P7FY

s0IvbpoC&oi=fnd&pg=PA359&dq=Pastor,+R.,+Coro

minas,+A.+and+Lusa,+A.,+2004.+Different+ways+of

+modelling+and+solving+precedence+and+incompati

bility+constraints+in+the+assembly+line+balancing+p

roblem.+Frontiers+in.

White, W.W., 1961. Comments on a Paper by Bowman.

Operations Research, 9(August 2015), pp.274–276.

Zhao, X. et al., 2016. A genetic algorithm for the multi-

objective optimization of mixed-model assembly line

based on the mental workload. Engineering

Applications of Artificial Intelligence, 47, pp.140–146.

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems

408