An Off-line Evaluation of Users’ Ranking Metrics

in Group Recommendation

Silvia Rossi

, Francesco Cervone

and Francesco Barile

Dipartimento di Ingegneria Elettrica e delle Tecnologie dell’Informazione,

Universit

a degli Studi di Napoli Federico II, Napoli, Italy

Dipartimento di Matematica e Applicazioni, Universit

a degli Studi di Napoli Federico II, Napoli, Italy

Keywords:

Group Recommendations, Weighted Utilities, Off-line Testing.

Abstract:

One of the major issue in designing group recommendation techniques relates to the difﬁculty of the evaluation

process. Up-today, no freely available dataset exists that contains information about groups, like, for example,

the group’s choices or social aspects that may characterize the group’s members. The objective of the paper

is to analyze the possibility to make an evaluation of ranking-based groups recommendation techniques by

using ofﬂine testing. Typically, the evaluation of group recommendations is computed, as in the classical

single user case, by comparing the predicted group’s ratings with respect to the single users’ ratings. Since the

information contained in the datasets are mainly such user’s ratings, here, ratings are used to deﬁne different

ranking metrics. Results suggest that such an attempt is hardly feasible. Performance seems not to be affected

by the choice of ranking technique, except for some particular cases. This could be due to the averaging effect

of the evaluation with respect to the single users’ ratings, so a deeper analysis or speciﬁc dataset are necessary.

1 INTRODUCTION

Group recommendation systems (GRSs) aim to re-

commend items or activities in domains where it is

expected that more than a person will participate in

the suggested activity. Examples include the choice

of a restaurant, a vacation package or a movie to wa-

tch (Rossi et al., 2016). Recently, several interesting

approaches to group recommendation have been pro-

posed in literature (Amer-Yahia et al., 2009; Baltru-

nas et al., 2010; Berkovsky and Freyne, 2010; Gar-

trell et al., 2010; O’Connor et al., 2001; Pera and Ng,

2013; Rossi and Cervone, 2016), and most of these

studies are based on collaborative ﬁltering, employing

some aggregation strategies (Masthoff, 2011).

One of the major issue in this research area re-

lates to the difﬁculty of evaluating the effectiveness

of group recommendations, i.e., comparing the ge-

nerated recommendations for a group with the true

preferences of the individual members. One gene-

ral approach for such an evaluation consists in in-

terviewing real users. However, on-line evaluations

can be performed on a very limited set of test cases

and cannot be used to extensively test alternative al-

gorithms. A second approach consists in performing

off-line evaluations, but up today, no freely available

dataset exists that consider groups choices. Hence,

when evaluating group recommendations, such evalu-

ation is computed, as in the classical single user case,

by comparing the predicted group ratings with the ra-

tings observed in the test set of the users. As shown

in (Baltrunas et al., 2010), the most popular datasets

(e.g. Movielens or Netﬂix) that contain just evaluati-

ons of individual users can be used to evaluate GRS.

Moreover, the simple aggregation of the indivi-

dual preferences cannot always lead to a good result.

Groups can be dynamic, and so the behavior of the

various members in different situations. For example,

the users’ personality, the relationships between them

and their experience in the domain of interest can be

decisive in the group decision phase. When aggrega-

ting the data of individual users, it is natural to allow

for some users to have more inﬂuence than others, so

considering a users’ ranking in the aggregation pro-

cess. Anyway, in order to keep the possibility of an

ofﬂine evaluation for a GRS, it is necessary to design

techniques for user rankings based on the available

information in a dataset. Since the information con-

tained in the datasets are mainly the user’s preferences

or the ratings that they gave to the various items, the

idea, here, is to use such preferences to deﬁne diffe-

rent ranking metrics.

252

Rossi S., Cervone F. and Barile F.

An Off-line Evaluation of Usersâ

Z Ranking Metrics in Group Recommendation.

DOI: 10.5220/0006200702520259

In Proceedings of the 9th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2017), pages 252-259

ISBN: 978-989-758-219-6

In this paper, starting from the generation of synt-

hetic groups (with various criteria), different ranking

aggregation methods and two aggregation strategies

are used to generate group recommendations. We eva-

luate how good this integrated ranking is, with respect

to the individual ratings contained in the users’ pro-

ﬁle (without any ranking process). We performed an

analysis of the generated group recommendations via

ranking varying the size of the groups, the inner group

members similarity, and the rank aggregation mecha-

nism.

The aim of the paper is to evaluate whether or not

the ranking mechanisms may have an impact on the

goodness of GRSs and whether this can be evaluated

in off-line testing. The ﬁrst results show that this kind

of evaluation is not very simple, and it seems not to

provide signiﬁcant information. Indeed, a more deep

analysis shows some correlation between the charac-

teristics of the groups and the evaluation of the re-

commendations. This suggests extending the analysis

crossing the data and evaluating the impact of each

ranking technique with respect to the internal charac-

teristics of each group.

2 RELATED WORKS

Typically, GRSs are obtained by merging the single

users’ proﬁles in order to obtain a preferences pro-

ﬁle for the whole group, and then, by using a sin-

gle user recommendation system on this virtual pro-

ﬁle to obtain the recommendations for the group.

On the contrary, a second approach relies on ﬁrstly

using a single user recommendation system on each

user’s proﬁle and merging these recommendations

using some group decision strategy (Masthoff, 2011).

In both cases, there is the problem to decide how to

combine preferences or recommendations.

Only few approaches considered that the decisions

taken within a group are inﬂuenced by many factors,

not only by the individual user preferences. PolyLens

(O’Connor et al., 2001) has been one of the ﬁrst ap-

proaches to include social characteristics (such as the

nature of a group, the rights of group members, and

social value functions for groups) within the group

recommendation process. Also in (Ardissono et al.,

2003), intra-group roles, such as children and the di-

sabled were contemplated; each group is subdivided

into homogeneous subgroups of similar members that

ﬁt a stereotype, and recommendations are predicted

for each subgroup and an overall preference is built

considering some subgroups more inﬂuential than ot-

hers.

The results on group recommendation, presented

in the literature, showed that there is no strategy that

can be deﬁned as the “best”, but different approa-

ches are better suited in different scenarios, depen-

ding from the characteristics of the speciﬁc group

(Masthoff, 2011). Besides, traditional aggregation

techniques do not seem to capture the features of real-

world scenarios, as, for example, the possibility of

weighting/ranking the users in the group in order to

compute the recommendation. On the contrary, in

(Gartrell et al., 2010), the authors started to evalu-

ate the group members’ weights, in terms of their

inﬂuence in a group relying on the concept of “ex-

pertise” (how many items they rated on a set of 100

popular movies) and “group dissimilarity” (a pair-

wise dissimilarity on ratings), and selecting a diffe-

rent aggregation function starting from a “social va-

lue” (that models the intra-group relationships) deri-

ved from questionnaires. The proposed approach was

tested on real groups and not on a dataset. In (Amer-

Yahia et al., 2009), the authors propose to use the

disagreement among users’ ratings to implement an

efﬁcient group recommendation algorithm. In (Ber-

kovsky and Freyne, 2010), an approach that provi-

des group recommendations with explicit relations-

hips within a family is proposed, investigating four

different models for weighting user data, related to

user’s function within a family or on the observed user

interactions. In (Rossi et al., 2015), the authors aimed

at identifying dominant users within a group by analy-

zing users’ interactions on social networks since their

opinions inﬂuence the group decision. The authors

developed a model weighed for group recommendati-

ons that calculates the leadership among users using

their popularity as a measure, and evaluated the sy-

stem with real users.

Finally, concerning the problem of group recom-

mendation evaluation, in the work of (Baltrunas et al.,

2010), the authors analyzes the effectiveness of group

recommendations obtained aggregating the individual

lists of recommendations produced by a collaborative

ﬁltering system. It is observed that the effectiveness

of a group recommendation does not necessarily de-

crease when the group size grows. Moreover, when

individual recommendations are not effective a user

could obtain better suggestions looking at the group

recommendations. Finally, it is shown that the more

alike the users in the group are, the more effective the

group recommendations are.

An Off-line Evaluation of Usersâ

Z Ranking Metrics in Group Recommendation

253

3 RANKING-BASED

AGGREGATIONS

We decide to use the merging recommendations

technique to generate groups recommendations. Ge-

nerally speaking, the aim of a Recommendation Sy-

stem (RS) is to predict the relevance and the impor-

tance of items (for example movies, restaurants and

so on) that the user never evaluated. More formally,

given a set U of n users and a set I of m items, the

RS aims at building, for each user u ∈ U, a Rating

Proﬁle 

over the complete set I, starting from some

ratings each user explicitly provides on a subset of

items (Rossi et al., 2017). We denote as r

u,i

∈ R the

rating given by the user u on an item i. Furthermore,

we denote as U

the set of users who explicitly evalu-

ated the item i and with I

the set of items evaluated

by the user u.

Once is evaluated a rating proﬁle 

for each user

u ∈ U, the goal of a GRS is to obtain, given a group

of users G ⊂ U, a rating proﬁle for the whole group



= {r

G,1

, . .. , r

G,m

}, where r

G,i

is the correspondent

ranking for the movie i as evaluated for the group.

Typically, this is obtained by implementing a social

choice function SC :

→

, that aggregates all the

ratings proﬁles in 

= {r

G,1

, . . . , r

G,m

3.1 Ranking Metrics

To obtain an ofﬂine evaluation based on a speciﬁc da-

taset, we must deﬁne users’ ranking metrics starting

from the available data. We decided to use the Mo-

vieTweetings dataset (Dooms et al., 2013), that con-

tains movie ratings derived from tweets on the Twit-

ter.com social network. So, the information available

are mainly related to the individual preferences (i.e.,

users’ rating proﬁles). Here, we identify four diffe-

rent ranking metrics. We will, then, use these me-

trics to obtain two different aggregation strategies, na-

mely, a Weighted Average Satisfaction (WAS), and a

Fairness-based algorithm (FAIR). These two techni-

ques will be evaluated with respect to two bench-

mark strategies: Least Misery (LM) and Average Sa-

tisfaction (AS).

3.1.1 Experience

The ﬁrst metric is inspired by the work of (Gartrell

et al., 2010), and it aims at giving a higher rank to

the users with respect to their experience, quantiﬁed

in the number of provided ratings. Hence, the score

assigned to each user is given by his experience de-

gree, and is computed on the number of his ratings in

the system, in this way:

= |I

| (1)

Since the computed weight is an integer greater

or equal to 0, the ranking is considered in descending

order.

3.1.2 Popularity

It can also be interesting to assess the popularity of

a user. We deﬁne a popular user if he/she evaluated

popular movies that are rated by many. Hence, in this

ranking strategy, the score of each user is given by the

sum of the number of users that evaluated each movie

the considered user evaluates too, as in the following

formula:

∑

i∈I

| (2)

In this case, the evaluated weight is an integer gre-

ater or equal to 0. As in the previous case, greater is

the score, greater will be the position of the user in the

ranking.

3.1.3 Total Distance

In this case, the weight of a user is computed on how

its ratings deviate from their average in the whole da-

taset. Therefore, it is given by the standard deviation

between his ratings and the average values, as follow:

ˆw

∑

i∈I

u,i

− avg(i))

(3)

where avg(i) is the average rating for the movie i

on the whole dataset. Differently from the previous

techniques, the ranking ordering is ascending with re-

spect to the scores because this value represents the

distance from the total average. Hence, if a user has a

great deviation from this average, he/she must have a

smaller inﬂuence on the ﬁnal decision. To align with

respect to the other techniques we inverted the obtai-

ned values.

Since ˆw

is the standard deviation between rating

pairs, the maximum value that it could have is the dif-

ference between the maximum rating r

max

and the mi-

nimum r

min

in the dataset. Therefore, we compute the

scores as in the following formula:

= (r

max

− r

min

) − ˆw

(4)

In this way, greater is the score w

of a user, smal-

ler will be the distance of his/her ratings with respect

to the average ratings in the dataset.

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

254

Table 1: Test results for individual recommendation

algorithms item-based.

precision@10 recall@10 nDCG

Cosine 8.394E-5 1.119E-4 7.500E-5

Pearson 2.518E-4 3.637E-4 3.022E-4

Euclidean 8.394E-5 1.119E-4 7.399E-5

Tanimoto 8.394E-5 1.119E-4 7.249E-5

City block 7.017E-2 0.117 0.113

Log likelihood 8.394E-5 1.119E-4 6.979E-5

Table 2: Test results for individual recommendation

algorithms user-based.

precision@10 recall@10 nDCG

Cosine 1.119E-4 1.376E-4 1.163E-4

Pearson 4.499E-4 8.117E-4 5.444E-4

Euclidean 1.119E-4 1.337E-4 1.476E-4

Tanimoto 1.399E-4 1.737E-4 1.897E-4

City block 1.567E-3 2.463E-3 2.051E-3

Log likelihood 1.679E-4 2.016E-4 2.095E-4

3.1.4 Group Distance

This last measure is very similar to the previous one

and it is based on the hypothesis that members who

give a rating that is too much different from the

average of the group may leading the RS to choose

a movie that the group will not like at all with a high

probability. The only difference, with respect to the

total distance, is that the average value is computed

using only the group members’ evaluations, as follow:

ˆw

∑

i∈I

u,i

− avg

(i))

(5)

where avg

(i) is the average rating for the movie

i in the group G. Also, in this case, the weights are

reversed in the following way:

= (r

max

− r

min

) − ˆw

(6)

3.1.5 Ranking Normalization

For each ranking technique, we obtain a value that

needs to be normalized, so that the sum of all weights

in a group will be equal to 1. This normalization is

obtained by the following formula:

¯w

∑

v∈G

(7)

For simplicity, we will refer as w

indicating ¯w

the rest of the paper.

3.2 Aggregation Strategies

Since the aim of the paper is not to evaluate the best

strategy to be used in a GRS, but to evaluate whet-

her or not the ranking mechanisms may have an im-

pact on the goodness of a decision and whether this

can be evaluated in off-line testing, we decided to use

two common aggregation strategies, namely a Weig-

hted Average Satisfaction (WAS) and a Fairness stra-

tegy (FAIR), that use the ranking process in a diffe-

rent way. In particular, the WAS treats the rankings

as multiplicative weights in the aggregation process,

while FAIR, that builds the recommendation with an

iterative process on individual users, uses the ranking

to order such users. Moreover, we decided to com-

pare them with two classical aggregation algorithms,

Average Satisfaction (AS), that simply computes the

groups rating averaging on each members ratings, and

Least Misery (LM), that assigns as group rating the

minimum in the group.

The WAS is given by the following equation:

G,i

∑

u∈G

· r

u,i

∑

u∈G

(8)

where w

is the weight of the generic user u within

the group.

Instead, the FAIR strategy uses also the same

weights to deﬁne a ranking within the group’s mem-

bers. Supposing we want to determine the K-best mo-

vies for the group G, the algorithm proceeds in an ite-

rative way as follows. Starting from the user u with

the highest weight w

, in the generic i − th step:

1. the t items with higher values for the user u are

considered (note that the choice of the number t is

not ﬁxed);

2. from these, the item that produces the higher least

misery for the other group’s members is selected;

3. we select the next user in the ranking, if there is

one. If the current user is the last in the ranking,

we select the ﬁrst one;

4. we repeat from the ﬁrst step until we have selected

k items.

On the basis of the deﬁned strategies and of

the ranking measures previously speciﬁed, we de-

ﬁne the effective strategies evaluated, and the re-

spective acronym, used for simplicity in the rest of

the paper. We use the Least Misery (LM), a not

weighted Average satisfaction strategy (AS), the re-

spective ranking weighted version, Total Distance

(TD-AS), Group Distance (GD-AS), Experience (EX-

AS) and Popularity (P-AS), and, ﬁnally, the ran-

ked fairness based strategies, Total Distance Fairness

(TD-FAIR), Group Distance Fairness (GD-FAIR),

Experience Fairness (EX-FAIR) and Popularity Fair-

ness (P-FAIR).

An Off-line Evaluation of Usersâ

Z Ranking Metrics in Group Recommendation

255

Table 3: F1 and nDCG scores: grouping by ranking strategy.

Ranking Average Total Distance Group Distance Popularity Experience ANOVA (F) p-value

Average F1 0.043 ± 0.021 0.043 ± 0.021 0.043 ± 0.021 0.043 ± 0.021 0.044 ± 0.022 0.022 0.999

Average nDCG 0.626 ± 0.150 0.626 ± 0.150 0.626 ± 0.150 0.625 ± 0.161 0.620 ± 0.161 0.018 0.999

Fairness F1 - 0.037 ± 0.019 0.037 ± 0.019 0.037 ± 0.019 0.037 ± 0.019 0.001 1.000

Fairness nDCG - 0.577 ± 0.176 0.578 ± 0.154 0.588 ± 0.165 0.581 ± 0.159 0.085 0.968

Table 4: F1 evaluation: grouping by aggregation strategy.

Aggregation Average Fairness ANOVA (F) p-value

Total Distance 0.043 ± 0.021 0.037 ± 0.019 4.399 0.037

Group Distance 0.043 ± 0.021 0.037 ± 0.019 4.389 0.038

Popularity 0.043 ± 0.021 0.037 ± 0.019 4.755 0.031

Experience 0.044 ± 0.022 0.037 ± 0.019 5.373 0.022

4 OFFLINE EVALUATION

As stated above, we decide to use the dataset MovieT-

weetings. The dataset does not contain information

about groups, and we decided to automatically ge-

nerate groups in a way that could provide relevant

results. The techniques used for the generation of

groups will be analyzed afterward. Firstly, the genera-

tion of the individual recommendations is illustrated

and then the determination of the group recommenda-

tions is explained. Finally, the group’s generation is

explained; in this step, an ad hoc algorithm is used, in

order to generate groups with different levels of cohe-

sion within the members.

4.1 Individual Recommendations

Since we use the merging recommendations techni-

que, we need to ﬁrstly use an individual recommen-

dation system to provide recommendations for each

group’s member. We conduct tests to determine the

most appropriate algorithm to produce these recom-

mendations in order to avoid errors that could be pro-

pagated in the group’s recommendations.

We analyze collaborative ﬁltering strategies, eva-

luating the effectiveness using both the item-based

and the user-based rating prediction, and, for each of

them, we evaluate different distance measures, in or-

der to ﬁnd the better one. In each test, for each user,

we remove part of the ratings, and then we generate

the individual recommendations; at the end, we com-

pute precision, recall and nDCG on the previously

removed elements. Recall that the Normalized Dis-

counted Cumulative Gain (nDCG) is an evaluation

metric that evaluates the goodness of a recommended

list taking into account the order of the recommenda-

tions.

Tables 1 and 2 contain, respectively, the results for

the item-based and for the user-based strategy, grou-

ped with respect to the distance measure used. We can

notice that the CityBlock has the best results in both

cases, so we decides to use the City block item-based

algorithm.

4.2 Group Recommendations

In order to create the group recommendation, we

should calculate the scores for all the items of the

data set that have not been previously evaluated by

users, and then aggregate those predictions and build

the recommendation list for the group. Since the da-

taset contains tens of thousands of items, this solution

would be computationally inefﬁcient. Hence, we de-

cided to generate the group’s recommendation only

for the k-best movies for each user, with respect to

the ratings evaluated by the individual recommenda-

tion system. Formally, we assume that the group G

is composed by |G| members. For each user u of the

group, we generate a list L

of k items to recommend.

Then, we construct the list L

of the whole group, by

merging the lists for all the group’s members.

4.3 Groups Generation

We generate groups with different levels of inner co-

hesion. We use the Pearson correlation to deter-

mine the cohesion between two group members, in-

dicated as ρ

(where X and Y are two statistic va-

riables). The value of ρ

is included in the clo-

sed interval [−1, 1], where a value close to 0 indica-

tes that the variables are no correlated, while a value

close to 1 indicates a positive correlation, and simi-

larly a value close to −1 indicates a negative one.

Hence, we distinguish three intervals of correlation,

weak correlation, if 0.1 ≤ ρ

≤ 0.3, moderate cor-

relation, if 0.3 ≤ ρ

≤ 0.7, and strong correlation,

when 0.7 ≤ ρ

≤ 1.

In the speciﬁc case, the two variables represent

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

256

Table 5: nDCG evaluation: grouping by aggregation strategy.

Aggregation Average Fairness ANOVA (F) p-value

Total Distance 0.626 ± 0.150 0.577 ± 0.176 3.818 0.052

Group Distance 0.626 ± 0.150 0.578 ± 0.154 4.096 0.045

Popularity 0.625 ± 0.161 0.588 ± 0.165 2.074 0.152

Experience 0.620 ± 0.161 0.581 ± 0.159 2.538 0.113

Table 6: F1 evaluation: grouping by correlation.

Correlation Random Weak Moderate Strong ANOVA (F) p-value

AS 0.037 ± 0.006 0.054 ± 0.014 0.054 ± 0.019 0.027 ± 0.026 12.8 < 0.01

EX-AS 0.038 ± 0.007 0.055 ± 0.015 0.055 ± 0.019 0.027 ± 0.027 12.323 < 0.01

EX-FAIR 0.031 ± 0.006 0.046 ± 0.013 0.046 ± 0.017 0.024 ± 0.023 10.371 < 0.01

GD-AS 0.037 ± 0.006 0.055 ± 0.014 0.054 ± 0.019 0.027 ± 0.026 12.853 < 0.01

GD-FAIR 0.031 ± 0.006 0.046 ± 0.013 0.046 ± 0.017 0.024 ± 0.023 10.432 < 0.01

LM 0.037 ± 0.007 0.053 ± 0.015 0.051 ± 0.019 0.028 ± 0.028 8.983 < 0.01

P-AS 0.037 ± 0.007 0.055 ± 0.015 0.054 ± 0.018 0.027 ± 0.027 12.196 < 0.01

P-FAIR 0.031 ± 0.006 0.046 ± 0.013 0.046 ± 0.017 0.024 ± 0.023 10.326 < 0.01

TD-AS 0.037 ± 0.007 0.055 ± 0.014 0.054 ± 0.019 0.027 ± 0.026 12.795 < 0.01

TD-FAIR 0.031 ± 0.006 0.046 ± 0.013 0.046 ± 0.017 0.024 ± 0.023 10.517 < 0.01

two users and are deﬁned as the vector of ratings of

the movies rated by both the users. Starting from

these correlations, we create groups from two to eight

members, and for each dimension, we associate users

with weak, moderate and strong correlation. To gene-

rate the groups, we deﬁne a sequential algorithm that

uses groups of size k to generate groups of size k + 1

(with k ≥ 2), adding a user to the group according to

the corresponding cohesion degree.

5 RESULTS ANALYSIS

We evaluate the effectiveness of aggregation stra-

tegies with respect to the different ranking mea-

sures, by varying dimensions and inner correlati-

ons of the groups. Hence, for each group size

m, with 2 ≤ m ≤ 8, and for each correlation x ∈

{random, weak, moderate, strong}, we evaluate the

F-measure (also known as F1-score) and the nDCG,

for recommendation lists of size 5, 10 and 20 movies.

5.1 Ranking Techniques

In this ﬁrst analysis, we evaluate the changing in

the F-measure and nDCG by ﬁxing the aggregation

strategy, and we compare the used ranking techni-

ques. Results are reported in Table 3 together with

the ANOVA values. Notice that the average values are

very similar for each technique and the p-values con-

ﬁrm that there are not signiﬁcant differences between

the different ranking strategies. Since the results seem

to be not signiﬁcant, we conduct a deeper analysis by

analyzing the results in relation to the used aggrega-

tion strategies, and to the type of groups, in terms of

internal cohesion and group size.

5.2 Aggregation Strategies

As second analysis, we compare the aggregation stra-

tegies (AVG and FAIR), by ﬁxing the ranking techni-

ques. Results of F1 measure are shown in Table 4.

In general, we can see that the weighted average stra-

tegy performs better than the fairness strategy. The

signiﬁcance of these conclusions is conﬁrmed by the

ANOVA test and the computed p-value. Similar re-

sults are obtained by evaluating the nDCG parame-

ters, as showed in Table 5. However, in the case of

nDCG signiﬁcant results are only in case of Total and

Group Distances, that are indeed ranking strategies

that rely on the difference in the individual ratings.

5.3 Group Correlation

Table 6 shows results of the F1 evaluation conside-

ring grouping by correlation. Also, in these analy-

ses, we can observe that the user ranking does not

seem to have an impact on the aggregation strategy

while keeping ﬁxed the group correlation. All the al-

gorithms show the best results in weak and moderate

correlation groups. The average extent of the worst F1

concerns the strong correlation groups. After a deeper

analysis on the groups, we believe that this could be

due to the fact that users with strong correlations eva-

An Off-line Evaluation of Usersâ

Z Ranking Metrics in Group Recommendation

257

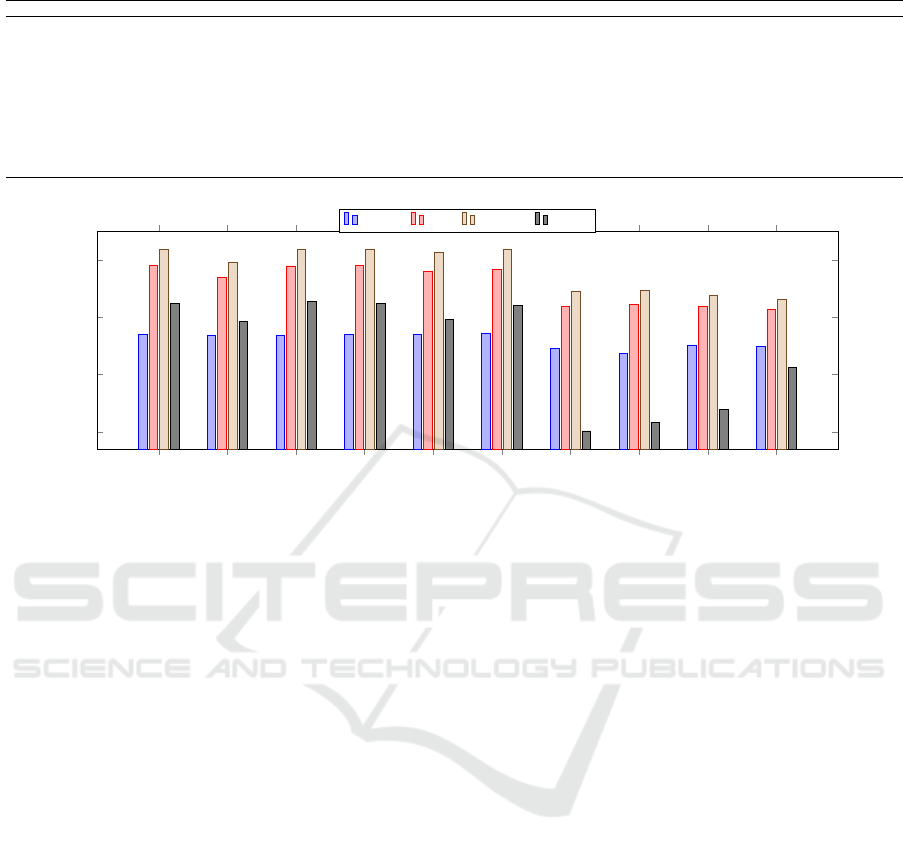
Table 7: F1 evaluation: grouping by group size.

Size 2 3 4 5 6 7 8 ANOVA (F) p-value

AS 0.054 ± 0.019 0.057 ± 0.018 0.053 ± 0.016 0.043 ± 0.017 0.035 ± 0.022 0.031 ± 0.02 0.028 ± 0.018 5.167 < 0.01

EX-AS 0.056 ± 0.02 0.058 ± 0.018 0.054 ± 0.016 0.044 ± 0.017 0.036 ± 0.022 0.031 ± 0.02 0.028 ± 0.019 4.931 < 0.01

EX-FAIR 0.05 ± 0.016 0.05 ± 0.016 0.045 ± 0.013 0.036 ± 0.014 0.029 ± 0.018 0.025 ± 0.016 0.022 ± 0.015 6.666 < 0.01

GD-AS 0.055 ± 0.019 0.057 ± 0.018 0.053 ± 0.016 0.043 ± 0.017 0.035 ± 0.022 0.031 ± 0.02 0.028 ± 0.019 5.112 < 0.01

GD-FAIR 0.049 ± 0.016 0.05 ± 0.016 0.045 ± 0.013 0.036 ± 0.014 0.029 ± 0.018 0.025 ± 0.016 0.022 ± 0.015 6.656 < 0.01

LM 0.057 ± 0.02 0.057 ± 0.017 0.053 ± 0.014 0.042 ± 0.016 0.033 ± 0.021 0.029 ± 0.019 0.026 ± 0.017 6.641 < 0.01

P-AS 0.055 ± 0.02 0.057 ± 0.018 0.054 ± 0.016 0.044 ± 0.017 0.035 ± 0.022 0.031 ± 0.02 0.028 ± 0.018 5.123 < 0.01

P-FAIR 0.049 ± 0.016 0.05 ± 0.016 0.045 ± 0.013 0.036 ± 0.014 0.029 ± 0.018 0.025 ± 0.016 0.022 ± 0.015 6.708 < 0.01

TD-AS 0.054 ± 0.019 0.057 ± 0.018 0.054 ± 0.016 0.043 ± 0.017 0.035 ± 0.022 0.031 ± 0.02 0.028 ± 0.019 5.107 < 0.01

TD-FAIR 0.049 ± 0.016 0.05 ± 0.016 0.045 ± 0.013 0.036 ± 0.014 0.029 ± 0.018 0.025 ± 0.016 0.022 ± 0.015 6.735 < 0.01

P-ASEX-ASGD-ASAS LM TD-AS EX-FAIR P-FAIRTD-FAIR GD-FAIR

0.5

0.55

0.6

0.65

Random Weak Moderate Strong

Figure 1: nDCG evaluation: grouping by correlation.

luated, on average, only ﬁve movies in common that

are too few to describe the correlation of the group.

Once set the algorithm, there are no signiﬁcant

differences between weak and moderate correlation

groups. In all other cases (i.e., the correlation between

random and weak, moderate and random, random and

strong, weak and strong, moderate and strong) the

differences are signiﬁcant. This implies that each

algorithm, by varying the correlation of the groups,

obtains different results. Hence, we can say that, in

general, the group cohesion affects the satisfaction of

its members. We also analyze the nDCG measure as

shown in Figure 1. Still, in this case, we can note that

the Fairness algorithms are worse than others. Ana-

lyzing each algorithm individually, there are signiﬁ-

cant differences in the case of AS, GD-AS and TD-AS

varying the correlation, particularly between random

and weak correlation and weak and moderate.

5.4 Group Size

At least, we analyze the results related to the size of

the group. Figure 2 shows the results. Also, in this

case, we can see that the Fairness strategies have the

worst results. Fixing the size of the groups and ana-

lyzing the average between the various algorithms in

pairs, the p − value resulting from the ANOVA sta-

tistical test is greater than 0.1, which means that all

differences are due to chance. So, we can state that

no algorithm prevails over by ﬁxing the number of

members. Fixing the algorithm, and varying the size

of the groups, there are many cases where the ANOVA

test shows signiﬁcant differences, as showed in Table

7. The best results are obtained for all the strategies

in groups composed of three members. We can see

that increasing the group’s size, the algorithms shows

worst results, as expected.

6 CONCLUSIONS

When designing group recommendation strategies

one of the major problems to address is the evaluation

process, since an ofﬂine evaluation is difﬁcult because

a dataset containing information about individual ra-

tings and group’s choices is missing, and online eva-

luations are usually conducted only on a small set of

cases and cannot be executed extensively.

In this work, we try to deﬁne ranking measures,

deﬁned on the basis of the information contained in

a well-known dataset for individual recommendati-

ons, the MovieTweetings dataset, that consists of mo-

vie ratings contained in tweets on the Twitter.com so-

cial network. We deﬁne two ranking-based aggrega-

tion strategies, a weighted average satisfaction and a

fairness based strategy, to generate groups recommen-

dations on groups automatically generated from the

users in the dataset to obtain an evaluation of the de-

ﬁned ranking measures.

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

258

EX-AS

EX-FAIR

GD-AS

GD-FAIR

P-AS

P-FAIR

TD-AS

TD-FAIR

·10

−2

Gr. size 2 Gr. size 3 Gr. size 4 Gr. size 5 Gr. size 6 Gr. size 7 Gr. size 8

Figure 2: F1 evaluation: grouping by group size.

To evaluate the strategies, measures like F1-score

and nDCG are computed, and then the results are ag-

gregated with different criteria to analyze different as-

pects of the group’s recommendations generated. Re-

sults suggest that in the case of off-line evaluation

classical aggregation strategies may produce different

results once applied on small groups, and so has the

cardinality of the group. More speciﬁcally, average

satisfaction based strategies seem to have best perfor-

mances than the fairness based. This could be related

to the evaluation metrics used, and so this should be

most deeply analyzed.

However, recent studies on small groups sho-

wed that their decision making relies on mechanisms

(e.g., interpersonal relationships and mutual inﬂuen-

ces) that are different with respect to the ones adopted

for larger groups (Levine and Moreland, 2008) that

are based on social choice functions. However, in this

case, off-line testing to show such differences seem to

be an impractical solution.

REFERENCES

Amer-Yahia, S., Roy, S. B., Chawlat, A., Das, G., and Yu,

C. (2009). Group recommendation: Semantics and

efﬁciency. Proc. VLDB Endow., 2(1):754–765.

Ardissono, L., Goy, A., Petrone, G., Segnan, M., and To-

rasso, P. (2003). Intrigue: Personalized recommenda-

tion of tourist attractions for desktop and handset de-

vices. Applied Artiﬁcial Intelligence, 17(8):687–714.

Baltrunas, L., Makcinskas, T., and Ricci, F. (2010). Group

recommendations with rank aggregation and collabo-

rative ﬁltering. In Proc. of the Fourth ACM RecSys

’10, pages 119–126. ACM.

Berkovsky, S. and Freyne, J. (2010). Group-based recipe

recommendations: Analysis of data aggregation stra-

tegies. In Proc. of the Fourth ACM RecSys ’10, pages

111–118. ACM.

Dooms, S., De Pessemier, T., and Martens, L. (2013). Mo-

vietweetings: a movie rating dataset collected from

twitter. In Workshop on Crowdsourcing and human

computation for recommender systems, volume 2013,

page 43.

Gartrell, M., Xing, X., Lv, Q., Beach, A., Han, R., Mishra,

S., and Seada, K. (2010). Enhancing group recom-

mendation by incorporating social relationship inte-

ractions. In Proceedings of the 16th ACM Internatio-

nal Conference on Supporting Group Work, GROUP

’10, pages 97–106. ACM.

Levine, J. M. and Moreland, R. L. (2008). Small groups:

key readings. Psychology Press.

Masthoff, J. (2011). Recommender Systems Handbook,

chapter Group Recommender Systems: Combining

Individual Models, pages 677–702. Springer US, Bos-

ton, MA.

O’Connor, M., Cosley, D., Konstan, J. A., and Riedl, J.

(2001). Polylens: A recommender system for groups

of users. In Proc. of the 7th European Conf. on CSCW,

pages 199–218.

Pera, M. S. and Ng, Y.-K. (2013). A group recommender

for movies based on content similarity and popularity.

Inf. Process. Manage., 49(3):673–687.

Rossi, S., Barile, F., Caso, A., and Rossi, A. (2016). Web

Information Systems and Technologies: 11th Interna-

tional Conference, WEBIST, Revised Selected Papers,

volume 246, chapter Pre-trip Ratings and Social Net-

works User Behaviors for Recommendations in Tou-

ristic Web Portals, pages 297–317. Springer Interna-

tional Publishing.

Rossi, S., Barile, F., Di Martino, S., and Improta, D. (2017).

A comparison of two preference elicitation approa-

ches for museum recommendations. Concurrency and

Computation: Practice and Experience, to appear.

Rossi, S., Caso, A., and Barile, F. (2015). Combining users

and items rankings for group decision support. Advan-

ces in Intelligent Systems and Computing, 372:151–

158.

Rossi, S. and Cervone, F. (2016). Social utilities and perso-

nality traits for group recommendation: A pilot user

study. In Proceedings of the 8th International Confe-

rence on Agents and Artiﬁcial Intelligence, pages 38–

46.

An Off-line Evaluation of Usersâ

Z Ranking Metrics in Group Recommendation

259