
CFS- InfoGain based Combined Shape-based Feature Vector for Signer
Independent ISL Database
Garima Joshi
1
, Renu Vig
1
and Sukhwinder Singh
2
1
Electronics and Communication Engineering Department, UIET, Panjab University, Chandigarh, India
2
Computer Science and Engineering Department, UIET, Panjab University, Chandigarh, India
joshi garima5@yahoo.com, renuvig@hotmail.com, sukhdalip@pu.ac.in
Keywords:
Sign language Recognition, Zernike Moments (ZM), Hu Moments (HM), Geometric features (GF), Info Gain
based Feature Normalization.
Abstract:
In Sign language Recognition (SLR) system, signs are identified on the basis of hand shapes. Zernike Mo-
ments (ZM) are used as an effective shape descriptor in the field of Pattern Recognition. These are derived
from orthogonal Zernike polynomial. The Zernike polynomial characteristics change as order and iteration
parameter are varied. Observing their behaviour gives an insight into the selection of a particular value of ZM
as a part of an optimal feature vector. The performance of ZMs can be improved by combining it with other
features, therefore, ZMs are combined with Hu Moments (HM) and Geometric features (GF). An optimal fea-
ture vector of size 56 is proposed for ISL dataset. The importance of the internal edge details to address issue
of hand-over-hand occlusion is also highlighted in the paper. The proposed feature set gives high accuracy for
Support Vector Machine (SVM), Logistic Model Tree (LMT) and Multilayer Perceptron (MLP). However, the
accuracy of Bayes Net (BN), Nave Bayes (NB), J48 and k- Nearest Neighbour (k-NN) improves significantly
for Info Gain based normalized feature set.
1 INTRODUCTION
Sign Language (SL) is a natural language of the deaf
community. The expression varies in terms of re-
gional accents and dialects in SL. Across the globe,
countries have their own SL, for example, the Ameri-
can Sign Language (ASL), the British Sign Language
(BSL), the Indian Sign Language (ISL), the French
Sign Language (FSL), and many more. ISL is highly
structured and there is some influence of BSL. ISL
and BSL use double hands mostly. SL interpreters are
required to facilitate communication between the per-
son using SL and a non-signing individual (Zeshan,
Vasishta and Sethna, 2005).
A system that can recognize SL can be used to
automatically act as an interpreter for SL. Sign Lan-
guage Recognition (SLR) system translates the in-
formation represented by hand gesture and converts
them into text (Rautaray and Agrawal, 2015). In fin-
ger spelled SL, English alphabets are represented by
hand shape. The name of people, places and abbre-
viations are finger-spelled in SL. SLR should be ca-
pable of classifying the signed alphabets. There is a
considerable variation in signs made by different peo-
ple. SLR system must be capable of recognizing the
sign performed by any user. It should be a user in-
dependent system. Ni et. al. (2015) presented a sur-
vey of signer-independent SLR system design. They
reported that system performance decreases consider-
ably in the case of a subject independent system as
the inter-subject difference can be large. They also
highlighted the need to design subject independent
datasets because the learning algorithms demand an
appropriate number of database samples to train the
system.
Various signer independent SLR systems are re-
ported in literature. A brief overview of these systems
is presented in Table 1. Important requisites associ-
ated with design of SLR system include a standard
signer independent database and to find the feature
set which is capable of representing the attributes of a
sign.
2 PROPOSED FRAMEWORK
The proposed framework is shown in Figure 1. It is
designed to evaluate the performance of shape based
features for a signer independent SL dataset. Exper-
iments have been performed to realize the following
Joshi, G., Vig, R. and Singh, S.
CFS- InfoGain based Combined Shape-based Feature Vector for Signer Independent ISL Database.
DOI: 10.5220/0006200905410548
In Proceedings of the 6th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2017), pages 541-548
ISBN: 978-989-758-222-6
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
541

Table 1: Literature Survey on Existing Signer Independent Vision based Systems.
Reference Sign Signer Repetition Features Classifier Accuracy
Ong and Ranganath (2004) 20 8 10 Geometric(6) BN 85
Rousan et. al. (2009) 30 18 50 DCT(50) HMM 94.2
Kelly et. al.(2010) 10 24 3 Eigen Space SVM 91.8
(SF+HM)
Shanableh and Assaleh (2011) 23 3 – DCT(70) kNN 87
Bhuyan et. al. (2011) 8 10 5 Hand Geometry+ Distance 93.4
HTD(186) Measure
Singha and Das (2013) 24 20 – PCA(50) Distance 96.25
Measure
Auephanwiriyakul et. al. (2013) 10 20 – SIFT(128) HMM 76.56
Kausar et. al. (2016) 37 – – Polynomial k-NN 92
Parameters
research objectives:
• To study the behavior of Zernike radial polyno-
mial with variation in its order and iterations.
• To study the performance of ZM and its combina-
tion with HM and GF.
• To propose an optimal feature vector and classifier
that provides a minimal error rate.
• To analyze performance of InfoGain based feature
normalization technique.
Figure 1: Proposed Framework.
2.1 Database
2.1.1 ISL Database
Figure 2 shows image data-set for 26 ISL alphabets.
It is created for 90 subjects and has a total of 2300
images. The images are captured by a web cam of 15
megapixels, on a uniform (black) background, with
Figure 2: ISL Alphabets.
varying illumination, at a fixed distance from the cam-
era with a resolution of 640 x 480 pixels. ISL alpha-
bets consists of 73% double hand signs. Use of dou-
ble hand gestures results in hand-over-hand occlusion.
Another challenge is imposed by signs having high
similarity among themselves. These are the signs of
alphabet ‘E’ - ‘F’, ‘H’ -‘M’ -‘N’, ‘P -‘Q’ and ‘S’ - ‘T’.
2.1.2 Treisch’s Database
The proposed system performance is also analyzed on
a standard Triesch’s Database from the Frankfurt In-
stitute for Advanced Studies. Images in light, dark
and complicated background for 12 hand gestures, 20
subjects are used in the present study (Triesch and
Malsburg, 2001).
2.2 Pre-processing
Figure 3: Skin Color Segmentation in Complex Back-
ground of Image from Treisch‘s Data-set a. Input Image
b. ‘L’ color component c. Color component ‘a’ d. Color
component ‘b’ e. Histogram of Skin and Entire Image.
Figure 4: ISL Alphabets H-M-N a. Without Internal Edge
Details b. With Internal Edge Details.
Using skin color segmentation in preprocessing
stage input colored images are converted to binary
images. An effective skin segmentation algorithm
must be capable of detecting skin colored pixels ef-
ficiently in the presence of light variations, shadows,
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
542

and noise (Kakumanu, Makrogiannis and Bourbakis,
2007). The input RGB image is converted to Com-
mission Internationale de l‘Eclairage (CIE) Lab color
model. Otsu‘s thresholding technique is clustering-
based method and it works best for bimodal histogram
characteristics. Therefore, it requires clearly distin-
guishable pixel values for hand and background. In
Figure 3(e), it is observed that the ‘a’ color compo-
nent has clear bimodal histograms. The ISL database
has been acquired in varying light conditions. The
effect of intensity variation are minimized if the in-
tensity component is separated from the image. Lab
color space separates ‘a’ and ‘b’ color component
from intensity ‘L’. Therefore, choice of Lab color
space makes it invariant to light intensity also. So
for pre-processing ‘a’ component of Lab color space
is used here. To preserve the internal edge details of
hand shapes, Laplacian of Gaussian (LoG) is used.
Laplacian filter highlights the regions with rapid in-
tensity changes and is highly sensitive to noise. To
reduce sensitivity, Gaussian blurring is used and then
Laplacian filter is applied. The pre-processed bi-
nary image includes the internal edges also. Figure 4
shows ISL alphabets ‘H’ -‘M’ -‘N’ without and with
internal edge details. These signs have similar outer
shape and can be distinguished only if inter edge in-
formation is added. Therefore, adding internal edge
details helps to overcome the problem of hand-over-
hand occlusion for double hand gesture.
2.3 Feature Extraction
Signs are represented as hand shapes. Recogni-
tion of SL can be defined as a linguistic analysis of
these hand shapes. Shape-based features that can
be used for shape recognition include Hu Moments
(HM), Zernike Moments (ZM), edge information and
Geometric Features (GF) (Mingqiang, Kidiyo, and
Joseph, (2008)). Appearance-based feature vectors
studied in this paper are summarized below:
2.3.1 Geometric Features
Geometric features are extracted for the binary hand
images using region based parameters (area, moments
and axis) and boundary parameters, the perimeter
(Zhang and Lu, 2004).
• Circularity Ratio is a measure of the degree to
which a shape differs from an ideal circle. It is
found to be invariant to scaling, rotation and trans-
lation. The range lies between 0 and 1.
CR =
Area
Shape
Area
Circle
(1)
• Spreadness is the measure of the spread of the
shape. It is calculated using, the central moments.
SR =
µ
20
+ µ
02
µ
00
+ µ
00
(2)
• Roundness is receptive to the elongation of image
boundary. Roundness is equal to 1 for a circle. It
has a less value for shapes other than a circle.
RO =
4πArea
Perimeter
2
(3)
• Solidity describes the roughness of a boundary.
Solidity is also equal to 1 for a region that has no
concavities. It is the degree to which the shape is
concave or convex. The solidity of a convex is 1.
S =
Areao f Shape
ConvexHullArea
(4)
• Average of Bending Energy (BE) is calculated
by finding a magnitude of discrete Fourier trans-
form,
|
X
n
( f )
|
of n boundary pixels. The bound-
ary pixels of a shape are listed in a clockwise di-
rection. Each pixel is represented as a complex-
valued vector. The Parseval’s energy relation is
applied to find the bending energy. Circle has a
minimum average bending energy.
BE =
n
∑
1
|
X
n
( f )
|
2
(5)
• Eccentricity or the aspect ratio is ratio of the
length of major axis (L) and minor axis (W) of
the area covering the shape.
E =
L
W
(6)
• Convexity is defined as the ratio of perimeter of
the convex hull over that of the original contour
of the shape.
CV =
ConvexHullPerimeter
ShapePerimeter
(7)
2.3.2 Hu Moments
Hu Moments (HM) were proposed by M.K. Hu
in 1962. HM are region-based invariant moments.
These are translation, scale and rotation invariant.
They represent the distribution of random variables
and bodies by their spatial distribution of mass. The
seven invariant moments are used as shape features.
Consider a binary image as 2D density distribution
function, here moments can be used to extract some
properties of the image. For a binary image, regular
moment m
uv
of order u+v is given by “Eq. (8)”:
m
uv
=
∑
0<x<=M−1,0<y<=N−1
x
u
y
v
f (x,y) (8)
CFS- InfoGain based Combined Shape-based Feature Vector for Signer Independent ISL Database
543
From the “Eq. (8)”, Hu derived seven set of moments
with respect to rotation, translation, scaling and were
computationally simple. First order moment locate
the centroid of the image calculated using “Eq. (9)”:
x
c
=
m
10
m
00
, y
c
=
m
01
m
00
(9)
To calculate the central moment centroid is subtracted
from all the coordinates as given by “Eq. (10)”.
These moment then become invariant to translation.
µ
uv
=
∑
0<x<=M−1,0<y<=N−1
(x −x
c
)
u
(y −y
c
)
v
f (x,y)
(10)
Scale invariance can be obtained by normalization.
η
uv
are normalized central moments. These can be
derived using “Eq. (11)”
η
uv
=
µ
uv
µ
u+v+2
2
00
(11)
The equations to derive seven Hu Moments listed by
Sabhara et. al. (2013). It may be noted that Hu mo-
ments and Geometric features are un-normalized set
of feature vector.
2.3.3 Analysis of Zernike Moments
Zernike Moments (ZM) are scale, rotation and trans-
lation invariant. Zhang and Lu (2004) reported ZM
as one of the best choices out of several shape rep-
resentation and description techniques. Sabhara et.
al. (2013) reported ZM to be more accurate, flexible,
and easier to reconstruct than HM. Also, increasing
the order of the ZM increased the accuracy and as
per the system requirement an optimal order of ZM
could be chosen. Goyal and Walia (2014) applied
ZMs as global features in achieving higher accuracy
for region-based shapes in a Shape-Based Image Re-
trieval (SBIR) system. ZM are known as global shape
descriptors. ZM are derived using orthogonal Zernike
polynomial. These polynomial are a product of angu-
lar function and radial polynomial. The angular func-
tions are the basis functions for the two-dimensional
rotation group, and the radial polynomials are devel-
oped from the Jacobi polynomials. “Eq. (12)” is an
expression for Radial polynomial R
uv
. These are
defined over interior of a unit circle, . V
uv
is the
orthogonal basis function of the image I(x,y), refer
“Eq. (14)”(Khalid and Hosny, (2010)).
R
uv
(r) =
(u−|v|)
2
∑
s=0
((−1)
s
(u −s)!)
s!
(u+|v|)
2
−s!
(u−|v|)
2
−s
r
(u−2s)
(12)
If u is the order and v is iteration in polar coordi-
nates.The condition that u −|v| is even and |v| < u
is always satisfied. r is length of vector from origin
to (x, y) pixel, θ is an azimuth angle between r and x
axis in counter clockwise direction. It varies from 0 to
2π. u is positive integer or zero, v is positive or nega-
tive (Nallasivan, Janakiraman and Ishwarya, (2015)).
ZM is given by “Eq. (13)”:
ZM
uv
=
u + 1
π
∑
(x
2
+y
2
)<=1
I(x, y)V
∗
uv
(x,y) (13)
Where V
∗
uv
, is complex conjugate of the Zernike ba-
sis function defined over the unit disk, derived using
“Eq. (14)”
V
uv
(x,y) = R
uv
(r)e
iuθ
,r <= 1 (14)
r =
q
(x
2
+ y
2
),r <= 1, θ = tan
−1
(
x
y
) (15)
ZP
even
=
p
(u + 1)R
uv
√
2cos(vθ) (16)
ZP
odd
=
p
(u + 1)R
uv
√
2sin(vθ) (17)
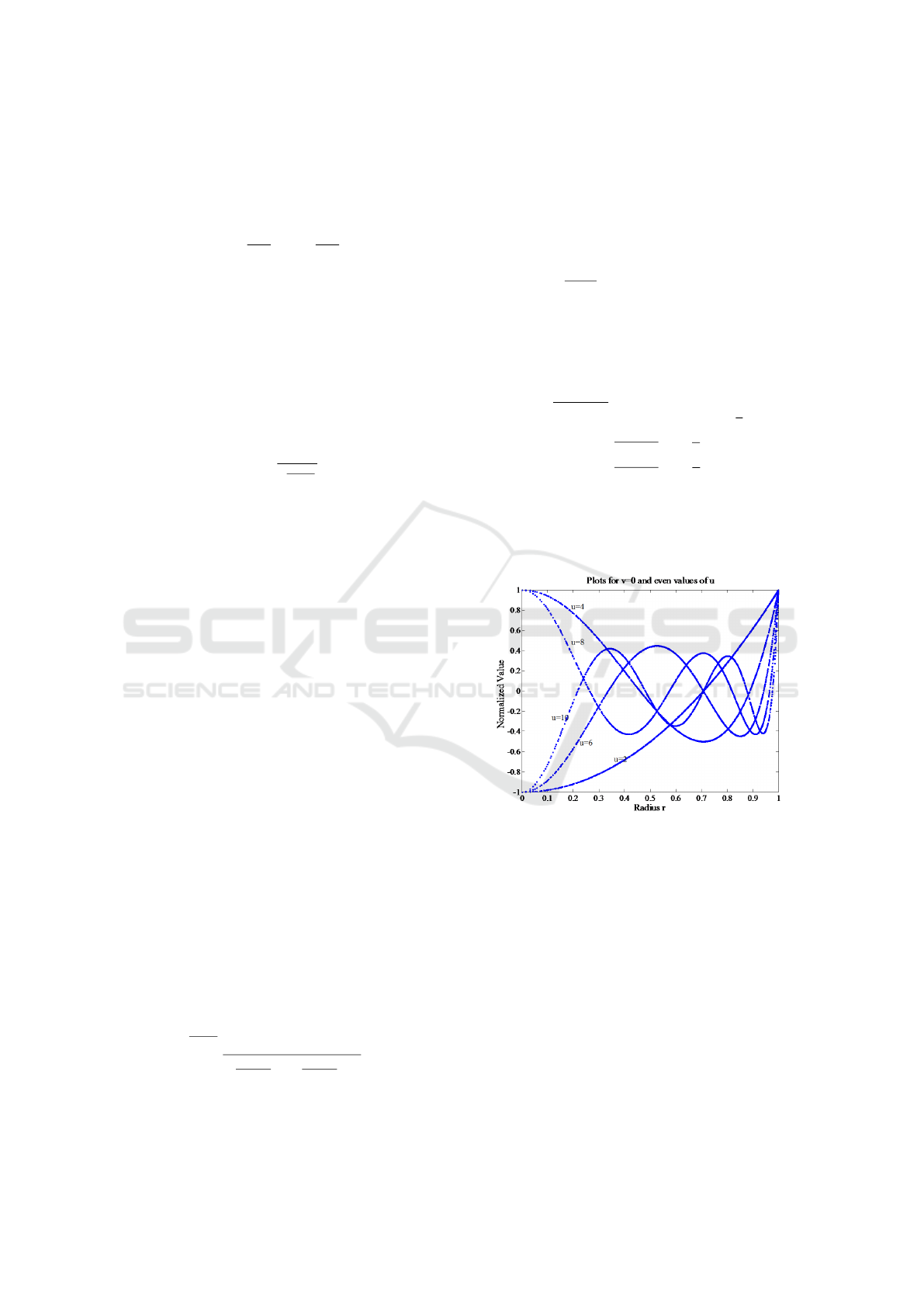
Figure 5 show that even Zernike Polynomial is a
cosine function and as order increases the number of
zero crossings increases, thus enhancing the ability of
ZMs to represent details within an image.
Figure 5: Zernike Polynomial plots for even values of u and
0th repetition.
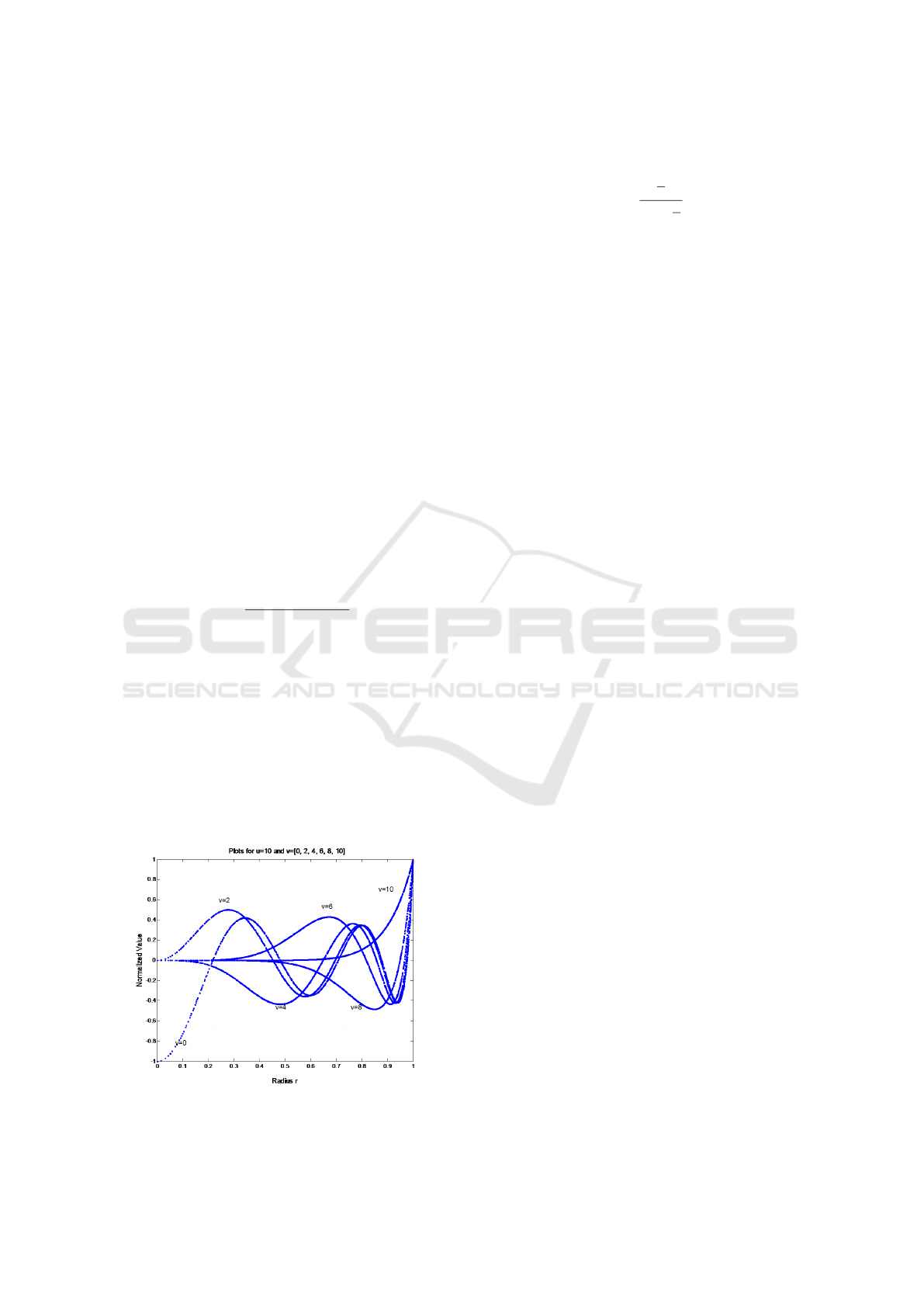
Figure 6 shows the behaviour of Zernike polyno-
mial for 10
th
order and for increasing values of repe-
titions. The valid values of v for 10
th
order are even
values from 0 to 10. Observing the shapes of the
curves in Figure 6, it is realized that as v increases,
the curves becomes flat near the origin and are less
oscillatory. This produces descriptions that the pix-
els lying closer to the perimeter of the unit disc will
have more weight than those lying closer to the origin.
Thus higher values of v are redundant in terms shape
representing properties. Therefore, ZM feature vec-
tor including higher order and lower repetitions may
prove useful. The highest value that v can acquire is
equal to u.
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
544
2.4 Feature Selection and
Normalization
In many classification problems, it is difficult to train
classifiers before removing redundant features due to
the huge size of the data. Reducing the number of
irrelevant features reduces the running time of the
learning algorithms and yields a more general clas-
sifier. Also ensures the better understanding of the
data and the classification rule. Some machine learn-
ing algorithms are known to degrade in performance
when faced with many irrelevant features. A set of
selected feature must be derived for a particular data-
set. Therefore, in this study an optimal set of features
is extracted by using Correlation based Feature Selec-
tion (CFS). CFS selects the features having high cor-
relation with the class and is not correlated with each
other (Duch, Wieczorek, Biesiada et. al., 2004). Info-
Gain (IG) is also known as mutual information. It is
the gain in information or decrease in uncertainty of a
class, when extra information is provided by attribute.
The measure of uncertainty of class is Entropy, de-
noted as H(Y). H(Y/X) is entropy of Y conditioned
on a particular value of X.
IG =
H(X) −H(Y /X )
H(Y )
(18)
Once the selected feature vector is obtained, the rank-
ing technique can find the feature listed in order of
their priority. Feature rank is r
i
(for i=1 to n),where,
n is number of features. Feature weights are calcu-
lated using a Rank Reciprocal technique, such that
sum of all the weights is 1. Each feature is multiplied
by its corresponding weight. This results in feature
normalization and now the feature vector values lie
between (0 to 1), only. By applying Rank Recipro-
cal technique, weight w
i
for each rank r
i
is calculated
by “Eq. (19)”. This neutralizes the effect of different
Figure 6: Zernike Polynomial plots for 10th order and all
repetitions.
scales across features.
w
i
=
1
r
i
∑
k
i=1
1
r
i
(19)
2.5 Supervised Machine Learning
Techniques
SLR system is a multi-class classification problem
with 26 classes of ISL alphabets. The classifiers con-
sidered in this paper are summarized here. Although,
the Support Vector Machine (SVM) is a binary clas-
sifier, it can still be extended for multi-classification
such as human activity recognition (Jakkula, 2011)
and hence in SLR in this case. SVM is supposed to be
effective in high dimensional spaces, in cases where
a number of feature dimensions are greater than the
number of samples. It uses a decision function called
support vectors. Different kernels can be specified for
the decision function. Penalty value, C can be from
0.01 to 100.The value of C=1 and a Polynomial ker-
nel is chosen for this work. Multi-Layer Perceptron
(MLP) with two hidden layer and back propagation
based iterative method is used. Naive Bayes (NB) and
Bayes Net (BN) are the statistical learning classifiers.
These are also considered in this work. k-Nearest
Neighbor (k-NN) is an instance-based learning. The
value of k=3 and the Euclidean distance function is
used to find neighbors. Several advantages of the de-
cision tree as a classification tool have been pointed
out in the literature. These are the non-parametric
method. They tend to perform well if a few highly
relevant features exist as compared to the case where
complex interactions exist (Kotsiantis, Zaharakis, and
Pintelas, 2006). In this study, J48 based on C4.5 al-
gorithm and Logistic Model Tree (LMT), are consid-
ered.
3 RESULTS AND DISCUSSION
3.1 ISL Database
Table 2 shows the proposed feature vector for ISL
database. In the case of ZM, MLP and SVM highest
accuracy is around 89.5%. On combining ZM with
HM and GF, a feature vector size of 135 is obtained.
Highest accuracy of 92.7% is obtained for SVM and
MLP. Next best performer is LMT with 91.2%. How-
ever, the concern with MLP is the time required to
build the model when a feature vector is large. In
terms of model building time, it is observed that SVM
CFS- InfoGain based Combined Shape-based Feature Vector for Signer Independent ISL Database
545

Table 2: Results of Feature Selection and Normalization for ISL database.
Feature Vector SVM MLP NB BN k-NN LMT J48
ZM(121) 89.4 89.5 76.5 74.7 81.1 87.7 79
Combined(135) 92.7 92.7 80.7 82.8 84 91.2 79.3
CFS (56) 93.4 93 89 87.3 86.8 92.1 80
Info Gain+ CFS (56) 96.3 96.7 97.8 96 89.7 96.3 86.3
performs better than MLP and LMT. For other classi-
fiers accuracy remains less than 85%. In order to min-
imize the feature vector size, the standard CFS tech-
nique is applied to the combined set of 135 features.
A reduced feature vector of size 56 is listed in Table
3. Among 56 CFS based selected features, there are
45 ZMs, 4 Hu Moments, and all Geometric features.
Focusing on the ZM order, it is observed that 71%
of selected feature vector are the lower order ZMs.
Therefore, these results are in line with the general-
ized conclusions drawn while analyzing the behavior
of Zernike Polynomial plots in section 2.3.2. It is
worth noting that for selected feature set the perfor-
mance of NB and BN improves significantly. Minor
improvement is also observed in all other classifiers.
Since the feature values have large variations. There-
fore, normalization is done to bring the range of fea-
tures within 0 and 1.For the normalized feature vec-
tor, the highest rise in accuracy is observed for NB,
BN, and J48. Some improvement is also observed for
SVM, MLP, k-NN, and LMT.
3.2 Triesch’s Dataset
The proposed systems performance is also studied on
standard Treisch’s dataset. It has 12 signs of 20 sign-
ers captured in different backgrounds. The results are
shown in Table 4. Three sets of Treisch‘s database are
made. Set 1 includes images of all the signs in both
uniform and complex background, Set 2 includes im-
ages of all the signs in uniform background only and
Set 3 includes images of only 6 distinctive signs in
uniform background. SVM gives higher accuracy in
all the three cases. For uniform background and 6 dis-
tinctive signs, accuracy is 93.2%. It drops to 82.5%
when all 12 signs are taken. The reason for this may
be the large similarity among single hand signs. Ac-
curacy dropped to 61.5% when images with compli-
cated background are also included.
4 CONCLUSION
For ISL database, the accuracy of combined feature
set, CFS based feature vector and normalized feature
vector is compared in Table 2. For combined feature
vector, MLP and SVM give the highest accuracy. It
is worth noting that for selected feature set the perfor-
mance of NB and BN improves significantly. There-
fore, following specific conclusions are drawn:
• Among individual feature sets, ZMs are better
than HM and GF. However, combining GF and
HM enhances the performance of ZM.
• For higher orders of ZM, the feature vector size
increases considerably while a significant im-
provement in accuracy is not achieved. Particu-
larly in the case of Naive Bayes and Bayes Net it
decreases due to the considerable increase in fea-
ture vector size.Therefore, a reduced feature set
is obtained using Correlation based Feature Se-
lection. In the reduced feature vector, 71% lower
order ZMs. The value of iteration, v <= 10 are
selected.
• For combined feature vector, SVM, Logistic
Model Tree, and MLP show similar results and are
better than other classifiers. The Logistic Model
Tree performs at par with MLP and SVM for com-
bined feature set. Therefore, it can be concluded
that Logistic Model Tree, MLP and SVM are ca-
pable of handling the larger feature vector.
• For CFS based reduced feature set the perfor-
mance of NB and BN improves while minor im-
provement is also observed in other classifiers.
SVM performed best for reduced feature set. Fur-
ther using InfoGain based feature weighing, the
performance is enhanced. The major improve-
ment is observed in the case of classifiers like NB,
BN, k-NN, and J48, as these classifiers do not use
an inherent feature normalization process. In case
of normalized feature vector, NB outperformed
SVM, giving the highest accuracy of 97.8%.
• In the proposed feature vector also contains some
higher order lower order ZMs and the value of it-
eration, v <= 10 are selected. Therefore, going
up to higher order and selecting the lower iteration
value has resulted in an optimal feature vector.
• For Treisch‘s dataset, SVM gave a good accuracy
for uniform background only.
The optimal shape-based feature set proposed in this
paper shall further be integrated into a dynamic ISL
recognition system. The proposed feature vector can
be utilized directly for representing the hand gestures
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
546

Table 3: Optimal Feature Vector for ISL Database.
Feature Vector Iteration (v) Selected Features, No. of Features
ZM
u
Selected
Zernike Moments (45) 0 ZM
0
, ZM
2
, ZM
4
, ZM
6
, ZM
8
, 9
ZM
10
, ZM
12
, ZM
14
, ZM
18
1 ZM
1
, ZM
3
, ZM
5
, ZM
7
, 7
ZM
9
, ZM
11
, ZM
17
2 ZM
2
, ZM
4
, ZM
6
, ZM
8
, 7
ZM
10
, ZM
12
, ZM
16
3 ZM
3
, ZM
5
, ZM
7
6
ZM
9
, ZM
11
, ZM
15
4 ZM
4
, ZM
6
, ZM
10
, 6
ZM
12
, ZM
16
, ZM
20
5 ZM
7
, ZM
13
, ZM
17
3
6 ZM
10
, ZM
12
, ZM
18
, 3
7 ZM
7
1
8 ZM
14
1
9 ZM
19
1
10 ZM
18
1
Hu Moments (4) —- H
1
, H
2
, H
3
, H
4
4
Geometric Features(7) —– All Features 7
Total Features 56
Table 4: Results on Triesch’s Dataset.
Dataset SVM MLP NB BN k-NN LMT J48
Set 1: Complex Background, 12 Signs 61.5 55.1 48.7 39.7 44.9 46.2 43.6
Set 2: Uniform Background, 12 Signs 82.5 80.8 60.3 58.6 61.1 78.2 56
Set 3: Uniform Background, 6 Distinctive 93.2 91.4 85 83.8 79.8 92.3 81.6
Signs
in a cluttered background if the images are captured
using depth camera. However, in future, the pro-
posed system pre-processing stage shall be upgraded
to work in the complicated background also.
REFERENCES
Auephanwiriyakul, S.,Phitakwinai, S. and Suttapak, W.
(2013), Thai Sign Language Translation using Scale
Invariant Feature Transform and Hidden Markov
Models, Pattern Recognition Letters, eds. P. Chanda,
and N. Theera-Umpon, 34, 1291-1298.
Bhuyan, M. K., Kar, M. K. and Neog, D. R. (2011), Hand
Pose Identification from Monocular Image for Sign
Language Recognition, IEEE International Confer-
ence on Signal and Image Processing Applications,
Kuala Lumpur, Malaysia, pp. 378-383.
Duch, W., Wieczorek, T. and Biesiada, J.(2004), Compar-
ison of Feature Ranking Methods Based on Informa-
tion Entropy, IEEE International Joint Conference on
Neural Networks, eds. K. Maczka, and S. Palucha, Bu-
dapest, pp. 1415-1419.
Goyal, A. and Walia, E. (2014), Variants of Dense De-
scriptors and Zernike Moments as Features for Accu-
rate Shape-Based Image Retrieval, Signal, Image and
Video Processing, 8, 1273-1289.
Jakkula, V., Tutorial on Support Vector Machine
(SVM), Retrieved from: http://www.ccs.neu.edu/
course/cs5100f11/resources, accessed on 15 March
2016.
Kakumanu, P., Makrogiannis, S. and Bourbakis, N. (2007),
A Survey of Skin-Color Modeling and Detection
Methods,Pattern Recognition, 40, 11061122.
Kausar, S., Javed, M. Y. and Tehsin, S. (2016), A Novel
Mathematical Modeling and Parameterization, Inter-
national Journal of Pattern Recognition and Artificial
Intelligence, 30, 1-21.
Kelly, D., McDonald, J. and Markham, C. (2010), A Person
Independent System for Recognition of Hand Postures
used in Sign Language, Pattern Recognition Letters,
31, 1359-1368.
Khalid, M. and Hosny (2010), A Systematic Method
for Fast Computation of Accurate Full and Subsets
Zernike Moments, Information Sciences, 180, 2299-
2313.
Kotsiantis, S., Zaharakis, I. and Pintelas, P. (2006), Super-
vised Machine Learning: A Review of Classification
and Combining Techniques, Artificial Intelligence Re-
view, 26, 159-190.
Mingqiang, Y., Kidiyo, K. and Joseph, R. (2008), A Sur-
CFS- InfoGain based Combined Shape-based Feature Vector for Signer Independent ISL Database
547

vey of Shape Feature Extraction Techniques, Pattern
Recognition Techniques Technology and Applications,
25, 43-90.
Nallasivan, G., Janakiraman, S. and Ishwarya (2015), Com-
parative Analysis of Zernike Moments with Region
Grows Algorithm on MRI Scan Images for Brain Tu-
mor Detection, Australian Journal of Basic and Ap-
plied Sciences, 9, 1-7.
Ni, X., Ding, G. and Ni, X. (2013), Signer-Independent
Sign Language Recognition Based on Manifold and
Discriminative Training, Information Computing and
Applications Communications in Computer and Infor-
mation Science, eds. Ni, X., Jing, Q., Ma, J., Li, P. and
Huang, T., 391, 263-272.
Ong, S. C. and Ranganath, S. (2004), Deciphering Ges-
tures with Layered Meanings and Signer Adaptation,
6
th
IEEE International Conference on Automatic
Face and Gesture Recognition, Korea, pp. 559-564.
Rautaray, S. and Agrawal, A. (2015), Vision Based Hand
Gesture Recognition for Human Computer Interac-
tion: A Survey, Artificial Intelligence Review, 43, 1-
54.
Rousan, M. A., Assaleh, K. and Tala, A. (2009), Video-
based Signer-Independent Arabic Sign Language
Recognition using Hidden Markov Models, Applied
Soft Computing, 9, 990-999.
Sabhara, R. K., Lee, C .P. and Lim, K. M. (2013), Com-
parative Study of Hu Moments and Zernike Moments
in Object Recognition, Smart Computing Review, 3,
166-173.
Shanableh, T. and Assaleh, K. (2011), User-Independent
Recognition of Arabic Sign Language for Facilitat-
ing Communication with the Deaf Community, Dig-
ital Signal Processing, 21, 535-542.
Singha, J. and Das, K. (2013), Recognition of Indian
Sign Language in Live Video, International Journal
of Computer Applications, 70, 17-22.
Triesch, J. and Malsburg, C. (2001), A System for Person-
Independent Hand Posture Recognition against Com-
plex Backgrounds, IEEE Transactions on Pattern
Analysis and Machine Intelligence, 23, 1449-1453.
Zeshan, U., Vasishta, M. M. and Sethna, M. (2005), Im-
plementation of Indian Sign Language in Educational
Settings, Asia Pacific Disability Rehabilitation Jour-
nal, 16 16-40.
Zhang and Lu, G. (2004), Review of Shape Representa-
tion and Description Techniques, Journal of Pattern
Recognition Society, 37, 1-90.
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
548
