Segmentation of Bone Structures by Removal of Skin and using a

Convex Relaxation Technique

José A. Pérez-Carrasco

, Begoña Acha

, C. Suárez

and Carmen Serrano

Signal Theory and Communications Department, University of Seville, Sevilla, Spain

Technological Innovation Group, Virgen del Rocío University Hospital, Sevilla, Spain

{jperez2, bacha, cserrano}@us.es, cristina.suarez.exts@juntadeandalucia.es

Keywords: CT, Bone Segmentation, Skin Extraction.

Abstract: In this paper an algorithm to extract the skin and obtain the segmentation of bones from patients in CT

volumes is described. The skin is extracted using an adaptive region growing algorithm followed by

morphological operations. The segmentation of bone structures is implemented by the minimization of an

energy function and using a convex relaxation minimization algorithm to minimize the energy term. The

cost terms in the energy function are computed using the distance between the mean and variance

parameters within bone structures in a training set and the mean and variance parameters computed locally

at each voxel position (x,y,z) in a test dataset. Several performance metrics have been computed to assess

the algorithm. Comparisons with two techniques (thresholding and level sets) have been carried out and the

results show that the algorithm proposed clearly outperform both techniques in terms of accuracy in the

delimitation results.

1 INTRODUCTION

The analysis of bone structures is interesting for

physicians, surgeons and radiologists in many

applications, such as bone fractures, cancer, analysis

of bone densities, diagnosis of some diseases

(osteoporosis, rheum, arthrosis), etc. Usually, in

these analysis, simple operations, such as

thresholding, are performed to extract bone

structures in CT 3D volumes. However, the

thresholding technique is not valid when some of

those diseases happen, as Hounsfield values within

bones may have different values as those expected.

Furthermore, Hounsfield values within bones vary

due to the different components (mainly periosteum,

compact (hard) bone, cancellous (spongy) bone and

bone marrow), making the segmentation of these

structures difficult. Fig. 1 shows a CT slice where

these Hounsfield differences can be appreciated.

Note that Hounsfield values in cancellous bone, for

instance, are quite similar to those values in

surrounding organs, making thresholding techniques

fail as they select either only the boundaries of bones

or some other soft tissues around the bone structures.

Besides, even boundaries in bone structures

(compact bone) can be difficult to be segmented due

to some of the diseases above mentioned.

Figure 1: Different parts within bones in CT volumes.

Another problem that physicians have to face is

the high computational cost when managing 3D CT

volumes. Thus, automatic algorithms able to

segment complete bone structures would be very

useful for specialists in the field, decreasing the time

in selecting them.

Many works have been presented to carry out the

Pérez-Carrasco, J., Acha, B., Suárez, C. and Serrano, C.

Segmentation of Bone Structures by Removal of Skin and using a Convex Relaxation Technique.

DOI: 10.5220/0006201105490556

In Proceedings of the 6th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2017), pages 549-556

ISBN: 978-989-758-222-6

549

segmentation of bone structures (Kang et al., 2003;

Sebastian et al., 2003; Cheng et al., 2013; Cervinka

et al., 2014; Aslan et al., 2009; Calder et al., 2011;

Kratky et al., 2008; Perez et al., 2015), being graph

cuts and level set algorithms (Kratky et al., 2008)

considered as representative of the state-of-the-art

methods. However, the main drawbacks in all these

works is that either they are focused in one or two

bone structures (hip, acetabulum, femoral head,

vertebral bodies, etc.), thus losing generality, or they

require high computational times or suffer from high

sensitivity to initialization (Kratky et al., 2008).

In this paper an algorithm to segment bone

structures is described. The procedure tries to be fast

and general to any kind of bone structures. The

paper is organized as follows: Section 2.1 describes

the extraction of the skin surface in order to facilitate

the selection of bone structures by removing

artificial structures that may have high Hounsfield

values outside the patient and reducing the areas

within each slice to be analyzed. Although there are

few works addressing the segmentation of skin in

CT volumes (Kang et al., 2014; Xiangrong et al.,

2004; Banik et al., 2010), the delimitation of the skin

can be very useful in order to facilitate the

segmentation of other organs or structures such as

liver, heart, muscle tissues, lung etc. Section 2.2

describes the algorithm developed to perform the

bone segmentation. Basically, the segmentation of

bone structures is implemented applying the

continuous max-flow algorithm by Yuan et al.,

(2010) building an energy function to be minimized.

The cost terms in the energy function are obtained

from distance images which are built by computing

the distance between the local mean and variance in

each CT voxel to the parameters mean and variance

computed from all the voxels in bone structures

within a training dataset. Section 3 shows the results

and finally, the conclusions and future work are

described.

2 METHODOLOGY

2.1 Skin Selection

In order to facilitate the segmentation of bone

structures, the first stage of the algorithm extracts

the surface skin of the patients in the CT volumes

under analysis. The common techniques to

delimitate the skin in CT volumes are based on the

use of global thresholds and edge detection

techniques (Kang et al., 2014; Zhou et al., 2004;

Banik et al., 2010). However, global thresholds are

not valid in all the cases and edge detection

techniques usually have problems with edge

delimitation and connection. As indicated in the

work by Zhou et al., (2004), skin has a depth of

about 2mms. Considering that the CT volumes

throughout this work have an xy spatial resolution of

about 0.781mm/pixel, 2mms corresponds to

approximately 3 pixels in the xy plane directions.

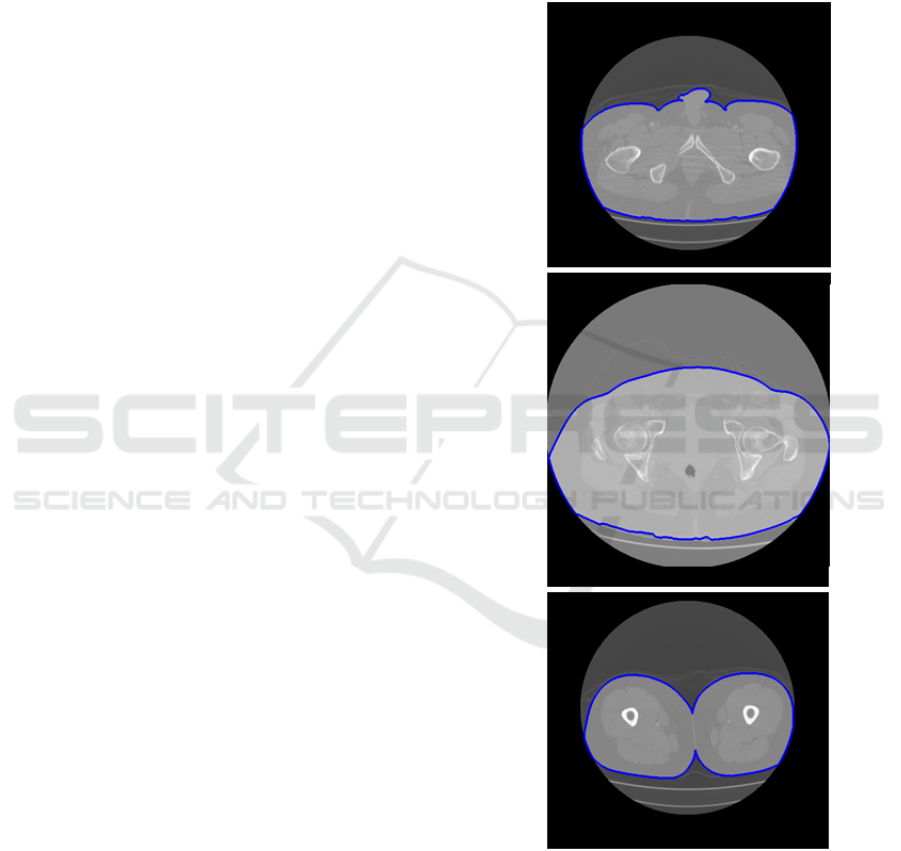
Figure 2: Skin (in blue) of three patients in different CT

slices.

The skin selection stage is performed in two

steps. In the first step, a neighbourhood-connected

region growing algorithm is applied to select inner

structures within the body. For this, some seeds

within the patient are selected. These seeds are

ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods

550

selected randomly and automatically by selecting

some voxels corresponding to bone (voxels with

Hounsfield values over 1700). The inclusion

criterion only takes into account Hounsfield values

within a range specified by the user by means of two

range values. Experimentally, the best lower and

upper inclusion values were 800 and 2500,

respectively. Only voxels with values within the

range are selected if also their neighbouring voxels

have Hounsfield values within the same range. With

this algorithm, artifacts or air (like in lungs or

outside the body) are discarded. The result is a

binarized image.

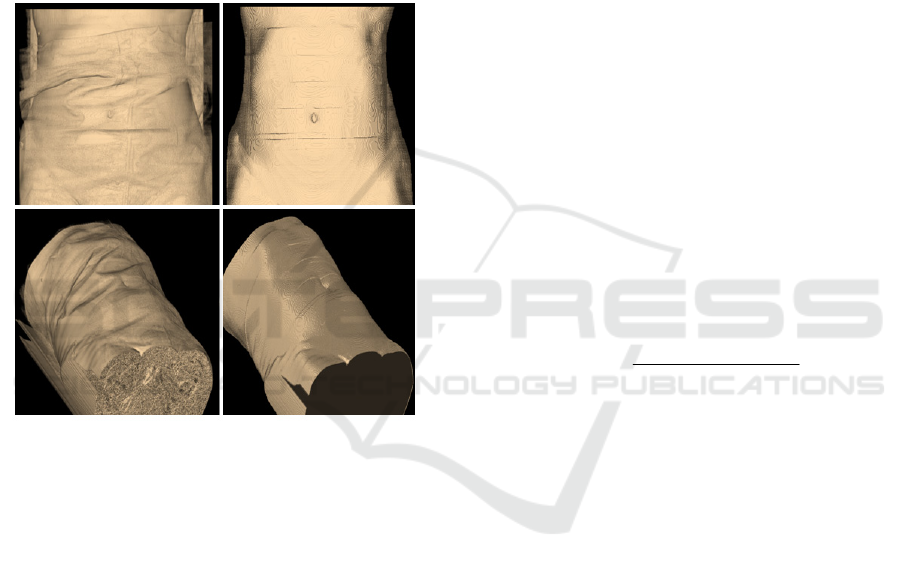
Figure 3: Examples of the 3D surface (skin) of a patient.

Left figures correspond to the surface before the skin

extraction operation. Right figures show the outer surface

of the patient.

The outer boundary of the binarized image will

correspond to the skin. Thus, in the second step, an

structure element of 3 voxels in the xy axis and 1

voxel in the z axis is employed. Using a simple

erosion morphological operation and substracting

the result to the original binarized image, the skin

can be obtained.

Fig. 2 shows the skin boundaries of three CT

slices corresponding to three different patients. Fig.

3 shows two examples of the 3D surface (skin) of a

patient. Left figures correspond to the surface before

the skin extraction operation. Right figures show the

outer surface (skin) of the patient. Note in Fig. 2 and

3 how artificial artefacts, such as sheets or bed, have

been removed.

2.2 Bone Segmentation

The algorithm for bone segmentation has three

different stages.

2.2.1 Normalization

In the first stage, a thresholding operation is

performed in order to remove soft tissue (such as fat

or some organs) with Hounsfield values below those

present in bones. To compute this threshold a set of

training CT slices were analyzed to determine the

minimum value present in all the bone structures.

More particularly, the training set was composed by

10 CT slices extracted from CTs of different patients

and different to those used in the test set.

Subsequently, a threshold was chosen under this

minimum value. The thresholding operation

guarantees that all the bone structures are maintained

in the CT slices while removing all those soft tissue

structures which could interfere in the bone structure

delimitation. The experimentally threshold obtained

had a value of 900 HU (Hounsfield Units). With this

thresholding operation all the bone structures are

still clearly visible while many of the soft tissues

have been removed.

Finally, the CT volumes are scaled with the

following scaling operation:

)_max(

Im_

Scaled_Im

settraining

Thresh



(1)

where Thresh_Im is the thresholded Image obtained

in the previous step and Scaled_im is the Image

obtained after the scaling operation. The maximum

value within the training set is used also to scale the

Dicom CT slices. Note that with this scaling

operation the Dicom slices will have values in the

range [0,1].

2.2.2 Computation of Statistical Distance

Image

In the second stage, using all the voxels within bone

structures in all the scaled CT slices belonging to the

training set, the mean and variance parameters are

extracted. This set of two parameters is denoted as

RSP (Reference Statistical Parameters). Then, for

each CT volume in the test dataset and at each voxel

position (x,y,z), the parameters mean and variance

are computed using a 5x5 local neighborhood around

the voxel position (x,y,z). Then, the Euclidean

distance from this computed set of parameters to the

reference parameter set RSP (mean and variance) is

obtained. This distance value is stored in the called

Segmentation of Bone Structures by Removal of Skin and using a Convex Relaxation Technique

551

SDI (Statistical Distance Image) image at the same

positions (x,y,z).

Fig 4 shows two slices corresponding to two

different patients (first row) and the corresponding

two SDI images obtained (second row). Note that

voxels belonging to bones have low values whereas

voxels not corresponding to bones present high

values.

2.2.3 Convex Relaxation to Implement Bone

Segmentation

In the last stage, the convex relaxation technique

proposed by Yuan et al.

(Yuan et al, 2010) is used to

perform the segmentation stage. Yuan et al.

modified the classical discrete min-cut max-flow in

graph-cut implementations by creating a continuous

domain and allowing the labeling terms to be

continuous. The fast max-flow implementation by

Yuan et al. provided a convex solution and, as

proved by Yuan et al., their implementation

outperformed the classical graph-cut techniques both

in terms of speed and accuracy. Yuan et al.

demonstrated that their fast max-flow

implementation is equivalent to the continuous s-t

min-cut problem as follows:









 dxxuxCdxxCxudxxCxu

)()()())(1()())((min

1,0)(

(2)

where u(x) is the continuous labeling function and

C and

are the cost terms in the energy function.

Note that according to Eq. (1), the cost term

should take low values inside bone structures and

high outside them. On the contrary,

should take

high values inside bone structures and low values

outside them. In our experiments, Cs and Ct were

computed as follows:

Cs-1Ct

SDI))/2-(1 (Scaled_Im=Cs





(3)

The most right term in Eq. (2) is a penalty term. C(x)

is a penalty function that penalizes voxels at

boundaries with low gradients.

This C(x) function is computed as follows:

)Im(_1

)(

xScaleda





(4)

where a and b are constants and were obtained

empirically. The parameters a and b took the values

10 and 0.2 respectively. In the third row of Fig. 4 the

cost terms Cs corresponding to two slices of two

different cases are shown.

The energy term described in Eq. (2) is

minimized using the algorithm described by Yuan et

al. in (Yuan et al., 2010).

3 RESULTS

Bone structures in 45 slices belonging to 15 different

CT volumes (and different to those in the training

set) were manually segmented by an expert and used

as groundtruth to assess the algorithm. The CT

volumes were composed on average of 250 CT

slices. The same CT slices were processed as

described in the previous section and several

evaluation metrics were computed. These metrics

have been computed in terms of TP (true positive

voxels), FP (False positive voxels), TN (true

negative voxels) and FN (False negative voxels). TP

are those voxels classified by the algorithm as bone

and also by the expert in their manual segmentation.

FP are those voxels classified as bone by the

algorithm but not by the expert. TN correspond to

voxels classified as not belonging to bones both by

the algorithm and by the groundtruth segmentation.

Finally, FN are those voxes classified as not

belonging to bones by the algorithm but they

correspond to bones according to the groundtruth.

The metrics used for the evaluation are DICE,

Jaccard, Sensitivity, Specificity, PPV and are

computed as follows:

FNFPTP







Dice

(5)

FNFPTP



dJaccar

(6)

FNTP

ySensitivit





(7)

TNFP

ySpecificit





(8)

FPTP

PPV





(9)

A conventional PC (Intel ® Core ™ i7-2670QM,

CPU @ 2,20GHz, 6GB RAM) was used in all of

these evaluations.

In order to compare the results obtained by the

algorithm with other state-of-the-art methodologies,

comparisons using the same evaluation metrics with

a level set implementation and with the classical

thresholding technique have been carried out.

Particularly, the level set methodology adopted in

the experiments is the Distance Regularized Level

Set Evolution (DRLSE) implementation (Li et al,

2010). The same test dataset was used to perform the

comparisons.

In the Level-Set implementation some

configurable parameters are selected to perform the

segmentation. Particularly, the parameter values

ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods

552

Figure 4: First row (a): Original CT slices. Second row (b): SDI images corresponding to the slices in the first row. Third

row (c): Cost Image terms used as input in the convex relaxation algorithm.

20



, timestep

5t

5.1



and

1



required

by the algorithm were used in our experiments. The

DRLSE algorithm was applied to the 45 scaled

dicoms (Scaled_Im) described in the previous

section.

Regarding to the thresholding implementation, a

threshold is selected and all Hounsfield values under

that threshold are set to zero. In our experiments the

threshold selected was that providing the best

results. Experimentally, using the training set, the

threshold value obtained was 1100.

Table 1 shows the evaluation metrics for the

algorithm described throughout this paper and the

two segmentation techniques above indicated. The

Segmentation of Bone Structures by Removal of Skin and using a Convex Relaxation Technique

553

average computational time required to segment one

slice for every algorithm is also indicated. Note that

the algorithm described throughout this paper was

the only providing good results, followed by the

thresholding implementation. The level set

implementation had difficulties when several bone

structures are present or when some bone structures

had diffuse boundaries or low gradient values. In

many of these cases the DRLSE algorithm required

a very high computational time (high number of

iterations) to provide acceptable results. Note,

according to Table 1, that the standard deviation

obtained in the different metrics when using the

DRLSE algorithm are high, thus showing that the

method performed very well in some slices (Dice

Coefficient of 0.94 in the best case), whereas it was

incapable of performing the segmentation in others

(Dice Coefficient of 0.04 in the worst case).

In terms of computational times, the thresholding

technique was the fastest one requiring only about

0.023 seconds to segment one slice. Considering a

CT volume composed of about 100 slices, this

would imply a processing time of only 2 seconds.

Table 1: Metrics obtained in the different experiments.

The values in the table represent the mean value of each

metric ± its standard deviation.

Thresholding DRLSE

Algorithm

proposed

Dice 0.79±0.09 0.59±0.35 0.9±0.053

Jaccard 0.66±0.13 0.49±0.34 0.83±0.087

PPV 0.80±0.13 0.52±0.37 0.86±+0.085

Sensitivity 0.80±0.16 0.94±0.21

0.97±0.049

Specificity 0.99±0.01 0.88±0.13 0.99±0.005

Computational

Time (

econds

per slice)

0.11±0.05 2752±657 89±6.73

In Fig. 5 the results obtained using the three

different methodologies are shown. Only some slices

are shown for visualization purposes. The red

contours correspond to the groundtruth segmentation

provided by the expert. Blue regions correspond to

the segmentation results obtained with each

algorithm. Note that the thresholding technique is

not able to select all the voxels within bones as they

present Hounsfield values under the specified

threshold. It can be also appreciated that the level set

technique had difficulties when the number of bone

structures is very high (second row, first colum) or

selected non bone tissue if it was enclosed within a

bone structure (third row, first colum).

4 CONCLUSIONS

In this paper a technique to implement the selection

of bone structures in CT volumes is described. The

first stage consists in the delimitation of the skin

(outer surface of the patient) in order to facilitate the

segmentation of the bone structures by reducing the

computational cost required. Note that the

computation of the Statistical Distance Image has a

considerable computational cost. Thus, discarding

the outer elements in the patient together with the

application of a threshold to discard soft tissues

decreases significantly the number of voxels to be

processed. Threfore, the computational time to

implement the segmentation is considerably

reduced.

A convex relaxation technique is applied using

the Histogram Distance Image as input. The convex

relaxation technique employed is the fast continuous

max-flow implementation by Yuan et al., (2010)

using the previously computed SDI image as cost

term in the energy function.

Comparison with an state-of-the-art algorithm

(DRLSE implementation) (Li et al., 2010) and the

thresholding technique, which is the preferred and

fastest technique in most of the tools used in the

clinical practice, show that the algorithm proposed

clearly outperform both techniques in terms of

accuracy in the delimitation results.

In future implementations, comparisons with

other techniques will be carried out. Note that the

performance results provided by the DRLSE

implementation were low and maybe other

techniques could be more suitable in the

segmentation of bone structures.

Besides, in future works, the two-label algorithm

described will be modified in order to identify a high

number of labels thus allowing the identification of

other kind of structures.

ACKNOWLEDGEMENTS

This research has been cofinanced by P11-TIC-7727

(Government of Andalusia, Spain) and

PT13/0006/0036RETIC (FEDER Funds and

Department of Health, Regional Government of

Andalusia).

ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods

554

Figure 5: First Column (a) shows the results (blue regions) provided by the DRLSE algorithm. Central column (b) shows

the results (blue regions) provided by the thresholding implementation. Right column shows the results provided by the

algorithm described (blue regions). The groundtruth segmentations are contoured in red.

REFERENCES

Aslan, M.S., Ali, A., Rara, H., Arnold, B., Farag, A.A.,

Fahmi, R. and Xiang, P., 2009. 'A novel 3D

segmentation of vertebral bones from volumetric CT

images using graph cuts'. ISVC '09 Proceedings of the

5th International Symposium on Advances in Visual

Computing: Part II. Lecture Notes in Computer

Science. 5876 LNCS, pp. 519-528.

Banik, S., Rangayyan, R. M. and Boag, G. S., 2010.

'Automatic Segmentation of the Ribs, the Vertebral

Column, and the Spinal Canal in Pediatric Computed

Tomographic Images'. Journal of Digital Imaging, vol.

23, no. 3, pp. 301–322. http://doi.org/10.1007/s10278-

009-9176-x

Calder, J., Tahmasebi, A.M. and Mansouri, A.-R., 2011.

'A variational approach to bone segmentation in CT

images'. In Progress in Biomedical Optics and

Imaging Proceedings of SPIE.

Cervinka, T., Hyttinen, J. and Sievnen, H.. 2014. 'Accurate

cortical bone detection in peripheral quantitative

computed tomography images'. In IFMBE

Proceedings, pp. 289–292.

Cheng, Y., Zhou, S., Wang, Y., Guo, C., Bai, J. and

Tamura, S., 2013. 'Automatic segmentation technique

Segmentation of Bone Structures by Removal of Skin and using a Convex Relaxation Technique

555

for acetabulum and femoral head in CT images'.

Pattern Recognition, vol. 46, no. 11, pp. 2969-2984.

Kang, H.-C., Shin, Y.-G. and Lee, J., 2014. 'Automatic

segmentation of skin and bone in CT images using

iterative thresholding and morphological image

processing'. In The 18th IEEE International

Symposium on Consumer Electronics (ISCE 2014),

JeJu Island, pp. 1-2. doi: 10.1109/ISCE.2014.6884320.

Kang, Y., Engelke, K. and Kalender, W.A., 2003. 'A new

accurate and precise 3-D segmentation method for

skeletal structures in volumetric CT data'. IEEE

Transactions on Medical Imaging, vol. 22, no. 5, pp.

586–598.

Kratky, J. and Kybic, J., 2008. 'Three-dimensional

segmentation of bones from CT and MRI using fast

level sets'. In Progress in Biomedical Optics and

Imaging Proceedings of SPIE.

Li, C., Xu, C., Gui, C. and Fox, M. D., 2010. 'Distance

Regularized Level Set Evolution and its Application to

Image Segmentation'. IEEE Trans. Image Processing,

vol. 19, no. 12, pp. 3243 – 3254.

Perez, J.-A., Acha, B., and Serrano, C., 2015.

'Segmentation of Bone Structures in 3D CT Images

Based on Continuous Max-flow Optimization'. In

SPIE Proceedings Proc. SPIE 9413, Medical Imaging

2015. Image Processing, vol. 94133Y.

Sebastian, T.B., Tek, H., Crisco, J.J. and Kimia, .B., 2003.

'Segmentation of carpal bones from CT images using

skeletally coupled deformable models'. Medical Image

Analysis, vol. 7. no. 1, pp. 2-45.

Yuan, J., Bae, E. and Tai, X.-C., 2010. 'A study on

continuous max-flow and min-cut approaches'. In

Proceedings of the IEEE Computer Society

Conference on Computer Vision and Pattern

Recognition, pp. 2217–2224.

Zhou, X., Hara, T., et al., 2004. 'Automated segmentations

of skin, soft-tissue, and skeleton from torso CT

images'. Medical Imaging. Image Processing,

Proceedings of SPIE 5370 (SPIE, Bellingham, WA).

ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods

556