Retrieving Similar X-ray Images from Big Image Data

using Radon Barcodes with Single Projections

Morteza Babaie

1,2

, H. R. Tizhoosh

, Shujin Zhu

and M. E. Shiri

KIMIA Lab, University of Waterloo, ON, Waterloo, Canada

SINA Lab, Mathematics & Computer Science Department, Amirkabir University of Technology, Tehran, Iran

School of Electronic & Optical Eng., Nanjing Univ. of Sci. & Tech., Jiangsu, China

Keywords: Radon Transform, Content-based Image Retrieval, Binary Barcode, Radon Barcodes, Big Data.

Abstract: The idea of Radon barcodes (RBC) has been introduced recently. In this paper, we propose a content-based

image retrieval approach for big datasets based on Radon barcodes. Our method (Single Projection Radon

Barcode, or SP-RBC) uses only a few Radon single projections for each image as global features that can

serve as a basis for weak learners. This is our most important contribution in this work, which improves the

results of the RBC considerably. As a matter of fact, only one projection of an image, as short as a single

SURF feature vector, can already achieve acceptable results. Nevertheless, using multiple projections in a

long vector will not deliver anticipated improvements. To exploit the information inherent in each projection,

our method uses the outcome of each projection separately and then applies more precise local search on the

small subset of retrieved images. We have tested our method using IRMA 2009 dataset a with 14,400 x-ray

images as part of imageCLEF initiative. Our approach leads to a substantial decrease in the error rate in

comparison with other non-learning methods.

1 INTRODUCTION

Nowadays, the role of computers has significantly in-

creased in our daily lives. As a result, most of the

computerized activities are stored as some sort of data

such as text, photos, videos, audio files and more.

Hence, it is not surprising that searching for data and

finding specific data in all these massive datasets is

not only a challenging task in many fields but also

quite often a necessary one (Rodríguez et al. 2015).

One of these challenges stems from the Content-

Based Image Retrieval (CBIR) which is considered as

an important task in “biomedicine, military, com-

merce, education, and Web image classification and

searching. In the biomedical domain, CBIR can be

used in patient digital libraries, clinical diagnosis,

searching of 2-D electrophoresis gels, and pathology

slides” (Wang 2001). CBIR is primarily concerned

with searching for and delivering similar images pro-

vided a query (input) image is given by a user.

One of the practical aspects of CBIR in medical

imaging is to assist clinicians for diagnostic purposes

by enabling them to compare the case they are

examining with previous (known) cases. It is

established pratcice that most hospitals do store their

patient data for a long periode of time; generally

images are stored in PACS (picture archiving and

communication system) and related documents such

as biopsy and treatment reports are stored in RIS

(radiology information system). Let us assume that a

diagnostic case is being inspected, by using a reliable

CIBR system clinicians can benefit from analogous

cases buried among millions of images, and hence

achieve higher diagnostic accuracy based on

comparative discrimination with previous (known)

cases (Kumar et al. 2013). A large number of CBIR

methods exist in the literature. Feature extraction,

learning, dictionary approaches, and binary

descriptions are among most commonly used

techniques to search for similar images.

In this paper, we propose compact features to fa-

cilitate fast image retrieval. Our method (Single Pro-

jection Radon Barcode, SP-RBC) benefit from the in-

formation inherent in single Radon projections, based

on the recently introduced Radon Barcodes (RBC)

that capture image information in short binary vec-

tors, or barcodes. We will report both cases where we

use the actual values of Radon projections as well as

their binary encodings known as Radon barcodes

(RBC).

The rest of this paper is organized as follows: Sec-

tion 2 provides a brief review of related works and

Babaie, M., Tizhoosh, H., Zhu, S. and Shiri, M.

Retrieving Similar X-ray Images from Big Image Data using Radon Barcodes with Single Projections.

DOI: 10.5220/0006202105570566

In Proceedings of the 6th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2017), pages 557-566

ISBN: 978-989-758-222-6

557

Radon transform. Section 3 will describe our pro-

posed method. The results of our experiments and

comparisons are reported in Section 4. The last sec-

tion provides some conclusions and suggestions for

the feature works.

2 RELATED WORK

Content-based image retrieval (CBIR) techniques au-

tomatically search for similar images in a database by

using visual features extracted to represent its

content, and not by a text description. In many cases,

textual descriptions may not be available, and in

many other cases, it is extremely difficult, if not im-

possible, to describe the image content (e.g., the

shape of an irregular tumor in a breast ultrasound

scan) adequately in all necessary details.

The major challenge for CBIR is to extract the rel-

evant image features based on relevant feature simi-

larity criteria and to organize the extracted features

into some sort of compact embeddings or representa-

tions for fast retrieval from big databases (Kumar et

al. 2013). The features or descriptors that represent

the properties/content of the images are often used in

CBIR systems. The choice of features or descriptors

should minimize the “semantic gap” between the ex-

tracted image features on one side and the human’s

interpretation of the image content on the other side.

Early CBIR systems often used the image fea-

tures/descriptor, such as histogram, shape and texture

descriptors (Gevers & Stokman 2004; Lee et al. 2003;

Saha et al. 2004). Gevers and Stokman proposed an

object recognition method based on the histograms

derived from photometric color invariants, which out-

performed the traditional color histogram scheme but

was very sensible to the noise (Gevers & Stokman,

2004). The edge histogram which contains the gen-

eral shape information and the moment that describes

the image pixel intensities were also used in early

CBIR systems (Shim et al. 2002; Zhu & Schaefer

2004).

The advanced features such as Scale Invariant

Feature Transform (SIFT) (Lowe 2004) and Speeded

Up Robust Features (SURF) (Bay et al. 2008) are

employed in CBIR systems to retrieve similar images

from different point of views and transformations (Do

et al. 2010; Velmurugan & Baboo 2011). As many of

these smart features are invariant to scale and rota-

tion, they are more robust than typical image trans-

forms. However, the features are typically large and

inefficient to conduct matching in big image data.

Ledwich et al. used the structure of typical indoor en-

vironments to reduce the need for rotational invari-

ance of the features, which has a minimal effect on

retrieval rate and significant improvement in effi-

ciency (Ledwich & Williams 2004). Velmurugan and

Babbo used the KD-tree with the Best Bin First (BBF)

(Beis & Lowe 1997) indexing method to accelerate

the similarity match of the SURF and color moments

combined features (Velmurugan & Baboo 2011).

With dramatic growth of image data in recent

years, one of the current trends in CBIR is to use

binary features such as Local Binary Patterns (LBP)

(Ojala et al. 2002), Binary Robust Invariant Scalable

Keypoints (BRISK) (Krig 2012), Binary Robust

Independent Elementary Features (BRIEF) (Calonder

et al. 2010), and Radon Barcodes (Tizhoosh 2015).

Comparing to non-binary features, the distance

computation between binary strings is much faster

for retrieving tasks. Bankar et al. proposed a CBIR

system based on LBP variance which characterized

the local contrast information into the one-dimen-

sional LBP histogram (Bankar et al. 2014). Subrah-

manyam et al. extended the LBP, which took ad-

vantage of the magnitude of the local difference be-

tween the center pixel and its neighbors which were

able to extract the edge information in the image, and

proposed the local maximum edge binary patterns

(LMEBP) descriptor (Subrahmanyam et al. 2012).

Other methods such as Deep Neural Networks

(DNNs), Convolutional Neural Networks (CNNs),

and Bag of Words (BoW) have been recently

developed for CBIR tasks. Learning from massive

annotated data in the deep learning networks, CNN

features would carry high-level and riche semantic in-

formation (Yan et al. 2016), which had been proved

to be successful in achieving state-of-the-art perfor-

mance (Babenko et al. 2014; Wan et al. 2014). Avni

et al. made use of SIFT descriptors to build the feature

dictionary with the bag of visual words approach, per-

forming outstandingly for the x-ray image retrieval

task in IRMA dataset (Avni et al. 2011). The best re-

sults so far have been reported by combining LBP and

saliency detection (Camlica et al. 2015).

However, most of CBIR methods face high com-

putational expenses and require considerable re-

sources during the learning phase. Besides, their im-

plementation requires sophisticated and complicated

design and data structures (Krig 2012).

In the medical field, CBIR systems can assist cli-

nicians to make more reliable clinical decisions by re-

trieving similar (proven) cases from the past stored in

their archives. But for the most of the afore-men-

tioned methods, they usually need to undergo param-

eter tuning to be applicable to medical image pro-

cessing (Huang et al. 2010). Not only because most

ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods

558

of the medical images have a known direction or

known scale (which means the global search would

not face related challenges), but also because at least

for the case of local descriptors in medical images,

experiments show they are generally not able to

achieve good results (Avni et al. 2011). It would be

acceptable if we use very simple content-based re-

trieval methods, rather than learning-based compli-

cated methods in order to save time for learning and

parameter tuning, even if we cannot reach top accura-

cies, but can provide comparable results.

As Radon transform can convert global detection

problem in the image domain into local peak detec-

tion problem in the parameter domain (Aundal &

Aasted 1996), it is widely applied in the medical field,

especially in Computed Tomography. Radon bar-

codes, RBC, are binary codes generated by Radon

Transform with projection binarization, proposed for

medical image retrieval system. RBCs have achieved

comparable results with many other methods from lit-

erature (Tizhoosh 2015) and are easy to implement

and efficient in matching and retrieving (via Ham-

ming distance) with low requirements for memory

and storage.

In this paper, a content-based image retrieval ap-

proach for big datasets is proposed. The multiple Ra-

don projections with selected angles are first ex-

tracted (considered as global features) for each image.

Each projection is used separately to search for simi-

lar images from the big dataset. The more precise lo-

cal features such as LBP and shifted Radon projec-

tions are then employed to refine the results. We use

the IRMA dataset of 14,400 x-ray images to validate

the approach.

2.1 Radon Transform

Radon introduced an integral transformation, which

calculates the sum of the values of an image along

parallel lines for various angels (Radon 1917). One

key factor of Radon transform is its ability to recon-

struct the main image from its transform. The Radon

transform has been applied in medical imaging, e.g.,

in computer tomography, for image reconstruction

(Gu & Sacchi 2009). The Radon transform is

generally given as for each given  as follows:



R( , )= ( , )

xy xcos ysin dxdy

    

 

 





(1)

In this equation, , refers to grey-level inten-

sities of image f at position



,



, and . is a Dirac

delta operator.

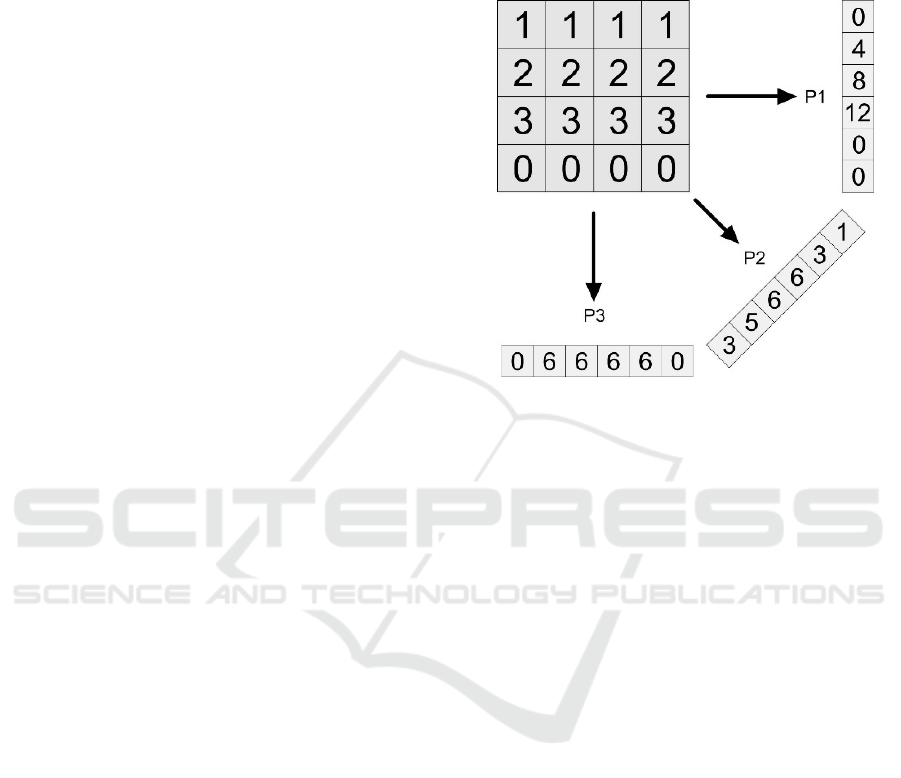
Figure 1 depicts an example for a small

matrix and three sample Radon projections which can

be used as image features and have been applied in

many fields of computer vision (Aundal & Aasted

1996). It also has been applied in form of Radon Bar-

codes for medical CBIR systems in large datasets

(Tizhoosh 2015).

Figure 1: Three Radon projections in 0, 45 and 90-degree

directions. Zero padding is applied to create same-length

vectors.

3 PROPOSED METHOD

In this section, we introduce the idea to use single Ra-

don projections for CBIR in its both forms, namely

real-valued (single projection Radon, SP-R) and bi-

nary (single projection Radon barcode, SP-RBC) im-

plementations. First, we describe the automated

preprocessing steps. In the next step, we explain how

we use Radon projections to reach top similarity for

each projection separately. We then introduce the ex-

ploitation method, which is used to find the most sim-

ilar images in the pre-selected set (Selection Pool).

Finally, we apply a binarization method to create SP-

RBC. For all our experiments, we use the IRMA da-

taset (Tommasi et al. 2009).

3.1 Pre-Processing Images

Data test images we use is quite challenging. For in-

stance, the imbalance in IRMA image dataset has

been noted as one of the most challenging aspects of

this dataset (Avni et al. 2011). There is major varia-

bility in IRMA images, not only in the term of a sam-

ple density in each category but also with respect to

image size, brightness, scale of body objects as well

as unrelated burned-in landmarks (Figure 2). To re-

duce the effects of these problems, we proposed a pre-

processing chain composed of three stages:

Retrieving Similar X-ray Images from Big Image Data using Radon Barcodes with Single Projections

559

1) resizing images to zero-padded squared im-

ages to avoid distortion due to necessary under-sam-

pling (most CBIR methods do require under-sam-

pling of images to reduce computational burden),

2) removing non-related parts such as burned-in

landmarks (e.g., letters) due to the digitization of x-

ray films, and

3) circular image margin suppression (super-im-

posing a circle on the image to eliminate the image

margin from the processing).

Figure 3 shows the output of our pre-processing

steps when applied on images from Figure 2.

Figure 2: Four samples from IRMA training set to illustrate

the variability of X-ray image data.

Figure 3: The pre-processing effect for same samples from

Figure 2 to create “normalized” inputs.

Figure 4 shows the difference between our

squaring method and simple image resize operations.

This operation preserves the original scale of image

whiteout distortion due to the resize operation which

shows significant improvements in the results (see

Table 4 in the result section) in comparison with pre-

vious works.

Figure 4: a) rectangular images, b) resized by our method

(squared with zero padding), and c) resized conventionally.

For the second pre-processing stage, we consider

the nature of summation operator in Radon vectors

which is clearly sensitive to bright parts of image. As

shown in Figure 2, most of the unrelated shapes

(letters, signs, landmarks etc.) in IRMA dataset are

depicted in (near-)white. To decrease their effect on

Radon projections, we remove these white parts by a

simple binary operation. Although this may

sometimes lead to eliminating some relevant

characteristics of some images. In general, however,

our results have shown that this stage of pre-

processing helps to deliver better results (see Table 4

in result section). In this stage, all images are

binarize by a threshold at 98% of maximum image in-

tensity to locate (near-)white image regions (Figure

5). Subsequently, these parts are replaced (filled) with

the median intensity value of their neighbors (we ac-

cess the neighbors by using some morphological op-

erators). Also, since artificial marks/signs appear

mostly close to the image border, replacing (near-

)white pixels is strictly restricted to the image mar-

gins.

Radon projections change their length based on

projection angel. All Radon operators consider the

maximum length

√

(where N is the largest of im-

age width/height) and use zero-padding for this pur-

pose. Based on (Tsai & Chiang 2010), we discard all

pixels out of circumference area from the image cen-

ter within a diameter of N/2.

ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods

560

Figure 3 shows sample images with superimposed

circles. This process helps to achieve shorter vectors;

the assumption, of course, is that image margins do

not offer much diagnostic information, hence we can

eliminate them. Our experiments confirm the

assumption for x-ray images in IRMA dataset. We

also can perform this step by selecting just N center

elements out of

√

elements in all Radon projec-

tions.

Figure 5: Removing irrelevant (near-)white landmarks: a)

original image, b) binary image with 98% thresholding, c)

the result after removing the irrelevant pixels by replacing

them with the median value of their neighborhood, d) mag-

nification of upper region of the image to show the bound-

aries which are used for median calculation.

3.2 Radon Projections

Using several Radon projections simultaneously has

been used successfully in many CBIRs woks (Zhu &

Tizhoosh 2016; Tizhoosh 2015; Liu et al. 2016). It

may be seen as obvious that using more projections

in all possible directions is associated with better re-

sults and naturally a more time-consuming search. In

our experiments, we examine a new approach by us-

ing only one projection for each retrieval attempt.

Obviously, we did not anticipate very promising

retrieval results for just one projection. However,

there was an interesting point in the results. If we, for

the sake of analysis, select the minimum IRMA error

for each projection, then the total IRMA error de-

creases dramatically (much better than concatenating

them into one vector). It means that although individ-

ual projection results are slightly better than of ran-

dom results (the error of each projection results is var-

ying between 570 to 640, and random search error is

around 900, see Table 3). This observation confirms

that separated projection results may have little over-

lap with each other. As a result, while one projection

(for example the projection at zero degree) fails to

find the most similar image, other projection (say the

45-degree direction) might be able to find it. By

choosing a certain number of “best matches” (say the

top three matches) for each Radon projection, we can

create a “Selection Pool” (see Figure 6).

Figure 6: A sample of Selection Pool for a test image and

top three images for each Radon projection. The final re-

sult(s) can be extracted from the Selection Pool after more

computationally demanding search methods are applied.

The surprising point is that the minimum error

rate for each test image in the Selection Pool consid-

erably decreases (e.g., error=196 for 8 projections).

Figure 7 motivates our idea of using single projec-

tions separately, where the error of the first hit (image

with the highest similarity to the query image) for 8

projections are depicted. The right side plot in

Retrieving Similar X-ray Images from Big Image Data using Radon Barcodes with Single Projections

561

Figure 7: The IRMA error of 1733 images for 8 single equidistant Radon projections. Black squares are the minimum error

for each test image. The sum of black squares amounts to 196. The right section magnifies an arbitrary test image results

(#619) for better visualization.

Figure 7 is the magnification of the errors of one spe-

cific test image (the image #619 in IRMA dataset). As

shown, each projection can be used to retrieve an im-

age as the first hit with different IRMA error. If we

record the lowest error for each projection, we can

reach a total error of 196 which, looking at the re-

ported numbers in literature, is quite low. For 10 top

images for each projection, the error even decreases

to 65, an error level not yet reached by any method in

literature. It means if we had an algorithm to identify

the best Radon projection for each image, we could

achieve the outstanding results. However, reliable

learning methods to select the best projection is ap-

parently quite challenging and subject to future

works. Hence, we attempt to exploit the discrimina-

tion power of single projections in a Selection Pool

via an exploitative approach.

3.3 Exploitation Search

After we have a small group of candidate images (Se-

lection Pool), retrieved from thousands of images in

training set, we can now apply a refined and more ex-

ploitative search to choose the best image from within

the Selection Pool. As mentioned before, if we man-

ually pick the best image from the top ones, we can

achieve the best scores. In this section, two methods

are combined to search the Selection Pool; Shifted

Radon and LBP.

Shifted Radon is proposed to eliminate the effect

of translation in images or image regions. Using eight

equi-distanced projections and shifting each Radon

projection in the test image to align with its counter-

part projection in the Selection Pool makes the algo-

rithm robust against translation (Figure 8 shows this

process for two sample images). We use the smallest

distance between the two projections using cross-

correlation (shifting by ± 10% the length of the

projection). By looking at cross-correlation between

each pair of Radon projections of two images, all

eight minimum distances (we use eight projections)

are summed up. After calculating the distance for all

images in the Selection Pool, we normalize this error

in [0,1].

LBP (local binary patterns) have been used in

many CBIRs based on thier power and speed (Avni et

al. 2011)(Nanni et al. 2010). In our method, LBP and

Shifted Radon are used together to improve the re-

sults. The LBP error rate is calculated by the

normalized sum of their absolute values. Final deci-

sion making is done by using the smallest value of the

sum of these two error vectors. Since both vectors

(Shifted Radon and LBP) are normalized between

zero and one, they are comparable to each other.

ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods

562

Figure 8: Two sample images with vertical subject shift and

their zero-degree Radon projections before and after cross-

correlation-based shifting.

3.4 Binarization of Projections

Computational complexity is one of the critical

features of any retrieval method. Our approach is very

light in comparison with most reported descriptors.

We just search the dataset using eight vectors as short

as the length of the resized image (under-sampled to

64x64 pixels in our experiments). Additionally, to

further shorten the search time, we have created the

binary version of projections to test SP-RBC which

employs two methods to create binary codes from Ra-

don projections. The MinMax and Median methods

have already been applied to threshold Radon projec-

tions (Tizhoosh 2015, Tizhoosh et al. 2016).

The Median method uses the median value of

each projection as a threshold, all elements below the

threshold are set to zero (Tizhoosh 2015). On the

other hand, the MinMax method sets zeros and ones

depending on the locations of minimums and maxi-

mums of each projection (Tizhoosh et al. 2016).

4 EXPERIMENTS AND RESULTS

This section introduces the data set used in our

research. We then detail our results and compare our

method with other methods.

4.1 Image Dataset: IRMA

The Image Retrieval in Medical Application, short

IRMA, is a challenging dataset, which has composed

of 12,677 images for training and 1,733 images for

evaluating any proposed retrieval method. Every

IRMA image is associated with a 13-digit code, and

each code is divided into four parts:

IRMA Code: TTTT-DDD-AAA-BBB

The first four digits describe the imaging modal-

ity, the next three represent the body orientation in the

image, the next four describe the body region and fi-

nally, the last four indicate the biological system ex-

amined. IRMA creators have also introduced a sys-

tem for measuring the error between two IRMA codes

and return an error number between zero and one

(Tommasi et al. 2009). So, retrieval algorithms

should return the most similar image for all 1733 test

images using the training dataset which supposed to

contain similar cases for every query image although

due to imbalance the easiness of finding similar cases

strongly varies.

4.2 Results

In this section, we first compare our best-achieved re-

sult with the results of other methods. After that, we

discuss the impact of each part of implementation on

achieved results. Finally, we show the results for each

Radon projection separately.

For comparing with other methods, we consider

approaches in two different groups, non-learning

methods and learning-based methods. The results for

RBC

, RBC

, and LBP are used from literature

(Tizhoosh 2015). However, since there is a different

way for error calculation in IRMA database than in

some papers, we recalculate the error for all men-

tioned methods based on (Tommasi et al. 2009) to

have consistent and fair comparisons.

In non-learning comparison, we consider L as the

length of descriptors, T as the type of searching (B for

Binary search and F for Floating point search), E

Total

as total IRMA error, and N

indicates the percentage

of zero-error cases (in case consider the classification

problem).

Table 1: IRMA error for non-learning methods (L=length,

T=type [B=binary; F=float], E=error, N

=percentage of re-

trieved cases with zero error).

Method L T E

Total

SP-R 8×64 F 311.80 45.76%

SP-RBC

Min-Max

8×64 B 356.57 42.30%

SP-RBC

Median

8×64 B 419.86 34.16%

LBP 1×135 F 365.23 38.26%

RBC

8×64 B 580.68 25.39%

RBC

16×64 B 564.54 23.54%

Table 1 shows that the proposed method SP-RBC

does loose some information in exchange for some

increase in speed compared to SP-R (single projection

Retrieving Similar X-ray Images from Big Image Data using Radon Barcodes with Single Projections

563

Radon) which simply uses the floating-point projec-

tions values without thresholding. But it can be

observed that the MinMax method is significantly

better than Median thresholding.

We also compared our results with the most suc-

cessful methods, which are applied on IRMA dataset.

Because all of them use some notion of learning, they

may only use labeled IRMA test images (94 images

in IRMA 2009 are not labelled; some works just ig-

nore them). Hence, their error might increase around

5-6%.

In the next part of this section, we have analyzed

the parameter tuning and the details of our observa-

tions. Firstly, we discuss the size of the Selection

Pool, which can affect the error rate significantly.

Figure 9 reflects the relationship between the error

rate and the number of top images per projection. As

it can be seen, the error rate has dropped substantially

between the first hit and the top five, while the de-

creasing rate tends to remain constant after number of

top choices reaches 10 for SP-R. The error rate seems

to continue to improve for SP-RBC beyond consider-

ing more than 10 top choices. The best answer is

reached by looking at top 14 images per projection. It

means we search among 112 images in the Selection

Pool (we use 8 separate projections).

Figure 9: Total IRMA error based on number of top similar

images for each projection.

Table 2: Best learning-based methods. All result marked

with * are reported in (Tommasi et al. 2009).

Learning method E

Total

(Camlica et al. 2015)

146.55

TAUbiomed

169.50

diap

178.93

VPA

242.46

FEITIJS

261.16

SP-R

311.8

MedGIFT

317.53

VPA

320.61

SP-RBC

356.57

IRMA

359.29

MedGIFT

420.91

Table 2

shows the results compared to learning-

based methods. The best results reported by Camlica

et al. is based on extensive saliency detection. The

second-best solution uses a dictionary approach ac-

companied by PCA application.

The results for each separate Radon projection, as

well as their binary version are provided in Table 3.

Each projection has a relatively high error.

Table 3: Results for SP-R and SP-RBC.

Learner SP-R

Total

SP-RBC

Total

0-degree Radon

567.67 644.52

22.5degree Radon

598.7 687.71

45-degree Radon

613.46 700.15

67.5-degree Radon

642.25 719.29

90-degree Radon

561.38 649.21

112.5-degree Radon

629.77 710.43

135-degree Radon

618.41 721.03

157.5-degree Radon

575.43 676.69

In Table 4, we share the results of concatenated Ra-

don projections as one vector. We also provide infor-

mation about the impact of preprocessing steps.

Normalization in general improves the results about

5%. Table 4 shows that there is some improvement

(approx. 10%) in white part removal and zero-padded

square resizing.

Table 4: Eight concatenated Radon projections.

Type of preprocessing E

Total

Radon whiteout preprocessing 439.93

Normal Radon 420.82

Normal Radon + resize method 389.10

Normal Radon + resize method +criclize 384.68

Normal Radon + removing white spots 385.75

All preprocessing steps 383.41

5 SUMMARY

In this paper, we proposed the idea of using single

Radon projections for medical image retrieval in large

archives. This can be considered an improvement of

previous works (Tizhoosh 2015) which introduced

the idea of Radon Barcodes by binarization of a se-

lected number of Radon projections.

In our method, a Selection Pool can be assembled

when multiple single Radon projections are applied

separately to retrieve many images from the database.

The single projection Radon Barcodes (SP-RBCs)

may lose some information due to the thresholding

process but they are compact and fast for retrieval in

big image data. Subsequently, more time consuming

ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods

564

local search can be performed on the Selection Pool

to retrieve the most similar cases. In this paper, we

employed LBP and Shifted Radon but many other al-

ternatives could be investigated.

In our future work, we will focus on improving

the exploitative search in the Selection Pool and

learning method to find the best projection to search

data set by just one projection.

REFERENCES

Aundal, P. & Aasted, J., 1996. The Radon Transform

Theory and Implementation Peter Toft Department of

Mathematical Modelling Section for Digital Signal

Processing Technical University of Denmark.

Avni, U. et al., 2011. X-ray categorization and retrieval on

the organ and pathology level, using patch-based visual

words. IEEE Transactions on Medical Imaging, 30(3),

pp.733–746.

Babenko, A. et al., 2014. Neural Codes for Image Retrieval.

CoRR, abs/1404.1. Available at: http://arxiv.org/

abs/1404.1777.

Bankar, R.T. et al., 2014. CBIR Representation In Terms of

Rotation Invariant Texture using LBP Variance.

International Journal of Emerging Science and

Engineering (IJESE), (5), pp.75–77.

Bay, H. et al., 2008. Speeded-Up Robust Features (SURF).

Computer Vision and Image Understanding, 110(3),

pp.346–359.

Beis, J.S. & Lowe, D.G., 1997. Shape indexing using

approximate nearest-neighbour search in high-

dimensional spaces. In Proceedings of IEEE Computer

Society Conference on Computer Vision and Pattern

Recognition. pp. 1000–1006.

Calonder, M. et al., 2010. BRIEF: Binary robust

independent elementary features. In Lecture Notes in

Computer Science (including subseries Lecture Notes

in Artificial Intelligence and Lecture Notes in

Bioinformatics). pp. 778–792.

Camlica, Z., Tizhoosh, H.R. & Khalvati, F., 2015. Medical

image classification via SVM using LBP features from

saliency-based folded data. Proceedings - 2015 IEEE

14th International Conference on Machine Learning

and Applications, ICMLA 2015, pp.128–132.

Do, T. et al., 2010. Deluding Image Recognition in SIFT-

based CBIR Systems. Analysis, (1), pp.7–12.

Gevers, T. & Stokman, H., 2004. Robust Histogram

Construction from Color Invariants for Object

Recognition. IEEE Transactions on Pattern Analysis

and Machine Intelligence, 26(1), pp.113–118.

Gu, Y.J. & Sacchi, M., 2009. Radon transform methods and

their applications in mapping mantle reflectivity

structure. Surveys in Geophysics, 30(4–5), pp.327–354.

Huang, W., Gao, Y. & Chan, K.L., 2010. A review of

region-based image retrieval. Journal of Signal

Processing Systems, 59(2), pp.143–161.

Krig, S., 2012. Computer vision metrics,

Kumar, A. et al., 2013. Content-based medical image

retrieval: a survey of applications to multidimensional

and multimodality data. Journal of digital imaging,

26(6), pp.1025–1039.

Ledwich, L. & Williams, S., 2004. Reduced SIFT features

for image retrieval and indoor localisation. Australian

conference on robotics and automation.

Lee, D.-J., Antani, S. & Long, L.R., 2003. Similarity

measurement using polygon curve representation and

fourier descriptors for shape-based vertebral image

retrieval. In Medical Imaging 2003. pp. 1283–1291.

Liu, X., Tizhoosh, H.R. & Kofman, J., 2016. Generating

Binary Tags for Fast Medical Image Retrieval Based on

Convolutional Nets and Radon Transform.

International Joint Conference on Neural Networks,

(Ijcnn). Available at: http://arxiv.org/abs/1604.04676.

Lowe, D.G., 2004. Distinctive image features from scale-

invariant keypoints. International Journal of Computer

Vision, 60(2), pp.91–110.

Nanni, L., Lumini, A. & Brahnam, S., 2010. Local binary

patterns variants as texture descriptors for medical

image analysis. Artificial Intelligence in Medicine,

49(2), pp.117–125.

Ojala, T., Pietikäinen, M. & Mäenpää, T., 2002.

Multiresolution gray-scale and rotation invariant

texture classification with local binary patterns. IEEE

Transactions on Pattern Analysis and Machine

Intelligence, 24(7), pp.971–987.

Radon, J., 1917. On determination of functions by their

integral values along certain multiplicities. Ber. der

Sachische Akademie der Wissenschaften

Leipzig,(Germany), 69, pp.262–277.

Rodríguez, F., Lecumberry, F. & Fernández, A., 2015.

Pattern Recognition Applications and Methods. Lecture

Notes in Computer Science (including subseries

Lecture Notes in Artificial Intelligence and Lecture

Notes in Bioinformatics), 9443, pp.196–205.

Saha, S.K., Das, A.K. & Chanda, B., 2004. CBIR using

perception based texture and colour measures. In

Proceedings of the 17Th International Conference on

Pattern Recognition, Vol 2. pp. 985–988.

Shim, S., Choi, T. & Member, S., 2002. Edge color

histogram for image retrieval. Science, pp.957–960.

Subrahmanyam, M., Maheshwari, R.P. &

Balasubramanian, R., 2012. Local maximum edge

binary patterns: A new descriptor for image retrieval

and object tracking. Signal Processing, 92(6), pp.1467–

1479. Available at: http://dx.doi.org/10.1016/

j.sigpro.2011.12.005.

Tizhoosh, H.R., 2015. Barcode annotations for medical

image retrieval: A preliminary investigation. In

Proceedings - International Conference on Image

Processing, ICIP. pp. 818–822.

Tizhoosh, H.R. et al., 2016. MinMax Radon Barcodes for

Medical Image Retrieval. In To appear in proceedings

of the 12th International Symposium on Visual

Computing. Available at: http://arxiv.org/abs/

1610.00318.

Retrieving Similar X-ray Images from Big Image Data using Radon Barcodes with Single Projections

565

Tommasi, T. et al., 2009. Overview of the CLEF 2009

medical image annotation track. In CEUR Workshop

Proceedings.

Tsai, H.-H. & Chiang, J.K., 2010. A Rotation Invariant

Image Descriptor based on Radon Transform Yudong.

In International Conference on New Trends in

Information Science and Service Science (NISS). pp.

671–676.

Velmurugan, K. & Baboo, S.S., 2011. Content-Based

Image Retrieval using SURF and Colour Moments.

Global Journal of Computer Science and Technology,

11(10), pp.1–4.

Wan, J. et al., 2014. Deep Learning for Content-Based

Image Retrieval. Proceedings of the ACM International

Conference on Multimedia - MM ’14, pp.157–166.

Wang, J.Z., 2001. Integrated Region-Based Image

Retrieval, Norwell, MA, USA: Kluwer Academic

Publishers.

Yan, K. et al., 2016. CNN vs. SIFT for Image Retrieval:

Alternative or Complementary? In Proceedings of the

2016 ACM on Multimedia Conference. MM ’16. New

York, NY, USA: ACM, pp. 407–411. Available at:

http://doi.acm.org/10.1145/2964284.2967252.

Zhu, S. & Tizhoosh, H.R., 2016. Radon Features and

Barcodes for Medical Image Retrieval via SVM.

Available at: http://arxiv.org/abs/1604.04675.

Zhu, S.Y. & Schaefer, G., 2004. Thermal Medical Image

Retrieval by Moment Invariants. In J. M. Barreiro et al.,

eds. Biological and Medical Data Analysis: 5th

International Symposium, ISBMDA 2004, Barcelona,

Spain, November 18-19, 2004. Proceedings. Berlin,

Heidelberg: Springer Berlin Heidelberg, pp. 182–187.

ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods

566