
Strategic Capacity Expansion of a Multi-item Process with Technology
Mixture under Demand Uncertainty: An Aggregate Robust MILP
Approach
Jorge Weston, Pablo Escalona, Alejandro Angulo and Ra
´
ul Stegmaier
Deparment of Industrial Engineering, Universidad T
´
ecnica Federico Santa Mar
´
ıa, Valpara
´
ıso, Chile
Keywords:
Capacity Expansion, Machine Requirement Planning, Work Shifts, Robust Optimization.
Abstract:
This paper analyzes the optimal capacity expansion strategy in terms of machine requirement, labor force, and
work shifts when the demand is deterministic and uncertain in the planning horizon. The use of machines of
different technologies are considered in the capacity expansion strategy to satisfy the demand in each period.
Previous work that considered the work shift as a decision variable presented an intractable nonlinear mix-
integer problem. In this paper we reformulate the problem as a MILP and propose a robust approach when
demand is uncertain, arriving at a tractable formulation. Computational results show that our deterministic
model can find the optimal solution in reasonable computational times, and for the uncertain model we obtain
good quality solutions within a maximum optimal gap of 10
−4
. For the tested instances, when the robust
model is applied with a confidence level of 99%, the upper limit of the total cost is, on average, 1.5 times the
total cost of the deterministic model.
1 INTRODUCTION
When a manufacturing industry faces a scenario of
increasing demand in the long term and its facilities
are close to maximum capacity, the how to expand its
production capacity is a key decision. Strategic ca-
pacity expansion should determine the level of differ-
ent production factors over time, such as the number
of machines and workers needed to satisfy the pro-
duction requirement. The objective of this paper is
to determine the optimal capacity expansion strategy
that minimizes the machinery investment cost, the la-
bor cost, the production cost, and the idle capacity
cost over a defined planning horizon, when the future
demand is uncertain and there is no knowledge of its
distribution. The decision variables are (i) the pro-
duction requirements needed to satisfy the demand
in each period, (ii) the number of machines of each
technology needed, (iii) the work shifts necessary to
cover the production requirement, and (iv) the work-
ers needed to perform the number of shifts. This con-
siders simultaneously the machine requirement plan-
ning (MRP) and the strategic capacity planning under
uncertainty.
In this paper, we developed a multi-item, and
multi-period model with technology mixture that de-
termines the optimal expansion strategy considering
the machine numbers of each technology, labor, and
work shifts needed to satisfy the demand. We consid-
ered two different cases: when the demand is deter-
ministic and when it is uncertain. For the first case, we
formulated a mixed integer linear program (MILP),
which can be solved efficiently with a mixed-integer
solver. Then, we incorporated the demand uncertainty
into the deterministic model, following a robust ap-
proach that considers the best worst case and a non-
anticipativity constraint. In this formulation, flexi-
bility is provided to the model via a box-type uncer-
tainty set obtaining a robust model with adjustable ro-
bustness; the non-anticipativity constraints, to make
the problem tractable, are represented by affine de-
cision rules. The model with demand uncertainty is
also an MILP and can be solved with a mixed-integer
solver. We used both models to evaluate the impact of
a technology mixture in the capacity expansion strat-
egy. We considered three types of technology that dif-
fer in terms of production rate, worker requirements,
investment cost and production cost.
The main contributions of this work are: (i) An
efficient formulation of a strategic capacity expansion
model that considers the work shifts as a decision
variable; and (ii) the inclusion of the uncertain nature
of the demand in the model under a robust approach.
The rest of this paper is structured as follows. In
Section 2, a brief literature review is presented, and
then, in Section 3 we present the model formulation
for the two cases, when the demand is deterministic
and when the demand is uncertain. In Section 4, we
Weston J., Escalona P., Angulo A. and Stegmaier R.
Strategic Capacity Expansion of a Multi-item Process with Technology Mixture under Demand Uncertainty: An Aggregate Robust MILP Approach.
DOI: 10.5220/0006202201810191
In Proceedings of the 6th International Conference on Operations Research and Enterprise Systems (ICORES 2017), pages 181-191
ISBN: 978-989-758-218-9
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
181

report our computational results, and finally, in Sec-
tion 5 we conclude and present future extensions to
this work.
2 RELATED WORK
A strategic capacity expansion problem consists of
defining the expansion sizes and expansion timing in
order to meet the incremental demands within a long-
term planning horizon. The objective is to minimize
the total costs with respect to the expansion process
(Luss, 1982). On the other hand, machine require-
ment planning (MRP) can be defined as the specifi-
cation of the number of each type of machine needed
in each period for a productive process (Miller and
Davis, 1977).
A comprehensive review of the strategic capac-
ity expansion problem can be found in Luss (1982),
Van Mieghem (2003), Wu et al. (2005), Julka et al.
(2007), and Geng et al. (2009) and a more recent
review in Mart
´
ınez-Costa et al. (2014). In particu-
lar, Mart
´
ınez-Costa et al. (2014) described the major
decisions and conditioning factors involved in strate-
gic capacity planning. They classified the strategic
capacity expansion models according to the number
of sites involved in the expansion process (a single
or multiple sites), the type of the capacity expansion
considered (expansion by investing/purchasing, out-
sourcing/subcontracting, reduction and replacement),
whether the uncertainty of the parameters is consid-
ered in the problem formulation, and finally, the type
of mathematical programming model and its solution
procedure.
Our model corresponds to a single-site and multi-
item capacity expansion problem under uncertain de-
mand. We consider that capacity expansion can be
achieved through machine acquisition and / or by us-
ing a flexible workforce in terms of increasing or de-
creasing the number of shifts. In this sense, the tra-
ditional structure of the strategic capacity expansion
problem does not consider the relationship between
the workforce planning and capacity acquisition de-
cisions. This is related to the natural separation be-
tween strategic and tactical decision making. How-
ever, when these decisions are addressed separately,
sub-optimal solutions are frequently the result. Since
workforce flexibility and capacity acquisition can rep-
resent substitutable magnitudes, flexible workforce
options could be also considered as a means of in-
creasing capacity. In particular, for capital intensive
companies, the implementation of one or more shift is
an additional tool that managers can use to increment
capacity continuously, avoiding the huge investment
cost related to equipment acquisition.
To the best of our knowledge, only Fleischmann
et al. (2006), Bihlmaier et al. (2009), and Escalona
and Ram
´
ırez (2012) considered the workforce in their
strategic capacity planning. Fleischmann et al. (2006)
studied a multi-site and multi-item strategic capac-
ity model with machine replacement and overtime as
a means to meeting demand. They considered the
same average cost for any overtime, such as prolonga-
tion of a shift, weekend shifts, night shifts, or regular
third shifts. The model is formulated as an MILP and
solved directly using CPLEX. Bihlmaier et al. (2009)
analyzed a multi-site and multi-item strategic capac-
ity model without machine replacement that inte-
grates tactical workforce planning via shift work im-
plementation. They consider a detailed set of shifts,
such as a late shift, night shift, Saturday shift, and Sat-
urday late shift. They presented a two-stage stochas-
tic MILP for strategic capacity planning under uncer-
tain demand that is solved by Benders decomposition.
Escalona and Ram
´
ırez (2012) studied the optimal ex-
pansion strategy of a process, in terms of machinery,
labor, and work shifts, through an aggregated model
without machine replacement. They considered that
in the process one, two, or three shifts can be worked
per time period. The main difficulty related to their
model is that shifts are not linear with the number of
machines and workers needed to meet the demand.
The model is formulated as a mixed integer nonlin-
ear problem and solved by complete enumeration by
fixing the shifts during the planning horizon.
Our strategic capacity model also considers un-
certain demand. Four primary approaches to consid-
ering uncertainty exist (Sahinidis, 2004), which ba-
sically comprise (i) stochastic programming, where
the uncertain parameters are considered random vari-
ables with known probability distributions; (ii) fuzzy
programming, where some variables are considered
as fuzzy numbers; (iii) stochastic dynamic program-
ming, where random variables are combined with dy-
namic programming; and (iv) robust optimization,
where the uncertainty of the parameters do not follow
a known probability distribution, and the solutions are
robust, i.e., they perform best in the worst case.
In the literature, two-stage stochastic program-
ming is a dominant approach to handling stochas-
tic capacity planning under various uncertainties
(Swaminathan, 2000), (Hood et al., 2003), (Barahona
et al., 2005), (Christie and Wu, 2002), (Karabuk and
Wu, 2003), (Geng et al., 2009), (Rastogi et al., 2011),
(Levis and Papageorgiou, 2004), and (Bihlmaier et al.,
2009). A major shortcoming of two-stage stochastic
programming is that it generates only a static capac-
ity expansion plan and neglects the dynamic adjust-
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
182

ments based on new information when the demand is
revealed in each period. Several studies have adapted
stochastic dynamic programming to overcome this is-
sue (Rajagopalan et al., 1998), (Asl and Ulsoy, 2003),
(Cheng et al., 2004), (Li et al., 2009), (Stephan et al.,
2010), (Wu and Chuang, 2010), (Pratikakis et al.,
2010), (Chien et al., 2012), (Pimentel et al., 2013),
and (Lin et al., 2014).
In summary, few previous research studies on
strategic capacity planning considered the workforce
as a tool for increasing or decreasing capacity, and to
the best of our knowledge, no robust optimization ap-
proach exists for dealing with demand uncertainty in
strategic capacity planning.
3 MODEL FORMULATION
Consider a capacity expansion problem of a process
over a planning horizon of T (t = 1, ..., τ) periods. In
this process, I (i = 1, ..., n) items are produced, and
J ( j = 1, ..., m) technologies are available for their
production. The demand for item i in the period t
is d
it
. Without loss of generality, we assume that the
aggregate demand (
∑
i∈I
d
it
) will increase on the long
term, i.e., the aggregate demand follows a positive
trend.
Let r
i j
be the production rate of item i produced
with technology type j, and let ¯µ
j
be the maximum
utilization for each machine of type j that will be con-
sidered by the design requirement. In each period it is
possible to work K shifts (k = 1, 2, 3); in each shift the
available working time is limited by H
1
. The number
of shifts that will be worked in the period t is deter-
mined by the binary variable W
kt
, which will be 1 if
k shifts are used in period t, else it will be 0. The
number of machines of type j needed in each shift to
satisfy the demand in period t working k turns is de-
noted by Y
jkt
; the number of machines of type j that
will be acquired in period t is denoted by V
jt
; and the
number of machines available at the beginning of the
planning horizon (t = 0) is B
j
.
To meet the demand in each period of the planning
horizon, the capacity expansion could happen by: (i)
acquiring new machines (expansion by investment) or
(ii) modifying the number of shifts (expansion by op-
erational cost). Therefore, in each period it is possi-
ble to hire or fire workers. Let Uh
jt
be the number
of workers hired at the beginning of the period t to
operate machines of type j, and let U f
jt
be the num-
ber of workers fired at the beginning of the period t
that operated machines of type j. The workers avail-
able to operate machines of type j in the period t is
denoted by O
jt
, with O
j0
= A
j
representing the work-
ers available at t = 0. The number of workers needed
to operate one machine of technology type j is repre-
sented by
¯
O
j
. Finally, the quantity of item i produced
with technology type j in each period t is represented
by the variable X
i jt
.
For this problem the costs that will be considered
are: (i) the investment cost of acquiring a machine
of type j in the period t (CI
jt
); (ii) the unitary labor
cost in period t (CL
t
); (iii) the production cost for one
item i produced in a machine of type j in the period
t (Cp
i jt
); (iv) the opportunity cost incurred by idle
capacity of technology type j (Cop
jt
); and, finally,
(v) the unitary cost of hiring and firing, denoted by
C
h
and C
f
respectively. It will be assumed that all
the mentioned costs are properly brought to present
value. A glossary of the terms used in the following
sections can be found in appendix A. For this work we
are going to consider the cost of opening or closing a
shift as negligible, even if in reality they are not cost-
free.
3.1 Deterministic Formulation
When demand is deterministic we propose the follow-
ing capacity expansion problem, denoted by (P0).
Problem (P0):
min
X,V,Y,Uh,Uf,W
TC =
(
∑
i jt
X
i jt
Cp
i jt
+
∑
jt
Cop
jt
B
j
+
∑
l=1..t
V
jl
−
∑
k
Y
jkt
!
+
∑
jt
V
jt
CI
jt
+
¯
O
j
∑
k
k Y
jkt
!
CL
t
+
∑
jt
Uh
jt
C
h
+
∑
jt
U f
jt
C
f
)
(1)
s.t:
∑
j∈J
X
i jt
≥ d
it
∀i,t (2)
∑
i∈I
X
i jt
r
i jt
≤ ¯µ
j
H
1
∑
k∈K
k Y
jkt
∀ j, t (3)
∑
k∈K
Y
jkt
≤ B
j
+
∑
l=1..t
V
jl
∀ j, t (4)
∑
k∈K
W
kt
= 1 ∀t (5)
Y
jtk
≤ M W
kt
∀ j, t, k (6)
∑
k∈K
k
Y
jkt
−Y
j,k,t−1
=
Uh
jt
−U f
jt
¯
O
j
∀ j, t (7)
∑
k∈K
k
Y
jk0
=
A
j
¯
O
j
∀ j (8)
X ≥ 0 (9)
Strategic Capacity Expansion of a Multi-item Process with Technology Mixture under Demand Uncertainty: An Aggregate Robust MILP
Approach
183

Y, Uh, Uf, V ∈ Z
+
(10)
W ∈
{
0, 1
}
(11)
The objective is to minimize the total cost (TC), con-
sidering the production cost, opportunity cost, invest-
ment cost, labor cost, and the cost of firing or hiring
workers. The satisfaction of demand is ensured by
(2). Constraint (3) restricts the total demanded time
by the total available time; (4) ensures that the num-
ber of machines of technology j available in the pe-
riod t is greater than the number of machines needed
to satisfy the demand assigned in that period to the
technology j. Constraints (5) and (6) ensure that the
number of work shifts used in period t are of only one
type, i.e., k = 1 or k = 2 or k = 3. Constraint (7) rep-
resents the continuity and requirement for workers in
each period t, and constraint (8) represents an initial
condition.
It is easy to show that the problem (P0) is equiv-
alent to the problem presented by Escalona and
Ram
´
ırez (2012) by incorporating the constraints (4)
and (5) and considering the following equivalences of
variables:
w
t
NN
jt
=
∑
k∈K
kY
jkt
(12)
V
jt
= ND
jt
− ND
j,t−1
(13)
ND
jt
= B
j
+
∑
l=1..t
V
jl
(14)
NN
jt
=
∑
k∈K
Y
jkt
(15)
where w
t
is the decision variable that determines the
number of shifts needed in period t, NN
jt
is the num-
ber of machines of type j needed in the period t to
satisfy the demand, and ND
jt
is the number of ma-
chines of type j available in the period t.
3.2 Uncertain Formulation
In this paper we use a robust approach, where the un-
certainty set is defined as a box, which is a partic-
ular case of the polyhedral set (Bertsimas and Sim,
2004),(Bertsimas and Thiele, 2006), (Guigues, 2009),
and the problem is formulated as an affine multi-stage
robust model with a simplified affine policy (Lorca
et al., 2016).
Given the uncertain nature of the demand, it can-
not be predicted with exactitude. In the best scenario,
the estimate of the demand will be close to the ac-
tual value, but this will not happen frequently. The
most frequent outcome is to have a variation (delta)
between the estimate and actual demand. This delta
tends to increase as the period analyzed is further in
the future. When the variation is positive, the com-
pany over-produces, incurring a cost for not selling
the excessive units produced; this cost can be esti-
mated using the production cost or an opportunity
cost. On the other hand, if this delta is negative, the
demand cannot be completely satisfied; in this case
the cost incurred by the company is one of lost sales.
The lost-sale cost is often discussed since it can result
in a loss of profit, a loss of future clients, or the loss of
clients whose demand could not be satisfied, causing
a bad reputation and loss of confidence in the com-
pany. Taking this into consideration, a negative delta
is highly undesirable, and therefore it is fundamen-
tal to determine how to address the uncertain nature
of the demand such that this delta is non-negative (or
even 0) most of the time.
Let D
it
=
d
it
| d
it
∈
¯
d
it
− Γ
ˆ
d
it
,
¯
d
it
+ Γ
ˆ
d
it
be
the uncertainty set of d
it
, where
¯
d
it
is the nominal
value of the demand, and let Γ represent the conserva-
tiveness of the model that can be associated with the
risk factor of the companies. Denote by D the aggre-
gate uncertainty set, i.e., D = ∪
it
D
it
.
Since we sought a robust model that can avoid
a negative delta, our worst case will be the one that
consider the maximum value that d
it
can take under
the uncertainty set D
it
; in this case this corresponds
to
¯
d
it
+ Γ
ˆ
d
it
. Therefore, the demand satisfaction con-
straint for the robust model can be written as
∑
j∈J
X
i jt
≥
¯
d
it
+ Γ
ˆ
d
it
∀i,t (16)
Replacing (2) in the problem (P0) by (16), we
obtain a robust model denoted by (P1). It is easily
noticed that the deterministic problem has two dif-
ferent types of decision variables: (i) strategic de-
cisions, i.e., decisions that affect the productivity in
the long term and cannot be modified at the moment
of demand realization; and (ii) operational decisions
that are made in each period and which therefore de-
pend on the realization of the demand. In the second
type we have the production quantity decision vari-
able (X). This variable has a clear dependence on
the demand realization, dependence that will be ad-
dressed via an affine decision rule of the form
X(d)
i jt
=
¯
χ
i jt
+ λ
i j
t
∑
τ=1
d
iτ
−
¯
d
iτ
, (17)
where the first term (
¯
χ
i jt
) represents the nominal value
of the quantity of item i to be produced in period t
with machines of type j, and λ
i j
is the percentage of
the accumulated over-demand assigned to the item i
and machines of technology j. Taking the definition
of the uncertain set (D) and the affine decision rules
defined by (17) and incorporating them in problem
(P0), we obtain our affine multi-stage robust model
denoted by (P2).
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
184

Problem (P2):
min
¯
χ,V,Y,Uh,Uf,W,λ,Z
(
Z +
∑
jt
V
jt
CI
jt
+
∑
jt
Cop
jt
B
j
+
∑
l=1..t
V
jl
−
∑
k
Y
jkt
!
+
∑
jt
¯
O
j
∑
k
k Y
jkt
!
CL
t
+
∑
jt
Uh
jt
C
h
+
∑
jt
U f
jt
C
f
)
(18)
s.t: (4), (5), (6), (7), (8), (9), (10), (11)
∑
j∈J
¯
χ
i jt
+ λ
i j
t
∑
τ=1
d
iτ
−
¯
d
iτ
!
≥ d
it
∀i,t,d (19)
∑
i∈I
¯
χ
i jt
+ λ
i j
∑
t
τ=1
d
iτ
−
¯
d
iτ
¯µ
j
H
1
r
i jt
≤
∑
k∈K
k Y
jkt
∀ j, t, d (20)
∑
i jt
¯
χ
i jt
+ λ
i j
t
∑
k=1
d
ik
−
¯
d
ik
!
Cp
i jt
≤ Z ∀d (21)
∑
i j
λ
i j
= 1 (22)
Z ∈ ℜ
+
, λ ∈ [0, 1] (23)
We created the auxiliary variable Z in constraint
(21) to denote the worst-case production cost. Con-
straints (19) and (20) are obtained by replacing the
variable X in constraints (2) and (3) by the affine de-
cision rule (17).
Making some straightforward arrangements, and
taking into consideration that constraints (19)-(21)
are robust constraints that should hold for all d ∈ D,
which is equivalent to maximizing each constraint
over the uncertainty set D, it is possible to replace
constraints (19)–(21) with the following set of con-
straints:
∑
j
¯
χ
i jt
≥ Γ
t
ˆ
d
it
1 −
∑
j
λ
i j
!
+
∑
j
λ
i j
t−1
∑
τ=1
Γ
τ
ˆ
d
iτ
+
¯
d
it
∀i,t
(24)
∑
i
¯
χ
i jt
r
i jt
+
∑
i
λ
i j
r
i jt
t
∑
τ=1
Γ
τ
ˆ
d
iτ
!
≤ ¯µ
j
H
1
∑
k∈K
k Y
jkt
∀ j, t
(25)
∑
i jt
¯
χ
i jt
Cp
i jt
+
∑
it
Γ
t
ˆ
d
it
T
∑
k=t
∑
j
C
i jk
λ
i j
!
≤ Z (26)
With these replacements, we obtained a MILP that
considers the uncertain nature of the demand and that
can be solved by a MIP solver in reasonable compu-
tational time. Note that if Γ
t
= 0, the solution is equal
to the problem (P0) (the nominal problem).
4 COMPUTATIONAL STUDY
The computational study was developed with the fol-
lowing objectives: (i) evaluate the computational per-
formance (in terms of CPU time) of the proposed
model compared with that presented in the literature;
(ii) analyze the behavior of the total cost to changes of
Γ, i.e., analyze how the total cost grows as more de-
mand (over its expected value) is considered; and (iii)
test the applicability of our model in an industrial-size
example. Since problems (P0) and (P1) are particular
cases of (P2), we will only analyze (P2).
All experiments were performed with an AMD A6
2.0 GHz processor with 6 GB RAM memory, and the
models were solved using CPLEX 12.6.
4.1 Industrial Size Example
We implemented our model using the information
presented by a cosmetic company about a packaging
process, in particular a sachet filling one, of four items
that have high growth potential in the long term. For
this process, three types of technology were evalu-
ated. These technologies differ in (i) investment cost,
(ii) unitary production cost, and (iii) workers required
to operated one machine. For this implementation, we
considered a time horizon of ten periods with each pe-
riod being one year.
The cosmetic company provided the demand fore-
cast for each item, i.e., the nominal value of the de-
mand and the standard deviation of the forecast er-
ror. For each item and each period, the company
treated the uncertainty through reliability intervals of
the form
ˆ
F
it
± σ
it
Z
1−
α
2
, where
ˆ
F
it
is the demand fore-
cast for the item i at period t, Z
1−
α
2
is the quantile
associated with a confidence level of 1 − α, and σ
it
corresponds to the standard deviation of the forecast
error for item i at period t. Note that for this reliability
interval, the company assumed that the forecast errors
are Gaussian white noise.
Treating the demand uncertainty via re-
liability intervals can be easily related to
the demand uncertainty set defined in Sec-
tion 3.2 through the following relationships
¯
d
it
=
ˆ
F
it
, Γ = Z
1−
α
2
, and
ˆ
d
it
= σ
it
, ∀i ∈ I, t ∈ T .
Therefore, the demand uncertainty set to be
used in this illustrative example is of the form
D
it
=
n
d
it
| d
it
∈
h
ˆ
F
it
− Z
1−
α
2
σ
it
,
ˆ
F
it
+ Z
1−
α
2
σ
it
io
,
where Z
1−
α
2
∈ {0, 0.25, 0.52, 0.84, 1.28, 1.64,
1.96, 2.33, 2.58, 3.29}, which corresponds to
confidence levels of 0%, 20%, 40%, 60%, 80%,
90%, 95%, 98%, 99%, and 99.9%, respectively.
Each problem has 343 variables (133 continuous,
Strategic Capacity Expansion of a Multi-item Process with Technology Mixture under Demand Uncertainty: An Aggregate Robust MILP
Approach
185
180 integer, and 30 binary variables) and 235 linear
constraints.
For this computational study we considered the
following set of parameters:
• Demand: The nominal value of demand and the
standard deviation of the forecast error are pre-
sented in Table 2 and Table 3 in B.
• Production rate (r
i j
): The production rate is the
same for each type of technology, i.e., r
i j
=
r
i
, ∀ j ∈ J, r
1
= 120, r
2
= 170, r
3
= 400, and
r
4
= 600.
• Maximum utilization (µ
j
): µ
1
= 0.8, µ
2
= 0.9,
µ
3
= 0.98.
• Available time per shift (H
1
): 2080[hours].
• Number of workers needed per machine of tech-
nology j (
¯
O
j
):
¯
O
1
= 3,
¯
O
2
= 2, and
¯
O
3
= 1.
• Investment cost (CI
jt
): CI
jt
= CI
j1
(1.15)
1−t
, ∀t =
{2, ..., T }, with CI
1,1
= $25000, CI
2,1
= $50000,
and CI
3,1
= $75000.
• Opportunity cost (Cop
jt
): Cop
jt
= CI
jt
f , ∀ j ∈
J, ∀t ∈ T , where f represents the relation between
the useful life and the depreciation time of the ma-
chine, and corresponds to 0.10.
• Annual labor cost per worker (CL
t
):
CL
t
= CL
1
(1.15)
1−t
, ∀t = {2, ..., T }, with
CL
1
= $16032.
• Unitary production cost (C p
i jt
): The produc-
tion cost will depend only on the type of
technology, i.e., Cp
i jt
= Cp
jt
, ∀i ∈ I, Cp
jt
=
Cp
j1
(1.15)
1−t
, ∀ j ∈ J, ∀t = {2, ..., T }, with
Cp
1,1
= $1, C p
2,1
= $0.75, and C p
3,1
= $0.5.
• Unitary firing and hiring cost: C
h
= $500 and
C
f
= $4500.
• Initial conditions: The number of workers and
machines available at the beginning of the plan-
ning horizon, for each technology, are 0, i.e.,
B
j
= A
j
= 0, ∀ j ∈ J.
4.2 Results of the Industrial Size
Example
The expansion route for this problem involves differ-
ent shifts and the use of only one type of technol-
ogy. According to the results, the technology type se-
lected is, regardless of the value of α, the one with the
highest investment cost but with the lowest produc-
tion cost and fewest required workers (type 3). The
nominal total cost for the expansion under determin-
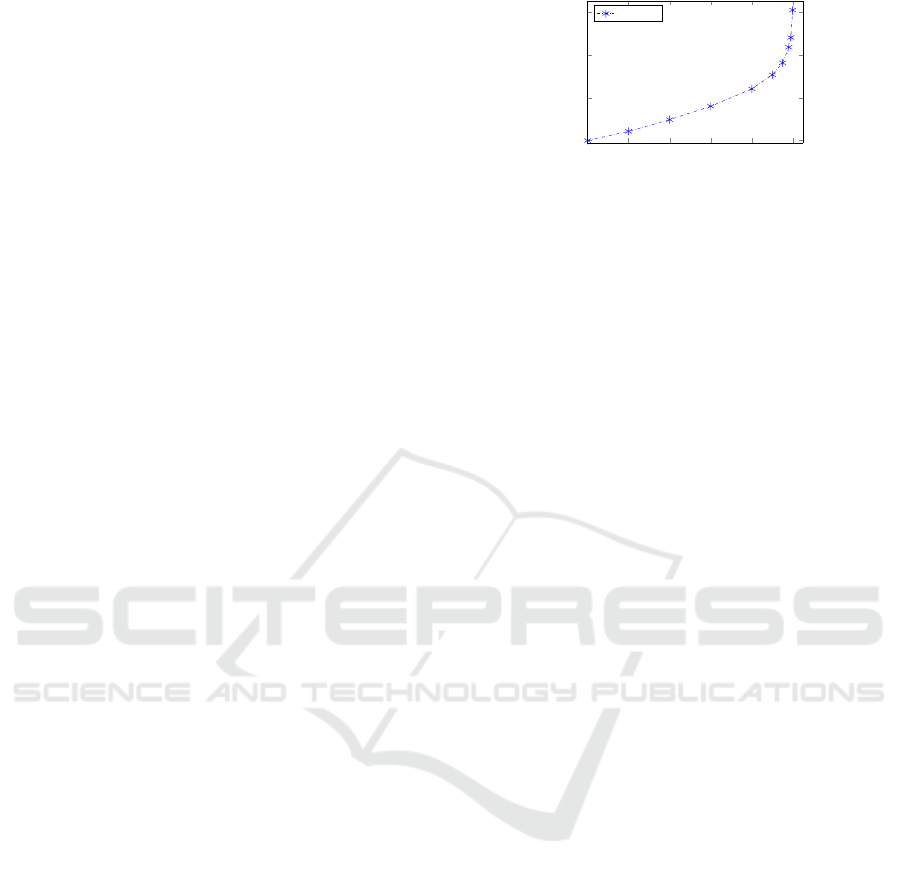
istic demand (1 − α = 0) is $8152716. In Figure 1 we
0 0.2 0.4
0.6
0.8 1
1
1.2
1.4
1.6
1 −α
Total Cost
Figure 1: Total cost behavior.
show the proportion of the total cost over the nominal
cost for each value of 1− α.
From Figure 1 we observe that the total cost in-
creases exponentially when more variable demand is
considered, and therefore each percentage increase is
more expensive than the previous one; for example, if
a reliability level (1−α) of 0.9 is selected, i.e., the de-
mand can be satisfied 95% of the time, the total cost
increases to 1.3 times the nominal cost, but if the reli-
ability level selected is 0.99 ,the total cost increases to
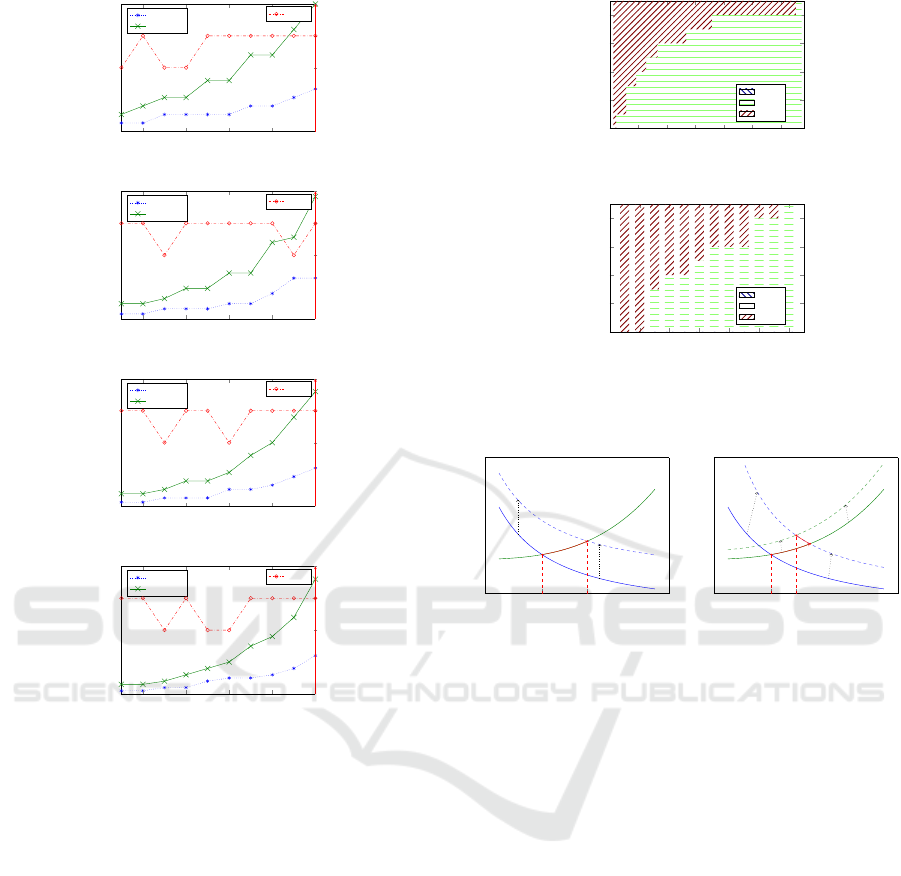
1.48 times the nominal cost. Figure 2 presents the ex-
pansion route in terms of shifts, total number of ma-
chines, and total number of workers needed in each
period for four different instances. In all instances,
we observed that the shifts changed along the plan-
ning horizon, and that an operational expansion (in-
creasing the number of shifts) is always preferred be-
fore realizing an investment; with this is possible to
determine that is more advisable to expand via shifts
before purchasing more machines. Therefore, if the
shifts are considered fixed, it is possible to arrive at
sub-optimal solutions.
4.3 Sensitivity Analysis
To analyze the impact of the parameters in the ex-
pansion strategy, we developed a sensitivity analy-
sis, where the following parameters were varied: (i)
investment cost, (ii) operational cost, and (iii) num-
ber of workers. For each one the technology mixture
and the shifts structure will be analyzed considering a
confidence level of 0.9, i.e., Γ = Z
0.95
= 1.64. The
shifts structure will be considered as the aggregate
number of shifts along the planning horizon (ANS),
i.e., ANS=
∑
t,k
kW
kt
.
Investment Cost. The investment cost of the actual
selected technology type ( j = 3) was increased until it
is not selected anymore. This increase was measured
with respect to technology type 1. Figure 3 shows
the technology mixture versus the investment cost of
technology type 3, (a) when the operational costs are
different for each type of technology and (b) when
they are the same.
From Figure 3 is possible to observe a gradual
transference from machines of technology type 3 to
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
186
2 4
6
8 10
0
Time Period
Workers - Machines
Machines
Workers
2 4
6
8 10
2
3
4
Shifts
Shifts
(a) 1 − α = 0 (Γ = 0)
2 4
6
8 10
0
Time Period
Workers - Machines
Machines
Workers
2 4
6
8 10
2
3
4
Shifts
Shifts
(b) 1 − α = 0.8 (Γ = 1.28)
2 4
6
8 10
0
Time Period
Workers - Machines
Machines
Workers
2 4
6
8 10
2
3
4
Shifts
Shifts
(c) 1 − α = 0.95 (Γ = 1.96)
2 4
6
8 10
0
Time Period
Workers - Machines
Machines
Workers
2 4
6
8 10
2
3
4
Shifts
Shifts
(d) 1 − α = 0.999 (Γ = 3.29)
Figure 2: Expansion route by Γ.
machines of technology type 2. Note that this trans-
ference happens sooner when the operational costs are
the same for all the technologies. In particular, from
Figure 3(a), total transference is achieved when the
investment cost of technology type 3 is at least 131
times CI
1
, and from Figure 3(b), total transference is
achieved when the investment cost of the machines of
type 3 is 14 times the investment cost of machines of
type 1.
We observe that the ANS increases when the in-
vestment cost increases. This behavior can be ex-
plained for two cases, when the rise of the invest-
ment cost (i) does not induce technology mixture, and
(ii) when it does induce technology mixture. Figure
4 shows the behavior of the cost equilibrium under
varying investment cost for both cases.
When the increase in the investment cost does not
induce technology mixture (Figure 4(a)), the aggre-
gate investment cost curve moves upwards and the
aggregate labor cost stays unchanged. This implies
0 20 40
60
80 100 120
0
2
4
6
8
Times CI
1
Number of machines
Type 1
Type 2
Type 3
(a) Different operational cost
(C p
i1t
> C p
i2t
> C p
i3t
)
2 4
6
8 10 12 14
0
2
4
6
8
Times CI
1
Number of machines
Type 1
Type 2
Type 3
(b) Same operational cost
(C p
i jt
= C p
it
∀ j ∈ J)
Figure 3: Sensitivity to investment cost.
ANS
A
ANS
A
0
A
A
0
(a) Without technology
mixture
ANS
B
ANS
B
0
B
C
B
0
(b) Under technology mix-
ture
Figure 4: Equilibrium dynamic under investment cost vari-
ation.
that the equilibrium moves from point A to point A
0
,
resulting in a higher cost and a higher ANS. In the
second case, when the increase in the investment cost
induces technology mixture (Figure 4(b)), the curve
dynamic can be explained in two stages: (i) the aggre-
gate investment cost increases and (ii) the aggregate
labor cost also simultaneously increases; with this the
equilibrium moves from point B to point C and finally
to point B
0
. Note that, since in this case the aggregate
investment cost increases significantly more than the
labor cost, the new equilibrium achieved at point B
0
implies a higher cost and a higher ANS.
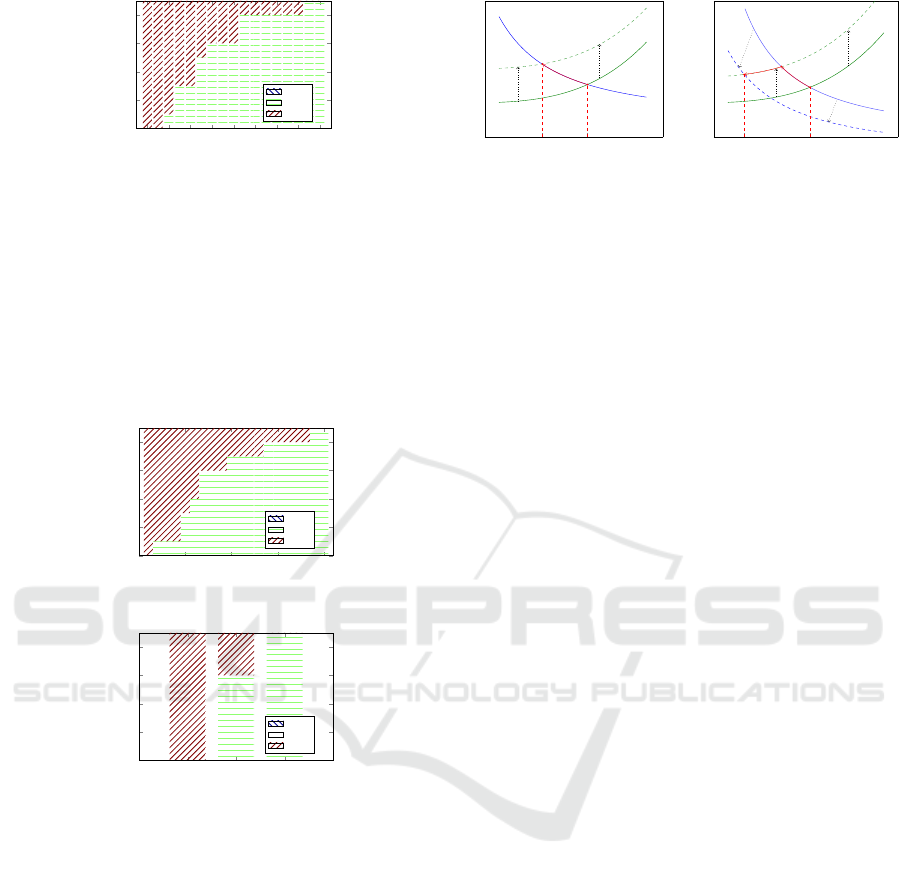
Operational Cost. The operational cost of the actual
selected technology ( j = 3) was increased until the
model stopped selecting it. This increase was mea-
sured with respect to technology type 1. Figure 5
shows the technology mixture under varying produc-
tion cost.
From Figure 5, it is possible to observe a gradual
transference from machines of technology type 3 to
machines of technology type 2. When the operational
cost of the machines of type 3 is 1.19 times that of ma-
chines of type 2, the technology transference is total.
Strategic Capacity Expansion of a Multi-item Process with Technology Mixture under Demand Uncertainty: An Aggregate Robust MILP
Approach
187
0.74
0.76
0.78 0.8 0.82 0.84
0.86
0.88 0.9
0
2
4
6
8
Times C p
i1t
Number of machines
Type 1
Type 2
Type 3
Figure 5: Sensitivity to operational cost.
We also observed that without technology mixture the
ANS does not change.
Number of Workers. Similar to the previous anal-
ysis the number of workers required for technology
type 3 was increased until the technology transfer-
ence was total. The resulting technology mixture is
presented in Figure 6, (a) when the operational costs
are different for each type of technology and (b) when
they are the same.
0
5
10
15
20
0
2
4
6
8
Number of workers needed (
¯
O
3
)
Number of machines
Type 1
Type 2
Type 3
(a) Different operational cost
(C p
i1t
> C p
i2t
> C p
i3t
)
1 2 3
0
2
4
6
8
Number of workers needed (
¯
O
3
)
Number of machines
Type 1
Type 2
Type 3
(b) Same operational cost
(C p
i jt
= C p
it
∀ j ∈ J)
Figure 6: Sensitivity to required number of workers.
From Figure 6 it is possible to observe a grad-
ual transference from machines of technology type
3 to machines of technology type 2. Note that this
transference starts when both technologies require the
same number of workers, and is more drastic when
the operational cost is the same for all the technolo-
gies (Figure 6(b)).
In this analysis is also possible to note a relation-
ship between the number of workers and the ANS. An
increase in the number of workers implies a decrease
in the ANS. Two cases can be recognized: when the
rise in the number of workers (i) does not induce tech-
nology mixture, and (ii) when it does induce technol-
ogy mixture. Figure 4 shows the behavior of the cost
equilibrium under a variation of the workers require-
ment for both cases.
ANS
D
0
ANS
D
D
0
D
(a) Without technology
mixture
ANS
F
0
ANS
F
F
0
F
E
(b) Under technology mix-
ture
Figure 7: Equilibrium dynamic under variation in the re-
quired number of workers.
When the increase in the number of workers does
not induce technology mixture (Figure 7(a)), the ag-
gregate labor cost curve moves upwards and the ag-
gregate investment cost stays unchanged. This im-
plies that the equilibrium moves from point D to point
D
0
, resulting in a higher cost with a lower ANS. In
the second case, when the increase in the number
of workers induces technology mixture (Figure 7(b)),
the curve dynamic can be explained in two stages: (i)
the aggregate labor cost increases and (ii) the aggre-
gate investment cost simultaneously decreases; with
this the equilibrium moves from point E to point F
and finally to point E
0
. Note that the aggregate la-
bor cost varies significantly more than the investment
cost and the new equilibrium is achieved at point E
0
,
implying a higher cost and a lower ANS.
For this industrial-size example, on average, 90%
of the cost can be explained as operational. Therefore,
when the operational costs are the same for all types
of technology, the technology mixture is more sen-
sitive under variation of the investment cost or num-
ber of workers. From the sensitivity analysis, we ob-
served that (i) the optimal capacity expansion strategy
is more sensitive to the cost that has more influence
over the total cost, (ii) the required number of work-
ers is always an important decision factor even when
the labor cost represents less than 10% of the total
cost, and (iii) the ANS has a direct relationship with
the investment cost and an inverse one with the labor
cost.
4.4 Computational Performance
To evaluate the computational performance of our
model and to cover a wide range of data, we generated
a set of 180 problems, each one randomly generated
around a base case with 10 different items, 5 types of
technologies, and a planning horizon of 10 periods,
with each problem having 881 variables (551 contin-
uous, 300 integer, and 30 binary variables) and 412
linear constraints. Figure 8 shows the computation
times in log
2
(sec) for all instances. In the abscissa
the cumulative percentage of instances is presented.
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
188

0.1 0.2 0.3 0.4
0.5 0.6
0.7 0.8 0.9 1
−2
0
2
4
6
8
10
Cumulative percentage
Time [log
2
(sec)]
Figure 8: Computation Times.
Figure 8 shows that we observed reasonable com-
putation times; 80% of the instances were solved in
less than 10 seconds and 94% of the instances were
solved in less than 100 seconds, with a geometric
mean of 2.8 seconds. The nominal problem of this
instances where solved with the formulation and algo-
rithm presented in Escalona and Ram
´
ırez (2012) ob-
taining an average computational of 584585 seconds
to arrive at the optimal solution, therefore our formu-
lation has an average speedup of 25175x.
5 CONCLUSION
In this paper, we develop a capacity expansion model
for multi-product, multi-machine manufacturing sys-
tems with uncertain demand. At first, a linear deter-
ministic model is presented and later the demand un-
certainty is incorporated using a robust approach for-
mulating an affine multi-stage robust model. In con-
trast with most of the works presented in the literature,
our model considers the shifts as a decision variable,
allowing more flexibility in the type of expansion that
can be used.
For instances that consider a planning horizon of
10 periods, 10 items, and with 5 types of technologies
available, the computation times prove to be reason-
able ones with times below 100 seconds for most of
them (94%), and therefore our model performs bet-
ter than the one presented in the literature, having an
average speedup of 25175x.
From the instances that we tested, we observed the
following managerial insights:
• Fixing beforehand the number of shifts to work
along the planning horizon can take us to sub-
optimal solutions.
• The technology mixture is most sensitive to the re-
quired number of workers and to the most impor-
tant cost.
• There exists an inverse relationship between la-
bor cost (number of workers) and the aggregate
available time and a direct relationship between
investment cost and the aggregate available time.
• The operational cost by itself does not change
the aggregate available time; in fact, if there is
no change in the investment cost and number of
workers, then the aggregate available time does
not change, i.e. the available time, and there-
fore the work shifts routed along that planning
horizon, depend only on the investment and labor
costs.
An interesting discussion that escaped the scope
of this work is the analysis of some costs, such as the
cost incurred when opening or closing a shift and the
opportunity cost which can be determined following
business logic instead of the accounting logic used in
this work.
Possible extensions of this problem that can be
considered are (i) the use of a scenario approach
with multi-stage programming (Ben-Tal et al., 2009),
(Shapiro, 2009), (ii) the use of CVaR
∆
to minimize
the variability of the solution (Rockafellar and Urya-
sev, 2000), (Pflug, 2000), (Rockafellar et al., 2006)
instead of cost minimization, and (iii) considering un-
certainty of other parameters such as the maintenance
times, production rates, costs, and/or available times.
REFERENCES
Asl, F. M. and Ulsoy, A. G. (2003). Stochastic optimal
capacity management in reconfigurable manufactur-
ing systems. CIRP Annals-Manufacturing Technol-
ogy, 52(1):371–374.
Barahona, F., Bermon, S., Gunluk, O., and Hood, S. (2005).
Robust capacity planning in semiconductor manufac-
turing. Naval Research Logistics, 52(5):459–468.
Ben-Tal, A., El Ghaoui, L., and Nemirovski, A. (2009). Ro-
bust optimization. Princeton University Press.
Bertsimas, D. and Sim, M. (2004). The price of robustness.
Operations research, 52(1):35–53.
Bertsimas, D. and Thiele, A. (2006). Robust and data-
driven optimization: Modern decision-making under
uncertainty. INFORMS Tutorials in Operations Re-
search: Models, Methods, and Applications for Inno-
vative Decision Making.
Bihlmaier, R., Koberstein, A., and Obst, R. (2009). Model-
ing and optimizing of strategic and tactical production
planning in the automotive industry under uncertainty.
OR spectrum, 31(2):311–336.
Cheng, L., Subrahmanian, E., and Westerberg, A. W.
(2004). Multi-objective decisions on capacity plan-
ning and production-inventory control under uncer-
tainty. Industrial & engineering chemistry research,
43(9):2192–2208.
Chien, C.-F., Wu, C.-H., and Chiang, Y.-S. (2012). Co-
ordinated capacity migration and expansion planning
for semiconductor manufacturing under demand un-
certainties. International Journal of Production Eco-
nomics, 135(2):860–869.
Strategic Capacity Expansion of a Multi-item Process with Technology Mixture under Demand Uncertainty: An Aggregate Robust MILP
Approach
189

Christie, R. M. and Wu, S. D. (2002). Semiconductor capac-
ity planning: stochastic modelingand computational
studies. IIE Transactions, 34(2):131–143.
Escalona, P. and Ram
´
ırez, D. (2012). Expansi
´
on de capaci-
dad para un proceso, m
´
ultiples
´
ıtems y mezcla de tec-
nolog
´
ıas. In 41 Jornadas Argentinas de Informatica.
Fleischmann, B., Ferber, S., and Henrich, P. (2006). Strate-
gic planning of bmw’s global production network. In-
terfaces, 36(3):194–208.
Geng, N., Jiang, Z., and Chen, F. (2009). Stochastic pro-
gramming based capacity planning for semiconductor
wafer fab with uncertain demand and capacity. Euro-
pean Journal of Operational Research, 198(3):899–
908.
Guigues, V. (2009). Robust production management. Opti-
mization and Engineering, 10(4):505–532.
Hood, S. J., Bermon, S., and Barahona, F. (2003). Capacity
planning under demand uncertainty for semiconductor
manufacturing. Semiconductor Manufacturing, IEEE
Transactions on, 16(2):273–280.
Julka, N., Baines, T., Tjahjono, B., Lendermann, P., and Vi-
tanov, V. (2007). A review of multi-factor capacity
expansion models for manufacturing plants: Search-
ing for a holistic decision aid. International Journal
of Production Economics, 106(2):607–621.
Karabuk, S. and Wu, S. D. (2003). Coordinating strategic
capacity planning in the semiconductor industry. Op-
erations Research, 51(6):839–849.
Levis, A. A. and Papageorgiou, L. G. (2004). A hierarchical
solution approach for multi-site capacity planning un-
der uncertainty in the pharmaceutical industry. Com-
puters & Chemical Engineering, 28(5):707–725.
Li, C., Liu, F., Cao, H., and Wang, Q. (2009). A
stochastic dynamic programming based model for un-
certain production planning of re-manufacturing sys-
tem. International Journal of Production Research,
47(13):3657–3668.
Lin, J. T., Chen, T.-L., and Chu, H.-C. (2014). A stochastic
dynamic programming approach for multi-site capac-
ity planning in tft-lcd manufacturing under demand
uncertainty. International Journal of Production Eco-
nomics, 148:21–36.
Lorca, A., Sun, X. A., Litvinov, E., and Zheng, T.
(2016). Multistage adaptive robust optimization for
the unit commitment problem. Operations Research,
64(1):32–51.
Luss, H. (1982). Operations research and capacity ex-
pansion problems: A survey. Operations research,
30(5):907–947.
Mart
´
ınez-Costa, C., Mas-Machuca, M., Benedito, E., and
Corominas, A. (2014). A review of mathematical pro-
gramming models for strategic capacity planning in
manufacturing. International Journal of Production
Economics, 153:66–85.
Miller, D. M. and Davis, R. P. (1977). The machine require-
ments problem. The International Journal of Produc-
tion Research, 15(2):219–231.
Pflug, G. C. (2000). Some remarks on the value-at-risk
and the conditional value-at-risk. In Probabilistic con-
strained optimization, pages 272–281. Springer.
Pimentel, B. S., Mateus, G. R., and Almeida, F. A. (2013).
Stochastic capacity planning and dynamic network
design. International Journal of Production Eco-
nomics, 145(1):139–149.
Pratikakis, N. E., Realff, M. J., and Lee, J. H. (2010). Strate-
gic capacity decision-making in a stochastic man-
ufacturing environment using real-time approximate
dynamic programming. Naval Research Logistics
(NRL), 57(3):211–224.
Rajagopalan, S., Singh, M. R., and Morton, T. E. (1998).
Capacity expansion and replacement in growing
markets with uncertain technological breakthroughs.
Management Science, 44(1):12–30.
Rastogi, A. P., Fowler, J. W., Carlyle, W. M., Araz, O. M.,
Maltz, A., and B
¨
uke, B. (2011). Supply network
capacity planning for semiconductor manufacturing
with uncertain demand and correlation in demand
considerations. International Journal of Production
Economics, 134(2):322–332.
Rockafellar, R. T. and Uryasev, S. (2000). Optimization of
conditional value-at-risk. Journal of risk, 2:21–42.
Rockafellar, R. T., Uryasev, S., and Zabarankin, M. (2006).
Optimality conditions in portfolio analysis with gen-
eral deviation measures. Mathematical Programming,
108(2-3):515–540.
Sahinidis, N. V. (2004). Optimization under uncertainty:
state-of-the-art and opportunities. Computers &
Chemical Engineering, 28(6):971–983.
Shapiro, A. (2009). On a time consistency concept in risk
averse multistage stochastic programming. Opera-
tions Research Letters, 37(3):143–147.
Stephan, H. A., Gschwind, T., and Minner, S. (2010). Man-
ufacturing capacity planning and the value of multi-
stage stochastic programming under markovian de-
mand. Flexible services and manufacturing journal,
22(3-4):143–162.
Swaminathan, J. M. (2000). Tool capacity planning for
semiconductor fabrication facilities under demand un-
certainty. European Journal of Operational Research,
120(3):545–558.
Van Mieghem, J. A. (2003). Commissioned paper: Capacity
management, investment, and hedging: Review and
recent developments. Manufacturing & Service Oper-
ations Management, 5(4):269–302.
Wu, C.-H. and Chuang, Y.-T. (2010). An innovative ap-
proach for strategic capacity portfolio planning under
uncertainties. European Journal of Operational Re-
search, 207(2):1002–1013.
Wu, S. D., Erkoc, M., and Karabuk, S. (2005). Managing
capacity in the high-tech industry: A review of litera-
ture. The Engineering Economist, 50(2):125–158.
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
190

APPENDIX
A Glossary of Terms
Table 1: Glossary of terms.
Sets Definition
I Set of items indexed by i
J Set of type of machines indexed by j
T Set of periods indexed by t
K Set of number of shifts indexed by k, with k = 1,2, 3
Parameters
Cp
i jt
Unitary production cost for item i produced with a machine of type j in period t
CI
jt
Investment cost of a machine of type j in period t
Cop
jt
Opportunity cost for a machine of type j in period t
CL
t
Unitary labor cost in period t
C
h
Hiring cost
C
f
Firing cost
B
j
Number of machines of type j available at the beginning of the planning horizon
A
j
Number of workers available to operate the machines of type j at the beginning of the planning horizon
d
it
Demand realization of item i in period t
¯
d
it
Nominal demand of item i in period t
ˆ
d
it
Maximum perturbation for the demand of item i in period t
r
i jt
Production rate of items i with machine of type j in period t
¯µ
j
Maximum utilization of machines type j
H
1
Available working time for each work shift
M A big enough number
¯
O
j
Number of workers needed to operate one machine of type j
Γ Level of conservativeness of the model
ˆ
F
it
Demand forecast of the item i at period t
σ
it
Standard deviation of the forecast error for item i at period t
Variables
X
i jt
Number of items i produced with machines of type j in period t
V
jt
Number of machines of type j bought in period t
Y
jkt
Number of machines of type j needed in each shift to satisfy the demand in period t, working k shifts
W
kt
1 if k shifts are worked in period t, 0 otherwise
Uh
jt
Number of workers hired in period t to work machines of type j
U f
jt
Number of workers fired in period t that worked machines of type j
w
t
Number of shifts to work in the period t
NN
jt
Number of machines of type j needed at period t to satisfy the demand
ND
jt
Number of machines of type j available at period t
λ
i j
Percentage of the accumulated over-demand assigned to the item i and machine j
¯
χ
i jt
Nominal quantity of item i to be produced in period t with machines of type j
Z Worst case production cost.
B Data for Illustrative Example
Table 2: Demand forecast of the item i at period t.
ˆ
X
it
[∗10
3
units]
i
t
1 2 3 4 5 6 7 8 9 10
1 100 111 122 138 177 236 330 411 483 605
2 328 420 549 662 788 950 1091 1479 1651 1830
3 367 470 650 762 1021 1140 1293 1736 2227 3111
4 180 226 308 391 523 686 942 1089 1452 1815
Table 3: Standard deviation of the forecast error for item i at period t.
σ
it
[∗10
2
]
i
t
1 2 3 4 5 6 7 8 9 10
1 30 44 53 70 99 179 292 416 515 858
2 83 130 210 343 532 823 1051 1771 2740 3823
3 142 243 468 747 1126 1335 1829 2590 4040 7805
4 67 96 155 236 423 742 1232 1685 3088 5054
Strategic Capacity Expansion of a Multi-item Process with Technology Mixture under Demand Uncertainty: An Aggregate Robust MILP
Approach
191
