Nested Rollout Policy Adaptation for Multiagent System Optimization in
Manufacturing
Stefan Edelkamp
1
and Christoph Greulich
2
1
Faculty 3 – Mathematics and Computer Science, University of Bremen, Bremen, Germany
2
International Graduate School for Dynamics in Logistics, University of Bremen, Bremen, Germany
Keywords:
Multiagent System Simulation, Optimization, Monte-Carlo Tree Search, Manufacturing.
Abstract:
In manufacturing there are not only flow lines with stations arranged one behind the other, but also more
complex networks of stations where assembly operations are performed. The considerable difference from
sequential flow lines is that a partially ordered set of required components are brought together in order to form
a single unit at the assembly stations in a competitive multiagent system scenario. In this paper we optimize
multiagent control for such flow production units with recent advances of Nested Monte-Carlo Search. The
optimization problem is implemented as a single-agent game in a generic search framework. In particular, we
employ Nested Monte-Carlo Search with Rollout Policy Adaptation and apply it to a modern flow production
unit, comparing it to solutions obtained with a simulator and with a model checker.
1 INTRODUCTION
In this paper, we propose Nested Monte-Carlo Search
for solving multiagent optimization problems by app-
plying a search framework that links a (domain-
specific) combinatorial problem to an implemented
(domain-independent) search algorithm. To solve the
problem, we selected a recent variant of Nested Roll-
out with Policy Adaptation (NRPA) (Edelkamp and
Cazenave, 2016).
The application scenario we consider is an
assembly-line network that is represented as a di-
rected graph. Between any two successive nodes in
the network, which represent entrances and exits of
assembly stations as well as junctions, we assume a
buffer of finite capacity. In those buffers, work pieces
are stored, waiting for service. At assembly stations,
service is given to work pieces. Travel time is mea-
sured and overall time optimized.
Especially in open, unpredictable, and complex
environments, Multiagent Systems (MASs) deter-
mine adequate solutions for transport problems. For
example, agent-based commercial systems are used
within the planning and control of industrial pro-
cesses (Dorer and Calisti, 2005; Himoff et al., 2006),
as well as within other areas of logistics (Fischer et al.,
1996; Bürckert et al., 2000), see (Parragh et al., 2008)
for a survey.
Flow line analysis is often done with queuing the-
ory (Manitz, 2008; Burman, 1995). Pioneering work
in analyzing assembly queuing systems with syn-
chronization constraints studies assembly-like queues
with unlimited buffer capacities (Harrison, 1973). It
shows that the time an item has to wait for synchro-
nization may grow without bound, while limitation of
the number of items in the system works as a control
mechanism and ensures stability. Work on assembly-
like queues with finite buffers all assume exponen-
tial service times (Bhat, 1986; Lipper and Sengupta,
1986; Hopp and Simon, 1989).
Our running case study is the so-called Z2, a phys-
ical monorail system for the assembling of tail-lights.
Unlike most production systems, Z2 employs agent
technology to represent autonomous products and as-
sembly stations. The techniques we develop, how-
ever, will be applicable to most flow production sys-
tems. We formalize the production floor as a system
of communicating agents and apply NRPA for ana-
lyzing its behavior optimizing the flow of production.
To make the paper self-contained we repeated the
description of the Z2 and of the multiagent system.
The contributions of this paper are: the encoding of
the optimization problem as a single-player game, a
flexible framework implementation, and a discussion
of the advantages of employing an MCTS optimizer.
The paper is structured as follows. We kick off by
introducing the Z2 as an example of a multiagent sim-
ulation system and formalize the multiagent optimiza-
284
Edelkamp S. and Greulich C.
Nested Rollout Policy Adaptation for Multiagent System Optimization in Manufacturing.
DOI: 10.5220/0006204502840290
In Proceedings of the 9th International Conference on Agents and Artificial Intelligence (ICAART 2017), pages 284-290
ISBN: 978-989-758-219-6
Copyright
c
 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

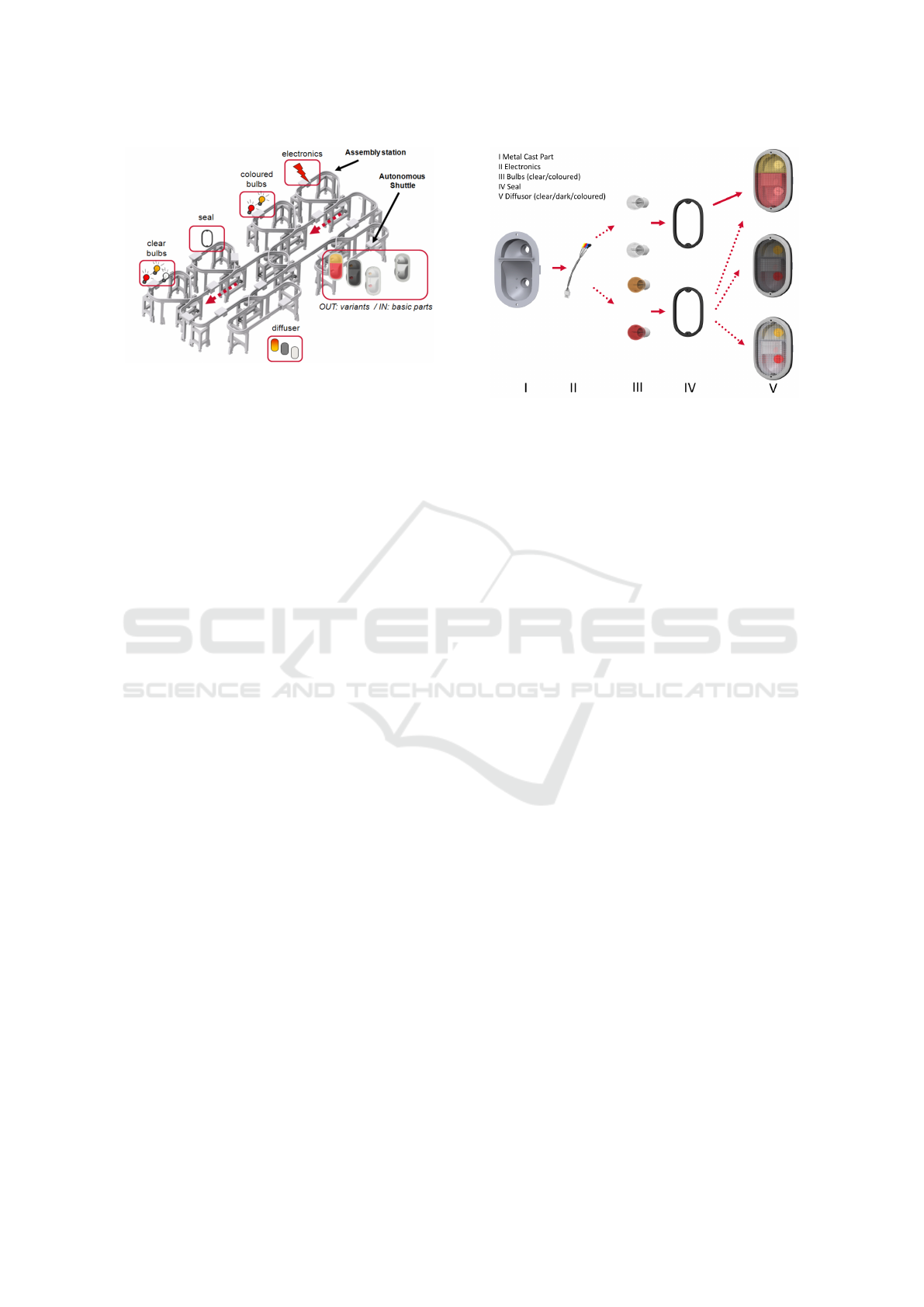
Figure 1: Assembly scenario for tail-lights (Morales Kluge
et al., 2010).
tion problem we face. Next, we present the family
of MCTS rollout algorithms including UCT, NMCS
and NRPA. In the following section, we map the opti-
mization problem to a single-player game which can
be solved in our NMCS framework. We will see that
the results compare positively with other optimization
approaches for the same multiagent system. Finally,
we conclude and discuss the impact of the work.
2 CASE STUDY: Z2
One of the few successful real-world implementations
of a multiagent flow production is the so called Z2
production floor unit (Ganji et al., 2010; Morales
Kluge et al., 2010). The Z2 unit consists of six work-
stations where human workers assemble parts of au-
tomotive tail-lights. The system allows production of
certain product variations as illustrated in Fig. 2 and
reacts dynamically to any change in the current or-
der situation, e.g., a decrease or an increase in the
number of orders of a certain variant. At the first sta-
tion, the basic metal-cast parts enter the manufactur-
ing system on a dedicated shuttle. A monorail con-
nects all stations, each station is assigned to one spe-
cific task, such as adding bulbs or electronics. The
structure of the transport system is shown in Fig. 1.
Each tail-light is transported from station to station
until it is assembled completely. The monorail sys-
tem has multiple switches which allow the shuttles
to enter, leave or pass workstations and the central
hubs. The goods transported by the shuttles are also
autonomous, which means that each product decides
on its own which variant to become and which sta-
tion to visit. This way, a decentralized control of the
production system is possible.
From the given case study, we derive a more
general notation of an assembly-line network. Sys-
tem progress is non-deterministic and asynchronous,
Figure 2: Assembly states of tail lights.(Ganji et al., 2010).
while the progress of time is monitored.
Definition 1 (Flow Production). A flow production
floor is tuple F = (A, P, G, ≺, S, Q) where
• A is a set of all possible assembling actions
• P is a set of n products; each P
i
∈ P, i ∈ {1, . . . , n},
is a set of assembling actions, i.e., P
i
⊆ A
• G = (V, E, w, s, t) is a graph with start node s, goal
node t, and weight function w : E → R
≥0
• ≺ = (≺
1
, . . . , ≺
n
) is a vector of assembling plans
with each ≺
i
⊆ A × A, i ∈ {1, . . . , n}, being a par-
tial order
• S ⊆ E is the set of assembling stations induced by
a labeling ρ : E → A ∪
/
0, i.e., S = {e ∈ E | ρ(e) 6=
/
0}
• Q is a set of (FIFO) queues, all of finite size to-
gether with a labeling ψ : E → Q
Products P
i
, i ∈ {1, . . . , n}, travel through the net-
work G, meeting their assembling plans/order ≺
i
⊆
A × A of the assembling actions A. The cost func-
tion uses a set of predecessor edges Pred(e) = {e
0
=
(u, v) ∈ E | e = (v, w)}.
Definition 2 (Run, Plan, and Path). Let F =
(A, P, G, ≺, S, Q) be a flow production floor. A run π
is a schedule of triples (e
j
,t
j
, l
j
) of edges e
j
, queue
insertion positions l
j
, and execution time-stamp t
j
,
j ∈ {1, . . . , n}. The set of all runs is denoted as
Π. The run partitions into a set of n plans π
i
=
(e
1
,t
1
, l
1
), . . . , (e
m
,t
i
, l
m
), one for each product P
i
, i ∈
{1, . . . , n}. Each plan π
i
corresponds to a path, start-
ing at the initial node s and terminating at goal node
t in G.
3 MULTIAGENT SYSTEM
In the real-world implementation of the Z2 system,
every assembly station, every monorail shuttle and ev-
Nested Rollout Policy Adaptation for Multiagent System Optimization in Manufacturing
285

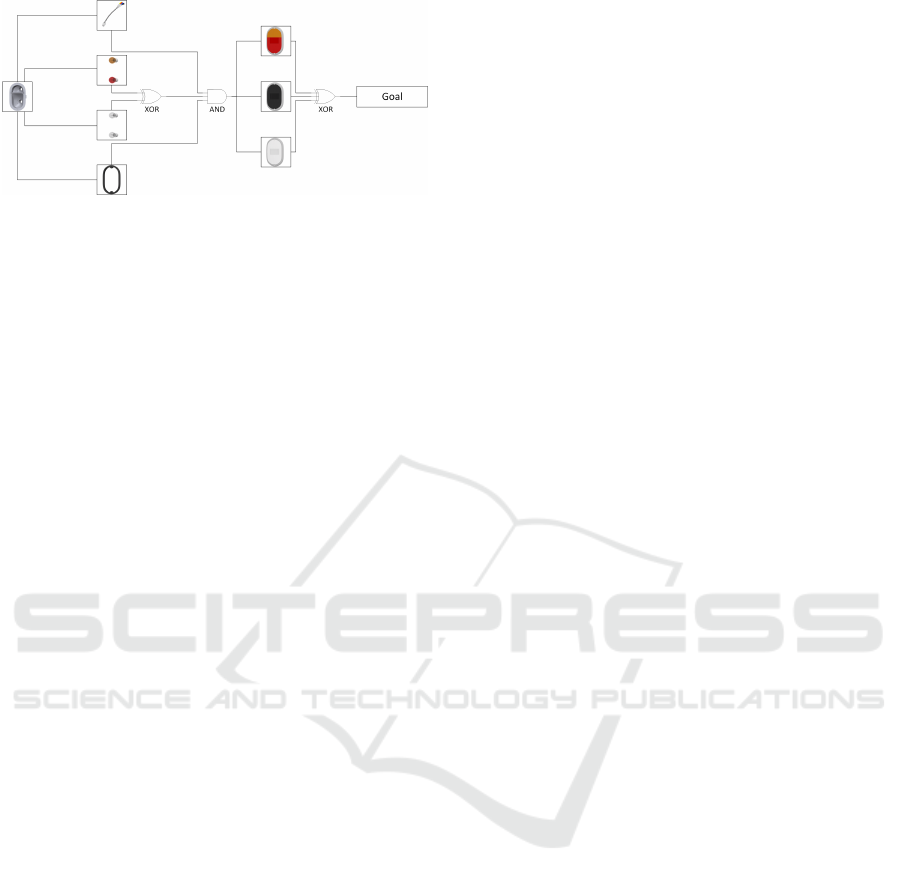
Figure 3: Preconditions of the various manufacturing
stages.
ery product is represented by a software agent. Most
agents in this MAS just react to requests or events
which were caused by other agents or the human
workers involved in the manufacturing process. In
contrast, the agents which represent products are ac-
tively working towards their individual goal of be-
coming a complete tail-light and reaching the storage
station. In order to complete its task, each product has
to reach sub-goals which may change during produc-
tion as the order situation may change. The number of
possible actions is limited by sub-goals which already
have been reached, since every possible production
step has preconditions as illustrated in Fig. 3.
The product agents constantly request updates re-
garding queue lengths at the various stations and the
overall order situation. The information is used to
compute the utility of the expected outcome of every
action which is currently available to the agent. High
utility is given when an action leads to fulfillment of
an outstanding order and takes as little time as possi-
ble. Time, in this case, is spent either on actions, such
as moving along the railway or being processed, or on
waiting in line at a station or a switch.
More generally, the objective of products in such
a flow production system can be formally described
as follows.
Definition 3 (Product Objective, Travel and Waiting
Time). The objective for product i is to minimize
max
1≤i≤n
wait(π
i
) + time(π
i
),
over all possible paths with initial node s and goal
node t, where
• time(π
i
) is the travel time of product P
i
, defined as
the sum of edge costs time(π
i
) =
∑
e∈π
i
w(e), and
• wait(π
i
) the waiting time, defined as wait(π
i
) =
∑
(e,t,l),(e
0
,t
0
,l
0
)∈π
i
,e
0
∈Pred(e)
t − (t
0
+ w(e
0
)).
For this study, we provided the MAS model with
timers to measure the time taken between two graph
nodes. Since the hardware includes many RFID read-
ers along the monorail, which all are represented by
an agent and a node within the simulation, we sim-
plified the graph and kept only three types of nodes:
switches, production station entrances and production
station exits. The resulting abstract model of the sys-
tem is a weighted graph, where the weight of an edge
denotes the traveling/processing time of the shuttle
between two respective nodes (Greulich et al., 2015).
4 MONTE-CARLO TREE
SEARCH
The randomized optimization scheme we consider be-
longs to the wider class of Monte-Carlo tree search
(MCTS) algorithms (Browne et al., 2004). The main
concept of MCTS is the random playout (or rollout)
of a position, whose outcome, in turn, changes the
likelihood of generating successors in subsequent tri-
als. Prominent members in this class of reinforcement
learning algorithms are upper confidence bounds ap-
plied to trees (UCT) (Kocsis and Szepesvári, 2006),
and nested monte-carlo search (NMCS) (Cazenave,
2009). MCTS is state-of-the-art in playing many two-
player games (Huang et al., 2013) or puzzles (Bouzy,
2016), and has been applied also to other prob-
lems than games like mixed-integer programming,
constraint problems, function approximation, physics
simulation, cooperative path finding, as well as plan-
ning and scheduling.
Cumulating in the success of AlphaGo (Silver
et al., 2016) in winning a match of Go against a pro-
fessional human player, the importance of MCTS in
playing games and AI search is no longer doubted.
5 NESTED MONTE-CARLO
SEARCH
Nested Monte-Carlo Search (NMCS) is a randomized
search method that has been successfully applied to
solve many challenging combinatorial problems, in-
cluding Klondike Solitaire, Morpion Solitaire, Same
Game, just to name a few. Recently, a large fraction
of TSP instances have been solved efficiently at or
close to the optimum (Cazenave and Teytaud, 2012a).
NMCS compares well with other heuristic methods
that include much more domain-specific information.
NMCS is parameterized with the recursion level of the
search which denotes the depth of the recursion tree
is, and with the number of iterations, that shows the
branching of the search tree. At each leaf of the recur-
sive search a rollout, which performs and evaluates a
random run.
What makes Nested Rollout Policy Adaptation
(NRPA) (Rosin, 2011) notably different to UCT and
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
286

NMCS is the concept of learning a policy through an
explicit mapping of moves to selection probabilities.
Beam-NRPA (Cazenave and Teytaud, 2012b) is an
extension of NRPA that maintains B instead of one
best solution in each level of the recursion. The mo-
tivation behind this is to warrant search progress by
an increased diversity of existing solutions to prevent
the algorithm from getting stuck in local optima. As
the NRPA recursion otherwise remains the same, the
number of playouts to a search with level L and (iter-
ation) width N rises from N
L
to (N · B)
L
. To control
the size of the beam, we allow different beam widths
B
l
in each level l of the tree (our values for B
l
in a
level 5 search were (1, 1, 10, 10, 10)). At the end of
the procedure, B
l
best solutions together with their
scores and policies are returned to the next higher re-
cursion level. For each level l of the search, one may
also allow the user to specify a varying iteration width
N
l
. This yields the algorithm Beam-NRPA to perform
∏
L
l=1
N
l
B
l
rollouts.
Beam-NRPA itself is inspired by the objective of
higher diversity in the solution space of NRPA. Still,
in very larger search spaces NRPA often dwells on
inferior solutions. It simply takes too long to back-
track to less determined policies in order to visit
other parts in the search space. High-Diversity NPRA
(HD-NRPA) (Edelkamp and Cazenave, 2016) elabo-
rates on this observation to increase the diversity of
the search and provides some further algorithmic ad-
vances (e.g., instead of the moves executed in a roll-
out the policy table address of the chosen move and
the code of its successors are stored, or the length of
the rollout and its score are stored for each bucket in
the beam).
6 GAME ENCODING
In the encoding as a single-player game, the amount
of acting agents is significantly reduced in compar-
ison to the original MAS. Similar to the encoding
for model-checker-based approaches (Edelkamp and
Greulich, 2016), decision making is modeled into the
nodes while shuttles are merely integer values which
are passed along the edges. Each edge is modeled
as a queue to make sure that no shuttle can pass an-
other. When put on an edge, a shuttle receives a wait-
ing time which corresponds to the cost of the spe-
cific edge. A synchronizing function (Greulich and
Edelkamp, 2016) ensures that time progresses for all
shuttles. The node at the end of a directed edge is al-
lowed to receive a shuttle only if it is first in its queue
and its waiting time has passed. If a shuttle can be re-
ceived by a node, the node provides a legal move for
cl as s A re na {
pu bl ic :
Mo ve rol lou t [ M ax L en g th ] ;
int leng th ;
Ar en a () {
le ng th = 0;
for ( i nt i = 0; i < S TA T IO NS ; i ++) {
sw i t ch 2 en t r an c e [ i ] - > c le ar ();
ex i t2 s wi t ch [ i ] - > c le ar ( );
en t ran c e2 e xi t [ i ]-> c le ar ( );
}
for ( i nt i = 0; i < S TA T IO NS + 2* H UBS ; i + +)
sw i tch 2 sw i tc h [ i ]-> c le ar ( );
for ( i nt i = 0; i < S H UT TLE S ; i ++ ) {
wa it [ i ] = 0; c os t [ i ] = i * 70;
go al s [ i ] = 0; c ol or [ i] = i %2 ;
me t al c as t [i] = 1; dif f us or [ i ] = 0 ;
el e ct r on i cs [ i ] = bu lb [ i ] = se al [ i ] = 0;
sw i t ch 2 en t r an c e [5] - > pu sh ( i );
}
}
% int cod e ( Mo ve m ) { r et ur n m ; }
int le ga l Mo v es (M ov e m ov es [ M a xL e ga l Mov e s ]) {
int m [3] , m vs = 0;
wh il e ( mv s == 0) {
for ( i nt p = 0; p < a ge nt . si ze ( ); p ++ ) {
int k = a ge nt [ p ]-> n e xt L eg a lMo v e ( m );
for ( i nt l =0 ; l < k ;l ++ )
mo ve s [ mvs + +] = p *3 + m [ l ];
}
if ( mv s == 0) i n cr e a se _ ti m e ();
}
re tu rn mv s ;
}
vo id p la y ( Move m ) {
ro ll o ut [ le ngt h ++ ] = m ;
ag en t [ m /3] - > e x ec u te M ove ( m % 3) ;
}
bo ol ter m in al () {
int re ac he d = 1 ;
for ( i nt j = 0; j < S HUT TL E S ; j ++ )
re ac h ed &= goa ls [ j ];
re tu rn ( r ea che d ) || l en g th = = Ma xL en gt h - 1;
}
do ub le s co re ( ) {
int ma xi mu m = 0 , to ta l = 0;
for ( i nt j = 0; j < S HUT TL E S ; j ++ )
if ( co st [ j ] > ma x im um ) m ax imu m = c os t [ j ];
int re ac he d = 0 ;
for ( i nt j = 0; j < S HUT TL E S ; j ++ )
re ac h ed += ! go al s [ j ];
re tu rn ( r ea che d * 1 000) + m axi mu m ;
}
}
Figure 4: Code for Z2 multiagent system optimization.
each outgoing edge. Hence, a set of all legal moves
over all active agents can be obtained.
To play the game, the player has to choose one
of the agents and one of its actions as the next move.
Goal of the game is to finish a predefined number of
Nested Rollout Policy Adaptation for Multiagent System Optimization in Manufacturing
287

cl as s A ge nt {
pu bl ic :
Ag en t () {}
vi rt u al voi d e x ec u te M ov e ( i nt m ) = 0;
vi rt u al int next L eg a lM o ve ( int * mo ve s ) = 0;
};
Figure 5: Code for abstract agent class.
cl as s S wit ch : p ub li c Age nt {
pu bl ic :
int In , Out , Sta ti on , B , C ;
Sw it ch ( i nt in , i nt out , in t s , in t b , in t c ) :
Ag en t () , In ( in ) , O ut ( ou t ) , S t at io n ( s) , B ( b ),C ( c ) {}
vo id ex ec u te M ov e ( i nt m ov e ) {
if ( mo ve == 0) {
int Sh ut tl e = s wi t c h2 s wi t ch [ In ] -> po p ( );
wa it [ S hu t tl e ] += C ; c os t [ Shu tt le ] += C;
sw i t ch 2 en t r an c e [ S ta t io n ] - > pu sh ( S hut tl e );
}
if ( mo ve == 1) {
int Sh ut tl e = s wi t c h2 s wi t ch [ In ] -> po p ( );
wa it [ S hu t tl e ] += B ; c os t [ Shu tt le ] += B;
sw i tch 2 sw i tc h [ O ut ] - > pu sh ( S hu t tl e );
}
if ( mo ve == 2) {
int Sh ut tl e = e xi t 2s w it c h [ S tat io n ] - > p op ( );
wa it [ S hu t tl e ] += B ; c os t [ Shu tt le ] += B;
sw i tch 2 sw i tc h [ O ut ] - > pu sh ( S hu t tl e );
}
}
int ne x tL e ga l Mov e ( int * m ov es ) {
int mvs = 0;
if ( r ec e iv es ( SW 2S W_E N , In , S t at io n ))
mo ve s [ mvs + +] = 0;
if ( r ec e iv es ( SW 2S W_ PA SS ,I n , S ta ti o n ))
mo ve s [ mvs + +] = 1;
if ( r ec e iv es ( E X2SW , S tat io n , S ta t io n ))
mo ve s [ mvs + +] = 2;
re tu rn mv s ;
}
};
Figure 6: Code for one agent.
products in the shortest possible time before a prede-
fined length is exceeded. The smaller the makespan
for each agent found by the algorithm the higher the
score of the play.
More formally, the (board) game is defined as
(B, b
0
, d, F, r) where B is the set of (board) positions,
in our case consisting of all queue content, shuttle lo-
cations, and their respective cost values. The start po-
sition s
0
has all shuttles and all queues being empty,
d : B → 2
B
specifies the set of allowed actions for each
q ∈ B, The set of final positions F consists of all states
in which either all the individual goals or the maximal
step sized is reached, and r : B → N is the score func-
tion adding a constant (e.g., 1000) for each individual
unreached goal, on top of the maximum of the indi-
vo id in cr e as e _ ti m e () {
int min = INF , d = 1;
for ( i nt p = 0; p < S H UT TLE S ; p ++ )
if (0 < w ai t [ p ] && wait [ p ] < min ) min = wa it [ p ];
if ( mi n < IN F ) d = mi n ;
for ( i nt p = 0; p < S H UT TLE S ; p ++ )
if ( wa it [ p ] - d >= 0 ) {
wa it [ p ] -= d ; cost [ p ] += d ;
}
el se w ai t [ p ] = 0;
}
bo ol rec e iv es ( int cha nne lt yp e , int i , int st at io n ) {
int resu lt = 0;
Ch an n el * c ha nn e l = N UL L ;
sw it ch ( c ha n ne l ty p e ) {
ca se EN2 EX : ch a nn el = ent r anc e 2e x it [ i ];
br ea k ;
ca se EX2 SW : ch a nn el = exi t 2s w it c h [ i ] ;
br ea k ;
ca se SW2S W_P ASS : c ha nn e l = swit c h2 s wi t ch [ i ];
br ea k ;
ca se SW2 S W_ EN : c ha nne l = swi t ch 2 sw i tch [ i ];
br ea k ;
ca se SW2 EN :
if ( e n tr a nc e 2ex i t [ s ta tio n ] - > le ng th ( ) >= 1 )
ch an n el = N ULL ;
el se cha nne l = s wi t ch 2 e nt r an c e [ s t at io n ];
br ea k ;
}
if ( c ha nne l != N UL L && c han ne l - > l en gt h () > 0) {
int sh ut tl e = ch ann el - > fr on t () ;
if ( wa it [ sh utt le ] <= 0)
re su lt = 1;
}
re tu rn r es ul t ;
}
Figure 7: Code for increase-time and receive action.
vidual cost values.
The components of the game induce a tree in the
natural way with B as nodes, root b
0
, d as edges and
the final positions as leaves. A play(out) is then a path
in the tree from b
0
to some leaf.
The software implementation (see Fig. 4–Fig. 7)
is based on a framework which allows to employ
several search algorithms such as MCTS, NMCS,
NRPA, BEAM-NRPA and HD-NRPA (Edelkamp and
Cazenave, 2016). For our experiments, we only fo-
cused on HD-NRPA since it is the most advanced im-
plementation and provided the best results.
7 EXPERIMENTS
For the evaluation we used a single core of a personal
computer infrastructure (Ubuntu 14.04 LTS (x64), In-
tel Core i7-4500U, 1.8 GHz, 8 GB).
We experiment with a rising number of vehicles
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
288

Table 1: Efficiency of MCTS for a rising number of shuttles,
compared to previously published results.
MCTS LVT DES
N Length Cost CPU Cost Cost
2 48 2:54 1s 3:24 2:53
3 72 2:59 1s 3:34 3:04
4 99 3:08 2s 3:56 3:13
5 123 3:13 2s 4:31 3:25
6 153 3:22 5s 4:31 3:34
7 186 3:38 5s 5:08 3:45
8 213 3:45 5s 5:43 3:55
9 240 3:52 5s 5:43 4:06
10 267 3:52 5s 5:43 4:15
20 540 5:16 5s 8:59 5:59
and compare the results with the discrete event sys-
tem (DES) model (Edelkamp and Greulich, 2016)
and local virtual time (LVT) model (Greulich and
Edelkamp, 2016), both implemented in the SPIN
model checker using its branch-and-bound facility.
While DES was faster than LVT, it had semantical
problems with the proper progression of time. There-
fore, in the MCTS implementation we decided to use
the semantics of the LVT model.
Table 1 shows that the MCTS implementation
scales best. It shows the length of the plan, the sim-
ulation time (Cost), and the runtime for a growing
number of vehicles. Here we do not enforce prereq-
uisites, namely that shuttles are protected from driv-
ing into a station if they have not all required com-
ponents available. Given that SPIN is a full-fledged
model checker that analyzes the encoding of the prob-
lem on the source-code level (resulting of traces that
have thousands of steps) the result could have been
expected, even though the search space is huge.
The CPU time bound for MCTS was 5 seconds,
the RAM requirements remained rather small, less
than 4MB for the largest instance, while the competi-
tors require hundreds of MBs. As with the DES/LVT
model, in cost we measure travel time plus some ini-
tial waiting time.
To help the solver to find valid solutions, we
extended the objective fuction (reached ∗ 1000) +
maximum by the term (e
r
∗10)+(b
r
∗10)+(s
r
∗10)+
(d
r
∗100), where e
r
, b
r
, s
r
, and d
r
are the violations to
the assembling status of electronics, bulbs, seals, and
diffusors, respectively.
We observe that there is a difference in the simu-
lation times of LVT and DES even for two shuttles.
Hence, we decided to reimplement LVT and have the
two cost functions in a close match. Table 2 shows
that (due to RAM usage) this implementation of LVT
has difficulties to scale and failed for four vehicles,
while the MCTS remained sufficiently fast (for larger
Table 2: Efficiency of MCTS for a rising number of shuttles,
compared to reimplementation.
MAS MCTS LVT
N Cost Cost CPU Cost CPU
2 4:01 3:17 5s 3:03 <1s
3 4:06 3:23 5s 3:19 79s
4 4:46 3:41 5s – –
5 4:16 3:59 5s – –
6 5:29 4:30 5s – –
models the bound of 5s turned out to be insufficient to
solve all models with no constraint violations).
In Table 2 we also added the results of the simu-
lated multiagent system, where the agents chose the
color of the lamp dynamically based on fuzzy logic
decision rules that take the incoming orders and ob-
served current queue lengths into account.
8 CONCLUSION AND
DISCUSSION
Monte-Carlo Tree Search is a general exploration
strategy that leads to concise solver prototypes not
only for games but for many combinatorial opti-
mization problems including multiagent optimization
problems.
We proposed the application of MCTS to evaluate
amultiagent system that controls the industrial pro-
duction of autonomous products. As the flow of ma-
terial is asynchronous at each station, queuing effects
arise and additional constraints make the problem NP-
hard. Besides validating the design of the system, the
core objective of this work was to find plans that op-
timize the throughput of the system.
We modeled the production line as a set of
communicating agents, with the movement of items
modeled as communication channels. Experiments
showed that the implementation is able to analyze the
movements of autonomous products for the model,
subject to the partial ordering of the product parts. It
derived valid and optimized plans with several hun-
dreds of steps using NRPA. A generic search frame-
work helped to perform policy-based benchmarking.
Considering the simplicity of the code, the sequen-
tiality of the execution on one CPU core, the obtained
results are promising.
NRPA is one means to find such needle in the
haystack. It intensify the search with increasing recur-
sion depth. The nestedness and policy refreshments
relate to exponential restarting strategies known to be
effective in the SAT community (Gomes et al., 2000).
An open problem is to find necessary/sufficient
Nested Rollout Policy Adaptation for Multiagent System Optimization in Manufacturing
289

criteria for the convergence of NMCS/NRPA. While
as in most MCTS algorithms based on rollouts, we
have probabilistic completeness in the sense that an
optimal solution can always be found by chance.
However, through nesting and adapting policies the
success likelihood can become arbitrarily small, so
that for now we cannot say by certain, that the op-
timum will be reached.
REFERENCES
Bhat, U. (1986). Finite capacity assembly-like queues.
Queueing Systems, 1:85–101.
Bouzy, B. (2016). An experimental investigation on the
pancake problem. In Computer Games: Fourth
Workshop on Computer Games, pages 30–43, Cham.
Springer International Publishing.
Browne, C. B., Powley, E., Whitehouse, D., Lucas, S. M.,
Cowling, P., Rohlfshagen, P., Tavener, S., Perez, D.,
Samothrakis, S., and Colton, S. (2004). A survey of
Monte Carlo tree search methods. 4(1):1–43.
Bürckert, H.-J., Fischer, K., and Vierke, G. (2000). Holonic
transport scheduling with teletruck. Applied Artificial
Intelligence, 14(7):697–725.
Burman, M. (1995). New results in flow line analysis. PhD
thesis, MIT.
Cazenave, T. (2009). Nested monte–carlo search. In IJCAI,
pages 456–461.
Cazenave, T. and Teytaud, F. (2012a). Application of
the Nested Rollout Policy Adaptation Algorithm to
the Traveling Salesman Problem with Time Windows,
pages 42–54. Springer.
Cazenave, T. and Teytaud, F. (2012b). Beam nested rollout
policy adaptation. In ECAI-Workshop on Computer
Games, pages 1–12.
Dorer, K. and Calisti, M. (2005). An adaptive solution to
dynamic transport optimization. In Proceedings of the
fourth international joint conference on Autonomous
agents and multiagent systems, pages 45–51. ACM.
Edelkamp, S. and Cazenave, T. (2016). Improved diversity
in nested rollout policy adaptation. In German Con-
ference on AI (KI 2016).
Edelkamp, S. and Greulich, C. (2016). Using SPIN for
the optimized scheduling of discrete event systems in
manufacturing. In SPIN 2016, pages 57–77. Springer.
Fischer, K., Müller, J. R. P., and Pischel, M. (1996). Coop-
erative transportation scheduling: an application do-
main for dai. Applied Artificial Intelligence, 10(1):1–
34.
Ganji, F., Morales Kluge, E., and Scholz-Reiter, B. (2010).
Bringing Agents into Application: Intelligent Prod-
ucts in Autonomous Logistics. In Artificial intel-
ligence and Logistics (AiLog) - Workshop at ECAI
2010, pages 37–42.
Gomes, C. P., Selman, B., Crato, N., and Kautz, H.
(2000). Heavy-tailed phenomena in satisfiability and
constraint satisfaction problems. J. Autom. Reason.,
24(1-2):67–100.
Greulich, C. and Edelkamp, S. (2016). Branch-and-bound
optimization of a multiagent system for flow produc-
tion using model checking. In ICAART 2016.
Greulich, C., Edelkamp, S., and Eicke, N. (2015). Cyber-
physical multiagent simulation in production logistics.
In MATES 2015.
Harrison, J. (1973). Assembly-like queues. Journal of Ap-
plied Probability, 10:354–367.
Himoff, J., Rzevski, G., and Skobelev, P. (2006). Ma-
genta technology multi-agent logistics i-scheduler for
road transportation. In AAMAS 06, pages 1514–1521.
ACM.
Hopp, W. and Simon, J. (1989). Bounds and heuristics for
assembly-like queues. Queueing Systems, 4:137–156.
Huang, S.-C., Arneson, B., Hayward, R. B., Mueller, M.,
and Pawlewicz, J. (2013). Mohex 2.0: A pattern-based
MCTS Hex player. In Computers and Games, pages
60–71.
Kocsis, L. and Szepesvári, C. (2006). Bandit based Monte-
Carlo planning. In ECML, pages 282–293.
Lipper, E. and Sengupta, E. (1986). Assembly-like queues
with finite capacity: bounds, asymptotics and approx-
imations. Queueing Systems, pages 67–83.
Manitz, M. (2008). Queueing-model based analysis of as-
sembly lines with finite buffers and general service
times. Computers & Operations Research, 35(8):2520
– 2536.
Morales Kluge, E., Ganji, F., and Scholz-Reiter, B. (2010).
Intelligent products - towards autonomous logistic
processes - a work in progress paper. In Intern. PLM
Conf.
Parragh, S. N., Doerner, K. F., and Hartl, R. F. (2008).
A Survey on Pickup and Delivery Problems Part II:
Transportation between Pickup and Delivery Loca-
tions. Journal für Betriebswirtschaft, 58(2):81–117.
Rosin, C. D. (2011). Nested rollout policy adaptation for
monte carlo tree search. In IJCAI, pages 649–654.
Silver, D., Huang, A., Maddison, C. J., Guez, A., Sifre, L.,
van den Driessche, G., Schrittwieser, J., Antonoglou,
I., Panneershelvam, V., Lanctot, M., Dieleman, S.,
Grewe, D., Nham, J., Kalchbrenner, N., Sutskever, I.,
Lillicrap, T., Leach, M., Kavukcuoglu, K., Graepel,
T., and Hassabis, D. (2016). Mastering the game of
go with deep neural networks and tree search. Nature,
529:484–503.
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
290