
Affinity-based Interpretation of Triangle Social Scenarios
Pratyusha Kalluri
1
and Pablo Gervás
2
1
Department of Electrical Engineering and Computer Science, MIT, Cambridge, MA, U.S.A.
2
Institute of Knowledge Technologies, Facultad de Informática, Universidad Complutense de Madrid, Madrid, Spain
Keywords: Social Perception, Social Cognition, Knowledge Representation, Bayesian Inference.
Abstract: Computational interpretation of social scenarios is a critical step towards more human-like artificial
intelligence. We present a model that interprets social scenarios by deducing the affinities of the constituent
relationships. First, our model deploys Bayesian inference with an action affinity lexicon to infer
probabilistic affinity relations characterizing the scenario. Subsequently, our model is able to use the
inferred affinity relations to choose the most probable statement from multiple plausible statements about
the scenario. We evaluate our approach on 80 Triangle-COPA multiple-choice problems that test
interpretation of social scenarios. Our approach correctly answers the majority (59) of the 80 questions
(73.75%), including questions about behaviors, emotions, social conventions, and complex constructs. Our
model maintains interpretive power while using knowledge captured in the lightweight action affinity
lexicon. Our model is a promising approach to interpretation of social scenarios, and we identify potential
applications to automated narrative analysis, AI narrative generation, and assistive technology.
1 INTRODUCTION
Given a brief social scenario, healthy humans
experience a number of social percepts; we infer
beliefs, goals, emotions, and social relationships
seemingly effortlessly (Rutherford and Kuhlmeier,
2013). Similar social perception is essential for
future artificial intelligence systems meant to
interact with or emulate humans.
Logic-based automated social inference can
provide rich interpretations of social scenarios but
comes with the steep cost of carefully curating large,
rich knowledge bases of psychology and sociology
axioms (Davis and Morgenstern, 2005; Gordon and
Hobbs, 2011; Gordon 2016). Standard sentiment
analysis of social scenarios makes use of simpler
knowledge: easily obtained sentiment lexicons; but
standard sentiment analysis only captures scenarios’
evolving positivity/negativity, precluding rich
interpretations (Reagan et al., 2016). For
computational interpretation of social scenarios to
become more useful and generalizable, novel
approaches must be developed, able to conduct
relatively rich interpretation using relatively
lightweight knowledge.
Studies from psychology reveal that one-year-old
infants recognize the underlying difference between
helping relationships and hindering relationships and
make assumptions about subsequent behaviors
(Premack and Premack, 1997; Kuhlmeier et al.,
2004). Motivated by these studies, we introduce a
model for interpreting social scenarios by deducing
the affinities of the constituent relationships. In
comparison to logic-based automated social
inference, our model for affinity-based automated
interpretation of social scenarios uses simpler
knowledge, like that of sentiment analysis, while
maintaining significant interpretive power.
2 FURTHER BACKGROUND
The term social perception is most closely
associated with the social psychologist Fritz Heider
(Rutherford and Kuhlmeier, 2013). Heider and
Simmel (1944) famously demonstrated that subjects
presented with a short film of geometric shapes
moving in relation to one another interpreted the
film in social terms.
The Triangle Choice of Plausible Alternatives
(Triangle-COPA) challenge problems by Maslan et
al. (2015) constitute a development test set, akin to
training data, for computational interpretation of
behavior. Each Triangle-COPA problem contains a
640
Kalluri P. and Gervà ˛as P.
Affinity-based Interpretation of Triangle Social Scenarios.
DOI: 10.5220/0006205506400647
In Proceedings of the 9th International Conference on Agents and Artificial Intelligence (ICAART 2017), pages 640-647
ISBN: 978-989-758-220-2
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

question describing a brief scenario in the style of
the Heider-Simmel film: two triangles and a circle
perform various actions in and around a room with a
door. Each question is accompanied by a correct
answer and an incorrect answer, where correctness
has been established by perfect agreement among
human raters. The task is to computationally
determine which is the correct answer. An example
Triangle-COPA challenge problem is as follows:
Question 10. A triangle and circle are arguing.
The circle turns around and leaves the room.
Why does the circle leave? (Correct: The circle is
annoyed with the triangle. Incorrect: The circle is
happy with the triangle.)
Triangle-COPA is an attractive framework for
developing computational interpretation of social
scenarios. Each Triangle-COPA problem is provided
in two forms, an English form and a logical literal
form using a fixed vocabulary. Researchers using
the logical form are free to concentrate on
interpretation while circumventing many natural
language processing challenges. Additionally, the
multiple-choice structure of Triangle-COPA enables
straightforward assessment of success.
Gordon (2016) presents a Triangle-COPA solver
that models interpretation of behavior as a
probabilistic logical abduction process: the model
identifies sets of assumptions that would account for
the behavior specified in a question and chooses the
answer associated with the more probable set.
Identifying assumptions that may account for
specified behavior relies on a hand-authored
knowledge base of 252 axioms, which explicitly
encode all necessary knowledge and probability
estimates based on the authors’ intuitions. While the
approach by Gordon correctly solves the large
majority (91) of 100 Triangle-COPA problems,
Gordon notes that this success relies on the laborious
task of hand-authoring the exact axioms and
probability estimates necessary to solve these
questions correctly.
Many probabilistic automated reasoning systems,
including the previous Triangle-COPA solver by
Gordon (2016), rely on being fed absolute prior
probabilities of many dissimilar events.
Mathematically, absolute prior probabilities are
minimally constrained. Conceptually, absolute prior
probabilities are ill defined and may have multiple,
mutually contradictory meanings for different
members of the public (Gigerenzer et al., 2005). As
a result, non-arbitrary, non-biased absolute prior
probabilities are problematic to obtain. We are
motivated to formulate a model for interpretation of
social scenarios that uses lightweight knowledge and
that does not use absolute prior probabilities.
3 COMPUTATIONAL
FRAMEWORK
3.1 Deduction of Affinity Relations
Given a social scenario, our model deploys Bayesian
inference with an action affinity lexicon to infer
probabilistic affinity relations characterizing the
scenario. Given a finite set of agents and a finite
sequence of actions
(
)
, we define a social scenario
as the finite sequence of events (
), where each
event
consists of an agent completing the action
, which is optionally directed at an object or
another agent.
3.1.1 Affinity Relation
According to our formulation, between any two
agents
,
∈, there exists a mutual affinity,
which takes on a discrete affinity state ∈
,,
. For the agent
pair (
,
), the probability () denotes the
model’s belief that the affinity state is the true
affinity of the pair. We underscore that these beliefs
are meant to represent those of an impartial
observer; our formulation does not currently
represent the subjective beliefs of agents. For the
agent pair
(
,
)
, the belief set, (),
(), and () sums to 1; we refer
to this belief set as the affinity relation linking
and
.
3.1.2 Action Affinity Lexicon
Our model relies on a static probabilistic action
affinity lexicon, which links actions to
corresponding affinities. For example, the lexicon
may capture that arguing commonly corresponds to
an unpleasant affinity. Formally, each entry in the
lexicon links an action to the relative observation
distribution of :
(
|
)
(
)
∶
∈
(1)
Intuitively, each entry contains an action and the
relative likelihood of witnessing that action in the
context of each affinity state. Table 1 presents a
sample action affinity lexicon. We note that our
model relies on relative observation distributions
Affinity-based Interpretation of Triangle Social Scenarios
641
and never relies on absolute prior probabilities.
Table 1: Sample action affinity lexicon that may be used
to interpret Triangle-COPA question 10 (presented in
Section 2). The lexicon consists of each action in the
logical literal form of question 10 and its relative
observation distribution over the affinity state space.
Action
Relative Observation Distribution
Unpleasant Neutral Pleasant
argue_with .50 (high) .25 (low) .25 (low)
turn .40 (high) .40 (high) .20 (low)
exit
.3
(high) .3
(high) .3
(high)
annoy .50 (high) .25 (low) .25 (low)
be_happy .25 (low) .25 (low) .50 (high)
3.1.3 Modified Bayesian Belief Updates
For the agent pair (
,
), until our model observes
interaction between
and
, the respective affinity
relation is uninformed and is accordingly
represented as a discrete uniform distribution:
(
)
=
1
3
,
∈
(2)
Upon observing agent
direct the action
at
agent
(e.g. Patti pokes Alex), the model queries
its action affinity lexicon for the relative observation
distribution of action
(e.g. the relative observation
distribution of poke) and uses this knowledge to
update the affinity relation linking
and
(e.g.
between Patti and Alex).
Further, our model can extract additional
information from object-directed and undirected
actions. Suppose, slightly later,
directs the action
at an object (e.g. Alex slams the door) or agent
’s action
is undirected (e.g. Alex yelps).
Humans intuitively interpret
as a reaction to
,
(e.g. a reaction to Patti’s poke) despite the fact that
is not explicitly directed at
. In order to glean
more social information from a given social
scenario, we provide our model with a baseline
formulation for handling these implicitly directed
actions: upon observing an object-directed or
undirected action such as
, our model proceeds as
though the action is implicitly directed at the last-
mentioned agent (in this case,
). As in the
explicitly directed case, our model then goes on to
update the affinity relation linking agents
and
.
We formulate a modified Bayesian belief update
function. Standard Bayesian belief updates place
equal weight on each piece of evidence encountered.
Yet, social descriptions often begin by describing
many minor events intended to set up subsequent
major events. Moreover, human judgment of an
experience tends to be inordinately affected by the
experience’s end (Kahneman et al., 1993). On these
grounds, our model uses a recency-weighted
reformulation of Bayesian belief updates, in which
recently observed actions have greater impact on the
model’s beliefs than earlier observed actions. Each
updated belief
() is a deterministic, recency-
weighted Bayesian function of the previous belief
(), the action
, and the timestep :
(
)
∝
(
)
(
|
)
(
)
(3)
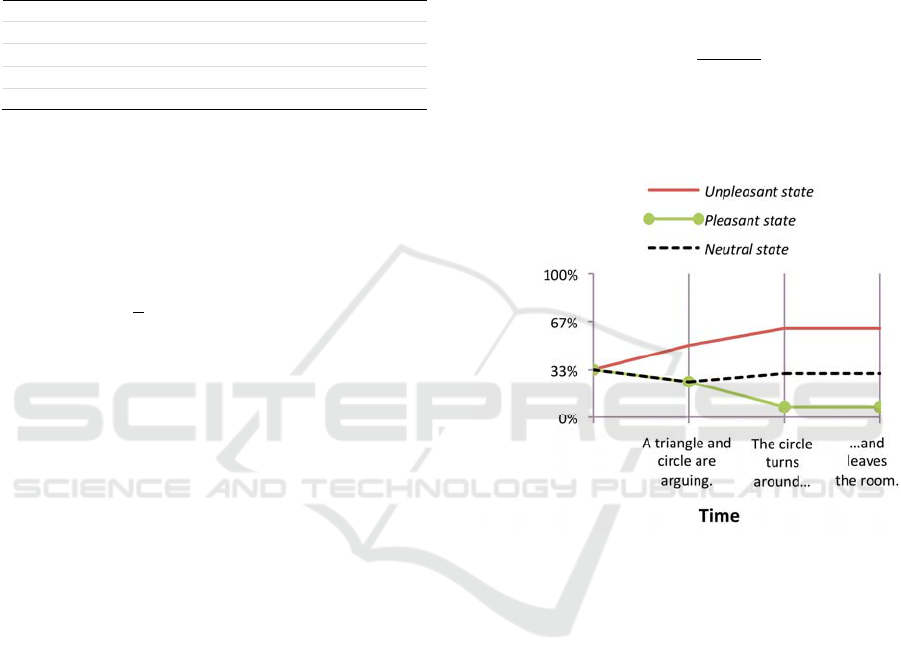
In Figure 1, we present a demonstrative example of
our model’s capacity to deduce affinity relations
from a brief social scenario.
Figure 1: Deduction of the affinity relation between the
Circle and the Big Triangle during Triangle-COPA
question 10. Before the first event, the observer believes
Unpleasant, Neutral, and Pleasant affinities are equally
probable. As events unfold, the observer increasingly
believes that an Unpleasant affinity is the most probable.
3.2 Multiple-choice Question
Answering
In order for our model to solve multiple-choice
problems about social scenarios such as the
Triangle-COPA problems, our model must be able
to interpret a descriptive question, evaluate a finite
set of plausible descriptive answers (choices) , and
choose the best answer in . We describe a method
for answer selection: having deduced a finite set of
underlying affinity relations from the question,
our model calculates the conditional probability for
each descriptive answer ∈ given ; our model
then chooses the answer with the highest conditional
probability.
Belief Regarding Affinity
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
642

We assume each answer is an interpretation
such that is itself a (possibly high-level) social
scenario in our sense. Our model calculates the
conditional probability of given by calculating
the joint conditional probability of the events in
given . When observing
of answer , in which
explicitly or implicitly directs action
at agent
(e.g. Patti annoys Alex), our model queries its
action affinity lexicon for the relative observation
distribution
(e.g. the relative observation
distribution of annoy), queries for the relevant
affinity relation (e.g. the affinity relation linking
Patti and Alex), and generates an expression for the
conditional probability of
given :
(
|
)
=
(
)
×
(
|
)
(
)
()
∈
(4)
As our model maintains no knowledge of absolute
prior probabilities of actions, at this point, the
conditional probability of event
remains in terms
of
(
)
.
We adopt the simplifying assumption that events
are conditionally independent. Thus, the joint
probability of the conjunction of events in can be
expressed as the product of the probabilities of the
events in . We must control, however, for the effect
of the number of events, so that longer answers are
not penalized. The normalized conditional
probability of each answer given is expressed as
follows:
(
|
)
=(
|)
(5)
where
denotes the number of events in answer ,
denotes the maximum number of events of any
potential answer in answer set , and
denotes the
average conditional probability of the events in .
Finally, the model should select the answer that
has the highest normalized conditional probability
(maximizing
(
|
)
). Recall, however, that
these expressions remain in terms of several prior
probabilities of actions, precluding immediate
comparison. Rather than engaging in the difficult
task of obtaining non-arbitrary, non-biased prior
probabilities, we assume a discrete uniform
distribution across action priors, allowing these
priors to fall out of the necessary inequalities. Our
model is thus able to choose the answer with the
highest normalized conditional probability.
4 SOLVING Triangle-COPA
PROBLEMS
In order to provide a baseline evaluation of our
approach, we implemented our model in a software
system, we fed the system Triangle-COPA problems
containing social scenarios, and we fed the system a
hand-authored action affinity lexicon of the
Triangle-COPA actions.
Our hand-authored action affinity lexicon
contained entries corresponding to each of the 119
standard first-order logical predicates used in
Triangle-COPA problems We completed this hand-
authoring task based on author intuition, and we
acknowledge that this approach comes with the risk
of systematic bias (Kahneman and Tversky, 1982).
We fed the software system the Triangle-COPA
problems in their logical literal form. The system
cast each logical literal as an event by extracting the
critical arguments from the literal: the actor, the
action, and the optional argument encoding who or
what the action was directed towards. Some
Triangle-COPA problems contain additional
notation encoding nested literals, concurrent literals,
or negation of literals (Maslan et al., 2015). It is not
obvious how these three cases (nested literals,
concurrent literals, and negation of literals) might be
simply interpreted. To provide our baseline approach
without having to solve many natural language
processing challenges, we handled these three cases
as follows. First, we serialized nested literals: we
cast the outer directed literal to an undirected literal,
and we included both the outer and inner literals in
the scenario description. Second, we serialized
concurrent literals: we removed special literals
distinguishing between in-sequence events and in-
parallel events, and we interpreted all literal
sequences as event sequences. Third, we removed
Triangle-COPA problems containing negation: 11
Triangle-COPA problems containing the special
literal not were removed from our Triangle-COPA
test set. Additionally, in order to use Triangle-COPA
to evaluate interpretation of social scenarios, we
removed the 9 Triangle-COPA problems that
describe only one character, on the grounds that they
contain no social relationships. Our final Triangle-
COPA test set contained 80 Triangle-COPA
problems.
For each of these Triangle-COPA problems, the
system first observed the ordered literals in the
Affinity-based Interpretation of Triangle Social Scenarios
643

Triangle-COPA question and, using our hand-
authored action affinity lexicon, deduced the
underlying affinity relations. Then, the system
observed the ordered literals in each of the two
Triangle-COPA plausible answers, and, using our
hand-authored action affinity lexicon and the
deduced affinity relations, the system chose the most
probable answer.
5 RESULTS AND DISCUSSION
Of the 80 problems in our Triangle-COPA problem
set, our approach correctly answers 59 problems
(73.75%) and incorrectly answers 8 problems
(10.00%). On the remaining 13 problems (16.25%),
our approach is unable to determine the better choice
between the two possible answers and accordingly
leaves these problems unanswered. Table 2 presents
the performance of our approach and the
performance of the previous Triangle-COPA solver
by Gordon (2016).
Table 2: Performance of our affinity-based approach and
the approach by Gordon (2016) on 80 Triangle-COPA
problems depicting social scenarios.
Correctly
answered
Incorrectly
answered Unanswered
Affinity-
based
59
(73.75%)
8
(10.00%)
13
(16.25%)
Gordon
(2016)
71
(88.75%)
8
(10.00%)
1
(1.25%)
The authors of Triangle-COPA have emphasized
that it is a development test set and is not valid for
competitive evaluations. Indeed, Gordon (2016)
credits the relative success of his Triangle-COPA
solver to laborious hand authoring of event
probabilities and axioms that target the correct
answers. In contrast, our affinity-based model relies
on a relatively lightweight action affinity lexicon; so
the relatively better performance of Gordon (2016)
is largely uninteresting to us. Instead, we are
primarily interested in examining our system’s
performance on specific problems to gauge how
automated deduction of affinity relations and related
strategies might facilitate aspects of computational
social perception.
The problems that our system answers correctly
span a wide range of social scenarios. For example,
the system correctly answers the following
questions:
Question 7. A circle examines a small triangle
from across the room. Why does the circle do
this? (Correct: The circle is curious. Incorrect: The
circle is angry.)
Question 10. A triangle and circle are arguing.
The circle turns around and leaves the room.
Why does the circle leave? (Correct: The circle is
annoyed with the triangle. Incorrect: The circle is
happy with the triangle.)
Question 12. Two triangles are playing with
each other outside. How do they feel? (Correct:
They feel happy. Incorrect: They feel angry.)
Question 31. Two triangles talk to each other
and then hug. Why? (Correct: The triangles are
friends. Incorrect answer: The triangles are
enemies.)
Question 49. The circle nods at the triangle.
Why? (Correct: The circle agrees with the triangle.
Incorrect: the circle disagrees with the triangle).
Question 88. A small triangle kisses a big
triangle. Why does the small triangle do this?
(Correct: The small triangle loves the big triangle.
Incorrect: The small triangle hates the big triangle.)
These successes indicate that our system is able
to answer questions about unpleasant affinities
(question 10), pleasant affinities (question 12), and
neutral affinities (question 7); and our system is able
to answer questions about single-event scenarios
(question 12) and multi-event scenarios (question
10). Further examining the correctly answered
questions (momentarily treating our system as a
black box), our system seems to demonstrate
significant social knowledge, including regarding
emotions such as happiness (questions 10 and 12),
social conventions such as nodding in agreement
(question 49), relationship types such as friends and
enemies (question 31), and complex constructs such
as love and hate (question 88).
These rich results are in stark contrast to the
simplicity of our model. These results demonstrate
that knowledge appropriately grounded in the
affinity states Unpleasant, Neutral, and Pleasant can
concisely encode significant social knowledge
applicable to many social scenarios. Future work
might benefit from a direct comparison between
affinity-based interpretation (reasoning about
positivity/negativity of relationships), valence-based
interpretation (reasoning about positivity/negativity
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
644

of individuals), and sentiment analysis (reasoning
about overall/authorial positivity/negativity). A
direct comparison might elucidate whether the
moderate success of our affinity-based model
derives more from the positivity/negativity
framework or the relationship-level focus of affinity.
We note that, in order to provide a baseline
evaluation of our system, we hand-authored the
action affinity lexicon of the Triangle-COPA
actions. While hand-authoring is simple and fast to
complete, careful design decisions have been made
to guarantee that hand-authoring will never impede
the generalizability of the system: for future use of
the system, the simple, numerical, and intuitively
meaningful content of the action affinity lexicon is
well-suited for crowd-sourcing or automated
learning. Further, unlike many probabilistic
automated reasoning systems, our model does not
rely on being fed absolute prior probabilities, thus
avoiding the difficult task of obtaining non-arbitrary,
non-biased absolute prior probabilities. Also in order
to provide a baseline evaluation of our system, we
serialized all logical Triangle-COPA literals,
including nested literals and literals indicated to
occur in parallel. Future work may investigate
strategies for more true-to-intention interpretation of
complex literal notation.
We now consider questions that were not
correctly answered. In two problems (questions 35
and 37), the possible Triangle-COPA answers are of
similar affinity, but only the correct answer is
consistent with certain nonsocial knowledge. For
example:
Question 35. A circle and a small triangle are
running alongside of each other. The circle slows
down and then stops. Why? (Correct: The circle is
exhausted from running. Incorrect: The circle is
sleepy.)
Human solvers access nonsocial commonsense
knowledge: for example, the knowledge that one
may be exhausted after one exerts oneself. Our
affinity-based model cannot capture this nonsocial
commonsense knowledge and, appropriately, leaves
these questions unanswered.
Two unanswered problems (questions 72 and 89)
depict the transitivity of affinity. For example:
Question 72. A big triangle and little triangle
are strolling together. A circle runs towards
them, picks up the little triangle and runs away.
How does the big triangle feel? (Correct: The big
triangle is upset. Incorrect: The big triangle is
happy.)
Our model correctly interprets that the Big
Triangle’s feelings (expressed in the possible
answers) are implicitly directed at the Circle. Yet,
the model believes the Big Triangle and the Circle
have not had any meaningful interactions and finds
the affinity relation between the Big Triangle and
the Circle to be uninformed. Consequently, our
model considers the Big Triangle’s negative feelings
(in the first answer) and the Big Triangle’s positive
feelings (in the second answer) to be equally
probable, and the question is left unanswered. We
note that our model readily perceives that the
affinity between the Big Triangle and Little Triangle
is pleasant and that the affinity between the Circle
and the Little Triangle is unpleasant; but, unlike
humans, our model does not conclude that the
affinity between the Big Triangle and the Circle is
therefore also unpleasant. This performance suggests
that in order to foster more human-like interpretation
our model should incorporate reasoning about the
transitivity of affinity. Social Balance Theory
mathematically characterizes the transitivity of
affinity in human social networks, and is well suited
to be incorporated into our system in future work
(Heider, 1946; Cartwright and Harary, 1956).
In one incorrectly answered problem (question
36) and seven unanswered problems (questions 2,
26, 40, 41, 54, 57, and 98), the Triangle-COPA
possible answers reflected similar underlying
affinity relations but differing underlying dominance
relations. For example:
Question 2. The triangle saw the circle and
started shaking. Why did the triangle start
shaking? (Correct: The triangle is scared. Incorrect:
The triangle is upset.)
Both answers are consistent with the negative
affinity relation between the Triangle and the Circle;
but only fear (the correct answer) is also consistent
with the Triangle’s submissiveness and the Circle’s
dominance in the Triangle-Circle relationship. The
significant number of questions requiring
interpretation regarding dominance suggests future
work should broaden the relationship model to
include the existing (undirected) affinity relation and
a novel directed dominance relation.
In order to more formally characterize the
deficiency in our model, we consider emotional
dimensions our model cannot currently capture. We
consider the three emotional dimensions proposed
by the Pleasure Arousal and Dominance (PAD)
emotional state model, which is often used for
emotion modeling and emotion measurement
(Mehrabian, 1996). In our current model, the PAD
dimension Pleasure, is captured by the skew of the
Affinity-based Interpretation of Triangle Social Scenarios
645

affinity relation (towards Pleasant or Unpleasant).
The PAD dimension Arousal is implicitly captured
by the centrality of the affinity relation (towards or
away from Neutral). The PAD dimension
Dominance is, however, not captured. This
reinforces our hypothesis that a broader relationship
model including an affinity relation and a dominance
relation may facilitate more human-like
interpretation of social scenarios.
6 CONCLUSIONS AND
FURTHER WORK
In this paper, we present affinity-based interpretation
of social scenarios. Logic-based automated social
inference requires carefully curating large, rich
knowledge bases. In contrast, our model conducts
affinity-based interpretation of social scenarios using
a relatively lightweight action affinity lexicon and
maintains significant interpretive power. First, our
model deduces affinity relations from a social
scenario. Then, using the deduced affinity relations,
our model is able to choose the more probable
statement from multiple plausible statements
regarding the social scenario. This model, in whole
and in part, may be developed for future
applications.
We evaluated a baseline implementation of our
approach on Triangle-COPA multiple-choice
problems describing social scenarios. Using our
hand-authored action affinity lexicon of Triangle-
COPA actions, the implemented system solves the
majority of problems, successfully answering
questions about behaviors, emotions, social
conventions, relationships, and complex constructs.
These rich results draw our attention to how
knowledge appropriately grounded in the affinity
states Unpleasant, Neutral, and Pleasant can
concisely encode significant social knowledge
applicable to many social scenarios.
By closely analyzing our model’s performance
on Triangle-COPA, we have identified key steps
towards model augmentation: incorporation of
Social Balance Theory and incorporation of a
directed dominance relation. Simultaneously,
potential applications have emerged. Our model is
well poised to enrich automated narrative analysis,
to guide AI narrative generation, and to assist
individuals suffering from impaired social cognition.
As large text corpora have become increasingly
available online, the demand has grown for
computational narrative analysis. Particularly
dominant is Social Network Analysis of literature,
yet standard character network extraction is based
only on character co-occurrence (Bonato et al.,
2016; Moretti, 2011). These character networks
represent familiarity, while disregarding many other
aspects of characters’ relationships. Affinity
relations deduced from literature may provide an
alternative to standard character networks.
Combining deduction of affinity relations with
extraction of character networks may produce
representations that are richer still. The challenge
will be adapting our model to features of longer
works (e.g. longer-range dependencies between
actions); yet our model will also benefit from the
significantly larger source material, as the task will
become more robust and fault-tolerant, and currently
sparse social interactions will be abundant.
Our model also has potential for guiding AI
narrative generation. Narrative generation may be
cast as repeatedly selecting an event to continue a
given context (a partial draft of a story) (Gervás,
2009). If a partial draft of a story can be considered
a social scenario in our sense, then our model could
be used to select continuations that are interesting
and believable.
Finally, certain individuals, including many
individuals with autism spectrum disorder (ASD),
experience impairment of social cognition. Reading
comprehension is critical for academic and
professional success, and these individuals struggle
to comprehend pervasive social aspects of texts
(Brown et al., 2013). As our model operates on text
to deduce affinities and to interpret social scenarios,
our model lays promising groundwork for easing the
difficulties these individuals face when reading.
Future work will aim to develop our model into an
autonomous service for these individuals, supporting
digital inclusion and accessibility.
Given the performance of our affinity-based
model and given the requisite lexicon is simple and
well suited for automated learning, we believe our
model is a promising approach for interpretation of
social scenarios and is well-poised for application.
ACKNOWLEDGEMENTS
This research is supported by the MIT-Spain
Program of the MIT International Science and
Technology Initiatives (MISTI) and by the IDiLyCo
project (TIN2015-66655-R) funded by the Spanish
Ministry of Economy, Industry and
Competitiveness.
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
646

REFERENCES
Brown, H., Oram-Cardy, J., and Johnson, A. 2013, A
Meta-Analysis of the Reading Comprehension Skills
of Individuals on the Autism Spectrum, Journal Of
Autism and Developmental Disorders, 43, 4, pp. 932-
955.
Bonato, A., D'Angelo, D., Elenberg, E., Gleich, D., and
Hou, Y. 2016, Mining and modeling character
networks, arXiv, EBSCOhost.
Cartwright, D. and Harary, F. 1956. Structural Balance: A
Generalization of Heider’s Theory, Psychology
Review, 63, 5.
Davis, E. and Morgenstern, L. 2005, A First-order Theory
of Communication and Multi-agent Plans, Journal Of
Logic and Computation, 15, 5, pp. 701-749.
Gervás, P. 2009. Computational Approaches to
Storytelling and Creativity, AI Magazine, 30, pp. 49-
62.
Gigerenzer, G., Hertwig, R., van den Broek, E., Fasolo,
B., and Katsikopoulos, K. 2005. “A 30% Chance of
Rain Tomorrow”: How Does the Public Understand
Probabilistic Weather Forecasts?, Risk Analysis: An
International Journal, 25, 3, pp. 623-629.
Gordon, A. S. 2016. Commonsense Interpretation of
Triangle Behavior, In Proceedings of the Thirtieth
AAAI Conference on Artificial Intelligence (AAAI-16).
Gordon, A. S. and Hobbs, J. R. 2011. A commonsense
theory of mind-body interaction, In Proceedings of the
2011 AAAI Spring Symposium on Logical
Formalizations of Commonsense Reasoning.
Heider, F. 1946. Attitudes and Cognitive Organization,
The Journal of Psychology, 21, pp. 107-112.
Heider, F. and Simmel, M. 1944. An experimental study
of apparent behavior, The American Journal of
Psychology, 57, 2, p. 243.
Kahneman, D., Fredrickson, B., Schreiber, C., and
Redelmeier, D. 1993, When More Pain Is Preferred To
Less: Adding a Better End, Psychological Science, 4,
6, pp. 401-405.
Kahneman, D. and Tversky, A. 1982, On the study of
statistical intuitions, Cognition, 11, pp. 123-141.
Kuhlmeier , V. A. , Wynn , K. , and Bloom , P. 2004.
Reasoning about present dispositions based on past
interactions, Paper presented at the International
Conference on Infant Studies.
Premack, D. and Premack, A. J. 1997. Infants attribute
value +/ – to the goal-directed actions of self-propelled
objects, Journal of Cognitive Neuroscience, 9, pp. 848
– 856 .
Maslan, N., Roemmele, M., and Gordon, A. 2015. One
Hundred Challenge Problems for Logical
Formalizations of Commonsense Psychology, Twelfth
International Symposium on Logical Formalizations of
Commonsense Reasoning (Commonsense-2015).
Mehrabian, A. 1996. Pleasure-arousal-dominance: a
general framework for describing and measuring
individual differences in temperament, Current
Psychology, 14, 4, pp. 261–292.
Moretti, F. 2011. Network Theory, Plot Analysis. New
Left Review, 68, pp. 80-102.
Reagan, A., Mitchell, L., Kiley, D., Danforth, C., and
Dodds, P. 2016. The emotional arcs of stories are
dominated by six basic shapes, EPJ Data Science, 5,
1, p. 1.
Rutherford, M. and Kuhlmeier, V. 2013. Social
Perception: Detection And Interpretation Of Animacy,
Agency, And Intention, n.p.: Cambridge,
Massachusetts : MIT Press, (2013).
Affinity-based Interpretation of Triangle Social Scenarios
647
