Fingerprint Class Recognition for Securing EMV Transaction
B. Vibert, J. M. Le Bars, C. Charrier and C. Rosenberger
Normandie Univ., UNICAEN, ENSICAEN, CNRS, GREYC, 14000 Caen, France
Keywords:
Transaction Security, Fingerprint Class Recognition, ISO Template, Biometric, EMV.
Abstract:
Fingerprint analysis is a very important issue in biometry. The minutiae representation of a fingerprint is the
most used modality to identify people or authorize access when using a biometric system. In this paper, we
propose some features based on triangle parameters from the Delaunay triangulation of minutiae. We show the
benefit of these features to recognize the type of a fingerprint without any access to the associated fingerprint
image.
1 INTRODUCTION
Fingerprint is usually associated to criminal investiga-
tion, since it is the oldest use case commonly known
by people and is well established in the human mind.
This can be a reason why such biometric modality is
quite well accepted and used by people to unlock ac-
cess on mobile devices or web services. In addition,
this kind of authentication yields to reach a high level
of trust in the security and privacy protection of dema-
terialized transactions. That way, fingerprint became
in few years a very popular biometric modality for
such use cases. In 2013, the first smartphone embed-
ding a fingerprint sensor has been deployed for public
use. In order to guarantee security and privacy issues,
the fingerprint processing is realized on a Secure Ele-
ment (SE) such as a SIM card or smartcard.
However SE is limited in computation process and
memory size. Due to this latter, it is not possible to
store the entire fingerprint image inside. The image is
then processed in order to obtain a relevant and com-
pact representation. This representation is based on
particular points of the fingerprint, known as minu-
tiae. Yet, all extracted minutiae, referred to as minu-
tiae template, can not be entirely stored inside a SE.
Actually, any minutiae template stored within a SE
should be in compliance with the ISO Compact Card
II (ISO, 2011) standard which provides the maximum
number of used minutiae that can be stored inside
a SE. Basically, a minutiae is described by its loca-
tion, type and orientation. All those informations are
stored inside the SE. When an authentication process
is required, a template comparison is performed be-
tween the embedded template and the request one to
determine how they are similar. This comparison step
is computed inside the SE using an embedded On-
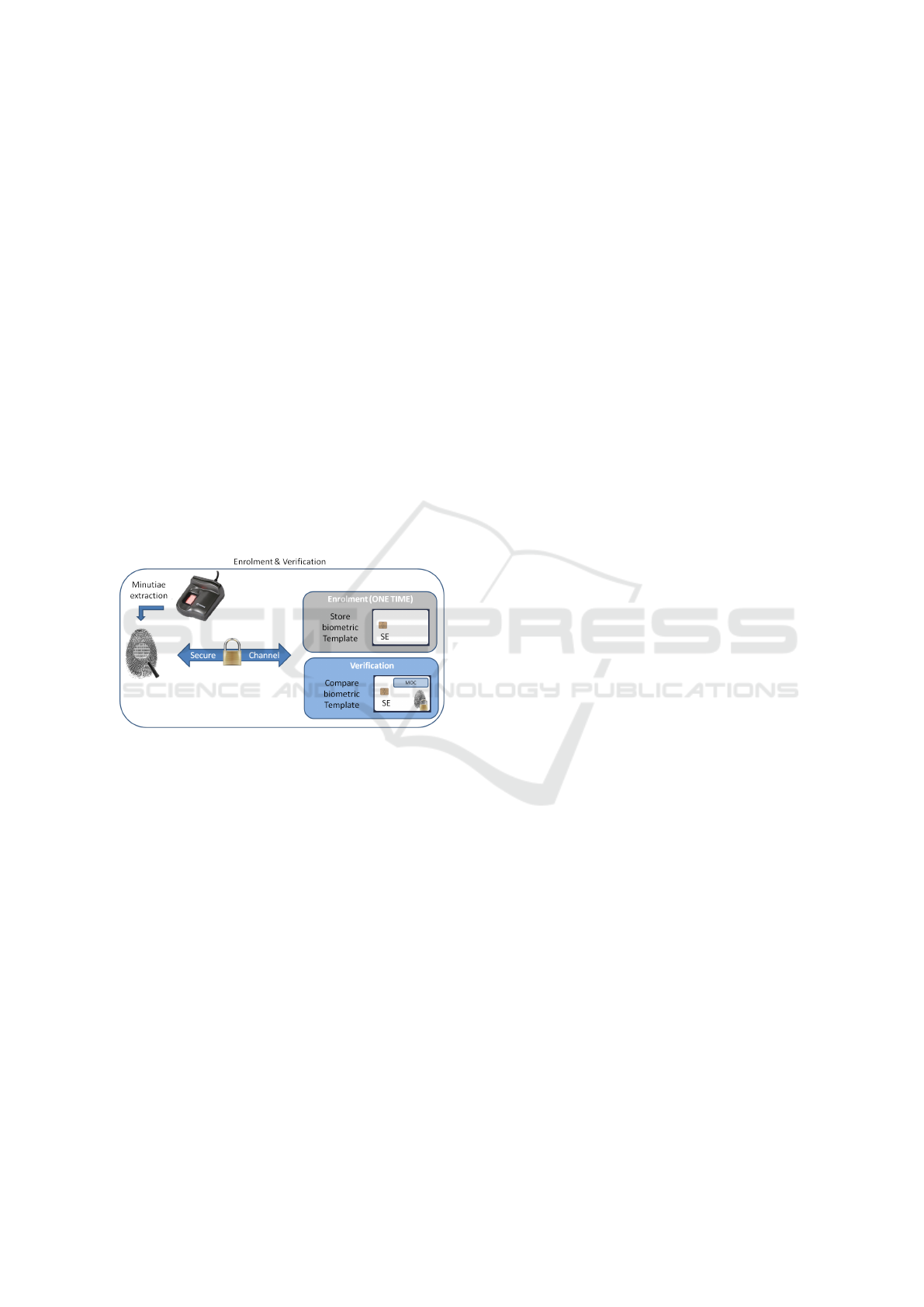
Card-Comparison (OCC) module (Cf. Figure 2). An-
other important feature about fingerprint concerns its
type. Even if a fingerprint is considered as unique,
it necessarily corresponds to one of the five classes
(know as Henry classes) as defined by Henry: Arch,
Left Loop, Right Loop, Tented arch and Whorl, as il-
lustrated in Figure 1.
This compliant standard representation can be
usefull for Europay Mastercard Visa (EMV) trans-
actions with biometric authentication. Indeed, since
2015, the EMVco (EMVCo, 2008) allows to use bio-
metric data in the Cardholder Verification part (Fig-
ure 3). This is the context of this study that justifies
the use of the ISO Compact Card II representation in-
stead of any other existing representation. In return,
new kinds of attack can be performed on SE.
(a) Arch (b) Left loop (c) Right Loop
(d) Tented arch (e) Whorl
Figure 1: The five classes of fingerprint defined by Henry.
Vibert, B., Bars, J., Rosenberger, C. and Charrier, C.
Fingerprint Class Recognition for Securing EMV Transaction.
DOI: 10.5220/0006205704030410
In Proceedings of the 3rd International Conference on Information Systems Security and Privacy (ICISSP 2017), pages 403-410
ISBN: 978-989-758-209-7
Copyright
c
 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
403

Among all possible attacks, one concerns the de-
tection of the class of the minutiae template, as de-
fined by Henry. The main assumption can be formu-
lated as follows: how the knowledge of the class of
the minutiae template increases the attack success ?
How the knowledge of the template allows to deter-
mine the class of the fingerprint ? In (Vibert et al.,
2016), the authors argue that the knowledge of the
class of the fingerprint significantly helps the attacker
to succeed from 2% to 50%. Based on this work,
we investigate how it is possible to block this kind
of attack. One way is to considered the addition of
a mechanism on the Payment terminal and the SE
which permit to detect the fingerprint class. The fin-
gerprint class is include in the Cardholder Verification
Result (CVR) and send to the terminal to process the
Terminal Risk Management and detect if the template
type is different between the one sent by the terminal
and the template received by the smartcard. In this
way, we investigate if the detection of a fingerprint
class change between the card and the terminal helps
to reduce the attack successful rate.
Figure 2: Explanation of an enroll en verification part on
SE.
This paper is organized as follows. In the next
section, we present the different works present on the
state-of-the-art which permit to determine the finger-
print type. Section 3 is focused on the proposed meth-
ods based on minutiae template. Section 4 is devoted
to the experimentation of fingerprint type recognition.
Finally, we conclude and give some perspectives of
this work.
2 RELATED WORKS
Many works have been done on the classification al-
gorithms, such as healthcare (Kumar and Inbarani,
2016; Zhang et al., 2016; Park et al., 2016), network
(Palmieri et al., 2013; Palmieri et al., 2014; Fiore
et al., 2013) and imaging (Li et al., 2015; Alok et al.,
2015; Elguebaly and Bouguila, 2015). On biometric
field some works have been done for the processing
of minutiae templates such as the orientation field re-
construction (Roy and Trivedi, 2014; Oehlmann et al.,
2015), the matching algorithm (Jain and Pankanti,
2000; Kumar et al., 2014), the fingerprint protection
(Jayaraman et al., 2014; Vigila et al., 2014). Few
works have considered the ISO Compact Card II rep-
resentation(Jain et al., 1999b; Zhang and Yan, 2004).
All methods which permit to detect the fingerprint
type are based on images and not on minutiae tem-
plate. Different methods reconstruct the image with
the minutiae template but need a lot of computation
resources and time since a SE doesn’t have enough
resources to reconstruct images and compute these
methods,the aim of the paper is to propose meth-
ods based only on minutiae template to determine the
class of fingerprints.
3 FINGERPRINT CLASS
RECOGNITION WITH ISO
TEMPLATE
Our work is based on the minutiae template computed
with ISO Compact Card II representation. This tem-
plate is composed of a set of minutiae represented by
3 octets and 4 values (x
i
, y
i
, T
i
, θ
i
), i = 1 : N
j
where:
• the coordinates (x
i
, y
i
) correspond to the location
of the minutiae in the image (that is not available),
• T
i
corresponds to the minutiae type (bifurcation,
ridge ending . . . ),
• θ
i
is the minutiae orientation (related to the ridge).
Note that this information is represented by 6 bits
(i.e. 64 different values).
• N
j
is the number of minutiae for the sample j of
the user.
Minutiae templates used in the experiments have
been extracted using the NBIS tool, MINDTCT (Wat-
son et al., 2007) from the NIST. From the ISO tem-
plate we have generated a statistical vector named
IsoStruct
jk
. Consedering a whole template, for all
minutiae we can construct four subsets considering 1)
the x coordinate, 2) the y coordinate, 3) the ISO angle
and 4)the minutiae type. From each subset, a normal-
ized histogram was computed with fix value of bins.
Then we obtain a IsoStruct
jk
vector of size 3 × N + 2
by concatening these histograms, where N is the num-
ber of bins in the histograms computation and 2 is
the histogram for the Type which contain only 2 val-
ues. This statistical vector IsoStruct
jk
is defined as
follows:
ICISSP 2017 - 3rd International Conference on Information Systems Security and Privacy
404

Figure 3: Flow of a complete EMV transaction.
IsoStruct
jk
= {HistoX
jk
,
HistoY
jk
, HistoIsoAngle
jk
,
HistoType
jk
} (1)
where HistoX
jk
, HistoY
jk
, HistoIsoAngle
jk
and
HistoType
jk
are normalized histograms. This his-
togram is generated with a variable number N of bins,
mainly to refine the shape of the histogram.
With this statistical vector IsoStruct
jk
, we want to
determine the fingerprint class, and after determine
which parameter is important for the fingerprint class
recognition. For that purpose, we use a support vector
machine (SVM) to create a model of each fingerprint
class.
3.1 SVM Learning
From all existing classification schemes, a Support
Vector Machine (SVM)-based technique has been se-
lected due to high classification rates obtained in
many previous works (Charrier et al., 2012; Hsu and
Lin, 2002; Kudo and Sklansky, 2000), and to their
high generalization abilities. The SVMs were devel-
oped by VAPNIK ET AL. (Vapnik, 1998) and are based
on the structural risk minimization principle from sta-
tistical learning theory. SVMs express predictions in
terms of a linear combination of kernel functions cen-
tered on a subset of the training data, known as sup-
port vectors (SV).
SVM being binary classifiers, several binary SVM
classifiers are induced for a multi-class problem. A
final decision is taken from the outputs of all binary
SVM (Hsu and Lin, 2002).
The kernel function choice is critical for the de-
sign of a machine learning expert. Radial Basis Func-
tion (RBF) kernel function is commonly used with
SVM. The most important reason is that RBF func-
tions work like a similarity measure between two ex-
amples. A final decision must be taken from all bi-
nary decision functions. Many combination strategies
can be used to obtain the final decision (Hsu and Lin,
2002). The majority vote is the usual way to do this.
3.2 Experimental Protocol
We list here all the elements to be defined to make
experiments.
3.2.1 SFinge Databases
FVC databases do not provide any information on the
fingerprint class. Nevertheless, it will be shown in dif-
ferent works (Maio et al., 2004; Fi
´
errez-Aguilar et al.,
2005) than SFinge has the same behavior and similar
performance than real databases. Hence, we may ex-
pect a similar performance of class recognition than
real databases. We have generated five databases with
the SFinge software, one for each class of fingerprint
described in Table 1. Each SFinge database has 800
templates.
3.2.2 SVM Setup
We need to create a database for the training and one
for the test. Multiple train-test sequences were run. In
Fingerprint Class Recognition for Securing EMV Transaction
405

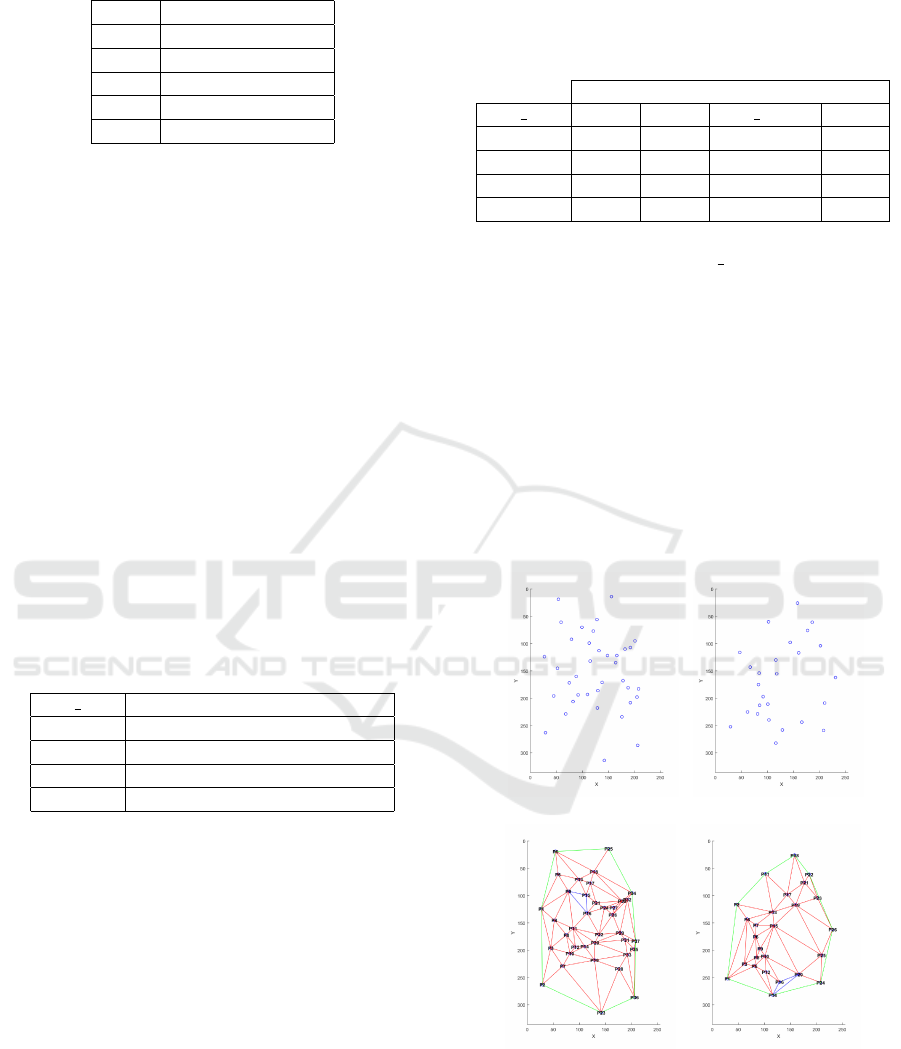
Table 1: Fingerprint classes databases label.
Label Fingerprint classes
1 Arch
2 Left Loop
3 Right Loop
4 Tented
5 Whorl
each, the fingerprint database was subdivided into dis-
tinct training and test sets. In each train-test sequence,
80% of the 5 SFinge database content was chosen for
training, and the 20% for testing. Specifically, each
training set contained 640 fingerprints, while each test
set contained the 260 remaining fingerprints. 10 ran-
domly chosen training and test sets were obtained and
the class recognition rate was run over the 10 itera-
tions. We have used the well known libsvm (Chang
and Lin, 2011) with the default parameters.
3.3 Experimental Results
Here, we want to determine the number of bins
needed to have the minimal impact on the recogni-
tion rate performance. We tested different values of
bins (8, 16, 32 and 64) on the feature structure. We
only consider the recognition results when 80% of
the databases is used for learning for the four value
of bins. Results are presented on Table 2.
Table 2: Table of Fingerprint class recognition with ISO
template for all feature at 80% for learning.
Nbr bins Recognition rate on test db(%)
8 79.43
16 80.37
32 80.06
64 60.80
We can observe than the best results are obtained
with 16 bins for the structure based feature. We can
explain this result by the fact that the redundancy with
64 bins is high for this application. With only a fea-
tures with 64 values (50 = 3 × 16 + 2), we obtain
80.37% of fingerprint class recognition with the stan-
dard svm parameters (without any optimization). In
the following, we keep this size of the feature vector.
The ISO template only contain four information,
and we want to know which information is impor-
tant for the fingerprint class recognition. The table
3 shows the recognition rate for each number of bins
and for each paramter present in the ISO template.
We can observe than the Type have the same recogni-
tion rate, this is due to the two possible values for this
parameter, we only have an histogram with 2 bins in
opposite with the other parameter. Concerning the X
and Y we have bad results around 40%. In opposite,
with ISO
A
ngle, we have the best recognition rate.
Table 3: ISO CC recognition rate for each element vs num-
ber of bins.
Recognition rate (%)
Nbr bins X Y ISO Angle Type
8 42.87 37.52 77.85 28.13
16 43.62 38.96 80.23 28.13
32 42.25 36.51 80.24 28.13
64 40.45 36.47 78.25 28.13
We can conclude than the ISO Angle is an important
information for the fingerprint class recognition. With
around 79% of recognition rate, this is the most im-
portant parameter present in the initial template. It is
a good result but we want to have more than one in-
formation to improve the fingerprint recognition rate.
4 NEW ATTRIBUTES
SELECTION
As alluded above, using ISO templates, we have few
information to characterize fingerprints.
(a) Left Loop Template (b) Right Loop Template
(c) Left Loop Triangula-
tion
(d) Right Loop Triangu-
lation
Figure 4: Spatial fingerprint minutiae point and associated
Delaunay triangulation.
As we can observed on both image 4(a) and
image 4(b), we see that the spatial distribution of
ICISSP 2017 - 3rd International Conference on Information Systems Security and Privacy
406

minuatiae differs. To take into account this observa-
tion, we modelize this difference using computational
geometry approach. Amoung all existing schemes,
we decided to use Delaunay triangulation (Auren-
hammer, 1991; Su and Drysdale, 1995). Delaunay
triangulation is used in various fields, such as com-
putational geometry (Shewchuk, 2002) for resolving
problems, or in surface reconstruction (Gopi et al.,
2000; Labatut et al., 2007). In our case Delaunay
triangulation allows to resolve the problem of trans-
lation and rotation of the ISO minutiae template and
also allows us to make an abstraction of the minutiae
space position. This yield us to create a structure
containing parameters describing each template, as
described in 4.1 and explained in Figure 5. These
structure parameters are composed of elements such
as shape, angles, area of the triangles, perimeter and
so on.
4.1 Feature Structure for Each
Template
For each template, we have computed the Delaunay
triangulation-based on minutiae (Figure 6 shows an
example of Triangulation).
For each obtained triangle, we extract different pa-
rameters:
• the three angles,
• the three edges lengths,
• the area.
To resume, the feature vector TriInf
jk
is generated
for the template j of the subject k and it consists of
three main characteristics:
TriInf
j,k
= {{AngleA
jkl
, AngleB
jkl
, AngleC
jkl
},
{LengthAB
jkl
, LengthAC
jkl
, LengthBC
jkl
},
{Area
jkl
}}, ∀l ∈ [1;M
j
], (2)
where {AngleA
jkl
, AngleB
jkl
, Angle C
jkl
}
is the vector of data related to angle val-
ues of the M
j
triangles of the template j,
{LengthAB
jkl
, LengthAC
jkl
, LengthBC
jkl
} rep-
resents the vector of data related to computed lengths
for the M
j
triangles of the template j, {Area
jkl
}
corresponds to the vector of data related to the area
of the M
j
triangles of the template j.
We also add parameter not related to the Delaunay
triangulation but issues of the original template:
• Minutiae orientation.
IsoAngleInf
j,k
= {{Orientation
jki
}
}, ∀i ∈ [1; N
j
], (3)
where Orientation
jki
represents the vector data con-
taining the ISO angle of the N
j
minutiae of the tem-
plate j.
4.2 Feature Probability Density
From this two feature vector (TriInf
jk
and
IsoAngleInfo
jk
), a new and statistical vector is
generated. We compute a normalized histogram to
approximate a probability density for each feature
which is not dependent to the number of minutiae
in the template. These histograms are computed
considering a fix value of bins. Then, we obtain a
TemplateStruct
jk
vector of size 4 × N, where N is the
number of bins in the histograms computation, by
concatening these histograms.
This statistical vector TemplateStruct
jk
is defined
as follows:
TemplateStruct
jk
= {HistoAngle
jk
,
HistoDistance
jk
, HistoArea
jk
,
HistoISOAngle
jk
} (4)
where HistoAngle
jk
, HistoDistance
jk
, HistoArea
jk
and HistoISOAngle
jk
are normalized histograms
computed from their associated subvector of TriInf
jk
and IsoAngleInfo
jk
. Those histograms are generated
with a variable number N of bins, mainly to refine the
shape of the histogram.
4.3 Fingerprint Class Recognition
Results
We have used the same protocol as defined in Section
3.2 and the number of bins defined in Section 3.3 with
N = 16.
The Table 4 gives the recognition results for the
new attributs selection.
Table 4: Fingerprint class recognition results for the new
attributs selection with 80% of learning.
Recognition rate (%)
ISO method 80.37
Proposed method 89.12
If we compare the results between only the ISO
template prensented in and the new feature, we have
a difference around 10%. The new feature present a
better fingerprint recognition rate with 89% of good
fingerprint class recognition.
Fingerprint Class Recognition for Securing EMV Transaction
407

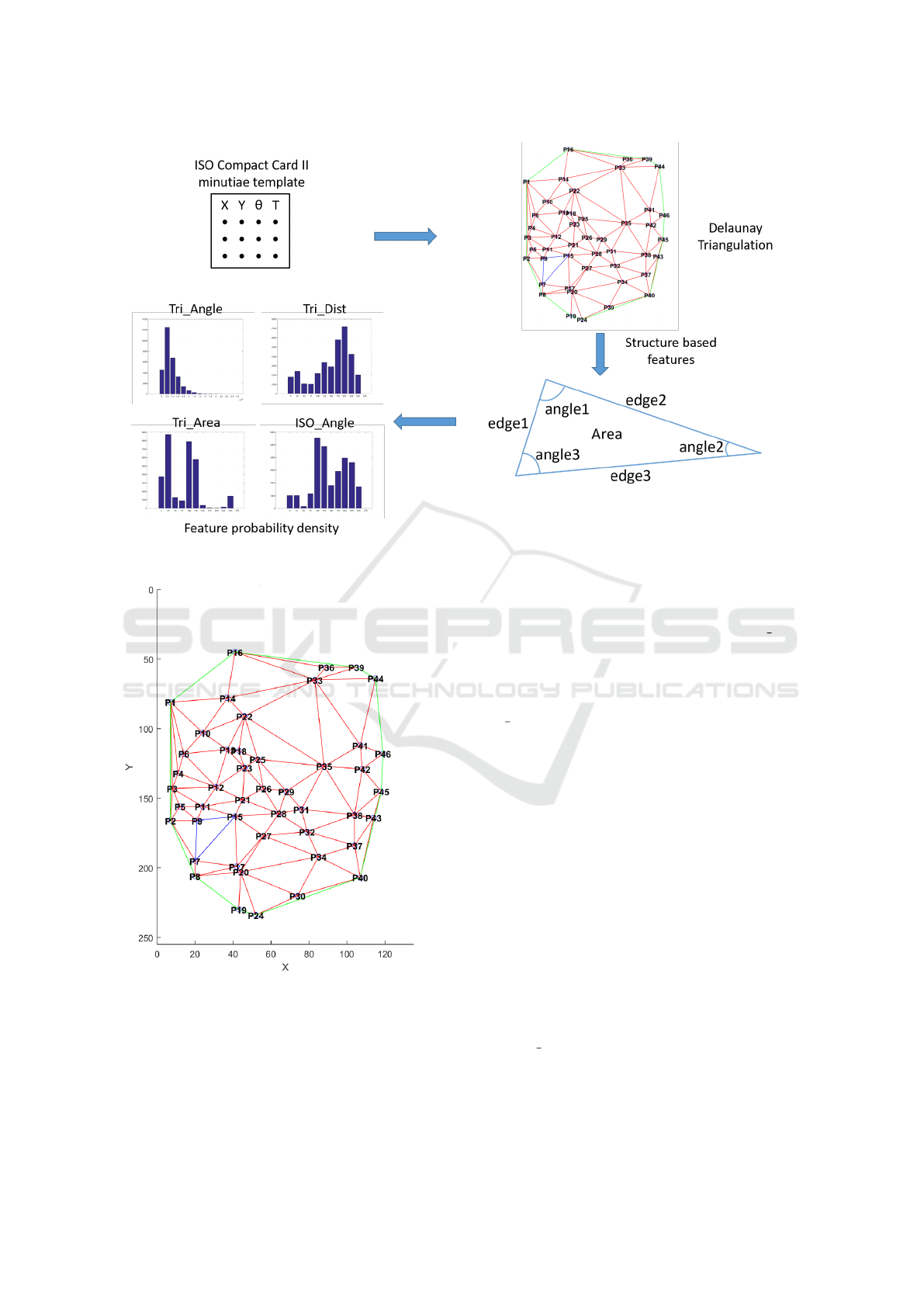
Figure 5: General scheme for the Attribute vector.
Figure 6: Delaunay Triangulation for one ISO Compact
Card II template.
5 DISCUSSION
Our problematic is to determine the fingerprint class
only with the ISO template informations. We create a
vector containing histogram for each parameter of the
ISO template. With this vector we obtain 80.37% of
recognition rate, but we have seen than the ISO Angle
is the parameter which permit to obtain a good recog-
nition rate alone 80.23%. This is why we proposed
a geometric approach based on the Delaunay trian-
gulation to obtain more parameters and also keep the
ISO Angle. With this approach, we increase by 9%
the recognition rate and we obtain 89%. From com-
parison, Jain et al. (Jain et al., 1999a) have developed
a method of fingerprint class recognition based on the
image and get a recognition rate of 90%. Our ap-
proach is nearest the recognition rate based on image,
this shows that the approach restraint is promising.
6 CONCLUSION AND
PERSPECTIVES
In this paper, we proposed two fingerprint class recog-
nition approach based only on ISO template with no
access on images or reconstructed images. We have
first of all determined the number of bins needed for
our statistical approach. After, we have determined
than ISO Angle parameter issued from the ISO tem-
plate is important for the fingerprint recognition rate.
We have proposed a new feature which permit to have
more than one information to determine the finger-
print class. With this method we obtain 89% of finger-
ICISSP 2017 - 3rd International Conference on Information Systems Security and Privacy
408

print class recognition rate in comparaison with 80%
for the ISO template. We have improved the recogni-
tion rate around 10%. In our case of study, an EMV
transaction, we have two approach and we have to
choose between more computation time, ressources
but 89% of recognition rate and few ressources and
quicker approach based on ISO template but only with
80% of fingerprint class recognition. We have shown
when one adds fingerprint recognition module, both
on smartcard and Point of sales we help to secure
EMV transaction when biometric is taking into ac-
count.
As perspectives, we plan to improve these recog-
nition rates of the fingerprint class by using other fea-
tures. And also to test in real condition on SE these
approach.
REFERENCES
Alok, A. K., Saha, S., and Ekbal, A. (2015). Multi-objective
semi-supervised clustering for automatic pixel classi-
fication from remote sensing imagery. Soft Comput-
ing, pages 1–19.
Aurenhammer, F. (1991). Voronoi diagramsa survey of a
fundamental geometric data structure. ACM Comput-
ing Surveys (CSUR), 23(3):345–405.
Chang, C.-C. and Lin, C.-J. (2011). Libsvm: A library for
support vector machines. ACM Transactions on Intel-
ligent Systems and Technology (TIST), 2(3):27.
Charrier, C., L
´
ezoray, O., and Lebrun, G. (2012). A
machine learning regression scheme to design a fr-
image quality assessment algorithm. In Conference
on Colour in Graphics, Imaging, and Vision, volume
2012, pages 35–42. Society for Imaging Science and
Technology.
Elguebaly, T. and Bouguila, N. (2015). A hierarchical
nonparametric bayesian approach for medical images
and gene expressions classification. Soft Computing,
19(1):189–204.
EMVCo (2008). EMV integrated circuit card specifications
for payment systems. Technical report, EMVCo.
Fi
´
errez-Aguilar, J., Nanni, L., Ortega-Garcia, J., Cappelli,
R., and Maltoni, D. (2005). Combining multiple
matchers for fingerprint verification: a case study in
fvc2004. In International Conference on Image Anal-
ysis and Processing, pages 1035–1042. Springer.
Fiore, U., Palmieri, F., Castiglione, A., and De Santis, A.
(2013). Network anomaly detection with the restricted
boltzmann machine. Neurocomputing, 122:13–23.
Gopi, M., Krishnan, S., and Silva, C. T. (2000). Surface
reconstruction based on lower dimensional localized
delaunay triangulation. In Computer Graphics Forum,
volume 19, pages 467–478.
Hsu, C.-W. and Lin, C.-J. (2002). A comparison of meth-
ods for multiclass support vector machines. Neural
Networks, IEEE Transactions on, 13(3):415–425.
ISO (2011). ISO/IEC 19794-2. information technology -
biometric data interchange format format - part 2 :
Finger minutiae data, 2011.
Jain, A. and Pankanti, S. (2000). Fingerprint classification
and matching. Handbook for Image and Video Pro-
cessing.
Jain, A. K., Prabhakar, S., , and Hong, L. (1999a). A multi-
channel approach to fingerprint classification. In Pat-
tern Analysis and Machine Intelligence, IEEE Trans-
actions on, volume 24, pages 248–359.
Jain, A. K., Prabhakar, S., and Hong, L. (1999b). A mul-
tichannel approach to fingerprint classification. Pat-
tern Analysis and Machine Intelligence, IEEE Trans-
actions on, 21(4):348–359.
Jayaraman, U., Gupta, A. K., and Gupta, P. (2014). An effi-
cient minutiae based geometric hashing for fingerprint
database. Neurocomputing, 137:115–126.
Kudo, M. and Sklansky, J. (2000). Comparison of algo-
rithms that select features for pattern classifiers. Pat-
tern Recognition, 33(1):25–41.
Kumar, M. et al. (2014). A novel fingerprint minutiae
matching using lbp. In Reliability, Infocom Technolo-
gies and Optimization (ICRITO)(Trends and Future
Directions), 2014 3rd International Conference on,
pages 1–4. IEEE.
Kumar, S. U. and Inbarani, H. H. (2016). Neighborhood
rough set based ecg signal classification for diagnosis
of cardiac diseases. Soft Computing, pages 1–13.
Labatut, P., Pons, J.-P., and Keriven, R. (2007). Efficient
multi-view reconstruction of large-scale scenes using
interest points, delaunay triangulation and graph cuts.
In Computer Vision, 2007. ICCV 2007. IEEE 11th In-
ternational Conference on, pages 1–8. IEEE.
Li, J., Du, Q., and Li, Y. (2015). An efficient radial ba-
sis function neural network for hyperspectral remote
sensing image classification. Soft Computing, pages
1–7.
Maio, D., Maltoni, D., Cappelli, R., Wayman, J. L., and
Jain, A. K. (2004). Fvc2004: Third fingerprint ver-
ification competition. In Biometric Authentication,
pages 1–7. Springer.
Oehlmann, L., Huckemann, S., and Gottschlich, C. (2015).
Performance evaluation of fingerprint orientation field
reconstruction methods. In Biometrics and Forensics
(IWBF), 2015 International Workshop on, pages 1–6.
IEEE.
Palmieri, F., Fiore, U., and Castiglione, A. (2014). A dis-
tributed approach to network anomaly detection based
on independent component analysis. Concurrency and
Computation: Practice and Experience, 26(5):1113–
1129.
Palmieri, F., Fiore, U., Castiglione, A., and De Santis,
A. (2013). On the detection of card-sharing traf-
fic through wavelet analysis and support vector ma-
chines. Applied Soft Computing, 13(1):615–627.
Park, J., Bhuiyan, M. Z. A., Kang, M., Son, J., and Kang, K.
(2016). Nearest neighbor search with locally weighted
linear regression for heartbeat classification. Soft
Computing, pages 1–12.
Roy, B. R. and Trivedi, A. K. (2014). Construction of fin-
gerprint orientation field from minutia points. In Ad-
Fingerprint Class Recognition for Securing EMV Transaction
409

vanced Communication Control and Computing Tech-
nologies (ICACCCT), 2014 International Conference
on, pages 1439–1442. IEEE.
Shewchuk, J. R. (2002). Delaunay refinement algorithms
for triangular mesh generation. Computational geom-
etry, 22(1):21–74.
Su, P. and Drysdale, R. L. S. (1995). A comparison of se-
quential delaunay triangulation algorithms. In Pro-
ceedings of the eleventh annual symposium on Com-
putational geometry, pages 61–70. ACM.
Vapnik, V. N. (1998). Statistical Learning Theory. Wiley,
New York.
Vibert, B., Christophe, C., Le Bars, J.-M., and Rosenberger,
C. (2016). In what way is it possible to impersonate
you bypassing fingerprint sensors ? In 15th Interna-
tional Conference of the Biometrics Special Interest
Group (BIOSIG), Darmstadt, Germany.
Vigila, S. A. M. C., Muneeswaran, K., and Antony, W. T.
B. A. (2014). Biometric security system over finite
field for mobile applications. IET Information Secu-
rity, 9(2):119–126.
Watson, C. I., Garris, M. D., Tabassi, E., Wilson, C. L., Mc-
cabe, R. M., Janet, S., and Ko, K. (2007). Users guide
to nist biometric image software (nbis). Technical re-
port, NIST.
Zhang, C., Lei, Y.-K., Zhang, S., Yang, J., and Hu,
Y. (2016). Orthogonal discriminant neighborhood
analysis for tumor classification. Soft Computing,
20(1):263–271.
Zhang, Q. and Yan, H. (2004). Fingerprint classification
based on extraction and analysis of singularities and
pseudo ridges. Pattern Recognition, 37(11):2233–
2243.
ICISSP 2017 - 3rd International Conference on Information Systems Security and Privacy
410