An Analysis of Virtual Loss in Parallel MCTS

S. Ali Mirsoleimani

1,2

, Aske Plaat

, Jaap van den Herik

and Jos Vermaseren

Leiden Centre of Data Science, Leiden University Niels Bohrweg 1, 2333 CA Leiden, The Netherlands

Nikhef Theory Group, Nikhef Science Park 105, 1098 XG Amsterdam, The Netherlands

Keywords:

MCTS, Virtual Loss, Tree Parallelization, Search Overhead, Exploitation-exploration Trade-off.

Abstract:

Monte Carlo tree search algorithms, such as UCT, select the best-root-child as a result of an iterative search

process consistent with path dependency. Recent work has provided parallel methods that make the search

process faster. However, these methods violate the path-dependent nature of the sequential UCT process.

Here, a more rapid search thus results in a higher search overhead. The cost thereof is a lower time efﬁciency.

The concept of virtual loss is proposed to compensate for this cost. In this paper, we study the role of virtual

loss. Therefore, we conduct an empirical analysis of two methods for lock-free tree parallelization, viz. one

without virtual loss and one with the virtual loss. We use the UCT algorithm in the High Energy Physics

domain. In particular, we methodologically evaluate the performance of the both methods for a broad set

of conﬁgurations regarding search overhead and time efﬁciency. The results show that using virtual loss for

lock-free tree parallelization still degrades the performance of the algorithm. Contrary to what we aimed at.

1 INTRODUCTION

Since its inception in 2006 (Coulom, 2006), the

Monte Carlo Tree Search (MCTS) algorithm has

acquired much interest among optimization resear-

chers. MCTS is a sampling algorithm that uses si-

mulation results to guide itself through the search

space, obviating the need for domain-dependent heu-

ristics. Starting with the game of Go, an Asian bo-

ard game (Chaslot et al., 2008a), MCTS has achieved

accomplishments in different domains such as High

Energy Physics (HEP) (Kuipers et al., 2013; Ruijl

et al., 2014). The success of MCTS depends on the

balance between exploitation (look in areas which ap-

pear to be promising) and exploration (look in areas

that have not been well sampled yet). The most po-

pular algorithm in the MCTS family which addresses

this dilemma is the Upper Conﬁdence Bound (UCB)

for Trees (UCT) (Kocsis and Szepesv

ari, 2006).

At each iteration, MCTS adds a new node to a

tree by ﬁrst selecting a path inside the tree and then

using Monte Carlo simulations. This iterative pro-

cess is path-dependent which means that the outco-

mes of previous iterations guide the future selections.

Recently, several studies have addressed the topic of

making parallel methods for MCTS such as tree, root,

and leaf parallelizations. Here we focus on tree paral-

lelization that distributes different iterations of MCTS

among parallel workers. Therefore, it has to violate

the path dependency feature of sequential MCTS to

make the algorithm faster.

In tree parallelization, the performance is decre-

asing when increasing the number of parallel wor-

kers. It is widely believed that the performance loss

is due to redundant search being done by separate pa-

rallel workers (i.e., Search Overhead)(Chaslot et al.,

2008a). Therefore, a method called virtual loss is pro-

posed for a lock-based tree parallelizations to force

parallel workers to traverse different paths inside the

MCTS tree. However, virtual loss then affects the ba-

lance between exploitation and exploration in UCT

algorithm (Chaslot et al., 2008a).

In this paper, we evaluate the beneﬁt of using

the virtual loss in lock-free (instead of locked-based)

tree parallelizations for a full conﬁguration of exploi-

tation/exploration factors in UCT and parallel wor-

ker threads. The result is reported concerning search

overhead and time efﬁciency.

The main contribution of this paper is to conduct

a methodological evaluation of using virtual loss for

lock-free tree parallelization, regarding search over-

head (SO) and time efﬁciency (Eff). The algorithms

are evaluated in problems from the High Energy Phy-

sics domain. Our goal is to ﬁnd a trade-off between

SO and Eff. The follow-up research would be to opti-

mize the trade-off for efﬁciency.

The remainder of this paper is structured as fol-

lows: Section 2 brieﬂy discusses the required back-

ground information. Section 3 discusses related work.

Section 4 gives the experimental setup, together with

the experimental results. Finally, a conclusion is gi-

ven in Section 5.

648

Mirsoleimani S., Plaat A., van den Herik J. and Vermaseren J.

An Analysis of Virtual Loss in Parallel MCTS.

DOI: 10.5220/0006205806480652

In Proceedings of the 9th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2017), pages 648-652

ISBN: 978-989-758-220-2

2 BACKGROUND

Below we provide some background information on

MCTS (Section 2.1) and the Horner schemes (Section

2.2).

2.1 Monte Carlo Tree Search

A search tree is the main building block of the MCTS

algorithm. Each node of the tree represents a posi-

tion in the search space. The algorithm constructs

the search tree incrementally, expanding one node in

each iteration (see Figure 1). Each iteration has four

steps (Chaslot et al., 2008b). (1) In the selection step,

beginning at the root of the tree, child nodes are se-

lected successively according to a selection criterion

until a leaf node is reached. (2) In the expansion step,

unless the selected leaf node ends the game, a random

unexplored child of the leaf node is added to the tree.

(3) In the simulation step (also called playout step),

the remainder of the path to a ﬁnal state is comple-

ted by playing random moves. In the end, a score ∆

is obtained that signiﬁes the score of the chosen path

through the state space. (4) In the back-propagation

step (also called backup step), the ∆ value is propaga-

ted back through the traversed path in the tree, which

updates the average score (win rate) of a node. The

number of times that each node in this path is visited

is incremented by one. Figure 1 shows the general

MCTS algorithm. Below we discuss the UCT algo-

rithm (2.1.1), tree parallelization (2.1.2), search over-

head (2.1.3), and time efﬁciency (2.1.4).

2.1.1 The UCT Algorithm

The UCT algorithm provides a solution for the pro-

blem of exploitation (look into existing promising

areas) and exploration (look for new promising areas)

in the selection phase of the MCTS algorithm (Kocsis

and Szepesv

ari, 2006). A child node j is selected to

maximize:

UCT ( j) = X

ln(n)

(1)

where X

, w

is the number of wins in child j, n

is the number of times child j has been visited, n is the

number of times the parent node has been visited, and

≥ 0 is a constant. The ﬁrst term in UCT equation is

for exploitation and the second one is for exploration.

The level of exploration of the UCT algorithm can be

adjusted by the C

constant. (High C

means more

exploration.)

function UCTSEARCH(r,m)

i ← 1

for i ≤ m do

n ← select(r)

n ← expand(n)

∆ ←playout(n)

backup(n,∆)

end for

return

end function

Figure 1: The general MCTS algorithm.

2.1.2 Tree Parallelization

In tree parallelization one MCTS tree is shared among

several threads that are performing simultaneous se-

arches (Chaslot et al., 2008a). The main challenge

in this method is using data locks to prevent data

corruption. A lock-free implementation of this al-

gorithm addresses the problem as mentioned earlier

with better scaling than a locked approach (Enzen-

berger and M

uller, 2010). Therefore, in our imple-

mentation of tree parallelization, locks are removed.

Figure 2 shows the tree parallelization algorithm wit-

hout locks.

Here we note that in tree parallelization with local

locks, it is still possible that different threads traverse

the tree in mostly the same way. This phenomenon

causes thread contention when two different threads

visit the same node concurrently, and one thread is

waiting for a lock that is currently being held by anot-

her thread. Increasing the number of threads exacer-

bate this problem. (Chaslot et al., 2008a) suggested

a solution to assign a temporary virtual loss (a mar-

ker) to a node when a thread selects it (Chaslot et al.,

2008a). Without the marker, there is a higher chance

for thread contention.

Implementing of the virtual loss is straight for-

ward. A thread is selecting a path inside the tree to

ﬁnd a leaf node. It is reducing the UCT value of all

of the nodes that belong to the path, assuming that the

playout from the leaf node results in a loss. Therefore,

The virtual loss will inspire other threads to traverse

different paths and avoid contention. A thread remo-

ves the assigned virtual loss immediately before the

backup step when updating the nodes with the real

playout result. It is worth mentioning that tree paral-

lelization with virtual loss is more explorative com-

pared to plain tree parallelization because the virtual

loss encourages different threads to explore different

parts of the tree regardless of the value of C

. Regar-

ding the virtual loss, UCT(j) decreases as more thre-

ads select node j, which encourage other threads to

favor other nodes.

An Analysis of Virtual Loss in Parallel MCTS

649

Figure 2: Tree parallelization without locks. The curly ar-

rows represent threads. The rectangles are leaf nodes.

2.1.3 Search Overhead

Parallel MCTS usually expands more nodes (i.e.,

more playouts) in the tree than the sequential MCTS.

In this paper, we deﬁne search overhead as

SO =

number of playouts in parallel

number of playouts in sequential

− 1.

2.1.4 Time Efﬁciency

Parallel MCTS that has more search overhead is less

time efﬁcient. In this paper, we deﬁne time efﬁciency

E f f =

time in sequential

number of workers in parallel · time in parallel

2.2 Horner Schemes

Horner’s rule is an algorithm for polynomial compu-

tation that reduces the number of multiplications and

results in a computationally efﬁcient form. For a po-

lynomial in one variable

p(x) = a

+ a

n−1

+ ... + a

, (2)

the rule simply factors out powers of x. Thus, the

polynomial can be written in the form

p(x) = ((a

x + a

n−1

)x + ...)x + a

. (3)

This representation reduces the number of multipli-

cation to n and has n additions. Therefore, the total

evaluation cost of the polynomial is 2n.

Horner’s rule can be generalized for multivariate

polynomials. Here, Eq. 3 applies on a polynomial

for each variable, treating the other variables as con-

stants. The order of choosing variables may be dif-

ferent, each order of the variables is called a Horner

scheme.

The number of operations can be reduced even

more by performing common subexpression elimina-

tion (CSE) after transforming a polynomial with Hor-

ner’s rule. CSE creates new symbols for each subex-

pression that appears twice or more and replaces them

inside the polynomial. Then, the subexpression has to

be computed only once.

3 RELATED WORK

(Chaslot et al., 2008a) reported that tree paralleliza-

tion with local locks and virtual loss performs as well

as root parallelization in the game of Go. However,

(Sephton et al., 2014) suggested that adding a virtual

loss to tree parallelization with local locks has almost

no effect on the performance for the game of Lords of

War.

(Soejima et al., 2010) also analyzed the perfor-

mance of root parallelism in detail. The authors found

that a majority voting scheme gives a better perfor-

mance than the conventional approach of playing the

move with the greatest total number of visits across

all trees. They suggested that the ﬁndings in (Chaslot

et al., 2008a) are explained by the fact that root paral-

lelism performs a shallower search, making it easier

for UCT to escape from local optima than the deeper

search conducted by plain UCT. In root parallelism,

each process does not build a search tree larger than

the sequential UCT. Moreover, each process has a lo-

cal tree that contains characteristics which differ from

tree to tree. Recently, (Teytaud and Dehos, 2015) pro-

posed a new idea by distinguishing between tactical

behavior and strategic behavior. They transferred the

RAVE (Rapid Action Value Estimate) ideas as deve-

loped by (Gelly and Silver, 2007), from the selection

phase to the simulation step. This transfer implied

that by inﬂuencing the tree policy also the Monte-

Carlo policy is inﬂuenced. It leads to a different se-

arch method.

4 EMPIRICAL STUDY

In this section, the experimental setup is described

(4.1), followed by the experimental results (4.2) and a

discussion (4.3).

4.1 Experimental Setup

We perform a sensitivity analysis of C

on the num-

ber of iterations for different thread conﬁgurations for

one expression, namely HEP(σ) which is a polyno-

mial from HEP domain with 15 variables (Kuipers

et al., 2013).

The plain UCT algorithm and parallel methods are

implemented in C++. Each data point represents the

average of 20 runs.

In our experiments, the maximum number of pla-

youts is 10,240. Throughout the experiments, the

number of threads is multiplied by a factor of two.

The results are measured on a dual socket machine

with 2 Intel Xeon E5-2596v2 processors running at

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

650

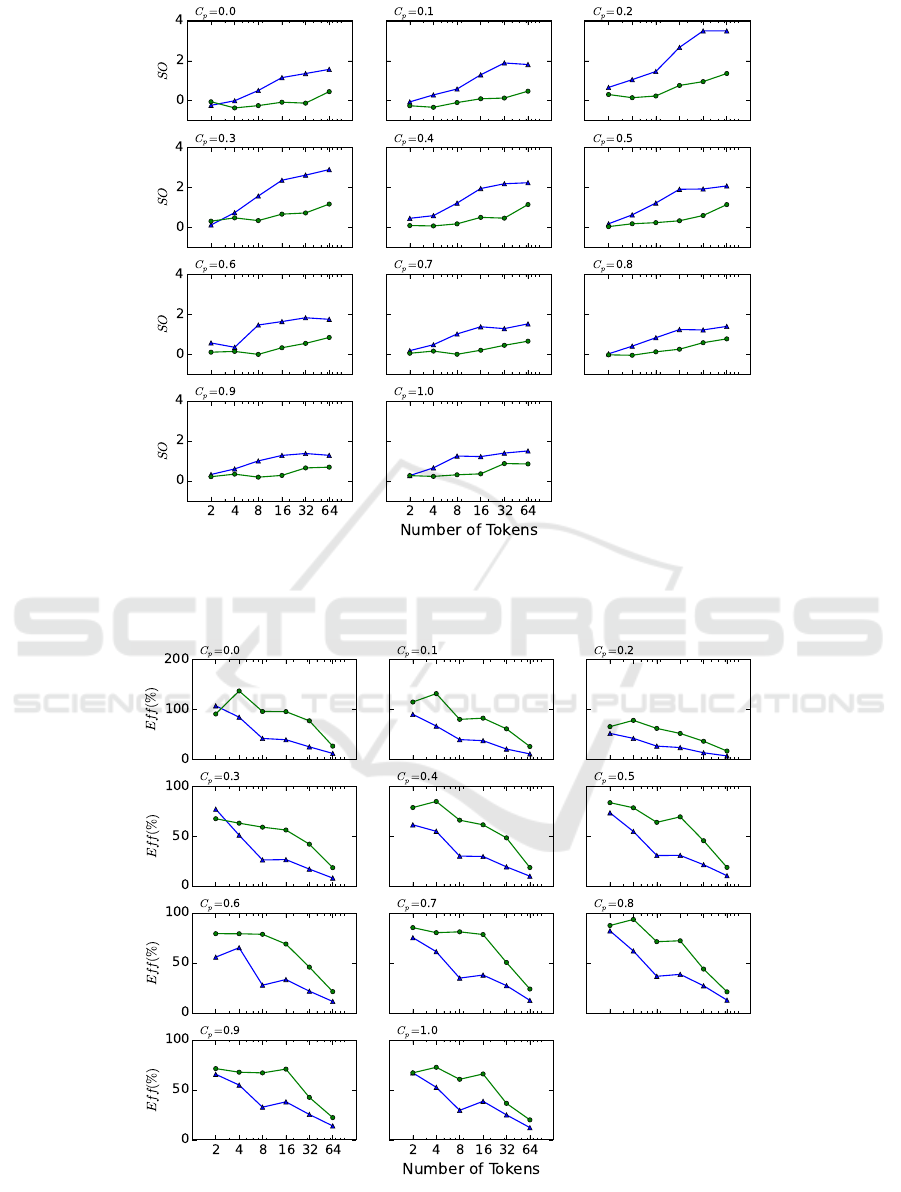
Figure 3: Search overhead (SO) for Horner (average of 20 instances for each data point). Tree parallelization is the green cir-

cle, and tree parallelization with virtual loss is the blue triangle. Note the higher SO of the blue triangle (lower performance).

Figure 4: Efﬁciency (Eff) for Horner (average of 20 instances for each data point). Tree parallelization is green circle and tree

parallelization with virtual loss is blue triangle. Note that the virtual loss have a lower efﬁciency (lower performance).

An Analysis of Virtual Loss in Parallel MCTS

651

2.40GHz. Each processor has 12 cores, 24 hyper-

threads and 30 MB L3 cache. Each physical core has

256KB L2 cache. The pack TurboBoost frequency is

3.2 GHz. The machine has 192GB physical memory.

Intel’s icc 14.0.1 compiler is used to compile the pro-

gram.

4.2 Experimental Results

Below we provide our experimental results. Figure

3 shows the SO of both methods. With four tokens

(a parallel thread can run each token) both methods

have similar SO for all values for C

. However, plain

tree parallelization has smaller SO than tree paralleli-

zation with the virtual loss on all points.

Figure 4 shows the Eff of each method. We see

that plain tree parallelization outperforms tree paral-

lelization with the virtual loss in almost all tokens for

all values of C

. The only exception is when the num-

ber of tokens is 4 and C

is 0 and 0.3.

4.3 Discussion

It is interesting that adding virtual loss degrades the

performance of lock-free tree parallelization in the se-

lected problems. This outcome may be due to the

several factors. We mention two of them. (1) Vir-

tual loss enables parallel threads to search different

parts of the shared tree, thus reducing the synchroni-

zation overhead caused by using the locks (Soejima

et al., 2010). However, when the algorithm is lock-

free, there is not such an overhead. (2) Virtual loss

disturbs the exploitation/exploration balance of UCT

algorithm. With these ideas we look again at Figures

3 and 4.

5 CONCLUSION

We investigated the virtual loss method for lock-free

tree parallelization and showed that the virtual loss

method suffered from a high search overhead, which

downsized the performance, thus the efﬁciency. Our

most important observations include: (1) In tree pa-

rallelization, search overhead is increased and time

efﬁciency is decreased when increasing the number

of parallel worker threads, (2) In a case that virtual

loss is used, there is almost no improvement in search

overhead and time efﬁciency. Originally virtual loss

was designed to improve the performance of lock-

based tree parallelization for the game of Go. Howe-

ver, our preliminary results using an application from

High Energy Physic domain shows that lock-free tree

parallelization can achieve better performances by a

lower search overhead and a higher efﬁciency without

using virtual loss. If this trend continues then this new

setting (without virtual loss) is to be preferred.

ACKNOWLEDGEMENTS

This work is supported in part by the ERC Advanced

Grant no. 320651, “HEPGAME.”

REFERENCES

Chaslot, G., Winands, M., and van den Herik, J. (2008a).

Parallel Monte-Carlo Tree Search. In the 6th Interna-

tioal Conference on Computers and Games, volume

5131, pages 60–71. Springer Berlin Heidelberg.

Chaslot, G. M. J. B., Winands, M. H. M., van den Herik, J.,

Uiterwijk, J. W. H. M., and Bouzy, B. (2008b). Pro-

gressive strategies for Monte-Carlo tree search. New

Mathematics and Natural Computation, 4(03):343–

357.

Coulom, R. (2006). Efﬁcient Selectivity and Backup Ope-

rators in Monte-Carlo Tree Search. In Proceedings

of the 5th International Conference on Computers

and Games, volume 4630 of CG’06, pages 72–83.

Springer-Verlag.

Enzenberger, M. and M

uller, M. (2010). A lock-free mul-

tithreaded Monte-Carlo tree search algorithm. Advan-

ces in Computer Games, 6048:14–20.

Gelly, S. and Silver, D. (2007). Combining online and

ofﬂine knowledge in UCT. In the 24th Internatio-

nal Conference on Machine Learning, pages 273–280,

New York, USA. ACM Press.

Kocsis, L. and Szepesv

ari, C. (2006). Bandit based Monte-

Carlo Planning Levente. In F

urnkranz, J., Scheffer,

T., and Spiliopoulou, M., editors, ECML’06 Procee-

dings of the 17th European conference on Machine

Learning, volume 4212 of Lecture Notes in Computer

Science, pages 282–293. Springer Berlin Heidelberg.

Kuipers, J., Plaat, A., Vermaseren, J., and van den Herik, J.

(2013). Improving Multivariate Horner Schemes with

Monte Carlo Tree Search. Computer Physics Commu-

nications, 184(11):2391–2395.

Ruijl, B., Vermaseren, J., Plaat, A., and van den Herik, J.

(2014). Combining Simulated Annealing and Monte

Carlo Tree Search for Expression Simpliﬁcation. Pro-

ceedings of ICAART Conference 2014, 1(1):724–731.

Sephton, N., Cowling, P. I., Powley, E., Whitehouse, D.,

and Slaven, N. H. (2014). Parallelization of Informa-

tion Set Monte Carlo Tree Search. In Evolutionary

Computation (CEC), 2014 IEEE Congress on, pages

2290–2297.

Soejima, Y., Kishimoto, A., and Watanabe, O. (2010). Eva-

luating Root Parallelization in Go. IEEE Transacti-

ons on Computational Intelligence and AI in Games,

2(4):278–287.

Teytaud, F. and Dehos, J. (2015). One the Tactical and Stra-

tegic Behaviour of MCTS When Biasing Random Si-

mulations. ICCA Journal, 38(2):67–80.

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

652