
Privacy Preserving Data Classification using Inner-product Functional
Encryption
Damien Ligier
1,2,3
, Sergiu Carpov
1
Caroline Fontaine
2,3
and Renaud Sirdey
1
1
CEA LIST, Point Courrier 172, 91191 Gif-sur-Yvette Cedex, France
2
CNRS/Lab-STICC and Telecom Bretagne, Brest, France
3
UBL, Rennes, France
{damien.ligier, sergiu.carpov, renaud.sirdey}@cea.fr, caroline.fontaine@telecom-bretagne.eu
Keywords:
Functional Encryption, Inner-Product Encryption, Classification, Linear Classification.
Abstract:
In the context of data outsourcing more and more concerns raise about the privacy of user’s data. Simultane-
ously, cryptographers are designing schemes enabling computation on ciphertexts (homomorphic encryption,
functional encryption, etc.). Their use in real world applications is difficult. In this work we focus on func-
tional encryption schemes enabling computation of inner-product on encrypted vectors and their use in real
world scenarios. We propose a protocol combining such type of functional encryption schemes with machine
learning algorithms. Indeed, we think that being able to perform classification over encrypted data is useful
in many scenarios, in particular when the owners of the data are not ready to share it. After explaining our
protocol, we detail the implemented handwritten digit recognition use case, and then, we study its security.
1 INTRODUCTION
With the generalization of data outsourcing, more and
more concerns raise about the privacy and the security
of outsourced data. In this context, machine learning
methods have to be conceived and deployed, but with
users privacy concerns addressed.
In a privacy preserving data classification process,
one has to be able to extract knowledge (e.g. in the
case of a classifier, deduction of the class label of an
individual without compromising his private data) by
assuring the protection of the sensitive data and, if
possible, by hiding data access patterns from which
useful properties could be inferred.
In this work we propose a privacy preserving clas-
sification algorithm based on functional encryption,
in particular the inner-product encryption. A multi-
class prediction algorithm with encrypted input data
is described. The privacy of input data is kept due to
the inner-product encryption scheme. Roughly speak-
ing the data item on which a prediction must be made
is encrypted. From the encrypted data, integer inner-
products are extracted and are used afterwards to pro-
duce the class of the input data item. The perfor-
mance of the classification algorithm is evaluated on
the MNIST database (LeCun et al., ).
The paper is structured as follows. In Sec. 2,
we recall machine learning and cryptographic back-
ground that we need in this paper. Sec. 3 presents the
protocol for performing classsification over encrypted
data, that we introduce. Sec. 4 gives the experimental
results we obtained with our protocol. Finally, Sec. 5
concludes this paper.
2 PRELIMINARIES AND
RELATED WORK
In the literature one can find several works on privacy-
preserving classification. In particular, we refer to
(Yang et al., 2005) for a privacy-preserving method
that allows to compute frequencies of values, (Man-
gasarian et al., 2008) for a support vector machine
classifier for a private data matrix. In this work we
present a new approach which uses functional encryp-
tion to perform classification on encrypted data.
2.1 Functional Encryption
Traditional public-key cryptography has been gener-
alized in many ways, among which recently raised the
concept of functional encryption (Sahai and Waters,
2005; Boneh et al., 2011). In this paradigm the au-
thority is holding a master secret-key MSK that allows
to derive a secret key sk
f
associated with a function
Ligier, D., Carpov, S., Fontaine, C. and Sirdey, R.
Privacy Preserving Data Classification using Inner-product Functional Encryption.
DOI: 10.5220/0006206704230430
In Proceedings of the 3rd International Conference on Information Systems Security and Privacy (ICISSP 2017), pages 423-430
ISBN: 978-989-758-209-7
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
423

f . It is possible to derive more secret keys associated
with different functions. Using the public key PUB
one can encrypt a message x into a ciphertext c. The
user who has sk
f
“decrypts” c and does not get x but
only the information f (x). Hence, this decryption is
not a real decryption in the common sense, but rather
an evaluation. Nevertheless, it is called “decryption”
in the literature, so we keep this terminology in this
paper.
The authority of a functional encryption scheme
delivers several secret keys (associated to different
functions) to the users. Hence, it requires that if a
user owns different secret keys {sk
f
i
}
i
and an en-
cryption of x, he cannot learn about x more than
{ f
i
(x)}
i
. This property is called collusion resistance,
and there are two ways to address it: one relies on
indistinguishability-based security and the other one
on simulation-based security.
The holy grail of this domain is to design a scheme
that enables to derive a secret key sk
f
for any polyno-
mial time computable function f . Goldwasser et al.
proposed a construction based on fully homomorphic
encryption (Goldwasser et al., 2013), Garg et al. pro-
posed another construction using an indistinguishabil-
ity obfuscator (Garg et al., 2013). At present, how-
ever, these constructions remain mostly of theorical
interest.
For some use cases one has to hide information
inside the function f associated with the decryption
keys sk
f
. This functionality is not covered by public-
key functional encryption. A solution to this problem
is to use functional encryption in a private-key set-
ting (Brakerski and Segev, 2015; Bishop et al., 2015)
(private-key functional encryption). There is no more
master public key and the encryption algorithm takes
as input the master secret key; consequently, an at-
tacker is not able to encrypt whatever he wants. We
do not focus on the private-key setting in this paper.
2.1.1 Definition
Boneh et al.. (Boneh et al., 2011) gave the following
standard definitions for functional encryption. In this
definition, the previous function f is represented with
the function F(K,·).
Definition 1. A functionality F defined with (K,X) is
a function F : K × X → Σ∪ {⊥}. The set K is the key
space, the set X is the plaintext space, and the set Σ
is the output space and does not contain the special
symbol ⊥.
Definition 2. A functional encryption scheme
for a functionality F is a tuple F E =
(Setup,Keygen, Encrypt,Decrypt) of four al-
gorithms with the following properties.
• The Setup algorithm takes as input the security
parameter 1
λ
and outputs a pair of a public key
and a master secret key (PUB,MSK).
• The KeyGen algorithm takes as inputs the master
secret key MSK and k ∈ K which is a key of the
functionality F. It outputs a secret key sk for k.
• The Encrypt algorithm takes as inputs the public
key PUB and a plaintext x ∈ X. This randomized
algorithm outputs a ciphertext c
x
for x.
• The Decrypt algorithm takes as inputs the public
key PUB, a secret key and a ciphertext. It outputs
y ∈ Σ ∪ {⊥}.
It is required that for all (PU B, MSK) ← Setup(1
λ
),
all keys k ∈ K and all plaintexts x ∈ X, if sk ←
KeyGer(MSK,k) and c ← Encrypt(PUB,x) we have
F(K,X ) = Decrypt(PUB,sk,c) except with a negli-
gible probability.
2.1.2 Inner-Product Functional Encryption
(IPFE)
Functional encryption schemes that enable the evalu-
ation of inner products are called functional encryp-
tion for the inner-product functionality, inner-product
functional encryption, or inner-product encryption. In
those schemes the plaintext space X and the function-
ality key space K are vector spaces K
n
, and F is the
inner-product function. We now consider a plaintext
W ∈ K
n
, and a secret key sk
V
which is associated with
a vector V ∈ K
n
. If c
W
is an encryption of W , when
one decrypts c
W
with sk
V
he only gets hv,wi, thus the
inner product of v and w. The owner of sk
V
has to
know V in order to decrypt with it, i.e. V cannot be
hidden to the decryptor.
Recently, Abdalla et al. (Abdalla et al., 2015)
proposed constructions for the inner product encryp-
tion schemes satisfying standard security definitions,
under well-understood assumptions like the Deci-
sional Diffie-Hellman (DDH) and Learning With Er-
rors. However they only proved their schemes to be
secure against selective adversaries. Agrawal et al.
(Agrawal et al., 2015) upgraded those schemes to pro-
vide them a full security (security against adaptive at-
tacks). In this work we focus on these inner prod-
uct schemes, thus on the fully secure functional en-
cryption for the inner product functionality under the
DDH assumption (Agrawal et al., 2015).
We now recall the functional encryption for inner-
product scheme of the Agrawal et al. (Agrawal et al.,
2015) that provides full security under the DDH as-
sumption. The notation α
R
←- K means that α is ran-
domly choosen from the set K.
ICISSP 2017 - 3rd International Conference on Information Systems Security and Privacy
424

Theorem 1. (Boneh, 1998) In a cyclic group G
of prime order q, the Decisional Diffie-Hellman
(DDH) problem is to distinguish the distribution
D
0
= {(g,g
a
,g
b
,g
ab
)|g
R
←- G, a, b
R
←- Z
q
} and D
1
=
{(g,g
a
,g
b
,g
c
)|g
R
←- G, a,b, c
R
←- Z
q
}.
We recall the four algorithms of the scheme.
Algorithm 1: Setup(1
λ
,1
m
).
1: choose a cyclic group G of prime order q > 2
λ
with generators g,h ∈ G
2: for all 1 ≤ i ≤ m do
3: s
i
,t
i
R
←- Z
q
4: h
i
← g
s
i
· h
t
i
5: PUB ← (G,g,h, {h
i
}
1≤i≤m
)
6: MSK ← ({s
i
}
1≤i≤m
,{t
i
}
1≤i≤m
)
7: return (PUB,MSK)
Let v = (v
1
,· ·· , v
m
) ∈ Z
m
q
be the vector we want
to associate a key.
Algorithm 2: Keygen(MSK,v).
1: s
v
←
∑
m
i=1
s
i
· v
i
2: t
v
←
∑
m
i=1
t
i
· v
i
3: return sk ← (s
v
,t
v
)
Let w = (w
1
,· ·· , w
m
) ∈ Z
m
q
be a plaintext we want
to encrypt.
Algorithm 3: Encrypt(PUB,w).
1: r
R
←- Z
q
2: C ← g
r
, D ← h
r
3: for all 1 ≤ i ≤ m do
4: E
i
= g
w
i
· h
r
i
5: return c ← (C,D,{E
i
}
1≤i≤m
)
Decryption algorithm uses a discrete logarithm
computation in a large size group (which in general
is hard to compute). Coefficients of the plaintext vec-
tor w and the key vector v belong to {−β,...,0,...,β}
where β is a small integer, so the possible interval
of hv
i
,wi is small as well. When the output interval
of the discrete logarithm is small and known we can
use Shank’s baby step giant step algorithm (Shanks,
1971) to compute it efficiently or simply use a lookup
table.
Algorithm 4: Decrypt(PUB,sk,c).
1: E ←
∏
m
i=1
E
v
i
i
/(C
s
v
· D
t
v
)
2: r ← log
g
(E)
3: return r
2.2 Classification
Machine learning (ML) is a sub-field of computer
science. It studies and builds algorithms for learn-
ing, predicting, classifying, and more generally ex-
tracting knowledge from data. In supervised ML, the
algorithms are trained with example input data and
desired output results, before being used as classi-
fiers. One can distinguish two phases in the applica-
tion of supervised ML algorithms: learning and pre-
diction (classification). During the first phase, ML al-
gorithms analyze example input data and learns how
to make proper predictions on such kind of data. Dur-
ing the prediction phase, ML algorithms predict how
new data has to be classified, as a function of the first
learning step.
Depending on the type of prediction results, ML
techniques can be of two different kinds: (i) classifi-
cation – when the result is a discrete value (e.g. pre-
dict class membership) or (ii) regression – when the
result is a continuous value (e.g. predict temperature).
In what follows we focus on the first kind, and de-
scribe two classification algorithms used in this work.
2.2.1 Linear Classifier
A linear classification algorithm makes a decision on
the membership of an input data object, based on
a linear combination of its features (characteristics).
For example, in an image classification algorithm the
input object is an image and the features can be im-
age pixels. In a binary classification, the decision is
made as a function of a threshold overrun by the dot
product between object features and linear classifier
coefficients. For multi-class classification, one can
distinguish two possibilities:
• One-vs.-rest, in which a binary classifier is built
for each class in order to distinguish between this
class and all the others. The decision is made as a
function of the resulting dot product amplitude.
• One-vs.-all, in which a binary classifier is built
for any pair of classes. The decision is made as a
function of the number of positive votes received
by each class.
More details about linear classification can be
found in (McCullagh and Nelder, 1989). In this work
we focus on one-vs.-rest multi-class classification.
Considering n ∈ N classes, n ≥ 2, we want to classify
vectors (objects features) in a specific subset of Z
m
,
m ∈ N. Let w
T
= (w
1
,w
2
,· ·· , w
m
) ∈ Z
m
be one of the
objects we want to classify. The set {v
i
}
1≤i≤n
con-
tains n vectors of Z
m
, each of them being associated
with one class. The vector v
i
= (v
i
1
,v
i
2
,· ·· , v
i
m
) ∈ Z
m
Privacy Preserving Data Classification using Inner-product Functional Encryption
425

represents binary classifier coefficients used to distin-
guish between class i and the other classes. For all
1 ≤ i ≤ n we compute ip
i
= hv
i
,wi. The class of in-
put object w
T
is given by arg max
1≤i≤n
r
i
.
2.2.2 Extremely Randomized Trees Classifier
In ensemble learning methods, the predictions of sev-
eral (usually small) base classifiers are combined in
order to make an aggregated classifier which is more
powerful and more robust than separate ones (Diet-
terich, 2000). One of the possibilities to build an en-
semble method is to average the decisions of many
base classifiers. The combined classifier is stronger
than any of the base classifiers.
A decision tree classifier (Safavian and Land-
grebe, 1991) represents a tree-like structure where an
internal node is a test on a single data feature, node
output edges are the outcomes of this test and the tree
leafs are decision classes. A decision tree classifier
prediction is built by following a tree path from the
root node to a leaf node. At each step a decision is
made as a function of node condition.
Extremely randomized trees (ERT) classifier is an
ensemble learning method in which base classifiers
are decision trees. Roughly speaking, an ERT clas-
sifier builds many decision trees on different sub-sets
of input data features. Prediction is performed by av-
eraging the classes resulting from each decision tree.
For more details, please refer to (Geurts et al., 2006).
2.2.3 MNIST Dataset
The performance of the privacy preserving classifica-
tion methods proposed in this work, is tested using the
MNIST dataset. The MNIST database is a collection
of handwritten digit images (LeCun et al., ). Fig. 1
presents sample images from it. Dataset images have
size 784 = 28 × 28 and each pixel has 256 levels of
grey. The handwritten digits are normalized in size
and are centered. There are 10 output classes in the
dataset (digits from 0 to 9). The MNIST dataset has
(a) (b)
Figure 1: Sample digit images from the MNIST database:
(a) is the 60th image and (b) is the 61st.
been extensively used by the ML community for clas-
sifier validation. For a review of ML methods applied
to MNIST, please refer to (Bottou et al., 1994; LeCun
et al., 1998).
3 CONTRIBUTION
In this work we propose a privacy preserving data
classification method. Input data is encrypted using
an inner product encryption scheme. In the context of
ML algorithms, the inner product encryption can be
seen as a linear binary classifier. In order to perform
a multi-class linear classification, we need to com-
pute several inner products on the same input data.
Usually, linear classifiers provide worse results when
compared to other more elaborate classification meth-
ods. Nevertheless, only a linear classifier is able to
provide a prediction for data encrypted using the in-
ner product encryption (if we don’t send more infor-
mation as encryption of some pieces of precalculus
for example).
3.1 Privacy Preserving Classification
Protocol
In our protocol, there is an entity called server that
has performed a training step of a linear classifier.
The server has a set of linear classification coefficients
{v
i
} and he wants to keep them secret, but he wants
to classify data with it, and not delegate its compu-
tation. There are many users which have information
that they want to keep secret but at the same time, they
also want to release classification results to the server
(for example in order to obtain a service). We intro-
duce a third party that both the server and the users
can trust. We call it authority and it is not meant
to perform computation. Its goal is in a first time
to check that the server’s {v
i
} are not dishonest (the
server is not trying to cheat) and in a second time, to
generate an instance of an inner-product encryption
scheme. We now describe in detail this protocol, il-
lustrated by Fig. 2. The initialization phase has two
steps:
First, the authority generates the public key and
the master secret key with the Setup algorithm of the
IPFE, and sends the public key to the users.
The following steps are repeated each time a new
server wants to join the system:
(A) The server uses the training algorithm on his
training set.
ICISSP 2017 - 3rd International Conference on Information Systems Security and Privacy
426
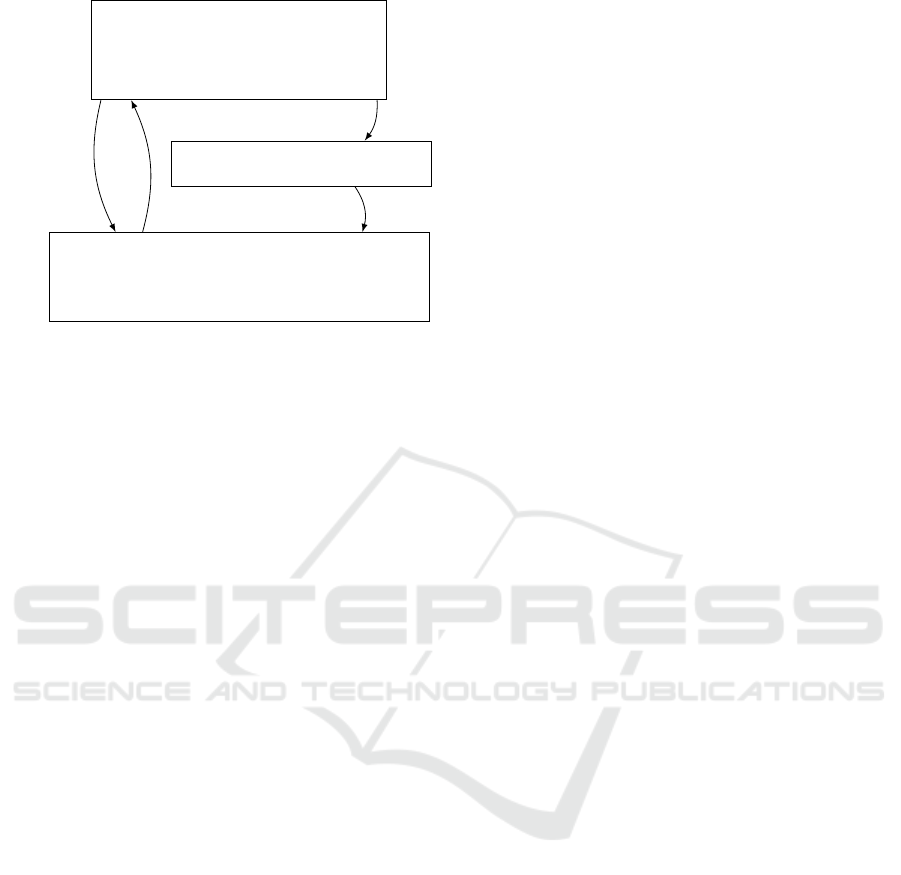
AUTHORITY
(PU B,MSK) ← IPFE.Setup(1
λ
,1
m
)
(B) {sk
v
i
} ← IPFE.Keygen(MSK,v
i
)
∀i
SERVER
(A) {v
i
} ← Classifier.Training(trainingSet)
(2) {ip
i
} ← IPFE.Decrypt(PUB,sk
v
i
,ct) ∀i
(3) c ← Classifier.Classify({ip
i
})
USER
(1) ct ← IPFE.Encrypt(PUB,w)
PU B
{v
i
}
PU B,{sk
v
i
}
ct
Figure 2: Privacy preserving classification protocol.
(B) The authority receives the {v
i
}
1≤i≤m
from the
server and generates the {sk
v
i
}
1≤i≤m
using the
Keygen algorithm of the IPFE, and afterwards
sends them to the server.
The following steps are repeated each time a user
wants to send its data to a server:
(1) A user encrypts a private data vector w with the
Encrypt algorithm of the IPFE, and sends it to the
server.
(2) The server decrypts it with all of his secret
keys {sk
v
i
}
1≤i≤m
using the Decrypt algorithm
of the IPFE, and gets {ip
i
}
1≤i≤m
such that ip
i
=
hv
i
,wi, ∀1 ≤ i ≤ m.
(3) The server uses a classification algorithm in order
to predict the class of w using the inner products
{ip
i
}
1≤i≤m
.
To illustrate the advantage of our construction, we
now describe a realistic scenario. We assume that
there is a pharmaceutical company which has con-
structed a classifier that takes as input medical and
private pieces of information. The company does not
want to divulge its secret classifier. However, it wants
to conduct a study on real human beings (for exam-
ple the patients of a hospital). The law about medical
data can be very restrictive depending on the country.
For example in France, a hospital cannot easily share
the data of its patients. Our construction provides a
possible solution. We simply need a third party that
can be trusted by the company and the hospital. A
governmental agency should be able to do it. So the
agency generates the public key and the secret keys
associated with the company classifier. The hospital
encrypts the data of its patients and sends it to the
company. The company decrypts them with its secret
keys. After decryption, the company only gets the re-
sult of a computation which involves the patients data.
It is important to notice that the critical data remained
encrypted during the whole process. Nevertheless, the
company can use the computation result to perform
the classification. Proceeding this way, it can perform
its study on real medical data without endangering the
patients data privacy. Moreover, our solution can in-
volve several hospitals and companies if needed (the
agency has to generate new secret keys for each new
classifier).
3.2 Combined Classifier
The simplest way to classify is to use a lin-
ear classifier. The only thing to perform is the
argMax({hv
i
,wi}
1≤i≤m
) which give the class of the
vector w.
In order to increase the results of linear classifi-
cation, we propose a combined classification method,
in which linear classification is applied to encrypted
data, then followed by a more complex classification
algorithm (for example an ensemble method in our
case but not limited to). For each piece of input en-
crypted data, several inner products are computed.
These products are then used as input features for a
second, more elaborate, classifier. In this way, we are
able to perform classification of encrypted data with
increased performance in terms of an evaluation met-
ric (e.g. error rate).
A linear one-vs.-rest classifier is applied on the
dataset. On the obtained output values of this clas-
sifier (i.e. dot products), we train an ERT classifier,
i.e. a pipeline of classifiers is used. The ERT clas-
sifier succeeds in extracting information from the n
(number of classes) inner products values. In order
to increase the success rate of the combined classifier,
we can further split each input class into several sub-
classes. This corresponds to assigning new “artificial”
labels to input data set (simply relabelling the target
values). The previously described combined classi-
fier is applied to the input data set with relabelled out-
comes except that for the second step “real” labels are
used instead of “artificial” ones.
3.3 Classification Security
In this section, we look beyond the cryptographic se-
curity of the IPFE scheme. Indeed, the result of the
computation provided by a secure IPFE scheme may
leak some information about the plaintext. If this in-
formation leakage can be used to recover enough in-
formation about the plaintext to compromise it, the
privacy preserving classification protocol may not be
considered as secure even if the underlying IPFE
scheme is proved to be secure.
Privacy Preserving Data Classification using Inner-product Functional Encryption
427

Let R be a ring. We consider a plaintext vector
w
T
= (w
1
,· ·· , w
m
) ∈ R
m
and c
w
one of its encryp-
tions. Let {sk
v
i
}
1≤i≤n
be a set of n secret keys. For
all 1 ≤ i ≤ n, sk
v
i
denotes the secret key associated
with the vector v
i
= (v
i
1
,· ·· , v
i
m
) ∈ R
m
. So the ques-
tion is: if we have c
w
and {sk
v
i
}
1≤i≤n
, what do we
exactly know about w? Using the decryption algo-
rithm we get {ip
i
}
1≤i≤n
. So we have the following
system with m unknowns: w
0
1
,· ·· , w
0
m
.
ip
1
=
∑
m
j=1
w
0
j
· v
1
j
ip
2
=
∑
m
j=1
w
0
j
· v
2
j
.
.
.
.
.
.
.
.
.
ip
n
=
∑
m
j=1
w
0
j
· v
n
j
(1)
Solving this system is equivalent to finding all the
vectors w
0
∈ R
m
that satisfy the equation:
ip = A · w
0
(2)
with ip
T
= (ip
1
,· ·· , ip
n
), w
0T
= (w
0
1
,· ·· , w
0
m
)
and the matrix A = (v
i
j
)
1≤i≤n,1≤ j≤m
with n lines and
m columns. The plaintext w is one of the solutions
of the system and the difficulty to find it depends on
m, n, R, {v
i
}
1≤i≤n
and on the intrinsic properties of
the used messages (images with properties, data with
properties, random, ...). To illustrate this we will con-
sider the following example.
Let R = Z, m = 16 and n = 4. The
plaintexts, are in {0, 1}
16
⊂ Z
16
. Let w
T
=
(0,1, 1,0,1, 0,1,0, 0,0,1, 0, 0,1,1, 1). Vectors v
1
=
(2,81, 80,82,3, 78,90,14, 66, 29,52, 36, 11,40,83, 31),
v
2
= (70,64,65, 46,74,10, 2, 85,23,54, 2,41,95, 83,
38,6), v
3
= (54,43, 98,0,93, 78,23,91, 52,39,43, 62,
19,57, 95,50) and v
4
=
(87,49, 3,33,28, 47,96,18, 17, 8,92, 69, 89,38,84, 10)
are randomly chosen in {0, ··· ,99}
16
. So, we have
ip
T
= (460,334,502, 400).
There are an infinite number of solutions in Z
m
but only one in the subset our plaintexts come from:
w ∈ {0,1}
16
. With a brute force attack we find it in
a few seconds even if the inner product encryption
scheme is secure!
A small space is clearly insecure. That is why on
the one hand the parameter m and the size of the ”re-
alistic” plaintext space has to be large enough, and on
the other hand the number of inner products n has to
be limited. Within our use case, a brute force attack is
unthinkable because of the size of our plaintext space:
2
8·784
. Nevertheless it does not mean that it is not pos-
sible to get more information than the inner-product
(e.g. about the handwriting we want to hide).
Now, with an explicit example we will discuss
an ideal property that would ensure an ideal security
level for our handwriting hiding scenario. Let us sup-
pose that x
fat
is the vector of the “fat” four (Fig. 1a),
x
thin
is the vector of the “thin” four (Fig. 1b), and that
A · x
fat
= A · x
thin
(which is not true in general). Let
us denote by ip this value (ip = A · x
fat
= A · x
thin
).
Now, let us suppose that someone encrypts one im-
age among x
fat
and x
thin
and sends it to us. After
its decryption we get ip. Using the classifier we get
the class of the image: 4. Of course, it is impossible
to know which of x
fat
or x
thin
was the original image.
However x
fat
and x
thin
do not have the same character
shape at all, so we can say that the handwriting is kept
secret in this case. Indeed, we know that an image of
a four has been encrypted but not if it is the thin four
or the fat four or even an other four. In the real life
A · x
fat
6= A · x
thin
. Let us denote ip
fat
= A · x
fat
and
ip
thin
= A · x
thin
. With the previous idea we searched
two things. First, x
0
fat
the closest
1
image to x
fat
such
that A·x
0
fat
= ip
thin
= A·x
thin
and we got Fig. 3a. Sim-
ilarly, in a second time, we searched for x
0
thin
the clos-
est image to x
thin
such that A · x
0
thin
= ip
fat
= A · x
fat
and we got Fig. 3b. Those two images are acceptable
in the sense that they are almost like an original im-
age. In both cases, we used CPLEX (ILOG, 2006) for
the search. More generally, if for any image x of a
digit there exists an other image y of the same digit
but with a different shape such that A · x = A · y, then
the handwriting is kept secret. This property depends
on the nature of the objects handled by the protocol
and the matrix A. In practice, this ideal property may
not be satisfied, but we can get close, as finding an
image really close to the original one when we only
know its ip vector value seems to be hard. Such a
study will be addressed in future work to better under-
stand how close we are from the ideal security model.
(a) (b)
Figure 3: (a) is a solution w
0
of Equation 2 that is the closest
to Fig. 1a where w is Fig. 1b. In the same way, (b) is
a solution w
0
of Equation 2 that is the closest to Fig. 1b
where w is Fig. 1a.
1
By closest we mean that we bound the maximum differ-
ence for each pixel.
ICISSP 2017 - 3rd International Conference on Information Systems Security and Privacy
428

4 EXPERIMENTATION &
RESULTS
We give the results and the performance of our im-
plementation when we use it to perform handwritten
digit recognition.
4.1 MNIST Digit Classification
In Sec. 3.2 we have introduced a combined classi-
fication algorithm which can be used with an inner
product encryption scheme. In our implementation
we have employed the scikit-learn
2
library. The scikit-
learn is an easy way to use machine learning library
with an extensive set of available ML algorithms. Lin-
ear and extremely randomized trees classifiers from
this library were used. These methods were called
with default parameters. Four classifiers were imple-
mented: linear classifier, combined classifier with 10,
20 and 30 intermediate classes.
As said earlier for the combined classifier with 10
intermediate classes we have simply used the inner
products from the linear classifier for a new learn-
ing process. In the case of the combined classifier
with 20 and 30 classes, each digit class was clustered
3
into 2 and respectively 3 “artificial” sub-classes.
Each classifier was trained on the MNIST training
set and the error rate on the test set was measured.
Linear classifier training method in scikit-learn returns
floating-point coefficients v
i
(recall Sec. 2.2.1). In or-
der to be able to use them in the inner product encryp-
tion scheme we scale and round these coefficients to
signed 8-bit integers
4
. The loss in classification pre-
cision is minor in this case and can be neglected.
We implemented the fully secured functional en-
cryption for inner product functionality (Agrawal
et al., 2015) within a prime field. Our group G is F
∗
p
such that p is a safe prime of approximatively 2048-
bits. So, the group where DDH is assumed to be dif-
ficult is the subgroup of F
∗
p
which has the prime or-
der size (p − 1)/2. The IPFE algorithms were imple-
mented in C++ using the FLINT library (Hart et al.,
2013) for field F
∗
p
computations. The experiments
were performed on a regular laptop computer with
an Intel Core i7-4650U CPU and 8GB of RAM. The
sizes of the elements we manipulate in the IPFE in-
stantiation are given in Table 1. The sizes are given
in the context of a classification algorithm applied to
2
http://scikit-learn.org
3
The k-means clustering was used.
4
We shall note that the range of coefficients is not limited to
[−127.. . 127] as regular signed 8-bit integers. The inner
product encryption scheme allows to encrypt any integer
modulo the prime order of the cyclic group (see Alg. 1).
Table 1: Size of the implementation. The secret key also
counts the coefficients of the vector that the secret key is
associated with.
plaintext ciphertext secret key
784 B 196 kB 1296 B
Table 2: Execution times (in seconds) for the inner prod-
uct encryption part of the classifier. The decryption column
contains the time needed for all the IPFE.Decrypt (not par-
allelized) and the computaion of the classification.
Classifier Keys gen Encryption Decryption
Linear or
0.0037
0.15
23
Combined 10
Combined 20 0.0079 46
Combined 30 0.012 69
Table 3: Execution results of the proposed classifiers.
Classifier Learning Prediction Error rate
Linear 6 sec.
< 0.1 sec.
13.93 %
Combined 10 30 sec. 7.32 %
Combined 20 77 sec. 4.86 %
Combined 30 94 sec. 4.36 %
the MNIST database: the plaintext is an image, the
ciphertext is an encrypted image.
The decryption of the IPFE scheme is per-
formed by computing a discrete logarithm. In our
case, the inner products obtained by the applica-
tion of the learned linear coefficients on the MNIST
database belong to a small interval. We have pre-
computed a lookup table with all the (α,g
α
) for α
in {−933197 . . .424769}. This pre-computation took
6.2 seconds and the size of the obtained lookup ta-
ble is about 337MB. The size of the lookup can be
reduced to 10.4MB if only the first 32-bits of all the
g
α
are kept, which can be seen as a hashing of g
α
(less than 0.1% of collisions are obtained in this case).
Solving the discrete logarithm using the lookup ta-
ble takes under 0.18 seconds. We measured the ex-
ecution time of the algorithms: 0.00037 seconds for
Keygen, 0.15 seconds for Encrypt and 2.3 seconds
for Decrypt (without the discrete logarithm part be-
cause we used the lookup table).
The execution times of the IPFE part are presented
in Tab. 2. The keys generation is fast. In the “encryp-
tion” column is provided the execution time for en-
crypting an image and the last column is the execution
time for computing the inner product values (several
IPFE decryptions). We shall note that this step can be
easily parallelized and then, the computation time can
be divided by 10.
In Tab. 3 we present execution results for the 4
proposed classifiers. The classification algorithms
were executed on the same laptop as previously.
Learning is executed only once for estimating clas-
Privacy Preserving Data Classification using Inner-product Functional Encryption
429

sifier models. Classifier error rate is the percentage
of miss-predictions reported to the total number of
predictions. As we can observe the introduction of
a second step after the linear classifier allows to de-
crease the error rate by at least 6 percentage points.
Using 20 intermediate inner products allows further-
more to decrease the percentage of miss-predictions
by ≈ 2.5%. In contrast using 30 intermediate inner
products instead of 20 increase the performance by
less than 0.5%. We suppose that using different num-
ber of “artificial” sub-classes for each digit will allow
to obtain better results.
5 CONCLUSION AND FUTURE
WORK
In this work we have used an instantiation of an inner-
product functional encryption scheme in order to per-
form classification over encrypted data. The learning
process is kept secret and only linear classifiers coeffi-
cients are shared with the authority. In the protocol we
introduce, we have a trusted authority, some servers
computing classifications and the users who encrypt
their data. Obtained execution times are reasonably
small (a prediction is made in approximatively 69 sec-
onds without any parallelization) just like the size of
the ciphertexts. We have studied a method for ensur-
ing that we cannot find the original image from the
inner product values. In perspective, we consider to
study more deeply the information leakage of inner
product encryption schemes used in classification and
to propose methods to lower it. We also consider to
improve our implementation (with elliptic curve for
example) in order to have smaller sizes.
REFERENCES
Abdalla, M., Bourse, F., De Caro, A., and Pointcheval,
D. (2015). Simple functional encryption schemes for
inner products. In IACR International Workshop on
Public Key Cryptography, pages 733–751. Springer.
Agrawal, S., Libert, B., and Stehl
´
e, D. (2015). Fully secure
functional encryption for inner products, from stan-
dard assumptions.
Bishop, A., Jain, A., and Kowalczyk, L. (2015). Function-
hiding inner product encryption. In International Con-
ference on the Theory and Application of Cryptology
and Information Security, pages 470–491. Springer.
Boneh, D. (1998). The decision diffie-hellman problem.
In International Algorithmic Number Theory Sympo-
sium, pages 48–63. Springer.
Boneh, D., Sahai, A., and Waters, B. (2011). Functional
encryption: Definitions and challenges. In Theory of
Cryptography Conference, pages 253–273. Springer.
Bottou, L., Cortes, C., Denker, J. S., Drucker, H., Guyon,
I., Jackel, L. D., LeCun, Y., Muller, U. A., Sackinger,
E., Simard, P., et al. (1994). Comparison of classifier
methods: a case study in handwritten digit recogni-
tion. In International conference on pattern recogni-
tion, pages 77–77. IEEE Computer Society Press.
Brakerski, Z. and Segev, G. (2015). Function-private
functional encryption in the private-key setting. In
Theory of Cryptography Conference, pages 306–324.
Springer.
Dietterich, T. G. (2000). Ensemble methods in machine
learning. In International workshop on multiple clas-
sifier systems, pages 1–15. Springer.
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A.,
and Waters, B. (2013). Candidate indistinguishabil-
ity obfuscation and functional encryption for all cir-
cuits. In Foundations of Computer Science (FOCS),
2013 IEEE 54th Annual Symposium on, pages 40–49.
IEEE.
Geurts, P., Ernst, D., and Wehenkel, L. (2006). Extremely
randomized trees. volume 63, pages 3–42. Springer.
Goldwasser, S., Kalai, Y., Popa, R. A., Vaikuntanathan, V.,
and Zeldovich, N. (2013). Reusable garbled circuits
and succinct functional encryption. In Proceedings of
the forty-fifth annual ACM symposium on Theory of
computing, pages 555–564. ACM.
Hart, W., Johansson, F., and Pancratz, S. (2013). FLINT:
Fast Library for Number Theory. Version 2.4.0,
http://flintlib.org.
ILOG, I. (2006). ILOG CPLEX: High-performance soft-
ware for mathematical programming and optimiza-
tion. http://www.ilog.com/products/cplex/.
LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998).
Gradient-based learning applied to document recogni-
tion. volume 86, pages 2278–2324. IEEE.
LeCun, Y., Cortes, C., and Burges, C. J. The MNIST
Database. http://yann.lecun.com/exdb/mnist/.
Mangasarian, O. L., Wild, E. W., and Fung, G. M. (2008).
Privacy-preserving classification of vertically parti-
tioned data via random kernels. ACM Trans. Knowl.
Discov. Data, 2(3):12:1–12:16.
McCullagh, P. and Nelder, J. A. (1989). Generalized linear
models, volume 37. CRC press.
Safavian, S. R. and Landgrebe, D. A. (1991). A survey
of decision tree classifier methodology. volume 21,
pages 660–674.
Sahai, A. and Waters, B. (2005). Fuzzy identity-based
encryption. In Annual International Conference on
the Theory and Applications of Cryptographic Tech-
niques, pages 457–473. Springer.
Shanks, D. (1971). Class number, a theory of factorization,
and genera. In Proc. Symp. Pure Math, volume 20,
pages 415–440.
Yang, Z., Zhong, S., and Wright, R. N. (2005). Privacy-
preserving classification of customer data without loss
of accuracy. In Proceedings of the 5th SIAM Interna-
tional Conference on Data Mining.
ICISSP 2017 - 3rd International Conference on Information Systems Security and Privacy
430
