
Malware Detection based on Graph Classification
∗
Khanh-Huu-The Dam
1
and Tayssir Touili
2
1
University Paris Diderot and LIPN, Villetaneuse, France
2
LIPN, CNRS and University Paris 13, Villetaneuse, France
Keywords:
Machine Learning, Graph Kernel, Malware Detection, Static Analysis.
Abstract:
Malware detection is nowadays a big challenge. The existing techniques for malware detection require a huge
effort of engineering to manually extract the malicious behaviors. To avoid this tedious task of manually
discovering malicious behaviors, we propose in this paper to apply learning for malware detection. Given a
set of malwares and a set of benign programs, we show how learning techniques can be applied in order to
detect malware. For that, we use abstract API graphs to represent programs. Abstract API graphs are graphs
whose nodes are API functions and whose edges represent the order of execution of the different calls to the
API functions (i.e., functions supported by the operating system). To learn malware, we apply well-known
learning techniques based on Random Walk Graph Kernel (combined with Support Vector Machines). We can
achieve a high detection rate with only few false alarms (98.93% for detection rate with 1.24% of false alarms).
Moreover, we show that our techniques are able to detect several malwares that could not be detected by well-
known and widely used antiviruses such as Avira, Kaspersky, Avast, Qihoo-360, McAfee, AVG, BitDefender,
ESET-NOD32, F-Secure, Symantec or Panda.
1 INTRODUCTION
The number of malwares is significantly increasing.
In 2014, there were more than 317 million new pieces
of malwares
1
compared to 286 millions in 2010. It is
estimated that there are nearly a million of new mal-
wares released every day. Thus, malware detection is
a big challenge.
The well-known technique to detect malware is
signature matching. It consists on searching for pat-
terns in the form of binary sequences (called signa-
tures) in the program. Signatures are manually intro-
duced in a database by experts. If a program contains
a signature in the database, it is declared as a virus. If
not, it is declared as benign. It is very easy for virus
writers to get around these signature matching tech-
niques. Indeed, obfuscation techniques can change
the structure of a malware so that it will not have a
known signature anymore while keeping its same be-
havior.
Another technique to detect malware is called dy-
namic analysis. It consists in running a malware in an
emulated environment and recording its behaviors in
real time. However, as the execution time is limited, it
∗
This work was partially funded by the FUI project AIC
2.0.
1
2015 Internet Security Threat Report, Volume 20,
Symantec
is hard to trigger the malicious behaviors, since these
may be hidden behind user interaction or require de-
lays.
To sidestep these limitations, static analysis tech-
niques that allow to analyse the behavior (not the syn-
tax) of the program without executing it were ap-
plied for malware detection (Bergeron et al., 1999;
Christodorescu and Jha, 2003; Kinder et al., 2010;
Song and Touili, 2013a). However, in these works,
the malicious behaviors are discovered after a man-
ual study of the assembly code of the malwares. That
task needs an enormous engineering effort and takes
an enormous amount of time. This is the reason why
only 7 malicious behaviors were considered in (Song
and Touili, 2013b), whereas there are much more ma-
licious behaviors that should be considered. Thus,
one needs techniques that prevent us from performing
this enormous amount of engineering effort of read-
ing assembly codes to discover malicious behaviors.
To solve this problem, we apply in this work
machine learning techniques for malware detection.
Given a set of malwares and a set of benign pro-
grams, we use machine learning techniques to teach
computers to automatically learn malicious behav-
iors. To do this, we need an abstract representa-
tion of programs (malicious behaviors) that we have
to learn. Following (Fredrikson et al., 2010; Babi
´
c
et al., 2011; Macedo and Touili, 2013), we use API
Dam, K-H-T. and Touili, T.
Malware Detection based on Graph Classification.
DOI: 10.5220/0006209504550463
In Proceedings of the 3rd International Conference on Information Systems Security and Pr ivacy (ICISSP 2017), pages 455-463
ISBN: 978-989-758-209-7
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
455

function calls to specify malicious behaviors. Indeed,
API (which stands for Application Programming In-
terface) is a collection of functions supported by the
operating system that allow users to interact with the
system. These API functions are mediators between
programs and their running environment (user data,
network access...) that are mostly used to access or
modify the system by malware authors. According
to a statistic study
2
, over 5TB of different samples of
malwares, there are 527, 992 samples that did import
at least one API, compared to 21, 043 samples with
no import. Thus, API functions and their usages in
the program are crucial to specify malicious behav-
iors. Let us consider a typical malicious behavior.
(a) (b)
Figure 1: The assembly code fragment of a trojan down-
loader (b) and the API call graph (a).
Figure 1(b) is a fragment of the assembly code of a
trojan downloader. First, the function GetTempPathA
is called. This allows the program to get the loca-
tion of the temporary directory in Windows OS. Then,
the function URLDownloadToFileA is called to down-
load a file to this directory. Finally, this file is exe-
cuted by calling the function CreateProcessA. This
is a typical behavior of a trojan downloader. In order
to represent this behavior we use an API call graph,
which is a graph whose vertices are pairs (n, f ) con-
sisting of an API function f and a control point n,
and whose edges ((n, f ),(n
0
, f
0
)) express that there
is a call to the API function f at the control point
n, followed by a call to the API function f
0
at the
control point n
0
, such that between the calls f and
f
0
, there is no other call to another API function.
Figure 1(a) represents the API call graph of the be-
havior of the trojan downloader. The edge ((n
2
,
GetTempPathA),(n
9
, URLDownloadToFileA)) ex-
presses that at the control point n
2
there is a call to the
function GetTempPathA followed by the call to the
function URLDownloadToFileA at the control point
n
9
. Since the size of such graphs is huge in the case of
malwares, we apply an abstraction to reduce the size
of these graphs by merging vertices corresponding to
the same API function into one vertex associated with
2
http://www.bnxnet.com/
the function name. Such graphs are called abstract
API graphs.
Using this representation, we apply machine
learning techniques on graphs to learn malicious be-
haviors, and detect malwares. Support Vector Ma-
chine (SVM) is one of the most successful techniques
in machine learning. It has been applied to several
fields in pattern recognition including text analysis
and bioinformatics. In this work, we apply Sup-
port Vector Machine based learning techniques for
malware detection. The choice of Support Vector
Machine is motivated by the fact that they are very
suitable for nonvectorial data (graphs in our setting),
whereas the other well-known learning techniques
like artificial neural network, k-nearest neighbor, de-
cision trees, etc. can only be applied to vectorial data.
This SVM method is highly dependent on the choice
of kernels. A kernel is a function which returns sim-
ilarity between data. Standard kernels (including lin-
ear, polynomial, etc) handle vectorial data. However,
for nonvectorial data such as graphs, these kernels be-
come non suitable. That is the reason why we need to
use specific kernels for graphs. In this work, we use
a variant of the random walk graph kernel that mea-
sures graph similarity as the number of common paths
of increasing lengths.
The main contribution of this paper is the application
of graph kernel based learning techniques for mal-
ware detection in a completely static way (no dynamic
analysis). As far as we know, this is the first time that
these techniques are applied for malware detection in
a static manner. We implemented our technique in a
tool and tested it on a dataset of 6291 malwares, that
are collected from Vx Heavens
3
, and obtained encour-
aging results. Our tool can achieve a high detection
rate with only few false alarms (98.93% for detection
rate with 1.24% of false alarms).
Moreover, we show that our techniques are able to
detect several malwares that could not be detected
by well-known and widely used antiviruses such as
Avira, Kaspersky, Avast, Qihoo-360, McAfee, AVG,
BitDefender, ESET-NOD32, F-Secure, Symantec or
Panda.
In this paper, we introduce our graph model in
Section 3. In Section 4, we discuss Support Vector
Machine techniques and the application of graph ker-
nels to our graphs in order to detect malwares. Exper-
iments are given in Section 5.
3
http://vxheavens.org
ICISSP 2017 - 3rd International Conference on Information Systems Security and Privacy
456

2 RELATED WORK
Machine learning techniques were applied for mal-
ware classification in (Schultz et al., 2001; Kolter
and Maloof, 2004; Gavrilut et al., 2009; Tahan et al.,
2012; Khammas et al., 2015). However, all these
works use either a vector of bits (Schultz et al., 2001;
Gavrilut et al., 2009) or n-grams (Kolter and Maloof,
2004; Tahan et al., 2012; Khammas et al., 2015) to
represent a program. Such vector models allow to
record some chosen information from the program,
they do not represent the program’s behaviors. Thus
they can easily be fooled by standard obfuscation
techniques, whereas our API graph representation is
more precise and represents the API call behavior of
programs and can thus resist to several obfuscation
techniques.
(Ravi and Manoharan, 2012) use sequences of API
function calls to represent programs and learn mali-
cious behaviors. Each program is represented by a
sequence of API functions which are captured while
executing the program. (Rieck et al., 2008) uses as
model a string that records the number of occurences
of every function in the program’s runs. Our model
is more precise and more robust than these two rep-
resentations as it allows to take into account several
API function sequences in the program while keep-
ing the order of their execution. Moreover, (Ravi and
Manoharan, 2012) and (Rieck et al., 2008) use dy-
namic analysis to extract a program’s representation.
As said above, our API graph extraction is done in a
static way.
(Christodorescu et al., 2007; Kinable and
Kostakis, 2011; Fredrikson et al., 2010; Macedo
and Touili, 2013; Elhadi et al., 2015) represent pro-
grams using graphs similar to our API call graphs.
(Christodorescu et al., 2007; Fredrikson et al., 2010;
Macedo and Touili, 2013) use graph mining algo-
rithms to compute the subgraphs that belong to mal-
wares and not to benign programs and they assume
that these correspond to malicious behaviors. We do
not make such assumption as two malwares may not
have any common subgraphs. Moreover, (Christodor-
escu et al., 2007; Fredrikson et al., 2010) use dynamic
analysis to compute the graphs, whereas our graph
extraction is made statically. (Kinable and Kostakis,
2011) uses clustering techniques. This approach de-
pends highly on the number of clusters that has to be
provided. The performance degrades if the number
of clusters is not optimal. (Elhadi et al., 2015) uses
graph similarity based on comparison of the longest
common subsequences. Our graph kernels are more
robust since, to compare graphs, we take into account
all paths existing in the graph.
(Nikolopoulos and Polenakis, 2016) use graphs sim-
ilar to our API graphs where each node corresponds
to a group of API function calls. Our graphs are more
precise since we do not group API functions together.
Moreover, (Nikolopoulos and Polenakis, 2016) uses
dynamic analysis to extract graphs, whereas our tech-
niques are static. Furthermore, they define their own
similarity metric to classify malwares whereas we use
the well-known SVM method for malware classifica-
tion.
(Kong and Yan, 2013; Xu et al., 2013) use graphs
where nodes are functions of the program (either API
functions or any other function of the program). Such
representations can easily be fooled by obfuscation
techniques such as function renaming. Moreover,
these works do not use graph kernel based SVM to
classify graphs.
Graph kernel based SVM for malware detection is
used in (Anderson et al., 2011; Wagner et al., 2009).
(Wagner et al., 2009) uses graphs to represent the sys-
tem’s behaviors (system commands, process IDs...)
not the program’s behaviors as we do. This approach
can only be done by dynamic analysis. Moreover,
(Wagner et al., 2009) uses a kind of random walk
graph kernel based SVM to learn malicious behav-
iors. Our random walk graph kernel is more precise
for graph comparison since our kernel takes into ac-
count path lengths in graphs in a more precise way.
As for (Anderson et al., 2011), they use graphs to rep-
resent the order of execution of the different instruc-
tions of the programs (not only API function calls).
Our API graph representation is more robust. Indeed,
considering all the instructions in the program makes
the representation very sensitive to basic obfuscation
techniques. Moreover, (Anderson et al., 2011) uses
graph kernel based SVM to learn malicious behaviors.
They use the Gaussian and spectral kernels which al-
low them to compare the structure of graphs. Our
random walk graph kernel compares the paths of the
graph instead. This allows us to compare the behav-
iors of the programs where a behavior is a sequence
of API functions.
3 BINARY CODE MODELING
Malwares are usually executables, i.e., binary codes.
Thus, we show in this section how to extract an
API call graph from a binary code. Given a binary
code, we apply the disassembly tools IDA Pro (Ea-
gle, 2011), Jakstab (Kinder and Veith, 2008) and
BePum (Nguyen et al., 2013) to extract a control flow
graph (CFG) (a standard representation of programs
in the program analysis community). Then, we use
this CFG to construct an API call graph. Since mal-
Malware Detection based on Graph Classification
457

wares contain a huge number of instructions in their
codes, the obtained API call graphs are huge (more
than 854 vertices in our dataset). Thus, the learn-
ing technique we applied took a lot of time. To be
more efficient, we introduce an abstraction of the API
call graph, called abstract API graph, that consists in
merging the vertices of the API call graph that corre-
spond to the same API function. In this section, we
first recall the definition of a control flow graph, then
we define API call graphs and abstract API graphs,
and show how to compute them from the CFG of the
program.
3.1 Control Flow Graph
A Control Flow Graph (CFG) is a tuple G = (N, I,E),
where N is a finite set of vertices, I is a finite set of
assembly instructions in a program, and E : N × I ×N
is a finite set of edges. Each vertex corresponds to
a control point of the program. Each edge connects
two control points in the program and is associated
with an assembly instruction. An edge (n
1
,i,n
2
) in
E expresses that in the program, the control point n
1
is followed by the control point n
2
and is associated
with the instruction i.
3.2 API Call Graph
Let A be the set of all API functions that are called
in the program. An API call graph is a directed graph
G
api
= (V
api
,E
api
), where V
api
: N × A is a finite set
of vertices and E
api
: (N × A)×(N × A ) is a finite set
of edges. We define the labeling function ` : V
api
→
A such that `((n, f )) = f (the label of a vertex is its
corresponding API function). A vertex (n, f ) means
that at a control point n, a call to the API function f
is made. An edge ((n
1
, f
1
),(n
2
, f
2
)) in E means that
the API function f
2
called at the control point n
2
is
executed after the API function f
1
called at the control
point n
1
. Moreover, between the control points n
1
and
n
2
, there is no call to another API function.
3.3 Abstract API Graph
As the size of the previous graph is quite huge in the
case of malwares, we apply an abstraction to reduce
the size of the API call graphs by merging vertices
corresponding to the same API function in one vertex
associated with the function name, i.e., the vertices
(n
1
, f ), (n
2
, f ), ..., (n
k
, f ) are merged in a single vertex
labeled by the API function f . By doing that, the size
of graphs in our dataset is reduced by about a quarter
while the accuracy is not changed so much. Thus, all
our experiments are made on abstract API graphs (not
on API call graphs).
Given an API call graph G
api
= (V
api
,E
api
), an
abstract API graph is a directed graph G
aapi
=
(V
aapi
,E
aapi
), where V
aapi
⊆ A is a set of vertices,
and E
aapi
is a set of edges. Each vertex is labeled
by an API function. There is an edge ( f
1
, f
2
) ∈ E
aapi
if there exist control points n
1
and n
2
, such that
((n
1
, f
1
),(n
2
, f
2
)) is in G
api
. We define the labeling
function ` : V
aapi
→ A such that `(v) = v for every
v ∈ V
aapi
(the label of a vertex is its corresponding
API function).
4 LEARNING MALICIOUS
BEHAVIORS
In order to detect malicious behaviors, we cast the
problem of malware detection as graph classification.
The goal is to check whether a given unseen data
4
belongs to the positive (malign) or the negative (be-
nign) class. For that purpose, we build a classifier,
that decides about this class membership using a la-
beled training set. The latter includes positive as well
as negative examples.
In what follows, we discuss the application of
kernel-based support vector machines (SVMs) in mal-
ware detection. The choice of SVMs is motivated by
their well established generalization ability in many
pattern classification problems, especially those in-
volving small or mid size training databases. More
importantly, and in contrast to other well known train-
ing algorithms, SVMs are very suitable when han-
dling semi-structured and non-vectorial data (such
as graphs), through the use of well dedicated kernel
functions as shown subsequently.
4.1 Kernel-based Support Vector
Machines
In this section, we recall the basic definitions used
in kernel-based support vector machine training and
show how we apply it for learning malicious behav-
iors. We refer the reader to (Burges, 1998) for a tuto-
rial on this technique.
Let’s consider a collection of training data
{(x
i
,y
i
)}
n
i=1
; with x
i
being a feature in a vector
space and y
i
its class label in {−1,+1}. Support
Vector Machine (SVM) training consists in finding
an optimal classifier (hyperplane), denoted h, that
separates labeled data in {(x
i
,y
i
)}
i
while maximizing
their margin. Considering w as the normal of that
4
Abstract API graph associated to a new program
ICISSP 2017 - 3rd International Conference on Information Systems Security and Privacy
458

hyperplane h, the SVM decision function of h can be
written as
h(x) = w
|
x + b, (1)
here x
|
stands for the transpose of x, w =
∑
n
i=1
α
i
y
i
x
i
(with {α
i
}
i
being the SVM training parameters) and
b is a shift. When training data are linearly separable,
the hyperplane h guarantees that y
i
(w
|
x
i
+ b) ≥ 1,
∀i ∈ {1, .. ., n}.
In the context of graph classification, the train-
ing set corresponds to {(G
i
,y
i
)}
i
with G
i
being an
abstract API graph and y
i
= +1 if G
i
is malign and
y
i
= −1 otherwise. As graphs are non-vectorial data,
we consider a function φ(.) which maps graphs into a
high dimensional vector space (denoted H ) that also
guarantees the linear separability of training data. Us-
ing φ, the decision function h, associated to graphs,
can be written as
h(G) = w
|
φ(G)+ b =
n
∑
i=1
α
i
y
i
hφ(G
i
),φ(G)i +b, (2)
where w =
∑
n
i=1
α
i
y
i
φ(G
i
) and hφ(G
i
),φ(G)i defines
an inner product. Instead of φ, one may use the in-
ner product hφ(G
i
),φ(G)i and this defines a kernel
function (denoted κ(G
i
,G)). Conversely, a symmet-
ric function κ defines an inner product, in some H , iff
κ is positive semi-definite(Vishwanathan et al., 2010).
With this kernel definition, Equation 2 can be rewrit-
ten as
h(G) =
n
∑
i=1
α
i
y
i
κ(G
i
,G) + b. (3)
Using (3) and a threshold τ, a given graph G is as-
signed to the malicious (resp. benign) class iff h(G) ≥
τ (resp. h(G) < τ) for τ ∈ R (see Figure 4 for results
w.r.t. different values of τ). The value of h(G) is also
seen as a confidence score of a given sample G w.r.t
the positive class.
In the remainder of this section, we define the ker-
nel function κ (used in SVMs) that implicitly maps
non-vectorial data (particularly graphs) into a high
dimensional vector space H ; this guarantees the lin-
ear separability of data in the mapping space H and
also provides a relevant similarity measure between
graphs in order to achieve malicious behavior detec-
tion and recognition effectively.
4.2 Random Walk Graph Kernel
Given two graphs G = (V, E) and G
0
= (V
0
,E
0
), the
random walk graph kernel (RDW) – introduced in
(G
¨
artner et al., 2003) – defines a similarity κ(G, G
0
),
as the number of common walks in their product
graph G
×
. The latter is a graph over pairs of
vertices from G and G
0
; two vertices in G
×
are
connected by an edge iff the corresponding ver-
tices in G and G
0
are both connected. More for-
mally, the product graph G
×
= (V
×
,E
×
) is defined
as V
×
= {(v, v
0
)|v ∈ V and v
0
∈ V
0
: `(v) = `(v
0
)}
and E
×
= {((v, v
0
),(w,w
0
))|(v,w) ∈ E,(v
0
,w
0
) ∈ E
0
:
`(v) = `(v
0
) and `(w) = `(w
0
)}, here ` is a label-
ing function
5
.
With this product graph, RDW is defined as
κ(G,G
0
) :=
T
∑
k=0
µ(k)q
|
×
A
k
×
p
×
, (4)
here
A
×
is the adjacency matrix of the product graph G
×
and A
k
×
is recursively defined as A
k
×
= A
k−1
×
A
×
,
p
×
(resp. q
×
) is a vector with as many entries as ver-
tices in G
i
(resp. G
j
). which characterizes the acces-
sibility of vertices in G
i
(resp. G
j
). In practice, p
×
and q
×
are set to uniform distributions, T is the max-
imum length of a random walk,
µ(k) = λ
k
∈ [0, 1] is a coefficient that controls the im-
portance of the length in random walks.
As a vertex in the product graph G
×
corresponds to
a pair of vertices (with the same API function) in the
call graphs G
i
, G
j
, a path (with any length k ≥ 0) in
G
×
represents a sequence of common API calls that
appears in both graphs G
i
and G
j
; this characterizes
a common behavior occurring in the two underlying
programs. With this RDW kernel, the similarity be-
tween training and test data is well captured as shown
through SVM classification experiments in the fol-
lowing section.
5 EXPERIMENTS
5.1 Dataset and Evaluation Measures
In order to evaluate the performance of our kernel-
based SVMs, we collect a dataset of 6291 malware
samples from Vx Heavens and 2323 benign programs
from system files and applications in Windows OS
and Cygwin. The proportion of malware categories
is shown in Figure 2. The dataset randomly split
into two partitions, a training and a testing partition.
For training partition, the quantity of malwares and
benign programs is balanced with 2000 samples for
each. The testing set consists of 4291 malwares and
323 benign programs. In order to capture the variabil-
ity of the dataset, we use 5 random splits of training
and test data, then we take the average of the perfor-
mances. Computing the kernel matrix for the whole
5
In the context of the abstract API graph, the label of a
vertex is an API function.
Malware Detection based on Graph Classification
459

dataset of 8614 graphs takes 3 days, but this is an of-
fline computation. Online computation to classify a
new program with size 15 KB takes 15 seconds.
Figure 2: The malware distribution in the dataset, showing
the percentage of different categories with respect to the to-
tal number of malware files.
Using this dataset, we consider two subtasks for eval-
uation.
• Malware detection. This is the principal task of
our contribution. We train a single monolithic
SVM classifier (h) using positive and negative
data in the training set. This classifier h is used
in order to check whether a given test graph G be-
longs to the malign (positive) or benign (negative)
class depending on the sign of h(G), i.e., τ = 0.
• Malware category recognition. As a secondary
task, the goal is to recognize the category of a
given malign graph G. For that purpose, we train
for each category (denoted c), a “one-versus-all”
SVM classifier h
c
that separates graphs belonging
to the c
th
category from all others. Given a test
graph G with h(G) ≥ 0, the category of G corre-
sponds to argmax
c
h
c
(G).
In both tasks, we plug the RDW kernel in SVMs and
we use the widely known library (LIBSVM)(Chang
and Lin, 2011) for SVM training.
We evaluate the performance of our SVM classi-
fiers (h and {h
c
}
c
) using well known measures: true
positive and false positive rates respectively defined
as TPR = TP/(TP + FN) and FPR = FP/(TN + FP);
here TP, TN, FP, FN respectively denote true pos-
itives, true negatives, false positives and false nega-
tives obtained after SVM classification. We also re-
port BCR (balanced correctness rate) as one minus
the average between false positive and false negative
rates (BCR = 1 − (FPR + FNR)/2) where the false
negative rate FNR = FN/(FN + TN). Finally, we re-
port the overall accuracy ACC = (TP + TN)/(TP +
TN +FP + FN). For all these measures, higher values
of TPR, BCR, ACC (with small values of FPR) imply
better performances.
5.2 Performances and Comparison
Performances of Malware Detection. Firstly, we
measure the performance of the RDW kernel (com-
(a) (b)
Figure 3: This diagram shows the evolution of the Accuracy
w.r.t λ (a) and T (b) in the RDW kernel.
bined with SVM) w.r.t different walk lengths (i.e.,
w.r.t parameter T in Eq. 4) and different values of
coefficient λ to control the importance of the length
in random walks in µ(k) = λ
k
of Eq. 4. Figure 3(a)
shows that the classification accuracy ACC increases
as λ increases from 0.2 to 0.8, then it decreases af-
ter reaching the max value at λ = 0.8. Figure 3(b)
shows that as T increases, the classification accuracy
ACC increases and stabilizes when T reaches 5 ran-
dom walks. Following these results, T is fixed to 5
and λ is fixed to 0.8 in all the remaining experiments;
with this setting, detection rates (TPR), reported in
Table 1 reach 98.93%, with a false positive rate FPR
of 1.24%.
Table 1: This table shows the performances of RDW kernel.
We obtain these results by averaging the results of 5 runs,
each run corresponds to a random split of the dataset into
training and test data.
TP TN FP FN TPR FPR ACC
4245 319 4 46 98.93% 1.24% 98.91%
Figure 4: This figure shows true positive rates vs. false
positive rates of our method and its comparison against
the two baseline kernels: structured histogram intersection
and convolution kernels (referred to as His012 and Con).
These results show that RDW achieves the best true positive
rate (around 99% with a small FPR; around 1%) compared
to histogram intersection and convolution kernels (which
achieve a TPR of 98%).
Secondly, we compare the performance of the RDW
kernel against two widely used baseline kernels for
graph comparison: (i) convolution kernel and (ii)
structured histogram intersection kernel. Given two
graphs G = (V,E) and G
0
= (V
0
,E
0
), the convolu-
ICISSP 2017 - 3rd International Conference on Information Systems Security and Privacy
460
tion kernel introduced in (Haussler, 1999) for semi-
structured data (including graphs), is defined as
κ(G,G
0
) =
1
|V |×|V
0
|
∑
v∈V
∑
v
0
∈V
0
1
{`(v)=`(v
0
)}
, here 1
{}
corresponds to the indicator function.
The second baseline kernel – structured histogram in-
tersection – is defined as
κ(G,G
0
) = κ
0
(G,G
0
) + κ
1
(G,G
0
) + κ
2
(G,G
0
), (5)
here κ
0
(G,G
0
), κ
1
(G,G
0
) and κ
2
(G,G
0
) correspond to
standard histogram intersection kernels associated to
cliques of order 0, 1 and 2 respectively (i.e., vertices,
edges and connected subgraphs with 3 vertices). Fol-
lowing (Barla et al., 2003; Maji et al., 2008), these
three kernels are defined as
κ
0
(G,G
0
) =
∑
L
i=1
min(g
0
(G,`
i
),g
0
(G
0
,`
i
))
κ
1
(G,G
0
) =
∑
L
i, j=1
min(g
1
(G,`
i
,`
j
),g
1
(G
0
,`
i
,`
j
))
κ
2
(G,G
0
) =
∑
L
i, j,k=1
min(g
2
(G,`
i
,`
j
,`
k
),g
2
(G
0
,`
i
,`
j
,`
k
)),
(6)
here L is |A|, i.e., is the number of API functions in
the program. g
0
(G,`
i
) is the probability of occurrence
of label `
i
in G, i.e., g
0
(G,`
i
) =
1
|V |
∑
v∈V
1
{`(v)=`
i
}
.
Similarly, g
1
(G,`
i
,`
j
) (resp. g
2
(G,`
i
,`
j
,`
k
)) corre-
sponds to the probability of occurrence of edges with
labels (`
i
,`
j
) (resp. connected triplet of vertices with
labels (`
i
,`
j
,`
k
)).
Figure 4 shows the evolution of the true positive rate
(TPR) and the false positive rate (FPR) w.r.t. different
and increasing values of τ, taken from min to max
value of h(G), i.e., τ ∈ [−4,6]. The interesting part of
these diagrams corresponds to small values of FPR;
indeed, for reasonably small and comparable FPRs,
our method based on the RDW kernel has high TPRs
and it clearly overtakes the convolution kernel as well
as structured histogram intersection kernel.
Performances of Malware Category Recognition.
Again, given a graph G (with h(G) ≥ 0), the goal is to
assign it to one of 13 malware categories (Backdoor,
Email-Worm, Exploit, P2P-Worm, Trojan, Trojan-
Clicker, Trojan-Downloader, Trojan-Dropper, Trojan-
Proxy, Trojan-PSW, Trojan-Spy, Virus and Worm)
based on argmax
c
h
c
(G) (thanks to Equation 3). Fig-
ure 5 shows the classwise TPR, Accuracy and BCR
rates of our RDW kernel and its comparison against
the two other baseline kernels.
Comparison with Well-known Antiviruses. We
compare the performance of our method with dif-
ferent existing antiviruses including Avira, Kasper-
sky, Avast, Qihoo-360, McAfee, AVG, BitDefender,
ESET-NOD32, F-Secure, Symantec and Panda. Since
known antiviruses update their signature database as
soon as a new malware is known, in order to have
a fair comparision with these antiviruses, we need to
consider new malwares. For this, we use three gener-
ators to create new malwares: NGVCK, RCWG and
(a)
(b)
(c)
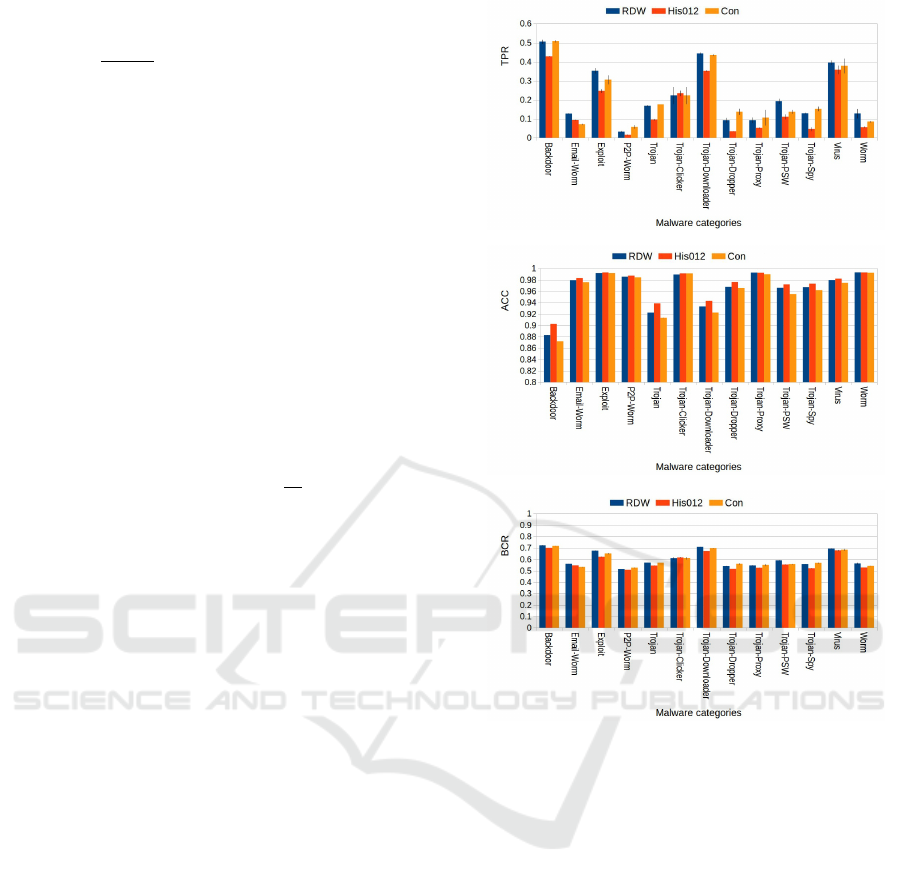
Figure 5: This figure shows class-by-class malware cate-
gory recognition performances of our RDW-based method
and the two other baselines kernels on 13 malware cate-
gories. Fig. (a), (b) and (c) show detection rate (TPR), ac-
curacy and balanced correctness rate (BCR) for each mal-
ware category and their variances. Our method reaches a
BCR of 60% while histogram intersection and convolution
kernels obtain 58% and 59% respectively. Results are aver-
aged over five experimental runs.
VCL32. The latter are able to create sophisticated
malwares with morphing code and other features to
avoid being detected by antiviruses. In total, we
generate 180 new malwares by RCWG, VCL32 and
NGVCK generators. After training our SVM classi-
fier on the training set, we are able to detect 100%
of new malwares while none of the well known an-
tiviruses can detect all of them. The results are shown
in Table ??.
Malware Detection based on Graph Classification
461

Table 2: This table shows a comparison of our method
against well-known antiviruses. Our tool achieves a detec-
tion rate of 100%.
Antivirus Detection Rates Antivirus Detection Rates
Our tool 100% Panda 19%
Avira 16% Kaspersky 81%
Avast 87% Qihoo-360 96%
McAfee 96% AVG 82%
BitDefender 87% ESET-NOD32 87%
F-Secure 87% Symantec 14%
6 CONCLUSION
The main contribution of this paper is the applica-
tion of graph kernel based learning techniques for
malware detection in a completely static way (no dy-
namic analysis). As far as we know, this is the first
time that these techniques are applied for malware
detection in a static manner. We introduced an auto-
matic malware detection algorithm based on SVMs.
First, we use static analysis in order to create ab-
stract API graphs from control flow graphs. Then, we
build SVMs that learn the malicious behaviors from
these API graphs and achieve malware detection and
recognition. These SVMs are built upon a well ded-
icated random walk graph kernel (RDW) that mea-
sures graph similarity as the number of common paths
of increasing lengths and characterizes common ma-
licious behaviors through training and test data. The
use of this kernel is clearly appropriate as it allows us
to handle non-vectorial data (i.e., graphs) without any
explicit generation of features on these graphs. Exper-
iments show that our RDW-based classifier achieves
a TPR of almost 99% with only 1.24% FPR for mal-
ware detection and an accuracy of 96.55% for mal-
ware category recognition. Compared to other ker-
nels (such as histogram intersection and convolution),
our RDW based method obtains the best classification
performances.
Note that we could have extracted vectorial features
from graphs and then applied other learning tech-
niques such as ANNs, but this would have led to loss
of information. Thus, we believe that applying graph
kernel based SVMs is the best choice to learn our ma-
licious behavior graphs.
REFERENCES
Anderson, B., Quist, D., Neil, J., Storlie, C., and Lane,
T. (2011). Graph-based malware detection using
dynamic analysis. Journal in Computer Virology,
7(4):247–258.
Babi
´
c, D., Reynaud, D., and Song, D. (2011). Malware
analysis with tree automata inference. CAV’11.
Barla, A., Odone, F., and Verri, A. (2003). Histogram inter-
section kernel for image classification. In ICIP 2003.
Bergeron, J., Debbabi, M., Erhioui, M., and Ktari, B.
(1999). Static analysis of binary code to isolate mali-
cious behaviors. In WET ICE ’99.
Burges, C. J. C. (1998). A tutorial on support vector ma-
chines for pattern recognition. Data Min. Knowl. Dis-
cov., 2(2).
Chang, C.-C. and Lin, C.-J. (2011). Libsvm: A library for
support vector machines. ACM Transactions on Intel-
ligent Systems and Technology, 2. Software available
at http://www.csie.ntu.edu.tw/ cjlin/libsvm.
Christodorescu, M. and Jha, S. (2003). Static analysis of
executables to detect malicious patterns. SSYM’03.
Christodorescu, M., Jha, S., and Kruegel, C. (2007). Mining
specifications of malicious behavior. ESEC-FSE ’07.
ACM.
Eagle, C. (2011). The IDA Pro Book. No Starch Press, 2nd
edition.
Elhadi, E., Maarof, M. A., and Barry, B. (2015). Improving
the detection of malware behaviour using simplified
data dependent api call graph.
Fredrikson, M., Jha, S., Christodorescu, M., Sailer, R., and
Yan, X. (2010). Synthesizing near-optimal malware
specifications from suspicious behaviors. SP ’10.
G
¨
artner, T., Flach, P., and Wrobel, S. (2003). On graph
kernels: Hardness results and efficient alternatives. In
Learning Theory and Kernel Machines.
Gavrilut, D., Cimpoesu, M., Anton, D., and Ciortuz, L.
(2009). Malware detection using perceptrons and sup-
port vector machines. In 2009 Computation World:
Future Computing, Service Computation, Cognitive,
Adaptive, Content, Patterns. IEEE.
Haussler, D. (1999). Convolution kernels on discrete struc-
tures.
Khammas, B. M., Monemi, A., Bassi, J. S., Ismail, I., Nor,
S. M., and Marsono, M. N. (2015). Feature selection
and machine learning classification for malware de-
tection. Jurnal Teknologi, 77.
Kinable, J. and Kostakis, O. (2011). Malware classification
based on call graph clustering. J. Comput. Virol., 7(4).
Kinder, J., Katzenbeisser, S., Schallhart, C., and Veith, H.
(2010). Proactive detection of computer worms using
model checking. Dependable and Secure Computing,
IEEE Transactions on, 7(4).
Kinder, J. and Veith, H. (2008). Jakstab: A static analy-
sis platform for binaries. In Gupta, A. and Malik, S.,
editors, Computer Aided Verification, volume 5123.
Kolter, J. Z. and Maloof, M. A. (2004). Learning to detect
malicious executables in the wild. KDD ’04.
Kong, D. and Yan, G. (2013). Discriminant malware dis-
tance learning on structural information for automated
malware classification. In Proceedings of the 19th
ACM SIGKDD international conference on Knowl-
edge discovery and data mining.
Macedo, H. and Touili, T. (2013). Mining malware spec-
ifications through static reachability analysis. In ES-
ORICS 2013.
ICISSP 2017 - 3rd International Conference on Information Systems Security and Privacy
462

Maji, S., Berg, A., and Malik, J. (2008). Classification us-
ing intersection kernel support vector machines is ef-
ficient. In CVPR 2008.
Nguyen, M. H., Nguyen, T. B., Quan, T. T., and Ogawa,
M. (2013). A hybrid approach for control flow graph
construction from binary code. In APSEC 2013, vol-
ume 2.
Nikolopoulos, S. D. and Polenakis, I. (2016). A graph-
based model for malware detection and classification
using system-call groups. Journal of Computer Virol-
ogy and Hacking Techniques, pages 1–18.
Ravi, C. and Manoharan, R. (2012). Malware detection us-
ing windows api sequence and machine learning. In-
ternational Journal of Computer Applications, 43.
Rieck, K., Holz, T., Willems, C., Dussel, P., and Laskov, P.
(2008). Learning and classification of malware behav-
ior. DIMVA ’08.
Schultz, M., Eskin, E., Zadok, E., and Stolfo, S. (2001).
Data mining methods for detection of new malicious
executables. In S P 2001.
Song, F. and Touili, T. (2013a). Ltl model-checking for mal-
ware detection. In Piterman, N. and Smolka, S., ed-
itors, Tools and Algorithms for the Construction and
Analysis of Systems, volume 7795.
Song, F. and Touili, T. (2013b). Pommade: Pushdown
model-checking for malware detection. ESEC/FSE
2013.
Tahan, G., Rokach, L., and Shahar, Y. (2012). Mal-id:
Automatic malware detection using common segment
analysis and meta-features. J. Mach. Learn. Res.,
13(1).
Vishwanathan, S. V. N., Schraudolph, N. N., Kondor, R.,
and Borgwardt, K. M. (2010). Graph kernels. J. Mach.
Learn. Res., 11.
Wagner, C., Wagener, G., State, R., and Engel, T. (2009).
Malware analysis with graph kernels and support vec-
tor machines. In MALWARE 2009. IEEE.
Xu, M., Wu, L., Qi, S., Xu, J., Zhang, H., Ren, Y., and
Zheng, N. (2013). A similarity metric method of ob-
fuscated malware using function-call graph. Jour-
nal of Computer Virology and Hacking Techniques,
9(1):35–47.
Malware Detection based on Graph Classification
463
