
Distributed In-network Processing of k-MaxRS in Wireless Sensor
Networks
Panitan Wongse-ammat
1
, Muhammed Mas-ud Hussain
1
, Goce Trajcevski
1
,
Besim Avci
1
and Ashfaq Khokhar
2
1
Department of Electrical Engineering and Computer Science, Northwestern University, Evanston, U.S.A.
2
Department of Electrical and Computer Engineering, Illinois Institute of Technology, Chicago, U.S.A.
Keywords:
k-MaxRS, Maximizing Range Sum, Distributed Query Processing, Wireless Sensor Networks.
Abstract:
We address the problem of in-network processing of k-Maximizing Range Sum (k-MaxRS) queries in Wireless
Sensor Networks (WSN). The traditional, Computational Geometry version of the MaxRS problem considers
the setting in which, given a set of (possibly weighted) 2D points, the goal is to determine the optimal location
for a given (axes-parallel) rectangle R to be placed so that the sum of the weights (or, a simple count) of the
input points in R’s interior is maximized. In WSN, this corresponds to finding the location of region R such
that the sum of the sensors’ readings inside R is maximized. The k-MaxRS problem deals with maximizing
the overall sum over k such rectangular regions. Since centralized processing – i.e., transmitting the raw read-
ings and subsequently determining the k-MaxRS in a dedicated sink – incur communication overheads, we
devised an efficient distributed algorithm for in-network computation of k-MaxRS. Our experimental obser-
vations show that the novel algorithm provides significant energy/communication savings when compared to
the centralized approach.
1 INTRODUCTION
Wireless Sensor Networks (WSN) consist of hun-
dreds, or even thousands of nodes capable of sensing
particular set of phenomena, performing basic com-
putations and, most importantly, communicating with
each other (Akyildiz et al., 2002). They are the em-
powering technology for a wide range of applications
including environmental monitoring, smart buildings
and cities, safety and hazard detection, agriculture,
medicine, military, traffic monitoring, etc. Due to the
types of sensors used and/or various deployment con-
straints (e.g., harsh and inaccessible environments),
re-charging nodes’ batteries is not always feasible.
Consequently, reducing the energy consumption is an
ever-important topic in WSN, facilitating an exten-
sion of overall network’s operational lifetime (Anas-
tasi et al., 2009). While periodic sampling and trans-
mission to a dedicated base-station may be applica-
ble for certain applications, they may incur signifi-
cant overhead in others – especially in event-based
monitoring and tracking. To minimize communi-
cation overheads, various works have tackled cou-
pling of routing schemes with aggregation and in-
network query processing (Fasolo et al., 2007; Krish-
namachari et al., 2002; Trigoni and Krishnamachari,
2012; Madden et al., 2005).
In this work, we take a first step towards providing
a distributed, energy-efficient solution in WSN set-
tings, to the problem known as (k-)MaxRS – which
can be described as follows. Given a collection of
weighted objects O and a rectangle R with fixed di-
mensions (i.e., d
1
× d
2
), the Maximizing Range Sum
(MaxRS) query retrieves the location at which (the
centroid of) R should be placed, so that the sum of
the weights of the objects in its interior is maximized.
In the context of WSNs, we can think of the set of
sensor nodes as the set of weighted objects, where
the “weights” are application dependent, e.g., mote
readings (event monitoring), information gain (track-
ing an object), uniform (counting), etc. We note that
MaxRS is rather different from the traditional range
query in the sense that when processing a range query,
the region is typically fixed and one is interested in
properties that hold in its interior. Contrary to this,
MaxRS determines where should a rectangle with
given dimensions be placed, so that some “interest-
ing” properties in its interior are maximized (modulo
all the other possible placements). An instance of the
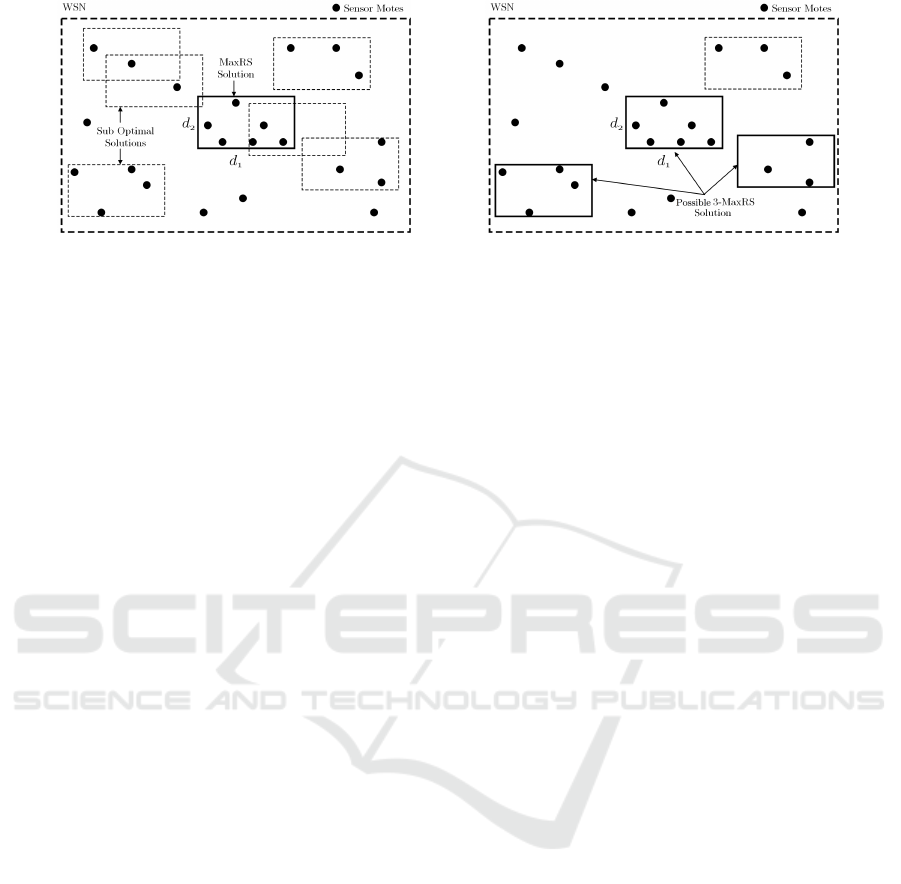
MaxRS in WSN is shown in Figure 1(a), assuming
108
Wonge-ammat P., Mas-ud Hussain M., Trajcevski G., Avci B. and Khokhar A.
Distributed In-Network Processing of k-MaxRS in Wireless Sensor Networks.
DOI: 10.5220/0006210701080117
In Proceedings of the 6th International Conference on Sensor Networks (SENSORNETS 2017), pages 108-117
ISBN: 421065/17
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
(a) (b)
Figure 1: An example of (a) MaxRS and (b) k-MaxRS problem in WSN.
that the weights of all the sensor nodes are uniform –
i.e., the “counting” variant.
Consider the following query:
Q1: “Where should we place k surveillance devices
(e.g., cameras, checkpoints, etc.) with a fixed-size
coverage region in a forest such that their cumula-
tive monitoring of forest-fire vulnerable regions (i.e.,
regions where temperature and light sensor readings
are higher) is maximized?”.
It is not hard to adapt Q1 to other applications
in which a simultaneous detection of top-k “popu-
lar” regions (k ≥ 2) may be of interest. Such ex-
amples are: discerning k herds of tracked animals
(e.g., gazelles) with largest density; aiding trans-
portation system management by identifying k re-
gions of the city with heaviest traffic; detecting con-
gestions/hotspots in WSN by setting a node’s cur-
rent incoming/outgoing network traffic as its weight.
One can also readily extrapolate to various collabora-
tive scenarios – e.g., guiding drones towards regions
where certain phenomenon has the largest weighted
sum. To the best of our knowledge, the existing solu-
tions (Hussain et al., 2015) to MaxRS queries in WSN
can only be applied to retrieve an optimal location for
a single rectangle R, whereas Q1 is an instance of the
k-MaxRS variant – which we tackle in this work.
The respective k-MaxRS query finds the
placement-locations for k rectangles such that
the weighted sums of all the objects in the (union of
the) interiors of each of R placed at those locations are
optimal. An example-solution of the k-MaxRS query
in WSN for uniformly weighted nodes is illustrated
in Figure 1(b) (k=3). Although the MaxRS problem
has been addressed by both computational geometry
and spatial databases communities (Choi et al., 2012;
Choi et al., 2014; Imai and Asano, 1983; Nandy and
Bhattacharya, 1995), to the best of our knowledge,
there has been no solution considering k optimal
placements in WSN settings. As mentioned, in
WSNs it is paramount to have energy-efficient query
processing, for which in-network aggregation of
partial results is often the approach of choice (Fasolo
et al., 2007; Krishnamachari et al., 2002). Another
challenge in this scenario is that the weights (i.e.,
sensor readings, information gain, etc.) of the sensor
nodes may change with time, although their locations
are fixed.
The main contribution of this paper can be sum-
marized as follows:
• We provide an efficient in-network distributed algo-
rithm to compute k-MaxRS via a hierarchy of clusters.
• We provide effective data-sharing schemes among
the cluster-heads (also called principals).
• We provide experimental observations quantifying
the benefits of the proposed approach.
The rest of the paper is organized as follows: Sec-
tion 2, introduces the necessary technical background
and presents the formal description of the k-MaxRS
problem. In Section 3, we discuss in details the pos-
sible centralized approaches and the different compo-
nents of our distributed solutions. Section 4 presents
the quantitative observations of the benefits of our ap-
proaches and Section 5 positions this work with re-
spect to the related literature. We conclude the paper
and outline directions for future work in Section 6.
2 PRELIMINARIES
We now introduce the basic notation, followed with
an overview of the MaxRS problem and formal
definition of the k-MaxRS query in WSN. We also
briefly describe the existing solutions for the MaxRS
problem to better motivate the algorithms and imple-
mentations proposed in this paper.
We assume a WSN covering an area
A
W SN
= l × w and consisting of n nodes, i.e.,
WSN = {sn
1
,sn
2
,. .. ,sn
n
}, where each sn
i
is
equipped with whatever sensors are appropriate for
the phenomena of interest for a given application.
In addition, we also assume that the WSN is dense
Distributed In-Network Processing of k-MaxRS in Wireless Sensor Networks
109

enough to ensure a coverage (i.e., every location in
A
W NS
is within the sensing range of at least one node)
and connectivity (i.e., every two nodes sn
i
and sn
j
can communicate with each other either directly or
via multiple hops).
MaxRS: Let C(p,R) denote the region covered by R
centered at a particular point p. We have:
Definition 1. (MaxRS) Given a set of n points O =
{o
1
,o
2
,. .. o
n
}, and each o
i
associated with a weight
w
i
, the MaxRS query retrieves a position p within the
given space for an isothetic rectangle R of size d
1
×d
2
such that
∑
{o
i
∈ O ∩C(p,R)}
w
i
is maximal.
In case of ties, one position is selected arbitrarily
as the MaxRS solution. Without loss of general-
ity, we assume that the set of points/objects O =
{o
1
,o
2
,. .. ,o
n
} coincides with the set of nodes in the
WSN = {sn
1
,sn
2
,. .. ,sn
n
}. The weight(s) associated
with a sensor node can be determined based on the
various readings, as needed by a specific application.
k-MaxRS: Let Interior(p,R,O) denote a function that
returns the subset of objects from O contained within
R, when the centroid of R is placed at a given point p.
Definition 2. (k-MaxRS) Given a set of n points O
= {o
1
,o
2
,. .. o
n
}, each o
i
associated with a weight w
i
,
and an integer k ≥ 2, the k-MaxRS problem finds a
set of locations P = {p
1
, p
2
,. .. p
k
} for the centroids
of k isothetic rectangles R
1
, R
2
,. .. , R
k
, each of size
d
1
× d
2
such that:
1. For each p
i
∈ P,
∑
{o
j
∈ O ∩C(p
i
,R
i
)}
w
j
≥
∑
{o
j
∈ O ∩C(p
0
,R
i
)}
w
j
, ∀p
0
/∈ P
2. Interior(p
i
,R, O) ∩ Interior(p
j
,R, O) =
/
0,
∀p
i
, p
j
∈ P and p
i
6= p
j
The second condition of the definition ensures
that there are no overlapping objects between any
two top-k solutions of the k-MaxRS problem. We
note that, just like in the case of MaxRS, there can
also be multiple possible solutions for the k-MaxRS
problem as shown in Figure 1(b) – another rectangle
(dashed) can also be taken as part of the solution, in
place of the bottom right one.
In-memory MaxRS Solution: To compute MaxRS
for static objects with fixed weights, the problem is
initially transformed into a “dual” rectangle intersec-
tion problem as follows (cf. (Nandy and Bhattacharya,
1995)). For simplicity, let us consider the counting
variant of the MaxRS problem here. We first draw a
rectangle of size d
1
× d
2
centered at each of the ob-
jects in O. R covers o
i
if and only if its center is in
the interior of the dual rectangle of o
i
. Thus a rect-
angle covering the maximum number of objects can
be centered at any location within the maximum in-
tersecting region of the dual rectangles. Using the
findings of (Imai and Asano, 1983) and this trans-
formation, (Nandy and Bhattacharya, 1995) provided
an in-memory algorithm to solve the MaxRS problem
in O(n logn) time. Considering the top and bottom
edges of the rectangles as horizontal intervals, an in-
terval tree – i.e., a binary tree on the intervals – is con-
structed, and subsequently a horizontal line is swept
in a bottom-up manner. The algorithm maintains the
count for each interval currently residing in the tree,
where the count of an interval represents the num-
ber (or, the sum of weights) of overlapping rectangles
within that interval. An interval with the maximum
count during the whole sweeping process is the final
solution.
3 PROCESSING k-MaxRS
We start this section with presenting two techniques to
compute k-MaxRS in centralized settings: Object Re-
moval Method (ORM) and List Method (LM). This
is followed by the details of our proposed in-network
algorithm for processing k-MaxRS that employs clus-
tering, routing, and data-aggregation schemes.
3.1 Centralized Algorithms for
k-MaxRS Processing
Objects Removal Method (ORM): The sim-
ple/intuitive idea behind this method is to use the
MaxRS algorithm (Nandy and Bhattacharya, 1995) it-
eratively k times, as follows:
1. Execute the MaxRS procedure over the current set
of objects, and retrieve the optimal location p for
the query rectangle R.
2. Set the current set of objects to be O −
Interior(p,R).
After performing steps (1) and (2) k times and
storing the solution from each iteration, we can
obtain the answer-set to the k-MaxRS problem. Since
MaxRS solution in (Nandy and Bhattacharya, 1995)
takes O(n log n) time, the overall complexity of this
technique is O(kn logn).
List Method (LM): This is a modified plane-sweep
procedure based on (Nandy and Bhattacharya, 1995),
where each internal node v of the interval tree main-
tains a field target – pointing to the interval with max-
imum count within the sub-tree rooted at v itself. To
compute k-MaxRS, we maintain an answer-set of size
k during the whole plane-sweep procedure. Whenever
SENSORNETS 2017 - 6th International Conference on Sensor Networks
110
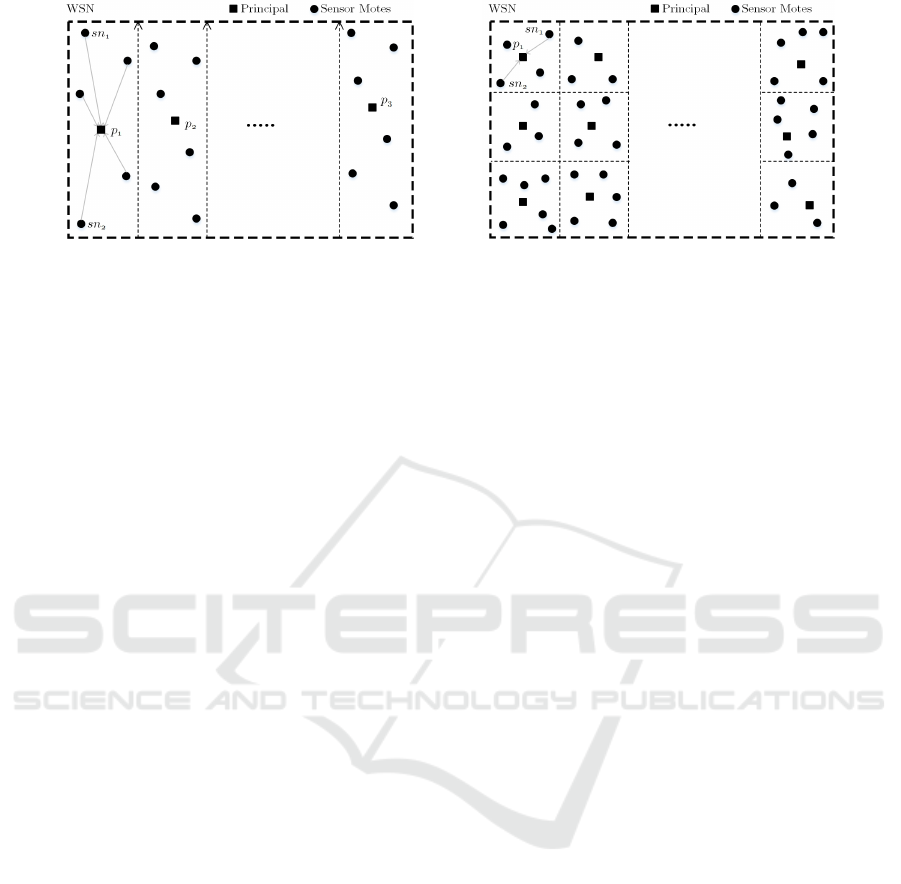
(a) (b)
Figure 2: Different types of clustering schemes: (a) vertical slabs (b) m × n grids.
a new interval (a.k.a. window) is added to or removed
from the tree, the target pointers of the affected in-
ternal nodes are updated accordingly. When an inter-
val is inserted/deleted – only a subset of the interval
tree is affected (all the nodes in path F
IN
, F
L
, and F
R
– cf. (Nandy and Bhattacharya, 1995)). Thus, after
insertion/deletion of an interval, the answer-set is up-
dated by comparing with the target values of these af-
fected nodes only. All such nodes can be traversed in
O(logn) time, and O(k) time is needed to update the
answer-set for a changed target value. The processing
time of a single plane-sweep event is thus O(k log n).
As there are O(n) events (2 for each rectangles, i.e.,
top and bottom edges), the time-complexity of this al-
gorithm is O(kn logn).
Additionally, suppose two intervals I
i
and I
j
over-
lap, and count(I
i
) ≥ count(I
j
). In such cases, I
j
would
be discarded from the answer-set even if its count puts
it in the top-k (due to violation of condition 2 of Def-
inition 2). Note that, we maintain a hash-table, dict,
where a key is an interval and corresponding value is
a set of intervals that have been discarded from con-
sideration due to overlapping with the key interval. If
we consider the previous example, one of the <key,
value> pair of the dict table will be < I
i
, {I
j
} >. This
aids us in retrieving the interval I
j
back, if later I
i
itself
is discarded for overlapping with another interval of
higher count. As we use a hash-table (i.e., amortized
access cost of O(1)), this does not affect the overall
time-complexity.
Extension & Comparison
Both LM and ORM can be used to process k-MaxRS
in WSN in a na
¨
ıve manner, i.e., all the sensed values
(or, current weights) are transmitted to the sink (di-
rectly or via multi-hop transmission), where the sink
can use either of the two techniques to compute cur-
rent MaxRS solution. ORM has two significant pit-
falls:
• Firstly, it can still produce answer-sets violating
condition 2 of Definition 2.
• Secondly, and more importantly, for some degen-
erated cases, it can produce sub-optimal k-MaxRS
answer-sets.
Regardless of these, though, any centralized process-
ing which takes place in a dedicated sink incurs a sig-
nificant communication overhead.
3.2 Distributed Algorithm for k-MaxRS
Processing
The basic idea behind our proposed in-network pro-
cessing is: (1) Divide the whole network into sub-
networks (clusters); (2) Localize the computation pro-
cess within the clusters; and (3) Execute a data ag-
gregation scheme between neighboring clusters – the
details of which we present in the sequel.
Geographical Clustering
In (Choi et al., 2014), a distributed solution to
the MaxRS problem was devised for large spatial
databases, extending the idea of the in-memory algo-
rithms to the settings in which data resides on a sec-
ondary storage. The work aimed at reducing the num-
ber of I/O’s – and the main idea was centered around
dividing the space into m vertical slabs along the X -
dimension, until the number of rectangles in a slab
can fit in the main memory. For each slab, a variant
of the in-memory sweep-line algorithm is performed
and the results are saved in a slab file. Finally, all the
local slab files are merged into one solution slab file.
Although the idea works well in spatial databases con-
text, its straightforward extension is not well-suited in
case of WSN. A vertical subdivision of a sensor net-
work (similar to (Choi et al., 2014)) is presented in
Figure 2(a). Each such slab (cluster) is assigned a
local principal (similar to cluster-heads), which is in
charge of gathering the raw data (i.e., weights) from
all the nodes in the interior of its own slab. As the
sensor field can be of a large size in both length and
width, some sensor nodes might still be far from the
Distributed In-Network Processing of k-MaxRS in Wireless Sensor Networks
111

local principal which will result in inefficient network
route to that principal – e.g., path to p
1
from nodes
sn
1
and sn
2
in Figure 2(a).
To avoid such cases, we propose to split the zone
of interest into m × n grid of equal-sized cells. Each
cell will be assigned a local principal, and the value of
m and n can be set based on some desired criteria, e.g.,
the average number of sensors within a cell, a limit
on the number of hops when communicating with the
principal, etc. The benefit of this space-clustering
method is shown in Figure 2(b), as now we can con-
trol the communication distance between nodes and
their local principal. Other similar space-partitioning
schemes (e.g., K-d tree (Mohamed et al., 2013)) can
be considered, but the important observation is that
subsequently the principals are organized in a hierar-
chical (tree-like) digraph – principal graph – rooted
in a dedicated sink (more details in the following sec-
tions). The impact of this geographic clustering and
hierarchical digraph for principals is two-fold: (1) It
helps in localizing the processing as each principal
can compute k-MaxRS for its own cell; and (2) It en-
ables a distributed solution even for the case when
some of the rectangles from the k-MaxRS answer-set
spans across ≥ 2 cells.
Base Method
For in-network processing, LM is more suited than
ORM, because ORM would need to execute MaxRS
k times iteratively, and doing the in-network process-
ing k times among the clusters would still incur sig-
nificant communication overhead – possibly even ex-
ceeding the centralized approach for a large k. On
the other hand, the sweep-line procedure is performed
only once for LM, i.e., a single in-network process-
ing cycle can retrieve the k-MaxRS answer-set. Thus
in our distributed technique, each local principal in a
given cluster uses LM to compute the answer-set in
that cluster.
Routing & Data Aggregation
One way to divide routing protocols in WSN is into
Figure 3: The safe region within a cell.
two categories: hierarchical and “flat”. In this work,
we employ a hierarchical digraph-based routing pro-
tocol among the principals, and data propagation and
aggregation is achieved by relaying messages from
predecessors to successors. As a result, the local prin-
cipals form a digraph, denoted principal graph, in
our distributed scheme. Before going into the details
about principal graph, we define the term safe region
(SR) for a cell as the geographical region within which
all the local processing of k-MaxRS for that cell is fi-
nal. In other words, no k-MaxRS solution can span
outside the safe region. The safe region of a cell for
a given query rectangle R of size d
1
× d
2
is illustrated
in Figure 3, and we observe that the information of all
the sensor nodes 6∈ SR (indicated in red in Figure 3)
must be shared with the neighboring cells when de-
termining the answer.
Figure 4: The principal graph and data aggregation to the
sink.
A cell can have as many as 8 neighbors (e.g., B
2
in Figure 4), and sharing data with all of them may
not be efficient. Instead, we use the principal graph as
shown in Figure 4. For a principal p
M
of the cell M
(under a suitable cell-addressing scheme), we will use
p
p
M
and p
s
M
to denote the set of its predecessors and
successors in the principal graph respectively. The
hierarchical digraph is formed by creating directed
edges from each principal to the principals of the cells
immediately up (“north”) and right (“west”) direc-
tions (if exists). Thus, a principal will have at most
two successors and two predecessors in the graph,
e.g., for A
2
in Figure 4 – p
p
A
2
={A
1
} and p
s
A
2
={A
3
,B
2
}.
Successors are considered to be in higher level in the
hierarchy than their predecessors, and the sink is kept
in the highest level of the hierarchy (i.e., has no suc-
cessors). In this scheme, each principal p
M
shares its
data with only at most two neighbors – its successors,
i.e., p
s
M
. Thus, p
A
2
in Figure 4 will share its data with
only p
A
3
and p
B
2
. A principal shares the following
data with its successors: (1) local k-MaxRS answer-
set; (2) the dict hash-table; and (3) the data of the
nodes in the unsafe region. In this setting, the prin-
cipal of cell A
3
has the valid k-MaxRS answer-set for
the region of the network between l
0
and l
1
(cf. Fig-
SENSORNETS 2017 - 6th International Conference on Sensor Networks
112

ure 4). Similarly, the principal of cell B
3
has valid
answers for the region l
1
and l
2
, and so on. Finally,
the sub-solutions can be merged in two ways: (1) In
the top-right cell (i.e., C
3
in Figure 4); and (2) In the
base-station (using dotted connections in Figure 4).
To eradicate any dependency on the base-station, we
employ the former method.
Algorithms
There are two types of nodes (entities) in our dis-
tributed scheme: (1) Sensing nodes; and (2) Local
principals. The behavior of a sensing node in k-
MaxRS processing is rather simple:
1. After a pre-determined (fixed) period, col-
lect/update its own application-specific weights
(e.g., sensed phenomena values, network traffic,
consumed energy, etc.).
2. If there is any update of the weight, send the new
value to the local principal.
The behavior of local principals is specified in Al-
gorithm 1, which we now explain. Initially a prin-
cipal receives the cell-boundary information, along
with two other values – (1) the dimensions of the
range R; and (2) λ – the re-evaluation frequency –
directly from the base-station. Using the received
parameters, the principal establishes connection with
Algorithm 1: k-MaxRS-Principal (R, λ, C).
Require: A rectangle R of size d
1
× d
2
, a time-
interval λ, and a principal’s own cell C
Ensure: Sending data to be shared with p
s
, or the
final answer-set kmaxrs to the sink
1: Establish connection with all sn
i
∈ WSN
C
2: Establish connection with p
p
and p
s
3: Compute safe region SR using C and R
4: while Not Interrupted do
5: Receive (location, w
i
) data from all sn
i
∈
WSN
C
6: Receive (kmaxrs
i
,dict
i
,unsafe
i
) from p
i
∈ p
p
7: if a time-interval ends after λ time then
8: Add unsafe
i
to WSN
C
9: (kmaxrs,dict) ← LM(WSN
C
,R)
10: Merge dict and dict
i
from p
i
∈ p
p
11: kmaxrs ← Compare(kmaxrs, kmaxrs
p
,
dict)
12: if p
s
={sink} then
13: return kmaxrs to the sink
14: else
15: return (kmaxrs,dict,unsafe) to p
s
16: end if
17: end if
18: end while
the relevant nodes, i.e., all the nodes in its cell, and
the principals corresponding to its p
p
and p
s
neigh-
bors (cf. Lines 1-2). SR is then computed and the
principal detects/marks the nodes in its unsafe region
(Line 3). Lines 5-17 are executed until new param-
eters are received from the base-station. In Lines 5-
6, the principal waits to receive relevant information
from the sensing nodes (i.e., the weights of their mea-
surements), and p
p
. At each time-interval λ, Lines
8-16 are processed. After adding the information of
nodes in the neighboring predecessor principals’ un-
safe regions, a principal performs the LM method to
compute its own local k-MaxRS answer-set (cf. Lines
8-9). Then it combines the dict tables from the neigh-
bors with its own in Line 10. In Line 11, Compare is
a method which takes all the local solutions – a cell’s
computed answer-set and from p
p
– and retrieves the
top-k non overlapping positions using the merged dict
hash-table. Finally, if the principal is the immediate
predecessor of the sink, it sends the final solution only
directly to the sink. Otherwise, relevant information
is sent to p
s
.
We re-iterate that there is the user-defined param-
eter λ (a.k.a. sampling rate) specifying the “fresh-
ness” of the answer-set, i.e., the frequency of re-
evaluating k-MaxRS. What this entails is if k-MaxRS
is computed at time t, only the nodes within the
answer-set rectangles are kept awoken between t and
t +λ, thereby limiting the awareness of the fluctuation
of the weights corresponding to the monitored phe-
nomenon. At time t + λ, all nodes are awakened, and
subsequently k-MaxRS is re-computed with updated
weights throughout the entire network and the states
(awake, or idle) of the nodes are changed accordingly.
4 EXPERIMENTAL EVALUATION
We now describe our experimental observations re-
garding the benefits of the proposed approaches
1
.
Tools and Setup: We conducted the experi-
ments in an open-source WSN simulator, SIDnet-
Swans (Ghica et al., 2008) – which has been used
as an experimental tool in prior works (Trajcevski
et al., 2011; Bai et al., 2011). The simulator is con-
figured as follows: (1) 20 Kbps radio data rate on
the MAC 802.15.4 protocol; (2) Shortest path geo-
graphical routing algorithm protocol (Banerjee et al.,
2012) between nodes; (3) Utilization of Heart-Beat
protocol (Li and Tan, 2007) to create the routing ta-
ble in the MAC layer for each node within the first
1
All the source codes and datasets for the experi-
ments reported in this paper are publicly available at:
http://www.eecs.northwestern.edu/˜pwa732
Distributed In-Network Processing of k-MaxRS in Wireless Sensor Networks
113
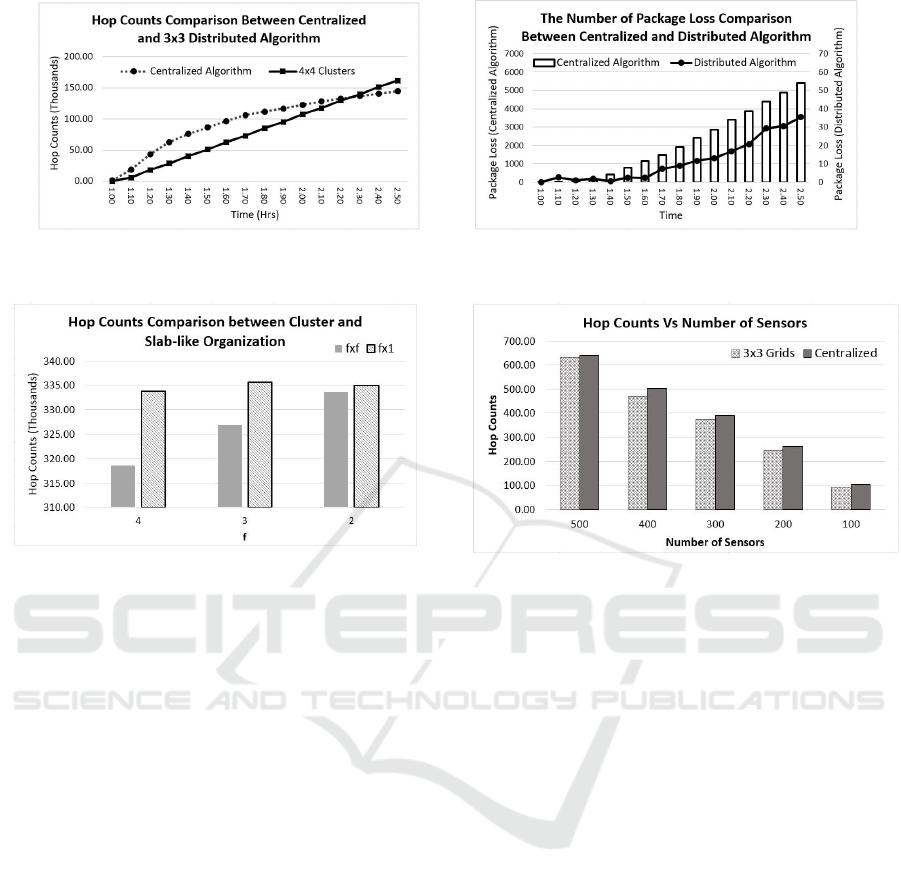
(a) (b)
Figure 5: (a) Hop count comparison, and (b) Amount of packet loss between centralized and distributed schemes.
Figure 6: Hop count comparison between different dis-
tributed schemes.
hour when the simulation starts; (4) Communication
range of 100 meters; (5) Power consumption model
according to the TelosB mote’s specifications; and
(6) Initial capacity of a fully-charged battery of 25
mAh. Note that, a fully-charged sensor can run for 48
active-hours during simulation before running out of
battery-charge. We used Java to implement the corre-
sponding algorithms in SIDnet-Swans.
Default Settings: We set |W SN|=300, i.e., 300 ho-
mogeneous sensors over a 640 × 640 m
2
field. We
used a rectangle of size 75 ×75 m
2
as query rectangle
(R) throughout our experiments, with k = 2. We set
sampling rate λ to 5 minutes, and default distributed
clustering to 3 × 3 cells.
We used the following configurations: (1) Centralized
– all nodes send data to the sink; and (2) Distributed
– all sensing nodes send weights to local principals.
Two types of sub-division are employed: (1) Grid-
based; and (2) Vertical Slab-like. Unless indicated
otherwise, we measure/report the raw hop counts of
all the algorithms’ run for 2 hours – assuming, as in-
dicated above, the typical TelosB mote energy con-
sumption per transmission.
Results: Figure 5 shows the hop counts of both the
centralized and distributed processing in the default
settings, running for 1.5 hours. As illustrated, the
number of hop counts of the distributed technique
is significantly smaller than the centralized one. As
Figure 7: Performance of algorithms on various cardinality
of objects.
time increases, the difference in hop count increases
as well, e.g., the difference is around 7500 at t = 1.1
hours while it steadily grows to be close to 14000 at
1.5 hours mark. Note that, the raw hop count is less
in the first hour for both schemes as most of that time
is spent in setting up the network.
The performance comparison of the vertical slab-
like and grid-based formation is shown in Figure 6.
We perform the experiments in three different sizes
for both formations – 2 × 1, 3 × 1, 4 × 1 for vertical
slabs, and 2 × 2, 3 × 3, 4 × 4 for grid-based cells –
and we note that in the figure itself, the legend lists
them as “ f × 1” and “ f × f ” configurations, with
the different values for f indicated on the x-axis.
As shown, in all the cases, grid-based clustering
scheme outperforms slab-like subdivision technique.
Section 3.2.
The effect of the varying number of clusters in dis-
tributed algorithms is shown in Figure 6. For both
grid-based cells and vertical slabs, hop count signif-
icantly decreases as we increase the number of clus-
ters. In case of grid-based cells, if we raise the count
of cells from 4 to 9, the hop count decreases by
more than 40000, while it further plummets by around
22000 when we use 4 × 4 (16) grid cells. Note that
complementary to this trend, when forming too many
clusters, there are added hindrances of increased num-
SENSORNETS 2017 - 6th International Conference on Sensor Networks
114

Figure 8: Average energy consumption comparison be-
tween distributed and centralized algorithm.
Figure 9: Performance k-MaxRS using different k values.
ber of resource-demanding principal sensors and the
relative decrease in the area of safe-regions for clus-
ters.
The effect of varying the size of WSN is illus-
trated in Figure 7. As expected, the rise in the num-
ber of nodes in WSN increases the hop count of both
the centralized and distributed algorithm. A notewor-
thy observation is that distributed technique (3 × 3)
performs better than the centralized scheme in all the
cases.
Figure 8 demonstrates an important feature of our
distributed scheme – overall less energy consumption,
which in turn increases overall network lifetime. We
ran both the distributed and centralized approach in
the default settings for 3.2 hours and computed aver-
age energy consumption over all the nodes in the net-
work. As can be seen in Figure 8, energy consump-
tion is at least 2-3 times more in centralized approach
than the distributed one. Also, as time increases, this
difference increases as well, indicating the efficacy of
our proposed algorithm in the long run.
This experiment measured the number of hop
counts when the k values are varied at the end of the
second hour. Figure 9 shows that hop counts increase
for larger k since, when k is high, our algorithm needs
to send more possible solutions to the neighbor clus-
ters, resulting in more hop counts.
Figure 10: Performance k-MaxRS using different k values.
We did another experiment by changing the
shapes and sizes of the query region with the scale
factor of 4, and we measured the hop counts of differ-
ent query regions. Figure 10 measures the number of
hop counts once the shapes and size of the query re-
gion are changed – confirming that the larger query
region is, more hop counts are needed. For larger
query region, each principle node has to transmit to
the neighbor clusters more data of the objects within
the area outside its cluster, extended by the size of
the specified query region. The larger extended area
would include more objects from other neighbor clus-
ters, and again each principle node has to send more
data/messages to other neighbor-clusters.
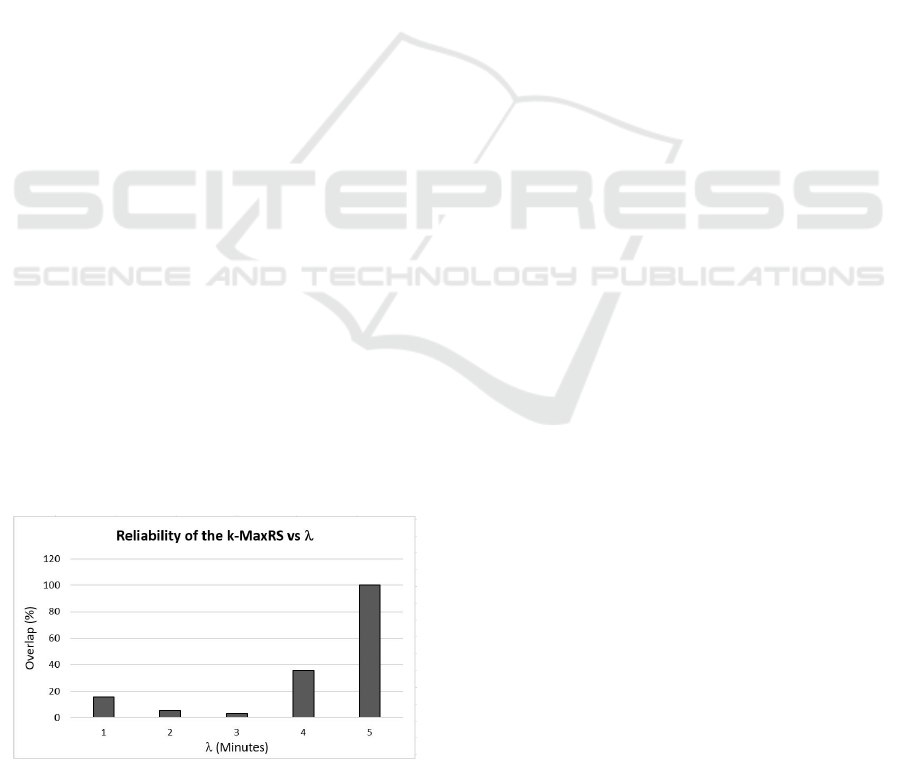
Our last experiments measured the variation of ac-
curacy of k-kMaxRS with the sampling rates (λ), re-
ported for two different sampling values: 1 and 5 min-
utes. We recorded the locations and weighted sums of
each MaxRS rectangle every minute, and compared
those outputs with the one where k-MaxRS is cal-
culated once every 5 minutes. We ran the experi-
ments for 10 times and averaged the percentage of
overlap of all k-MaxRSs – and we did the same for
the weights (measured in the optimally-located rect-
angles). The results, shown in Figure 11 illustrate that
the k-MaxRS at the lower sampling rate may induce
significant errors in terms of keeping the sink up to
date – both in terms of the locations of R as well as
the values of the weighted sums. More specifically,
the results show the percentage of overlap of the val-
ues between the once-in-5 minutes sampling vs. sam-
pling every minute. The overlaps tend to reach 100%
by the end which, in a sense, is expected since the
phenomenon of interest is measured at t = 5 by both
setups. We note that the difference in energy con-
sumption was almost-linear – i.e., the sampling with
λ = 1 consumed approximately 5 times more energy
than the case of λ = 5. The investigation of balancing
the trade-off between the (im)precision and residual
energy (or overall lifetime) of the WSN, however, is
beyond the scope of this work.
Distributed In-Network Processing of k-MaxRS in Wireless Sensor Networks
115
5 RELATED WORKS
The MaxRS and its variants were first tackled by
the researchers from computational geometry, de-
vising in-memory algorithms of O(n log n) time-
complexity (Imai and Asano, 1983; Nandy and Bhat-
tacharya, 1995). Motivated by applications from the
class of Location-Based Services (e.g., best location
for a new franchise store with a specified delivery
range; most attractive place for a tourist with a re-
stricted reachability), scalable solution for MaxRS in
spatial databases were proposed (Choi et al., 2012;
Choi et al., 2014). The distribution schemes proposed
in (Choi et al., 2014) work nicely for secondary mem-
ory settings but, it appears that the vertical subdivi-
sion of space used in those works is not well-suited
for WSN settings (cf. Section 3 and 4).
Recently, different variants of the MaxRS prob-
lem were investigated: – constraining locations of
the objects to an underlying spatial network (Phan
et al., 2014); – monitoring MaxRS over spatial
data streams (Amagata and Hara, 2016); – rotating-
MaxRS problem, i.e., allowing non axis-parallel rect-
angles (Chen et al., 2015). While interesting variants
of the traditional MaxRS problem, these works did
not consider the distributed processing aspects which
are typical for WSN settings, nor the multiple (k) so-
lutions.
A system implementing in-network solution to (a
single, k = 1) MaxRS query in WSN was presented
in (Hussain et al., 2015). We note that a similar phi-
losophy of hybrid hierarchical clustering and rout-
ing scheme (although tree-based, not digraph-based)
were used in (Avci et al., 014b), for different settings
– i.e., detecting and tracking evolving shapes in WSN.
Although there have been numerous works addressing
energy conservation in WSN (Anastasi et al., 2009),
to our knowledge, no energy-aware aggregation and
routing approaches exist for the k-MaxRS problem in
sensor networks.
Figure 11: Performance k-MaxRS processing using differ-
ent λ values.
6 SUMMARY & FUTURE
DIRECTION
We presented an efficient distributed algorithm for
processing k-MaxRS queries in WSNs. The unique
nature of the k-MaxRS is that a collection of k fixed-
size rectangles needs to be placed at distinct locations,
in a manner that ensures that the sum of the respective
(weighted) density/values in their interiors is maxi-
mized. We proposed a geographic clustering scheme
where principal nodes (i.e., cluster heads) not only
collect and aggregate data from their children, but
also communicate with the siblings (i.e., other prin-
cipals – predecessors and successors) in order to de-
tect the answer to the k-MaxRS query as early in the
hierarchy as possible, while reducing the overhead of
communicating with all the possible neighbors.
To the best of our knowledge, k-MaxRS has not
been addressed before in the context of WSNs and
there are multiple extensions and variants to be inves-
tigated, some of which we plan to address in the near
future. There are three distinct facets of the prob-
lem that we are currently focusing upon from com-
plementary perspectives: (1) The incorporation of the
(un)reliability of the links and transmission errors,
along with more detailed consideration of different
power-consumption models; (2) The investigation of
the impact of the discrepancy of the nodes locations
distribution; and (3) Dynamically adjusting the size
of the query-rectangle and/or k based on trade-offs
among different constraints (e.g., turnaround time,
overall energy consumption, “freshness” of the data
in the sink, etc.). In addition, we would like to inves-
tigate the incorporation of other kinds of dynamics-
related contexts: from the impact of the different
partitioning values (i.e., “m” and “n”) and adap-
tive congestion management (Ren et al., 2011; Wan
et al., 2003), through dynamic routing and aggrega-
tion structures (Fasolo et al., 2007), to incorporating
mobile nodes/sink (Mohamed et al., 2013).
ACKNOWLEDGMENTS
Research supported by NSF grants CNS-0910952 and
III 1213038, and ONR grant N00014-14-1-0215.
REFERENCES
Akyildiz, I. F., Su, W., Sankarasubramaniam, Y., and
Cayirci, E. (2002). Wireless sensor networks: A sur-
vey. Comput. Netw., 38(4):393–422.
SENSORNETS 2017 - 6th International Conference on Sensor Networks
116

Amagata, D. and Hara, T. (2016). Monitoring MaxRS in
spatial data streams. In EDBT, pages 317–328.
Anastasi, G., Conti, M., Di Francesco, M., and Passarella,
A. (2009). Energy conservation in wireless sensor net-
works: A survey. Ad hoc networks, 7(3):537–568.
Avci, B., Trajcevski, G., and Scheuermann, P. (2014b).
Managing evolving shapes in sensor networks. In
Proceedings of the 26th International Conference
on Scientific and Statistical Database Management,
page 22. ACM.
Bai, L. S., Dick, R. P., Chou, P. H., and Dinda, P. A.
(2011). Automated construction of fast and accurate
system-level models for wireless sensor networks. In
2011 Design, Automation & Test in Europe, pages 1–
6. IEEE.
Banerjee, I., Roy, I., Choudhury, A. R., Sharma, B. D.,
and Samanta, T. (2012). Shortest path based geo-
graphical routing algorithm in wireless sensor net-
work. In Communications, Devices and Intelligent
Systems (CODIS), 2012 International Conference on,
pages 262–265.
Chen, Z., Liu, Y., Wong, R. C.-W., Xiong, J., Cheng, X.,
and Chen, P. (2015). Rotating MaxRS queries. Infor-
mation Sciences, 305:110–129.
Choi, D.-W., Chung, C.-W., and Tao, Y. (2012). A scal-
able algorithm for Maximizing Range Sum in spa-
tial databases. Proceedings of the VLDB Endowment,
5(11):1088–1099.
Choi, D. W., Chung, C. W., and Tao, Y. (2014). Maxi-
mizing Range Sum in external memory. ACM Trans.
Database Syst., 39(3):21:1–21:44.
Fasolo, E., Rossi, M., Widmer, J., and Zorzi, M. (2007).
In-network aggregation techniques for wireless sensor
networks: A survey. Wireless Communications, IEEE,
14(2):70–87.
Ghica, O. C., Trajcevski, G., Scheuermann, P., Bischof, Z.,
and Valtchanov, N. (2008). Sidnet-swans: A simu-
lator and integrated development platform for sensor
networks applications. In Proceedings of the 6th ACM
Conference on Embedded Network Sensor Systems,
pages 385–386. ACM.
Hussain, M. M., Wongse-ammat, P., and Trajcevski, G.
(2015). Demo: Distributed MaxRS in wireless sensor
networks. In Proceedings of the 13th ACM Confer-
ence on Embedded Networked Sensor Systems, Sen-
Sys ’15, pages 479–480. ACM.
Imai, H. and Asano, T. (1983). Finding the connected
components and a maximum clique of an intersec-
tion graph of rectangles in the plane. Journal of al-
gorithms, 4(4):310–323.
Krishnamachari, B., Estrin, D., and Wicker, S. (2002).
The impact of data aggregation in wireless sensor
networks. In Distributed Computing Systems Work-
shops, 2002. Proceedings. 22nd International Confer-
ence on, pages 575–578. IEEE.
Li, H. and Tan, J. (2007). Heartbeat driven medium access
control for body sensor networks. In HealthNet, pages
25–30. ACM.
Madden, S. R., Franklin, M. J., Hellerstein, J. M., and
Hong, W. (2005). TinyDB: An acquisitional query
processing system for sensor networks. ACM Trans-
actions on database systems (TODS), 30(1):122–173.
Mohamed, M. M. A., Khokhar, A., and Trajcevski, G.
(2013). Energy efficient in-network data indexing
for mobile wireless sensor networks. In Advances
in Spatial and Temporal Databases, pages 165–182.
Springer.
Nandy, S. C. and Bhattacharya, B. B. (1995). A unified
algorithm for finding maximum and minimum object
enclosing rectangles and cuboids. Computers & Math-
ematics with Applications, 29(8):45–61.
Phan, T.-K., Jung, H., and Kim, U.-M. (2014). An effi-
cient algorithm for Maximizing Range Sum queries in
a road network. The Scientific World Journal, 2014.
Ren, F., He, T., Das, S. K., and Lin, C. (2011). Traffic-
aware dynamic routing to alleviate congestion in wire-
less sensor networks. IEEE Trans. Parallel Distrib.
Syst., 22(9):1585–1599.
Trajcevski, G., Zhou, F., Tamassia, R., Avci, B., Scheuer-
mann, P., and Khokhar, A. (2011). Bypassing
holes in sensor networks: load-balance vs. latency.
In Global Telecommunications Conference (GLOBE-
COM 2011), 2011 IEEE, pages 1–5. IEEE.
Trigoni, N. and Krishnamachari, B. (2012). Sensor network
algorithms and applications. Philosophical Transac-
tions of the Royal Society of London A: Mathematical,
Physical and Engineering Sciences, 370(1958):5–10.
Wan, C.-Y., Eisenman, S. B., and Campbell, A. T. (2003).
CODA: Congestion detection and avoidance in sen-
sor networks. In Proceedings of the 1st international
conference on Embedded networked sensor systems,
pages 266–279. ACM.
Distributed In-Network Processing of k-MaxRS in Wireless Sensor Networks
117
