Distance-bounding Identification
Ahmad Ahmadi and Reihaneh Safavi-Naini
Department of Computer Science, University of Calgary, Calgary, Canada
Keywords:
Distance-bounding, Identification, Public-key, MiM.
Abstract:
Distance bounding (DB) protocols allow a prover to convince a verifier that they are within a distance bound.
We propose a new approach to formalizing the security of DB protocols that we call distance-bounding iden-
tification (DBID), and is inspired by the security definition of cryptographic identification protocols. Our
model provides a natural way of modeling the strongest man-in-the-middle attack, making security of DB
protocols in line with identification protocols. We compare our model with other existing models, and give a
construction that is secure in the proposed model.
1 INTRODUCTION
Distance bounding protocols were first proposed
(Desmedt, 1988) as a mechanism for providing secu-
rity against Man-in-the-middle (MiM) attacks in au-
thentication protocols. In a MiM attack, the attacker
does not have access to the secret key of the user,
but exploits their communications to get accepted by
the verifier. DB protocols use the distance between
the prover and the verifier as a second factor in au-
thentication. Distance bounding protocols have been
widely studied in recent years and the security argu-
ments have been formalized (D
¨
urholz et al., 2011),
(Boureanu et al., 2013). Most DB protocols are sym-
metric key protocols requiring the prover and the ver-
ifier to share a secret key. More recently public-key
protocols –where the prover has a registered public-
key– have been proposed. In this paper we consider
public-key DB protocol.
Distance-bounding (DB) protocols are authentica-
tion protocols that consider the distance between the
prover and the verifier as an extra factor, and guar-
antee that the prover knows (i) the correct secret and,
(ii) their distance to the verifier is upper-bounded. The
distance between the two parties is measured by run-
ning a fast challenge and response message exchange
phase consisting of a sequence of single bit challenges
sent by the verifier. The prover’s response to each
challenge bit depends on their secret key and the re-
ceived bit. If the prover is located within a defined
distance bound D to the verifier, then they are able to
respond within a certain time period and their authen-
tication claim will be accepted.
In a DB setting, the participants who are located
within the distance D to the verifier, are called close-
by participants, and those who are outside the range
are called far-away participants. DB protocols have
been studied under the following attacks. We use
prover to refer to a participant who has a shared key
with the verifier, and adversary for one who does not
have a shared key.
(A1) Distance-Fraud (Brands and Chaum, 1994);
a dishonest far-away prover tries to succeed
in the protocol. In a sub-class of this at-
tack, called Distance-Hijacking (Cremers et al.,
2012), a far-away prover takes advantage of
honest close-by provers to succeed in the pro-
tocol.
(A2) Mafia-Fraud (Desmedt, 1988); an adversary
who is close to the verifier tries to use the com-
munications of a far-away honest prover, to suc-
ceed in the protocol.
(A3) Impersonation (Avoine et al., 2011); a close-by
adversary tries to impersonate the prover in a
new session. This original definition does not
include a learning phase for the adversary.
(A4) Strong-Impersonation (this paper); a close-by
adversary learns from past executions of the
protocol by an honest prover and tries to imper-
sonate the prover in a new execution when the
prover is not close-by.
(A5) Slow-Impersonation (D
¨
urholz et al., 2011); an
adversary communicates simultaneously with
the prover and the verifier, and tries to suc-
ceed in the protocol. The adversary will modify
the protocol messages that are sent in the slow-
202
Ahmadi, A. and Safavi-Naini, R.
Distance-bounding Identification.
DOI: 10.5220/0006211102020212
In Proceedings of the 3rd International Conference on Information Systems Security and Privacy (ICISSP 2017), pages 202-212
ISBN: 978-989-758-209-7
Copyright
c
 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

phase of the protocol but can relay the messages
of the fast-phase.
(A6) Terrorist-Fraud (Desmedt, 1988); this is a col-
luding attack by a dishonest far-away prover
and a close-by helper. The prover tries to suc-
ceed in the protocol with the requirement that
their secret key will not be leaked to the helper.
DB protocols are commonly shown to be secure
against a subset of these attacks. Shared-key DB pro-
tocols have application in the authentication of small
devices such as RFID tags, while public-key DB pro-
tocols are used when more computation is affordable
and one needs to protect the privacy of users against
the verifier. In public-key DB model, a prover has a
unique secret-key and the verifier has all the public-
keys. Public-key DB protocols have the convenience
of not needing to share a secret key but are signifi-
cantly slower than shared-key DB protocols, and need
more complex design to deal with individual bits of
the private-key.
Related Works. The main models and construc-
tions of public-key DB protocols are in (Hermans
et al., 2013), (Ahmadi and Safavi-Naini, 2014),
(Gambs et al., 2014), and (Vaudenay, 2014). In the
following, we discuss and contrast the security model
of these works to be able to put our new work in con-
text.
(Hermans et al., 2013) presented an informal
model for Distance-Fraud, Mafia-Fraud and Imper-
sonation attack as defined above, and provided a
secure protocol according to the model. (Ahmadi
and Safavi-Naini, 2014) formally defined Distance-
Fraud, Mafia-Fraud, Impersonation, Terrorist-Fraud
and Distance-Hijacking attack. The Distance-Fraud
adversary has a learning phase before the attack ses-
sion and is therefore stronger than the definition in
A2. During the learning phase, the adversary has ac-
cess to the communications of the honest provers that
are close-by. The security proofs of the proposed pro-
tocol have been deferred to the full version, which is
not available yet.
(Gambs et al., 2014) uses an informal model
that captures Distance-Fraud, Mafia-Fraud, Imper-
sonation, Terrorist-Fraud, Distance-Hijacking and a
new type of attack called Slow-Impersonation that
is defined in A5. In their model, the definition of
Terrorist-Fraud is slightly different from A6: a TF at-
tack is successful if it allows the adversary to succeed
in future Mafia-Fraud attacks.
For the first time in distance-bounding literature,
(D
¨
urholz et al., 2011) considered normal MiM attack-
ing scenario where both the honest prover and the ad-
versary are close to the verifier. The adversary inter-
acts with the prover in order to succeed in a separate
protocol session with the verifier. The adversary has
to change some of the received messages in the slow
phases of protocol in order to be considered success-
ful. The attack is called Slow-Impersonation (A5) and
is inspired by the basic MiM attack in authentication
protocols. Although the basic MiM attack is proper
for DB models, it may not be strictly possible in one
phase of the protocol as their action could influence
or be influenced by other phases of the protocol.
A MiM adversary may, during the learning phase,
only relay the slow-phase messages but, by manipu-
lating the messages of the fast phase, learn the key
information and later succeed in impersonation. Ac-
cording to the definitions in (Gambs et al., 2014) and
(D
¨
urholz et al., 2011), the protocol is secure against
Slow-Impersonation, however it is not secure againt
Strong-Impersonation (A4). This scenario shows that
Slow-Impersonation does not necessarily capture Im-
personation attacks in general. Moreover, it’s hard to
distinguish the success in slow phases of a protocol
without considering the fast phase, as those phases
have mutual influences on each other.
As an alternative definition, we propose Strong-
Impersonation (A4), in which the MiM adversary has
an active learning phase that allows them to change
the messages. Strong-Impersonation captures the
MiM attack without the need to define success in
the slow rounds. One of the incentives of Strong-
Impersonation is capturing the case when the prover
is close to the verifier, but is not participating in any
instance of the protocol. In this case, any acceptance
by the verifier means that the adversary has succeeded
in impersonating an inactive prover.
In (Vaudenay, 2014) an elegant formal model
for public-key distance-bounding protocols in terms
of proof of proximity of knowledge has been
proposed. The model captures Distance-Fraud,
Distance-Hijacking, Mafia-Fraud, Impersonation and
Terrorist-Fraud. In this approach, a public-key DB
protocol is a special type of proof of knowledge
(proximity of knowledge): a protocol is considered
sound if the acceptance of the verifier implies exis-
tence of an extractor algorithm that takes the view
of all close-by participants and returns the prover’s
private-key. This captures security against Terrorist-
Fraud where a dishonest far-away prover must suc-
ceed without sharing their key with the close-by
helper.
According to the soundness definition in (Vaude-
nay, 2014) however, if the adversary succeeds while
there is an inactive close-by prover, the protocol is
sound because the verifier accepts, and there is an ex-
tractor for the key simply because there is an inactive
Distance-bounding Identification
203

close-by prover and their secret key is part of the ex-
tractor’s view. Existence of an extractor is a demand-
ing requirement for the success of attacks against au-
thentication: obviously an adversary who can extract
the key will succeed in the protocol, however it is pos-
sible to have an adversary who succeeds without ex-
tracting the key, but providing the required responses
to the verifier. Our goal in introducing identification
based model is to capture this weaker requirement of
success in authentication, while providing a model
that includes realistic attacks against DB protocols.
Our Work. We follow the formalization of crypto-
graphic identification protocols due to (Kurosawa and
Heng, 2006), and extend it to include the proximity
of the prover as an extra required property. By replac-
ing the framework of authentication protocols/proof-
of-knowledge in (Vaudenay, 2014), with that of iden-
tification protocols, we can provide appropriate se-
curity definitions that realistically capture security of
public-key DB protocols. A basic identification pro-
tocol, referred to as Σ-protocol, is a three round pro-
tocol between a prover and a verifier in which the
prover convinces the verifier of their identity. Secu-
rity is defined as a game between a challenger and an
adversary, and the success of the adversary depends
on its ability to provide a new valid protocol tran-
script, given their knowledge of the past transcripts.
This is a weaker requirement for adversary’s success
in the sense that an adversary that can extract the se-
cret key of the prover can construct a valid transcript,
but constructing a transcript does not imply success
in extracting the key. Using this approach we can
model a MiM setting where an honest prover and the
adversary are close-by, and the adversary uses the past
communications of the prover, to launch an imperson-
ation attack. Our soundness definition correctly cap-
tures this setting in the sense that success of the adver-
sary in this setting implies violation of the soundness
in our model. Our model of public-key DB proto-
cols captures Distance-Fraud, Mafia-Fraud, Strong-
Impersonation and Terrorist-Fraud. We provide a
construction that is provably secure in this model.
The organization of the paper is as follows:
Section2 is preliminaries; Section3 includes the
model and definitions; Section4 presents a proto-
col and proves their security in our proposed model;
Section5 concludes the paper.
2 PRELIMINARIES
In the following we recall a widely used definition of
identification schemes.
Identification Scheme (Kurosawa and Heng,
2006). An identification scheme (ID), a prover P
convinces a verifier V that they know a witness
w
I
related to a public value p
I
. The scheme is
given by the tuple ID=(KeyGen; Commit;Response;
Check) which consists of a PPT algorithm KeyGen
that generates (w
I
, p
I
), and the algorithms, Commit,
Response and Check that specify an interactive pro-
tocol (P,V ) between the prover P and the verifier V
as follows. Let CMD, CMT, CHA and RES denote
domains of the three variables denoting committed,
commitment, challenge and response.
Step 1. P chooses a ∈
R
CMD, computes the commit-
ment A = Commit(a) ∈ CMT and sends to V .
Step 2. V chooses c ∈
R
CHA and sends it to P.
Step 3. P computes r = Response(w
I
,a, c) ∈ RES
and sends to V .
Step 4. V accepts if the following check holds;
A = Check(p
I
,c, r), (2.1)
The above protocol is called Σ-protocol. We say
that (A, c,r) ∈ CMT × CHA × RES is a valid tran-
script for p
I
if it satisfies Equation2.1. The main prop-
erties of ID-schemes are:
• Completeness. If a prover is honest, then
Equation2.1 holds.
• Soundness. It is hard to compute two valid tran-
scripts (A, c,r) and (A, c
0
,r
0
) such that c 6= c
0
on
input p
I
.
This definition of soundness is against an adver-
sary who observes transcripts of the protocol and will
succeed if they can construct a new one. (Bellare
and Palacio, 2002) however considers soundness as
a game between the adversary, prover and the verifier,
in two distinct steps.
• Impersonation under Concurrent Attack. The
adversary A = (V
∗
,P
∗
) is a pair of randomized
polynomial algorithms, called cheating verifier
and cheating prover. Consider a game having
two phases; In the first phase the key-pair of the
prover (w
I
, p
I
) is generated and V
∗
(p
I
) interacts
concurrently with multiple clones of the prover
P(w
I
, p
I
) with independent randomness. In the
second phase, the cheating prover P
∗
(View
V
∗
)
that is initialized with the final view of V
∗
, in-
teracts with V (p
I
). A protocol is imp-ca secure if
the acceptance probability of V is negligible.
In a stronger definition of MiM attack (Lyuba-
shevsky and Masny, 2013), the attacker simultane-
ously interacts with the prover and the verifier.
ICISSP 2017 - 3rd International Conference on Information Systems Security and Privacy
204

• MiM Resistance. Consider an adversary who
can interact with the prover and the verifier at
the same time and run this interaction over mul-
tiple instances of the protocol. Upon receiving a
message from a party, the adversary adds some
value to the message and sends it to the other
party, hence replacing the message A with A + A
0
,
c with c + c
0
and r with r + r
0
. Note that this cap-
tures the most general modification of such ad-
versary, as they effectively change the received
protocol message to anything they like. A proto-
col is MiM-resistant if the success chance of ad-
versary in finding (A
0
,c
0
,r
0
) 6= (0,0,0), such that
(A+A
0
,c, r +r
0
) is a valid transcript, is negligible.
3 SECURITY MODEL AND
DEFINITION
In our model, each participant has a location which is
an element of a metric space S and stays the same dur-
ing the protocol execution. There is a distance func-
tion d(loc
1
,loc
2
) that returns the distance between
any two locations. When a participant I
1
(located at
loc
1
), sends a message m at time t to another partic-
ipant I
2
(located at loc
2
), the message is received by
I
2
at time t +
d(loc
1
,loc
2
)
L
, where L indicates the speed
of light. The message that is delivered to P
2
is a noisy
version of the sent message m, i.e. each bit of m may
have been flipped with probability p
noise
.
A message sent by I
1
may be seen and modified
by other participants. A malicious participant I
3
lo-
cated at loc
3
, can send a malicious signal (message)
at time t
0
. This can only affect a message sent from I
1
to I
2
at time t, if t +d(loc
1
,loc
2
) ≥ t
0
+d(loc
3
,loc
2
).
If this happens, the message of I
1
may not be received
by I
2
. We allow I
1
to send multiple messages to mul-
tiple destinations at the same time, or receive multiple
messages simultaneously. In the latter case, the recip-
ients will receive a message that is the combination
of all the messages that are received at the same time.
If the signal strength of a message m
1
is much higher
than that of a message m
2
, then m
1
would stay recov-
erable and m
2
would appear as noise. This extends the
communication model of (Vaudenay, 2014) to better
capture the setting of many communicating devices.
In this system, we consider a set of users U =
{u
1
,. .., u
m
} that are registered and identifiable with
their secret-key. We assume that a single user can be
associated with multiple devices (called provers) of
the user that share the same secret-key, but possibly
have different locations.
We consider one protocol between the verifier and
a user (with provers’ of the user) at each time, and
consider the following three types of participants in
the system; a list of provers P = {P
1
,. .., P
k
} that
share the secret-key of a single user (u
i
), a verifier
V who has access to the public parameters of sys-
tem, and a set of actors. The actors set consists of
all other users (i.e. their provers) and adversaries that
may be active at the time. The difference between
a malicious prover and a malicious actor is that the
malicious prover has access to the secret-key that is
needed for execution of the protocol, while a mali-
cious actor does not.
When a prover of a user is compromised, then
the user’s key is compromised and the adversary can
choose devices with that key at locations of their
choice. We refer to these as corrupted provers who
are controlled by the adversary. We assume provers
that are not corrupted follow the protocol, and that a
user uses only one of its devices at a time. Corrupted
provers that are controlled by the adversary however
can be invoked simultaneously.
3.1 Distance-bounding Identification
In this section we describe the setting, operations and
properties of DBID protocols. The approach is to en-
hance Σ-protocol to include distance-bounding prop-
erties.
Definition 1. (Distance-bounding Identifi-
cation). Let λ denote the security parameter.
A distance-bounding identification (DBID)
is a tuple (K; KeyGen; Commit;Response;
Check;D; p
noise
), where K the key space whose
size is determined by a trusted party; KeyGen
that generate a pair (x,y) of public and private
key; a two-party probabilistic polynomial-time
(PPT) distance-bounding protocol (P(x),V (y)),
where P(x) is the prover algorithm and V(y)
is the verifier algorithm; and a distance bound
D. A trusted party runs the key generation
algorithm, gives the private-key x to the user and
the corresponding public-key to the verifier. To
run an instance of the protocol, the following
steps are taken.
1. P randomly chooses a from the set CMD
and computes the commitment of that A =
Commit(a). P then sends A to V . They
use a reliable channel (using error correcting
codes).
2. Fast challenge/response over noisy channel:
(a) V randomly chooses a challenge c from the
domain CHA
F
and sends it to P.
(b) P computes the response r =
Response(x,a, c) that is from a cer-
tain domain RES
F
and sends r to V .
Distance-bounding Identification
205

Steps 2-(a) and 2-(b) are repeated multiple
times, over a physical channel that is noisy
and may cause the challenge or response to
flip (with a constant probability).
3. In Step 2, let t
1
and t
2
denote the clock values
at the verifier when the challenge c is sent, and
the response r is received, respectively. V ver-
ifies if t
2
− t
1
<
D
L
, where L is the speed of
light.
4. Slow challenge/response over noise-free
channel:
(a) V chooses a challenge c at random from a
certain domain CHA
S
and sends it to P.
(b) P computes the response r =
Response(x,a,c) that is in a certain
domain RES
S
and sends r to V .
In this phase the communication is over reli-
able channel.
5. V accepts only if the following holds;
Accept = Check(y,[c], [r],A), (3.1)
Here [c] and [r] are the sequence of challenges
and the sequence of corresponding responses, in
the fast and the slow phases of the protocol. V
outputs Out
V
= 1 for accept, or 0 for reject.
Note that in this paper, the notation [.] indicates
a list of variables. In the rest of this section we will
define the security properties. We start by defining an
experiment that describes the operation of a distance-
bounding identification protocol.
Definition 2. (DBID Experiment). An experi-
ment exp for a DBID scheme (K; KeyGen; Commit;
Response;Check; D; p
noise
) is defined by a set of
participants and interactions between them. Par-
ticipants are; a verifier V , an ordered list of
provers P that share the same secret-key (a user
is a set of provers that share the same key), and
other actors from a set C (including potential ad-
versaries). Participants who are within the dis-
tance at most D from V are called close-by par-
ticipants. Participants who are at a distance more
than D to V are called far-away participants.
If provers are honest, the secret-key x ∈ K of
their associated user is randomly chosen and the
public-key y = KeyGen(x) is generated using a
trusted process. Note that the values (x,y) are
chosen before the experiment. x is given to mem-
bers of P and the first prover is activated. Each
active prover runs the defined algorithm, then
stops and activates the next prover in the sequence
of P . All members of P run the algorithm P(x),
and this continues until all provers in P are fin-
ished.
If provers are malicious, the key pair (x,y) is
set arbitrarily, and provers are allowed to be at
any location and run any PPT algorithm concur-
rently.
The actors can run any PPT algorithms and
can communicate with other participants simulta-
neously. The value of y is given to all participants.
The verifier follows the algorithm V(y) in an in-
stance of the protocol with any participant, and
returns Out
V
at the end of that instance. The ex-
periment finishes by returning the last output of
verifier.
We define four distinct properties for public-key
DB protocols using games between the adversary and
a challenger.
Game Setting. The challenger assigns the keys
of users and their provers. The adversary can corrupt
a user, gain their secret-key, set the location of their
provers and control those provers. The adversary can
also corrupt some actors, set their locations and con-
trol them.
Property 1. (Completeness). Consider
a DBID (K;KeyGen; Commit; Response;
Check;D; p
noise
) protocol between the veri-
fier and a honest close-by prover, as defined in
Definition1. Let p
noise
denote the flip probability
of noise in the environment.
The protocol is (τ, δ)-complete, 0 ≤ τ,δ ≤ 1,
if the verifier returns Out
V
= 1 with probability at
least 1 − δ, under the following assumption;
• for all bits of prover’s secret, we have at least τ
fraction of fast challenge/response rounds not
affected by the noise, and
• τ < 1 − p
noise
− ε for some constant ε > 0.
Completeness requires the absence of an adver-
sary. A robust protocol must have negligible δ to
be able to function in the presence of physical layer
noise.
Next we consider a setting where the prover is
honest, but there is a MiM adversary.
Property 2. (MiM-resistance). Let an adversary
A select a set of honest provers, corrupt a set of
actors (both sets of polynomial size in the secu-
rity parameter), and set their locations, and runs
the DBID experiment in Definition2. The cor-
rupted actors are controlled by the adversary, and
can communicate with provers and V at the same
time. i.e. A can receive a message m from P
and send m
0
to V , and vice versa. A protocol
is γ-MiM-resistant if for any such experiment, the
probability of verifier outputting Out
V
= 1 , while
there is no active close-by prover during the ses-
sion is limited by γ.
ICISSP 2017 - 3rd International Conference on Information Systems Security and Privacy
206

This general definition captures relay attack
(Brands and Chaum, 1994), mafia-fraud (Desmedt,
1988) and impersonation attack (Avoine et al., 2011).
In addition, this definition captures the case that there
are some close-by provers, but they are inactive. In
this case, if there is a successful protocol session, then
the protocol is not considered as MiM-resistant.
We consider two types of attacks by a dishonest
prover: a stand alone dishonest prover (Property3),
and a dishonest prover with a helper (Property4).
Property 3. (Distance-Fraud). Let the adver-
sary A corrupt the provers and set their locations
far-away from the verifier. The experiment is run
after this setting.
A protocol is called α-DF-resistant if, for any
DBID experiment exp, where all participants (ex-
cept V ) are far-away from V , we have Pr[Out
V
=
1] ≤ α.
In the following we define the soundness of
public-key DB protocols that captures security against
Terrorist-Fraud.
Definition 3. Let O be an oracle that takes the
key pair of a user and the locations of partici-
pants and actors, simulates a DBID experiment as
in Definition2, and supplies the view of close-by
participants, including the verifier, to the caller al-
gorithm.
A transcript sampler algorithm is an algorithm
that calls O once and generates a valid transcript
σ = (A,[c],[r]). A covering sampler algorithm S
calls O once to generate a set of valid transcripts
Σ = {σ
1
,..., σ
m
} such that, (i) all transcripts in Σ
have the same commitment value A, (ii) for each
round of the fast challenge/response phase (Step
2) there is a pair of transcripts (σ
0
,σ
00
) ∈ Σ such
that the challenge values of the two transcripts of
that round are different (complement), and (iii)
there are at least two transcripts (σ
0
,σ
00
) ∈ Σ that
have different challenge values for the slow chal-
lenge/response phase (Step 3).
A response sampler algorithm R is an algo-
rithm that calls O once and is able to generate a
valid transcript σ = (A
0
,[c
0
],[r
0
]) for any value of
[c
0
].
Property 4. (Soundness). Consider an adversary
who corrupts provers and actors, and sets the loca-
tion of actors and provers, close-by and far-away
respectively. For a key assignment of the prover,
and location set of provers and actors with the
above restrictions, a protocol is sound if the fol-
lowing holds:
If there is a covering sampler S as de-
fined in Definition3 that is successful with non-
negligible probability, then there is a PPT
response sampler R as defined in Definition3 that
is successful with non-negligible probability.
In the rest of this section we show that terrorist-
fraud (A6) is captured by the soundness (Property4).
First we rephrase the definition of terrorist-fraud re-
sistance.
Definition 4. (TF-resistance). Consider an ex-
periment in which provers are far-away from the
verifier while the actors are close-by and all are
controlled by the adversary. A DB protocol is TF-
resistant if the following statement holds:
If there is a TF adversary that succeeds with
non-negligible probability, then there exists a PPT
close-by adversary that takes the view of all close-
by actors as input and is able to impersonate the
prover with non-negligible probability.
Lemma 1. A DBID protocol that is sound ac-
cording to Property4, is TF-resistant according to
Definition4.
Proof. Consider the following diagram that starts
with a successful TF attack and ends with a successful
impersonation.
Success f ul T F
(i)
−→ S
(ii)
−→ R
(iii)
−−→ Impersonation
Our soundness definition of DBID protocols imply
that this diagram holds for the protocol. We will show
that (i) and (iii) hold for any DBID protocol, and so if
the protocol is sound, then the link in (ii) holds, and
the diagram is complete.
To show (iii), we note that for a DBID protocol, if
there is a response sampler R that takes the view of
close-by participants, and returns a valid transcript for
any challenge sequence (concatenated fast and slow
challenges), then R can be used to construct a suc-
cessful impersonation attacker. This immediately fol-
lows from the definition of a successful impersonation
attacker and R : the impersonation attacker runs a
learning phase during which it plays the role of the
verifier for a close-by prover, and provides the view
of the close-by participants to R . In the attack phase,
the impersonation attacker will provide the commit-
ment of the close-by prover in the learning phase, to
the verifier, and use R to provide responses for the
challenges of the verifier. The success of the imper-
sonation attacker follows because R is able to gener-
ate correct response to any challenge sequence.
To show (i) we need to show that if there is a
successful TF attacker (Definition4) then there is a
covering sampler. Suppose there is a TF adversary
A that succeeds with non-negligible probability p
1
.
The challenge sequence [c] is chosen randomly by
the honest verifier after they receive the commitment
A. During the fast phase, the response to the verifier
Distance-bounding Identification
207

cannot depend on the response in the same round, of
the far-away prover as such responses will be dropped
because they are outside the acceptable time-interval
(associated with the bound). The view of the close-by
participants however can be used to construct a valid
transcript with non-negligible probability p
1
. This
means that there is a sampler algorithm J that uses
this view and succeeds with non-negligible probabil-
ity p
1
in constructing a valid transcript. J can simu-
late the behavior of the honest verifier, which is gen-
erating the challenge bits randomly. We divide J into
two sub-algorithms (J
1
,J
2
) based on time. J
1
is the
sub-algorithm from the beginning of J up to the gen-
eration of commitment A, and J
2
is the sub-algorithm
from after generation of A up to the end of J .
To construct a covering sampler S we do the fol-
lowing: run J
1
once, followed by ` times of J
2
. Be-
fore running J
2
at any time, we rewind the memory
state of the algorithm to the end of J
1
. Let n denote
the number of challenge rounds in the fast exchange
round, and for simplicity assume binary challenges.
The following calculation shows that the probability
of constructing a covering sampler approaches 1 for
any n and p
1
, if ` is chosen sufficiently large.
Suppose the covering sampler algorithm S has
generated ` transcripts Σ = {σ
1
,σ
2
,..., σ
`
}, each with
n challenge bits. Each transcript is valid with prob-
ability p
1
. For a bit 1 ≤ i ≤ n, consider the list of
` bits
ˆ
b
i
= (b
i
1
,b
i
2
,...b
i
`
) belonging to σ
1
,σ
2
·· ·σ
`
re-
spectively. The bit is bad, if no pair of transcripts in
Σ have complementary values in this position. This
only happens if all the bits of
ˆ
b
i
are 0, or all are 1. So
the probability that the bit is good is, assuming all bits
belong to valid transcripts, is 1 −2
−`+1
. Note that out
of the ` bits, `× p
1
bits belong to valid transcripts and
so probability that the bit is good is, is 1 − 2
−p
1
`+1
.
This means the probability that all n bits are covered
is, (1− 2
−p
1
`+1
)
n
≥ 1 − n × 2
−p
1
`+1
. Since p
1
is con-
stant, and ` and n are polynomial in the security pa-
rameter, then for any n, ` can be chosen such that the
success chance of constructing the covering sampler
is arbitrarily close to 1. This implies that we can build
a covering sampler S that follows the success chance
the TF attack (i.e. p
1
).
4 PROPROX PROTOCOL
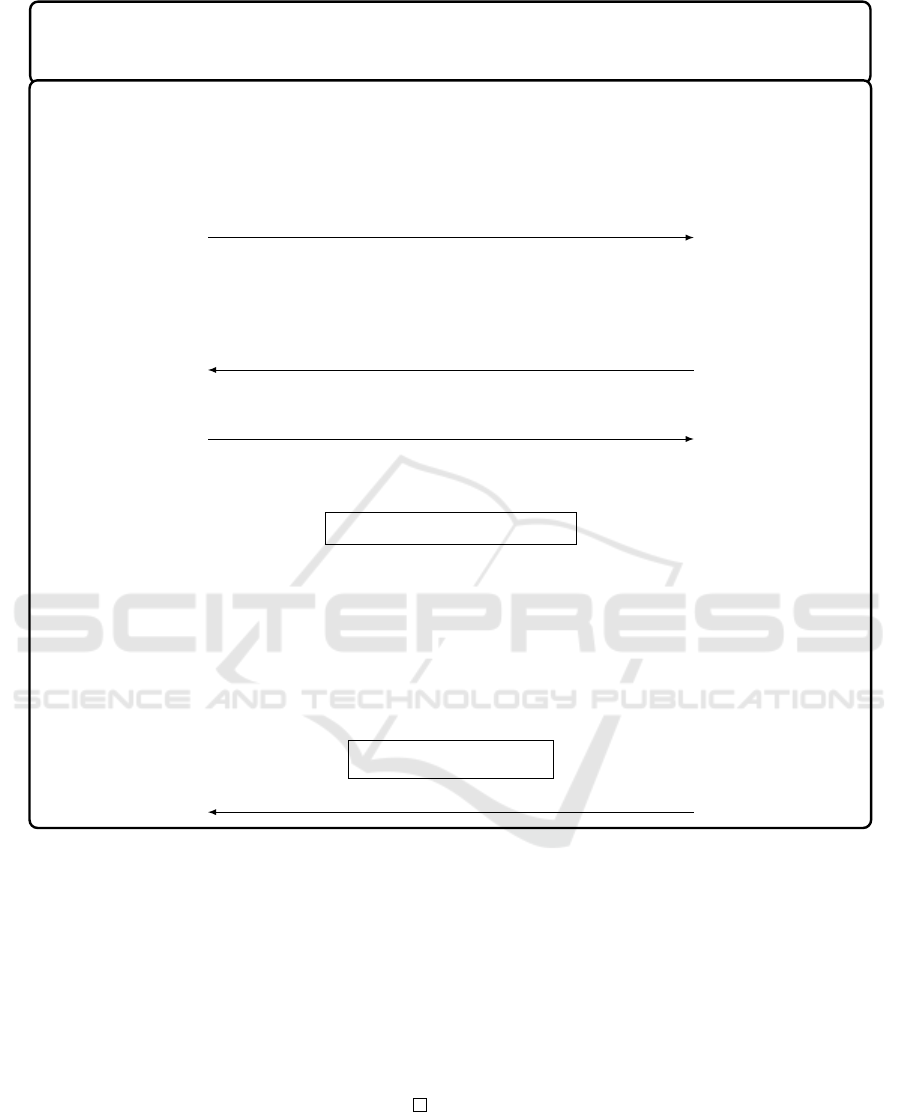
In this section we introduce ProProx (Figure1)
public-key DB protocol (Vaudenay, 2014) and show
that the protocol fits in DBID model. We also prove
security of the protocol in this model.
ProProx has λ as the secret the size, n as the num-
ber of rounds that is linear in λ, and t as the minimum
ratio of number of noiseless rounds to all rounds. The
vector b ∈ Z
n
2
has Hamming weight b
n
2
c and is fixed.
The j
th
bit of public-key is y
j
=KeyGen(x
j
) =
Com(x
j
;H(x, j)) where Com(b; ρ) = θ
b
ρ
2
(mod N)
for a bit b, and the random value ρ is given by
Goldwasser-Micali cryptosystem (Goldwasser and
Micali, 1984). For a fixed θ that is a residue modulo
N = P.Q such that (θ/P) = (θ/Q) = −1, for example
θ = −1, the algorithm Com is a homomorphic com-
mitment scheme that provides computational hiding
in the sense of zero-knowledgeness. More details can
be found in (Vaudenay, 2014).
In the verification phase, the prover and the veri-
fier determine a set I
j
of τ.n round indices that they
believe has not been affected by noise. The verifier
checks whether I
j
has cardinality τ.n and responses
are within the required time interval. The prover and
the verifier then run an interactive zero-knowledge
proof (ZKP
κ
) to show that the responses r
i, j
’s are con-
sistent with A
i, j
’s and y
j
’s. If the verification fails, the
verifier aborts the protocol by sending Out
V
= 0. Oth-
erwise, they send Out
V
= 1.
Theorem 1. ProProx is (τ,δ)-complete, sound,
γ-MiM-resistant and α-DF-resistant DBID proto-
col for negligible values of δ, γ and α, when
n.(1 − p
noise−ε
) > n.τ ≥ n − (
1
2
−2ε)d
n
2
e for some
constant ε > 0.
ProProx is shown to be distance-fraud resis-
tant and zero-knowledge (Definition8) in (Vaudenay,
2014). Our definitions of those properties remain un-
changed and so we only need to prove completeness,
soundness and MiM-resistance properties of DBID
model about ProProx protocol.
Lemma 2. (Completeness). ProProx is a com-
plete DBID protocol.
Proof. Let’s assume the verifier sends challenge se-
quence C = ([c],[ ¯c]), where [c] = [[c
1
]...[c
λ
]], [c
j
] =
[c
j
1
...c
j
n
] for all j ∈ {1,...,λ}, and [ ¯c] = [ ¯c
1
... ¯c
m
] for
some m ≥ 0, while the prover receives C
0
= ([c
0
],[ ¯c])
such that Pr[c
j
i
= c
0 j
i
] = 1 − p
noise
for all j ∈ {1,...,λ}
and i ∈ {1,..., n}. Correspondingly, the prover sends
the response sequence R = ([r],[¯r]) and the verifier re-
ceives R
0
= ([r
0
],[¯r]) such that Pr[r
j
i
= r
0 j
i
] = 1 − p
noise
for all j ∈ {1,...,λ} and i ∈ {1, ...,n}.
The verifier is honest and for an honest prover,
they are able to find and agree on the set of uncor-
rupted (noiseless) messages and so the protocol suc-
ceeds if for all values of j ∈ {1,...,λ} there exist at
least τ.n noiseless challenge/response rounds. The
failure chance of the protocol is not more than the
chance of having at least one j ∈ {1,..., λ} that has
less than τ.n noiseless challenge/response rounds.
The probability of having at least τ.n noiseless
ICISSP 2017 - 3rd International Conference on Information Systems Security and Privacy
208

P
i
V
j
(secret: x) (public: y = Com
H
(x))
commitment phase
∀ j ∈ {1,. .., λ},∀i ∈ {1, ... ,n}:
a
i, j
∈
R
Z
2
,ρ
i, j
∈
R
Z
∗
N
• A
i, j
= Com(a
i, j
;ρ
i, j
)
A
i, j
fast challenge/response phase
∀ j ∈ {1,. ..,λ},∀i ∈ {1, ... ,n}:
c
i, j
∈
R
Z
2
start timer •
c
i, j
receive c
0
i, j
• r
i, j
= a
i, j
+ c
i, j
b
i
+ c
i, j
x
j
r
i, j
receive r
0
i, j
stop timer •
verification phase
agree on I
1
,. .., I
s
⊂ {1,...,n}
∀ j ∈ {1,. .., λ}:
check |I
j
| = τ.n
check timer
i, j
≤ 2B
∀ j ∈ {1,. .., λ},i ∈ I
j
:
• v
j
= H(x, j)
• α
i, j
= ρ
i, j
v
c
i, j
j
z
i, j
= A
i, j
(θ
b
i
y
j
)
c
i, j
θ
−r
0
i, j
•
ZKP
κ,ζ
(α
i, j
: z
i, j
= α
2
i, j
)
Out
V
Figure 1: ProProx Protocol.
challenge/response rounds for a single j ∈ {1,...,λ}
is equal to Tail(n,τ.n,ρ) =
n
∑
i=τ.n

n
i

(ρ)
i
(1 − ρ)
n−i
for
ρ = 1 − p
noise
. As a result, the failure chance of the
protocol is limited by λ.(1 − Tail(n,τ.n,1 − p
noise
)).
Based on Chernoff bound (Lemma5) we know
that 1 − Tail(n,τ.n,1 − p
noise
) < e
−2ε
2
n
. Therefore,
the failure chance of the protocol is limited by
λ.e
−2ε
2
n
, which is negligible.
Lemma 3. (Soundness). ProProx is a sound
DBID protocol.
Proof. The challenger sets the secret of the provers.
The adversary sets the location of provers and actors
before start of the experiment and possibly corrupts
provers that are outside the bound.
According to the soundness definition
(Property4), we need to show that if there is a
PPT covering sampler (S ) that can create a covering
set of valid transcripts using the view of close-by
participants, then there exists a response sampler for
the protocol. In the following we will achieve this by
first proving a stronger property: we will show that
existence of S implies existence of a PPT extractor
(E) that uses S to find an x
0
such that KeyGen(x
0
) = y.
That is the extractor algorithm J will use S as a
subroutine to extract x
0
.
In ProProx the relation between each challenge
and response bit in the fast phase is r
i, j
= a
i, j
+c
i, j
b
i
+
c
i, j
x
j
. Since S can find a covering set σ = {σ
1
,..., σ
m
}
Distance-bounding Identification
209

that for any j ∈ {1,...,λ}, there is at least one pair of
transcripts (σ
0
,σ
00
) ∈ σ that c
0
i, j
6= c
00
i, j
, where c
0
i, j
be-
longs to σ
0
and c
00
i, j
belongs to σ
00
. Since the commit-
ted values (a
i, j
) are fixed in the two transcripts and
the value of b
i
is public and fixed in the protocol,
then we have r
0
i, j
− r
00
i, j
= a
i, j
+ c
0
i, j
b
i
+ c
0
i, j
x
j
− (a
i, j
+
c
00
i, j
b
i
+ c
00
i, j
x
j
) = (c
0
i, j
− c
00
i, j
)b
i
+ (c
0
i, j
− c
00
i, j
)x
j
. So for
all j ∈ {1, ...λ}, the value of x
j
can be computed as
x
j
=
r
0
i, j
−r
00
i, j
−(c
0
i, j
−c
00
i, j
)b
i
c
0
i, j
−c
00
i, j
. By using the extracted key
x in honest prover algorithm P(x), we build the re-
sponse sampler of Property4.
Lemma 4. (MiM-resistance). ProProx is a
γ-MiM-resistant DBID (Prop2) protocol for γ =
negl(λ), if the followings hold: τ.n ≥ n − (
1
2
−
2ε)d
n
2
e for some constant ε; Com
H
is one-way;
Com is homomorphic bit commitment with all
properties of Definition6; ZKP
κ
is a κ-sound
(Definition5) and ζ-zero-knowledge authentica-
tion (Definition8) for negligible κ and ζ.
Proof. The adversary A sets the locations of provers
and actors, and can control the actors who can com-
municate with P and V simultaneously. P and V
are assumed to behave honestly. The P ’s input in
an experiment consist of challenge values (i.e. {c
i, j
}
bits and challenge values of ZKP
κ
), that can take ar-
bitrary values, and will be responded by the prover
only once. Because of zero-knowledge property of
ProProx against any PPT verifier (that can be mali-
cious), the learning phase of the MiM adversary can-
not provide any information to the adversary as other-
wise there will be a malicious verifier that will violate
negl(λ)-zero-knowledge property of the protocol.
There are two possible participant arrangements
for winning conditions of a MiM adversary that result
in the verifier accepting a DBID instance: (i) all ac-
tive provers are far-away from the verifier, (ii) there
is no active prover during this session. In the follow-
ing we show that the success probability of the adver-
sary in both cases is negligible. In the first case, the
adversary cannot simply relay the messages because
of the extra delay and the fact that the responses are
from out of bound locations. In this case the veri-
fier will reject the instance. If there is a PPT adver-
sary A that can guess at least τ.n out of n responses
for each key bit with non-negligible probability (i.e.
guessing all bits of ∀ j ∈ {1,..., λ}I
j
⊂ {1, ...,n} such
that |I
j
| ≥ τ.n), then they can find the response ta-
ble for at least τ.n elements for each j ∈ {1,...,λ}
with the same probability. So for τ.n out of n val-
ues of i they can find correct x
j
=
r
i, j
− ¯r
i, j
−(c
i, j
− ¯c
i, j
)b
i
c
i, j
− ¯c
i, j
with probability ≥ poly(λ). Therefore by taking the
majority, they can find the correct key bit with proba-
bility ≥ 1 − (1 − poly(λ))
τ.n
.
Thus if the adversary succeeds in the first case
with non-negligible probability, then they can find
the secret-key with considerably higher probability
than random guessing and this contradicts the zero-
knowledge property of ProProx. Therefore, the ad-
versary’s success chance will be negligible in this
case.
In the second case, the adversary succeeds in the
protocol by providing the correct response to V for
at least τ.n correct queries out of n fast rounds for all
key bits.
We noted that the learning phase of the adver-
sary cannot provide information about the secret-key
({x
j
}) or the committed values ({a
i, j
}) as otherwise
the zero-knowledge property of the protocol, or the
commitment scheme will be violated, respectively.
In order to succeed in the protocol with
non-negligible probability, the adversary must
succeed in ZKP
κ
, for at least τ.n values of i,
so they need to find at least τ.n valid tuples
π
i
= (X ∈ G,Y ∈ {0,1},Z ∈ Z
∗
N
) for random chal-
lenge bits such that Z
2
= X(θ
b
i
y
j
)
c
i, j
θ
−Y
without hav-
ing information about x
j
. For π = [π
i
], |π| ≥ τ.n and
chg : challenge variables, Pr[valid π| random chg] =
∏
γ
i=1
Pr[valid π
i
| random chg]. So if
Pr[π is valid | random chg] ≥ negl(λ), then there
is a value of i that Pr[π
i
is valid | random chg] ≥
1
2
+ poly(λ). Since X is sent to the ver-
ifier before seeing c
i, j
, therefore we have
Pr[valid (X,Y, Z)|c
i, j
= 0] ≥
1
2
+ poly(λ) and
also Pr[valid (X,Y
0
,Z
0
)|c
i, j
= 1] ≥
1
2
+ poly(λ).
Since both tuples are valid, then we have Z
2
= Xθ
−Y
and Z
02
= X(θ
b
i
y
j
)θ
−Y
0
. Therefore we have the
following for y
j
= θ
x
j
(v
j
);
(
Z
0
Z
)
2
= y
j
θ
b
i
−Y
0
+Y
= θ
x
j
+b
i
−Y
0
+Y
(v
j
)
2
Therefore, the adversary can conclude x
j
+ b
i
−Y
0
+
Y /∈ {1,3} for the known bits b
i
, Y
0
and Y . So they
gain some information about x
j
, which is in contradic-
tion with zero-knowledge property of ProProx.
5 CONCLUSION
We motivated and proposed a new formal model
(DBID) for distance-bounding protocols, inline with
the cryptographic identification protocols, that cap-
tures and strengthens the main attacks on public-
key distance-bounding protocols. This effectively in-
cludes physical distance as an additional attribute of
the prover in identification protocol.
ICISSP 2017 - 3rd International Conference on Information Systems Security and Privacy
210

We motivated our work by examining the proof of
proximity of knowledge that incorporates the prover’s
distance as an extra attribute in proof of knowledge
systems, and showed that the soundness definition
cannot correctly capture the situation that the prover
is close-by but inactive. The DBID framework how-
ever correctly captures the soundness in this case. We
also showed the ProProx protocol fits our model and
proved its security in this model. Our future work in-
cludes designing more efficient DBID protocols, and
extending the model to include the anonymity of the
prover against the verifier.
REFERENCES
Ahmadi, A. and Safavi-Naini, R. (2014). Privacy-
preserving distance-bounding proof-of-knowledge. In
16th International Conference on Information and
Communications Security.
Avoine, G., Bing
¨
ol, M. A., Kardas¸, S., Lauradoux, C., and
Martin, B. (2011). A framework for analyzing RFID
distance bounding protocols. Journal of Computer Se-
curity, pages 289–317.
Bellare, M. and Palacio, A. (2002). Gq and schnorr identifi-
cation schemes: Proofs of security against imperson-
ation under active and concurrent attacks. In Annual
International Cryptology Conference, pages 162–177.
Springer.
Boureanu, I., Mitrokotsa, A., and Vaudenay, S. (2013).
Practical & provably secure distance-bounding. In
The 16th Information Security Conference.
Brands, S. and Chaum, D. (1994). Distance-bounding pro-
tocols. In Advances in Cryptology–EUROCRYPT’93,
pages 344–359. Springer.
Chernoff, H. (1952). A measure of asymptotic efficiency
for tests of a hypothesis based on the sum of ob-
servations. The Annals of Mathematical Statistics,
23(4):493–507.
Cremers, C., Rasmussen, K. B., Schmidt, B., and Cap-
kun, S. (2012). Distance hijacking attacks on distance
bounding protocols. In Security and Privacy, pages
113–127.
Desmedt, Y. (1988). Major security problems with the
¨
unforgeable
¨
(feige-)fiat-shamir proofs of identity and
how to overcome them. In Congress on Computer
and Communication Security and Protection Securi-
com’88, pages 147–159.
D
¨
urholz, U., Fischlin, M., Kasper, M., and Onete, C.
(2011). A formal approach to distance-bounding
RFID protocols. In Information Security, pages 47–
62. Springer.
Gambs, S., Killijian, M.-O., Lauradoux, C., Onete, C., Roy,
M., and Traor
´
e, M. (2014). Vssdb: A verifiable secret-
sharing and distance-bounding protocol. In Interna-
tional Conference on Cryptography and Information
security (BalkanCryptSec’14).
Goldwasser, S. and Micali, S. (1984). Probabilistic en-
cryption. Journal of computer and system sciences,
28(2):270–299.
Hermans, J., Peeters, R., and Onete, C. (2013). Efficient, se-
cure, private distance bounding without key updates.
In Proceedings of the sixth ACM conference on Se-
curity and privacy in wireless and mobile networks,
pages 207–218. ACM.
Hoeffding, W. (1963). Probability inequalities for sums of
bounded random variables. Journal of the American
statistical association, 58(301):13–30.
Kurosawa, K. and Heng, S.-H. (2006). The power of iden-
tification schemes. In Public Key Cryptography-PKC
2006, pages 364–377. Springer.
Lyubashevsky, V. and Masny, D. (2013). Man-in-the-
middle secure authentication schemes from lpn and
weak prfs. In Advances in Cryptology – CRYPTO’13,
pages 308–325. Springer.
Vaudenay, S. (2014). Proof of proximity of knowledge.
IACR Eprint, 695.
APPENDIX
Definition 5. (Authentication). An authentica-
tion protocol is an interactive pair of protocols
(P(ζ),V (z)) of PPT algorithms operating on a
language L and relation R = {(z,ζ) : z ∈ L,ζ ∈
W (z)}, where W(z) is the set of all witnesses for
z that should be accepted in authentication. This
protocol has the following properties:
• complete: ∀(z,ζ) ∈ R, we have Pr(Out
V
= 1 :
P(ζ) ↔ V (z)) = 1.
• κ-sound: Pr(Out
V
= 1 : P
∗
↔ V (z)) ≤ κ in
any of the following two cases; (i) z /∈ L, (ii)
z ∈ L while algorithm P
∗
is independent from
any ζ ∈ W (z). Pr(Out
V
= 1 : A
2
(View
A
1
) ↔
V (z)) ≤ negl.
Definition 6. (Homomorphic Bit Commit-
ment). A homomorphic bit commitment function
is a PPT algorithm Com operating on a mul-
tiplicative group G with parameter λ, that
takes b ∈ Z
2
and ρ ∈ G as input, and returns
Com(b; ρ) ∈ G. This function has the following
properties:
• homomorphic: ∀b,b
0
∈ Z
2
and ∀ρ, ρ
0
∈ G,
we have Com(b; ρ)Com(b
0
;ρ
0
) = Com(b +
b
0
;ρρ
0
).
• perfect binding: ∀b,b
0
∈ Z
2
and ∀ρ,ρ
0
∈ G,
the equality Com(b;ρ) = Com(b
0
;ρ
0
) implies
b = b
0
.
• computational hiding: for a random ρ ∈
R
G,
the distributions Com(0,ρ) and Com(1, ρ) are
computationally indistinguishable.
Distance-bounding Identification
211

Definition 7. (One-way Function). By consid-
ering λ as the security parameter, an efficiently
computable function OUT ← FUNC(IN), is one-
way if there is no PPT algorithm that takes OUT
as input and returns IN with non-negligible prob-
ability in terms of λ.
Definition 8. (Zero-Knowledge Protocol).
A pair of protocols (P(α),V (z)) is ζ-zero-
knowledge for P(α), if for any PPT interactive
machine V
∗
(z,aux) there is a PPT simulator
S(z,aux) such that for any PPT distinguisher,
any (α : z) ∈ L, and any aux ∈ {0,1}
∗
, the
distinguishing advantage between the final view
of V
∗
, in the interaction P(α) ↔ V
∗
(z,aux), and
output of the simulator S(z,aux) is bounded by ζ.
Lemma 5. (Chernoff-Hoeffding Bound (Cher-
noff, 1952), (Hoeffding, 1963)). For any
(ε,n, τ,q), we have the following inequalities
about the function Tail(n,τ,ρ) =
n
∑
i=τ

n
i

ρ
i
(1 −
ρ)
n−i
;
• if
τ
n
< q − ε, then Tail(n, τ,q) > 1 − e
−2ε
2
n
• if
τ
n
> q + ε, then Tail(n, τ,q) < e
−2ε
2
n
ICISSP 2017 - 3rd International Conference on Information Systems Security and Privacy
212