Instrumenting a Context-free Language Recognizer
Paulo Roberto Massa Cereda and João José Neto
Escola Politécnica, Departamento de Engenharia de Computação e Sistemas Digitais, Universidade de São Paulo,
Av. Prof. Luciano Gualberto, s/n, Travessa 3, 158, CEP: 05508-900, São Paulo, SP, Brasil
Keywords:
Context-free Language, Structured Pushdown Automaton, Instrumentation.
Abstract:
Instrumentation plays a crucial role when building language recognizers, as collected data provide basis for
achieving better performance and model improvements, thus offering a balance between time and space, as
demanded by practical applications. This paper presents a simple yet functional semiautomatic approach for
generating a instrumentation-aware context-free language recognizer, enhanced with hooks, from a grammar
written using the Wirth syntax notation. The entire process is aided by a set of command line tools, freely
available for download. We also introduce the concept of an instrumentation layer enclosing the underlying
recognizer, acting as observer for each computational step and collecting data for later use.
1 INTRODUCTION
Instrumentation is the capability of monitoring or
measuring performance of a device, as well as trac-
ing information during its life cycle (Wert et al.,
2015). Such metrics allow an accurate understand-
ing of the device’s inner workings and provide base
for improvements on the model (Paul and Vahren-
hold, 2013; Ball and Larus, 1994). In general, it
is advisable to combine different metrics in order to
obtain a more comprehensive representation of the
device’s collected data, in an attempt to reduce bias
(which might cause misjudgement of the model as a
whole) (Wert et al., 2015).
Language recognition devices are mechanisms ca-
pable of reading strings built from an set Σ of sym-
bols (also known as language alphabet) and decide
whether such strings are in the language they de-
scribe (Aho and Ullman, 1995). These devices play
an important role in several areas, including program-
ming languages; context-free language recognizers
are widely used to design parsers (syntactic analy-
sers), which work out the grammatical structure of
strings according to a set of rules. It is highly ad-
visable to have deterministic devices, although that is
not always possible (Sebesta, 2013).
Recognizers need to be reasonably efficient, in
time and space, when analysing a string. Practical ap-
plications demand a balance between these two fac-
tors (Cooper and Torczon, 2011). Hence, understand-
ing the inner workings of such devices and particu-
lar features of the languages for which they are con-
structed is crucial to achieving better performance
and providing model improvements (Ball and Larus,
1994). Designing instrumentation-aware recognizers
allows performance monitoring and information trac-
ing, as well as gathering potential findings about the
languages themselves and their formation rules.
We present a simple yet functional semiauto-
matic approach for generating a instrumentation-
aware context-free language recognizer from a gram-
mar written using the Wirth syntax notation, as well
as querying the recognizer and collecting instrumen-
tation data based on a set of metrics. The entire pro-
cess is aided by a set of command line tools, freely
available for download.
This paper is organized as follows: Section 2 in-
troduces the basic concepts of a context-free language
recognizer, the Wirth syntax notation used to describe
programming languages, and a process to automate
the generation of a structured pushdown automaton
given a WSN grammar. Section 3 presents the instru-
mentation layer, the set of metrics and its operational
semantics. Conclusions are presented in Section 4.
2 BACKGROUND
In this paper, we will use a structured pushdown au-
tomaton as our recognizer for context-free languages.
We aim at generating a recognizer instance from a
language grammar written using the Wirth syntax no-
tation and then instrumenting it later. The generation
Cereda, P. and Neto, J.
Instrumenting a Context-free Language Recognizer.
DOI: 10.5220/0006212002030210
In Proceedings of the 19th International Conference on Enterprise Information Systems (ICEIS 2017) - Volume 2, pages 203-210
ISBN: 978-989-758-248-6
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
203

will be aided by a set of command line tools written
for this purpose. Before we proceed, let us formally
introduce the concepts.
The structured pushdown automaton (SPA) (José
Neto and Magalhães, 1981; José Neto, 1993) is a kind
of pushdown automaton composed of a set of mutu-
ally recursive finite automata, also known as subma-
chines. Unlike the traditional pushdown automaton,
the stack is only used to store references to return
states on each submachine call. Calls and returns con-
sist on transferring control from one submachine to
another; this special transition uses the input symbol
to make a decision on which transition should be ex-
ecuted (the symbol is then consumed in the next tran-
sition) (José Neto, 1993; José Neto, 1994).
A structured pushdown automaton M is defined as
M = (Q,A,Σ,Γ,P,Z
0
,q
0
,F), in which Q is the set of
states, A is the set of submachines, defined as fol-
lows, Σ is the automaton alphabet, corresponding to
the non-empty set of input symbols, Γ is the set of
stack symbols, P is the transition relation, q
0
∈ Q
is the initial state (of the first submachine), Z
0
is a
special symbol acting as an empty stack marker, and
F ⊆ Q is the set of accepting states (of the first sub-
machine) (José Neto and Magalhães, 1981; José Neto,
1993).
A submachine a
i
∈ A is defined as a traditional fi-
nite automaton a
i
= (Q
i
,Σ
i
,P
i
,q
i,0
,F
i
), in which Q
i
⊆
Q is the set of states of a
i
, Σ
i
⊆ Σ is the set of input
symbols of a
i
, q
i,0
is the entry state of a
i
, P
i
⊆ P is the
transition relation of a
i
, and F
i
⊆ F is the set of return
states of a
i
.
The transition relation P is defined as P ⊆ Γ ×
Q × Σ × Γ × Q, in the form (γg,e,sα) → (γg
′
,e
′
,α),
in which e,e
′
are the current and target states, respec-
tively, s is the consumed symbol, α is the remainder of
the input string, g is the current top of the stack, g
′
is
the new top of the stack, and γ is the remainder of the
stack. A configuration is an element of Q × Σ
∗
× Γ
∗
,
and a relation between successive configurations ⊢ is
defined as follows:
– Symbol consumption: (q,σw,uv) ⊢ (p,w,xv), with
p,q ∈ Q, u,x ∈ Γ, v ∈ Γ
∗
, σ ∈ Σ∪{ε}, w ∈ Σ
∗
, if σ
was consumed, x = u, e (γ, q, σα) → (γ, p,α) ∈ P.
– Submachine call: (q,w,uv) ⊢ (r,w, xv), with q,r ∈
Q, u ∈ Γ, v, x ∈ Γ
∗
, w ∈ Σ
∗
, x = pu, with a call to
the submachine R, initial state r, return in p, and
(γ,q,α) → (γp, r,α) ∈ P.
– Submachine return: (q,w, uv) ⊢ (p, w,v), with
p,q ∈ Q, u,x ∈ Γ, v ∈ Γ
∗
, w ∈ Σ
∗
, u = p, with sub-
machine return to p, and (γg,q,α) → (γ,g,α) ∈ P.
The language recognized by a structured push-
down automaton M is given by L(M) = {w ∈ Σ
∗
|
(q
0
,w, Z
0
) ⊢
∗
( f,ε,Z
0
), f ∈ F}.
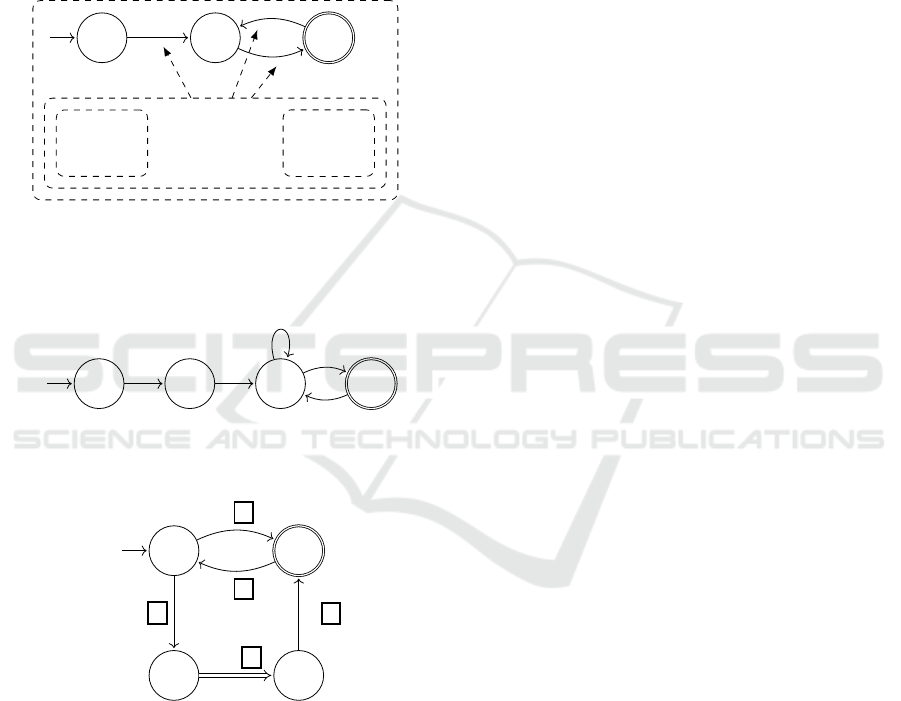
A submachine call can be graphically represented
by a transition with double lines as illustrated in Fig-
ure 1. Note that, from state q
im
of submachine a
i
,
execution is transferred to the submachine a
j
and the
address regarding the return state q
in
is inserted into
the top of the stack. In the example, the current state
becomes q
i0
, which is the initial of the submachine
a
j
.
q
im
q
in
q
j0
a
j
...
a
j
Figure 1: Example of call to the submachine a
j
.
It is important to note that, as a matter of
model organization, it is assumed that a
i
,a
j
∈ A,
a
i
= (Q
i
,Σ
i
,P
i
,q
i,0
,F
i
), a
j
= (Q
j
,Σ
j
,P
j
,q
j,0
,F
j
), Q
i
∩
Q
j
=
/
0 and P
i
∩P
j
=
/
0, i.e. sets of states and mappings
of submachines are disjoint.
Automata are devices that, based on a set of for-
mation rules of a language, can decide whether an in-
put string is a valid sentence, i.e. the input string is a
element of the set of all sentences in that language. In
the late 1970s, Wirth (Wirth, 1977) presented a met-
alanguage for describing programming languages, in
an attempt to provide a simplified notation as alterna-
tive to existing initiatives, specially the Backus-Naur
Form (BNF); such metalanguage became known as
Wirth syntax notation (WSN) and has the following
properties:
i) The notation shows a clear distinction between
metasymbols, terminal and nonterminal symbols.
Existing metasymbols are =, ., (, ), [, ], {, },
| and ". A nonterminal symbol is denoted by an
identifier, i.e. one letter followed by zero or more
letters and digits (as an usual variable definition
in a programming language), while the terminal
symbol is expressed by a string enclosed in dou-
ble quotes.
ii) There is no restriction regarding the use of meta-
symbols as symbols of language being described.
For example, the metasymbol | differs from ter-
minal symbol "|".
iii) The notation avoids heavy use of recursion to ex-
press simple repetitions by having a construct to
express explicit iteration. Repetition is denoted
by curly brackets.
iv) There is no need to use an explicit symbol to
represent the empty string, such as hemptyi in
BNF or ε, because the notation already has con-
structs that address this situation. Optionality is
expressed by square brackets.
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
204

According to Wirth (Wirth, 1977), the repeti-
tion is denoted by curly braces, i.e. { a } repre-
sents ε | a | aa | aaa | ... (Kleene star). Op-
tional elements are expressed through square brack-
ets, i.e. [ a ] represents a | ε. Parentheses are used
to represent grouping, i.e. ( a | b ) c represents
ac | bc. Terminal symbols are expressed enclosed
in double quotes; if the double quotes appear as literal
symbols, these are duplicated. Some alternative rep-
resentations express literal double quotes like "\""
instead of """"; Wirth’s original article prefers dupli-
cating double quotes.
The simplicity of the Wirth syntax notation al-
lows a trivial representation of the grammar ele-
ments as internal and external transitions of the SPA
(symbol consumption and submachine calls, respec-
tively) (José Neto, 1987; José Neto et al., 1999).
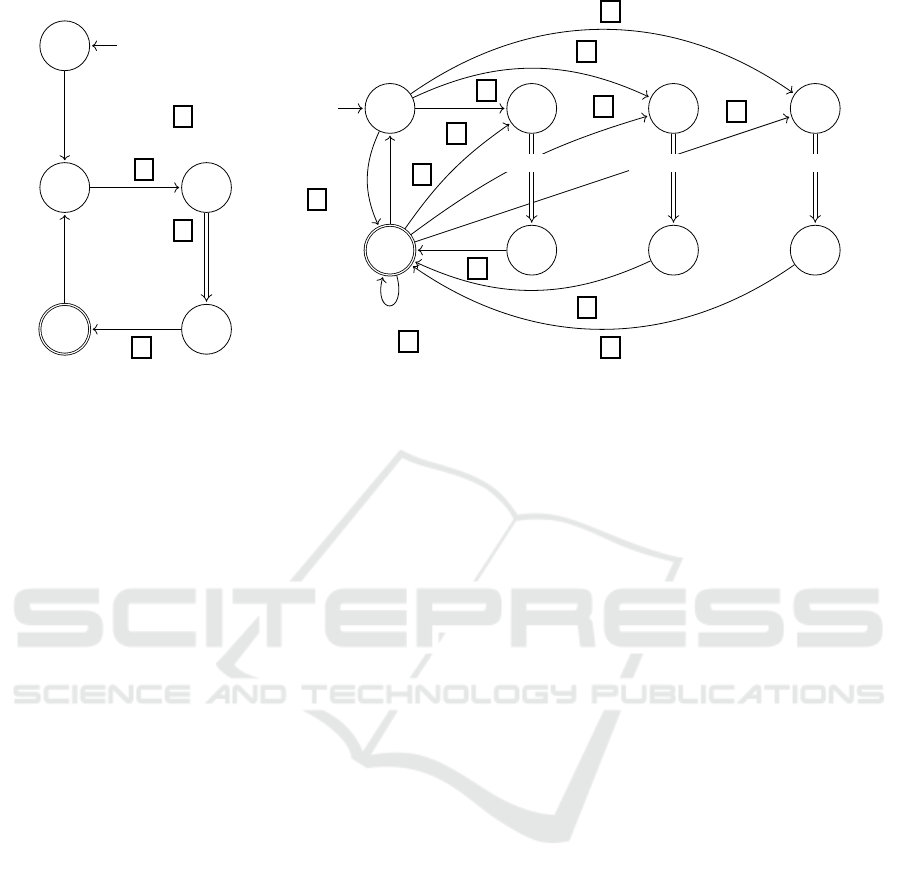
Given a grammar written in WSN, we can use the
SPA presented in Figure 2 in order to obtain a result-
ing SPA that recognizes sentences from the language
expressed in the provided grammar (José Neto, 1987;
José Neto et al., 1999; Cereda and José Neto, 2015).
Semantic actions associated with transitions are de-
scribed in Figure 3.
The resulting SPA is potentially nondeterminis-
tic; however, as each submachine is in itself a fi-
nite automaton, the automaton could be translated to
an equivalent deterministic SPA using classic subset
construction algorithms (Cooper and Torczon, 2011;
Sebesta, 2013). Also, each submachine could be re-
duced to an equivalent automaton with a minimum
number of states through minimization (Hopcroft,
1971).
We willuse a command line tool named wsn2spa
1
in order to automate the SPA generation from a gram-
mar written in WSN; there are options for determin-
istic translation and state minimization as well. The
tool is written in Java and it is released under GPLv3
(the GNU General Public License 3.0). The default
output is a DOT (plain text graph description lan-
guage) file, but we are also interested in the secondary
format, a YAML (human-friendly data serialization
standard) file, which provides a textual, structural rep-
resentation of the resulting SPA. We will discuss the
usage later on, in the next section.
3 INSTRUMENTING A
RECOGNIZER
Consider the automation flow presented in Figure 4.
From a grammar, written in WSN, representing arith-
1
Official repository: https://goo.gl/pULqpm
metic expressions (for simplicity purposes, we are
only considering addition and nested parentheses),
wsn2spa generates a SPA spec. The language is
clearly context-free; validsentences include a, a + a,
(a + a), a + (a + a), and so on. The graphical
representation of this specific SPA spec is presented
in Figure 5.
Note that the call to wsn2spa shown in Figure 4
included two optional flags, -c and -m. As the output
indicates, the generated SPA had the submachine AE
translated to its equivalentminimized deterministic fi-
nite automaton. The tool also generated a DOT file
representing the submachine AE (and each additional
operation applied to it); the file can be compiled with
the dot command (from GraphViz). If the SPA had
more submachines, the tool would generate a set of
DOT and YAML files representing each submachine.
Once we have the SPA spec (possibly comprised
of individual submachine specs), we can use another
helper tool, named spa2run
2
, in order to submit
string queries to the automaton and check whether
they are valid sentences in the language the SPA rec-
ognizes. The tool is also written in Java and it is re-
leased under GPLv3, just as wsn2spa. The input takes
a list of submachine specs written in YAML (being
the first item in the list the main submachine); once
this list is provided, the tool generates an on-the-fly
executable code and grants a shell session in order to
query the automaton. The user can abort the session
at any time by pressing a certain combination of keys
or using the reserved keyword :quit as input string.
Figure 6 shows spa2run in action, as it instantiates
the SPA spec generated in Figure 4 into a proper au-
tomaton and allows querying it.
Now that we have means of describing a context-
free language through WSN, generate its correspond-
ing recognizer (namely, a SPA) and query an automa-
ton instance to check whether an input string is a valid
sentence of that language, we are able to go further
and instrument the recognizer. But first, let us for-
mally introduce the operational semantics of our in-
strumentation.
Let us define a set B = {b | b: P 7→ R} of instru-
mentation metrics, i.e. a set of functions that takes an
element of the transition relation and returns a real
value. This approach allows us to simultaneously ap-
ply several metrics to the very same recognition in-
stance.
In order to keep track of each metric, the instru-
mentation layer (presented in Figure 7) provides a list
V of real variables, |V| = |B|, such that each variable
v
i
∈ V is associated with a function b ∈ B. At first,
∀v
i
∈ V, v
i
← 0. For each computational step in the
2
Official repository: https://goo.gl/MvCnQs
Instrumenting a Context-free Language Recognizer
205

1
Grammar
2
3
4
5
nonterminal
1
=
2
.
3
nonterminal
1
Expression
6
Expression
7
8
9
10
11
12
13
nonterminal,
terminal,
ε
4
|
7
nonterminal,
terminal, ε
4
(
2
[
5
{
6
)
3
]
3
}
3
(
2
[
5
{
6
Expression Expression Expression
Figure 2: SPA that generates another SPA given a grammar written in WSN.
Semantic action 1
stack.empty(); current := 0; counter := 1
Semantic action 2
stack.push(pair(current, counter))
counter := counter + 1
Semantic action 3
stack.empty()
transitions.add(transition(current,
epsilon, stack.top().second())
current := stack.top().second()
stack.pop()
Semantic action 4
transitions.add(transition(current,
token, counter))
counter := counter
Semantic action 5
transitions.add(transition(current,
epsilon, counter))
stack.push(pair(current, counter))
counter := counter + 1
Semantic action 6
transitions.add(transition(current,
epsilon, counter))
current := counter
stack.push(pair(counter, counter))
counter := counter + 1
Semantic action 7
transitions.add(transition(current,
epsilon, stack.top().second()))
current := stack.top().first()
Figure 3: Semantic actions associated with transitions of the SPA from Figure 2.
Grammar, written in WSN
AE = ( "a" | "(" AE ")" )
{ "+" ( "a" | "(" AE ")" ) } .
Running the tool...
$ java -jar wsn2spa.jar grammar.txt \
-o dot%s.dot -y spec%s.yaml -c -m
[lines omitted]
- Submachines translated to DFA’s.
- State minimization applied.
YAML spec for the main submachine
name: AE
initial: 0
accepting: [1]
transitions:
- { from: 0, symbol: a, to: 1 }
- { from: 0, symbol: (, to: 2 }
- { from: 1, symbol: +, to: 0 }
- { from: 2, symbol: AE (call), to: 3 }
- { from: 3, symbol: ), to: 1 }
Figure 4: Automation flow from a grammar representing simple arithmetic expressions (only addition and nested parentheses),
written in WSN, to the corresponding SPA spec.
recognition process of a string w, the current matched
transition p ∈ P is measured through each function
b
i
∈ B and the result is added to its correspondingvari-
able v
i
∈ V, such that v
i
← v
i
+ b
i
(p). It is important
to observe that we require every function in B to be
total, thus ∀p ∈ P, if b
i
(p) is not explicitly defined,
b
i
(p) = 0 by definition.
As an example, consider the SPA presented in Fig-
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
206

Minimized,
deterministic version
0
AE
1
2
3
a
+
(
)
AE
Highlighting the regular and
context-free parts
0
AE
1
2
3
a
+
(
)
AE
Regular part
Context-free part
Figure 5: Graphical representation of the SPA spec from
Figure 4.
ure 8. For simplicity’s sake, the stack was omitted.
This particular automaton recognizes sentences from
a regular language L, defined as L = {w ∈ {a, b}
∗
|
w = abb
∗
a(bb
∗
a)
∗
}. Now, let us introduce a set
B = {b
1
,b
2
} of instrumentation metrics such that:
– b
1
is a total function, b
1
: P 7→ R, in which
b
1
(h0,a,1i) = 1.0, b
1
(h1,b,2i) = 3.0,
b
1
(h2,b,2i) = 2.0, b
1
(h2,a,3i) = 4.0,
b
1
(h3,b,2i) = 6.0.
– b
2
is a total function, b
2
: P 7→ R, in which
b
2
(h0,a,1i) = 0.34, b
2
(h1,b,2i) = 1.42,
b
2
(h2,b,2i) = 3.87, b
2
(h2,a,3i) = 3.21,
b
2
(h3,b,2i) = 5.16.
Given a string w = abbaba, the instrumentation
layer collects each measurement during the recogni-
tion process and updates the variables accordingly.
When the automaton effectively stops, as there are
no valid transitions to apply given the current symbol
(none, actually), the variables hold the instrumenta-
tion results, namely v
1
= 20.0 and v
2
= 17.21 (values
corresponding to the sum of the application of a func-
tion b
i
∈ B to each matched transition p ∈ P when
recognizing w).
In this paper, the set B of instrumentation met-
rics is solely composed of functions that take an el-
ement p ∈ P and return a real value; also, being
M = hm
1
...m
n
i, ∀m
i
∈ M, m
i
∈ P, the sequence of all
matched transitions during the recognition process of
a string w, the instrumentation results are stored in a
listV of variables, such that ∀v
i
∈ V,v
i
=
∑
|M|
j=1
b
i
(m
j
),
i.e. each variable holds the sum of its corresponding
instrumentation function taking each element in the
list of matched transitions. However, these concepts
could be generalized in order to cover other domains,
as well as applying complex data manipulation and
computation.
Now that the concept has been formally intro-
duced, let us see how one can use spa2run to in-
strument a SPA recognizer and collect metrics accord-
ingly. But first, we need to add hooks to our automa-
ton spec in order to make it instrumentation-aware,
so the layer can detect whether a computational step
should be measured.
As to reduce verbosity, each transition p ∈ P is la-
beled with a positive integer k ∈ Z,k > 0, acting as a
unique identifier and hook regarding p. This approach
favours the design principle of separation of concerns,
as it provides a straightforward interface such that
each potential layer enclosing an underlying recog-
nizer and acting as an observer for each computational
step addresses a separate processing based on hooks.
Figure 9 presents the SPA from Figure 5 enhanced
with hooks, graphically represented as framed num-
bers. Note that the notation for representing hooks
was informally introduced in Figure 2, in which tran-
sitions are associated with semantic actions; this is no
coincidence, as hooks act an interface to layers, re-
gardless of their underlying processing. We will dis-
cuss this later on, in the next section.
According to Figure 9, every transition p ∈ P
contains an associated positive integer i,i ∈ Z, act-
ing as a unique identifier and hook. Now, let us in-
troduce a set B = {b
1
} of instrumentation metrics,
such that b
1
is a total function, b
1
: P 7→ R, in which
b
1
(h0,a,γ,1,ε,γi) = 2.0, b
1
(h1,+,γ,0,ε,γi) = 6.0,
b
1
(h0,(,γ,2,ε,γi) = 7.0, and b
1
(h3,),γ,1,ε,γi) =
5.0. Note that we deliberately omitted the subma-
chine call, namely 2 → 3, as such transition will not
be measured; hence, by definition, ∀p
′
∈ P, p
′
is a
submachine call, b
1
(p
′
) = 0.
The spa2run tool uses a lookup function ψ,
such that ψ: Z 7→ P, i.e. the function maps identi-
fiers to their corresponding transitions. Given the
SPA from Figure 9 and the set B of instrumentation
metrics previously defined, ψ(1) = h0,a,γ,1,ε,γi,
ψ(2) = h1,+,γ,0,ε,γi, ψ(3) = h0,(,γ,2,ε,γi, ψ(4) =
h3,),γ,1,ε,γi, and ψ(5) = h2,σ,γ,0,σ,3γi. The tool
combines the provided set B of instrumentation met-
rics with its lookup function in order to query values
based on transition identifiers, e.g. b
1
(ψ(1)) = 2.0,
which is much more understandable from the user’s
point of view.
As the next step, we need to update the SPA spec
from Figure 4 in order to make it instrumentation-
aware. The update is straightforward, as it suffices to
include an identifier key to each transition defini-
tion, matching the numbering scheme from Figure 9.
An excerpt of the new spec is presented in Figure 10.
Once the SPA is updated with the corresponding
transition identifiers (as seen in Figure 10), spa2run
Instrumenting a Context-free Language Recognizer
207

Running the tool...
$ java -jar spa2run.jar \
specEA.yaml
[lines omitted]
Starting shell, please wait...
(press CTRL+C or type ‘:quit’
to exit the application)
Queries
[1] query> (a+(a+a+a))
[1] result> true (deterministic)
[2] query> (a+(a+a)
[2] result> false (deterministic)
Figure 6: The spa2run tool instantiates the SPA spec generated from wsn2spa (Figure 4) as a proper automaton and provides
a shell session for queries.
v
1
...
v
n
metric 1
metric n
Instrumentation layer
Figure 7: The instrumentation layer, enclosing an underly-
ing recognizer. Note that the layer acts as an observer for
each computational step and updates the list of variables ac-
cording to their corresponding instrumentation metrics.
0
1 2
3
a b
b
a
b
Figure 8: SPA that recognizes sentences from L = {w ∈
{a,b}
∗
| w = abb
∗
a(bb
∗
a)
∗
}.
0
AE
1
2
3
a
1
+
2
(
3
)
4
AE
5
Figure 9: SPA from Figure 5 enhanced with hooks, graphi-
cally represented as framed numbers.
can now take a list of metrics specs, using the -i flag,
and instrument the recognizer accordingly. Figure 11
illustrates the instrumentation metric b
1
∈ B, previ-
ously defined and codified as a spec in the YAML for-
mat, as well as the new instrumentation-aware shell
session. Note that the metric spec deliberately om-
mits the submachine call, as it will not be measured.
Consider a second instrumentation metric b
2
added to the set B of instrumentation metrics de-
fined previously, such that b
2
∈ B,B = {b
1
,b
2
},
transitions:
- { from: 0, symbol: a, to: 1, identifier: 1 }
- { from: 0, symbol: (, to: 2, identifier: 3 }
- { from: 1, symbol: +, to: 0, identifier: 2 }
- { from: 2, symbol: AE (call),
to: 3, identifier: 5 }
- { from: 3, symbol: ), to: 1, identifier: 4 }
Figure 10: Excerpt of the new YAML spec for the SPA from
Figure 9, including the transition identifiers (associated pos-
itive integers) in order to make it instrumentation-aware.
and b
2
is a total function, b
2
: P 7→ R, in which
b
2
(h0,a,γ,1,ε,γi) = 3.2, b
2
(h1,+,γ,0,ε,γi) = 1.78,
b
2
(h0,(,γ,2,ε,γi) = 5.57, and b
2
(h3,),γ,1,ε,γi) =
4.23. As in b
1
, note that we deliberately omitted the
submachine call, namely 2 → 3, as such transition
will not be measured; hence, by definition, ∀p
′
∈ P,
p
′
is a submachine call, b
2
(p
′
) = 0. Figure 12 shows
the corresponding metric spec codified in the YAML
format, as well as queries from spa2run using the set
B of instrumentation metrics.
Instrumentation metrics can be used to evaluate
the recognizer’s behaviour over time and study char-
acteristics of the language itself, based on individ-
ual analysis of a group of strings. For instance,
consider the SPA from Figure 5, the set B of in-
strumentation metrics, previosuly defined, L
i
is de-
fined as L
i
= {w ∈ L | |w| = i}, i.e. a subset of lan-
guage L in which all valid strings have length i, and
∀i ∈ Z,i mod 2 = 0,L
i
=
/
0, i.e. only strings with odd
lengths are valid (the subset of valid strings with even
lengths is empty); let us write an evaluation test and
instrument every string w ∈ L
i
,3 ≤ i ≤ 11,i mod 2 6=
0, such that x
i, j
=
∑
L
i
w∈L
i
v
j
/|L
i
|, with 1 ≤ j ≤ |B|, i.e.
x
i, j
holds the arithmetic mean of the instrumentation
results from v
j
applied to all valid strings of length i,
and v
j
is associated to the sum of the application of
a function b
j
∈ B to each matched transition p ∈ P
when recognizing w ∈ L
i
. We applied a string genera-
tor based on the WSN grammar of L in order to gener-
ate all valid strings w ∈ L
i
and then used spa2run as
an instrumentation interface to the SPA. The obtained
results are presented in Figure 13.
According to Figure 13, the instrumentation re-
sults grow proportionally to the length of a string
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
208

Metric codified as a YAML spec
name: B1
mapping:
- { identifier: 1, value: 2.0 }
- { identifier: 2, value: 6.0 }
- { identifier: 3, value: 7.0 }
- { identifier: 4, value: 5.0 }
Running the tool...
$ java -jar spa2run.jar \
specEA.yaml -i b1.yaml
Queries
[1] query> (a+(a+a+a))
[1] result> true (deterministic)
B1: 50.0
[2] query> ((a))
[2] result> true (deterministic)
B1: 26.0
Figure 11: Instrumentation metric b
1
, codified as a spec in the YAML format, and a instrumentation-aware shell session from
spa2run, using the new SPA spec from Figure 10. Note that the instrumentation metric used by spa2run relies on identifiers
instead of transitions, as to reduce verbosity.
Metric codified as a YAML spec
name: B2
mapping:
- { identifier: 1, value: 3.20 }
- { identifier: 2, value: 1.78 }
- { identifier: 3, value: 5.57 }
- { identifier: 4, value: 4.23 }
Running the tool...
$ java -jar spa2run.jar \
specEA.yaml -i b1.yaml b2.yaml
Queries
[1] query> (a+(a+a+a))
[1] result> true (deterministic)
B1: 50.0 B2: 37.74
[2] query> a+(a+a)
[2] result> true (deterministic)
B1: 30.0 B2: 22.96
Figure 12: Instrumentation metric b
2
, codified as a spec in the YAML format, and a instrumentation-aware shell session from
spa2run, using the new SPA spec from Figure 10 and the set B = {b
1
,b
2
} of instrumentation metrics.
4
6
8 10
20
40
60
index i, for L
i
= {w ∈ L | |w| = i}
arithmetic mean of v
j
(R)
b
1
b
2
Figure 13: Arithmetic mean of the instrumentation results
from v
j
applied to all valid strings of length i, 3 ≤ i ≤ 11,
with v
j
associated to the sum of the application of a function
b
j
∈ B to each matched transition p ∈ P when recognizing
w ∈ L
i
.
w ∈ L, given the formation rules of this particular lan-
guage, its corresponding recognition device and set of
instrumentation metrics. These clues might provide
subsidies for further studies, e.g. improving sections
of a syntactic analyser in order to avoid costly paths
(in our case, balanced parentheses could be checked
with a counter instead of a submachine call and stack
operations, as they do not influence the result in an
arithmetic expression only containing addition opera-
tions).
4 CONCLUSIONS
This paper presented a semiautomatic approach for
generating a instrumentation-aware context-free lan-
guage recognizer, enhanced with hooks, from a gram-
mar written using the Wirth syntax notation. The en-
tire process was aided by a set of command line tools,
freely available for download. We also introduced the
concept of an instrumentation layer enclosing the un-
derlying recognizer, acting as observer for each com-
putational step and collecting data for later use.
Observe that the unique identifiers associated to
transitions can be extended beyond instrumentation,
as they provide a convenient feature for appending
metrics, data structures and semantic actions. Fig-
ure 2 illustrates how hooks are associated with seman-
tic actions, in this case, generating another SPA given
a grammar written in WSN. Semantic actions are trig-
gered whenever their corresponding transitions match
the device’s current configuration.
We are working on a syntax for specifying com-
Instrumenting a Context-free Language Recognizer
209

plex operations in spa2run using scripting languages
running on the Java Virtual Machine, such as Groovy,
Scala and BeanShell. To this end, the instrumentation
layer is being generalized in order to natively accom-
modate more elements, such as data structures and
semantic actions. Furthermore, there is an ongoing
research on instrumenting context-sensitive language
recognizers, namely adaptive automata (José Neto,
1994; José Neto, 2001) (rule-driven devices exploit-
ing self-modification by adding an adaptive layer on
top of the underlying rule set); we are using a library
named AA4J (Cereda and José Neto, 2016), which
allows an straightforward implementation of adaptive
automata, and extending it with hooks for later in-
strumentation. Preliminary results look promising,
although there are challenges regarding the compu-
tational costs when modifying the underlying device
(which is, by definition, a SPA enclosed by an adap-
tive layer).
Instrumenting language recognizers allows a bet-
ter understanding of the inner workings of such de-
vices as well as particular features of the languages
for which they are constructed. Collected data from
instrumentation provide basis for achieving better
performance and model improvements, thus offering
a balance between time and space, as demanded by
practical applications. Besides, the use of an instru-
mentation layer enclosing an underlying recognizer
provides a framework generic enough to cover several
domains.
REFERENCES
Aho, A. V. and Ullman, J. D. (1995). Foundations of Com-
puter Science. W. H. Freeman and Company.
Ball, T. and Larus, J. R. (1994). Optimally profiling and
tracing programs. ACM Transactions on Program-
ming Languages and Systems, 16(4):1319–1360.
Cereda, P. R. M. and José Neto, J. (2015). Um arcabouço
para extensibilidade em linguagens de programação.
In Memórias do IX Workshop de Tecnologia Adapta-
tiva – WTA 2015, pages 18–28, São Paulo.
Cereda, P. R. M. and José Neto, J. (2016). AA4J: uma
biblioteca para implementação de autômatos adapta-
tivos. In Memórias do X Workshop de Tecnologia
Adaptativa – WTA 2016, pages 16–26.
Cooper, K. and Torczon, L. (2011). Engineering a com-
piler. Morgan Kaufmann Publishers Inc., San Fran-
cisco, CA, USA.
Hopcroft, J. E. (1971). An nlogn algorithm for minimiz-
ing states in a finite automaton. In Proceedings of the
International Symposium on the Theory of Machines
and Computations, pages 189–196, Haifa, Israel. Aca-
demic Press.
José Neto, J. (1987). Introdução à compilação. Engenharia
de Computação. LTC – Livros Técnicos e Científicos.
José Neto, J. (1993). Contribuições à metodologia de cons-
trução de compiladores. Postdoctoral thesis, Escola
Politécnica da Universidade de São Paulo, São Paulo.
José Neto, J. (1994). Adaptive automata for context -
sensitive languages. SIGPLAN Notices, 29(9):115–
124.
José Neto, J. (2001). Adaptive rule-driven devices: general
formulation and case study. In International Confer-
ence on Implementation and Application of Automata.
José Neto, J. and Magalhães, M. E. S. (1981). Reconhece-
dores sintáticos: Uma alternativa didática para uso em
cursos de engenharia. In XIV Congresso Nacional de
Informática, pages 171–181.
José Neto, J., Pariente, C. B., and Leonardi, F. (1999).
Compiler construction: a pedagogical approach. In
Proceedings of the V International Congress on In-
formatic Engineering – ICIE 99, Buenos Aires, Ar-
gentina.
Paul, W. and Vahrenhold, J. (2013). Hunting high and low:
Instruments to detect misconceptions related to algo-
rithms and data structures. In Proceeding of the 44th
ACM Technical Symposium on Computer Science Ed-
ucation, pages 29–34, New York, NY, USA. ACM.
Sebesta, R. W. (2013). Concepts of Programming Lan-
guages. Pearson, 10 edition.
Wert, A., Schulz, H., Heger, C., and Farahbod, R. (2015).
Generic instrumentation and monitoring description
for software performance evaluation. In Proceedings
of the 6th ACM/SPEC International Conference on
Performance Engineering, pages 203–206, New York,
NY, USA. ACM.
Wirth, N. (1977). What can we do about the unnecessary
diversity of notation for syntactic definitions? Com-
munications of the ACM, 10(11):822–823.
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
210