Fast Polarization Switch for Polarization-based Quantum

Communication

Vinicius M. Lima, Gustavo C. Amaral, Felipe Calliari, Guilherme P. Tempor

ao,

Jean Pierre von der Weid, Joaquim D. Garcia and Jo

ao Pedro Garcia

Center for Telecommunication Studies, Pontiﬁcal Catholic University of Rio de Janeiro, Rio de Janeiro 22451-900, Brazil

Keywords:

Polarization Switching, FPGA, Polarimeter.

Abstract:

We present a complete optoelectronic unit for polarization visualization, switching and control. The system is

based on a Field Programmable Gate Array (FPGA) unit and comprises: an acquisition unit containing an ana-

log polarimeter and digital-to-analog converters; an FPGA capable of implementing an optimal algorithm for

three-stage arbitrary polarization tracking; and an electronic driver with analog-to-digital converters capable

of interfacing with Lithium-Niobate-based Polarization Controllers. The results, determined via simulation of

real-parameter devices, show that fast polarization switch is achievable.

1 INTRODUCTION

Polarization stabilization and control is a matter of

particular interest in the area of quantum commu-

nication mainly due to the possibility of encoding

qubits in polarization states (Gisin et al., 2002). Re-

cently, quantum communication protocols based on

two-photon interference have been given a lot of at-

tention, specially with the advent of the Measurement

Device Independent Quantum Key Distribution Pro-

tocol (Lo et al., 2012). This protocol, in particular,

makes use of the photon-bunching effect in a Bell-

State Projection (BSP) which is highly dependent on

the indistinguishability between quantum states and,

thus, on the aligned polarization states at the BSP

(Ferreira da Silva et al., 2013). Therefore, polariza-

tion stabilization along the quantum channel becomes

an important issue.

Recently, a scheme for active polarization stabi-

lization along the optical quantum channel employ-

ing current optical ﬁbre technology has been success-

fully demonstrated (Xavier et al., 2008; da Silva et al.,

2012). Such scheme makes use of a reference laser

which is launched in the ﬁber in a DWDM channel ad-

jacent to that of the quantum communication channel

in a counter-propagating manner, such that the trans-

mitter receives the reference signal from the receiver

(Xavier et al., 2008). A simpliﬁed scheme of the pro-

posed system is depicted in Fig.1.

By rotating the received polarization state to

match what should be its original state, the transmitter

Figure 1: Simpliﬁed setup for on-time polarization tracking

in wavelength multiplexed optical quantum channels.

gains access to the optical link transfer function and

can produce the inverse transformation on the outgo-

ing optical pulses (Xavier et al., 2008). Not only the

polarization has been shown to stabilize during long-

term communication periods but it was also proven

that the noise contribution from the adjacent counter-

propagating channels was negligible, enabling the use

of the technique in quantum communication channels

(Xavier et al., 2008).

However efﬁcient, the polarization control en-

forced by the system described above only enables

the stabilization of the polarization state rather than

its fast switching. As the quantum states must be en-

coded in the polarization, the rapid switching between

polarization states becomes a rather important task,

even more when the mathematical security proofs for

quantum communication channels rely on the rate of

secret key generation (Ma et al., 2005; L

utkenhaus,

2000). By associating the polarization stabilization

setup proposed in (Xavier et al., 2008) and an ac-

tive feedback system based on a sample of the out-

going polarization state, a mixed analog-digital polar-

288

Lima V., Amaral G., Calliari F., TemporÃ

co G., von der Weid J., D. Garcia J. and Pedro Garcia J.

Fast Polarization Switch for Polarization-based Quantum Communication.

DOI: 10.5220/0006212202880293

In Proceedings of the 5th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2017), pages 288-293

ISBN: 978-989-758-223-3

ization switch is proposed. The scheme is supposed

to rapidly switch between arbitrary polarization states

whilst protecting the quantum state alignment from

ﬂuctuations of the optical channel, a claim supported

by the numerical simulation results of each individual

system that comprise the main unit.

The paper is divide as follows. In Section II, the

mathematical formalism necessary to represent states

of polarization and the lithium-niobate-based polar-

ization controller is presented. In Section III, the in-

dividual units are detailed and the complete optoelec-

tronic polarization switch unit is presented. The sim-

ulation results and discussions appear in Section IV.

Finally, in Section V, the conclusions are drawn and

the real implementation of the envisioned system is

discussed.

2 THEORETICAL

FORMULATION

2.1 Mathematical Representation of

Polarization

The state of polarization of light has been represented

mathematically as Jones Vectors and Stokes Vectors

(Saleh et al., 1991). Even though the conversion be-

tween these two representations require straightfor-

ward computations, we shall stick to the Stokes rep-

resentation since visualization in the Poincar

e Sphere

is direct (Saleh et al., 1991). Stokes vectors are 4-

dimensional vectors that carry information about the

State of Polarization (SOP) of light. Since the ﬁrst

component (S

) is associated to the total light inten-

sity, it is common to normalize the Stokes Vector by

dividing all of its entries by S

. In the case of po-

larized light, the 3-dimensional Stokes Vector formed

of the remaining three normalized components of the

former 4-dimensional vector, has norm 1. Indeed, the

degree of polarization of light is given by the norm

of the Stokes vector. Assuming that light is polar-

ized enables one to simplify the representation. The

usual representation of the 3-dimensional normalized

Stokes vector, assuming polarized light (and, hence

norm 1), is a point in the 3-sphere known as the

Poincar

e Sphere. Since all SOPs are mapped bijec-

tively in the 3-sphere, we shall treat, from now on, an

SOP as a point in the 3-sphere.

SOP changes that do not affect the light intensity

can be represented by rotations in 3-space. These

rotations are a class of unitary transformations and

can be represented by orthonormal matrices (Strang,

2009). The rotation matrix in 3-space has a very in-

teresting characterization via the Spectral Theorem: it

always has 3 eigenvalues (since they are normal); all

of the eigenvalues have norm 1; one of the eigenvalues

is always equal to 1 and its eigenvector is the rotation

axis, e; the remaining eigenvalues are complex conju-

gate numbers whose real part correspond to the cosine

of the rotation angle, θ, and whose imaginary part cor-

respond to the sine of the rotation angle. A simple and

robust way of manipulating 3-space rotation matrices

is through the quaternions number system (Karlsson

and Petersson, 2004; Garcia and Amaral, 2016). De-

spite the fact that polarisers affect the light intensity

and, as such, cannot be represented by orthonormal

matrices, they can be represented by projection matri-

ces.

2.2 Lithium-niobate-based Polarization

Controller Characteristics

Literature around polarization control is very rich

and diverse techniques were proposed and veriﬁed

over the last years (Heismann, 1994) (Imai et al.,

1985)(No

e et al., 1988) (Heismann, 1989). Our

methodology focuses on the electro-optic LiNbO

EOSpace Polarization Controller Module (PCM)

which is available commercially as a multi-stage com-

ponent to which the input voltage may vary within a

±70 Volts range (Saleh et al., 1991).

A single stage of the PCM has 3 electrodes

(EOSpace, ) and realizes an arbitrary Linear Retarder.

A linear retarder is a linear wave-plate capable of in-

ducing a relative phase difference between the two po-

larization axes. This accomplished through the bire-

fringent characteristic of the wave-plate, which cause

two orthogonal polarization axes to experiment differ-

ent indexes of refraction while traversing the material.

The difference in propagation time is, thus, responsi-

ble for enforcing the relative phase shift between po-

larization axes.

Linear Retarders have a main polarization axis,

also known as eigen-mode, e ∈ {v ∈ R

|z = 0}, and a

characteristic phase delay, θ ∈ [0,2π). It is possible to

show that, by changing the eigen-mode and the phase

delay of a linear retarder, one can shift from one SOP

to any other SOP (Garcia and Amaral, 2016). In order

to set the eigen-mode to e = (cos(α/2),sin(α/2),0)

and the phase delay to θ = 2πδ the electrodes volt-

ages of the lithium-niobate-based PCM must be set to

(EOSpace, ):

= 2V

δ sin (α) −V

δ cos (α) +V

(1)

= 0 (2)

= 2V

δ sin (α) −V

δ cos (α) +V

(3)

Fast Polarization Switch for Polarization-based Quantum Communication

289

where V

is the voltage required to induce a 180

phase shift between the TE and TM modes for a sin-

gle stage, V

is the voltage required to rotate all power

from the TE to the TM mode, or vice versa, for a

single stage, and V

and V

are the bias voltages re-

quired on electrodes A and C, respectively, in order

to achieve zero birefringence between the TE and TM

modes (EOSpace, ). Even though the data-sheet of

the device provides the voltage range for V

, V

and V

, their actual values for an arbitrary stage must

be determined via a calibration procedure.

Algorithms for both the calibration procedure

and for identifying the required rotation in order to

achieve a desired polarization state at the output of

the polarization controller are presented in (Xi et al.,

2010) (Garcia and Amaral, 2016). We shall focus on

the hardware implementation of the control system.

3 OPTOELECTRONIC SETUP

PROPOSAL

The representation of a polarization state in the

Poincar

e Sphere is achieved by measuring the Stokes

vector of the incident light, which can be performed

in a number of ways with either a set of optical split-

ters, wave plates and detectors or with a polarization

rotator and a polarization state reference (Saleh and

Teich, 2007). The proposed architecture makes use

of the FPGA-based polarimeter for polarization state

visualization proposed in (Calliari et al., 2014). The

FPGA’s internal schematic is presented in Fig.2.

Figure 2: Block diagram of the FPGA’s internal structure

for polarization visualization. The results acquired by the

polarimeter are sent to the FPGA and the result is displayed

graphically.

The polarimeter measures the intensities on each

of the three main polarization basis, the rectilinear, di-

agonal, and circular basis, from which one is capable

of determining the corresponding Stokes vector. The

measurement is represented by a voltage value, which

is sent to an Analog-to-Digital Converter (ADC) so

the digitized values can be interpreted by the FPGA.

Inside the FPGA structure, a series of sub-blocks per-

form the signal interpretation: the Int to Float block is

responsible for representing the digitized voltage val-

ues as ﬂoating point numbers; the AD to Volts block

converts the digitized values back to their original

voltage values represented as a ﬂoating point number;

the Calibration Matrix block permits one to associate

the voltage value measured by the polarimeter to each

of the four un-normalized entries of the Stokes vector

(this block is dependent on the device and on the op-

erating wavelength); up to the Normalize block, the

digital structure deals with the 4-dimensional Stokes

vector, but after they are normalized, we need only to

deal with the 3-dimensional vector; the Isometric Ma-

trix block enables the 2-dimensional visualization of

the Poincar

e Sphere; the remaining Correct and Off-

set blocks associate the pixels in the graphic display

with the values of the SOP vector.

The goal is to combine the setups of Figs. 1 and

2 in a feedback loop enabling visualization and con-

trol of the output SOP (Garcia and Amaral, 2016).

The electronic implementation of the feedback sys-

tem, depicted in Fig. 3, is composed of: an analog

polarimeter; an array of analog-to-digital converters

(ADC); an FPGA unit; an array digital-to-analog con-

verters (DAC); an electronic driver unit; a Lithium-

Niobate-based PCM; and a power supply.

Figure 3: Mixed analog-digital feedback loop for polariza-

tion visualization, selection, and stabilization.

Running in parallel inside the FPGA is the algo-

rithm developed in (Garcia and Amaral, 2016). The

algorithm takes the current state of polarization and

the target state of polarization as inputs and attempts

to output voltage levels which perform a rotation (ac-

cording to the equations describing the PCM behav-

ioral) so that the current and target SOPs match each

other. The electronic driver that follows the DAC

guarantees that the low power signals sent from the

FPGA are converted to match the Lithium-Niobate

based PCM. Each stage of the PCM demands two

electronic drivers capable of reaching an output volt-

age swing between ±70 Volts for which the full elec-

trical schematic of a single driver stage is presented in

Fig. 4.

The setup presented in Fig.3 is suited for classical

communication channels since a sample of the out-

PHOTOPTICS 2017 - 5th International Conference on Photonics, Optics and Laser Technology

290

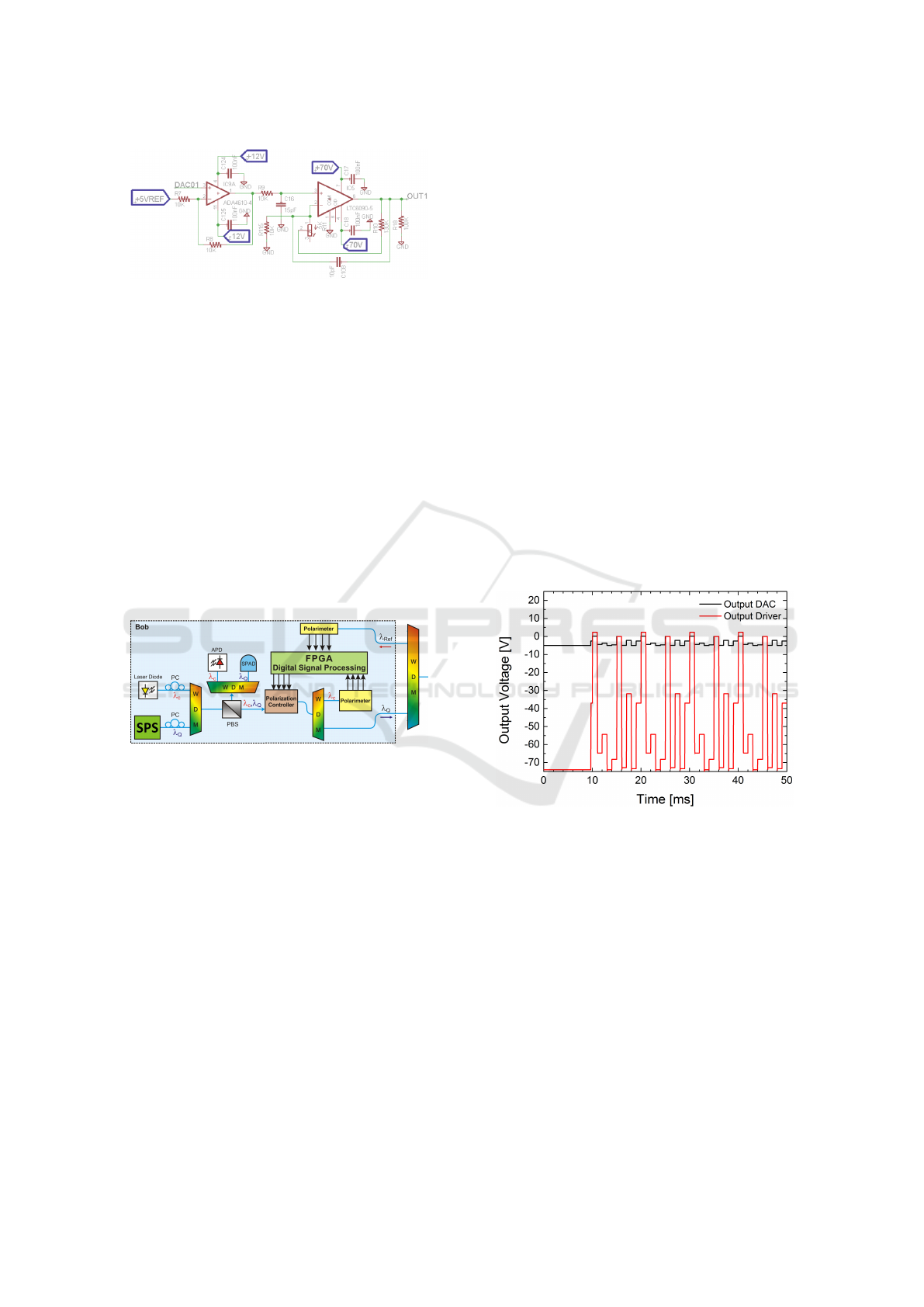
Figure 4: Electronic schematic of a single ±70 Volts driver

stage of the lithium-niobate-based PCM.

put signal can be measured by the polarimeter. When

one is interested in transmitting quantum states, as for

quantum communication purposes, however, the state

cannot be measured without being destroyed. Also, a

sample of the quantum state cannot be taken. Thus,

a different approach should be considered: the mea-

sured polarization state cannot be a sample of the out-

going quantum state so it must be a classical state.

It should, however, be polarization-aligned with the

outgoing quantum state so, by measuring the classi-

cal state, one gains information over the polarization

state of the outgoing quantum state. If we suppose the

quantum state is generated by an ideal single-photon

source (SPS), the block diagram depicted in Fig. 5

should be able to perform its polarization control.

Figure 5: Proposed full polarization stabilization and selec-

tion scheme for quantum communication channels. SPS:

Single-Photon Source; WDM: Wavelength Division Mul-

tiplexer; PBS: Optical Polarizing Beam Splitter; APD:

Avalanche Photodiode SPAD: Single-Photon Avalanche

Photodiode; PC: Mechanical Polarization Controller.

In the input of the polarization control setup, a

reference optical signal from a tunable laser diode is

directed to a WDM combiner together with the out-

put of the SPS. It is important that each source oc-

cupies different WDM channels so they can be mul-

tiplexed and later demultiplexed. A polarizing beam

splitter (PBS) is then connected to the output of the

WDM to act as a polarization aligner. By minimiz-

ing the outputs from detectors SPAD

ad j

and APD

ad j

the alignment of the polarization states of both chan-

nels at the remaining PBS output arm is enforced

(Amaral et al., 2016). The polarization-aligned chan-

nels are then directed to a PCM where they experi-

ment the same polarization rotation given the wave-

lengths do not differ greatly (Xavier et al., 2008). The

polarization-rotated signals are divided by a WDM

splitter so λ

is directed to the output of Bob’s station

and λ

is directed to the mixed analog-digital feed-

back system. Combining the information of which

polarization state should be keyed at the output and

how the optical channel inﬂuences the polarization

of light, the outgoing state is composed. Note that

the quantum state is not measured at any time in the

polarization control system and we infer its polariza-

tion state taking the measurement over the classical

polarization-aligned state as a reference.

4 RESULTS

The simulation results were acquired using the Spice

simulation tool. All the electronic devices were re-

placed by their real-parameter model which take into

account the supply saturation, frequency response

(slew-rate), and gain limitations. In Fig. 6, we de-

pict the simulation results for various digital inputs at

the DAC and the corresponding output from both the

DAC and the power driver.

Figure 6: Voltage swing at the driver output as a function of

the DAC output. The FPGA is responsible for conﬁguring

the DAC output.

We observe that the voltage swing is respected

by the power driver unit. An important information,

however, is the one regarding the switching time be-

tween one voltage level to the other since, ultimately,

it determines our maximum achievable transmission

rate in polarization-encoded quantum communication

channels. In Fig. 7, we detail the switching time and

show that the proposed system is capable of achiev-

ing an up to 125 KHz transmission rate. It should be

noted, however, that the slew-rate of the LTC6090-

5 is dependent on its gain. Throughout the simu-

lation runs, we enforced a 14V/V gain which limits

the transition time to 8kHz. By introducing a pre-

ampliﬁer stage with 3V/V gain before the LTC6090-

Fast Polarization Switch for Polarization-based Quantum Communication

291

5, we could operate under a 5V/V gain achieving a

1MHz switching rate (Linear Technology, ).

Figure 7: Detailed transition time in the full ±70 voltage

swing at the electronic driver’s output.

5 CONCLUSION

An optoelectronic unit comprised of a mixed analog-

digital control loop and a polarization alignment state

is presented. The system’s application in polarization-

based quantum communication links is studied with

respect to the switching rate, usually above 1MHz.

Considering the device’s frequency response, we

show, through numerical simulations, that the de-

mands are matched. We also show that polariza-

tion visualization can be performed throughout the

switched operation of the system and a polariza-

tion visualization unit is proposed and experimentally

demonstrated. Fast and embeddable signal process-

ing tools that permit state of polarization control have

been described in the literature and are directly imple-

mentable in the proposed scheme.

ACKNOWLEDGMENT

The authors would like to thank brazilian agency

CNPq for ﬁnancial support.

SUPPLEMENTAL MATERIAL

The authors provide digital supplemental material to

accompany the article: a video ﬁle depicting the sim-

ulation run of the polarimeter can be accessed in (Cal-

liari et al., ).

REFERENCES

Amaral, G. C., da Silva, T. F., Tempor

ao, G., and von der

Weid, J. (2016). Few-photon heterodyne spec-

troscopy. Optics Letters, 41(7):1502–1505.

Calliari, F., Amaral, G. C., and von der Weid, J.-

P. (2014). Development of a graphics inter-

face for analysis of the state of polarization

of light through fpga platform. Monogra-

phy available at http://www.maxwell.vrac.puc-

rio.br/Busca etds.php?strSecao=resultado&nrSeq=

237902,.

Calliari, F., Lima, V., Garcia, J. a. P. D., and Ama-

ral, G. C. Fpga-based polarimeter simulation.

https://www.youtube.com/watch?v=s9F0D0HKb4E.

da Silva, T. F., Vitoreti, D., Xavier, G. B., Temporao, G. P.,

and von der Weid, J. P. (2012). Polarization-stable

long-distance interference of independent photons for

quantum communications. page QW2A.4.

EOSpace. Lithium niobate polarization controller.

http://www.hanamuraoptics.com/device/EOSPACE/

PC030123 EO.pdf. Accessed: 2016-01-22.

Ferreira da Silva, T., Vitoreti, D., Xavier, G. B., do Ama-

ral, G. C., Temporao, G. P., and von der Weid,

J. P. (2013). Proof-of-principle demonstration of

measurement-device-independent quantum key dis-

tribution using polarization qubits. Phys. Rev. A,

88:052303.

Garcia, J. D. and Amaral, G. C. (2016). An op-

timal polarization tracking algorithm for lithium-

niobate-based polarization controllers. arXiv preprint

arXiv:1603.06751, cs.SY.

Gisin, N., Ribordy, G., Tittel, W., and Zbinden, H. (2002).

Quantum cryptography. Rev. Mod. Phys., 74:145–195.

Heismann, F. (1989). Integrated-optic polarization trans-

former for reset-free endless polarization control.

Quantum Electronics, IEEE Journal of, 25(8):1898–

1906.

Heismann, F. (1994). Analysis of a reset-free polarization

controller for fast automatic polarization stabilization

in ﬁber-optic transmission systems. Lightwave Tech-

nology, Journal of, 12(4):690–699.

Imai, T., Nosu, K., and Yamaguchi, H. (1985). Optical po-

larisation control utilising an optical heterodyne de-

tection scheme. Electronics Letters, 21(2):52–53.

Karlsson, M. and Petersson, M. (2004). Quaternion ap-

proach to pmd and pdl phenomena in optical ﬁber sys-

tems. Lightwave Technology, Journal of, 22(4):1137–

1146.

Linear Technology. 140v cmos rail-to-rail

ouput, picoamp input current op amp.

http://cds.linear.com/docs/en/datasheet/6090fe.pdf.

Accessed: 2016-04-22.

Lo, H.-K., Curty, M., and Qi, B. (2012). Measurement-

device-independent quantum key distribution. Phys.

Rev. Lett., 108:130503.

utkenhaus, N. (2000). Security against individual attacks

for realistic quantum key distribution. Phys. Rev. A,

61:052304.

PHOTOPTICS 2017 - 5th International Conference on Photonics, Optics and Laser Technology

292

Ma, X., Qi, B., Zhao, Y., and Lo, H.-K. (2005). Practical

decoy state for quantum key distribution. Phys. Rev.

A, 72:012326.

e, R., Heidrich, H., and Hoffmann, D. (1988). Au-

tomatic endless polarization control with integrated-

optical ti: Linbo 3 polarization transformers. Optics

letters, 13(6):527–529.

Saleh, B. E., Teich, M. C., and Saleh, B. E. (1991). Funda-

mentals of photonics, volume 22. Wiley New York.

Saleh, B. E. A. and Teich, M. C. (2007). Fundamentals of

Photonics. John Wiley & Sons, Inc.

Strang, G. (2009). Linear Algebra and Its Applications.

Wellesley-Cambridge Press, Wellesley, MA.

Xavier, G. B., de Faria, G. V., Temporao, G. P., and von der

Weid, J. P. (2008). Full polarization control for ﬁber

optical quantum communication systems using polar-

ization encoding. Opt. Express, 16:1867–1873.

Xi, L., Zhang, X., Tang, X., Weng, X., and Tian, F. (2010).

A novel method to calibrate linbo3-based polarization

controllers. Chinese Optics Letters, 8(8):804–806.

Fast Polarization Switch for Polarization-based Quantum Communication

293