Graphics Processing Units for Constraint Satisfaction

Malek Mouhouband and Ahmed Mobaraki

Dept. of Computer Science, Univ. of Regina, Regina, Canada

Keywords:

Constraint Satisfaction, Graphics Processing Units, Parallel Computing.

Abstract:

A Constraint Satisfaction Problem (CSP) is a powerful formalism to represent constrained problems. A CSP

includes a set of variables where each is deﬁned over a set of possible values, and a set of relations restricting

the values that the variables can simultaneously take. There are numerous problems that can be represented

as CSPs. Solving CSPs is known to be quite challenging in general. The literature poses a great body of

work geared towards ﬁnding efﬁcient techniques to solve CSPs. These techniques are usually implemented

in a system commonly referred to as a constraint solver. While many enhancements have been achieved over

earlier ones, solvers still require powerful resources and techniques to solve a given problem in a reasonable

running time. In this paper, a new parallel-based approach is proposed for solving CSPs. In particular, we

design a new CSP solver that exploits the power of graphics processing units (GPU), which exist in modern

day computers, as an affordable parallel computing architecture.

1 INTRODUCTION

A Constraint Satisfaction Problem (CSP) is a math-

ematical formalism used for representing a variety

of constrained problems ranging from scheduling to

bioinformatics (Dechter, 2003). More formally, a

CSP includes a set of variables, each deﬁned on a do-

main of ﬁnite and discrete values, and a set of con-

straints restricting the values tha the variables can si-

multaneously take. A solution to a CSP is a set of

assignments of values to variables such that all con-

straints are satisﬁed. A CSP is known to be a NP-

hard problem and requires a solving algorithm of ex-

ponential time cost. Therefore, given a CSP, one usu-

ally needs advanced solvers and techniques to ﬁnd

one or more feasible solutions (Mackworth, 1977;

Haralick and Elliott, 1980; Dechter, 2003; Bessi`ere

et al., 2005; Lecoutre and Tabary, 2008; Balafoutis

and Stergiou, 2010; Mouhoub and Jashmi, 2011; Ab-

basian and Mouhoub, 2016). There are several sys-

tems that are developed speciﬁcally for solving CSPs

(Lecoutre and Tabary, 2008). Such systems have been

developed in many different manners to meet the re-

quirements of different CSP problems. Still, most of

the systems suffer some limitations with regards to

how fast they can ﬁnd a solution. Most solvers are

dedicated to run on personal computers. This means

they run in sequential order until a solution is found,

if it exists. This becomes more challenging when the

problem has a very large number of variables with a

large domain size. Even though there are several im-

provements that have been proposed to enhance the

performance of CSP solvers (Bessi`ere et al., 2005;

Lecoutre and Tabary, 2008; Balafoutis and Stergiou,

2010; Mouhoub and Jashmi, 2011; Abbasian and

Mouhoub, 2016), there are still some difﬁculties with

hard to solve problems. One well-known improve-

ment is to build a parallel CSP solver that uses mul-

tiple processors. Such an idea performs very well as

long as the user has the ability to acquire powerful

machines. Besides, such machines often come with

unaffordablecost. Another suggested idea is to imple-

ment a parallel CSP solver that takes advantage of the

multi-core processor of the personal computer plat-

form. This approach seems very promising, as it only

requires a personal computer. However, the system

developer would need to maintain balance within the

multi-core processor usability. That is to say, while

an application is using multiple cores, this application

would be required to assign tasks to each of the cores

in such way all of them are used equally.

In this paper, we propose a new GPU-based sys-

tem for solving CSPs. This is achieved by adopting

the CUDA framework (Cook, 2012). CUDA is a pro-

gramming platform that was developed by NVIDA to

allow programmers to use a NVIDIA Graphics Pro-

cessing Unit (GPU). As a programmable and general-

purpose architecture, GPU can be purchased as cheap

as ﬁfty dollars. Moreover, a GPU outperforms the

Central Processing Unit (CPU), in various regards.

Mouhoub M. and Mobaraki A.

Graphics Processing Units for Constraint Satisfaction.

DOI: 10.5220/0006214806530657

In Proceedings of the 9th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2017), pages 653-657

ISBN: 978-989-758-220-2

653

For example, while the CPU often involves up to

16 cores, GPU can have thousands cores due to the

fact that GPU has been developed to work as a paral-

lel computing architecture, mainly for image render-

ing and other graphics and media computations. An-

other advantage of using GPU as a parallel platform is

that NVIDIA has introduced a new programming lan-

guage called CUDA C, which is an extended version

of C language, to help developers monopolize all the

resources of the GPU without having to learn a new

programming language. The CUDA platform will be

responsible for scheduling the threads and avoiding

any misbalancing which could lead to starvation.

The rest of the paper is organized as follows.

First, Section 2 offers background information about

CUDA, along with some details for the advantages of

using this new computing platform. Then, a descrip-

tion of the proposed system for solving CSPs with a

GPU is presented in Section 3. Finally, concluding

remarks and future works are reported in Section 4.

2 COMPUTE UNIFIED DEVICE

ARCHITECTURE (CUDA)

The GPU has been designed to relieve the CPU from

the highly computation processes. The GPU has been

responsible for graphics processing like image render-

ing. This is why it comes with a large number of tran-

sistors which are mostly dedicated for data process-

ing, in comparison to the CPU which requires more

processing control and caching the memory. More-

over, GPU memory has a higher bandwidth than CPU

which speeds up the performance of the arithmetic

operations on the data. The reason for this is because

the main task of the GPUs is to execute the same op-

erations on a larger number of data, which is what the

image rendering is about. However, CPUs are general

architecture designed to execute all types of functions.

In the image rendering processing, or any other graph-

ics processing, the main idea is to divide the problem

data into smaller blocks in which a block can perform

the same work on the sub-problem. Thus, any prob-

lem that processes a repeatedly arithmetic operation

on a larger number of data can be partitioned into

a smaller size and tackled with as independent from

other partitions of the problem as long as the parti-

tioned data elements are independent from each other.

In 2006, NVIDIA announced a new parallel comput-

ing architecture called Compute Uniﬁed Device Ar-

chitecture, or CUDA (Cook, 2012). It exploits the

parallelism of the GPU hardware to its highly compu-

tation for solving highly computational problem out

the ﬁeld of graphics. In contradiction with CPU,

CUDA architecture would perform parallel comput-

ing work in a more professional way than CPU. Also,

NVIDA has developed a software programming envi-

ronment that allows the developers to use it for im-

plementing their applications with a CUDA C that

is an extension programming language of the C Lan-

guage. One of the obstacles of a multicore processor

is that developers need to develop an application that

not just uses the multicore technology in the CPU,

but also maximizes the beneﬁts of the parallel com-

putation to its high level to reach the top speedup that

can be achieved by the multicore processor. Still, this

requires a lot of programming experience and under-

standing of the CPU architecture. These difﬁculties

have been tackled with CUDA by introducing the new

programming model with instructions sets based on

the C programming language. Developers who are

not familiar with the CUDA platform can still perform

well in programming with CUDA C and reach a very

high leverage of the GPU parallel computing ability.

A developer needs only to write the kernel that will

run on the GPU, and the CUDA platform will execute

this kernel on all of the elements of the data. CUDA

C also allows the users to write a heterogeneous code

that runs on the CPU and GPU in the same ﬁle. The

code that concerns the CPU called host code while the

part that runs on the GPU is called the device code. In

CUDA C, there are a few new instructions that are

added to the extension of C programming language.

ThreadIdx is the keyword for accessing the current

thread ID. It is used to direct the speciﬁc thread work.

In Figure 1, a sample code, for example, shows

how to add two vectors and store the results in a third

one. The developer only needs to write two functions;

one that will be executed on the CPU and will be re-

sponsible for copying the data from the from CPU

memory to GPU memory, triggering the kernel, syn-

chronizing, then copying back the result form device

memory to the CPU memory. This code is written in

the main function and it is executed only once. While

in the Kernel section, the code will run equal to the

number of threads that are already speciﬁed by the

host code in the many function when the kernel is trig-

gered. In this example, the thread number is equal to

the number of array elements. Each thread will ac-

cess different elements in the array of A and adds it to

the correspondent element in array B, then store the

result in the correspondent element in array C. After

the kernel function is complete, the main function of

the host will be to direct the CPU to copy back the

elements of array C from the device memory to the

CPU memory, and the program will terminate.

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

654

// Kernel definition

__global__ void VecAdd(float* A,

float* B,

float* C)

{

int i = threadIdx.x;

C[i] = A[i] + B[i];

}

int main()

{

...

// Kernel invocation with N threads

VecAdd<<<1, N>>>(A, B, C);

...

}

Figure 1: Vectors Addition in CUDA C language.

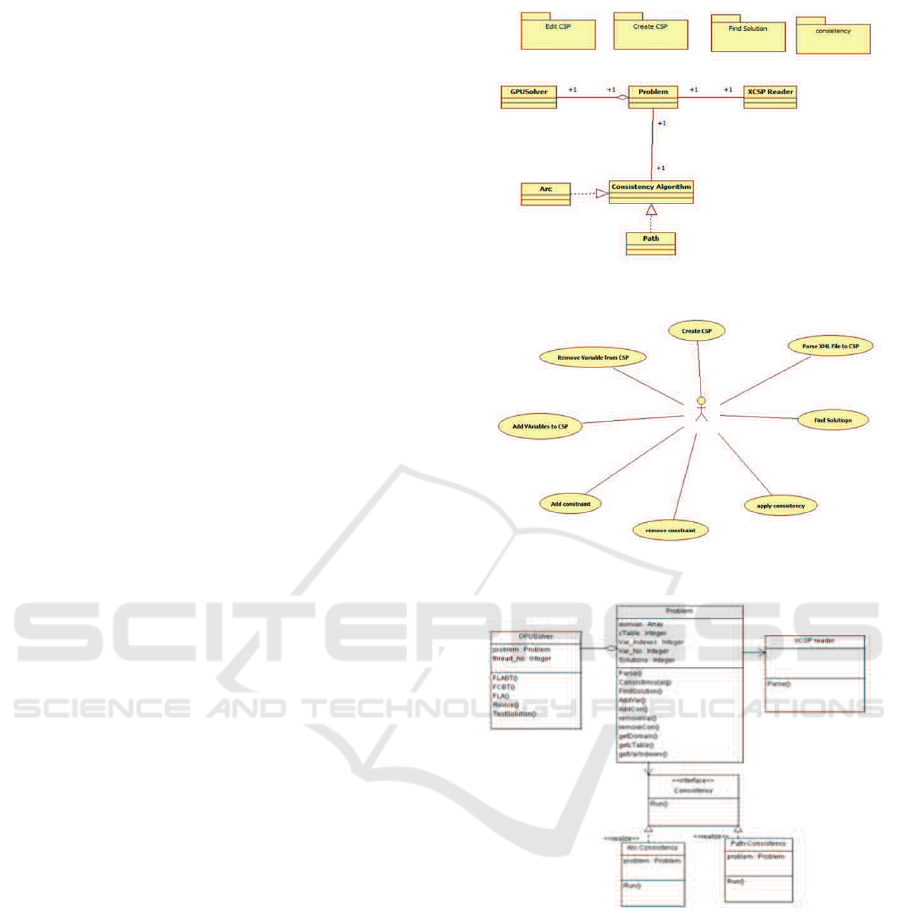
3 PROPOSED SYSTEM

3.1 System Overview

Our proposed system is composed of four major com-

ponents that are running on the same local machine

or platform. The components are Problem, XCSP

Parser (Lecoutre and Tabary, 2008), Consistency Al-

gorithm (Dechter, 2003; Bessi`ere et al., 2005), and

ﬁnally GPU Solver. Each one of them, except Prob-

lem, performs a different task. The system is dis-

cussed in more details in the next subsection. The

main component of the whole system is the Problem

class. This latter is provided with the basic function-

alities that are required to create, manage, and ﬁnd

the solution for a CSP. These functionalities are: cre-

ate a CSP, add and remove variables, add and remove

constraints and ﬁnd solutions. It is also provided with

the ability to retrieve a CSP data that is stored in an

XML ﬁle, parse them, and feed that data to the prob-

lem class. In addition, the Problem class can also run

a local consistency algorithm on a problem in order to

trim the CSP variables domain before submitting it to

the GPU Solver component. The Consistency com-

ponent is composed of two types of consistency tech-

niques: arc (Dechter, 2003; Bessi`ere et al., 2005) and

path consistency (Bessi`ere, 1996) algorithms. Both

of them are concrete classes that implement the inter-

face class called Consistency. Consistency interface

deﬁnes the basic attributes and methods of local con-

sistency algorithms. The most important here, the in-

terface declares a function called run in which the tar-

get algorithm will be triggered over the CSP. There-

fore, both of the implementations, or any other future

classes, must implement this function. At the concrete

classes, arc and path, the corresponding technique is

implemented. Thus, when the consistency function

of the problem class is invoked, one of these imple-

mentations is triggered based on the choice given by

the user. The GPU Solver is a new implementation

that is proposed to improve the CSP solver system by

using CUDA architecture for parallel computing. Us-

ing the Cudafy library, we can create several system

running threads that match the number of all differ-

ent locally consistent variable assignments that can

be generated by a given CSP problem. Each thread

will ﬁnd the corresponding assignment for the vari-

ables based on its identiﬁcation number that is as-

signed to each thread by the GPU. Certainly, each

GPU has a maximum number of threads that can

be used. Those variables considered in the process

of generating the combinations are called partitioned

variables. Consequently, the unselected variables are

called unpartitioned variables, and are assigned to a

value from there domains sequentially using the back-

tracking algorithm following a given constraint prop-

agation strategy (Haralick and Elliott, 1980). The

GPU Solver class is composed of two main functions.

The ﬁrst is FLABT, which implements the backtrack-

ing algorithm with Full Look Ahead as a propagation

strategy. The other function is FCBT, which imple-

ments the backtracking algorithm with the Forward

checking strategy. Either of them is to be invoked

from function problem. FindSolution and the selec-

tion will be based on the user choice that is pro-

vided as a parameter for this function. Based on the

CSP data, the GPU Solverwill instantiate an adequate

number of threads that is equal to number of all the

combinations of the given CSP as long as it does not

exceed the maximal number threads that can be cre-

ated by the GPU. In case a CSP combination number

is larger than the maximal number of threads, some of

these variables’ domains will be partitioned while the

rest will be solved using the backtracking algorithm.

Once the required number of threads is speciﬁed, the

CSP problem data will be copied from the CPU mem-

ory to the GPU memory, and then the correspondence

kernel will be invoked to run on the GPU. The sys-

tem needs to synchronize now until all the executions

of the GPU are performed. Once this step is com-

plete, the system retrieves the results from the GPU

memory and frees all the resource allocations being

used by the GPU, and the next step will be storing

the results in the problem class data structure, namely

solutions. However, this is how the GPU Solver per-

forms on ﬁnding the solution, but not how it is done

on the GPU kernel. For the FLABT kernel, the data

required to solve a CSP is domains, constraints, vari-

Graphics Processing Units for Constraint Satisfaction

655

ables indexes, in additions to the number of threads.

There are as many versions of all the variables’ do-

mains as the number of threads so that each of the

threads can access a separate version of all the vari-

ables’ domains and update them separately. The ﬁrst

step is that each thread ﬁnds a unique combination

based on its ID number that is assigned by the GPU.

If all the combinations of the given CSP can be gener-

ated by the threads, each thread will invoke a function

called a propagation function for testing the legibility

of this solution using the constraints table of the CSP.

Thus, the kernel function will terminate itself at that

level. On the other hand, if the number of threads is

less than the entire combinations, the selected vari-

ables will be assigned via each of the threads, those

assignments are tested through the propagation func-

tion. Only those threads that carry legal combinations

are considered, and all other threads will be termi-

nated. Afterward, the backtracking algorithm com-

bined with a constraint propagation technique, either

forward checking or Full Look ahead, will be exe-

cuted on the rest of threads. The third step after the

completion of backtracking algorithm is to examine

all the threads against the constraints table to ﬁnd

combinations that satisfy all the constraints.

3.2 Software Architecture and

Description

The layout of the system (see Figure 2) consists of two

interfaces, the core system and the hardware. The user

can enter a CSP data via graphics user interface or by

submitting XML ﬁle constraints that includes all the

information needed to create a problem. XML Parser

is responsible for parsing the XML ﬁle and extracting

the data of the CSP and feeding it to the core system.

The problem data has to be written in a certain format

that is speciﬁed in (Lecoutre and Tabary, 2008). Once

a problem has been created, the core system is ready

to be initiated and perform its functionalities over the

problem. The system use cases diagram is depicted in

Figure 3.

As described before, our proposed software im-

plements four main classes: Problem, XCSP parser,

consistency, and GPU Solver. Their tasks are to rep-

resent a CSP problem, reading a problem data from

a ﬁle, performing consistency algorithm, and ﬁnding

the solution, respectively. The main class is the prob-

lem class, in which all other classes’ functionalities

are accessed. Figure 4 describes all the classes and

the integrations between them.

There are two main functionalities for the systems,

removing inconsistent values and ﬁnding the solution

of the problem. The Problem Class implements each

Figure 2: System interaction component.

Figure 3: Use Case Diagram.

Figure 4: Class diagram.

of these functionalities in a function that can be called

from the main class. FindSolution functionality is de-

picted in Figure 4. The function requires a string pa-

rameter and has no value to return since the results

will be stored in an array of two dimensions, namely

solutions. FindSolution will invoke the proper algo-

rithm function of the GPUSolver class depending on

the parameter being passed to the function. There are

two implementations of the backtracking algorithms,

FCBT and FLABT. Each one of the backtracking al-

gorithm functions invoke in turn a different kernel to

run on GPU cores. More speciﬁcally, FCBT will in-

voke FindWithFC kerenel, while FLABT will invoke

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

656

the FindwithFLA kernel. The FindSolution function

will pass its class, problem, as a parameter to the

backtracking function in GPUSolver class, and the

backtracking function in turn will copy the problem

data from CPU memory to the GPU memory. Right

now, everything is ready for the kernel to be invoked.

The backtracking function, either FCBT or FLABT,

needs to synchronize until the kernel ﬁnishes its work.

The kernel will store all the solutions that are paral-

lelized in a two-dimension array, namely Solutions.

This is the array that will be retrieved from the GPU

memory by the FLADBT function after the CPU has

been synchronized in order for the kernel to ﬁnish its

task. Of course, not all the solutions found are legit-

imate. That is why there is another array called Flag,

which holds a ﬂag value for each corresponding solu-

tion.

Our system is an open source programming envi-

ronment produced by NVIDA that allows a developer

to implement a kernel and execute it on the graphics

processing unit. The programming language used is

an extended C language. Cudafy is a library devel-

oped by C# to allow developers to develop their ap-

plications in a high level programming language like

C# and they do not need prior knowledge about the C

language structure or the parallel computing architect.

Still, the application needed to have a NVCC com-

piler to compile and execute the output of the Cuadfy

code. This library target .Net is designed to be used in

the Visual Studio.Net Framework, particularly for C#

programmers, so that the developed application can

be executed, partially not entirely, in a parallel man-

ner.

4 CONCLUSION AND FUTURE

WORK

In this work, we proposed a GPU-based solver for

CSPs. Most of the solvers existing today rely on a

CPU processing to solve a CSP problem. After en-

forcing constraint propagation, the CSP can be com-

posed of locally consistent combinations such that

some of them form a consistent solution. GPU can be

programmed to distribute multiple threads over these

combinations and ﬁnd which of those combinations

would satisfy the constraints. The GPU is easily pro-

grammable and does not require any advance knowl-

edge for thread scheduling, maintaining, or synchro-

nizing. Finally, the GPU can outperform classic solv-

ing methods by partitioning the CSPs and paralleliz-

ing the threads. This often leads to large savings in

terms of computations. The following will be consid-

ered in the near future: developing a Graphics User

Interface, implementing more constraint techniques

including variable ordering heuristics (Balafoutis and

Stergiou, 2010; Mouhoub and Jashmi, 2011), consid-

ering other forms of paralllel architectures for solv-

ing CSPs (Abbasian and Mouhoub, 2013; Abbasian

and Mouhoub, 2016), and generalizing the system to

adopt other types of NVIDIA GPU.

REFERENCES

Abbasian, R. and Mouhoub, M. (2013). A hierarchical par-

allel genetic approach for the graph coloring problem.

Applied Intelligence, 39(3):510–528.

Abbasian, R. and Mouhoub, M. (2016). A new parallel ga-

based method for constraint satisfaction problems. In-

ternational Journal of Computational Intelligence and

Applications, 15(03).

Balafoutis, T. and Stergiou, K. (2010). Conﬂict directed

variable selection strategies for constraint satisfaction

problems. In Hellenic Conference on Artiﬁcial Intel-

ligence, pages 29–38. Springer.

Bessi`ere, C. (1996). A simple way to improve path con-

sistency processing in interval algebra networks. In

AAAI’96, pages 375–380, Portland.

Bessi`ere, C., R´egin, J., Yap, R. H. C., and Zhang, Y. (2005).

An optimal coarse-grained arc consistency algorithm.

Artif. Intell., 165(2):165–185.

Cook, S. (2012). CUDA programming: a developer’s guide

to parallel computing with GPUs. Newnes.

Dechter, R. (2003). Constraint Processing. Morgan Kauf-

mann.

Haralick, R. and Elliott, G. (1980). Increasing tree search

efﬁciency for Constraint Satisfaction Problems. Arti-

ﬁcial Intelligence, 14:263–313.

Lecoutre, C. and Tabary, S. (2008). Abscon 109: a generic

csp solver. In 2nd International Constraint Solver

Competition, held with CP’06 (CSC’06), pages 55–

63.

Mackworth, A. K. (1977). Consistency in networks of rela-

tions. Artiﬁcial Intelligence, 8:99–118.

Mouhoub, M. and Jashmi, B. J. (2011). Heuristic tech-

niques for variable and value ordering in csps. In

Krasnogor, N. and Lanzi, P. L., editors, GECCO,

pages 457–464. ACM.

Graphics Processing Units for Constraint Satisfaction

657