Subjective Assessment Method for Multiple Displays

with and without Super Resolution

Chinatsu Mori and Seiichi Gohshi

Department of Informatics, Kogakuin University, 1-24-2 Nishi-Shinjuku Shinjuku-ku, 163-8677, Tokyo, Japan

ed15002@ns.kogakuin.ac.jp, gohshi@cc.kogakuin.ac.jp

Keywords: Display, Image Quality, Subjective Assessment, Paired Comparison, 4K TV, Super Resolution.

Abstract: At present, although 4K TV sets are available in the market, the provision of 4K TV content is still not

sufficient. Almost all TV content is in high-definition television (HDTV) broadcasting, and images/videos

with insufficient resolution are up-converted to the resolution of the display. Thus, almost all 4K TV sets are

equipped with super-resolution (SR) technology to improve the resolution of the content. However, the

performance of SR on TV sets has not been guaranteed. Although the capability of SR needs to be assessed,

there has been no standard method for such an assessment. In this paper, a subjective assessment method for

multiple displays is proposed. Subjective assessment experiments of displays with and without SR are

conducted to confirm the ability of an SR method. As the results of statistical analysis, the superiority of the

SR in resolution quality is proved by the significant differences indicating the reproducible results. As the

reproducible results are obtainable, the proposed method is useful to assess multiple displays. In this paper,

the methodology of the proposed assessment method is described and the experimental results are presented.

1 INTRODUCTION

Digital high-definition television (HDTV)

broadcasting has begun, and home-use television

(TV) displays have evolved from cathode-ray tubes

to liquid crystal displays. In 2011, 4K TV sets,

which have four times the resolution (3,840 × 2,160)

of HDTV (1,920 × 1,080), were introduced in the

market, and in 2014, 4K satellite broadcasting

started in Japan. However, 4K video content is still

not widespread, resulting in the release of 4K TV

sets ahead of the 4K broadcasting. Almost all TV

content available currently is in HDTV, and thus,

format conversion is necessary to play conventional

HDTV content on 4K TV sets. However, enlarging

an image causes blurring.

To improve image/video quality, almost all TV

sets are equipped with signal processing

technologies such as an enhancer. However, the

enhancer only enhances the edges of an image and

cannot actually improve resolution. Super-resolution

(SR) technology is one way to increase resolution.

4K TV sets equipped with SR have been released by

some manufacturers (Toshiba, 2013; Sony, 2015).

A popular SR method is super-resolution image

reconstruction (SRR), which uses multiple low-

resolution images to reconstruct a high-resolution

image (Farsiu, 2004). Although 4K TV sets

equipped with SRR are available (Toshiba, 2013),

the inability of SRR to improve the resolution of the

TV content has been discussed (Mori, 2016). Note

that SR is a catchphrase used in TV marketing, and

the performance of SR on TV sets is not guaranteed.

Although the assessment of SR performance on

TV sets is required, there is no method for such an

assessment at present. The simplest evaluation of SR

is signal analysis, which is a comparison of the

signals with and without SR in the frequency

domain. However, there is no way to measure the

signals after the SR processing on the TV sets. As

signal analysis cannot be used, a subjective

assessment is the only way to evaluate the

performance of SR embedded in video devices.

There are various TV sets equipped with signal

processing technologies including SR by different

manufacturers. Consumers compare these products

when they purchase a TV set. Although image

quality is frequently considered in the decision, there

is no way for consumers to evaluate the relative

merits of image quality between the products. A

standardized assessment methodology for television

video quality is described in BT.500 (ITU-R, 2002).

However, BT.500 is not adaptable for assessing

multiple displays leading to a product comparison.

260

Mori C. and Gohshi S.

Subjective Assessment Method for Multiple Displays with and without Super Resolution.

DOI: 10.5220/0006215202600265

In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 260-265

ISBN: 978-989-758-225-7

In other method, a paired comparison (Scheffe,

1952), was applied to image quality assessments

(Nakamae, 1996), and also applied to assess

different display panels (Kubota, 2008); however,

these assessments are for still-images. The typical

use for TV sets is video appreciation. The usefulness

of the method for video assessments on multiple

displays has not been verified. The purpose of this

study is to propose an assessment method for

multiple displays enabling to obtain consumers’

subjective impressions. Another purpose is to assess

TV sets equipped with different SR methods. In

authors’ previous work, a novel SR method using

non-linear signal processing (NLSP) was proposed

(Gohshi, 2014). The effect of NLSP is assessed by

the proposed method (Sugie, 2014; Mori, 2015). The

methodology of the assessment and the experimental

results are presented. The proposed method is

applicable to product comparisons.

2 SUBJECTIVE ASSESSMENT

Subjective image quality is a psychophysical

quantification of how a viewer perceives images and

videos. Human perceptions vary individually. Thus,

statistical analysis is essential to validate the

reproducibility of assessments. The reproducibility

is evaluated with the significant difference. Thus,

significant differences must be detectable because

the result without them makes no sense. Note that

psychophysical quantities are susceptible to various

factors, and we must carefully select the assessment

method and experimental conditions to obtain

reproducible measurements.

One of the most common subjective assessment

tools is BT.500 (ITU-R, 2002). BT.500 is useful in

evaluating the relationship between subjective image

quality and bitrate of the image coding. However,

BT.500 assessments must use a single display to

present assessment videos, and it is not directly

adaptable for multiple display assessments. A paired

comparison method and ranking method are

commonly used for sensory evaluation and it is

adaptable to multiple display assessments involving

simultaneous comparisons. The ranking method is a

comparison of all samples, whereas the paired

comparison is that of every pair of samples. The

ranking method is inferior to the paired comparison

method with respect to the sensitivity of the

assessment (Nakamae, 2000). In this paper, the

paired comparison method is combined with some of

the BT.500 experimental conditions, such as the

eligibilities of test sequences and observers. The

proposed method copes with the inadaptability of

BT.500 assessments to multiple display assessments.

3 PROPOSED METHOD

3.1 Scheffe’s Paired Comparison

A paired comparison method is a round-robin paired

comparison that helps in obtaining a statistical order

for image quality. The process of Scheffe’s paired

comparison method is as follows. Using a pair of

target and reference samples, observers score their

quality on a five-grade scale from -2 to +2 (+2:

Excellent, +1: Good, 0: Even, -1: Poor, -2: Bad).

The same assessments are repeated for all pairs of

samples. Figure 1 shows the actual experiment using

the paired comparison method. The observer

compares the quality of multiple displays placed

together. This situation reproduces an environment

in which shoppers compare multiple items at a store.

3.2 Observers and Test Sequences

BT.500 specifies that observers must be non-experts

who do not work in the video industry and have

normal visual acuity and color vision. Moreover, the

number of observers must be at least 15. The

proposed method adopts these conditions.

BT.500 specifies that each test sequence used in

the assessment must last for 10-15 s and at least four

test sequences must be used. The proposed method

also adopts these specifications. Although BT.500

does not specify assessment areas, it is not easy for

non-expert observers to recognize the difference in

quality. To stabilize the observers’ decisions, the

proposed method specifies assessment areas that

make it easier to assess image quality in each of the

test sequences. Examples of the test sequences and

the assessment areas are shown in Figures 2 and 3.

The ovals indicate the assessment areas, and the

observers judge the image qualities in these areas.

3.3 Experimental Environments

A training session is conducted in advance to

explain the meaning of high- and low-quality images

Figure 1: Experimental setup.

Subjective Assessment Method for Multiple Displays with and without Super Resolution

261

and the experimental method to observers. The

experimental process and evaluation points are

effectively explained to observers using a dummy

test sequence. The test sequence is repeated for each

display during the assessment. There is no time limit

for the assessment. The observers can freely move to

the front of each display and view the test sequences

to decide on their opinion. BT.500 specifies an

observation angle of ±30° from the front of the

screen. The proposed method maintains this angle,

and the observers are asked to view the videos from

the front of the display. A viewing distance of three

times the display height is specified in BT.500;

however, the appropriate viewing distances vary for

individuals according to their visual acuity. In the

proposed method, observers can freely select their

viewing distance during the assessment.

4 EXPERIMENTS

4.1 Experiment 1

Subjective assessment experiments were conducted

to verify the effect of NLSP. In experiment 1, the

effect of NLSP was assessed on multiple TV

displays. We used a pair of the same consumer-

grade 4K TV sets to present different assessment

videos. Figure 4 shows the 4K TV set used in the

experiment. NLSP was applied to one of the TV sets

by using the additional hardware shown in Figure 6.

Figure 7 shows a system diagram of the experiment.

The solid arrow indicates the process for presenting

the NLSP video signal, and the dashed arrow

indicates the process for presenting the original vi-

(1) Cherry tree (2) Bus

(3) Cruise ship 1 (4) Cruise ship 2

(5) Red brick

Figure 2: 4K test sequences.

deo signal. The 4K video player outputs a video

signal with 4K resolution. For the NLSP process, the

signal is input to the NLSP hardware and is

processed with NLSP. The processed video signal is

then displayed through the 4K TV set. For the

original process, the original 4K video signal is

directly input and displayed through the 4K TV set.

4.2 Experiment 2

The qualities of NLSP and conventional up-

conversion methods were compared. Experiment 2

also considered the effect of different display panels.

The same and different display sets were used for

the experiments. The stimuli are the 4K signals up-

converted from a 2K (1,920 × 1,080) signal by three

methods: NLSP, SRR, and the Lanczos filter

(Burger, 2010), which is a common interpolation

algorithm. Experiment 2-A uses two consumer-

grade 4K TV sets, as shown in Figure 4, and

experiment 2-B uses the 4K TV set shown in Figure

4 and a professional 4K display, shown in Figure 5.

The 4K TV set shown in Figure 4 is equipped with

SRR and implements it when the resolution of an

input signal is less than that of its display resolution

(4K), but it does not work with the same resolution.

The system diagrams for two experiments are shown

in Figures 8 and 9, respectively. They are the same

experiment except for the types of display devices.

The solid arrow indicates the process for presenting

the NLSP or original video signal. The dashed arrow

indicates the process for presenting the SRR video

signal. The video player outputs a video signal with

2K resolution. For the NLSP process, the 2K signal

is input to the NLSP hardware and is first up-

converted to 4K using the Lanczos filter. Then, the

(1) Ruins (2) Bricks

(3) Plaza (4) Castle

(5) Cathedral

Figure 3: 2K test sequences.

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

262

NLSP is implemented with the SR processing on the

hardware enabled (ON). If this setting is disabled

(OFF), the unprocessed 4K signal is output. The

output signal is either displayed through the 4K TV

set or the professional 4K display. For the SRR

process, the original 2K signal is directly input to the

consumer-grade 4K TV set. The signal is then up-

converted to 4K by the SRR embedded in the 4K TV

set and displayed through the 4K TV set.

4.3 Experimental Conditions

Thirty non-expert observers participated in the

experiments. The observers assessed image quality

using the five-grade scale from -2 to +2. They were

asked to assess resolution only. Other quality

factors, such as noise and color, were not considered

in the assessment. Five test sequences were used in

each experiment: the 4K test sequences shown in

Figure 2 were used in experiment 1, and the 2K test

sequences shown in Figure 3 were used in

experiment 2. These sequences do not include pan

and tilt scenes. The assessment areas indicated by

ovals in Figures 2 and 3 were specified. These areas

have high-resolution elements and are appropriate

for recognizing resolution differences.

5 RESULTS AND DISCUSSION

5.1 Results of Experiment 1

The stimuli of experiment 1 are the original 4Kvideo

signal (original) and 4K video signal processed by

NLSP (NLSP). The assessment results for the

“Cherry tree” sequence are shown in Figure 10,

which shows the average and standard deviation of

the assessment score for each stimulus. The

horizontal axis shows an assessment score, and the

marks show the average score of original and NLSP

(rhombus and square, respectively). The bars

extending from the marks show the range of the

Figure 4: 4K TV. Figure 5: 4K display.

Figure 6: NLSP hardware.

standard deviation, which indicates the dispersion of

the score from its average. A higher average

indicates a higher assessment. The average of NLSP

(1.73) is higher than that of original (-1.27).

A reproducibility test is necessary to guarantee

the difference in averages. Reproducibility is

evaluated by the average score and range of the

standard deviation. The separation of the ranges

between the stimuli indicates the reproducibility of

the assessments. Comparing the ranges of the NLSP

and original values shown in Figure 10, there is a

complete separation of the range. Similar results are

obtained from the assessments for other test

sequences. All results prove the reproducibility and

the superiority of NLSP’s scores.

5.2 Results of Experiment 2

The stimuli of experiment 2 are signals up-converted

by the Lanczos filter (Lanczos), SRR equipped on

the 4K TV set (SRR), and SR with NLSP (NLSP).

Table 1 is the cross table for the “Ruins” sequence.

Row  indicates the reference stimulus for

comparison, and column  indicates the target

stimulus. The values in Table 1 are the sums of the

assessment scores for all observers. Further, 



and





represent the sums of each row and column, 





Figure 7: Experiment 1. Figure 8: Experiment 2-A. Figure 9: Experiment 2-B.

Subjective Assessment Method for Multiple Displays with and without Super Resolution

263





is the difference of 



and 



, and 

…

represents

the total of each row or column.

Here, analysis of variance (ANOVA) was used to

assess the significant differences in the assessment

scores of the stimuli. The ANOVA results for the

“Ruins” sequence are shown in Table 2. The sum of

squares, degrees of freedom, and mean squares were

calculated for each factor (Fukuda, 2009). The 



score is a statistical value for the F-test, and it is

obtained by dividing the mean square of a specific

factor and that of the residual factor. Further, 

%

a critical F value for the 1% significance level. If 



of the stimuli factor is greater than 

%

, there is a

significant difference in the assessment scores of

stimuli. Here, 



of the stimuli factor is 





582.96

%

4.881. Thus, a 1% significant

difference between the stimuli is observed. Owing to

space limitations, the results for the other test

sequences cannot be shown, but all the ANOVA

results are the same in that there are significant

differences for the stimuli factor.

The significant differences in each pair of stimuli

were assessed because the ANOVA results

guarantee the significant differences of least one of

the pairs of stimuli. The yardstick values α for each

stimulus are calculated by 







/2, where

 is the number of observers (30) and N is the

number of stimuli (3). The yardstick values for the

“Ruins” sequence are shown in Figure 11. In Figure

11, the horizontal axis is the yardstick value, and the

marks (rhombus, square, and triangle) show the

values of each stimulus. Higher values indicate

higher assessment. The values on the arrows show

the differences between the stimuli. A critical value

of the difference in yardstick values with

significance level  is calculated as follows:











2

,

(1)

where 



is the mean square of the residual factor

(0.26), as shown in Table 2. Further,  is obtained

from the Student’s t-distribution with the degrees of

freedom for the residual factor (89) and number of

stimuli N (3). Let significance level be 0.01. Then

4.282, and thus, 

.

0.164. If the difference

in yardstick values is greater than 

.

, there is a

significant difference between the yardstick values.

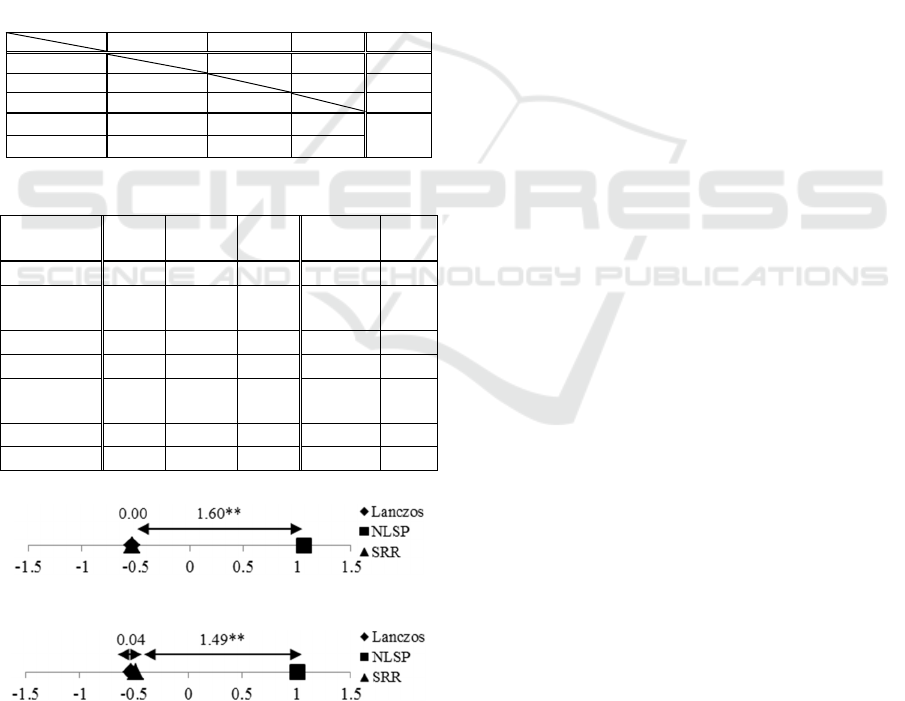
In the results of the “Ruins” sequence, the yardstick

values in Figure 11 are the highest for NLSP, SRR,

and Lanczos, in that order. The differences in the

yardstick values of adjacent stimuli, NLSP with

SRR (α

NLSP

α

SRR

), and SRR with Lanczos (α

SRR



Lanczos

) are as follows:



α



1.60Y

.

(2)



α



0.00Y

.

(3)

Because α

NLSP

α

SRR

is greater than 

.

, a 1%

significant difference between NLSP and SRR is

observed. The value of α

SRR

α

Lanczos

is not greater

than 

.

, and thus, a significant difference between

SRR and Lanczos is not guaranteed. The asterisks

(**) in Figure 11 indicate 1% significant differences

between the stimuli. The significance level of the

difference is the error decision probability. The

complement value 99% to “**” is the probability of

the difference. Thus, a quality difference practically

exists with a 99% probability. All results have

similar tendencies; NLSP has the highest evaluation,

and there are significant differences between NLSP

and SRR as well as NLSP and Lanczos in all cases.

Significant differences between SRR and Lanczos

are obtained for “Plaza,” “Castle,” and “Cathedral.”

The results of experiment 2-B were analyzed in the

same way as those of experiment 2-A. As the

ANOVA results, the 1% significant difference

between the stimuli is observed in all test sequences.

Figure 12 show the results of yardstick values for the

“Ruins” sequence. All the results are similar to those

of experiment 2-A. The yardstick values of NLSP

are the highest of all stimuli in all cases. The

significant differences are revealed between NLSP

and the other two stimuli, SRR and Lanczos.

Significant differences between SRR and Lanczos

are obtained for “Bricks” and “Castle.”

5.3 Discussion

As a result of experiment 1, a quality difference in

resolution with and without NLSP was observed.

The reproducibility of the results was proven, and

thus, the effect of NLSP on 4K TV sets is

guaranteed. In experiment 2, the superiority of

NLSP is proven from the results of two experiments

with the same and different displays. The same

results were obtained regardless of the different

displays. The quality differences between SRR and

Lanczos are too small to guarantee because they

depend on the display and sequence. The essential

limits of the ability of SRR to improve the resolution

of the TV content were discussed (Mori, 2016), and

the results of the experiments are consistent with

these discussions. All the results prove its

reproducibility, regardless of the different displays.

Figure 10: Assessment results (experiment 1 Cherry tree).

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

264

The proposed assessment method is useful for

assessing multiple displays with SR.

6 CONCLUSIONS

In this paper, a subjective assessment method for

multiple displays was proposed, and the subjective

assessment experiments of different displays with

and without SR were conducted. The results prove

the superiority of NLSP in resolution quality. Since

the statistical differences were observed from all

assessment results, the proposed method is useful to

reproducible assessments. The proposed method is

adaptable for measuring other quality factors, such

as noise or color; the measurement of overall image

quality by proposed method is the future work.

Table 1: Cross table (experiment 2-A Ruins).





Lanczos NLSP SRR





Lanczos 55 8 63

NLSP -42 -39 -81

SRR 9 56 65







-33 111 -31



…













-96 192 -96

Table 2: ANOVA results (experiment 2-A Ruins).

Factor

Sum of

Squares

Degree of

Freedom

Mean

Square







%

Stimuli 307.20 2 153.60 582.96** 4.881

Stimuli 

Observers

39.47 58 0.68 2.58** 1.746

Combination 0.05 1 0.05 0.19 6.963

Position 12.27 1 12.27 46.58** 6.963

Position 

Observers

8.56 29 0.30 1.12 1.944

Residual 23.45 89 0.26 - -

Overall result 391.00 180 2.17 - -

**: 1% significant difference

Figure 11: Assessment results (experiment 2-A Ruins).

Figure 12: Assessment results (experiment 2-B Ruins).

**: 1% significant difference

REFERENCES

Toshiba, 2013, http://us.toshiba.com/tv/research-

center/technology-guides/what-is-4k

Sony, 2015,http://www.sony.com/electronics/bravia/extra

S. Farsiu, M. Dirk Robinson, “Fast and Robust Multi-

Frame Super-Resolution”, IEEE Trans Image Pro-

cess.2004, Vol.13, no.10, pp.1327-1344, Oct.2004.

Rec. ITU-R BT.500-11, “Methodology for the subjective

assessment of the quality of television pictures”, ITU-

R, 2002.

H. Scheffe, “An analysis of variance for paired

comparisons,” J. Am. Stat. Assoc. 47(259), pp.381-

400, 1952.

M. Nakamae, Y. Tabata, Y. Ohga, M. Kakuta, F. Uto, T.

Okunishi, T. Ochi, K. Maeda, “Method of Subjective

Evaluation by Scheffe's Method of Paired

Comparisons”, Japanese Journal of Radiological

Technology, Vol.52, No.11, pp.1561-1565, 1996. (in

Japanese)

M. Nakamae, “Study of the Reliability of Visual

Evaluation by the Ranking Method: Analysis of

Ordinal Scale and Psychological Scaling Using the

Normalized-rank Approach”, Japanese Journal of

Radiological Technology 56.5, pp.725-730, 2000. (in

Japanese)

S. Kubota, “Evaluation of Image Quality of Organic

Light-emitting Diode Displays”, The Journal of The

Institute of Image Information and Television

Engineers Vol. 62, No.1, pp.122-125, 2008. (in

Japanese)

W. Burger, M. J. Burge, “Principles of Digital Image

Processing: Core Algorithms”, Springer Science &

Business Media,2010. pp.223-225

T. Fukuda, R. Fukuda, “Ergonomics handbook”, Scientist

press co.ltd, Tokyo, 2009. (in Japanese)

C. Mori, K. Tanioka, S. Gohshi, “Relationship between

Super Resolution Image Reconstruction and Image

Device”, IIEEJ Transactions on Image Electronics and

Visual Computing, Vol.4, No.1, pp.12-19, 2016.

M. Sugie, S. Gohshi, H. Takeshita C. Mori, “Subjective

assessment of super-resolution 4K video using paired

comparison”, Intelligent Signal Processing and

Communication Systems (ISPACS) 2014, pp.17-22,

2014.

C. Mori, M. Sugie, H. Takeshita, S. Gohshi, “Subjective

Assessment of Super-Resolution: High-Resolution

Effect of Nonlinear Signal Processing”, Asia-Pacific

Symposium on Information and Telecommunication

Technologies (APSITT) 2015, pp.46-48, 2015.

S. Gohshi, “Real Time Super Resolution for 4K/8K with

Non-linear Signal Processing”, Journal of SMPTE,

124/7, pp. 51-56, 2014.

Subjective Assessment Method for Multiple Displays with and without Super Resolution

265