On Robust Reachability of Input/State Switched Asynchronous
Sequential Machines
Seong Woo Kwak
1
and Jung–Min Yang
2
1
Department of Electronic Engineering, Keimyung University, 1095 Dalgubeol-daero, Dalseogu, Daegu, 42601, Korea
2
School of Electronics Engineering, Kyungpook National University, 80 Daehakro, Bukgu, Daegu, 41566, Korea
Keywords:
Asynchronous Sequential Machines, Switched Systems, Robust Reachability, Fault Tolerance.
Abstract:
Switched asynchronous sequential machines are composite systems consisting of a number of single asyn-
chronous machines, or submachines, and a rule that orchestrates switching operations between submachines.
In this paper, we investigate robust reachability of switched asynchronous machines. If each submachine has
equivalent state space with one another, it can be used in fault recovery against any unauthorized state tran-
sition caused by transient faults. The robust reachability of switched asynchronous machines is addressed in
terms of simple matrix expressions. The use of robust reachability in fault-tolerant corrective control is also
outlined.
1 INTRODUCTION
Asynchronous sequential machines are hard-
ware/software systems that operate sequentially with
no global synchronizing clock (Sparsø and Furber,
2001). Since first invented in mid 1950’s (Huffman,
1954), asynchronous sequential machines have been
used in various areas as an important building block
of the system, e.g., digital systems (Unger, 1995),
communication networks (Schwartz, 1996), parallel
computation, etc. It is also expected that the notion
and control of asynchronous sequential machines
can be applied to the field of systems biology
and bioinformatics (Hammer, 1995; Saadatpour,
Albert, and Albert, 2010), as biological systems
inherently have the feature of asynchrony, and the
state space of biological systems can be expressed in
discrete dynamics, which fits into the mechanism of
asynchronous machines.
In this paper, we address robust reachability of
switched asynchronous sequential machines. The
switched systems are a kind of hybrid systems that
consist of several submachines and a rule that co-
ordinates switching operations between them. Due
to their importance in both theoretical and practi-
cal applicability, the study of switched systems has
drawn a great attention, especially in the field of lin-
ear systems (Sun and Ge, 2006). In event-driven dy-
namics, however, few studies on switched systems
have been reported so far. Notable among them
are switched Boolean networks for gene regulatory
networks (Zhang and Feng, 2012) and control of
switched asynchronous sequential machines by the
authors (Yang, 2016).
In the prior work (Yang, 2016), the problem of
model matching for switched asynchronous sequen-
tial machines is investigated in the framework of cor-
rective control, which is a novel automatic control
theory developed exclusively for asynchronous ma-
chines (Murphy, Geng, and Hammer, 2003). The
control objective in Yang (2016) is to elucidate the
existence condition and design algorithm for a cor-
rective controller that matches the stable-state behav-
ior of the closed-loop system to that of a prescribed
reference model. In the present study, we are con-
cerned with fault-tolerant controllability of switched
asynchronous machines. We assume that the con-
sidered switched machine may suffer from transient
faults (Krishna and Shin, 1997). Transient faults
cause unauthorized state transitions to the machine,
making the next behavior unpredictable if not recov-
ered. Note that our study can be also applied to in-
termittent faults. While the adverse effect of transient
faults vanish immediately after the fault occurrence,
that of intermittent faults lasts for finite time. Hence
once an asynchronous machine undergoes an unau-
thorized transition by the intermittent fault, it cannot
return to the original state immediately and more rig-
orous procedure of fault tolerance is needed.
In this paper, we derive and quantify inherent
190
Kwak S. and Yang J.
On Robust Reachability of Input/State Switched Asynchronous Sequential Machines.
DOI: 10.5220/0006220401900195
In Proceedings of the 10th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2017), pages 190-195
ISBN: 978-989-758-214-1
Copyright
c
 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

reachability of switched asynchronous sequential ma-
chines necessary to overcome both transient and inter-
mittent faults. We show that compared with the case
of transient faults, the switched machine must have
more reachability to tolerate the effect of intermittent
faults. Though this reachability analysis is a requisite
for designing a fault-tolerant corrective controller, in
this study we omit the controller construction and in-
stead outline the correction procedure as a remark.
The rest of this work is organized as follows. Sec-
tion 2 provides a modeling formalism of switched
asynchronous machines with transient faults. In Sec-
tion 3, the reachability of switched asynchronous ma-
chines is described in terms of numerical matrices and
the condition for fault-tolerant controllability is ad-
dressed. A simple example is provided in Section 4 to
support the proposed methodology. Finally, Section 5
concludes the paper.
2 PRELIMINARIES
2.1 Switched Asynchronous Sequential
Machines
Let us consider a switched asynchronous sequential
machine Σ with m submachines. Assume that each
submachine is a single input/state asynchronous se-
quential machine, namely the present state of the ma-
chine is given as the output. Σ is represented as
Σ = {Σ
i
|i ∈ M}
Σ
i
= (A, X, f
i
)
where M = {1, . . . , m}, Σ
i
is the ith submachine, A
is the input set, X is the state set with n states, and
f
i
: X × A → X is the state transition function of Σ
i
partially defined on X × A. Since every submachine
is assumed to have an equal operational domain, the
input and state set of Σ
i
is the same for every i ∈ M. A
is further divided intoA = A
n
˙
∪A
d
where A
n
and A
d
are
the set of normal and adversarial inputs, respectively.
Each submachine Σ
i
is operated according to the
characteristics of a single asynchronous sequential
machine, that is, it is not governed by any synchroniz-
ing clock and the state transition is executed only in
response to changes of external inputs. A state–input
pair (x, v
′
) ∈ X × A is a stable pair of Σ
i
if f
i
(x, v
′
) = x
and x is a stable state. If f
i
(x, v
′
) 6= x, on the other
hand, x is a transient state and (x, v
′
) is a transient
pair. Note that x may be stable or transient depending
on the value of the present input. Denote by
U
i
(x) = {v ∈ A
n
| f
i
(x, v) = x}
the set of normal inputs that make a stable pair with x
in Σ
i
. Owing to the absence of a synchronizing clock,
Σ
i
stays at a stable pair (x, v
′
) indefinitely. If the in-
put v
′
changes to another value v for which (x, v) is
a transient pair, Σ
i
engages in a series of transient
transitions f
i
(x, v) = x
1
, f
i
(x
1
, v) = x
2
, . . . where v re-
mains fixed. Assuming no infinite cycles, Σ
i
reaches
the next stable state x
k
such that x
k
= f
i
(x
k
, v) at the
end of the chain with k transient transitions. Since
the transition speed of asynchronous sequential ma-
chines is very fast, the meaningful behavior of asyn-
chronous sequential machines may be described only
in terms of stable states. To this end, we introduce the
stable recursion function s as follows (Murphy et al.,
2003): s
i
: X × A → X, and s
i
(x, v) = x
′
where x
′
is
the next stable state of a valid state–input pair (x, v).
A chain of transient transitions from a stable state to
its next stable state, as represented by s
i
, is termed a
stable transition. The domain of s
i
can be expanded to
X × A
+
in a natural way as follows, where A
+
is the
set of all nonempty strings of characters in A.
s
i
(x, v
1
v
2
···v
k
) = s
i
(s
i
(x, v
1
), v
2
···v
k
),
v
1
v
2
···v
k
∈ A
+
2.2 Control Configuration
C D
1
Σ
m
Σ
P
u
v
(i,x)
σ
σ
w
1
w
m
x
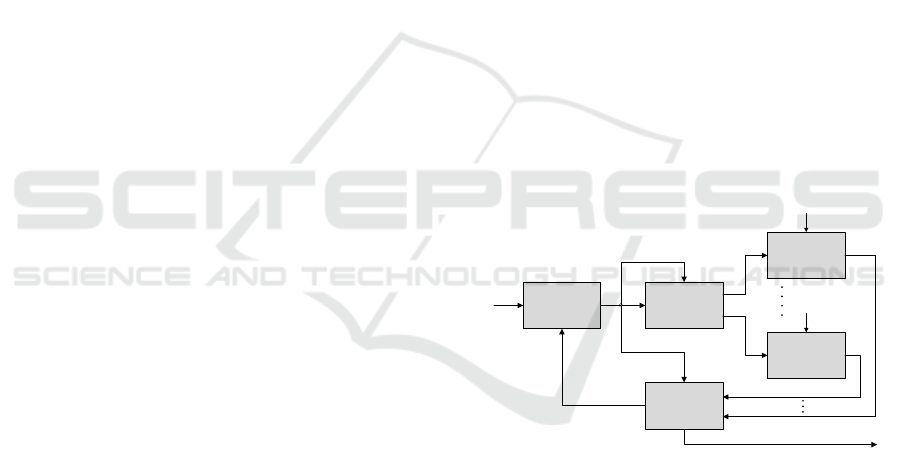
Figure 1: Control configuration for the switched asyn-
chronous sequential machine Σ with transient faults.
A control configuration for the switched asyn-
chronous sequential machine Σ is shown in Figure
1. C is the corrective controller, also designed in the
form of an asynchronous sequential machine. C pro-
vides Σ with the control signal u ∈ A
n
or the switch-
ing signal σ ∈ M, either of which is generated at a
time, but not simultaneously. The control input is de-
livered to D, the demultiplexer. D plays the role of
determining the active submachine whose dynamics
is manifested by Σ. The latter is realized by changing
the value of σ. Whenever σ is changed to a new value
in M, D gives the new active submachine the control
signal u, which can be interpreted as the switching op-
eration. P, the multiplexer, receives m state feedback
On Robust Reachability of Input/State Switched Asynchronous Sequential Machines
191

values from all submachines Σ
1
, . . . , Σ
m
and selects x,
the feedback value generated by the active subma-
chine Σ
σ
. P forwards x and i ∈ M, the index of the
active submachine, to C. Let Σ
c
denote the closed-
loop system consisting of C, D, P, and Σ.
In Figure 1, v ∈ A
n
is the external input and
w
1
, . . . , w
m
∈ A
d
are the adversarial input occurring to
Σ
1
, . . . , Σ
m
, respectively. When w
i
occurs, Σ
i
experi-
ences an unauthorized state transition. For instance,
if the active submachine of Σ is Σ
i
staying at a stable
state x at which w
i
is defined, Σ
i
must be forced to
reach s
i
(x, w
i
) as the result of the fault. If an imme-
diate fault recovery to the original state is not con-
ducted, the next behavior of Σ with respect to the
new external input would show incorrect state/input
behavior. Thus the objective of fault diagnosis and
tolerance is that the corrective controller C must be
designed such that the closed-loop system Σ
c
can
achieve instantaneous fault recovery upon diagnosing
an occurrence of a fault.
One point to be reminded is that immediate fault
recovery is impossible in the case that the fault shows
intermittent characteristics. When w
i
represents the
intermittent fault, Σ
i
cannot return to x upon diag-
nosing an occurrence of w
i
. But since Σ has m sub-
machines and each submachine has the same state
space made of X, we can regard that fault tolerance
is achieved if Σ returns to the state x of another sub-
machine. Whether Σ has such robust reachability will
be discussed in detail in the next section.
To avoid unpredictable behaviors caused by the
absence of a synchronizing clock, we assume that Σ
c
always preserves the principle of fundamental mode
operations (Kohavi and Jha, 2010) whereby a variable
must change its value when both C and Σ are in sta-
ble states, and no two or more variables can be altered
simultaneously.
3 ROBUST REACHABILITY
3.1 Skeleton Matrix
Assuming |X| = n, we denote the state set by X =
{x
1
, . . . , x
n
}. Reachability of switched asynchronous
sequential machines is classified into to two aspects:
(i) stable reachability of each submachine, and (ii)
switching capability between different submachines.
In corrective control of single asynchronous ma-
chines, reachability of a machine is described by a
Boolean matrix, termed the skeleton matrix (Murphy
et al., 2003; Peng and Hammer, 2012), as follows.
Definition 1. K(Σ
i
), the skeleton matrix of Σ
i
=
(A, X, f
i
), is an n× n matrix whose (p, q) entry is
K
p,q
(Σ
i
) =

1 ∃t ∈ A
+
n
s.t. x
q
= s
i
(x
p
, t)
0 otherwise
If K
p,q
(Σ
i
) = 1, a corrective controller can be con-
structed that takes Σ
i
from x
p
toward x
q
in the asyn-
chronous mechanism using an input string t ∈ A
+
n
such that x
q
= s
i
(x
p
, t). For a detailed procedure
of controller construction, the readers are referred to
Murphy et al. (2003); Peng and Hammer (2012).
Switching capability of Σ implies the ability of Σ
to change its mode from a submachine to another sub-
machine at a specific stable state. In the prior work
(Yang, 2016), a constraint is imposed on the switch-
ing operation that as the result of switching, the active
submachine always takes the same state possessed by
the previous submachine. In this study, we general-
ize the switching operation by relaxing the foregoing
constraint. In other words, the new active subma-
chine does not necessarily transfer to the same state
at which the old one has stayed before switching. To
address the switching relation between two subma-
chines, we define the following matrix.
Definition 2. W(i, j), the switching incidence ma-
trix of two submachines Σ
i
and Σ
j
, is an n × n matrix
whose (p, q) entry is
W
p,q
(i, j) =



1 Σ switches the mode from Σ
i
at x
p
to Σ
j
at x
q
0 otherwise
W(i, j) represents switching capability of Σ in the
most general way, that is, the state of the present
submachine may differ from the previous one after
switching. The motivation for introducing W(i, j)
stems from the fact that some switched machines have
multiple submachines that share the same system
module to realize the state space. As the switching op-
eration depends on this implementation restraint, the
next state may be different from the previous one.
Note that for switching from Σ
i
at x
p
to Σ
j
at x
q
,
there must exist an input a ∈ A
n
that makes a stable
pair with both x
p
of Σ
i
and x
q
of Σ
j
, i.e.,
W
p,q
(i, j) = 1 ⇒ U
i
(x
p
) ∩U
j
(x
q
) 6=
/
0 (1)
Under the principle of fundamental mode operations,
Σ
i
should stay at the stable state x
p
at the moment that
the switching signal σ changes. Hence the present
control signal is u ∈ U
i
(x
p
). Moreover, u must also
make a stable pair with x
q
in Σ
j
, namely u ∈ U
j
(x
q
);
otherwise Σ
j
could not maintain x
q
upon completion
of the switching operation. However, the condition
u ∈ U
j
(x
q
) may not be always valid since u is deter-
mined only by the past state trajectory of Σ
i
. Still, as
long as U
i
(x
p
)∩U
j
(x
q
) 6=
/
0 is held true, C can achieve
BIOINFORMATICS 2017 - 8th International Conference on Bioinformatics Models, Methods and Algorithms
192

the switching operation by changing the control sig-
nal to u
′
∈ U
i
(x
p
) ∩ U
j
(x
q
) right before transmitting
the switching signal σ = j. In this sense, (1) is a req-
uisite for guaranteeing consistent switching.
The following definitions depict stable reachabil-
ity and switching capability of Σ in a single matrix,
respectively.
Definition 3. K(Σ), the skeleton matrix of Σ for sub-
machines, is an nm× nm matrix defined as
K(Σ) =




K(Σ
1
) 0
n×n
·· · 0
n×n
0
n×n
K(Σ
2
) ··· 0
n×n
.
.
.
.
.
.
.
.
.
.
.
.
0
n×n
0
n×n
·· · K(Σ
m
)




W(Σ), the switching incidence matrix of Σ, is an nm×
nm matrix defined as
W(Σ) =




0
n×n
W(1, 2) ·· · W(1, m)
W(2, 1) 0
n×n
·· · W(2, m)
.
.
.
.
.
.
.
.
.
.
.
.
W(m, 1) ·· · W(m, m− 1) 0
n×n




Definition 4. The one-step switching skeleton matrix
S
1
(Σ) is an nm× nm Boolean matrix defined as
S
1
(Σ) =




K(Σ
1
) W(1, 2) ·· · W(1, m)
W(2, 1) K(Σ
2
) ·· · W(2, m)
.
.
.
.
.
.
.
.
.
.
.
.
W(m, 1) ·· · W(m, m− 1) K(Σ
m
)




The k-step switching skeleton matrix S
k
(Σ) (k ≥ 2)
is recursively defined as
S
k
(Σ) = S
k−1
(Σ) ×
B
S
1
(Σ)
where ‘×
B
’ denotes the Boolean product of two
Boolean matrices where logic AND and OR are used
instead of multiplication and plus operations in the
matrix product.
Definition 5. The combined switching skeleton ma-
trix Z(Σ) of the switched asynchronoussequential ma-
chine Σ is an nm× nm Boolean matrix defined as
Z(Σ) =
nm−1
∑
k=1
+
B
S
k
(Σ)
where ‘+
B
’ denotes the Boolean addition of two ma-
trices.
Note that in the above definitions, state x
p
(p ∈
{1, . . . , n}) of the ith submachine Σ
i
is assigned the
index p
′
∈ {1, . . . , nm} such that
p
′
= (i− 1)n+ p
K(Σ) just assembles stable reachability of all the
submachines. Referring to Definition 3, K(Σ) does
not contain any reachability information between dif-
ferent submachines. If K
p
′
,q
′
(Σ) = 1 for some p
′
, q
′
∈
{1, . . . , nm}, p
′
= (i− 1)n + p, and q
′
= (i − 1)n + q,
it follows that K
p,q
(Σ
i
) = 1, which means x
q
is stably
reachable from x
p
in submachine Σ
i
.
W(Σ) epitomizes switching capability of Σ. In
contrast to K(Σ), W(Σ) does not contain any stable
reachability measured within a single submachine.
Having W(i, j) as sub-blocks, W(Σ) shows whether
Σ can transfer from a state of a submachine to another
state of another submachine through switching oper-
ations. If W
p
′
,q
′
(Σ) = 1 for some p
′
, q
′
∈ {1, . . . , nm},
p
′
= (i − 1)n + p, and q
′
= ( j − 1)n + q, we have
W
p,q
(i, j) = 1. Thus Σ can move from x
p
of Σ
i
to x
q
of Σ
j
via the switching operation.
S
1
(Σ) in Definition 4 contains both stable reacha-
bility and switching capability of Σ. Here, “one-step”
implies that Σ takes either one switching operation or
correction procedure. Indeed, a correction procedure
by the controller involves more than one stable transi-
tions if the length of the used input sequence is greater
than one (Murphy et al., 2003).
The combined switching skeleton matrix Z(Σ) is
a generalized description of stable reachability for the
switched asynchronous sequential machine Σ. Not
only does Z(Σ) represent stable reachability within
each submachine, it also elucidates whether a state
of a submachine can be reached from another state
of a different submachine by a combination of stable
transitions and switching operations. Since Σ has nm
states in total, any state in Σ can be reached within
nm− 1 steps of switching and correction procedures.
Hence S
1
(Σ), . . . , S
nm−1
(Σ) are sufficient to express
the entire reachability of Σ.
3.2 Robust Reachability Analysis
In order to address the robust reachability of Σ, we
must quantify the adverse effect of fault inputs. De-
fine F
i
(x) ⊂ A
d
for x ∈ X and i ∈ M as
F
i
(x) = {w ∈ A
d
|s
i
(x, w)! and s
i
(x, w) 6= x}
where s
i
(x, w)! means s
i
(x, w) is defined in Σ
i
. F
i
(x)
is the set of adversarial inputs that cause unauthorized
transitions at x of Σ
i
. In a similar way to K(Σ
i
), we ex-
press the characteristics of all unauthorized state tran-
sitions by a simple matrix as follows.
Definition 6. K
d
(Σ
i
), the adversarial skeleton matrix
of submachine Σ
i
, is an n × n matrix whose (p, q) en-
try is
K
d
p,q
(Σ
i
) =

1 ∃w ∈ F
i
(x
p
) s.t. s
i
(x
p
, w) = x
q
0 otherwise
On Robust Reachability of Input/State Switched Asynchronous Sequential Machines
193

In particular, assume that there exists an adversar-
ial input w
i
∈ F
i
(x
p
) such that s
i
(x
p
, w
i
) = x
q
. Ac-
cording to the above definition, we have K
d
p,q
(Σ
i
) = 1.
The fact that the unauthorized transition from x
p
to
x
q
is manifested means that Σ
i
is serving as the active
submachine of Σ. The condition for robust reacha-
bility varies depending on how many steps and sub-
machines will be used for realizing the fault-tolerant
control process.
First, assume an extreme case that we would like
to maintain the active submachine as the same despite
an occurrence of the fault. In the foregoing case, this
means that submachine Σ
i
must have fault-tolerance
capability against w
i
. Clearly, the condition for driv-
ing Σ
i
back to the original state x
p
is that Σ
i
must have
stable reachability from x
q
to x
p
. Thus, we have
K
d
p,q
(Σ
i
) = 1 ⇒ K
q, p
(Σ
i
)
Generalizing the above relation, we derive as follows
the robust reachability for fault tolerance using a sin-
gle submachine.
(K
d
(Σ
i
))
T
≤ K(Σ
i
) (2)
where the inequality is taken entry by entry and
(K
d
(Σ
i
))
T
denotes the transpose of K
d
(Σ
i
). Note that
an intermittent fault cannot be tolerated using this ro-
bust reachability, since the instantaneous recovery to
x
p
is infeasible.
Next, assume that we would like to involve one
more submachine in realizing fault-tolerant control.
This means that upon diagnosing a fault occurrence,
the controller will provide a switching signal, with
which Σ will change its mode to another submachine,
say Σ
j
. Then fault tolerance is conducted in Σ
j
by
enforcing Σ
j
to reach the desired state x
p
. With the
skeleton matrices, the reachability condition for the
latter case is described as
W
q,r
(i, j) = 1 and K
r, p
(Σ
j
) = 1
where we suppose that Σ reaches x
r
of Σ
j
as the result
of the switching operation from Σ
i
at x
q
. Submachine
Σ
j
can be arbitrarily chosen so long as the above con-
dition is satisfied. We represent in formal terms this
robust reachability condition as follows.
∀i ∈ M, ∃ j ∈ M such that
(K
d
(Σ
i
))
T
≤ W(i, j) ×
B
K(Σ
j
) (3)
Finally, assume that fault-tolerant procedures can
be implemented using either only submachine Σ
i
or
Σ
i
and another submachine, and that different subma-
chines can be used in the entire fault-tolerant control
procedure. To this end, we introduce another Boolean
matrix as follows.
Definition 7. For Σ, let
K (Σ) = W(Σ) +
B
W(Σ) ×
B
K(Σ)
Z(Σ
i
), the augmented skeleton matrix of submachine
Σ
i
, is an n× n matrix whose (p, q) entry is
Z
p,q
(Σ
i
) = max
j∈M, j6=i
K
p
′
i
,q
′
j
(Σ)
where p
′
i
= (i− 1)n+ p and q
′
j
= ( j − 1)n+ q.
Using Z(Σ
i
), we derive the following robust
reachability condition for fault-tolerant controllabil-
ity of Σ.
∀i ∈ M, (K
d
(Σ
i
))
T
≤ Z(Σ
i
) (4)
Whereas (2) cannot solve fault tolerance against
intermittent faults, (3) and (4) ensure fault-tolerant
controllability against them, since Σ does not return to
the original state at which the fault occurs. Although
not used in this paper, the combined skeleton ma-
trix Z(Σ) in Definition 5 can be applied to represent
the overall fault-tolerant controllability of Σ, namely
whether Σ can overcome any unauthorized state tran-
sition using arbitrary number of submachines and cor-
rection procedures. Once the robust reachability con-
ditions (2)–(4) are guaranteed, a fault-tolerant correc-
tive controller can be easily designed based on the
previous algorithm for the model matching problem
(see, e.g, Murphy et al. (2003); Peng and Hammer
(2012); Yang (2016)).
4 EXAMPLE
x
2
x
3
c
c
b
b
c,w
2
2
Σ
x
1
a
a
x
2
x
3
c
c
b
b a,w
1
1
Σ
x
1
a
Figure 2: Switched asynchronous machine Σ = {Σ
1
, Σ
2
}.
Consider a simple switched asynchronous machine
Σ = {Σ
1
, Σ
2
} (M = {1, 2}) shown in Figure 2, where
X = {x
1
, x
2
, x
3
}, A
n
= {a, b, c}, and A
d
= {w
1
, w
2
}.
For simplicity, we set f
i
(x, v) = s
i
(x, v) for all i = 1, 2
and (x, v) ∈ X × A. A slight examination of Figure 2
leads to
K(Σ
1
) =


1 1 1
1 1 1
1 1 1


K(Σ
2
) =


1 1 1
1 1 1
0 0 1


BIOINFORMATICS 2017 - 8th International Conference on Bioinformatics Models, Methods and Algorithms
194

We assume that Σ has switching capability expressed
by the following switching skeleton matrix.
W(1, 2) = W(2, 1) =


1 0 0
0 1 0
0 1 0


Following Definition 6 and referring to Figure 2, we
quantify the adverse effect of A
d
by
K
d
(Σ
1
) =


0 0 0
0 0 0
1 0 0


K
d
(Σ
2
) =


0 0 1
0 0 0
0 0 0


Consider the adversarial input w
1
in the first.
Clearly, we have (K
d
(Σ
1
))
T
≤ K(Σ
1
). Hence the
unauthorized transition s
1
(x
3
, w
1
) = x
1
caused by w
1
can be invalidated (if w
1
has the transient feature) by
employing only Σ
1
, as Σ
1
has sufficient robust reach-
ability (K
1,3
(Σ
1
) = 1 and s
1
(x
1
, bc) = x
3
). Next, con-
sider the case of w
2
. We see that K
d
1,3
(Σ
2
) = 1 but
K
3,1
(Σ
2
) = 0. This implies that fault tolerance cannot
be achieved within Σ
2
. However, since W
3,2
(2, 1) = 1
and K
2,1
(Σ
1
) = 1, fault-tolerant control may be real-
ized by activating a two-step procedure: switching to
Σ
1
(σ = 1) upon diagnosing an occurrence of w
2
, and
initiating the correction procedure from x
2
to x
1
in Σ
1
.
This argument can be also asserted by applying con-
dition (4).
5 CONCLUSION
In this study, fault-tolerant controllability for a class
of switched asynchronous sequential machines has
been investigated. We have presented matrix ex-
pressions to describe robust reachability of switched
asynchronous sequential machines in a quantitative
manner. We have found that the condition for fault-
tolerant controllability is determined by the number
of submachines that are used in fault-tolerant control
procedures. The examination of the controller exis-
tence has been demonstrated in a simple example.
ACKNOWLEDGEMENTS
The research of S. W. Kwak was supported
by Basic Science Research Program through
the National Research Foundation of Korea
(NRF) funded by the Ministry of Education
(No. 2016R1D1A1B02012959). The research
of J.–M. Yang was supported by Basic Science
Research Program through the National Research
Foundation of Korea (NRF) funded by the Ministry
of Education (No. 2015R1D1A1A01056764) and by
the Ministry of Science, ICT and future Planning
(No. 2015R1A2A1A15054026).
REFERENCES
Hammer, J. (1995). On the modeling and control of biolog-
ical signaling chains. In Proceedings of IEEE Interna-
tional Conference on Decision and Control, pp. 3742–
3752.
Huffman, D. A. (1954). The synthesis of sequential switch-
ing circuits. Journal of The Franklin Institute, 257,
161–190.
Kohavi, Z., Jha, N. K.(2010). Switching and finite automata
theory (3rd ed.). Cambridge, UK: Cambridge Univer-
sity Press.
Krishna, C. M., Shin, K. G. (1997). Real-time systems.
NewYork: McGraw-Hill.
Murphy, T. E., Geng, X., Hammer, J. (2003). On the control
of asynchronous machines with races. IEEE Transac-
tions on Automatic Control, 48(6), 1073–1081.
Peng, J., Hammer, J. (2012). Bursts and output feedback
control of non-deterministic asynchronous sequential
machines. European Journal of Control, 18(3), 286–
300.
Saadatpour, A., Albert, I., Albert, R. (2010). Attractor
analysis of asynchronous Boolean models of signal
transduction networks. Journal of Theoretical Biol-
ogy, 266(4), 641–656.
Schwartz, M. (1996). Broadband integrated networks. New
Jersey: Prentice Hall.
Sparsø, J., Furber, S. (2001). Principles of asynchronous
circuit design — a systems perspective. Kluwer Aca-
demic Publishers.
Sun, Z., Ge, S. S. (2006) Switched linear systems: control
and design. London: Springer-Verlag.
Unger, S. H. (1995). Hazards, critical races, and metasta-
bility. IEEE Transactions on Computers. 44(6), 754–
768.
Yang, J. M. (2016). Modeling and control of switched asyn-
chronous sequential machines. IEEE Transactions on
Automatic Control, 61(9), 2714–2719.
Zhang, L., Feng, J. (2012). Controllability and observabil-
ity of switched Boolean control networks. IET Control
Theory & Applications, 6(16), 2477–2484.
On Robust Reachability of Input/State Switched Asynchronous Sequential Machines
195