
A Prime Number Approach to Matching an XML Twig Pattern including
Parent-Child Edges
Shtwai Alsubai and Siobh
´
an North
Department of Computer Science, The University of Sheffield, Sheffield, U.K.
Keywords:
XML, Holistic Algorithm, Twig Pattern Query.
Abstract:
Twig pattern matching is a core operation in XML query processing because it is how all the occurrences
of a twig pattern in an XML document are found. In the past decade, many algorithms have been propo-
sed to perform twig pattern matching. They rely on labelling schemes to determine relationships between
elements corresponding to query nodes in constant time. In this paper, a new algorithm TwigStackPrime is
proposed, which is an improvement to TwigStack (Bruno et al., 2002). To reduce the memory consumption and
computation overhead of twig pattern matching algorithms when Parent-Child (P-C) edges are involved, Twig-
StackPrime efficiently filters out a tremendous number of irrelevant elements by introducing a new labelling
scheme, called Child Prime Label (CPL). Extensive performance studies on various real-world and artificial
datasets were conducted to demonstrate the significant improvement of CPL over the previous indexing and
querying techniques. The experimental results show that the new technique has a superior performance to the
previous approaches.
1 INTRODUCTION
The extensible markup language XML has emerged
as a standard format for information representation
and communication over the internet. Due to the defi-
nition of relationships in XML as nested tags, data in
XML documents are self-describing and flexibly or-
ganized (Li and Wang, 2008). The basic XML data
model is a labelled and ordered tree. A query in the
context of XML is defined as a complex selection on
elements of an XML document specified by structural
information of the selected elements (Wu et al., 2012).
In most XML query languages, such as XPath and
XQuery, a twig (small tree) pattern can be represented
as a node-labelled tree whose edges specify the relati-
onship constraints among its nodes and they are either
Parent-Child or Ancestor-Descendant. Generally, the
purpose of XML indexing is to improve the efficiency
and the scalability of query processing by reducing
the search space. Without an index, XML retrieval
algorithms have to scan all the data. In XML, the ty-
pes of structural index can be divided into two main
groups; node and graph indexing. A well-known ex-
ample of node indexing is range-based (Zhang et al.,
2001). In a range-based labelling scheme, every node
in an XML document is assigned an unique label
to record its position within the original XML tree.
The labelling scheme must enable determination of
all structural relationships by computation. In order
to detect the twig patterns, previous algorithms need
to access only the labels corresponding to the query
nodes without traversing the original XML tree by
utilizing a clustering mechanism called tag streaming
where all elements with the same tag are grouped to-
gether (Chen et al., 2005). The alternative usually
summarizes all paths in an XML document starting
from the root. Early work on processing twig pat-
tern matching decomposed twigs into a set of binary
structures, then performed structural joins to obtain
individual binary matchings. The final solution of the
twig query is computed by stitching together the bi-
nary matches.
In (Bruno et al., 2002), the authors introduced the
first holistic twig join algorithm for matching an XML
twig pattern, called TwigStack. It works in two pha-
ses. Firstly, twig patterns are decomposed into a set
of root-to-leaf paths queries and the solutions to these
individual paths are computed from the data tree.
Then, the intermediate paths are merge joined to form
the final result. The authors of (Bruno et al., 2002)
proposed a novel prefix filtering technique to reduce
the number of irrelevant elements in the intermediate
paths. TwigStack is optimal for twig patterns when all
the structural relationships are Ancestor-Descendant,
204
Alsubai, S. and North, S.
A Prime Number Approach to Matching an XML Twig Pattern including Parent-Child Edges.
DOI: 10.5220/0006225602040211
In Proceedings of the 13th International Conference on Web Information Systems and Technologies (WEBIST 2017), pages 204-211
ISBN: 978-989-758-246-2
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

and it guarantees all the intermediate path solutions
contribute to the final result, but it generates useless
intermediate path results when the twig pattern query
contains Parent-Child axes.
In this paper, we proposed a new indexing technique
to identify P-C relationships efficiently, called Child
Prime Labels. We extended the original holistic twig
pattern matching algorithm to process XML twig pat-
terns with P-C axes efficiently and reduce memory
consumption and CPU overheads. In addition, we
have conducted an extensive set of experiments to
compare the performance of the new algorithm to the
previous approaches.
The rest of this paper is organized as follows: the
novel indexing and twig algorithm are presented in
Section 2 and Section 3, respectively. In Section 4 the
experimental results are reported. The discussion of
related work in Section 5, then the paper is concluded
in the last section 6.
2 NODE LABELLING SCHEME
Node indexing (also referred to as a labelling or num-
bering scheme) is commonly used to label an XML
document to accelerate XML query performance by
recording information on the path of an element to
capture structural relationships rapidly during query
processing with no need to access the XML document
physically (Lu et al., 2004). In this approach, every
node in an XML document is indexed and assigned an
unique label which records its positional information
within an XML tree. The information gained from la-
bels vary according to the chosen labelling scheme.
Most of the previous twig join algorithms rely on la-
belling schemes where nodes are considered as the
basic unit of a query which provides a great flexibi-
lity in performing any structural query matching effi-
ciently.
To determine the effects of the range-based labelling
scheme, (Zhang et al., 2001) proposed multi-predict
merge-join algorithm based on the positional infor-
mation of the XML tree. An alternative representa-
tion, a prefix scheme, of labels of an XML tree can
be seen in (Lu et al., 2011). In this sort of labelling
scheme, each node is associated with a sequence of
integers that represents the node-ID path from the root
to the node. This approach can be exemplified by De-
wey, the sequence of components in a Dewey label
is separated by ”.” where the last component is cal-
led the self label (i.e., the local order of the node) and
the rest of the components are called the parent la-
bel. For instance, {1.2.3} is the parent of {1.2.3.1}.
Another approach, (Alireza Aghili et al., 2006) ad-
dressed the limitations of information encoded within
labels produced by existing labelling schemes. It fo-
cus on performing join operations earlier, at leaf le-
vels, where the selectivity of query nodes is at its peak
for data-centric XML documents. The significance of
the proposed approach stems from a comprehensive
labelling scheme that could infer additional structural
information, called Nearest Common Ancestor, NCA
for short rather than the basic relationships among
elements of XML documents. None of the previous
approaches have taken the breadth of every node into
account. We propose a novel approach to overcome
the previous limitations. The key idea of our work is
to find an appropriate, refined labelling scheme such
that, for any given query node in the query, the set
of its child query nodes in the XML document which
forms the major bottleneck in determining structural
relationship because parent-child can be resolved ef-
ficiently. This novel approach results in considerably
fewer single paths stored than TwigStack algorithm.
It also increases the overall performance and reduces
the memory overhead, and the result is shown clearly
in our experiments. During depth-first scanning, a
node is assigned the next available prime number if its
tag has not been examined. After that, we check the
CPL parameter of its parent element to see whether it
is divisible by the assigned prime number or not. If it
is, we process the next element, otherwise the product
of parent element’s CPL is multiple by the new prime
number. For illustration, assume we have two nodes
u and v labelled by a triplet(start,end, level) where
start and end record the positional information of the
opening tag and the ending tag, respectively, while
level is the number of edge(s) to the root. A set of
structural relationships can be determined as follows:
Property 1. Ancestor-Descendant and Parent-Child
relationships, For two nodes u and v encoded using
the range-based labelling scheme can be described
as v=( start
u
, end
u
, level
u
) and u=( start
v
, end
v
, level
v
). From that positional information, u is the
ancestor of v if and only if start
u
< start
v
< end
u
.
Property 2. Parent-Child relationship, From that
positional information, u is the parent of v if and only
if start
u
< start
v
< end
u
and level
u
+ 1 = level
v
.
Definition 1. (Child Prime Label) A child prime la-
bel is assigned to each element in an XML docu-
ment as an extra parameter into the range-based la-
bel. A child prime label indicates the multiplication
of distinct prime numbers for every internal elements
within the document. For example, node u is encoded
quadruple =( start
u
, end
u
, level
u
, CPL
u
).
Property 3. In any XML labelling scheme that
is augmented with Child Prime Label, for any
A Prime Number Approach to Matching an XML Twig Pattern including Parent-Child Edges
205

(a) (b)
Figure 1: An example of an XML tree labelled using the original range-based labelling scheme in Figure 1a and the new child
prime label parameter assigned to each element along with the tag index in the top right of Figure 1b.
nodes x,y and z in an XML document, x has
at least one or more child nodes of tag(y)
and tag(z) if CPL
x
mod key
tag(y)
× key
tag(z)
=
0 where key
tag(y)
and key
tag(y)
are unique prime numbers.
Figure 1a and 1b are a sample of an XML tree la-
belled with the original range-based and child prime
label augmentation, respectively. To demonstrate the
effect of child prime label, consider the XML tree
in Figure 1b and the tag indexing table on the top
right, queries in XML are expressed as twigs since
data is represented as tree. The answer to an XML
query is all occurrences of it in an XML document
under investigation. So, if we issue the simple twig
query Q = a[x]/y, only two elements will be con-
sidered for further processing, namely a
2
and a
4
.
This is because of CPL
a
2
mod key
tag(x)
× key
tag(y)
=
77 mod 7 × 11 equals 0.
3 TWIG JOIN ALGORITHM
There is abstract data type called a stream, which is
a set of elements with the same node label, where
the elements are sorted in ascending document or-
der. Each query node q in a twig pattern is associ-
ated with an element stream, named T
q
which has a
cursor C
q
which initially points to the first element in
T
q
at the beginning of a query processing. We de-
fine the following operations on streams and query
nodes to facilitate the processing. children(q) returns
all child nodes of q. subtree(q) returns all child no-
des which are in the subtree rooted at q. childre-
nAD(q) returns all child nodes which have ancestor-
descendant relationship with q. childrenPC(q) returns
all child nodes which have parent-child relationship
with q. isRoot(q) tests if q is the root or not. pa-
rent(q) returns the parent query node of q. isLeaf(q)
tests if q is a leaf node or not. getStart(C
q
) returns the
start attribute of q. getEnd(C
q
) returns the end attri-
bute of q. getLevel(C
q
) returns the level attribute of
q. advance(C
q
) forward the cursor of q to the next
element. eo f (T
q
) to judge whether C
q
points to the
end of stream of T
q
. The structure of the main al-
gorithm, TwigStackPrime presented in Algorithm 2 is
not much different from the original holistic twig join
algorithm TwigStack (Bruno et al., 2002) which uses
two phases to compute an answer to a twig query.
TwigStackPrime modifies TwigStack in order to use
CPL. getNext is an essential function which is called
by the main algorithm to decide the next query node
to be processed. It is fundamental to guarantee that
the current label associated with the returned node is
part of the final output since all the basic structural re-
lationships are thoroughly checked by getNext or its
supporting subroutine getElement. The basic Twig-
Stack algorithm remains the same with the only dif-
ference being the key supporting algorithm getNext.
The main difference between two getNext algorithms
in TwigStack and TwigStackPrime can be summarized
as follows. In TwigStack, element e
n
returned by get-
Next is considered likely to contribute to the result if
and only if: it has a descendant element e
n
i
in each of
the streams corresponding to its child elements where
e
n
i
= children(n) and each of its child elements satis-
fies recursively the first property. While in TwigStack-
Prime, if element e
n
has parent-child edge(s), it has
to satisfy that in getElement procedure (Line 30-31).
Finally, all individual paths are merged to produce the
final results.
3.1 Analysis of TwigStackPrime
In this section, we show the correctness of our al-
gorithms. The correctness of TwigStackPrime algo-
rithm can be shown analogously to TwigStack due to
the fact that they both use the same stack mechanism.
In other words, the correctness of Algorithm 2 fol-
lows from the correctness of TwigStack (Bruno et al.,
2002). Since the getNext() with CPL increases the fil-
tering ability of the original, we prove its correctness
here, while the proof of the main algorithm is in the
original work of (Bruno et al., 2002).
Definition 2. (Child and Descendant Extension)
WEBIST 2017 - 13th International Conference on Web Information Systems and Technologies
206

query node q has the child and descendant extension
if the following properties hold:
• ∀ n
i
∈ childrenAD(q), there is an element e
i
which
is the head of T
n
i
and a descendant of e
q
which is
the head of T
q
.
• ∀ n
i
∈ childrenPC(q), there is an element e
q
which is the head of T
q
and its CPL parameter
is divisible by Key
tag
(n
i
)
• ∀ n
i
∈ children(q), n
i
must have the child and des-
cendant extension.
The above definition is a key for establishing the
correctness of the following lemma:
Lemma 1. For any arbitrary query node q
0
which is
returned by getNext(q), the following properties hold:
1. q
0
has the child and descendant extension.
2. Either q == q
0
or q
0
violates the child and des-
cendant extension of the head element e
q
of its
parent(q
0
).
Proof. (Induction on the number of child and descen-
dants of q
0
). If q
0
is a leaf query node, we return it in
line 2 because it verifies all the properties 1 and 2.
Otherwise, we recursively have g
i
= getNext(n
i
) for
each child of q in line 4. If for some i, we get g
i
6= n
i
,
and we know by inductive hypothesis that g
i
verifies
the properties 1 and 2b with respect to q, so we re-
turn g
i
in line 6. Otherwise, we know by inductive
hypothesis that all q’s child nodes satisfy properties
1 and 2 with their corresponding sub-queries. At ge-
tElement(q) (line 21-23), we advance from T
q
all seg-
ments that do not satisfy the divisibility by the product
of prime numbers in childrenPC(q) returned from ge-
tQNChildExtension. After that, we advance from T
q
(line 9-10) all segments that are beyond the maximum
start value of n
i
. Then, if q satisfies properties 1 and 2,
we return it at line 12. Otherwise, line 13 guarantees
that n
i
with the smallest start value satisfies proper-
ties 1 and 2b with respect to start value of q’s head
element.
Theorem 1. Given a twig pattern query Q and an
XML document D, Algorithm TwigStackPrime cor-
rectly returns answer to Q on D.
Proof(Sketch). We prove Theorem 1 by using
Lemma 1 and the proof of TwigStack to verify that
the chain of stacks represents paths containing the si-
milar chain of nodes as appear in XML document D
(Bruno et al., 2002). In Algorithm TwigStackPrime,
we repeatedly find getNext(root) to determine the next
node to be processed. Using lemma 1, we know that
all elements returned by q
act
= getNext(root) have the
child and descendant extension. If q
act
6= root, line
4, we pop from S
parent(q
act
)
all elements that are not
ancestors of C
q
act
. After that, we already know q
act
has a child and descendant extension so that we check
whether S
parent(q
act
)
is empty or not. If so, it indica-
tes that it does not have the ancestor extension, line 5,
and can be discarded safely to continue with the next
iteration. Otherwise, C
q
act
has both the ancestor and
child and descendant extensions which guarantee its
participation in at least one root-to-leaf path. Then,
we clean S
q
act
to maintain pointers from itself to the
root. Finally, if q
act
is a leaf node, we compute all
possible combinations of single paths with respect to
q
act
, line 8-9.
It can be shown that TwigStackPrime algorithm is op-
timal when P-C axes exist only in the deepest level of
a twig query.
Example 1. Consider the XML tree and a twig query
in Figure 2, the head elements in their streams are
a → a
1
, x → x
1
, y → y
1
and f → f
1
. The first call
A Prime Number Approach to Matching an XML Twig Pattern including Parent-Child Edges
207

e
a
1
x
1
a
2
x
2
y
1
f
1
y
2
a
4
x
4
y
3
(a) an XML tree.
a
x
y
f
(b) a twig query.
Figure 2: Sub-optimal evaluation of TwigStackPrime where
redundant paths might be generated.
of getNext(root) inside the main algorithm will return
a → a
1
because it has A-D relationship with all head
elements and satisfies CPL with x and y, and its des-
cendant y → y
1
also satisfies the child and descendant
extension with respect to f. However, TwigStackPrime
produces the useless path (a
1
,x
1
)
4 EXPERIMENTAL EVALUATION
In this section we present the performance compari-
son of twig join algorithms, namely: TwigStackPrime
the new algorithm based on Child Prime Labels, al-
ong with TwigStack (Bruno et al., 2002). The original
twig join algorithm that was reported to have optimal
worst-case processing with A-D relationship in all ed-
ges, and TwigStackList is the first refined version of
TwigStack to handle P-C efficiently (Lu et al., 2004).
TwigStackList was chosen in this experiment because
it utilizes a simple buffering technique to prune irrele-
vant elements from the stream. We evaluated the per-
formance of these algorithms against both real-world
and artificial data sets. The performance comparison
of these algorithms was based on the following me-
trics:
1. Number of intermediate solutions: the individual
root-to-leaf paths generated by each algorithm.
2. Processing time: the main-memory running time
without counting I/O costs. All twig pattern que-
ries were executed 103 times and the first three
runs were excluded for cold cache issues. We did
not count the I/O cost for tag indexing files for
TwigStackPrime algorithm because it s negligible,
and the cost to read the tag indexing is constant
over a series of twig pattern queries.
4.1 Experimental Settings
All the algorithms were implemented in Java JDK 1.8.
The experiments were performed on 2.9 GHz Intel
Core i5 with 8GB RAM running in Mac OS X El Ca-
pitan. The benchmarked datasets used in the experi-
ments and their characteristics are shown in Tables 1
and 2. The selected datasets and benchmark are the
most frequent in the literature of XML query proces-
sing (Bruno et al., 2002; Lu et al., 2004; Grimsmo
et al., 2010; Wu et al., 2012; Li and Wang, 2008; Qin
et al., 2007). We generated Random dataset similar
to that in (Lu et al., 2004) but we vary the two pa-
rameters: depth and fan-out. The depth of randomly
generated tree has maximum value sets to 13 and fan-
out has range from 0 to 6, respectively. This data set
was created to test the performance where the XML
combines the features of DBLP and TreeBank, being
structured and deeply-recursive at the same time.
Table 1: Benchmark real-world datasets used in the experi-
ments.
DBLP TreeBank
Rangae-based MB 65.3 43
CPL MB 70.3 47.9
4 size MB 5 4.9
Tag Indexing Size KB 0.48 3
Nodes (Millions) 3.73 2.43
Max/Avg depth 6/2.9 36/7.8
Distinct Tags 40 251
Largest Prime Numbers 151 1597
Table 2: Benchmark artificial datasets used in the experi-
ments.
XMark Random
Rangae-based MB 35.3 69.4
CPL MB 40.1 74.1
4 size MB 4.8 4.7
Tag Indexing Size KB 1 0.049
Nodes (Millions) 2.04 3.94
Max/Avg depth 12/5.5 13/7
Distinct Tags 83 6
Largest Prime Numbers 379 19
The XML structured queries for evaluation over these
dataset were chosen specifically because it is not
common for queries, which contain both ’//’ and
’/’, to have a significant difference in performance
for tightly-structured document such as DBLP and
XMark. TreeBank twig queries were obtained from
(Lu et al., 2004) and (Grimsmo et al., 2010). Twig
pattens over the random data set were also randomly
generated. Table 3 shows the XPath expressions for
the chosen twig patterns. The code indicates the data
set and its twig query, for instance, TQ2 refers to the
second query issued over TreeBank dataset.
WEBIST 2017 - 13th International Conference on Web Information Systems and Technologies
208

Table 3: Benchmark twig pattern queries used in the expe-
riments.
Code Query
DQ
1
dblp/inproceedings[//title]//author
DQ
2
//www[editor]/url
DQ
3
//article[//sup]//title//sub
DQ
4
//article[/sup]//title/sub
XQ
1
/site/closed auctions/closed auction
[annotation/description/text/keyword]/date
XQ
2
/site/closed auctions/closed auction
[//keyword]/date
XQ
3
/site/people/person[profile[gender][age]]
/name
XQ
4
/site/people/person[profile[gender][age]]
/name
XQ
5
//item[location][//mailbox//mail//emph]
/description/keyword
XQ
6
//people/person[//address/zipcode]/profile
/education
T Q
1
//S[//MD]//ADJ
T Q
2
//S/VP/PP[/NP/VBN]/IN
T Q
3
//VP[/DT]//PRP DOLLAR
T Q
4
//S[/JJ]/NP
T Q
5
//S/VP/PP[/IN]/NP/VBN
T Q
6
//S[//VP/IN]//NP
T Q
7
//S/VP/PP[//NP/VBN]/IN
T Q
8
//EMPTY/S//NP[/SBAR/WHNP/PP//NN]
/ COMMA
T Q
9
//SINV//NP[/PP//JJR][//S]//NN
RQ
1
//b//e//a[//f][d]
RQ
2
//a//b[//e][c]
RQ
3
//e//a[/b][c]
RQ
4
//a[//b/d]//c
RQ
5
//b[d/f]/c[e]/a
RQ
6
//c[//b][a]/f
RQ
7
//a[c//e]/f[d]
RQ
8
//d[a//e/f]/c[b]
RQ
9
//a[d][c][b][e]//f
4.2 Experimental Result
We compared TwigStackPrime algorithm with Twig-
Stack and TwigStackList over the above mentioned
twig pattern queries against the data sets selected. The
Kruskal-Wallis test is a non-parametric statistical pro-
cedure was carried out on processing time, the p-value
turns out to be nearly zero (p-value less than 2.2 to the
power of -16), it strongly suggests that there is a dif-
ference in processing time between two algorithms at
least as shown in Figure 3.
4.2.1 DBLP and XMark Datasets
We tested twig queries over DBLP and XMark da-
tasets, they are both considered as data-oriented and
have a very strong structure. In these two datasets
both TwigStackPrime and TwigStackList are optimal,
but TwigStack still produces irrelevant paths. This can
be shown in Table 4. Since there is a difference in
performance, we ran pairwise comparison based on
Manny-Whitney test showed that in most tested twig
queries TwigStackPrime outperformed TwigStackList
and TwigStack. TwigStackPrime and TwigStackList
have same performance in XQ
2
, XQ
3
and XQ
6
see
Figure 3a and 3b.
4.2.2 TreeBank Dataset
None of the algorithms compared are optimal in this
dataset because TreeBank has redundant paths and
many tags are deeply recursive. The number of in-
dividual paths produced by each algorithm for the
twig pattern queries tested over Treebank is presen-
ted in Table 3. TwigStackPrime showed a superior
performance in avoiding the storage of unnecessary
paths while processing time is improved. T Q
6
is a
very expensive query, it touches a very large portion
of the document and the answer is quite large. Pai-
rwise comparison based on Manny-Whitney test be-
tween TwigStackPrime and TwigStackList resulted in
p − value < .001 which suggests a significant diffe-
rence and TwigStackPrime has the best performance
see Figure 3e. It can be seen in Figure 3d the only
twig queries where TwigStackPrime has slower per-
formance comparing to the others is T Q
3
and T Q
9
because they touch very little of the dataset.
4.2.3 Random Dataset
We have generated twig queries over this dataset to
test the performance of the algorithms by varying the
parent-child edges and increasing their numbers. RQ4
is optimal for TwigStackList because it does not have
P-C in branching axes, and TwigStackPrime does the
same (see Table 3). While in RQ9 where all branching
edges are P-C, none of the algorithms compared gua-
rantee optimal evaluation except TwigStackPrime in
which RQ9 is its optimal class of query. When evalu-
ating RQ6, TwigStackPrime has the best performance,
it is roughly twice as fast than TwigStackList and five
time faster than TwigStack see Figure 3c and 3e.
5 RELATED WORK
The growing number of XML documents leads to the
need for appropriate XML querying algorithms. Over
the past decade, most research in structured XML
query processing has emphasized the use of node
indexing approaches (Bruno et al., 2002; Lu et al.,
2004; Grimsmo et al., 2010; Wu et al., 2012; Li and
A Prime Number Approach to Matching an XML Twig Pattern including Parent-Child Edges
209
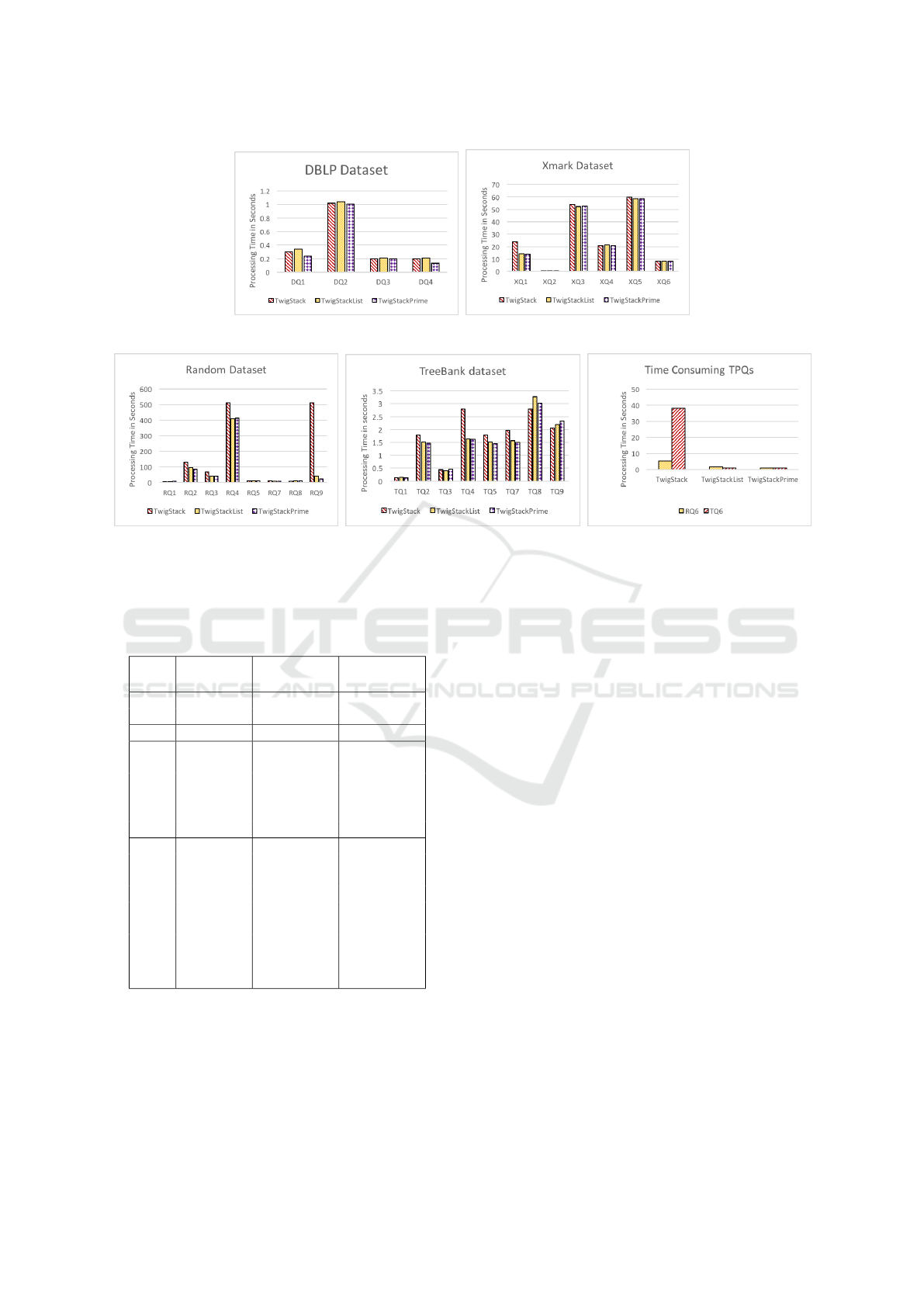
(a) DBLP. (b) XMark.
(c) Random. (d) TreeBank. (e) Time consuming TPQs.
Figure 3: Processing time for twig pattern queries against DBLP in 3a and XMark in 3b. 3c and 3d shows processing time
for twig queries on Random and TreeBank datasets, respectively. Figure 3e illustrates the processing time taken by each
algorithm to run the two most expensive queries in the experiments, normalizing query times to 1 for the fastest algorithm for
each query.
Table 4: Single paths produced by each algorithm.
Code TwigStack TwigStack
List
TwigStack
Prime
DQ
1
147 139 139
DQ
4
98 0 0
XQ
1
9414 6701 6701
T Q
2
2236 388 441
T Q
3
10663 11 5
T Q
4
70988 30 10
T Q
6
702391 22565 22565
T Q
8
58 27 26
T Q
9
29 17 8
RQ
1
2076 1843 1795
RQ
2
29914 24235 23057
RQ
3
20558 16102 15505
RQ
4
67005 57753 57753
RQ
5
3765 901 1093
RQ
6
201835 98600 72084
RQ
7
6880 2791 3219
RQ
8
746 322 406
RQ
9
179546 26114 8786
Wang, 2008; Qin et al., 2007). One of the most im-
portant problems in XML query processing is tree
pattern matching. Generally, tree pattern matching is
defined as mapping function M between a given tree
pattern query Q and an XML data D, M : Q → D
that maps nodes of Q into nodes of D where struc-
tural relationships are preserved and the predicates
of Q are satisfied. Formally, tree pattern matching
must find all matches of a given tree pattern query Q
on an XML document D. The classical holistic twig
join algorithm TwigStack only considers the ancestor-
descendant relationship between query nodes to pro-
cess a twig query efficiently without storing irrele-
vant paths in intermediate storage. It has been re-
ported (Bruno et al., 2002) that it has the worst-case
I/O and CPU complexities when all edges in twigs are
“//” (AD relationship) linear in the sum of the size of
the input and output lists. However, TwigStack’s per-
formance suffers from generating useless intermedi-
ate results when twig queries encounter Parent-Child
relationships. The authors of (Lu et al., 2004) pro-
posed a new buffering technique to process twig que-
ries with P-C relationships more efficiently by look-
ing ahead some elements with P-C in lists to eliminate
redundant path solutions. TwigStackList guarantees
every single path generated is a part of the final re-
sult if twig queries do not have P-C under branching
query nodes (Lu et al., 2004). The authors of (Choi
et al., 2003) have proven that the TwigStack algorithm
and its variants which depend on a single sequentially
scan of the input lists can not be optimal for evalu-
ation of tree pattern queries with any arbitrary com-
bination of ancestor-descendant and parent-child re-
WEBIST 2017 - 13th International Conference on Web Information Systems and Technologies
210

lationships. However, the approach to examine XML
queries against document elements in post-order was
first introduced by (Chen et al., 2006), Twig
2
Stack.
The decomposition of twigs into a set of single paths
and the enumeration of these paths is not necessary to
process twig pattern queries. The key idea of their ap-
proach is based on the proposition that when visiting
document elements in post-order, it can be determi-
ned whether or not they contribute to the final result
before storing them in intermediate storage, which
is trees of stacks, to ensure linear processing. Twi-
gList (Qin et al., 2007) replaced the complex interme-
diate storage proposed in Twig
2
Stack with lists (one
for every query node) and pointers with simple inter-
vals to capture structural relationships. The authors
in (Grimsmo et al., 2010) proposed a new storage
scheme, level vector split which splits the list con-
nected to its parent list with P-C edge to a number of
levels equals to the depth of the XML tree.
6 CONCLUSION
In this paper we have proposed a new mechanism to
improve the pre-filtering strategy in twig join algo-
rithms when P-C edges exist in twig patterns. The
new technique has the ability to ensure pruning of un-
necessary elements from the streams which can en-
hance runtime efficiency and relieve memory con-
sumption by avoiding the storage of redundant paths.
We are currently working to extend our approach to
combine with the previous orthogonal algorithms to
propose a new one-phase twig join algorithm that we
hope will be faster in average worst-case than the pre-
vious algorithms. Furthermore, we plan to examine
processing ordered twig patterns and positional pre-
dicate in a way that would consume less time and me-
mory than the existing approaches.
REFERENCES
Alireza Aghili, S., Alireza Aghili, S., Hua-Gang, L., Hua-
Gang, L., Agrawal, D., Agrawal, D., El Abbadi, A.,
and El Abbadi, A. (2006). TWIX: twig structure and
content matching of selective queries using. InfoScale
’06: Proceedings of the 1st international conference
on, page 42.
Bruno, N., Koudas, N., and Srivastava, D. (2002). Holis-
tic twig joins: optimal XML pattern matching. In
Proceedings of the 2002 ACM SIGMOD international
conference on Management of data, pages 310–321,
Madison, Wisconsin. ACM.
Chen, S., Li, H.-G., Tatemura, J., Hsiung, W.-P., Agra-
wal, D., Sel, K., #231, uk Candan, and Candan,
K. S. (2006). Twig2Stack: bottom-up processing
of generalized-tree-pattern queries over XML docu-
ments.
Chen, T., Lu, J., and Ling, T. W. (2005). On Boosting Ho-
lism in XML Twig Pattern Matching Using Structural
Indexing Techniques. Science, pages 455–466.
Choi, B., Mahoui, M., and Wood, D. (2003). On the optima-
lity of holistic algorithms for twig queries. Database
and Expert Systems Applications, pages 28–37.
Grimsmo, N., Bjørklund, T. A., and Hetland, M. L. (2010).
Fast optimal twig joins. VLDB, 3(1-2):894–905.
Li, J. and Wang, J. (2008). Fast Matching of Twig Patterns.
Lecture Notes in Computer Science (including subse-
ries Lecture Notes in Artificial Intelligence and Lec-
ture Notes in Bioinformatics), 5181 LNCS:523–536.
Lu, J., Chen, T., and Ling, T. W. T. (2004). Efficient Proces-
sing of XML Twig Patterns with Parent Child Edges :
A Look-ahead Approach. In Proceedings of the thir-
teenth ACM international conference on Information
and knowledge management, number i, pages 533–
542, Washington, D.C., USA. ACM.
Lu, J., Meng, X., and Ling, T. W. (2011). Indexing and que-
rying XML using extended Dewey labeling scheme.
Data & Knowledge Engineering, 70(1):35–59.
Qin, L., Yu, J. X., and Ding, B. (2007). TwigList: Make
Twig Pattern Matching Fast. In Kotagiri, R., Krishna,
P. R., Mohania, M., and Nantajeewarawat, E., edi-
tors, Advances in Databases: Concepts, Systems and
Applications: 12th International Conference on Da-
tabase Systems for Advanced Applications, DASFAA
2007, Bangkok, Thailand, April 9-12, 2007. Procee-
dings, pages 850–862. Springer Berlin Heidelberg,
Berlin, Heidelberg.
Wu, H., Lin, C., Ling, T. W., and Lu, J. (2012). Processing
XML twig pattern query with wildcards. Lecture No-
tes in Computer Science (including subseries Lecture
Notes in Artificial Intelligence and Lecture Notes in
Bioinformatics), 7446 LNCS:326–341.
Zhang, C., Naughton, J., DeWitt, D., Luo, Q., and Lohman,
G. (2001). On supporting containment queries in rela-
tional database management systems. ACM SIGMOD
Record, 30:425–436.
A Prime Number Approach to Matching an XML Twig Pattern including Parent-Child Edges
211
