Deadlock Prevention in Rendezvous Generation for On-demand

Inter-robot Resource Delivery

Yin Chen, Xinjun Mao and Fu Hou

College of Computer, National University of Defense Technology, Changsha, Hunan, China

Keywords:

Deadlock, Rendezvous, Resource, Multi-robot System.

Abstract:

In this paper, we consider a multi-robot system (MRS) which executes task points associated with 2-D loca-

tions. Each task point demands certain physical resources for its execution. A robot can fetch these resources

either from ﬁxed stations, or by conducting rendezvouses with other robots who happen to possess these

resources, provided that the latter option can be more beneﬁcial in terms of cost or resource availability. How-

ever, applying rendezvouses may cause deadlock among robots, through (1) the tangling among rendezvouses,

or (2) sabotaging the resource consistency of the schedule of a robot which is originally holding the resources.

We analyse these problems and introduce a series of deadlock prevention rules that are embedded into an

A*-based rendezvous planning algorithm, so that both type of deadlocks can be avoided in the rendezvouses.

1 INTRODUCTION

Multi-robot systems (MRS) are applied in many do-

mains where their task execution requires retrieving

physical resources from the environment. The re-

quired resources may not be available in the vicinity

of a robot or may be held by other robots, making it a

desirable choice for a robot in urgent need of a partic-

ular set of resources to rendezvous with other robots

and fetch the resources from these robots, rather than

travel to the ﬁxed resource stations which are either

far from the robot or depleted. Assume each robot

possesses a sequence of task points, each demanding

a speciﬁc set of resources, which can be fetched from

stations or via rendezvous with other robots. However

rendezvouses for resource delivery may cause two

types of inter-robot deadlocks which may block task

execution: (1) Rendezvous tangling, i.e., the ren-

dezvouses form a loop waiting for each other to com-

plete, blocking the execution forever. (2) Demand

looping, i.e., when all robots are self-interested, they

may be unable to achieve a globally feasible ren-

dezvous plan that satisfy each robot’s own demands

without jeopardising others’ demands.

In this paper we present deadlock prevention

mechanisms for the two types of deadlocks respec-

tively. The ﬁrst type is tackled by constraining the

insertion index of each rendezvous so as to prevent

tangling. The second type is tackled by coordinating

the rendezvous planning on different robots so that

each rendezvous respects the demands of entire MRS

rather than only individual robots. We then present a

centralised A*-based algorithm (which will be trans-

formed into a distributed version in the future) that

searches for the best rendezvous insertion sequence

for satisfying the resource demands of entire MRS,

while respecting all the deadlock prevention rules.

2 RELATED WORK

Our work deals with the resource demands of sched-

ules of a MRS by dynamically generating ren-

dezvouses for fetching resources. In robotics litera-

ture, our work is similar in some way to the multi-

robot recharging problem, in which the robots (espe-

cially UAVs) rendezvous with ground-based charging

robots in order to charge their batteries. (Keshmiri,

2011) presents an opportunistic control approach to

address the multi-robot multi-rendezvous recharg-

ing problem, which combines centralised and dis-

tributed decision-making. (Neil Mathew, 2013) and

(Neil Mathew, 2015) present a method for multi-robot

recharging problem by modelling the rendezvous

planning problem into an integer linear program and

transform it into a travelling salesperson problem.

Despite their similarity: (1) our work considers het-

erogeneous demands by different task points for phys-

ical resources, and the types of resource are not lim-

ited to energy; (2) in stead of absolutely differenti-

670

Chen Y., Mao X. and Hou F.

Deadlock Prevention in Rendezvous Generation for On-demand Inter-robot Resource Delivery.

DOI: 10.5220/0006225806700675

In Proceedings of the 9th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2017), pages 670-675

ISBN: 978-989-758-220-2

ating between resource provider and consumer, we

make it possible for each robot to take any of both

roles according to the demands, so that the system can

more ﬂexibly react to environment changes; (3) the

deadlock problem is raised because of the interdepen-

dency among different task points in the schedules,

which is largely omitted in the traditional recharging

problem. For the resource-caused deadlock problem,

(Han Lei, 2014) presents a Petri-Net-based multi-

robot scheduling approach for ﬂexible manufacturing

system, which embeds deadlock control policies into

heuristic (e.g., genetic) search algorithm. Our work

is partially inspired by their idea of embedding dead-

lock prevention mechanisms into search algorithm.

In comparison, our work assumes dynamic environ-

ment and unforeseeable requirement resources, which

make our work potentially more applicable to a dy-

namic environment rather than a relatively ﬁxed in-

dustrial environment.

3 PROBLEM FORMATION

3.1 Preliminaries

Task Point. Each task point π is a unit of task

execution on each robot, and is written as a tuple

hκ, l, R



, R

−

, R

i, where (1) κ is the action to be per-

formed by the robot to which the task point π is as-

signed; (2) l ∈ R

is the 2-D location at which the π

is to be executed; (3) R



is the set of resources re-

quired by π for its successful execution; (4) R

−

⊆ R



is the set of resources consumed by π; (5) R

is the

set of resources generated by π, provided that κ is a

resource-fetching action.

Schedule. Task points are organised into schedules

in order to be executed on robots. Each robot pos-

sesses a schedule σ which is deﬁned as a sequence of

task points π

, ..., π

, where |σ| = n is the length of

the schedule. For each i = 1, ..., |σ|, σ(i) = π

is the

task point of the σ, and σ(0) is a presumed (but not

really existing) task point which marks the very be-

ginning of the schedule. The index of π is ι

(π). For

each task point π ∈ σ, we make the following deﬁni-

tions: (1) the set of task points preceding π is Π



(π) =

{π

∈ σ : ι

(π

) < ι

(π)}; (2) the set of task points

succeeding π is Π



(π) = {π

∈ σ : ι

(π

) > ι

(π)}.

Resource. Each resource r is deﬁned as a tuple

hy, mi, where (1) y is the type of r; (2) m is the amount

of resource of type y shown by r. A set of resources

R can thus be deﬁned as {r = hy, mi : y ∈ Y, m ∈ R}.

Operations of Resources. In this work, we assume

the resources are linear, and deﬁne their operations:

(1) hy, m

i + hy, m

i = hy, m

+ m

i; (2) hy, m

i −

hy, m

i = hy, m

− m

i; (3) k · hy, mi = hy, k · mi.

Operations of Sets of Resources. We deﬁne the

type set Y (R) = {y ∈ Y : ∃m ∈ R

: hy, mi ∈ R}. We

further deﬁne the operations (union, intersect, and mi-

nus) on set of resources: (1) R

∪ R

= ς(R

∪ R

);

(2) R

∩ R

= ς(R

∩ R

); (3) R

\ R

= ς(R

∪ −R

where −R = {−r : r ∈ R}. The function ς is deﬁned

as ς(R) = {r

∈

y∈Y (R)

{hy,

∑

r∈R,r.y=y

r.mi} : r

.m > 0},

which means that the resources with the same type

(r.y = y) will be combined into one, and all the re-

sources whose amount is below zero will be removed.

Required and Provided Resources. For each

schedule σ, and task point π ∈ σ, we can deﬁne:

(1) R



(π) is the set of resources required by π,

which is deﬁned by R



(π) = π.R



; (2) R



(π) is the

set of resources provided by σ after executing π,

which is recursively deﬁned by R



(σ(i)) = (R



(σ(i −

1))

∪ π.R

)

\ π.R

−

Resource Holder. This concept is introduced to

uniformly analyse the change of the resource conﬁg-

uration of the entire system (including both the MRS

and its environment). Each resource holder h is a tu-

ple hl, R, σi, where (1) l is the location of h; (2) R is

the set of resources currently possessed by h; (3) σ is

the sequence of task points which are not yet executed

and which will take effects on either the location l or

the set of resources R after being executed. A holder

h can be either a robot or a station. If h is a station,

then its σ ﬁeld is simply a representation of those re-

sources scheduled to be given out to robots. If h is

a robot, then its σ ﬁeld shows the sequence of task

points to be actually executed by the robot.

Rendezvous. Each rendezvous υ represents multi-

ple robots meeting at a common time and location,

and is deﬁned as a tuple hl, Π, H, pi, where (1) l is

the location of the rendezvous; (2) Π is the set of task

points attending υ; (3) H is the set of resource hold-

ers attending υ; (4) p is a function which corresponds

each h ∈ H to π ∈ Π, so that p(h) = π shows that h

attending υ through executing π.

Resource-delivering Rendezvous. In this work, all

rendezvouses are used for delivering resources, and

therefore should contain only two task points: (1)

Deadlock Prevention in Rendezvous Generation for On-demand Inter-robot Resource Delivery

671

snd

for sending a set of resources R, which is exe-

cuted by the resource provider; (2) π

rcv

for receiving

a set of resources R, which is executed by the robot

demanding the resources. Thus for each resource-

delivering rendezvous υ, there exists π

snd

, π

rcv

, and

R, so that: υ.Π = {π

snd

, π

rcv

}, υ.H = {h

snd

, h

rcv

}, and

p = {hh

snd

, π

snd

i, hh

rcv

, π

rcv

i}.

3.2 Rendezvous Tangling

1 1

2 2

3 3

4 4

2 2

4 4

1 1

2 2

4 4

(a) Not tangled

(b) Two rendezvouses tangled

with each other directly

with each other indirectly

The schedule of a robot

Task points of a rendezvous

A rendezvous

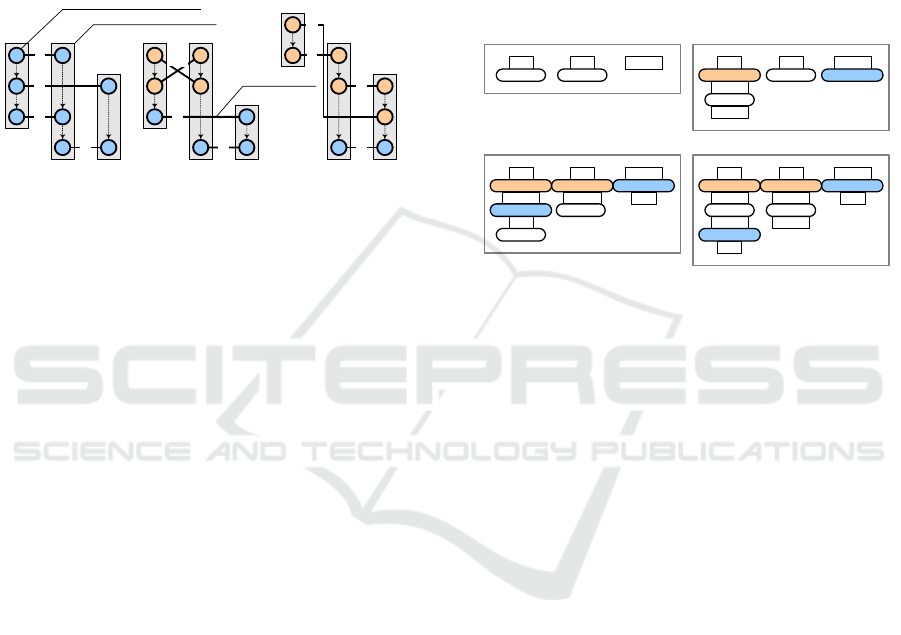
Figure 1: Tangling among robots.

Fig. 1 compares 3 cases related to deadlock

among rendezvous: (1) Not tangled (Fig. 1-a). The

task points of all rendezvouses can be completed

without interfering with each other. No rendezvous-

caused deadlock will occur. (2) Directly tangled

(Fig. 1-b). In this case, we have

∃υ, υ

∈ ϒ : ∃π

, π

∈ υ.Π, π

, π

∈ υ

.Π

[π

, π

∈ σ

, π

∈ σ

] :

(π

) < ι

(π

) ∧ ι

(π

) > ι

(π

)

indicating a waiting loop that makes schedules not ex-

ecutable: (i) π

waits for π

(because π

, π

∈ υ.Π);

(ii) π

waits for π

(because ι

(π

) > ι

(π

)); (iii)

waits for π

(because π

, π

∈ υ

.Π); (iv) π

waits

for π

(because ι

(π

) < ι

(π

)). (3) Indirectly

tangled (Fig. 1-b). In this case, we have:

∃υ

, ..., υ

∈ ϒ :

∃π

1,1

, π

1,2

∈ υ

.Π, ..., π

n,1

, π

n,2

∈ υ

.Π

[(∀i ∈ {2, ..., n} : π

i−1,2

, π

i,1

∈ σ

) ∧ π

n,2

, π

1,1

∈ σ

] :

(∀i ∈ {2, ..., n} : ι

(π

i−1,2

) < ι

(π

i,1

)))

∧ ι

(π

1,1

) > ι

(π

n,2

)

indicating a waiting loop that makes schedules not

executable: π

1,1

waits for π

n,2

which waits for π

n,1

which waits for π

n−1,2

, ..., π

2,1

, π

1,2

, π

1,1

3.3 Demand Looping

Assume initially the resource demands of all task

points in the MRS are not satisﬁed. A straightfor-

ward way to satisfy these demands is to make each

robot to traverse its entire schedule, where for each

task point π whose resource demands π.R



are not

satisﬁed, the robot will generate a set of rendezvouses

prv

(π) to fetch π.R



from stations or other robots.

If no inter-robot coordination strategy is present, an

extreme situation known as demand looping may oc-

cur, in which robots will endlessly “argue” with each

other about who should use the particular set of re-

sources to satisfy itself, without reaching any conclu-

sion. In this section we present two examples to show

the need to introduce inter-robot coordination strat-

egy so as to decide prudently (1) the insertion index

of each rendezvous, and (2) the robot providing re-

quired resources; and the consequences of not to do

so.

Robot h

Station h

0 0 knife

Robot h

Station h

0 0 knife

1-1

knife

Robot h

Station h

0 0 knife

1-1-1

knife 0

Robot h

Station h

0 0 knife

1-1-2

knife 0

knife

(a) The initial status of the system, when no robot

has scheduled to obtain the knife

(b) The robot h

has scheduled to obtain the knife

gives up the knife

to robot h

. If h

does the same thing in the next

step, the system will be stuck, with both robots

discussing who will use the knife first.

(d) In another situation, the robot h

first uses the

knife, and then give the knife to robot h

, which

will satisfy all without causing any infinite loops.

cut◄knife cut◄knife

cut◄knife

cut◄knifeRcv

, knife Snd

, knife

cut◄knife

Rcv

, knife Snd

, knife

cut◄knife cut◄knife

Rcv

, knife Snd

, knife

Snd

, knife

Rcv

, knife

Snd

, knife

Rcv

, knife

Figure 2: A simple case showing demand looping.

Fig. 2 shows the need to constrain the insertion

index of each rendezvous among robots, in order to

prevent the resource demands of one robot from be-

ing sabotaged by rendezvous with another robot. Fig.

2-a shows the initial state. Each robot has a task point

for cutting with a knife. In Fig. 2-b, robot h

sets

up the rendezvous for fetching the knife from station

. Since initially both robots possess no knife, and

there is only one knife, intuitively, h

and h

must take

turns using the knife, and therefore the ideal next step

would be to let h

obtain the knife after h

has com-

pleted using it. However, due to the lack of coordina-

tion, in Fig. 2-c, h

abruptly schedules to take away

the knife from h

without considering h

’s need, mak-

ing h

unable to complete its schedule. If in the fol-

lowing steps, e.g., Fig. 2-d, they still repeat the same

ruthless decision, then it is possible the rendezvouses

for sending/receiving knife will be repeated for many

times among h

and h

, while the knife can never have

the chance to be actually used. Note that in order to

prevent this, we can forbid all robot from giving out

resources that are already scheduled to be used by it-

self, i.e., to constrain the insertion of rendezvouses in

the schedules of potential resource providers.

Fig. 3 shows that the MRS must be prudent in

choosing the proper resource provider and receiver

at each step. Fig. 3-a and Fig. 3-b descends from the

same initial status when both robots have no resources

and all resources are in h

. Based on different choices

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

672

Robot h

Station h

0 0 7

1-1

Robot h

Station h

0 0 7

1-2

Robot h

Station h

0 0 7

1-2-1

Robot h

Station h

0 0 7

1-2-1-1

Robot h

Station h

0 0 7

1-1-1

4 34

0 5

Robot h

Station h

0 0 7

1-1-1-1

4 34

0 5

(a) In this case, the robot h

accepts resources first

soon is forced to give up the

resource to enable robot h

to execute

(b) In this case, the robot h

accepts resources first

(d) Since it has little consumption, it still can provide

robot h

with resources after it has completed

(e) Although also successful, this branch generates

more zigzags which require further processing

(f) This branch successfully generated a series of

rendezvouses which satisfy all resource demands

◄4, -3

◄2, 0

◄5, -1

◄3, -1

Rcv

, 4 Snd

, 4 ◄4, -3

◄2, 0 ◄5, -1

◄3, -1

Snd

, 5Rcv

, 5

◄4, -3

◄2, 0

◄5, -1

◄3, -1

Snd

, 5Rcv

, 5

Snd

, 2

Snd

, 2

Rcv

, 2

Rcv

, 2

◄4, -3

◄2, 0

◄5, -1

◄3, -1

Snd

, 5Rcv

, 5

Snd

, 2

Snd

, 2

Rcv

, 2

Rcv

, 2

Snd-4, 1

Rcv

, 1

◄4, -3

◄2, 0

◄5, -1

◄3, -1π

Rcv

, 4 Snd

, 4

Snd

, 4 Snd

, 1

Rcv

, 4

Rcv

, 1

◄4, -3

◄2, 0

◄5, -1

◄3, -1

Rcv

, 4 Snd

, 4

Snd

, 4 Snd

, 1

Rcv

, 4

Rcv

, 1

Snd

, 2Rcv

, 2

Rcv

, 2

Snd-5, 2

Snd-6, 1Rcv

, 1

Figure 3: The case where initial choices are important.

made at the very ﬁrst step about who should obtain

the resources ﬁrst, the system may undergo different

journeys: (1) Fig. 3-a,c,e, shows the branch when h

ﬁrst obtains the resources for its task point π

; (2) Fig.

3-b,d,f, shows the branch when h

ﬁrst obtains the re-

sources for π

. In Fig. 3-a,c,e, since satisfying π

has

used up a lot of resources, leaving no resources for

any other task points of h

and h

, in Fig. 3-c, h

has

no choice but to give up part of its resources and π

to let others run. In Fig. 3-b,d,f, even after all task

points of h

are satisﬁed, there are still remaining re-

sources in h

, h

, making it possible to satisfy h

’s

demands. Although both branches can ultimately sat-

isfying all the resources, Fig. 3-a,c,e branch creates

some zigzags which involve robots planning to deliver

resources forwards and backwards among them with-

out using the resources, due to improper earlier choice

of who would provide and/or receive the resources.

4 ANALYSIS AND SOLUTION

4.1 Prevention of Rendezvous Tangling

Reachable Set of a Rendezvous. We ﬁrst deﬁne

several functions based on reachable sets: (1) the

directly preceding set of rendezvouses ϒ

←

(υ) =

π∈υ.Π



(π); (2) the directly succeeding set of ren-

dezvouses ϒ

→

(υ) =

π∈υ.Π



(π); (3) the preceding

reachable set of rendezvouses is recursively deﬁned

by ϒ

←

(υ) ⊆ ϒ

←

(υ) and ∀υ

∈ ϒ

←

(υ) : ϒ

←

(υ

) ⊆

←

(υ); (4) the succeeding reachable set of ren-

dezvouses is recursively deﬁned by ϒ

→

(υ) ⊆ ϒ

→

(υ)

and ∀υ

∈ ϒ

→

(υ) : ϒ

→

(υ

) ⊆ ϒ

→

(υ). The no-

tangling rule can be written as ∀υ ∈ ϒ : ϒ

←

(υ) ∩

→

(υ) =

0, which is expected to be satisﬁed by all

the rendezvouses in the schedules at any given time.

In order to ensure there is no tangling, we con-

strain the insertion index of each rendezvous υ when

it is inserted or moved in the schedules. For υ, if

the insertion index ι

(π) of any π ∈ υ.Π has been

speciﬁed, ι

(π) poses constraints to the possible in-

sertion indexes of other task points in υ.Π. Assume

⊆ υ.Π is the set of task points that have been in-

serted into the schedules without tangling. If we want

to insert one more task point π ∈ υ.Π \ Π

without

introducing tangling, its insertion index i in schedule

σ should satisfy the following constraint:

max

∈ϒ

←

(υ)

(π

) < i ≤ min

∈ϒ

→

(υ)

(π

)

where {π

} = υ

.Π ∩ σ 6=

0. It can be proven that as

long as the insertion index of any task point of a ren-

dezvous satisfy the above constraint, the no-tangling

rule can always be ensured, and there will be no dead-

lock among robots caused by rendezvous tangling.

4.2 Prevention of Demand Looping

For preventing demand looping, all robots should col-

laborate to determine (1) which robot will generate

the next rendezvous υ for satisfying one of its task

points, (2) which resource holder will provide re-

source for υ. It should prevent the situation of hav-

ing one robot generate all its rendezvouses at one shot

without regarding other robot’s demands. Also, each

robot should consider the degree to which inserting υ

may deprive the chance of the resource provider from

further satisfying its own resource demands. For ex-

ample, if by inserting υ, all further task points would

lost their chances to obtain any resources from any

resource holders, then deﬁnitely υ should not be in-

serted, provided there is a better choice.

Crosscut. In order to better depict such thought,

we introduce the concept of crosscut. A crosscut is

a function χ : H → Z, which returns the currently

concerned index in the schedule of each resource

holder. Given a crosscut χ, (1) the set of resources

provided by holder h is R



(h.σ(χ(h))), which shows

Deadlock Prevention in Rendezvous Generation for On-demand Inter-robot Resource Delivery

673

from where other robots can obtain their required re-

sources; (2) the set of resources required by holder

h is R



(h.σ(χ(h))), which is used to compare to the

provided resources R



(h.σ(χ(h))) to see whether χ is

unsatisﬁed; (3) the preceding crosscut of χ is written

as χ − 1, which is deﬁned as

(χ − 1)(h) =



χ(h) −1 χ(h) > 0

0 otherwise

(4) the succeeding crosscut of χ is written as χ + 1,

which is deﬁned as

(χ + 1)(h) =



χ(h) + 1 χ(h) < |h.σ|

∞ otherwise

(5) we use χ = 0 to represent ∀h ∈ H : χ(h) = 0; (6)

we use χ = ∞ to represent ∀h ∈ H : χ(h) = ∞.

Boundary Crosscut. We deﬁne boundary crosscut

χ for depicting the progress of rendezvous generation:

∀h ∈ H :

χ(h) =







i i ≤ |h.σ| ∧ h.σ(1, ..., i − 1)issatisﬁed

∧ h.σ(i)isnotsatisﬁed

∞ h.σ(1, ..., |h.σ|)issatisﬁed

The χ is an upper limit beyond which all task points

are not satisﬁed. With the rendezvous generation pro-

ceeding, we can imagine a great frontier of satisﬁed

task points marked by χ gradually pushing forwards

and approaches the ends of all schedules (where χ =

∞), signifying the satisfaction of all task points.

We now make some rules about the process of ap-

proaching χ = ∞ in order to prevent demand looping.

1. The χ and χ should advance to the goal χ = ∞,

and should always choose the way to achieve that

goal with lowest cost.

2. The insertion index of each rendezvous should

be within (χ, χ), so that the task points satisﬁed

through previous rendezvous planning, should re-

main satisﬁed in the later rendezvous planning,

and the planning will not omit any task point’s de-

mands nor sabotage any satisﬁed task points.

3. The task point to be satisﬁed in the next step of

rendezvous planning should be chosen in such a

way that maximises the opportunity of other task

points to be satisﬁed in the future planning, so that

entire MRS has the best chance to be all satisﬁed.

4.3 A*-based Rendezvous Planning

In this section we present a centralised A*-based

Rendezvous Planning Algorithm (ARPA), which tra-

verses all schedules to generate a set of rendezvouses

that satisfy as many task points as possible. The dead-

lock prevention mechanisms shown in Section 4.1 and

Section 4.2 are embedded in ARPA. ARPA can be fur-

ther converted into an equivalent distributed version

in which each robot processes its schedule while per-

sistently communicating with other robots to obtain

information for its own decision-making and to pre-

vent deadlocks (of both types) among robots.

A sub-tree of schedule-level A*-based search

A*-based search(task point level)

=¥

(

)

is sati.

sfied

æö

ç÷

æö

ç÷

èø

(

)

is satisfie

æö

ç÷

èø

… …

…

Generating rendezvous

Inserting a rendezvous

Chosen for its optimality

about total cost, and the

opportunity given to

other task points.

For satisfying

(

)

1 1

æö

ç÷

èø

A*-based search

For satisfying

(

)

(

)

… …

…

()

(

)

1 1

æö

ç÷

èø

prv

Generating rendezvous

A*-based search

For satisfying

(

)

(

)

…

()

(

)

1 1

æö

ç÷

èø

prv

Generating rendezvous

(

)

1 1

i i

æö

ç÷

æö

ç÷

èø

prv

Generating rendezvous

A*-based search

For satisfying

(

)

122

i ii

æö

ç÷

èø

…

(

)

122

iii

æö

ç÷

æö

ç÷

prv

A*-based search

For satisfying

(

)

(

)

…

Generating rendezvous

()

(

)

æö

ç÷

èø

prv

Apply optimal set of rendezvous

(

)

1 1

i i

æö

ç÷

æö

ç÷

èø

prv

Adapt this set of

rendezvous according to

(

)

1 1

i i

æö

ç÷

æö

ç÷

èø

prv

Search for next optimal set of rendezvous based on A* algorithm, until it reaches

…

=¥

Update the current crosscut and boundary crosscut

()

1111

,Apply,, .

iiii

c c cc sc

æö

ç÷

æö

ç÷

èø

¡¬

prv

Connected to

other sub-trees

on the

schedule-level

…

Figure 4: The search tree of A*-based rendezvous planning

algorithm that combines two granularity levels.

Fig. 4 shows the search tree of ARPA. Assume

initially all robots are without any resources, and all

resources are in the ﬁxed stations. The search begins

with χ = χ = 0, to reach the goal χ = ∞. The search is

divided into two granularity levels: (1) schedule level,

which deals with the goal to make χ = ∞; (2) task

point level, which deals with the sub-goal to satisfy

the demands of each task point.

Schedule Level. In this level, A* algorithm is used

to reach the goal χ = ∞. The algorithm will try

to use the calculation at task point level to satisfy

each task point π on χ, and generate the set of ren-

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

674

dezvouses ϒ

prv

(π) which fetch resources for π. Based

on {ϒ

prv

(π) : πis on χ}, it ﬁnds the optimal task point

∗

= arg max

πis on χ

(hϒ

prv

(π

), ..., ϒ

prv

(π

)i, ϒ

prv

(π))

where f

: (P(ϒ))

∗

× P(ϒ) → R is a heuristic ﬁtness

function, which collectively considers following fac-

tors: (1) the cost of completing ϒ

prv

(π); (2) the cost of

previously applied hϒ

prv

(π

), ..., ϒ

prv

(π

)i; (3) the es-

timated distance from current search step to the goal

χ = ∞, given the current χ and χ; (4) the estimated

inﬂuence of applying ϒ

prv

(π) on the opportunities of

other task points becoming satisﬁed in the future. Af-

ter π

∗

is chosen, it will be put into a frontier set χ

which records all the optimal paths at the schedule

level up to now, and will be the starting point of next

round of schedule-level search. Each node ν

of the

search tree at the schedule level is deﬁned as a tuple

hπ, χ, χ

, ϒ

prv

(π), ν

←s

i, where (1) π is the task point

to be satisﬁed by ϒ

prv

(π) (generated by the corre-

sponding task point level search); (2) χ is the cross-

cut reached by ν

; all task points before χ will not be

modiﬁed by any searches succeeding ν

; (3) χ

is the

boundary crosscut reached by ν

; (4) ϒ

prv

(π) is the

rendezvous sequence generated by the corresponding

task point level search to satisfy R



(π). (5) ν

←s

is the

node that precedes ν

in the search tree, from which

we can get the optimal path from χ = χ to ν

Task Point Level. In this level, A* algorithm is

used to satisfy R



(π) — the demands of each task

point π on χ by ﬁnding the best rendezvous sequence

prv

(π). The providing task point will be chosen from

the section of crosscuts (χ, χ). At each step, the al-

gorithm will try to insert a new rendezvous into the

prv

(π) until R



(π) is fully satisﬁed. Similar to the

schedule level, in this level, we also choose among

all possible rendezvouses the optimal rendezvous υ

∗

based on the following formula:

∗

= arg max

υ∈ϒ

prv

(π)

(ϒ

prv

(π), υ)

where f

: ϒ

∗

× ϒ → R is the heuristic ﬁtness function

of rendezvous, which is deﬁned similar to f

. The

most signiﬁcant difference is that f

considers the dis-

tance to the sub-goal where π is satisﬁed, rather than

the satisfaction of entire schedule. Each node ν

the search tree at the task point level is deﬁned as a

tuple hυ, χ, χ, ν

←t

i, where (1) υ is the rendezvous to

be inserted after ν

is chosen as optimal; (2) χ is the

crosscut reached by ν

; (3)

χ is the boundary cross-

cut reached by ν

; (4) ν

←t

is the node that precedes

in the search tree, from which we can obtain the

optimal path from ϒ

prv

(π) =

0 to ν

. The search will

turn to the schedule level when the task point level

search has completed for each task point in χ. In the

task point level, when it is found that currently con-

cerned task point cannot be satisﬁed without sabotag-

ing other task points, the corresponding search will be

postponed until next round of schedule level search.

5 CONCLUSION

In this paper we analyse the two types of deadlock that

can be introduced into a multi-robot system (MRS) by

uncoordinated generation of resource-delivering ren-

dezvouses among robots. The ﬁrst type is caused by

rendezvous tangling and is tackled by constraining the

insertion index of each rendezvous according to its

preceding/succeeding reachable set. The second type

is caused by one robot’s resource demands being sab-

otaged by another robot’s rendezvous, and is tackled

by prudent selection of insertion index of each ren-

dezvous and of resource provider/receiver when plan-

ning rendezvouses. We present the sketch of an A*-

based Rendezvous Planning Algorithm (ARPA) that

respects the constraints regarding both types of dead-

lock.

Our future work includes: (1) Determine the spe-

ciﬁc form of the ﬁtness functions f

and f

as speci-

ﬁed in Section 4.3. (2) Conduct an experiment which

shows ARPA can generate efﬁcient and effective ren-

dezvouses for inter-robot delivery. (3) Implement a

distributed version of ARPA with lower computation

and communication cost, which facilitates its applica-

tion on a real-world MRS. (4) Deal with the interac-

tion between ARPA and the rescheduling and reallo-

cating algorithms on MRS.

REFERENCES

Han Lei, Keyi Xing, L. H. F. X. Z. G. (2014). Deadlock-

free scheduling for ﬂexible manufacturing system us-

ing petri-nets and heursitic search. In Computers and

Industrial Engineering, v. 72, n. 1, p. 297-305.

Keshmiri, S. (2011). Multi-robot, multi-rendezvous

recharging paradigm: an opportunistic control strat-

egy. In IEEE ROSE.

Neil Mathew, Stephen L. Smith, S. L. W. (2013). A graph-

based approach to multi-robot rendezvous for recharg-

ing in persistent tasks. In International Conference on

Robotics and Automation.

Neil Mathew, Stephen L. Smith, S. L. W. (2015). Multi-

robot rendezvous planning for recharging in persistent

tasks. In IEEE Transaction on Robotics, v. 31, n. 1, p.

128-142.

Deadlock Prevention in Rendezvous Generation for On-demand Inter-robot Resource Delivery

675