Hybrid Numerical Simulation of Fluid Flow and

Light Distribution in a Bubble Column Photobioreactor

Christopher McHardy

, Giovanni Luzi

, Jose Rodriguez Agudo

Antonio Delgado

2,3

and Cornelia Rauh

1,2,3

Institute of Food Biotechnology and Food Process Engineering, Technische Universität Berlin, Königin-Luise Str. 22,

Berlin, Germany

Institute of Fluid Mechanics, FAU Campus Busan, University of Erlangen-Nuremberg, 618-230 Busan, Republic of Korea

Institute of Fluid Mechanics, University of Erlangen-Nuremberg, Cauerstr. 4, Erlangen, Germany

Keywords: Photobioreactor, Microalgae, Light-Matter Interaction, Computational Fluid Dynamics, Radiation

Transport, Lattice Boltzmann, Hybrid Method.

Abstract: Cultivation of phototrophic microorganisms occurs often in closed photobioreactors (PBR). Thereby, the

distribution of light inside PBR is a key factor for phototrophic growth and reactor productivity. To predict

local light intensities, it is often assumed that the absorption rate is constant in space, and scattering by

microorganisms is negligible. The present contribution aims to present a hybrid model to simulate fluid flow

characteristics and its impact on light fields in a bubble column PBR. First, numerical simulations of bubble

column flow have been performed. Afterwards, the computed local air volume fractions have been used to

obtain local radiation characteristics of the gassed suspension, and polychromatic light fields were

computed and compared to the optically homogeneous case.

1 INTRODUCTION

Phototrophic microorganisms are characterized by

the ability to use light energy to drive their cellular

metabolism by means of photosynthesis. By doing

so, the energy of light is used for the conversion of

carbon dioxide into biomass. The ability to

accumulate huge amounts of proteins or

triacylglycerides into the biomass makes

phototrophs a promising option for sustainable

production of food, feed and fuels (Williams and

Laurens, 2010).

Technical cultivation of phototrophs commonly

occurs in closed PBR. Since the rate of

photosynthesis is directly linked to the light intensity

a cell is exposed to (Williams and Laurens, 2010),

the distribution of light inside PBR is a key factor

for phototrophic growth and productivity. The

distribution of light is primarily determined by the

presence of microorganisms. Light is absorbed along

the path and consequently intensity is attenuated.

Thereby, the local rate of absorption is directly

proportional to the density of cells in the culture

suspension (Pilon et al. 2011). Moreover, anisotropic

scattering of light causes a major difficulty for an

accurate prediction of local light intensities because

of two reasons. First, the scattering characteristics of

the microorganisms must be measured (directly or

indirectly), which is already a non-trivial task

(Dauchet et al., 2015; Kandilian et al., 2016).

Second, the computation of scattering requires an

adequate discretization of the light angular

distribution (Hunter and Guo, 2015). Due to these

difficulties, a common approach in bioengineering is

to neglect scattering and approximate light

propagation by Lambert Beer’s law instead of

solving the full Radiative Transfer Equation (RTE).

It is often assumed that cells are homogeneously

distributed in a PBR, and consequently also the

radiation characteristics of the suspension are

assumed to show no spatial variance. However, in

most PBR gassing occurs to supply carbon dioxide

to the suspension, remove oxygen and provide

energy for mixing of the liquid phase (Olivieri et al.,

2014). Since the light absorption of gas bubbles is

negligible, and their scattering characteristics

deviate from those of phototrophic cells, the

assumption of an optically homogeneous suspension

does not hold anymore in presence of bubbles.

304

McHardy C., Luzi G., Agudo J., Delgado A. and Rauh C.

Hybrid Numerical Simulation of Fluid Flow and Light Distribution in a Bubble Column Photobioreactor.

DOI: 10.5220/0006226003040311

In Proceedings of the 5th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2017), pages 304-311

ISBN: 978-989-758-223-3

The present contribution aims at presenting a

methodology for computing radiation fields in

multiphase flows. It is based on the assumption that

the radiation characteristics of a mixture can be

obtained by superimposing those of single

components. Therefore, the hydrodynamic

characterization of a PBR is required, for which

Computational Fluid Dynamics (CFD) is a suitable

tool. Two dimensional numerical simulations of

fluid flow inside bioreactors are among the firsts that

have been performed, since they require a lower

numerical effort. However, they were found to be

highly grid dependent (Bech, 2005). Three

dimensional unsteady simulations are more adequate

to reproduce the real complex flow patterns of

bubble column flows. Examples of numerical

simulations of fluid flow in a cylindrical bioreactor

are reported in literature (Pfleger and Becker, 2001;

Lobaton et al., 2011), but the so called “non-drag

forces” are absent in their model. In recent and more

complete models lift, virtual mass, wall lubrication

and turbulent dispersion forces have been

considered, since they strongly affect the flow field

(Masood and Delgado, 2014). More sophisticated

models integrate CFD, light distribution and kinetics

growth of algae cells. Combination of CFD with

Lambert Beer law and Aiba model (Zhang et al.,

2015), or with optical ray tracing simulations based

on an empirical three-parametric model (Krujatz et

al. 2015) are reported. In other contributions

compartmental modelling approach and

photosynthetic factory model (Nauha et al., 2013),

considering also light directionality and day and

night conditions (Nauha et al., 2013) are presented.

In the present contribution, first, the bubble

column flow inside a cylindrical PBR is simulated.

Next, the local radiation characteristics of the gassed

turbid suspension are computed. The RTE is solved

afterwards by means of a Lattice Boltzmann solver

(McHardy et al., 2016).

2 THEORY

Here, the mathematical models of fluid flow and

light distribution are presented. The Eulerian-

Eulerian formulation of two-phase flow and the

applied Lattice Boltzmann method are described in

detail.

2.1 Fluid Flow Model

An Eulerian-Eulerian approach is chosen to simulate

the bubble column flow. Both, the continuous and

the disperse phase are modelled as an interpenetrated

continuum, where the inter-phase forces are taken

into account by an extra term in the momentum

equation. The corresponding mass conservation

equations, both for the liquid and the gas phase read

 

kk kkk

 









 u

(1)

where

,kLG



. Here,

stands for liquid and

for

gas. The other symbols



and



denote the

velocity vector, the volume fraction and the density

of each phase, respectively. The momentum

equations are

 



kkk kkkk

kkkkksk

 





 



  

uuu







(2)

where



. The terms on the left-hand side

represent the temporal and convective acceleration,

while those on the right-hand side represent the

pressure gradient, the turbulent stress tensor, gravity

and interphase forces (Masood and Delgado, 2014).

The stress tensor is defined as



kkeff k k















uu

(3)

where incompressibility has been assumed for both

phases. The effective viscosity for each phase is the

sum of the molecular and the turbulent one

,, ,keff kLam kTurb

 



(4)

Finally, the last term of Eq. (2) reads

,, ,,,

,,, ,

ADL

sk LG LG LG LG

VM WL TD

LG LG LG GL









MM FFF

FFF M

(5)

where the terms on right hand side of Eq. (5) are the

drag

, the lift, the virtual mass, the wall lubrication

and the turbulent dispersion forces (Masood and

Delgado, 2014)

. The drag force is due to viscous

shear stress and pressure distribution around the

bubble surface



GGLGLGL





uuuu

(6)

Hybrid Numerical Simulation of Fluid Flow and Light Distribution in a Bubble Column Photobioreactor

305

where

is the drag force coefficient and

is the

bubble diameter. The Grace correlation is used to

model

(Grace et al., 1976). The lift force acting

on the gas phase due to a rotational liquid phase can

be written as





LG G L L G L L



Fuuu

(7)

where

is computed according to the Legendre

Magnaudet model (Legendre et al., 1998). The

virtual mass force represents the added inertia to gas

bubbles since they are moving through the liquid

phase

LG G L VM











(8)

where

0.5

C 

is the virtual mass coefficient. The

wall lubrication force is an artificial force that

models the situation where bubbles concentrate in a

region close to a wall

GWLGLLGW



Fuun

(9)

where

is the normal to a reactor surface and the

coefficient

is computed with the Frank model

(Frank et al., 2004; Frank et al., 2008). Finally, the

turbulent dispersion force is responsible for the

dispersion of phases and it can be expressed as

LTurb

LG TD D

LTurb L G

















(10)

according to the Favre averaged model (Burns et al.,

2004). Here,

Turb



is the turbulent Schmidt number

for the continuous phase, and

C 

is a multiplier.

2.1.1 Turbulence Model

A two-equation model is able to accurately compute

the turbulent viscosity of the continuous phase

,LTurb L







(11)

where

k is the turbulent kinetic energy and



is the

turbulent frequency.

These two quantities are here

computed according to the Shear Stress Transport

(SST) model (Menter, 1994) by solving two

independent scalar transport equations for

k and for



. A simple algebraic turbulence model is chosen

for the gas phase

Turb

GTurb

LTurb











(12)

2.2 Radiative Transport Model

The RTE is a Boltzmann-type transport equation,

which balances the spatio-temporal evolution of

intensity of radiation (or radiance)



,,Itxs









ˆˆ

ˆˆˆˆ

,, , , , d

It I t









 















sxs

xs xs' s's



(13)

In Eq. (13),

, t ,





and

denote speed of

light, time, solid angle, extinction coefficient, unit

direction and position vector. The scattering albedo



is defined as

sca













(14)

where



and



denote the absorption and

scattering coefficients, which are related to the

extinction coefficient by









is the

scattering phase function, which describes the

angular distribution of scattered light. In Eq. (13),

the emission of radiation by microorganisms is

neglected, due to its minor relevance for the light

field in photobioreactors. Properties of the RTE are

described in detail elsewhere (Modest, 2013) and

need not to be repeated here.

2.2.1 Radiation Transport Lattice

Boltzmann Method (RT-LBM)

To solve Eq. (13), a lattice Boltzmann method

(McHardy et al., 2016) is applied in this work.

Following the usual lattice Boltzmann formalism, a

discrete representation of Eq. (13) reads



(,)(,)

(,) (,)

ii i

IttIt

ItIt





  

 

xx x

(15)

PHOTOPTICS 2017 - 5th International Conference on Photonics, Optics and Laser Technology

306

Herein,



is discretized in the momentum space,

which consists of directional and frequency

components. Therefore, a monochromatic radiation

propagating along a trajectory, which is given by the

connection of two nodes in a cubic lattice, is

considered. The scattering from the

into the

trajectory is captured by the function





which is a discrete representation of the in-scattering

integral in Eq. (13).

 

,,,,

iijijij

twItf











(16)

Thereby, the integral is replaced by a summation and

the scattering phase function is represented by a

symmetric

matrix which is computed by

means of an algebraic method, proposed in

(McHardy et al., 2016). A correction function

,ij

considers that the propagation distance depends on

the direction of propagation on a cubic lattice. The

absorption and scattering coefficients may have

spectral dependency, so





is also spectrally

distributed. For a D3Q26 model (3 dimensions, 26

discrete trajectories), the nodes and weights

of the

quadrature are shown in table 1. The quantity

,ii







 x

(17)

is the collision frequency and relates grid spacing to

the mean free path of radiation. The collision

frequency depends on direction, because the

probability of collision increases with increasing

path length.

The macroscopic quantities of the radiation field,

namely mean intensity

and radiation flux

, can

be obtained by computing moments of



wI d









(18a)

ii i

wI d









(18b)

While the integration over solid angles is

approximated by the summation over directions, the

integration across the spectral component of

momentum is approximated by composite

Simpson’s Rule, using a step length of



 nm.

Table 1: Lebedev quadrature on a unit sphere, used for

discretization of the RTE. The nodes of the quadrature

result from all possible permutations of the typical nodes.

i typical node (x,y,z) weights

1 - 6 (1,0,0) 1/21

7 - 14 1/√3 (1,1,1) 4/105

15 - 26 1/√2 (1,1,0) 9/280

2.2.2 Radiation Characteristics of

Multiphase Suspensions

A major assumption of the presented methodology is

that the radiation properties of a mixture can be

obtained by superimposing those of the single

components. This is true, if single particles scatter

independently of each other. For suspensions of

point-like scatterers, several criteria for estimating

scattering-regimes can be found in literature. Baillis

and Sacadura (2000) as well as Modest (2013) refer

to a scattering regime map, which estimates the

scattering regime with respect to the particle volume

fraction and a size parameter. Jonasz and Fournier

(2007) suggest as a criterion the relation





11g





x

, where

is the cosine of the mean

scattering angle. For suspensions of microalgae at

concentrations in the single-digit gram-per-litre

range, typical for PBR, the suggested criteria are

generally fulfilled. Therefore the radiation

characteristics of a microalgae suspension can be

obtained from

A A ABS





(19a)

AASCA





(19b)

where

is the mass concentration of scatterers in

the suspension and

is the mass-specific

absorption or scattering cross-section, respectively.

For dispersed bubbles, the absorption and

scattering coefficients can be computed analogously,

by multiplying the number density of gas bubbles

by the absorption or scattering cross-section. It is

assumed that bubble absorption is negligible

compared to absorption by microalgae, therefore





. The number density of bubbles inside a

control volume can be computed from the local air

volume fraction and the volume of a single bubble

, in case of monodisperse bubbles.

The scattering

cross-section can be obtained by the geometrical

Hybrid Numerical Simulation of Fluid Flow and Light Distribution in a Bubble Column Photobioreactor

307

cross-section of a bubble

and the scattering

efficiency

. Therefore, the scattering coefficient

for dispersed bubbles becomes

 



xx

(20)

In a gassed suspension of microalgae, the effects

of the single components superimpose (Pilon et al.,

2011; Berberoglu et al., 2007). The effective

absorption and scattering coefficients of the mixture

are given by















xx

(21a)













A GB



 

 xx

(21b)

In Eq. (21) it is considered that the liquid volume

and therefore the volumetric concentration of

microalgae are reduced by the presence of air. Since

microalgae scatter light differently compared to gas

bubbles, an effective scattering phase function must

be computed. Pilon et al. (2011) suggests to use the

scattering coefficients of microalgae and gas bubbles

as weighting coefficients, so that the effective

scattering phase function becomes













GAABB

GAB

 









(22)

3 PHOTOBIOREACTOR MODEL

Here, details concerning simulation set-up are given.

The physical parameters are described first, followed

by the outline of geometry and grid generation, as

well as numerical solutions of fluid flow and light

distribution.

3.1 Physical Parameters

An isothermal cylindrical bubble column PBR of

diameter

9.4D  cm and height 50H  cm with an

air headspace of 10 cm is considered. The reactor is

aerated from a small inlet of diameter



mm,

located at the bottom of the column. Spherical

monodisperse bubbles have a constant mean

diameter

d 

mm and mass flow rate

9.85 10







kg/s. The PBR is illuminated by red

LED from four sides. The spectrum of the LED is

approximated by a Gauss distribution with peak

emission at

655 nm and 15 nm standard deviation.

A suspension of microalgae is located inside the

PBR. The absorption and scattering cross-sections of

the microalgae are assumed to be the same as

measured by Kandilian et al. (2016) and cells are

assumed to be present as individuals and no

agglomeration occurs. Mie-scattering of cells is

expressed by the Henyey-Greenstein phase function



1.5

12cos











(23)

where

0.98g



(Kandilian et al., 2016). For gas

bubbles, the asymmetry factor

was set to 0.86

and the scattering efficiency

sca

Q 

was chosen as

an approximation for Mie-scattering of large spheres

(Pilon et al., 2011).

3.2 Fluid Flow Simulation

Both, the geometry and the grid have been created

using the commercial software ANSYS ICEM

. The

domain is covered with a structured mesh, obtained

by using two O grids, and a mesh of

59059

volumes was selected. All numerical simulations

were carried out using the commercial software

ANSYS CFX

15.0 which is a finite volume based

solver. At the inlet, an air mass flow rate was set,

and an opening boundary condition was set at the

outlet. The remaining parts of the geometry have

been set as walls, and a no slip condition for both air

and water has been imposed.

Simulations with an air mass flow rate

4.85 10







kg/s were run up to 60 s to initialize

the flow field. A time step of 5·10

-4

s was chosen to

advance the solution in time. Afterwards, the time

step has been increased to 10

-3

s, and the mass flow

rate has been raised to the value of

9.85 10







kg/s. Simulations have been run up to 140 s, the cut-

off value of the residuals was set equal to 10

-4

and a

maximum number of thirty iterations for the inner

cycle was imposed. The air volume fraction at every

grid node has been extracted at the time step

 110t



3.3 Simulation of Light Distribution

Solutions of the D3Q26 RT-LBM were computed in

MATLAB

, using an in-house code. The computed

local air-volume fractions were interpolated on a

PHOTOPTICS 2017 - 5th International Conference on Photonics, Optics and Laser Technology

308

lattice with 201 nodes along the column diameter. In

total, the lattice was composed of approx.

1.16 10

nodes. The lattice was proven to produce converged

solutions in a grid refinement study and is also used

for computation in the RT-LBM.

At the side walls of the reactor parallel light

enters the turbid suspension from four sides.

Focussing of light by the curved reactor wall is not

taken into account for the boundary modelling. It is

assumed that the walls are non-reflective so that

backscattered light can leave the computational

domain. For each concentration of biomass

(

0.6

g/L, 1.0 g/L), 7 monochromatic solutions were

computed and integrated by means of Simpson’s

Rule to obtain the polychromatic solution. All

parameters are shown in table 2. Achievement of

steady-state in monochromatic simulations was

estimated by introducing a relative error criterion.



max 1 10

Itt









 

(24)

Table 2: Spectral radiation characteristics of biomass and

light source at the simulated wavelengths.

λ [nm] 610 625 640 655

abs

/kg] 136 156 176 259

sca

/kg] 1628 1599 1538 1360

0,λ

1E-04 [-] 3 36 161 266

λ [nm] 670 685 700

abs

/kg] 358 311 70

sca

/kg] 1139 1305 1941

0,λ

1E-04 [-] 161 36 3

4 RESULTS AND DISCUSSION

In this section, preliminary results are shown to

demonstrate the applicability of the proposed hybrid

methodology. It is shown how different biomass

concentrations and presence of bubbles affect the

light distribution inside a PBR. While the former has

a strong impact on the intensity profile, the latter

exhibits only a weak effect on it, probably due to the

low mass flow rate used in this work.

4.1 Flow Field

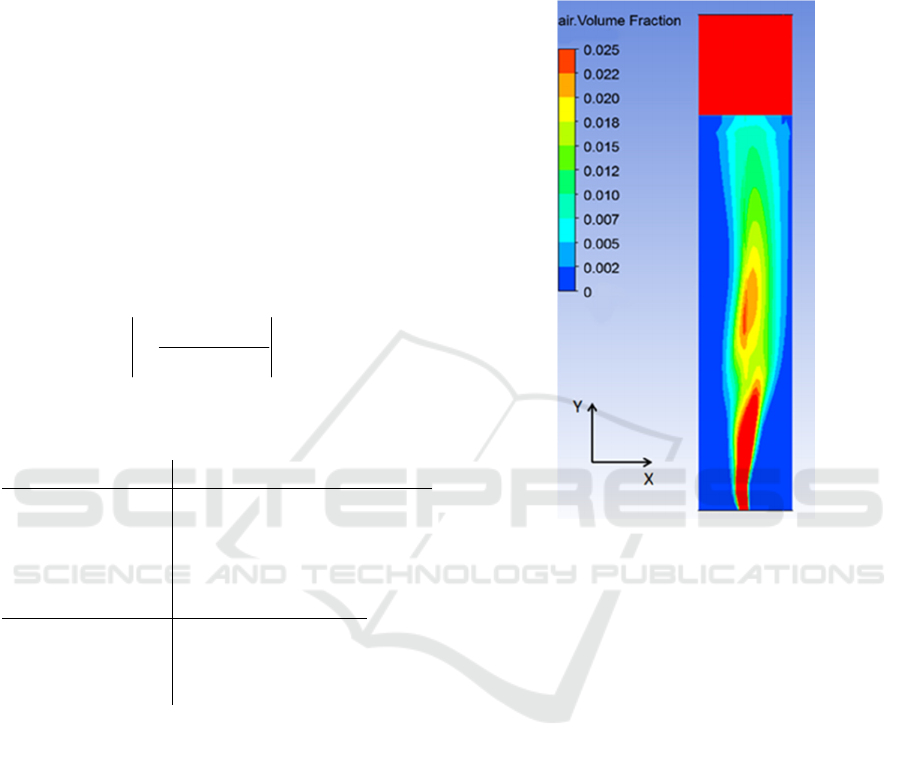
Figure 1 shows a contour of air-volume fraction in a

cross-sectional (x-y) plane at 0z  at the time step

110t  s. It is an oscillating air bubble “plume”,

typical of an aerated bioreactor. The air volume

fraction at each grid node is extracted at the selected

time instant, so that optical properties of the

suspension can be computed.

Figure 1: a) Air volume fraction on an x-y plane at

0z 

the time instant

110t 

s. The mass flow rate is

9.85 10







kg/s.

4.2 Radiation Field

The local air volume fractions were interpolated on a

cubic lattice and grid independence was found for a

grid resolution higher than 50 nodes along the

column diameter (results not shown).

To evaluate the radiation field, profiles on the

plane

0.3y 

m of the bubble column were

computed. Figure 2 shows profiles of normalized

monochromatic radiation at different wavelengths.

Near the boundaries, the radiation emitted from

different lamps overlap so that the magnitude of the

normalized radiation field becomes greater than 1.

Figure 3 shows the polychromatic intensity

profiles for two different concentrations of

microalgae. For comparison, simulations of an

optically homogeneous suspension (without gas)

were performed. Although the profiles do not

deviate much, slight differences (up to 6 %, not

shown) were found in presence of gas.

Hybrid Numerical Simulation of Fluid Flow and Light Distribution in a Bubble Column Photobioreactor

309

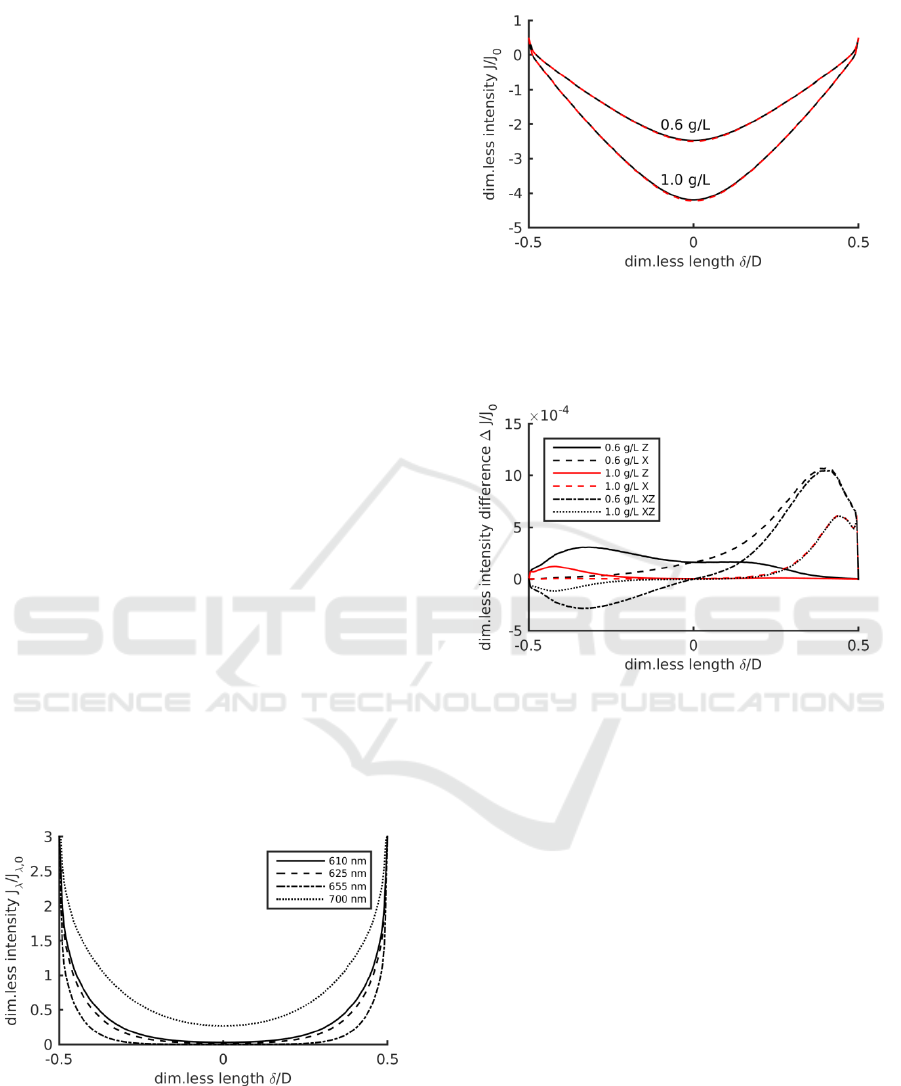
Figure 4 shows the effect of gas bubbles on the

light field more in detail. It can be seen that increase

of biomass concentration damps the effect of the gas

on the light field and biomass absorption becomes

the dominant characteristic. However, the light field

becomes asymmetric due to differences in local gas

concentrations as it can be seen by comparing

intensity profiles along the x- and z-axes or rather by

the difference of the profiles (Dash-dotted and

dotted lines in Figure 4).

Generally, the effect of gas bubbles on the light

field is weak in the present case. However, the air

volume fraction is higher at higher gas mass flow

rates, and further investigations will address this

effect. Moreover, the present study considers red

LED lamps, which emit in the absorption maximum

of microalgae (Williams and Laurens, 2010). It can

be expected, that the effect of bubbles increases if

light across the full visible spectrum is considered,

due to the lower absorption in other spectral regions.

Further model improvement will also consider the

directional emission of light sources as well as

focussing effects at the boundaries.

It is well known that flashing light has great

potential to improve the productivity of PBR

(Williams and Laurens, 2010). From a Lagrangian

point of view, flashing light is realized if cells travel

between bright and dark regions in the reactor.

Investigations on this effect in PBR require transient

simulations techniques, since optical accessibility

and therefore experimental investigations are

limited. The presented hybrid model offers the

required functionality to investigate transient effects

of the flow on the light field, and to trace virtual

particles through the transient light field.

Figure 2: Profiles of monochromatic light intensity along

the x-axis at

0.3y  m and 0z  in the PBR for

0.6

c 

g/L. δ is the radial coordinate.

Figure 3: Profiles of polychromatic light intensity (log-

scale) along the x-axis at

0.3y



m and 0z  in the PBR

for different biomass concentrations with (solid lines) and

without gas (dashed lines). δ is the radial coordinate.

Figure 4: Effect of gas bubbles on light intensity. Solid

and dashed lines compare the effect of gas bubbles to an

optically homogeneous suspension at

0.3y  m along the

x- and z-axis, respectively. Dash-dotted and dotted lines

show the difference of light intensity along x and z axis in

the presence of gas bubbles. δ is the radial coordinate.

5 CONCLUSIONS

In this work a simulation framework was presented

to couple fluid dynamics and radiation transfer. The

method is innovative and no coupling of CFD and

RT-LBM has been reported in literature before. This

is, in particular, due to the fact that the development

of RT-LBM is still a new field of research.

The methodology was applied to simulate flow

and light fields in a bubble column PBR. Although

the effect of gas bubbles on the light field was weak,

further investigations will proof the generality of this

result. To make use of the full power of the

modelling framework, future work should also

address transient impacts of gas bubbles on the light

field to realize flashing-light regimes in PBR.

PHOTOPTICS 2017 - 5th International Conference on Photonics, Optics and Laser Technology

310

The link between CFD and RT-LBM was

realized by computing local radiation properties

from air-volume fractions and radiation properties of

bubbles and single cells. If the cell density is not too

high, the underlying assumption that radiation

properties of a mixture can be obtained by

superimposing those of single components remains

valid. This enables to take local cell concentrations

into account if mass transport of cells in

incorporated into the CFD model. As shown by

Dauchet et al. (2015), information as particle size

distributions can also be considered for the

calculation of radiation properties to obtain more

realistic representative values, if desired. Similarly,

it seems to be possible to treat mixtures of different

cell species with different particle size.

REFERENCES

Baillis, D., Sacadura, J.-F., 2000. Thermal radiation

properties of dispersed media: theoretical predication

and experimental characterization. In J. Quant.

Spectrosc. Ra., 67(5): 327-363.

Bech, K., 2005. Dynamic simulation of a 2D bubble

column. In Chem. Ing. Sci., 60(19): 5294-5304.

Berberoglu, H., Yin, J., Pilon, L., 2007. Light transfer in

bubble sparged photobioreactors for H

production and

mitigation. In Int. J. Hydrogen Energ., 32(13):

2273-2285.

Burns, A.D.B., Frank, Th., Hamill, I., and Shi, J-M., 2004.

The Favre Averaged Drag Model for Turbulent

Dispersion in Eulerian Multi-Phase Flows. 5th

International Conference on Multiphase Flow

Dauchet, J., Blanco, S., Cornet, J.-F., Fournier, R., 2015.

Calculation of radiative properties of photosynthetic

microorganisms. In J. Quant. Spectrosc. Ra., 161: 60-

84.

Frank, Th., Shi, J.M., Burns, A.D., 2004. Validation of

Eulerian Multiphase Flow Models for Nuclear Safety

Applications. In 3rd International Symposium on

Two-Phase Flow Modelling and Experimentation,

Pisa, Italy.

Frank, Th., Zwart, P.J., Krepper, E., Prasser, H.-M.,

Lucas, D., 2008. Validation of CFD models for mono-

and polydisperse air-water two-phase flows in pipes.

In J. Nuclear Engineering & Design, 238(3): 647–659.

Grace, J.R., Wairegi, T., Nguyen, T.H., 1976. Shapes and

velocities of single drops and bubbles moving freely

through immiscible liquids. In Trans. Inst. Chem.

Eng., 54 (3): 167-173.

Hunter, B., Guo, Z., 2015. Numerical smearing, ray effect,

and angular false scattering in radiation transfer

computation. Int. J. Heat Mass Transfer, 81: 63–74.

Jonasz, M., Fournier G.R.., 2007. Light Scattering by

Particles in Water, Academic Press. Amsterdam, 1

edition.

Krujatz, F., Illing, R.

, Krautwer, T., Liao, J., Helbig

K., Goy, K., Opitz, J., Cuniberti, G., Bley, T., Weber,

J., 2015, Light-field-characterization in a continuous

hydrogen-producing photobioreactor by optical

simulation and computational fluid dynamics. In

Biotechnol Bioeng., 112(12): 2439-2449

Kandilian, R., Pruvost, J., Artu, A., Lemasson, C.,

Legrand, J., Pilon, L., 2016. Comparison of

experimentally and theoretically determined radiation

characteristics of photosynthetic microorganisms. In J.

Quant. Spectrosc. Ra., 175: 30-54.

Legendre, D., Magnaudet, J., 1998. The lift force on a

spherical bubble in a viscous linear shear flow. In J.

Fluid Mech., 368: 81-126.

Lobaton, H.F.Q., Suarez, C.A., Molina, A., 2011. CFD-

facilitated flow field analysis of bubble columns with

concentric plates for biological applications. In Chem.

Eng. Technol., 34(9):1490-1496.

Masood, R.M.A., Delgado, A., 2014. Numerical

investigation of the interphase forces and turbulence

closure in 3D square bubble columns. In Chem. Eng.

Sci., 108(28), 154-168.

Menter, F.R., 1994. Two-equation eddy-viscosity

turbulence models for engineering applications. In

AIAA Journal, 32(8): 1598-1605.

McHardy, C., Horneber, T., Rauh, C., 2016. New lattice

Boltzmann method for the simulation of three-

dimensional radiation transfer in turbid media. In Opt.

Express, 24(15): 16999-17017.

Modest M.F., 2013. Radiative Heat Transfer, Academic

Press. Amsterdam, 3

edition.

Nauha, E., K., Alopaeus, V. 2013. Modeling method for

combining fluid dynamic and algal growth in a bubble

column photobioreactor. In Chem. Eng. Journal, 229:

559-568

Nauha, E., K., Alopaeus, V. 2015. Modeling outdoors

algal cultivation with compartmental approach. In

Chem. Eng. Journal, 259: 945-960

Pilon, L., Berberoglu, H., Kandilian, R., 2011. Radiation

transfer in photobiological carbon dioxide fixation and

fuel production by microalgae. In J. Quant. Spectrosc.

Ra., 112(17): 2639-2660.

Pfleger, D., Becker, S., 2001. Modelling and simulation of

the dynamic flow behavior in a bubble column. In

Chem. Eng. Sci., 56(4): 1737-1747.

Olivieri, G., Salatino, P., Marzocchella, A., 2014.

Advances in photobioreactors for intensive microalgal

production: configurations, operating strategies and

applications. In J. Chem. Technol. Biotechnol., 89:

178-195

Williams, P.J.le B., Laurens, L.M.L., 2010. Microalgae as

biodiesel & biomass feedstocks: Review & analysis of

the biochemistry, energetics & economics. In Energy

Environ. Sci., 3(5): 554-590.

Zhang, D., Dechatiwongse, P., Hellgardt, K., 2015.

Modeling light transmission, cyanobacterial growth

kinetics and fluid dynamics in a laboratory scale

multiphase phot-bioreactor for biological hydrogen

production”, Algal Research 8, pp. 99-107.

Hybrid Numerical Simulation of Fluid Flow and Light Distribution in a Bubble Column Photobioreactor

311