On Efficient Computation of Tensor Subspace Kernels for
Multi-dimensional Data
Bogusław Cyganek
1
and Michał Woźniak
2
1
AGH University of Science and Technology, Al. Mickiewicza 30, 30-059, Kraków, Poland
2
Wroclaw University of Science and Technology, Wroclaw, Poland
Keywords: Reproducing Kernel Hilbert Spaces, Chordal Kernel, Multi-dimensional Patterns, Tensors, Grassmannian
Manifolds, Pattern Classification.
Abstract: In pattern classification problems kernel based methods and multi-dimensional methods have shown many
advantages. However, since the well-known kernel functions are defined over one-dimensional vector spaces,
it is not straightforward to join these two domains. Nevertheless, there are attempts to develop kernel functions
which can directly operate with multi-dimensional patterns, such as the recently proposed kernels operating
on the Grassmannian manifolds. These are based on the concept of the principal angles between the orthogonal
spaces rather than simple distances between vectors. An example is the chordal kernel operating on the
subspaces obtained after tensor unfolding. However, a real problem with these methods are their high
computational demands. In this paper we address the problem of efficient implementation of the chordal
kernel for operation with tensors in classification tasks of real computer vision problems. The paper extends
our previous works in this field. The proposed method was tested in the problems of object recognition in
computer vision. The experiments show good accuracy and accelerated performance.
1 INTRODUCTION
Kernel based methods found broad applications in
variety of object classification problems. This is due
to their ability of transforming patterns into higher
dimensional space in which their separation allows
more reliable pattern separation. The well-known
example are the support vector machines (SVM)
proposed by Cortes and Vapnik (Cortes and Vapnik,
1995). On the other track, tensor methods allow direct
processing of the multi-dimensional patterns, such as
images, video streams, etc. The methods were
developed in sixties, although their application in
signal processing was started by de Lathauwer (de
Lathauwer, 1997). Since then, many tensor based
methods were developed for pattern classification,
such as for instance tensor faces (Vasilescu and
Terzopoulos, 2002, Cyganek, 2010). However, since
the well-known kernel functions are defined over
one-dimensional vector spaces, whereas the tensor
methods assume multi-dimensional objects, it is not
straightforward to find functions that are Hilbert
kernels and directly operate with the tensor objects.
Nevertheless, recent research on the concept of the
principal angles between subspaces (Hamm, 2005),
as well as distances on the Grassmannian manifolds
led to development of kernels that can operate with
tensor objects. Based on the works by Hamm
Signoretto et al. proposed a chordal tensor that can
operate with tensor and showed their superior abilities
in signal and video processing (Signoretto et al.,
2011). A version of the chordal tensor, but operating
on slightly different subspaces, was proposed by Liu
et al. (Liu et al. 2013). Both chordal versions are
based on a sequence of singular value decompositions
(SVD) applied to the unfolded matrices obtained from
the input tensors. This way two versions of the
chordal tensor are obtained: the S-subspace and D-
subspace type, respectively. This will be further
explained in this paper. The chordal tensor was
analyzed by Cyganek et al. (Cyganek et al. 2015) in
broad group of pattern classification tasks. These
works showed very good accuracy of this approach.
However, direct computation of the chordal tensor is
burdened with high computational costs.
To solve this problem we proposed a number of
improvements. In our previous work (Cyganek et al.
2016) a fast eigenvalue computation algorithm was
proposed which allows fast computation of the
chordal kernel based on the so called S-spaces.
378
Cyganek B. and WoÅžniak M.
On Efficient Computation of Tensor Subspace Kernels for Multi-dimensional Data.
DOI: 10.5220/0006229003780383
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 378-383
ISBN: 978-989-758-226-4
Copyright
c
 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

However, it was not shown how to use this algorithm
for the D-spaces. In this paper we address this
problem and show its solution which constitutes the
main contribution.
The rest of this paper is organized as follows:
Section 2 presents a short introduction to kernel
methods operating on tensor subspaces. In Section 3
we present methods of efficient computations of the
chordal kernels. Section 3.1 briefly outlines fast
computation of the S-subspace chordal distance,
which was presented in our previous work (Cyganek
et al. 2016). On the other hand, Section 3.2 introduces
a novel approach to the computation of the D-
subspace chordal distance. This is the main
contribution of this paper. The paper ends with
discussion of implementation and experimental
results, as shown in Section 4. Finally, Section 5
contains conclusions and directions of further work.
2 INTRODUCTION TO KERNELS
ON TENSOR SUBSPACES
The presented in this paper chordal kernel allows
direct computation of the kernel function directly out
of the tensor objects. As shown by many authors,
application of the high dimensional tensor methods
and kernels, in many domains leads to superior results
(Signoretto et al. 2011, Liu et al. 2013, Cyganek et al.
2015). In this section we present only a brief outline
of the chordal kernel and tensor methods. However,
further details can be found in the aforementioned
publications.
The chordal kernel tensor, which is the main
subject of this paper, relies on computation of the
chordal distance, which is defined on the spaces
spanned by the unfolded representations of the two
tensors. In order to come to the proper expressions,
let us briefly recall basic facts on tensor algebra (for
a more complete description see papers by
Lathauwer, Kolda, Cichocki, Cyganek). A tensor is
defined as follows
××
∈ℜ

12 L
NN N

,
(1)
which can be seen as an L-dimensional cube of real
data; Its dimensions correspond to different factors of
the measurements. A j-th flattening, or unfolding, of
a tensor  is a matrix defined as follows
()
()
−+
×
∈ℜ

12 1 1jjjL
NNNNN N
j
A
,
(2)
where columns of
()
j
A are the j-mode vectors of .
Let us notice, that j in the above denotes a row index
of
()
j
A . On the other hand, column index is a product
of all the rest L-1 indices of the tensor  (Cichocki,
2009) (Lathauwer, 1997) (Lathauwer, 2000)
(Cyganek, 2013). Having defined the
()
j
A
flattening
of the tensor let us compute its SVD
decomposition, as follows
() () () ()
() ()
()
()
()
==











,1
,1
,1 ,2
,2
.
jjjTj
Tj
j
jj
Tj
A
A
AA
A
ASVD
D
V0
SS
00
D
(3)
Further on, let us observe that columns of
()
,1
j
A
D
and columns of
()
,1
j
A
S
constitute orthogonal bases,
called the D-space and S-space, respectively. Both
correspond to the ranges
()



Tj
R A and
()



j
R A ,
respectively. Based on this observation, two types of
projectors can be defined, as follows (Cyganek, 2016)
()
() ()




=
,1 ,1
j
jTj
R
AA
A
PSS
,
(4)
as well as
()
() ()




=
,1 ,1
Tj
jTj
R
AA
A
PDD
.
(5)
The two above projectors directly lead to the two
chordal distances and chordal kernels, respectively,
as follows (Signoretto et al. 2011)
()
() () () ()
σ
=
=

−
−


∏
1
2
,1 ,1 ,1 ,1
2
1
,
1
exp
2
L
jTj jTj
F
j
K
AA BB
DD DD

,
(6)
and (Liu et al. 2013)
()
() () () ()
σ
=
=

−
−


∏
2
2
,1 ,1 ,1 ,1
2
1
,
1
exp
2
L
jTj jTj
F
j
K
AA BB
SS SS

.
(7)
In one of our previous papers on this subject we
investigated properties of the kernel (6), showing its
superior performance in many classification tasks of
the visual objects (Cyganek et al. 2014). However,
the computational burden was very high and the
subsequent research led to development of new fast
computation methods of the kernel (7) (Cyganek et
al. 2016), and finally to the kernel (6) (this paper).
On Efficient Computation of Tensor Subspace Kernels for Multi-dimensional Data
379

3 EFFICIENT COMPUTATION
OF THE CHORDAL KERNELS
The previous discussion has shown that computation
of the two types of the chordal kernel requires
a number of decompositions of the unfolding
matrices obtained from the input tensor. A more
detailed investigation shows that this is the main
bottleneck of the whole method. Therefore, a faster
algorithm would help in this respect. Algorithm 1
presents such an algorithm which is based on the
work by Bingham and Hyvärinen (Bingham and
Hyvärinen, 2000). This is the fast eigen-
decomposition based on the fixed point theorem,
which allows alleviation of the much slower full SVD
decomposition algorithm (Golub and van Loan,
1996). However, contrary to the latter, the Algorithm
1 requires a symmetric matrix on its input. In the next
sections we show how to fulfill this requirements
when computing the S-space, as well as the D-space
versions of the chordal distance, respectively. The
latter constitutes the main contribution of this paper.
Algorithm 1. Fast eigen-decomposition of a symmetrical
matrix
Input – a symmetric matrix C,
a number of eigenvectors k
max
,
a threshold
ρ
th
.
Output – k
max
first eigenvectors of C.
Random initialize vector
()
0
0
e
k ← 0
for k < k
ma
x
i ← 1
do
() ( )
−
←
1ii
kk
eCe
G-S orthogonalization:
() () ()
()
−
=
←−

1
0
k
ii Ti
kk kjj
j
ee eee
Normalize vector:
() () ()
←
2
iii
kkk
eee
()()
ρ
−
=−
1
1
Ti i
kk
ee
i ← i + 1
while
ρρ
>
th
end for
After finding the k
max
leading eigenvectors, the
corresponding eigenvalues are computed as follows
(Cyganek et al. 2016)
λ =
T
kkk
eAe
. (8)
The method computes the k
max
leading
eigenvectors of a symmetric matrix C. However, the
algorithm is iterative. Nevertheless, in practice it
converges fast. Also, on its input, the threshold
ρ
th
,
which controls a degree of orthogonality of the
vectors, must be provided. Detailed discussion of the
steps of the above algorithm is presented in our
previous publication (Cyganek et al. 2016). In the
next two subsections we provide details on efficient
computation of the both S and D subspaces,
respectively, which constitute the core of
computations of both types of the chordal kernel for
tensor data.
3.1 Efficient Computation of the
S-Subspace
A method of efficient computation of the S-space
based on the fast eigen-decomposition algorithm was
proposed in our previous work (Cyganek 2016). Here,
for completeness, we recall the main steps of this
derivation.
In this case, we arrive to the following
computation
() () () () ()
==
2jTj j jTj
S
CAA SVS
,
(9)
where A
(j)
denotes the j-th flattening matrix of the
input tensor. In the following we will skip the
superscript (j) from for clarity. Thus, the product
=
T
S
CAA
in (9) is always symmetric and, for
majority of tensors used in real cases, it contains
much less elements than the matrix A alone. Thus, C
S
can be directly used with the Algorithm 1 for
computation of the S-type chordal kernel of tensor
data.
3.2 Efficient Computation of the
D-Subspace
As alluded to previously, computation of the chordal
kernel in accordance with the proposition of
Signoretto et al. requires computation of a series of D
subspace matrices, from the decompositions of the
two input tensors of this kernel. In this case, to come
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
380

with a symmetric matrix and to employ the Algorithm
1, the following derivation is proposed.
In this case, starting from (3) the following is
obtained
() () () () ()
=
2Tj j Tj j j
AA DVD.
(10)
However, computation of the D matrix based on
(10) from the series of unfolded tensor matrices, in
most of the cases would be inefficient due their much
larger number of columns than rows, i.e. N«M.
Therefore in this case we propose to proceed slightly
different, taking as a starting point eigen-
decomposition of the AA
T
, exactly as in (9). In this
case, computation of the eigenvectors can be stated as
follows
μ
=
T
kkk
AA e e
.
(11)
where
k
e
denote k-th eigenvector and
μ
k
its
corresponding eigenvalue. Since AA
T
is of
dimensions N×N, there is at most N eigenvectors
k
e
,
i.e. k≤N. For clarity, in the above formula we also
skipped the superscript (j) from (9). Solution to (11)
can be efficient, since the product AA
T
is a symmetric
matrix of relatively small size.
Now, left multiplying (11) by A
T
yields
μ =
TT T
kkk
AAAe Ae
.
(12)
which can be interpreted as follows
()()()
μ
Ξ
=







kk
TT T
kk k
qq
AA Ae Ae
.
(13)
So, we see that the vectors q
k
are eigenvectors of the
matrix Ξ=A
T
A of dimensions M×M, thus they provide
columns of the sought matrix D in (10) without
explicit computation of the A
T
A, however. Thus, to
find out q
k
the following product
=
T
kk
qAe
(14)
needs to be computed. If we consider all possible
eigenvectors q
k
, the following matrix is obtained
=
T
QAE,
(15)
where columns of the matrices Q∈ℜ
M×N
and
E∈ℜ
N×N
, constitute eigenvectors q
k
and e
k
,
respectively.
Since q
k
are eigenvectors of the symmetric matrix
Ξ=A
T
A, they are orthogonal. However, in general
case they do not need to be orthonormal. Thus, the
last step is to normalize columns of the matrix Q in
(15), so the Frobenius norm of each of them is 1.
Thus, an estimate of the N eigenvectors of the matrix
,1A
D
in (3) is obtained as follows
=
,1A
DQ
,
(16)
where
Q
is a column normalized version of the
matrix Q in (15). It is worth noticing however, that
the rank of the matrix
()
,1
j
A
D
never exceeds N. Thus,
the above procedure is exact up to the numerical
errors associated with matrix multiplications.
Summarizing, efficient computation of the matrix
,1A
D
proceeds as follows:
1. Compute the symmetric matrix C= AA
T
;
2. Compute eigenvectors e
k
of C (see the
previous section);
3. From e
k
, form matrix E and compute matrix
Q in accordance with (15);
4. Normalize columns of Q and from (16)
compute
,1A
D
.
That is, in other words, efficient computation of
D-type constitutes of two steps: computation of the
eigenvectors exactly as in the S-type, then followed
by one matrix multiplication and matrix
normalization. In effect, both computations, i.e. of the
D-type and S-type of the chordal kernel, can be
almost identically efficiently computed, thanks to the
fast eigen-decomposition and the D-type and S-type
algorithms proposed in this paper.
4 IMPLEMENTATION AND
EXPERIMENTAL RESULTS
All of the algorithms presented in this paper were
implemented in C++ in the Microsoft Visual 2015
Studio.
The experiments were run on a computer
endowed with the Intel® Core™ i7-4800MQ CPU
@2.7GHz, 32GB RAM, and OS 64-bit Windows 7.
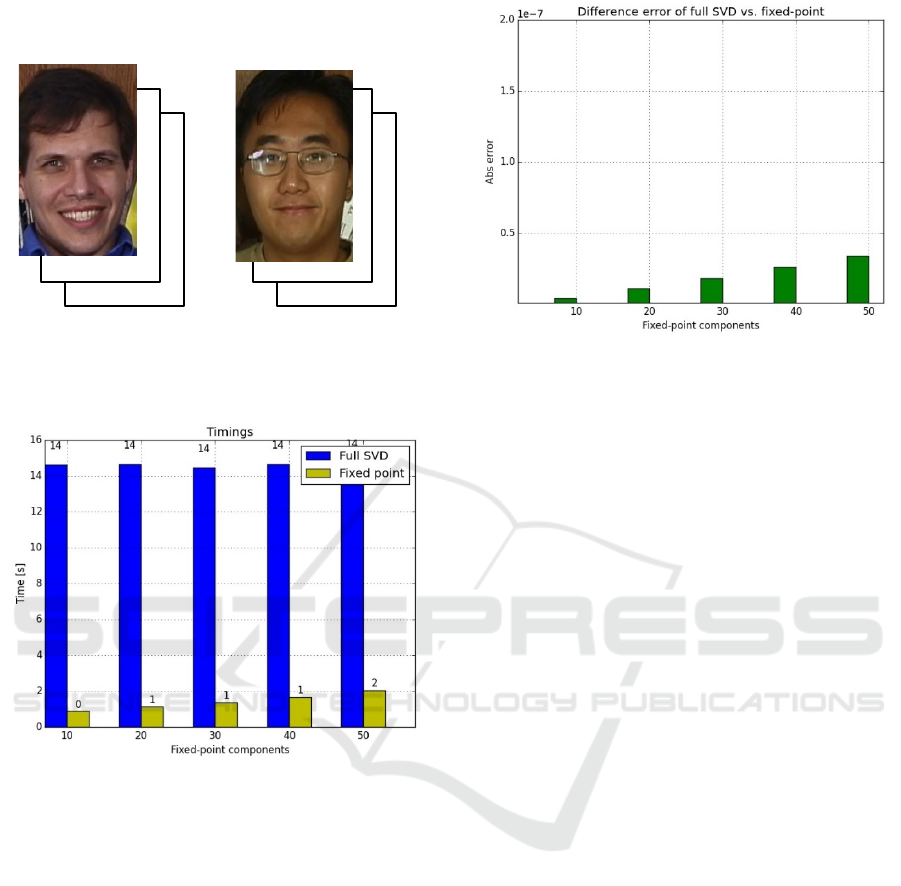
The input tensors were two video objects created
from the images of the Georgia Tech Face Database
of the two persons shown in Figure 1.
Both tensors used for testing were of dimensions
181x241x3x5, i.e. these were composed of 5 color
frames. Figure 2 depicts execution times of the full
SVD decomposition compared to the fixed-point
On Efficient Computation of Tensor Subspace Kernels for Multi-dimensional Data
381

version for the D-subspace tensor kernels for the
video streams shown in Figure 1.
Figure 1: Two video streams composed of the frames from
the Georgia Tech Face Database which constitute two 4D
tensors used to compute chordal kernels.
Figure 2: Comparison of execution time of the full SVD
decomposition and the fixed-point version for the D-
subspace tensor kernels of size 181x241x3x5.
Observing Figure 2 it becomes evident that the
obtained with our method speed up ratio is an order
of magnitude faster compared to the full SVD
decomposition. On the other hand, there are no
significant differences in computation speed between
the D-space and S-space, computed with the fixed
point algorithm proposed in this paper.
It is also in order to compare computation
accuracy between the full SVD decomposition in
relation to the proposed fixed point approximation of
a number of leading eigenvectors. Results of this
computations are shown in Figure 3.
Although the error is different for a different
number of eigenvectors, the total error does not
exceed 5e-08 which is well accepted in many
applications.
Figure 3: Difference error in computation of the D-subspace
tensor kernel of the full SVD vs. fixed point algorithm for
a given number of the leading eigenvectors. Error does not
exceed 5e-08.
5 CONCLUSIONS
This paper extends and completes the method
proposed in our previous work (Cyganek 2016) by
providing a method of efficient computation of the
chordal kernel for tensor data from the respective D
sub-spaces of the input tensors. We show two
efficient algorithms for computation of both versions
of the chordal kernel operating on tensor data. This
type of kernels opens new way of classifying tensor
(multi-dimensional) objects, such as images, video
streams, etc. with the broad category of kernel
methods, such as SVM or KPCA. Our experimental
results showed that the achieved speed up ration in an
order of magnitude thanks to the proposed
methodology. Further investigation will focus upon
observing further properties of the two types of the
chordal kernels, as well as upon development of new
kernels capable of operation with tensor objects.
ACKNOWLEDGEMENTS
This work was supported by the Polish National
Science Center under the grant no. DEC-
2014/15/B/ST6/00609.
REFERENCES
Bingham E., Hyvärinen A.: A Fast Fixed-Point Algorithm
For Independent Component Analysis of Complex
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
382

Valued Signals. International Journal of Neural
Systems, Vol. 10, No. 1, World Scientic Publishing
Company (2000)
Cichocki, A., Zdunek, R., Amari, S.: Nonnegative Matrix
and Tensor Factorization. IEEE Signal Processing
Magazine, Vol. 25, No. 1, 142-145 (2008)
Cortes C., Vapnik V.: Support-vector
networks.Mach.Learn.20, pp. 273–297 (1995)
Cyganek B., An Analysis of the Road Signs Classification
Based on the Higher-Order Singular Value
Decomposition of the Deformable Pattern Tensors,
Advanced Concepts for Intelligent Vision Systems:
12th International Conference, ACIVS 2010, Sydney,
Australia, December 13-16, pp. 191–202 (2010)
Cyganek, B., Object Detection and Recognition in Digital
Images: Theory and Practice, Wiley (2013)
Cyganek B., Krawczyk B., Woźniak M.: Multidimensional
Data Classification with Chordal Distance Based
Kernel and Support Vector Machines. Engineering
Applications of Artificial Intelligence, Elsevier, Vol.
46, Part A, pp. 10–22 (2015)
Demmel J.W.: Applied Numerical Linear Algebra. Siam
(1997)
Georgia Tech Face Database, 2013.
http://www.anefian.com/research/face_reco.htm
Golub, G.H., van Loan, C.F.: Matrix Computations. Johns
Hopkins Studies in the Mathematical Sciences. Johns
Hopkins University Press (2013)
Hamm, J., Lee, D.: Grassmann discriminant analysis: a
unifying view on subspace-based learning. In
Proceedings of the 25th international conference on
machine learning (pp. 376–383). ACM
Kolda, T.G., Bader, B.W.: Tensor Decompositions and
Applications. SIAM Review, 455-500 (2008)
Krawczyk B.: One-class classifier ensemble pruning and
weighting with firefly algorithm. Neurocomputing 150,
pp. 490-500 (2015)
Kung S.Y.: Kernel Methods and Machine Learning.
Cambridge Universisty Press (2014)
Lathauwer, de L.: Signal Processing Based on Multilinear
Algebra. PhD dissertation, Katholieke Universiteit
Leuven (1997)
Lathauwer, de L., Moor de, B., Vandewalle, J.: A
Multilinear Singular Value Decomposition. SIAM
Journal of Matrix Analysis and Applications, Vol. 21,
No. 4, 1253-1278 (2000)
Liu C., Wei-sheng X., Qi-di W.: Tensorial Kernel Principal
Component Analysis for Action Recognition.
Mathematical Problems in Engineering, Vol. 2013,
Article ID 816836, 16 pages, 2013.
doi:10.1155/2013/816836.
Marot J., Fossati C., Bourennane S.: About Advances in
Tensor Data Denoising Methods. EURASIP Journal on
Advances in Signal Processing, (2008)
Meyer C.D.: Matrix Analysis and Applied Linear Algebra
Book and Solutions Manual. SIAM (2001)
Signoretto M., De Lathauwer L., Suykens J.A.K. : A
kernel-based framework to tensorial data analysis.
Neural Networks 24, pp. 861–874 (2011)
Vasilescu M.A., Terzopoulos D.: Multilinear analysis of
image ensembles: TensorFaces. Proceedings of
Eurpoean Conference on Computer Vision, pp. 447–
460, (2002)
Q. Zhao, G. Zhou, T. Adali, L. Zhang and A. Cichocki,
Kernelization of Tensor-Based Models for Multiway
Data Analysis: Processing of Multidimensional
Structured Data, in IEEE Signal Processing Magazine,
vol. 30, no. 4, pp. 137-148, July 2013. doi:
10.1109/MSP.2013.2255334
On Efficient Computation of Tensor Subspace Kernels for Multi-dimensional Data
383