A Serendipity-Oriented Greedy Algorithm

for Recommendations

Denis Kotkov

, Jari Veijalainen

and Shuaiqiang Wang

2∗

University of Jyvaskyla, Faculty of Information Technology,

P.O.Box 35, FI-40014 University of Jyvaskyla, Jyvaskyla, Finland

Manchester Business School, The University of Manchester, Manchester, U.K.

Keywords:

Recommender Systems, Learning to Rank, Serendipity, Novelty, Unexpectedness, Algorithms, Evaluation.

Abstract:

Most recommender systems suggest items to a user that are popular among all users and similar to items the

user usually consumes. As a result, a user receives recommendations that she/he is already familiar with or

would ﬁnd anyway, leading to low satisfaction. To overcome this problem, a recommender system should sug-

gest novel, relevant and unexpected, i.e. serendipitous items. In this paper, we propose a serendipity-oriented

algorithm, which improves serendipity through feature diversiﬁcation and helps overcome the overspecial-

ization problem. To evaluate our algorithm and compare it with others, we employ a serendipity metric that

captures each component of serendipity, unlike the most common metric.

1 INTRODUCTION

Recommender systems are software tools that suggest

items of use to users (Ricci et al., 2011; Kotkov et al.,

2016a). An item is “a piece of information that refers

to a tangible or digital object, such as a good, a service

or a process that a recommender system suggests to

the user in an interaction through the Web, email or

text message” (Kotkov et al., 2016a). For example,

an item could refer to a movie, a song or a new friend.

To increase the number of items that will receive

high ratings most recommender systems tend to sug-

gest items that are (1) popular, as these items are con-

sumed by many individuals and often of high qual-

ity in many domains (Celma Herrada, 2009) and (2)

similar to which the user has assigned high ratings,

as these items correspond to user’s preferences (Tac-

chini, 2012; Kotkov et al., 2016a; Kotkov et al.,

2016b). As a result, users might become bored with

the suggestions provided, as (1) users are likely to

be familiar with popular items, while the main rea-

son these users would use a recommender system is to

ﬁnd novel and relevant items (Celma Herrada, 2009)

and (2) users often lose interest in using the system

when they are offered only items similar to highly

rated ones from their proﬁles (the so-called overspe-

cialization problem) (Tacchini, 2012; Kotkov et al.,

∗

The research was conducted while the author was

working for the University of Jyvaskyla, Finland

2016a; Kotkov et al., 2016b). Here the term user pro-

ﬁle refers to the set of items rated by the target user,

though it might include information, such as name, ID

and age in other papers.

To suggest novel and interesting items and over-

come the overspecialization problem, recommender

systems should suggest serendipitous items. Some

researchers consider novel and unexpected items

serendipitous (Zhang et al., 2012), while others sug-

gest that serendipitous items are relevant and unex-

pected (Maksai et al., 2015). Although there is no

agreement on the deﬁnition of serendipity (Kotkov

et al., 2016b), in this paper, the term serendipitous

items refers to items relevant, novel and unexpected

to a user (Kotkov et al., 2016a; Kotkov et al., 2016b):

• An item is relevant to a user if the user has ex-

pressed or will express preference for the item.

The user might express his/her preference by lik-

ing or consuming the item depending on the appli-

cation scenario of a particular recommender sys-

tem (Kotkov et al., 2016a; Kotkov et al., 2016b).

In different scenarios, ways to express preference

might vary. For example, we might regard a

movie relevant to a user if the user gave it more

than 3 stars out of 5 (Zheng et al., 2015; Lu et al.,

), while we might regard a song relevant to a user

if the user listened to it more than twice. The sys-

tem is aware that a particular item is relevant to a

user if the user rates the item, and unaware of this

Kotkov, D., Veijalainen, J. and Wang, S.

A Serendipity-Oriented Greedy Algorithm for Recommendations.

DOI: 10.5220/0006232800320040

In Proceedings of the 13th International Conference on Web Information Systems and Technologies (WEBIST 2017), pages 32-40

ISBN: 978-989-758-246-2

relevance otherwise.

• An item is novel to a user if the user has not con-

sumed it yet (Kotkov et al., 2016a; Kotkov et al.,

2016b). Items novel to a user are usually unpopu-

lar, as users are often familiar with popular items,

where popularity can be measured by the number

of ratings given in a recommender system (Kotkov

et al., 2016a; Kotkov et al., 2016b; Celma Her-

rada, 2009). Novel items also have to be relatively

dissimilar to a user proﬁle, as the user is likely to

be familiar with items similar to the ones she/he

has rated (Kotkov et al., 2016a; Kotkov et al.,

2016b).

• An item is unexpected to a user if the user does not

anticipate this item to be recommended to him/her

(Kotkov et al., 2016a; Kotkov et al., 2016b). The

user does not expect items that are dissimilar to

the ones usually recommended to him/her. Gener-

ally, recommender systems suggest items similar

to items rated by the user (Tacchini, 2012; Kotkov

et al., 2016a; Kotkov et al., 2016b). Consequently,

an item dissimilar to the rated ones is regarded as

unexpected (Kotkov et al., 2016a; Kotkov et al.,

2016b). The measure of dissimilarity could be

based on user ratings or item attributes depend-

ing on the application scenario of a recommender

system (Kaminskas and Bridge, 2014).

State-of-the-art serendipity-oriented recommen-

dation algorithms are barely compared with one an-

other and often employ different serendipity metrics

and deﬁnitions of the concept, as there is no agree-

ment on the deﬁnition of serendipity in recommender

systems (Zhang et al., 2012; Lu et al., ; Kotkov et al.,

2016b).

In this paper, we propose a serendipity-oriented

recommendation algorithm based on our deﬁnition

above. We compare our algorithm with state-of-the-

art serendipity-oriented algorithms. We also show

that the serendipity metric we use in the experiments

includes each of the three components of serendipity,

unlike the most common serendipity metric.

Our serendipity-oriented algorithm reranks rec-

ommendations provided by an accuracy-oriented al-

gorithm and improves serendipity through feature

diversiﬁcation. The proposed algorithm is based

on an existing reranking algorithm and outperforms

this algorithm in terms of accuracy and serendipity.

Our algorithm also outperforms the state-of-the-art

serendipity-oriented algorithms in terms of serendip-

ity and diversity.

The paper has the following contributions:

• We propose a serendipity-oriented recommenda-

tion algorithm.

Table 1: Notations.

I = {i

, i

, ...,i

} the set of items

, I

⊆ I

the set of items rated by

user u (user proﬁle)

F = { f

, f

, ..., f

} the set of features

, F

⊆ F

the set of features of item i

U = {u

, u

, ..., u

} the set of users

⊆ U

the set of users who rated

item i

(n), RS

(n) ⊆ I

the set of top–n

recommendations provided

by an algorithm to user u

u,i

the rating given by user u

to item i

ˆr

u,i

the prediction of the rating

given by user u to item i

• We evaluate existing serendipity-oriented recom-

mendation alorithms.

The rest of the paper is organized as follows. Sec-

tion 2 describes the proposed algorithm. Section 3 is

dedicated to experimental setting, while section 4 re-

ports the results of the experiments. Finally, section 5

draws conclusions and indicates future work.

2 A SERENDIPITY-ORIENTED

GREEDY ALGORITHM

To describe the proposed algorithm, we present the

notation in Table 1. Let I be a set of available items

and U be a set of users. User u rates or interacts

with items I

, I

⊆ I. A recommender system suggests

(n) items to user u. Each item can have a number

of features F

= { f

i,1

, f

i,2

, ..., f

i,n

F,i

}. The rating user

u has gaven to item i is represented by r

u,i

, while the

predicted rating is represented by ˆr

u,i

2.1 Description

We propose a serendipity-oriented greedy (SOG) al-

gorithm, which is based on a topic diversiﬁcation al-

gorithm (TD) (Ziegler et al., 2005). The objective

of TD is to increase the diversity of a recommenda-

tion list. Both SOG and TD belong to the group of

greedy reranking algorithms (Castells et al., 2015).

According to the classiﬁcation provided in (Kotkov

et al., 2016b), we propose a hybrid reranking algo-

rithm following the post-ﬁltering paradigm and con-

sidering unpopularity and dissimilarity.

Algorithm 1 describes the proposed approach. An

accuracy-oriented algorithm predicts item ratings ˆr

u,i

A Serendipity-Oriented Greedy Algorithm for Recommendations

Input : RS

(n): top–n recommendation set,

: damping factor

Output: Res: picked item list

: candidate set,

ˆr

u,i

: predicted rating of an item,

ˆr

u, f

: predicted rating of a feature;

Res[0] ← i with max ˆr

u,i

;

for z ← 1 to n do

B ← set(Res);// set converts a list to a set

← RS

(n)\B;

calculate c

u,B,i

, i ∈ B

;

normalize c

u,B,i

, ˆr

u, f

and ˆr

u,i

, i ∈ B

to [0, 1];

forall the i ∈ B

calculate score

u,i

end

Res[z] ← i with max score

u,i

;

end

Algorithm 1: Description of SOG.

and generates top–n suggestions RS

(n) for user u.

SOG iteratively picks items from set RS

(n) to ﬁll di-

versiﬁed list Res. In each iteration the algorithm gen-

erates a candidate set B

which contains top–n recom-

mendations RS

(n) except picked items from list Res

(or from set B). A candidate item with the highest

score is added to diversiﬁed list Res. The score is cal-

culated as follows:

score

u,i

= (1 − Θ

) · ˆr

u,i

+ Θ

· c

u,B,i

, (1)

u,B,i

= d

u,B

+ Θ

· ( max

f ∈(F

)

(ˆr

u, f

) + unexp

u,i

), (2)

where Θ

is a serendipity weight, while Θ

is a

damping factor, which is responsible for diversity of

reranked recommendation list Res. The predicted rat-

ing of feature f for user u is represented by ˆr

u, f

ˆr

u, f

∈ [0, 1]. Feature rating indicates how likely a user

is to like an item that has a particular feature. As an

item might have several features, we select the rating

of a feature that is novel and most relevant to a user.

If an item does not have any novel features F

then max

f ∈(F

)

(ˆr

u, f

) = 0. Unexpectedness is based

on the number of new features of an item for a user:

unexp

u,i

||F

||F\F

, (3)

where F corresponds to the set of all features,

corresponds to features of item i, and F

cor-

responds to features of items rated by user u.

Suppose selected features correspond to movie

genres F = {comedy, drama, horror, adventure,

crime}, the movie “The Shawshank Redemp-

tion” could be represented as follows F

shawshank

{drama, crime}, while the user might rate come-

dies and dramas F

= {comedy, drama}. For

i1 i2 i3 i4

5 4

2 2 5

4 4

4 3

2 5 5

user-item matrix

f1 f2 f3

2 2 5

4 4

2 5

user-feature matrix

4.5

3.5

F {f1, f2}i1=

F {f1}i2=

F {f2}i3=

F {f3}i4=

;;

Figure 1: An example of user-item and user-feature

matrices.

user u the movie “The Shawshank Redemption” has

the following unexpectedness: unexp

u,shawshank

||{drama,crime}\{comedy,drama}||

||{comedy,drama,horror,adventure,crime}\{comedy,drama}||

If the user rates items of all features F, we regard the

feature that is the least familiar to the user as novel.

If the user has not rated any features F

0, all the

features are regarded as novel.

Dissimilarity of an item to picked items is calcu-

lated as follows:

i,B

||B||

∑

j∈B

1 − sim

i, j

, (4)

where similarity sim

i, j

can be any kind of similarity

measure. In our experiments we used content-based

Jaccard similarity:

sim

i, j

||F

∩ F

||F

∪ F

. (5)

To predict feature ratings ˆr

u, f

, we apply an

accuracy-oriented algorithm to a user-feature matrix.

A user-feature matrix is based on user-item matrix,

where a rating given by a user to a feature corresponds

to the mean rating given to items having this feature

by this user:

u, f

||I

u, f

∑

i∈I

u, f

u,i

, (6)

where I

u, f

is a set of items having feature f and rated

by user u.

Figure 1 demonstrates an example of user-item

and user-feature matrices. Suppose users have rated

items i1, i2, i3 and i4 on the scale from 1 to 5 (user-

item matrix). Each item has a number of features. For

example, item i1 has features f 1 and f 2, while item

i2 only has feature f 1. User-feature matrix contains

feature ratings based on user-item matrix (eq. 6). For

example, the rating of feature f 1 for user u1 is 4.5, as

items i1 and i2 have feature f 1 and the user gave a 5

to item i1 and a 4 to item i2.

2.2 Analysis

Our algorithm considers each component of serendip-

ity:

WEBIST 2017 - 13th International Conference on Web Information Systems and Technologies

• Ratings ˆr

u,i

and ˆr

u, f

correspond to relevance.

• unexp

u,i

corresponds to unexpectedness.

• Novelty is handled implicitly. SOG suggests

items with features novel to users, leading to the

relative unpopularity of the items, as they have un-

popular features.

Although SOG is based on TD, our algorithm has

three key differences with respect to TD:

• SOG considers item scores instead of positions of

items in lists, which leads to more accurate scores

(score

u,i

• SOG employs a serendipity weight that controls

how likely the algorithm is to suggest an item with

a novel feature.

• SOG predicts features a user will like.

Our algorithm has four main advantages:

• The algorithm considers each component of

serendipity.

• As our algorithm is based on the diversiﬁcation al-

gorithm, SOG improves both serendipity and di-

versity.

• As SOG is a reranking algorithm, it can be ap-

plied to any accuracy-oriented algorithm, which

might be useful for a live recommender system

(reranking can be conducted on the client’s side

of a client-server application).

• Our algorithm has two parameters, which adjust

the algorithm according to different requirements.

The parameters could be different for each user

and be adjusted as the user becomes familiar with

the system.

The computational complexity of the algorithm is

O(n

) (excluding pre-calculation), where n is a num-

ber of items in input set RS

(n) (in our experiments

n = 20).

3 EXPERIMENTS

To evaluate existing algorithms and test the pro-

posed serendipity metric, we conducted experiments

using two datasets: HetRec (Harper and Konstan,

2015) and 100K MovieLens. The HetRec dataset

contains 855,598 ratings given by 2,113 users to

10,197 movies (density 3.97%). The 100K Movie-

Lens (100K ML) dataset contains 100,000 ratings

given by 943 users to 1,682 movies (density 6.3%).

The HetRec dataset is based on the MovieLens10M

dataset published by grouplens

. Movies in the Het-

Rec dataset are linked with movies on IMDb

and

Rotten Tomatoes

websites.

In our experimental setting, we hid 20 ratings of

each evaluated user and regarded the rest of the rat-

ings as training data. We performed a 5-fold cross-

validation. Each evaluated algorithm ranked test

items for a particular user based on training data.

This experimental setting was chosen due to the

evaluation task. Other settings either let an algorithm

rank all the items in the system or a limited number

of them assuming that items unknown by a user are

irrelevant. This assumption is not suitable for evalu-

ation of serendipity, as serendipitous items are novel

by deﬁnition (Iaquinta et al., 2010; Adamopoulos and

Tuzhilin, 2014; Kotkov et al., 2016a). The experi-

ments were conducted using Lenskit framework (Ek-

strand et al., 2011).

3.1 Baselines

We implemented the following baseline algorithms:

• POP ranks items according to the number of rat-

ings each item received in descending order.

• SVD is a singular value decomposition algorithm

which ranks items according to generated scores

(Zheng et al., 2015). The objective function of the

algorithm is the following:

min

∑

u∈U

∑

i∈I

u,i

− p

)

+ β(||p

+ ||q

(7)

where p

and q

are user-factor vector and

item-factor vector, respectively, while β(||p

||q

) represents the regularization term.

• SPR (serendipitous personalized ranking) is an

algorithm based on SVD that maximizes the

serendipitous area under the ROC (receiver oper-

ating characteristic) curve (Lu et al., ):

max

∑

u∈U

f (u), (8)

f (u) =

∑

i∈I

∑

j∈I

· σ(0, ˆr

u,i

− ˆr

u, j

)(||U

||)

(9)

where I

is a set of items a user likes. We consid-

ered that a user likes items that she/he rates higher

than threshold θ (in our experiments θ = 3). Nor-

malization term z

is calculated as follows: z

||I

||||I

. We used hinge loss function to calcu-

late σ(x) and set popularity weight α to 0.5, as the

http://www.grouplens.org

http://www.imdb.com

http://www.rottentomatoes.com

A Serendipity-Oriented Greedy Algorithm for Recommendations

algorithm performs the best with these parameters

according to (Lu et al., ).

• Zheng’s is an algorithm based on SVD that

considers observed and unobserved ratings and

weights the error with unexpectedness (Zheng

et al., 2015):

min

∑

u∈U

∑

i∈I

(˜r

u,i

− p

)

· w

u,i

+β(||p

+ ||q

(10)

where ˜r

u,i

corresponds to observed and unob-

served ratings a user u gave to item i. The un-

obseved ratings equal to 0. The weight w is calcu-

lated as follows:



1 −

||U

max

j∈I

(||U

||)



∑

j∈I

di f f (i, j)

||I

(11)

where max

j∈I

(||U

||) is the maximum number of

ratings given to an item. A collaborative dissim-

ilarity between items i and j is represented by

di f f (i, j). The dissimilarity is calculated as fol-

lows di f f (i, j) = 1 − ρ

i, j

, where similarity ρ

i, j

corresponds to the Pearson correlation coefﬁcient:

i, j

∑

u∈S

i, j

u,i

− r

)(r

u, j

− r

)

∑

u∈S

i, j

u,i

− r

)

∑

u∈S

i, j

u j

− r

)

(12)

where S

i, j

is the set of users rated both items i and

j, while

corresponds to an average rating for

user u.

• TD is a topic diversiﬁcation algorithm, where dis-

similarity corresponds to eq. 4. Similarly to

(Ziegler et al., 2005), we set Θ

= 0.9.

• SOG is the proposed serendipity-oriented greedy

algorithm (Θ

= 0.9, Θ

= 0.6). We set Θ

sim-

ilarly to (Ziegler et al., 2005) and Θ

slightly

higher than 0.5 to emphasize the difference be-

tween SOG and TD. To predict feature ratings

we used SVD, which received user-genre matrix.

User ratings in the matrix correspond to mean rat-

ings given by a user to items with those genres.

• SOGBasic is SOG algorithm without predicting

genre ratings (ˆr

u f

= 0).

3.2 Evaluation Metrics

The main objective of our algorithm is to improve

serendipity of a recommender system. A change of

serendipity might affect other properties of a recom-

mender system. To demonstrate the dependence of

different properties and features of the baselines, we

employed evaluation metrics to measure four prop-

erties of recommender systems: (1) accuracy, as it

is a common property (Kotkov et al., 2016b), (2)

serendipity, as SPR, Zhengs, SOG and SOGBasic are

designed to improve this property (Lu et al., ; Zheng

et al., 2015), (3) diversity, as this is one of the objec-

tives of TD, SOG and SOGBasic (Ziegler et al., 2005)

and (4) novelty, as SPR, Zhengs, SOG and SOGBa-

sic are designed to improve this property (Lu et al., ;

Zheng et al., 2015).

To measure serendipity, we employed two met-

rics: traditional serendipity metric and our serendip-

ity metric. The traditional serendipity metric disre-

gards unexpectedness of items to a user, while our

serendipity metric takes into account each component

of serendipity. We provided results for both metrics

to demonstrate their difference. Overall, we used ﬁve

metrics:

• To measure a ranking ability of an algorithm,

we use normalized discounted cumulative gain

(NDCG), which, in turn, is based on discounted

cumulative gain (DCG) (J

arvelin and Kek

ainen,

2000):

DCG

@n = rel

(1) +

∑

i=2

rel

(i)

log

(i)

, (13)

where rel

(i) indicates relevance of an item with

rank i for user u, while n indicates the number of

top recommendations selected. The NDCG met-

ric is calculated as follows:

NDCG

@n =

DCG

IDCG

, (14)

where IDCG

@n is DCG

@n value calculated

for a recommendation list with an ideal order ac-

cording to relevance.

• The traditional serendipity metric is based on a

primitive recommender system which suggests

items known and expected by a user. Evalu-

ated recommendation algorithms are penalized for

suggesting items that are irrelevant or generated

by a primitive recommender system. Similarly to

(Zheng et al., 2015), we used a slight modiﬁcation

of the serendipity metric:

SerPop

@n =

(n)\PM ∩ REL

, (15)

where PM is a set of items generated by the prim-

itive recommender system. We selected the 100

most popular items for PM following one of the

most common strategies (Zheng et al., 2015; Lu

et al., ). Items relevant to user u are represented

by REL

, REL

= {i ∈ TestSet

> θ}, where

TestSet

is a ground truth for user u, while θ is the

WEBIST 2017 - 13th International Conference on Web Information Systems and Technologies

threshold rating, which in our experiments equals

to 3.

• Our serendipity metric is based on the traditional

one. Although the traditional serendipity met-

ric successfully captures relevance and novelty of

recommendations by setting a threshold for rat-

ings and taking into account the number of rat-

ings assigned to an item, the metric disregards un-

expectedness. In this paper, we consider an item

unexpected to a user if the item has at least one

feature novel to the user e.g. a feature, of which

the user has not yet rated an item. We therefore

calculate the serendipity metric as follows:

Ser

@n =

(n)\PM ∩ REL

∩UNEXP

(16)

where UNEXP

is a set of items that have at least

one feature novel to user u. In our experiments, a

movie with at least one genre, which the user has

not rated a movie of is considered unexpected.

• To measure diversity, we employed an intra-list

dissimilarity metric (Zheng et al., 2015):

Div

@n =

n · (n − 1)

∑

i∈RS

(n)

∑

j6=i∈RS

(n)

1 − sim

i, j

(17)

where similarity sim

i, j

is based on Jaccard simi-

larity using item sets based on movie genres (eq.

5).

• Novelty is based on the number of ratings as-

signed to an item (Zhang et al., 2012):

nov

= 1 −

||U

max

j∈I

(||U

||)

. (18)

4 RESULTS

Table 2 demonstrates performance of baselines mea-

sured with different evaluation metrics. The following

observations can be observed for both datasets:

1. SOG outperforms TD in terms of accuracy and

slightly underperforms it in terms of diversity. For

example, the improvement of NDCG@10 is 5.3%

on the HetRec dataset, while on the 100K ML

dataset the improvement is 5.9%. The decrease

of Div@10 is less than 2%.

2. SOG outperforms other algorithms in terms of

our serendipity metric and the state-of-the-art

serendipity-oriented algorithms in terms of di-

versity, while the highest value of traditional

serendipity metric belongs to SPR. TD achieves

the highest diversity among the presented algo-

rithms.

3. SOG outperforms SOGBasic in terms of our

serendipity metric. For example, the improve-

ment of Ser@10 is 5.9% on the HetRec dataset,

while on the 100K ML dataset the improvement

is 10.9%.

4. SOG slightly outperforms SOGBasic in terms of

NDCG@n (< 1%) and the traditional serendipity

metric SerPop@n (< 1%) and underperforms in

terms of Div@n (< 1% for the HetRec dataset and

1 − 2% for the 100K ML dataset).

5. Popularity baseline outperforms SOGBasic, SOG

and TD in terms of NDCG@n, but underperforms

all the presented algorithms in terms of serendip-

ity.

Observation 1 indicates that our algorithm im-

proves TD in terms of both serendipity and accu-

racy, having an insigniﬁcant decrease in diversity.

TD provides slightly more diverse recommendations

than SOG, as these algorithms have different objec-

tives. The main objective of TD is to increase di-

versity (Ziegler et al., 2005), while SOG is designed

not only to diversify recommendations, but also ex-

pose more recommendations with novel genres to a

user. SOG therefore picks movies less expected and

slightly less diverse than TD. Surprisingly, suggesting

movies with genres novel to a user increases accuracy,

which might be caused by diverse user preferences re-

garding movies. The improvements of accuracy and

serendipity seem to overcompensate for the insigniﬁ-

cant decrease of diversity.

Observation 2 suggests that our algorithm

provides the most serendipitous recommendations

among the presented baselines, which is partly due

to Θ

= 0.9 for our algorithm. This parameter also

causes the high diversity of TD. We set Θ

the same

as (Ziegler et al., 2005) to emphasize the difference

between SOG and TD. SPR achieves the highest tra-

ditional serendipity due to its objective function (Lu

et al., ). This algorithm is designed to suggest relevant

unpopular items to users.

The prediction of genres a user is likely to ﬁnd

relevant improves serendipity, according to observa-

tion 3. Meanwhile, accuracy, traditional serendipity

and diversity remain almost the same, as observation

4 suggests. SOG appears to increase the number of

relevant, novel and unexpected movies and supplant

some relevant and expected movies from recommen-

dation lists with respect to SOGBasic, as novel and

unexpected movies suggested by SOG are more likely

to also be relevant to users than those suggested by

SOGBasic.

According to observation 5, our algorithm under-

performs the non-personalized baseline in terms of

NDCG@n. Accuracy of POP is generally relatively

A Serendipity-Oriented Greedy Algorithm for Recommendations

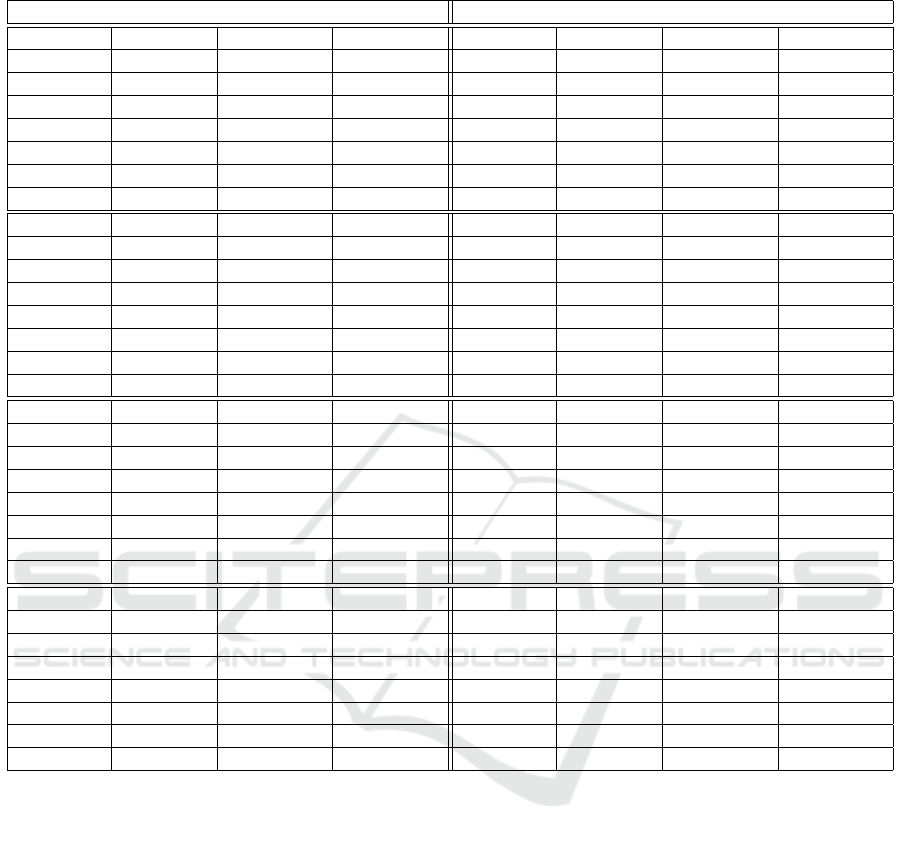
Table 2: Performance of algorithms.

HetRec dataset 100K ML dataset

Algorithm NDCG@5 NDCG@10 NDCG@15 Algorithm NDCG@5 NDCG@10 NDCG@15

TD 0,761 0,800 0,840 TD 0,736 0,776 0,823

SOGBasic 0,824 0,841 0,873 SOGBasic 0,800 0,821 0,859

SOG 0,825 0,842 0,873 SOG 0,801 0,822 0,859

POP 0,824 0,848 0,878 POP 0,804 0,833 0,869

SPR 0,854 0,873 0,894 SPR 0,821 0,839 0,868

Zheng’s 0,857 0,874 0,898 Zheng’s 0,836 0,859 0,887

SVD 0,871 0,894 0,916 SVD 0,844 0,868 0,897

Algorithm SerPop@5 SerPop@10 SerPop@15 Algorithm SerPop@5 SerPop@10 SerPop@15

POP 0,224 0,393 0,476 POP 0,039 0,178 0,297

Zheng’s 0,323 0,440 0,497 Zheng’s 0,215 0,284 0,328

TD 0,457 0,482 0,493 TD 0,318 0,324 0,328

SOGBasic 0,493 0,494 0,501 SOGBasic 0,332 0,331 0,333

SOG 0,493 0,495 0,501 SOG 0,333 0,332 0,333

SVD 0,501 0,544 0,546 SVD 0,338 0,353 0,357

SPR 0,431 0,550 0,563 SPR 0,255 0,373 0,394

Algorithm Ser@5 Ser@10 Ser@15 Algorithm Ser@5 Ser@10 Ser@15

POP 0,072 0,112 0,136 POP 0,010 0,055 0,114

Zheng’s 0,100 0,122 0,135 Zheng’s 0,061 0,094 0,127

SVD 0,159 0,156 0,151 SVD 0,129 0,136 0,144

SPR 0,128 0,162 0,158 SPR 0,086 0,150 0,165

TD 0,192 0,177 0,158 TD 0,166 0,171 0,156

SOGBasic 0,284 0,204 0,168 SOGBasic 0,239 0,193 0,166

SOG 0,305 0,216 0,174 SOG 0,278 0,214 0,174

Algorithm Div@5 Div@10 Div@15 Algorithm Div@5 Div@10 Div@15

Zheng’s 0,782 0,795 0,798 SPR 0,788 0,792 0,796

SVD 0,787 0,795 0,799 Zheng’s 0,783 0,794 0,799

SPR 0,797 0,797 0,796 SVD 0,787 0,795 0,800

POP 0,794 0,803 0,803 POP 0,813 0,810 0,808

SOG 0,944 0,891 0,850 SOG 0,938 0,891 0,853

SOGBasic 0,948 0,893 0,851 SOGBasic 0,959 0,901 0,856

TD 0,952 0,894 0,852 TD 0,964 0,903 0,857

high, as users on average tend to give high ratings

to popular movies (Amatriain and Basilico, 2015).

However, accuracy in this case is unlikely to reﬂect

user satisfaction, as users are often already familiar

with popular movies suggested. Despite being rel-

atively accurate, POP suggests familiar and obvious

movies, which is supported by both serendipity met-

rics. The relatively low accuracy of our algorithm was

caused by the high damping factor Θ

4.1 Serendipity Weight Analysis

Figure 2 indicates performance of SOG and SOGBa-

sic algorithms with the change of serendipity weight

from 0 to 1 with the step of 0.1 (without cross-

validation) on the HetRec dataset (on the 100K ML

dataset the observations are the same). The two

following trends can be observed: (1) serendipity

declines with the increase of accuracy, as with the

growth of Θ

our algorithms tend to suggest more

movies that users do not usually rate, and (2) diver-

sity declines with the increase of serendipity, as with

the growth of Θ

our algorithms tend to suggest more

movies of genres novel to the user limiting the num-

ber of genres recommended.

As SOG predicts genres a user likes, its Ser@10

is slightly higher than that of SOGBasic for the same

values of NDCG@10. SOG tends to suggest more

movies of genres not only novel, but also interesting

to a user, which slightly hurts diversity, but improves

serendipity.

4.2 Qualitative Analysis

Table 3 demonstrates the recommendations provided

for a randomly selected user, who rated 25 movies in

WEBIST 2017 - 13th International Conference on Web Information Systems and Technologies

0,17

0,175

0,18

0,185

0,19

0,195

0,2

0,205

0,21

0,215

0,22

0,84 0,841 0,842 0,843 0,844

Ser@10

NDCG@10

SOGBasic

SOG

0,8895

0,89

0,8905

0,891

0,8915

0,892

0,8925

0,893

0,8935

0,894

0,8945

0,895

0,17 0,19 0,21 0,23

Div@10

Ser@10

SOGBasic

SOG

Figure 2: Performance of SOG and SOGBasic algorithms on the Hetrec dataset.

Table 3: Suggestions generated to a random user from the Hetrec dataset (novel genres are in bold).

User proﬁle

Name Genres Rating nov

Major League Comedy 3.5 0.882

The Shawshank Redemption Drama 4.5 0.137

Stargate Action Adventure Sci-Fi 4.5 0.572

Robin Hood: Men in Tights Comedy 3.5 0.684

The Three Musketeers Action Adventure Comedy 3.5 0.789

SPR recommendations

Name Genres Rating nov

V for Vendetta Thriller 5 0.438

Enemy of the State Action Thriller 3.5 0.620

The Count of Monte Cristo Drama 3.5 0.787

Free Enterprise Comedy Romance Sci-Fi 4.5 0.989

First Knight Action Drama Romance 3.5 0.962

SOG recommendations

Name Genres Rating nov

V for Vendetta Thriller 5 0.438

The Untouchables Thriller Crime Drama 4.5 0.604

Monsters. Inc. Animation Children Comedy Fantasy 4 0.331

Minority Report Action Crime Mystery Sci-Fi Thriller 3 0.260

Grease Comedy Musical Romance 3 0.615

the HetRec dataset. The algorithms received 5 ratings

as the training set and regarded 20 ratings as the test

set for the user. We provided recommendations gener-

ated by two algorithms: (1) SOG due to high Ser@n,

and (2) SPR due to high SerPop@n.

Although SPR suggested less popular movies than

SOG, our algorithm outperformed SPR at overcoming

the overspecialization problem, as it introduced more

novel genres (8 genres) to the user than SPR (2 gen-

res). Our algorithm also provided a more diversiﬁed

recommendation list than SPR.

The suggestion of the movie “Monsters Inc.”

seems to signiﬁcantly broaden user tastes, as the sug-

gestion is relevant and introduces three new genres to

the user. Provided that the movie is serendipitous to

the user, it is likely to inspire the user to watch more

cartoons in the future.

Analysis of tables 2 and 3 suggests that the tra-

ditional serendipity metric captures only novelty and

relevance by penalizing algorithms for suggesting

popular and irrelevant items, while Ser@n takes into

account each component of serendipity, which allows

assessment of the ability of the algorithm to overcome

overspecialization.

5 CONCLUSIONS AND FUTURE

RESEARCH

We proposed a serendipity-oriented greedy (SOG)

recommendation algorithm. We also provided eval-

A Serendipity-Oriented Greedy Algorithm for Recommendations

uation results of our algorithm and state-of-the-art al-

gorithms using different serendipity metrics.

SOG is based on the topic diversiﬁcation (TD) al-

gorithm (Ziegler et al., 2005) and improves its accu-

racy and serendipity for the insigniﬁcant price of di-

versity.

Our serendipity-oriented algorithm outperforms

the state-of-the-art serendipity-oriented algorithms in

terms of serendipity and diversity, and underperforms

them in terms of accuracy.

Unlike the traditional serendipity metric, the

serendipity metric we employed in this study captures

each component of serendipity. The choice of this

metric is supported by qualitative analysis.

In our future research, we intend to further inves-

tigate serendipity-oriented algorithms. We will also

involve real users to validate our results.

ACKNOWLEDGEMENTS

The research at the University of Jyv

askyl

a was per-

formed in the MineSocMed project, partially sup-

ported by the Academy of Finland, grant #268078.

REFERENCES

Adamopoulos, P. and Tuzhilin, A. (2014). On unexpected-

ness in recommender systems: Or how to better ex-

pect the unexpected. ACM Transactions on Intelligent

Systems and Technology, 5(4):1–32.

Amatriain, X. and Basilico, J. (2015). Recommender sys-

tems in industry: A netﬂix case study. In Recom-

mender Systems Handbook, pages 385–419. Springer.

Castells, P., Hurley, N. J., and Vargas, S. (2015). Novelty

and diversity in recommender systems. In Recom-

mender Systems Handbook, pages 881–918. Springer.

Celma Herrada,

O. (2009). Music recommendation and dis-

covery in the long tail. PhD thesis, Universitat Pom-

peu Fabra.

Ekstrand, M. D., Ludwig, M., Konstan, J. A., and Riedl,

J. T. (2011). Rethinking the recommender research

ecosystem: Reproducibility, openness, and lenskit.

In Proceedings of the 5th ACM Conference on Rec-

ommender Systems, pages 133–140, New York, NY,

USA. ACM.

Harper, F. M. and Konstan, J. A. (2015). The movielens

datasets: History and context. ACM Transactions on

Interactive Intelligent Systems, 5(4):19:1–19:19.

Iaquinta, L., Semeraro, G., de Gemmis, M., Lops, P., and

Molino, P. (2010). Can a recommender system induce

serendipitous encounters? InTech.

arvelin, K. and Kek

ainen, J. (2000). Ir evaluation meth-

ods for retrieving highly relevant documents. In Pro-

ceedings of the 23rd Annual International ACM SIGIR

Conference on Research and Development in Infor-

mation Retrieval, pages 41–48, New York, NY, USA.

ACM.

Kaminskas, M. and Bridge, D. (2014). Measuring surprise

in recommender systems. In Proceedings of the Work-

shop on Recommender Systems Evaluation: Dimen-

sions and Design (Workshop Programme of the 8th

ACM Conference on Recommender Systems).

Kotkov, D., Veijalainen, J., and Wang, S. (2016a). Chal-

lenges of serendipity in recommender systems. In

Proceedings of the 12th International conference on

web information systems and technologies., volume 2,

pages 251–256. SCITEPRESS.

Kotkov, D., Wang, S., and Veijalainen, J. (2016b). A survey

of serendipity in recommender systems. Knowledge-

Based Systems, 111:180–192.

Lu, Q., Chen, T., Zhang, W., Yang, D., and Yu, Y. Serendip-

itous personalized ranking for top-n recommendation.

In Proceedings of the The IEEE/WIC/ACM Interna-

tional Joint Conferences on Web Intelligence and In-

telligent Agent Technology, volume 1.

Maksai, A., Garcin, F., and Faltings, B. (2015). Predict-

ing online performance of news recommender sys-

tems through richer evaluation metrics. In Proceed-

ings of the 9th ACM Conference on Recommender

Systems, pages 179–186, New York, NY, USA. ACM.

Ricci, F., Rokach, L., and Shapira, B. (2011). Recommender

Systems Handbook, chapter Introduction to Recom-

mender Systems Handbook, pages 1–35. Springer US.

Tacchini, E. (2012). Serendipitous mentorship in music rec-

ommender systems. PhD thesis.

Zhang, Y. C., S

eaghdha, D. O., Quercia, D., and Jambor, T.

(2012). Auralist: Introducing serendipity into music

recommendation. In Proceedings of the 5th ACM In-

ternational Conference on Web Search and Data Min-

ing, pages 13–22, New York, NY, USA. ACM.

Zheng, Q., Chan, C.-K., and Ip, H. H. (2015). An

unexpectedness-augmented utility model for making

serendipitous recommendation. In Advances in Data

Mining: Applications and Theoretical Aspects, vol-

ume 9165, pages 216–230. Springer International

Publishing.

Ziegler, C.-N., McNee, S. M., Konstan, J. A., and Lausen,

G. (2005). Improving recommendation lists through

topic diversiﬁcation. In Proceedings of the 14th Inter-

national Conference on World Wide Web, pages 22–

32, New York, NY, USA. ACM.

WEBIST 2017 - 13th International Conference on Web Information Systems and Technologies